1

SZKIC DO WYKŁADÓW Z PRZEDMIOTU

MASZYNY ELEKTRYCZNE

kier. Energetyka,

studia stacjonarne, 1-szego stopnia, sem. IV

cz. 2

TRANSFORMATORY

SZKIC DO WYKŁADÓW Z PRZEDMIOTU

MASZYNY ELEKTRYCZNE

kier. Energetyka,

studia stacjonarne, 1-szego stopnia, sem. IV

cz. 2

TRANSFORMATORY

Mieczysław RONKOWSKI

Politechnika Gdańska

Wydział Elektrotechniki i Automatyki

Katedra Energoelektroniki

i Maszyn Elektrycznych

MODELOWANIE TRANSFORMATORA

MODELOWANIE TRANSFORMATORA

MODEL FIZYCZNY

IDEALIZACJA TRANSFORMATORA

RZECZYWISTEGO

MODEL FIZYCZNY

IDEALIZACJA TRANSFORMATORA

RZECZYWISTEGO

ROZWAŻANIE ZACHODZĄCYCH

ZJAWISK FIZYCZNYCH

ISTOTNYCH DLA ROZWAŻANEGO STANU PRACY

I CELÓW ANALIZY (OBLICZEŃ)

ROZWAŻANIE ZACHODZĄCYCH

ZJAWISK FIZYCZNYCH

ISTOTNYCH DLA ROZWAŻANEGO STANU PRACY

I CELÓW ANALIZY (OBLICZEŃ)

2

MODELOWANIE TRANSFORMATORA

MODELOWANIE TRANSFORMATORA

MODEL MATEMATYCZNY

ODWZOROWANIE ZJAWISK I PROCESÓW

FIZYCZNYCH

POSZUKIWANIE WZORÓW

MODEL MATEMATYCZNY

ODWZOROWANIE ZJAWISK I PROCESÓW

FIZYCZNYCH

POSZUKIWANIE WZORÓW

MODELE MATEMATYCZNE:

•MODEL POLOWY - STAŁE ROZŁOŻONE)
•MODEL OBWODOWY (SCHEMAT ZASTĘPCZY)

– STAŁE SKUPIONE

MODELE MATEMATYCZNE:

•MODEL POLOWY - STAŁE ROZŁOŻONE)
•MODEL OBWODOWY (SCHEMAT ZASTĘPCZY)

– STAŁE SKUPIONE

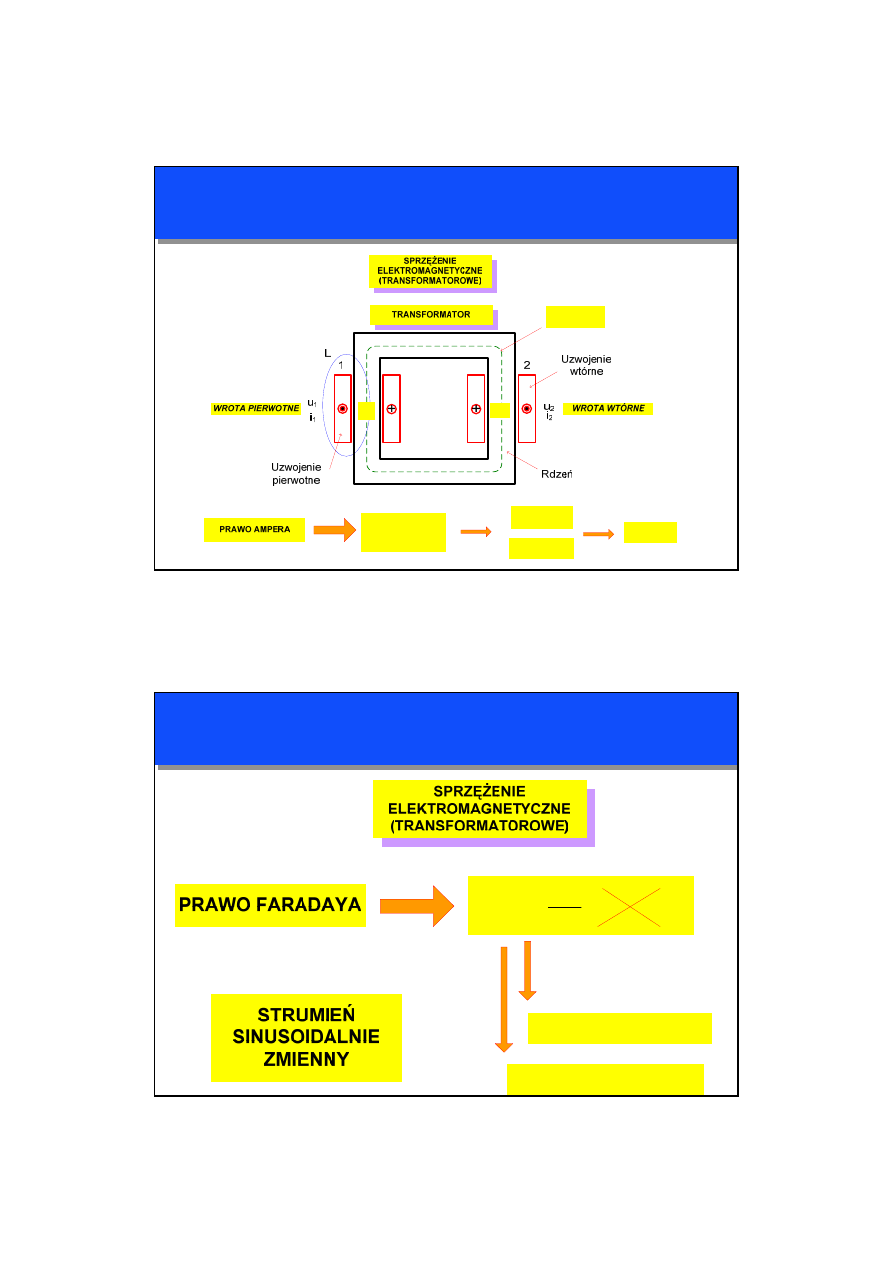
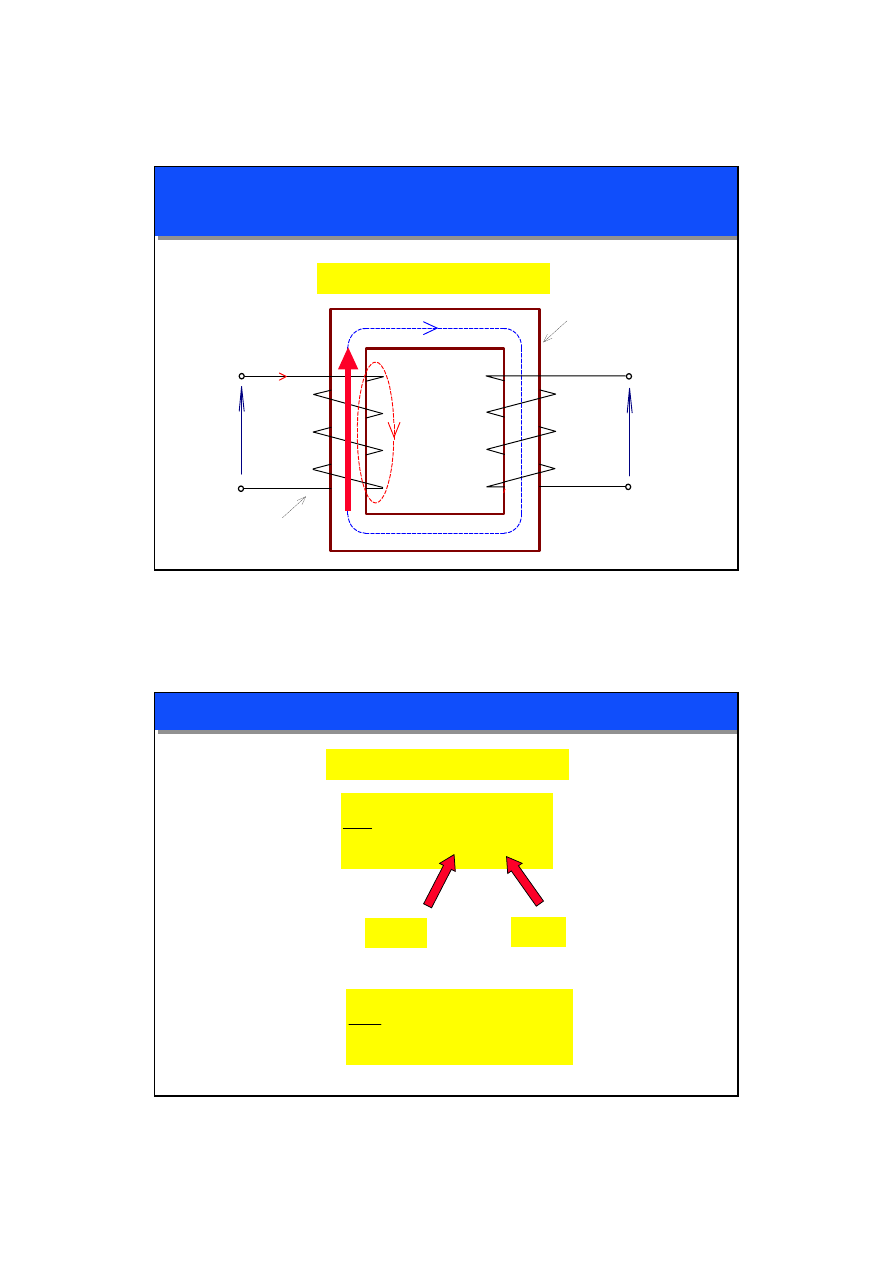
TRANSFORMATOR RZECZYWISTY

TRANSFORMATOR RZECZYWISTY

UZWOJENIA TRÓJFAZOWE

UMIESZCZONE NA KOLUMNACH

WYKONANE Z MIEDZI

TRANSFORMATOR TRÓJFAZOWY

RDZEŃ TRÓJKOLUMNOWY

WYKONANY Z BLACHY

ELEKTROTECHNICZNEJ

CHŁODZENIE OLEJOWE

3

MODEL FIZYCZNY TRANSFORMATORA

PODSTAWOWE PRAWA I ZJAWISKA FIZYCZNE

MODEL FIZYCZNY TRANSFORMATORA

PODSTAWOWE PRAWA I ZJAWISKA FIZYCZNE

Θ

=

∫ ⋅

L

dl

H

1

Θ

2

Θ

m

Φ

1

1

1

i

z

=

Θ

2

2

2

Θ

i

z

=

m

Φ

MODEL FIZYCZNY TRANSFORMATORA

PODSTAWOWE PRAWA I ZJAWISKA FIZYCZNE

MODEL FIZYCZNY TRANSFORMATORA

PODSTAWOWE PRAWA I ZJAWISKA FIZYCZNE

Φ

∇

⋅

−

∂

Φ

∂

−

=

v

t

e

1

1

44

,

4

z

f

E

m

Φ

=

2

1

2

44

,

4

z

f

E

m

Φ

=

4

PODEJŚCIE RICHARD’a FEYNMAN’a:

FEYNMAN’a WYKŁADY Z FIZYKI. T.2, Cz.1, s. 83

„Wyrazić to wszystko w postaci matematycznej –

to jedno, a stosować swobodnie, z pewną dozą

pomysłowości – to zupełnie coś innego”

PODEJŚCIE RICHARD’a FEYNMAN’a:

FEYNMAN’a WYKŁADY Z FIZYKI. T.2, Cz.1, s. 83

„Wyrazić to wszystko w postaci matematycznej –

to jedno, a stosować swobodnie, z pewną dozą

pomysłowości – to zupełnie coś innego”

TRANSFORMATOR

FORMUŁOWANIE MODELU OBWODOWEGO

(SCHEMATU ZASTĘPCZEGO)

TRANSFORMATOR

FORMUŁOWANIE MODELU OBWODOWEGO

(SCHEMATU ZASTĘPCZEGO)

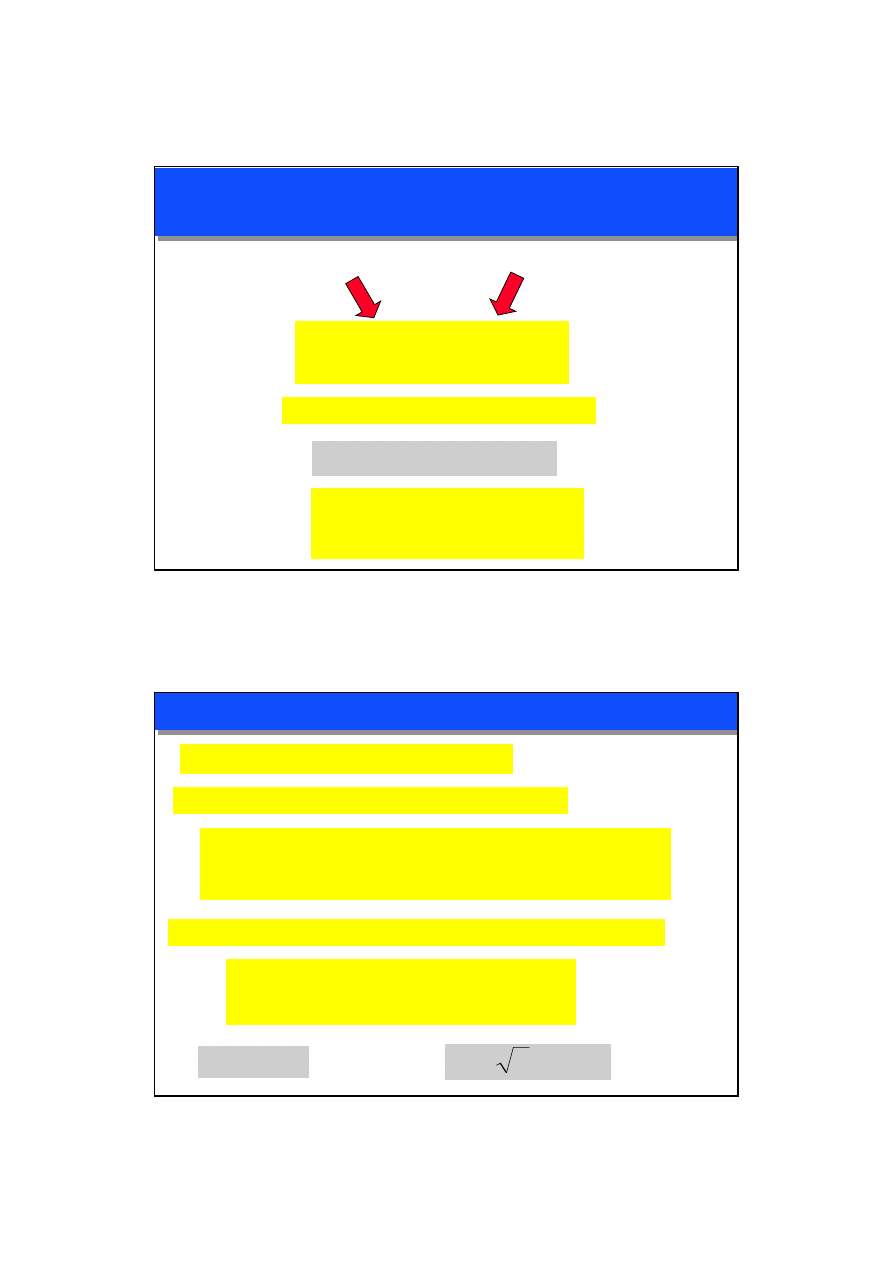
TRANSFORMATOR IDEALNY

RELACJE WIELKOŚCI ZACISKOWYCH

TRANSFORMATOR IDEALNY

RELACJE WIELKOŚCI ZACISKOWYCH

U

1

U

2

I

1

I

2

BRAK PRĄDU MAGNESOWANIA,

STRUMIENI ROZPROSZENIA

I SPRAWNOŚĆ = 100%

P

2

> 0

P

P

2

2

< 0

< 0

P

1

= - P

2

P

1

> 0

U

1

I

1

= -

U

2

I

2

?

?

5

TRANSFORMATOR IDEALNY

RELACJE WIELKOŚCI ZACISKOWYCH

TRANSFORMATOR IDEALNY

RELACJE WIELKOŚCI ZACISKOWYCH

P

1

= - P

2

U

1

I

1

= - U

2

I

2

υ

I

I

U

U

1

2

2

1

=

=

PRZEKŁADNIA

IDEALNA

REALNA

OGÓLNE RÓWNANIA NAPIĘCIOWO- PRĄDOWE – STR.

TRANSFORMATOR

MODEL OBWODOWY (SCHEMAT ZASTĘPCZY)

TRANSFORMATOR

MODEL OBWODOWY (SCHEMAT ZASTĘPCZY)

dt

d

i

R

u

1

1

1

1

ψ

+

=

dt

d

i

R

u

2

2

2

2

ψ

+

=

ψ

1

=

ψ

1

(i

1

, i

2

)

ψ

2

=

ψ

2

(i

1

, i

2

)

Gdzie, strumienie skojarzone:

6

OGÓLNE RÓWNANIA NAPIĘCIOWO- PRĄDOWE

TRANSFORMATOR

MODEL OBWODOWY (SCHEMAT ZASTĘPCZY)

TRANSFORMATOR

MODEL OBWODOWY (SCHEMAT ZASTĘPCZY)

dt

di

dt

di

M

L

i

R

u

2

1

11

1

1

1

+

+

=

dt

di

dt

di

M

L

i

R

u

1

2

22

2

2

2

+

+

=

Gdzie, strumienie skojarzone:

ψ

1

= L

11

i

1

+ M i

2

ψ

2

=L

22

i

2

+ M i

1

INDUKCYJNOŚĆ WZAJEMNA

TRANSFORMATOR

MODEL OBWODOWY (SCHEMAT ZASTĘPCZY)

TRANSFORMATOR

MODEL OBWODOWY (SCHEMAT ZASTĘPCZY)

22

11

L

L

k

M

=

k - współczynnik sprzężenia

1

1

≤

≤

−

k

7

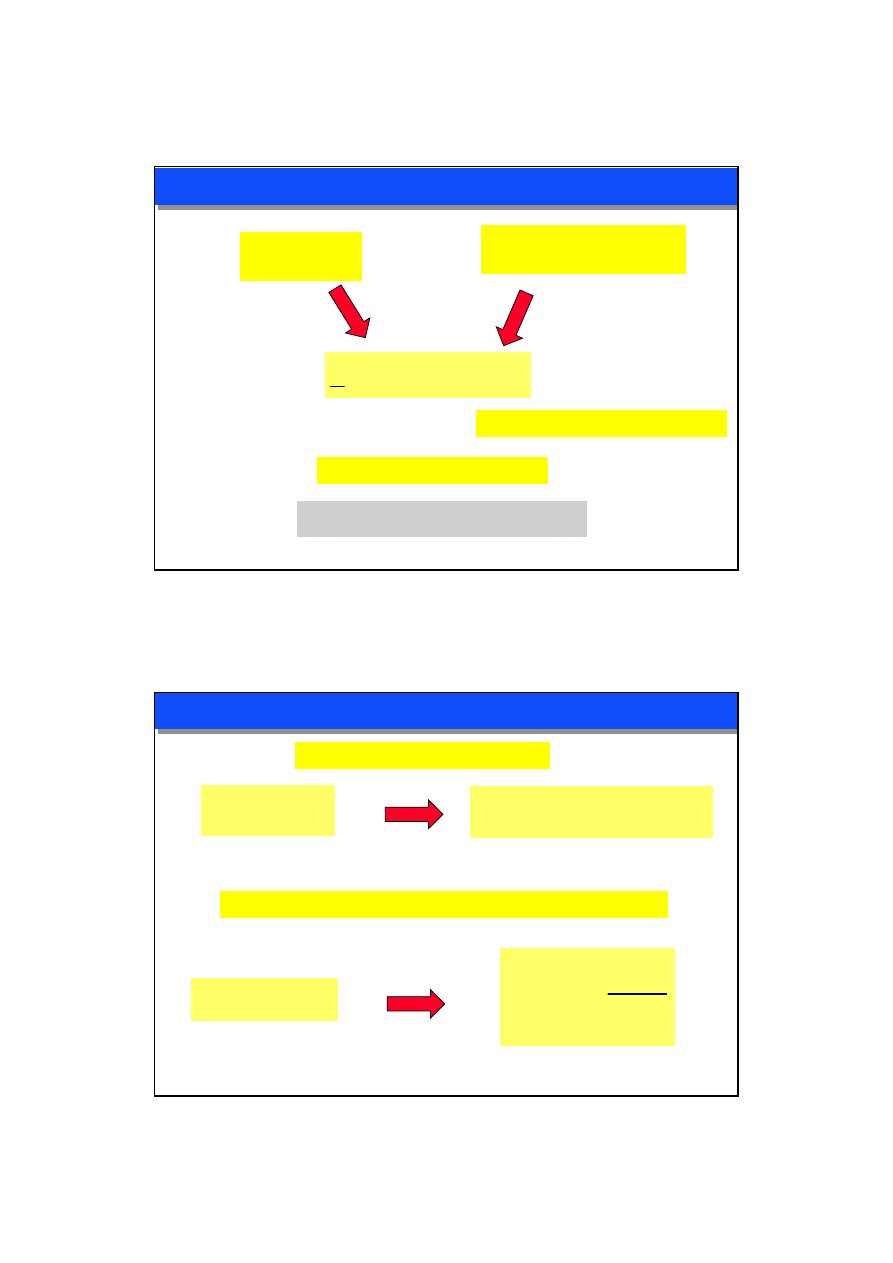
TRANSFORMATOR REALNY - MODEL FIZYCZNY

STAN JAŁOWY: I

1

= I

0

I

2

= 0 U

2

= U

20

TRANSFORMATOR REALNY - MODEL FIZYCZNY

STAN JAŁOWY: I

1

= I

0

I

2

= 0 U

2

= U

20

Δ P

Cu 1

ΔP

Fe

Φ

m

U

1

U

2

z

1

z

2

I

1

Φ

1

σ

Φ

2

σ

Θ

1

∗

∗

SPRAWNOŚĆ < 100%

PRĄD I MOC STANU JAŁOWEGO

PRĄD I MOC STANU JAŁOWEGO

TYPOWE PROPORCJE

TYPOWE PROPORCJE

)%

10

1

(

100

0

÷

=

n

I

I

)%

3

3

,

0

(

100

0

÷

=

n

S

P

MVA

MVA

kVA

kVA

8

SKŁADOWE STRUMIENIA:

ROZPROSZENIA I MAGNESOWANIA

SKŁADOWE STRUMIENIA:

ROZPROSZENIA I MAGNESOWANIA

%

90

%

10

%

100

+

=

m

φ

φ

φ

σ

1

1

+

=

Strumie

Strumie

ń

ń

magnesuj

magnesuj

ą

ą

cy (g

cy (g

ł

ł

ó

ó

wny)

wny)

Strumie

Strumie

ń

ń

rozproszenia

rozproszenia

Typowe proporcje podzia

Typowe proporcje podzia

ł

ł

u strumienia

u strumienia

m

φ

φ

≅

10

SEM INDUKOWANA

SEM INDUKOWANA

f

z

Φ

4,44

E

=

Z PRAWA

Z PRAWA

FARADAY

FARADAY

’

’

a

a

WYNIKA:

WYNIKA:

Φ

z

ω

Ψ

ω

E

max

=

=

AMPLITUDA PRZEBIEGU SINUSOIDALNEGO:

AMPLITUDA PRZEBIEGU SINUSOIDALNEGO:

WARTO

WARTO

ŚĆ

ŚĆ

SKUTECZNA PRZEBIEGU SINUSOIDALNEGO:

SKUTECZNA PRZEBIEGU SINUSOIDALNEGO:

4,44

2

≅

2

/

π

f

2

π

ω

=

9

SKŁADOWE SEM INDUKOWANYCH

SKŁADOWE SEM INDUKOWANYCH

f

z

4,44Φ

E

1

σ1

σ1

=

Strumie

Strumie

ń

ń

magnesuj

magnesuj

ą

ą

cy (g

cy (g

ł

ł

ó

ó

wny) indukuje:

wny) indukuje:

Strumie

Strumie

ń

ń

rozproszenia indukuje:

rozproszenia indukuje:

f

z

4,44Φ

E

1

m

1

=

f

z

4,44Φ

E

2

m

2

=

2

20

E

U

=

1

1

E

U

>

1

1

E

U

σ

>>

1

1

E

U

≅

PRZEKŁADANIA TRANSFORMATORA

PRZEKŁADANIA TRANSFORMATORA

z

def

υ

=

=

z

z

E

E

2

1

2

1

1

1

E

U

≅

U

U

20

1

u

def

υ

=

z

z

2

1

≅

u

υ

Przek

Przek

ł

ł

adania zwojowa

adania zwojowa

Przek

Przek

ł

ł

adania napi

adania napi

ę

ę

ciowa (dodany indeks

ciowa (dodany indeks

„

„

u

u

”

”

)

)

lub kr

lub kr

ó

ó

tko

tko

υ

υ

=

z

10

SKŁADOWE ENERGII W STANIE JAŁOWYM

SKŁADOWE ENERGII W STANIE JAŁOWYM

%

90

%

10

%

100

j

+

≅

m

cz

I

j

I

I

0

0

+

=

Typowe proporcje podzia

Typowe proporcje podzia

ł

ł

u:

u:

Straty energii

Straty energii

(ciep

(ciep

ł

ł

o)

o)

Magazynowanie energii

Magazynowanie energii

(magnesowanie)

(magnesowanie)

j

j

–

–

operator obrotu o 90 stopni

operator obrotu o 90 stopni

RÓWNANIE PRZEPŁYWÓW W STANIE JAŁOWYM

RÓWNANIE PRZEPŁYWÓW W STANIE JAŁOWYM

m

m

m

R

Θ

=

Φ

0

m

1

m

Θ

I

z

Θ

≅

=

m

I

z

1

m

=

Θ

0

1

0

I

z

Θ

=

Z PRAWA AMPERA WYNIKA:

Z PRAWA AMPERA WYNIKA:

PRAWO

PRAWO

OHM

OHM

’

’

a

a

DLA OBWODU MAGNETYCZNEGO :

DLA OBWODU MAGNETYCZNEGO :

11

SEM INDUKOWANA – STAN JAŁOWY

SEM INDUKOWANA – STAN JAŁOWY

Φ

σ1

I

X

E

0

σ1

def

σ1

=

f

z

4,44Φ

E

1

σ1

σ1

=

1

def

0

1

1

L

I

z

Φ

σ

σ

=

1

1

1

ωL

L

f

2

X

σ

σ

σ

π

=

=

Strumie

Strumie

ń

ń

rozproszenia indukuje:

rozproszenia indukuje:

Gdzie, definicja indukcyjno

Gdzie, definicja indukcyjno

ś

ś

ci/reaktancji rozproszenia:

ci/reaktancji rozproszenia:

SEM INDUKOWANA – STAN JAŁOWY

SEM INDUKOWANA – STAN JAŁOWY

m

Φ

I

X

E

m

m

def

1

=

f

z

4,44Φ

E

1

m

1

=

m

def

m

1

m

L

I

z

Φ

=

ωL

L

f

2

X

m

m

m

=

=

π

Strumie

Strumie

ń

ń

magnesowania indukuje:

magnesowania indukuje:

Gdzie, definicja indukcyjno

Gdzie, definicja indukcyjno

ś

ś

ci rozproszenia:

ci rozproszenia:

12

STRATY MOCY – STAN JAŁOWY

STRATY MOCY – STAN JAŁOWY

m

Φ

E

ΔP

I

1

Fe

0cz

def

=

2
0cz

Fe

Fe

I

ΔP

R

=

Fe

ΔP

I

E

R

0cz

1

Fe

=

n

I

I

1

0

<<

2
0

1

Cu0

I

R

ΔP

=

0

ΔP

0

≅

Cu

STAN JAŁOWY

PRZEZWOJENIE UZWOJENIA STRONY WTÓRNEJ

STAN JAŁOWY

PRZEZWOJENIE UZWOJENIA STRONY WTÓRNEJ

2

z

PRZEZWOJENIE (REDUKCJA) UZWOJENIA STRONY

WTÓRNEJ DO LICZBY ZWOJÓW RÓWNEJ LICZBIE

ZWOJÓW UZWOJENIA STRONY PIERWOTNEJ.

1

2

z

z

=

′

20

1

2

U

E

E

′

=

=

′

Cel: zr

Cel: zr

ó

ó

wnanie poziom

wnanie poziom

ó

ó

w napi

w napi

ęć

ęć

i

i

SEM

SEM

obu uzwoje

obu uzwoje

ń

ń

:

:

f

z

4,44Φ

E

2

m

2

′

=

′

13

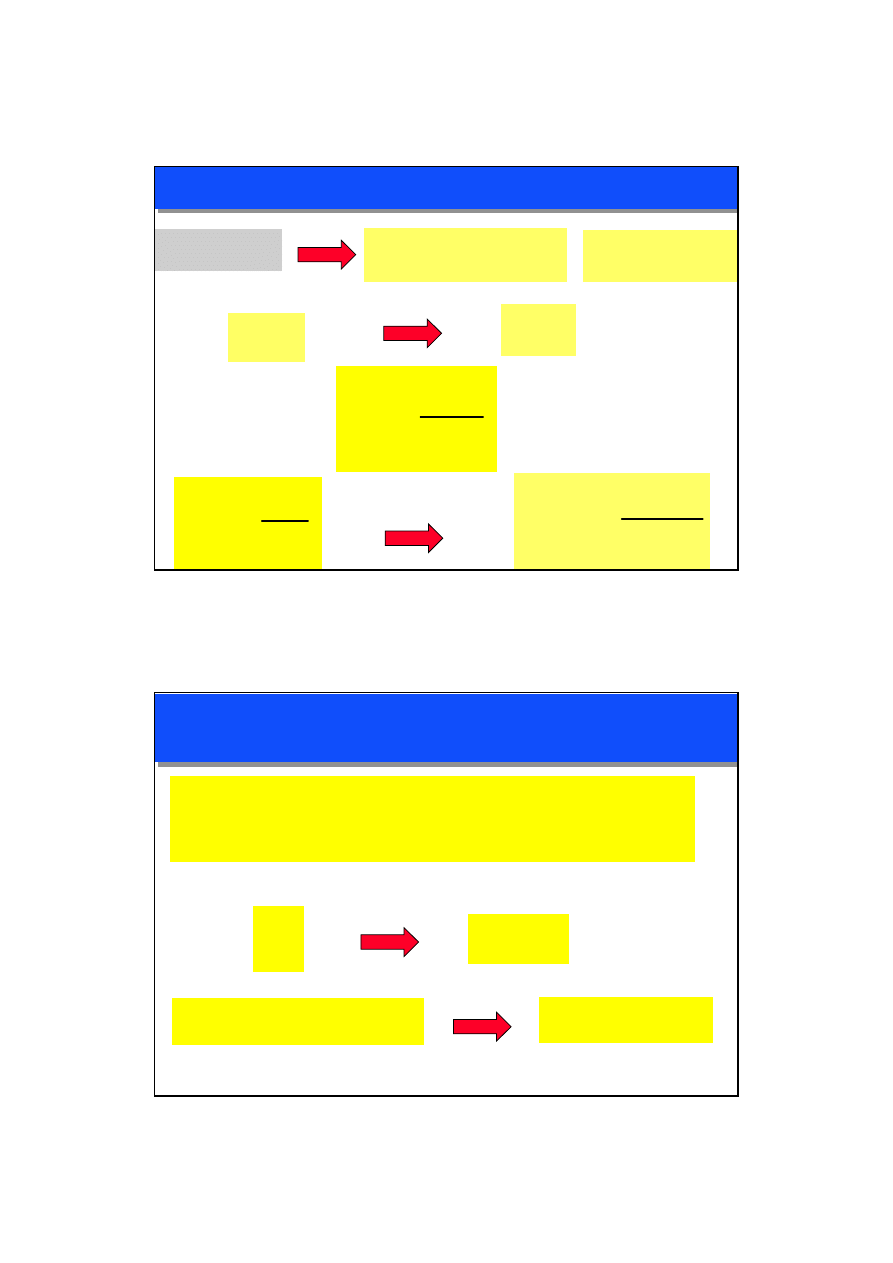
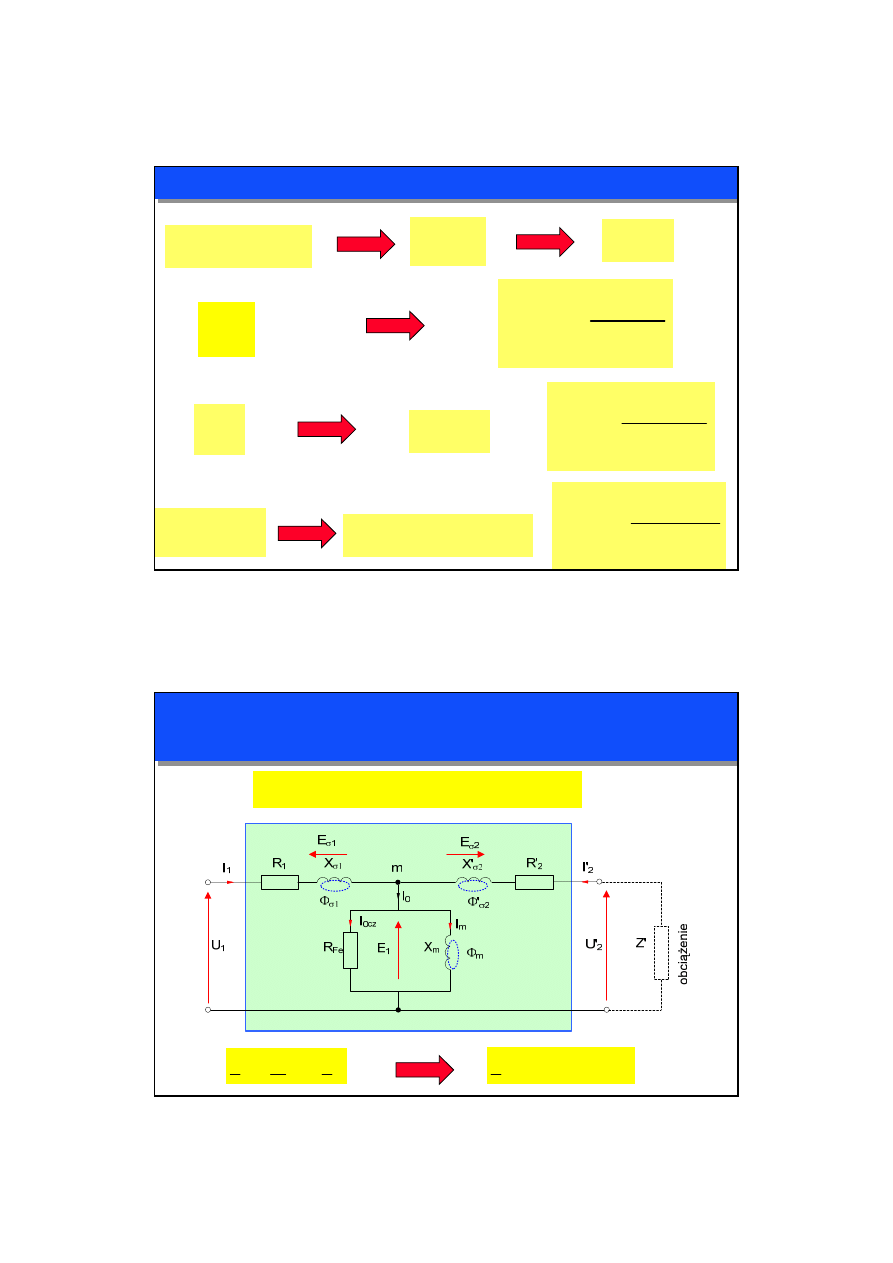
MODEL OBWODOWY TRANSFORMATORA

STAN JAŁOWY

MODEL OBWODOWY TRANSFORMATORA

STAN JAŁOWY

ZMIENNE ZESPOLONE

0

1

I

I

=

m

cz

I

j

I

I

0

0

+

=

1

2

z

z

=

′

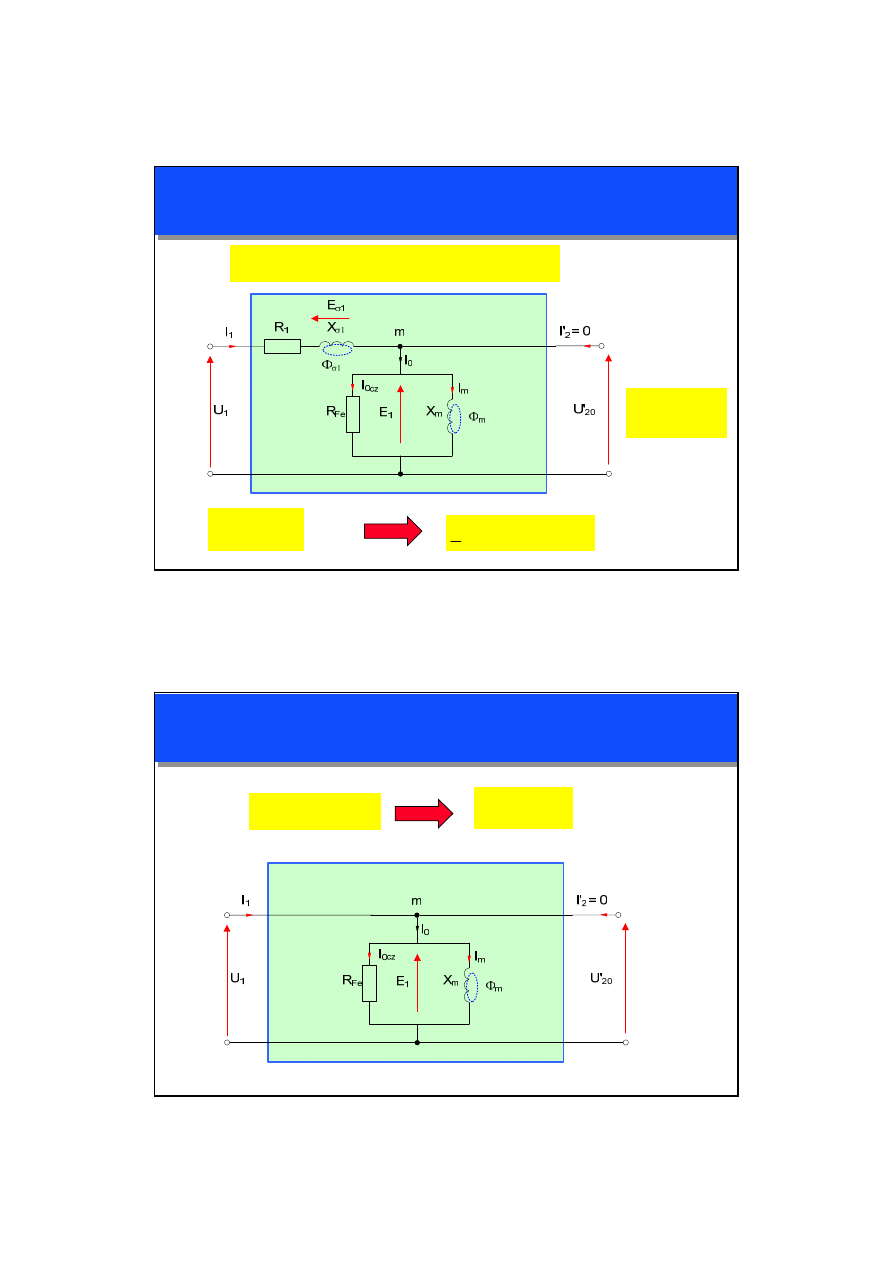
MODEL OBWODOWY TRANSFORMATORA

STAN JAŁOWY – MODEL UPROSZCZONY

MODEL OBWODOWY TRANSFORMATORA

STAN JAŁOWY – MODEL UPROSZCZONY

Założenie:

1

1

E

U

≅

14

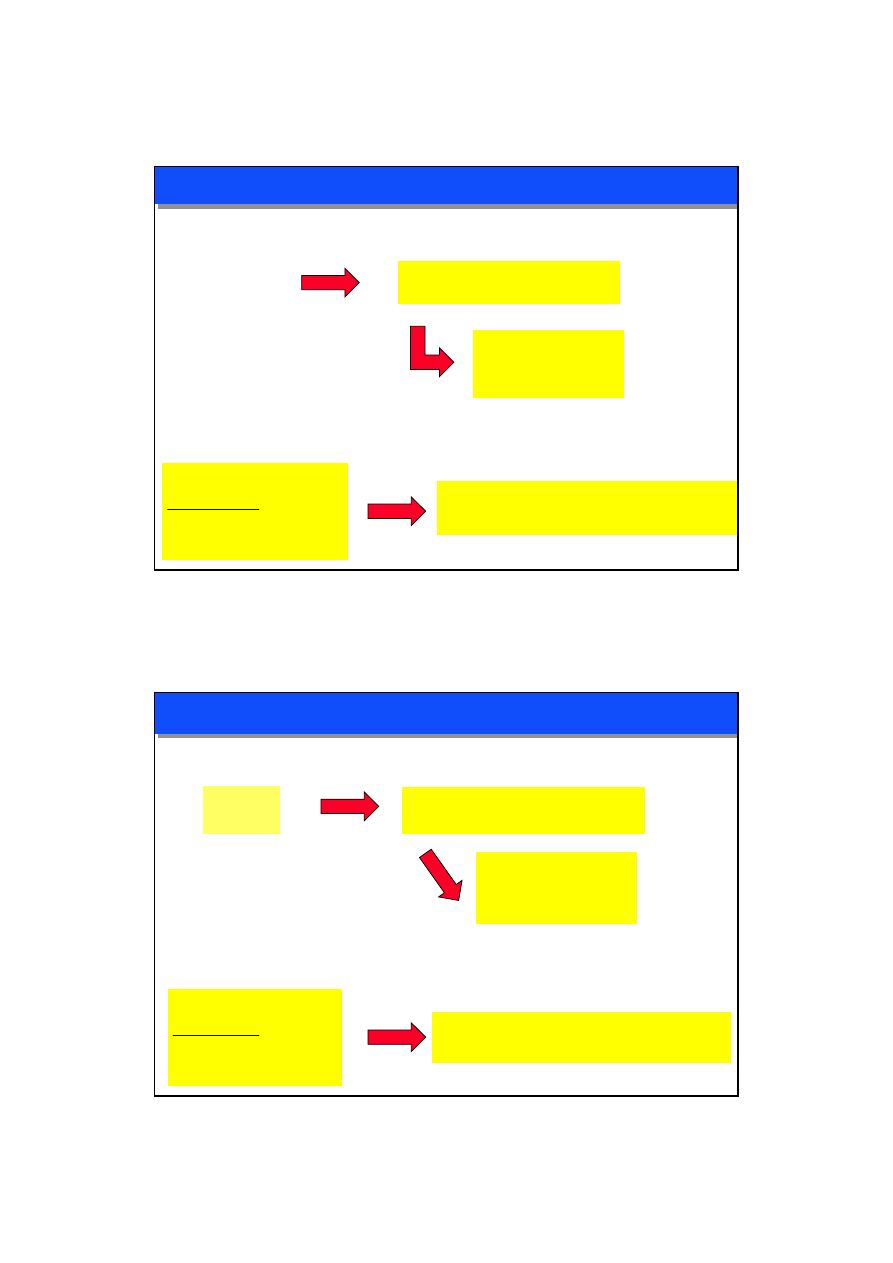
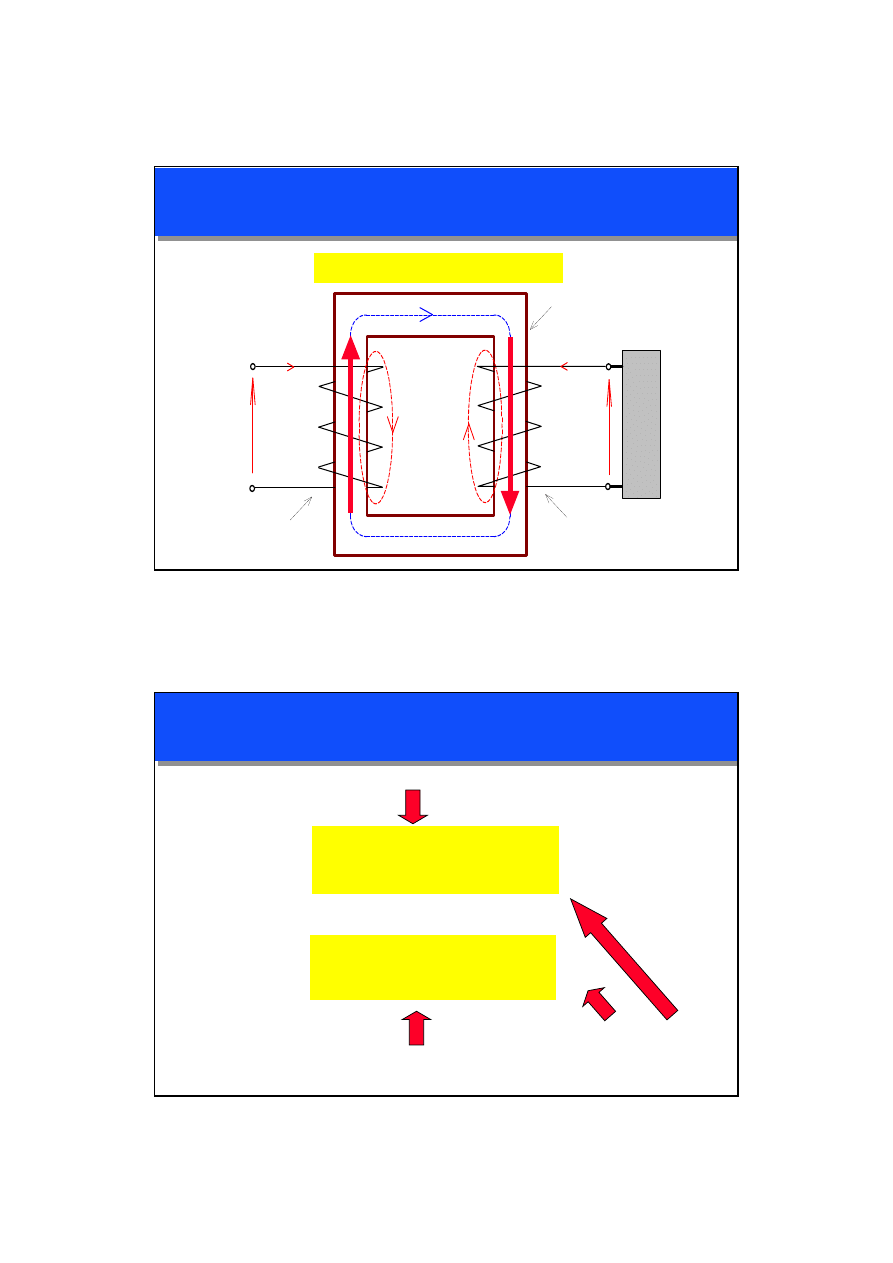
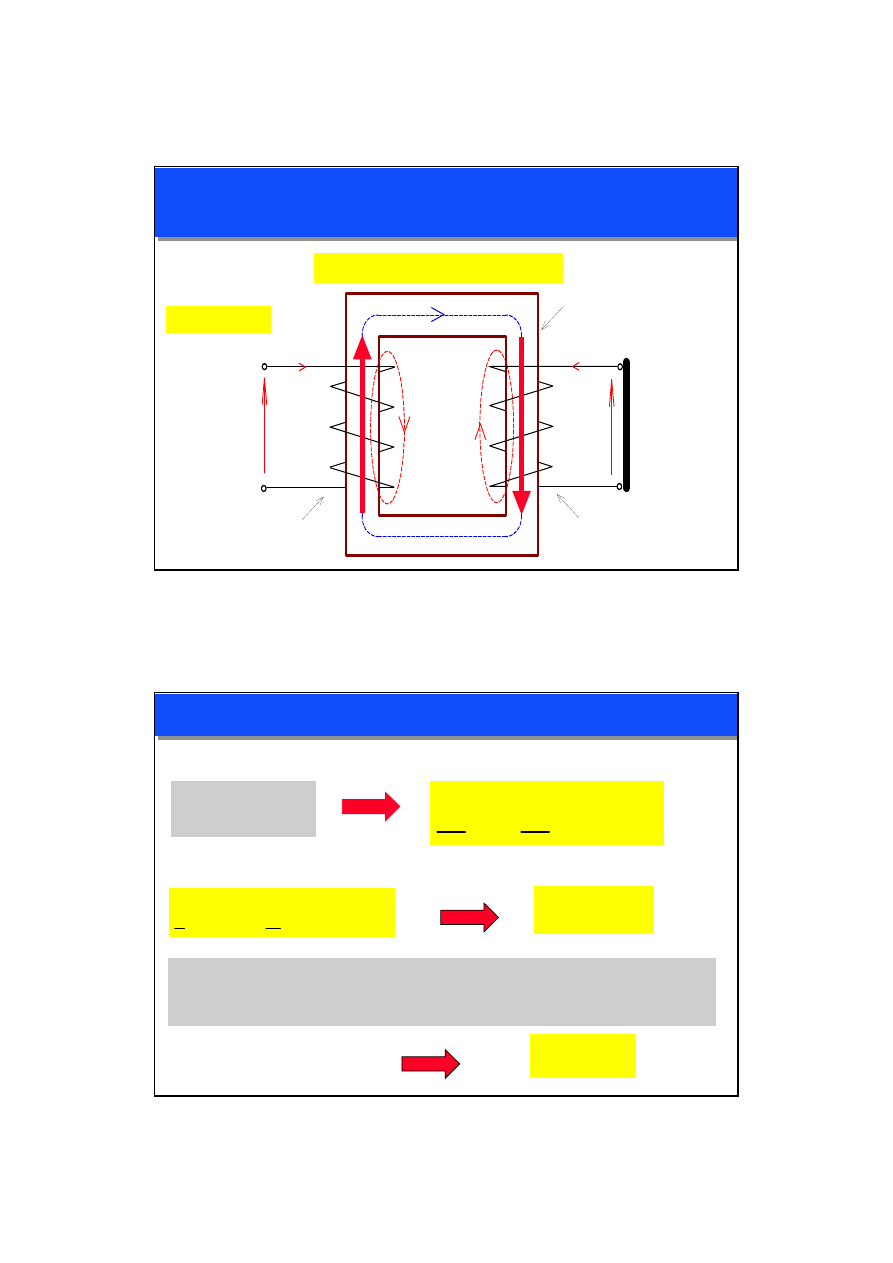
TRANSFORMATOR REALNY - MODEL FIZYCZNY

STAN OBCIĄŻENIA: I

1

> I

0

I

2

> 0

TRANSFORMATOR REALNY - MODEL FIZYCZNY

STAN OBCIĄŻENIA: I

1

> I

0

I

2

> 0

ΔP

Cu1

ΔP

Cu2

ΔP

Fe

Φ

m

U

1

U

2

z

1

z

2

I

1

I

2

Φ

1

σ

Φ

2

σ

Θ

2

Θ

1

OBC.

SPRAWNOŚĆ

η

< 100%

SKŁADOWE STRUMIENIA:

ROZPROSZENIA I MAGNESOWANIA

SKŁADOWE STRUMIENIA:

ROZPROSZENIA I MAGNESOWANIA

m

φ

φ

φ

σ

1

1

+

=

m

φ

φ

φ

σ

2

2

+

=

Strumie

Strumie

ń

ń

magnesuj

magnesuj

ą

ą

cy

cy

(g

(g

ł

ł

ó

ó

wny)

wny)

Strumie

Strumie

ń

ń

rozproszenia

rozproszenia

Strumie

Strumie

ń

ń

rozproszenia

rozproszenia

15

SKŁADOWE STRUMIENIA:

ROZPROSZENIA I MAGNESOWANIA

SKŁADOWE STRUMIENIA:

ROZPROSZENIA I MAGNESOWANIA

(t)

Θ

1

(t)

Θ

2

m

φ

φ

φ

σ

1

1

+

=

m

φ

φ

φ

σ

2

2

+

=

Przep

Przep

ł

ł

yw wypadkowy

yw wypadkowy

(t)]

Θ

(t)

[Θ

2

1

+

RÓWNANIE PRZEPŁYWÓW – STAN OBCIĄŻENIA

RÓWNANIE PRZEPŁYWÓW – STAN OBCIĄŻENIA

[A]

z

I

z

I

z

I

o

1

1

2

2

1

=

+

Θ

Θ

Θ

0

2

1

=

+

WEKTORY „CZASOWE” - WSKAZY

WARTOŚCI CHWILOWE

(t)

Θ

(t)

Θ

(t)

Θ

o

2

1

=

+

N

I

I

2

2

≤

ZAŁOŻENIE:

16

RÓWNANIE PRZEPŁYWÓW – STAN OBCIĄŻENIA

RÓWNANIE PRZEPŁYWÓW – STAN OBCIĄŻENIA

[A]

z

I

z

I

z

I

o

1

1

2

2

1

=

+

REDUKCJA/PRZEZWOJENIE UZWOJENIA WTÓRNEGO

DO LICZBY ZWOJÓW UZWOJENIA PIERWOTNEGO

2

2

2

2

1

2

2

I

z

z

z

z

′

′

=

Θ′

=

Θ

⇒

=

′

⇒

o

I

I

I

=

+

2

1

'

UWAGA: SUMOWANIE PRZEPŁYWÓW

MOŻNA ZASTĄPIĆ SUMOWANIEM PRĄDÓW!!!

1

2

2

E

E

E

=

′

⇒

Φ

Φ

m0

m

≅

)

(

2

1

Θ

+

Θ

f

z

E

m

44

,

4

1

1

Φ

=

f

z

E

m

44

,

4

2

2

Φ

=

1

2

2

z

z

z

=

′

⇒

RÓWNANIE PRZEPŁYWÓW – STAN OBCIĄŻENIA

RÓWNANIE PRZEPŁYWÓW – STAN OBCIĄŻENIA

17

m

m

m

R

Θ

=

Φ

0

m

Θ

≅

Θ

m

I

z

1

m

=

Θ

m

cz

I

j

I

I

0

0

+

=

%

90

%

10

%

100

j

+

≅

RÓWNANIE PRZEPŁYWÓW – STAN OBCIĄŻENIA

RÓWNANIE PRZEPŁYWÓW – STAN OBCIĄŻENIA

PRAWO

PRAWO

OHM

OHM

’

’

a

a

DLA OBWODU MAGNETYCZNEGO :

DLA OBWODU MAGNETYCZNEGO :

SKŁADOWE SEM INDUKOWANE

– STAN OBCIĄŻENIA

SKŁADOWE SEM INDUKOWANE

– STAN OBCIĄŻENIA

1

σ

φ

2

σ

φ

1

Θ

2

Θ

1

1

1

I

X

E

σ

σ

=

2

2

2

X

I

E

σ

σ

=

2

2

2

I

X

E

′

′

=

′

σ

σ

2

2

2

1

2

)

(

σ

σ

X

z

z

X

=

′

m

Φ

)

(

2

1

Θ

+

Θ

1

m

m

I

X

E

=

18

STRATY W RDZENIU I UZWOJENIACH

– STAN OBCIĄŻENIA

STRATY W RDZENIU I UZWOJENIACH

– STAN OBCIĄŻENIA

2

0

cz

Fe

Fe

I

P

R

Δ

=

2

1

1

1

I

P

R

Cu

Δ

=

2

2

2

2

I

P

R

Cu

′

Δ

=

′

2

2

Cu

Cu

P

P

′

Δ

=

Δ

cz

I

0

m

Φ

Fe

P

Δ

1

Cu

P

Δ

1

I

)

I

(

I

2

2

′

m

I

z

1

m

=

Θ

MODEL OBWODOWY TRANSFORMATORA

STAN OBCIĄŻENIA

MODEL OBWODOWY TRANSFORMATORA

STAN OBCIĄŻENIA

ZMIENNE ZESPOLONE

0

2

1

I

I

I

=

′

+

m

cz

I

j

I

I

0

0

+

=

19

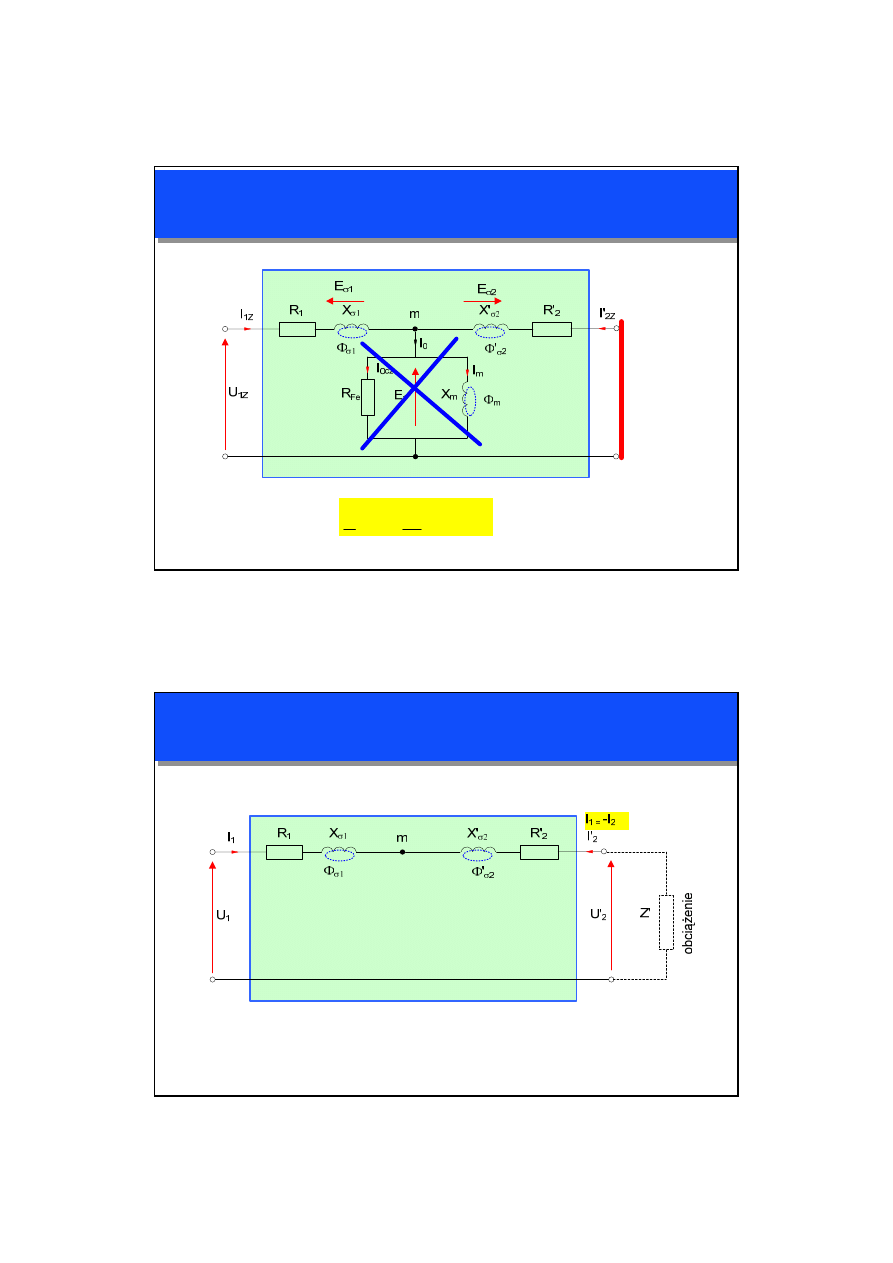
TRANSFORMATOR REALNY - MODEL FIZYCZNY

STAN ZWARCIA: I

1Z

= I

1N

I

2Z

= I

2N

TRANSFORMATOR REALNY - MODEL FIZYCZNY

STAN ZWARCIA: I

1Z

= I

1N

I

2Z

= I

2N

ΔP

Cu1

ΔP

Cu2

ΔP

Fez

Φ

mz

U

1Z

U

2

z

1

z

2

I

1Z

I

2Z

Φ

1

σ

Φ

2

σ

Θ

2Z

Θ

1Z

= 0

ΔP

Fe0

<<

<<

Φ

m0

SPRAWNOŚĆ

η

< 100%

U

1Z

<< U

1N

RÓWNANIE PRZEPŁYWÓW – STAN ZWARCIA

RÓWNANIE PRZEPŁYWÓW – STAN ZWARCIA

N

Z

I

I

2

2

=

0

I

2

2

1

1Z

≅

+

z

I

z

Z

0

Θ

Θ

2

1

≅

+

Φ

Φ

m0

mz

<<

0

≅

Fe

P

Δ

0

Φ

mz

≅

UWAGA: STRUMIEŃ NIE OSIĄGA WARTOŚCI

RÓWNEJ ZERO !!!!!

20

MODEL OBWODOWY TRANSFORMATORA

STAN ZWARCIA

MODEL OBWODOWY TRANSFORMATORA

STAN ZWARCIA

0

2

1

≅

′

+

Z

Z

I

I

MODEL OBWODOWY TRANSFORMATORA

STAN ZWARCIA

MODEL OBWODOWY TRANSFORMATORA

STAN ZWARCIA

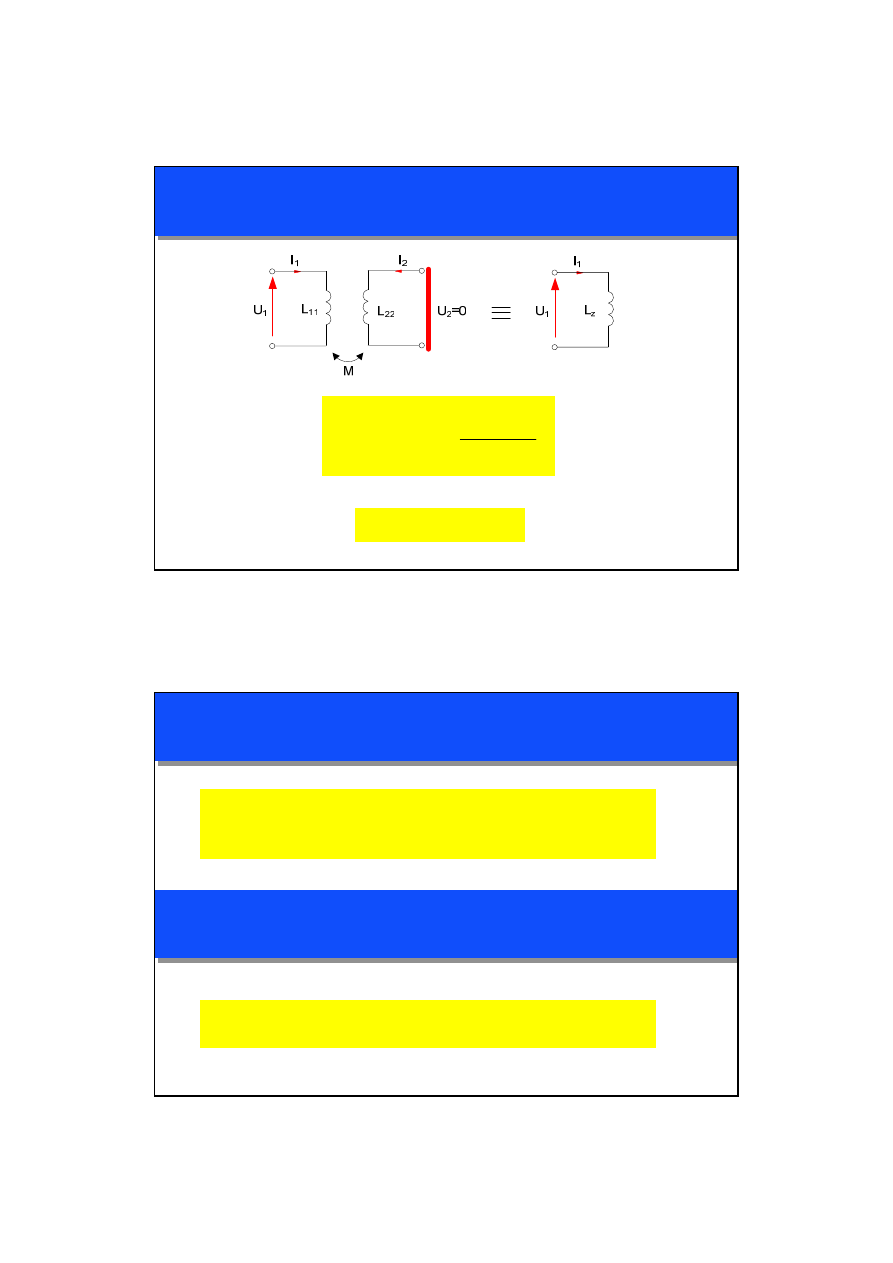
21

MODEL OBWODOWY TRANSFORMATORA

STAN ZWARCIA

MODEL OBWODOWY TRANSFORMATORA

STAN ZWARCIA

)

22

11

2

11

1

(

L

L

M

L

L

z

−

=

2

1

σ

σ

L

L

L

z

′

+

≅

ZASTOSOWANIE

MODELU OBWODOWEGO TRANSFORMATORA

ZASTOSOWANIE

MODELU OBWODOWEGO TRANSFORMATORA

•

WYZNACZANIE ZMIENNOŚCI NAPIĘCIA

•

WYZNACZANIE SPRAWNOŚCI

WYZNACZANIE PARAMETRÓW

MODELU OBWODOWEGO TRANSFORMATORA

WYZNACZANIE PARAMETRÓW

MODELU OBWODOWEGO TRANSFORMATORA

•

WYZNACZANIE PRZEKŁADNI

•

PRÓBA STANU

•

PRÓBA ZWARCIA