Moc w obwodach prądu sinusoidalnie zmiennego

MOC CHWILOWA

W obwodzie prądu sinusoidalnie zmiennego może

występować kilka rodzajów mocy.

Pierwszą z analizowanych jej postaci jest moc

chwilowa.

Mocą chwilowa nazywa się iloczyn wartości

chwilowych napięcia i prądu:

p = ui

W obwodzie prądu zmiennego moc pobierana przez

odbiornik ze źródła nie jest stała (jak w przypadku układu
prądu stałego), lecz ze względu na fakt, iż energia jest
dostarczana w rożnych wartościach w stałych przedziałach
czasu posiada ona różne wartości w poszczególnych
chwilach. Taki przebieg zmian mocy jest związany z tym,
że zarówno prąd jak i napięcie zmieniają w funkcji czasu
swój kierunek oraz wartość bezwzględną.

Podstawiając do wzoru na moc chwilową wartości

chwilowe napięcia i prądu, po dokonaniu uzyskujemy
zależność analityczną określającą wartość mocy chwilowej:

Moc w obwodach prądu sinusoidalnie zmiennego

p = ui = U

m

sin



t



I

m

sin(



t





) =

2

m

m

I

U

[cos





sin(2



t





)] =

= UI[cos





cos(2



t





)] = UIcos





UIcos(2



t





)

W wzorze tym można wyróżnić dwie składowe mocy

chwilowej:

stałą daną członem UIcos



,

składową sinusoidalnie zmienną równą: UIcos(2



t





).

Częstotliwość mocy sinusoidalnie zmiennej jest

dwukrotnie wyższa od częstotliwości prądu i napięcia,
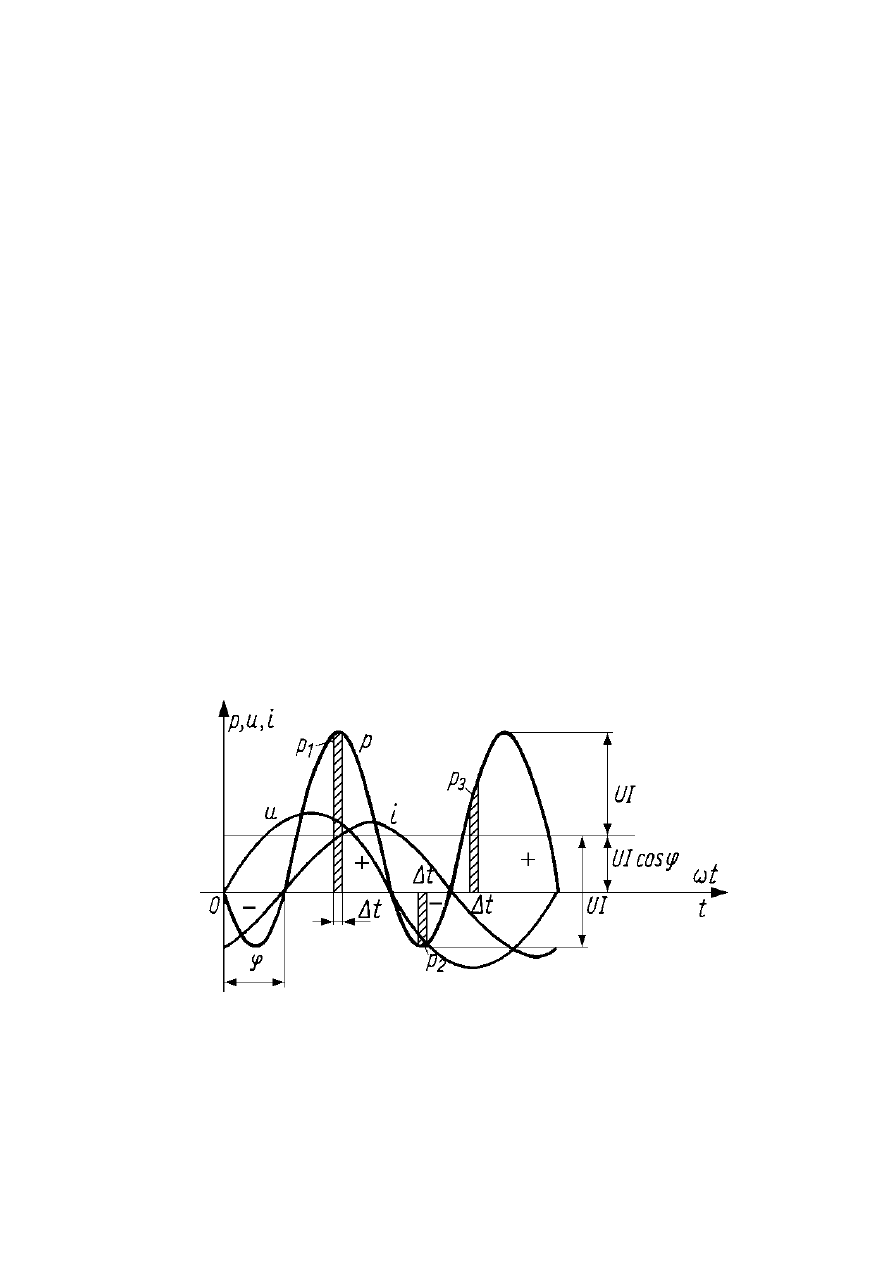
natomiast jej amplituda wynosi UI. Energia dostarczona do
odbiornika w równych przedziałach czasu ma różną
wartość. Całkowita energia dodatnia dostarczona do
odbiornika odpowiada polu ograniczonemu przez sinusoidę
nad osią czasu, natomiast ujemna odebrana od odbiornika
poniżej osi.

Moc w obwodach prądu sinusoidalnie zmiennego

MOC CZYNNA, BIERNA I POZORNA.

Przyjmując czas równy wielokrotności okresu można

wyznaczyć wartość średnią mocy chwilowej. Na podstawie
podanych powyżej zależności określających moc chwilową,
oraz wykresu przedstawionego na powyższym rysunku
można stwierdzić, że wartość średnia mocy chwilowej
równa jest składowej stałej mocy chwilowej:

P

śr

= UIcos



Mocą czynną nazywa się wartość średnią mocy

chwilowej, jest ona zatem dana następującą zależnością:

P = UIcos



Jednostką mocy czynnej jest 1 wat (1W).
Moc pozorna oznaczana jest ona przez S i obliczana

jest jako iloczyn wartości skutecznych napięcia i prądu:

S = UI

Jej jednostką jest 1 woltoamper (1V



A).

Moc bierna oznaczana jest przez Q i definiuje się ją

jako iloczyn wartości skutecznych prądu i napięcia oraz
sinusa kąta zawartego pomiędzy tymi wielkościami:

Q = UIsin



Jednostką mocy biernej jest 1 war (1 var).
Pomiędzy wspomnianymi trzema rodzajami mocy prądu

sinusoidalnego istnieją następujące zależności:

S

2

= P

2

+ Q

2

S =

2

2

Q

P



tg



=

P

Q

; cos



=

S

P

Moc w obwodach prądu sinusoidalnie zmiennego

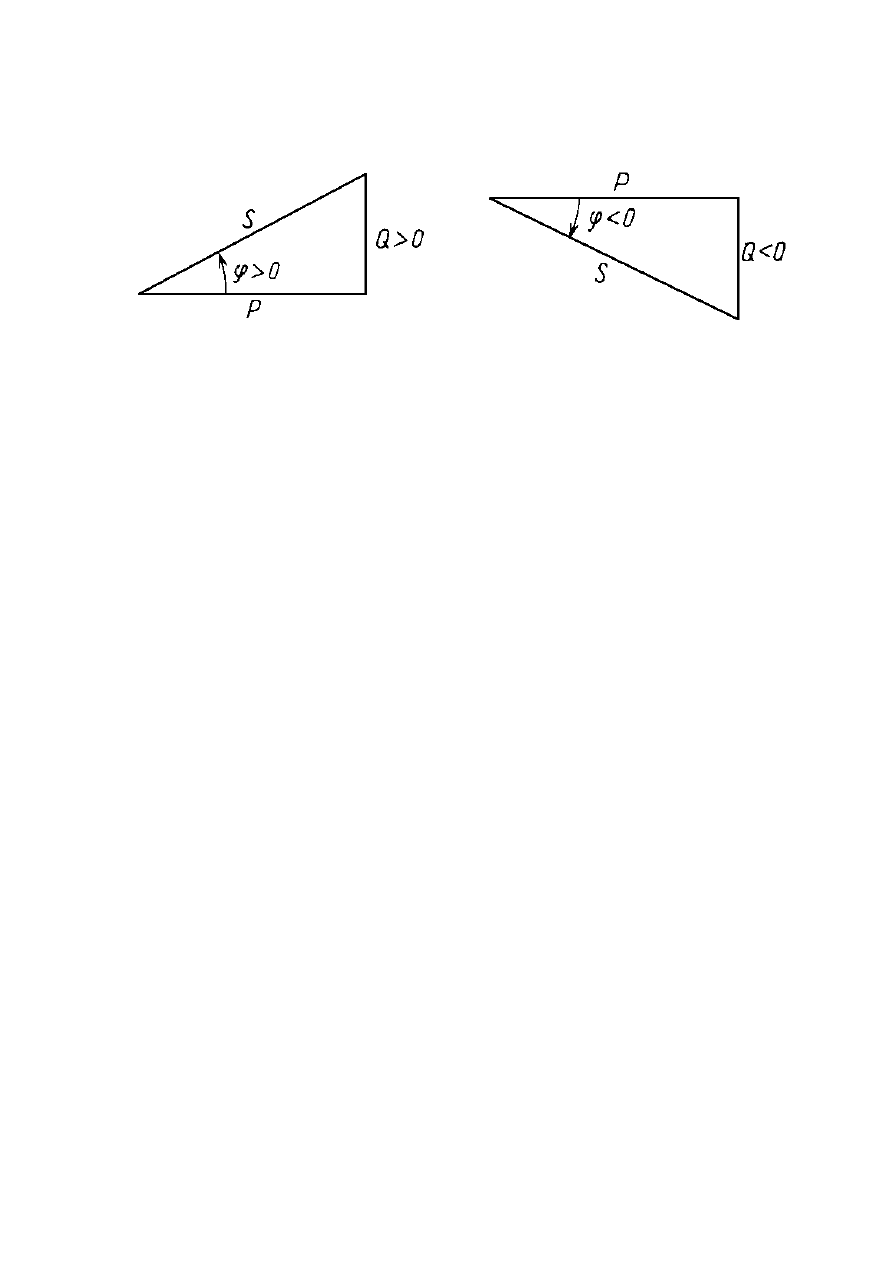
Przykładowe trójkąty mocy dla dwóch przypadków:

Q>0 i Q<0 przedstawione są poniżej:

Moc w obwodach prądu sinusoidalnie zmiennego

POSTAĆ ZESPOLONA MOCY POZORNEJ.

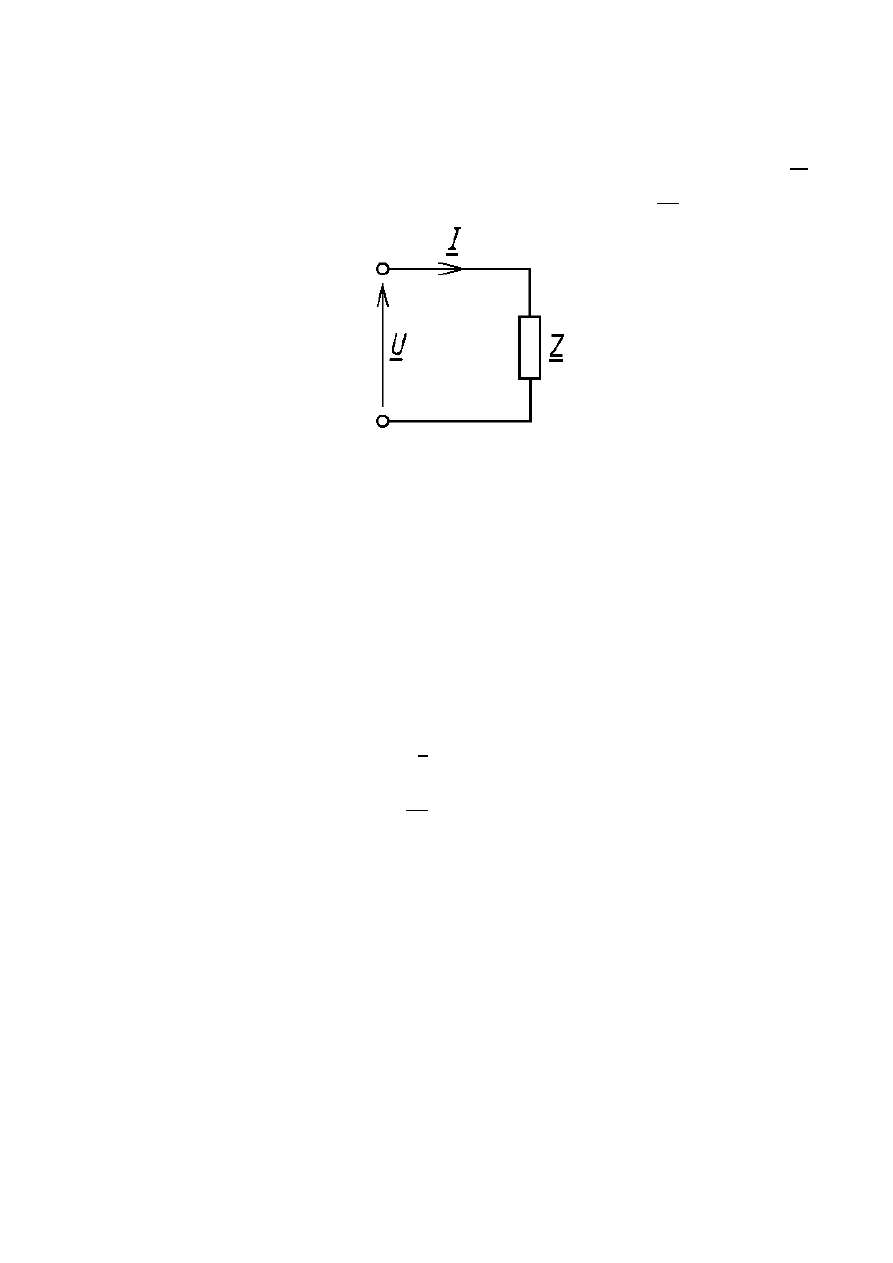
Do zacisków dwójnika o impedancji zespolonej Z

przyłożone jest napięcie sinusoidalnie zmienne U.

Przyjmujemy, że odbiornik ma charakter reystancyjno-

indukcyjny i przesunięcie pomiędzy napięciem i prądem
wynosi



, to:

i = I

m

sin(



t +



i

)

u = U

m

sin(



t +



u

)

W postaci zespolonej będą przedstawione wzorami:

I =

i

j

Ie



U =

u

j

Ue



Kąt przesunięcia fazowego:



=



u

-



i

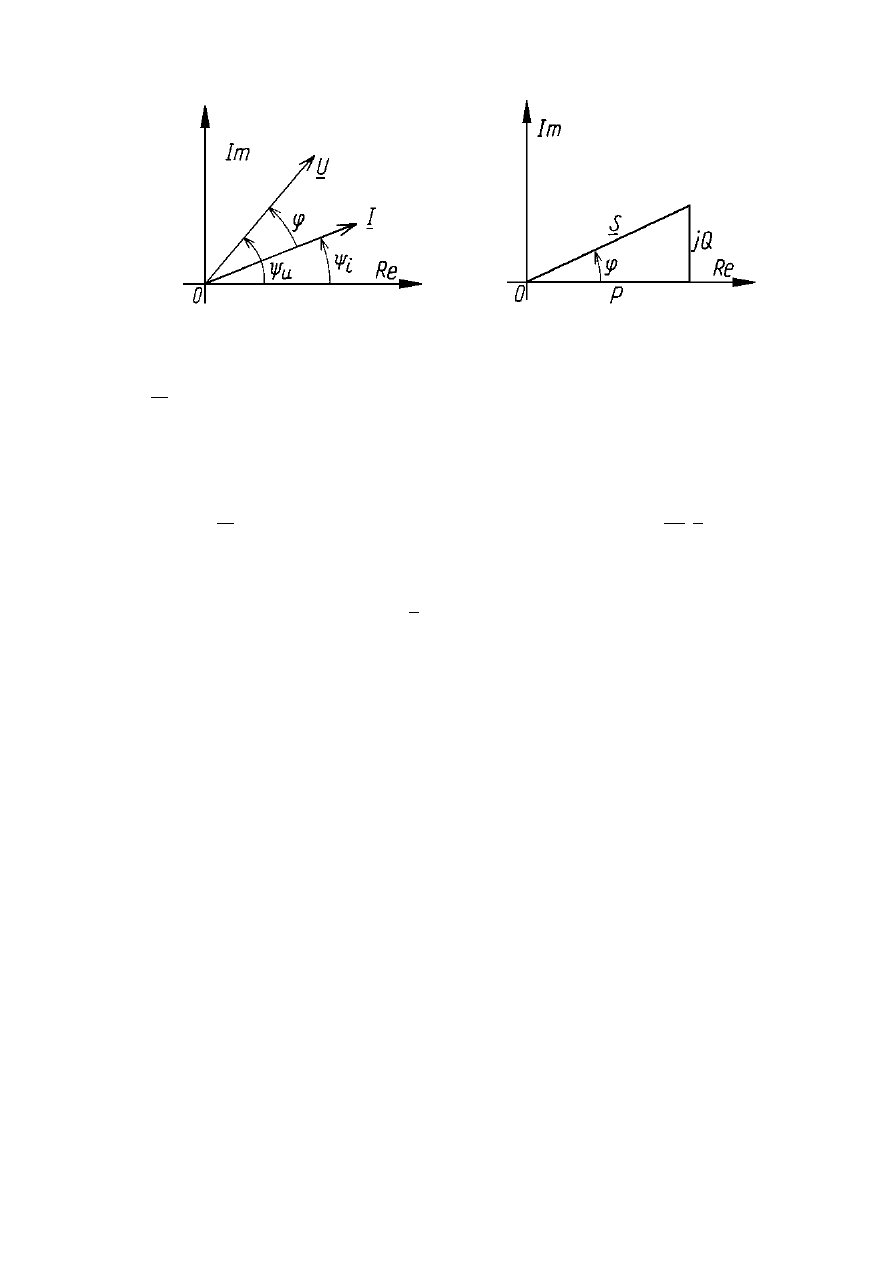
Napięcie i prąd w postaci zespolonej przedstawione

jako wektory:

Moc w obwodach prądu sinusoidalnie zmiennego

Z trójkąta mocy wynika:

S = P + jQ = UIcos



+ jUIsin



= UI(cos



+ jsin



) =

UIe

j



= Se

j



Równoważna zależność:

S = UIe

j



=

i

u

i

u

j

j

j

Ie

Ue

UIe















)

(

=U



I*

ponieważ:

I*=

i

j

Ie





Moc w obwodach prądu sinusoidalnie zmiennego

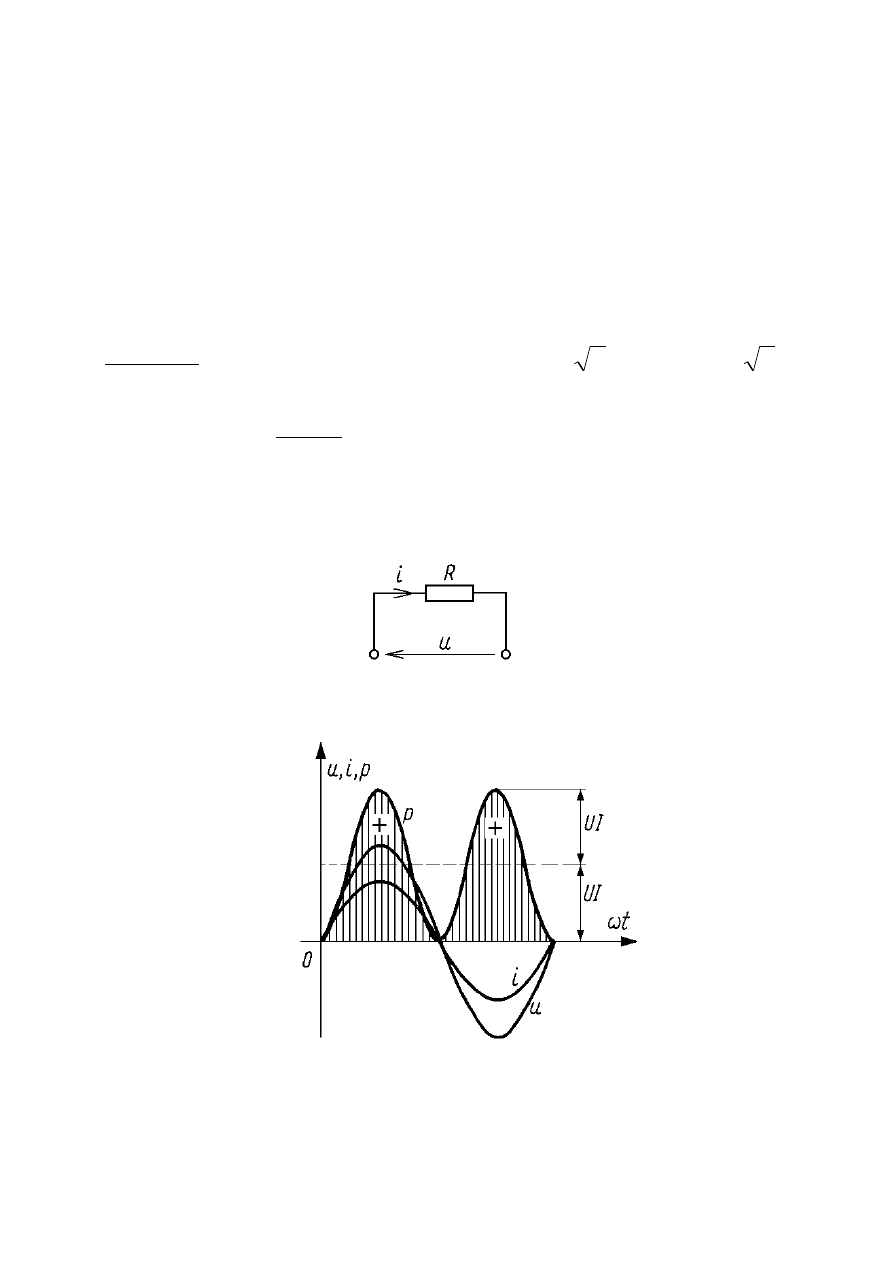
MOC W REZYSTORZE IDEALNYM O

REZYSTANCJI R

Prąd i napięcie w rezystorze występują w fazie.
Moc chwilowa to:

p = ui = U

m

I

m

sin

2



t

Po dokonaniu przekształceń trygonometrycznych (sin

2



=

2

2

cos

1





), oraz uwzględniając, że: U

m

=

2

U oraz I

m

=

2

I:

p =

2

m

m

I

U

(1



cos2



t) = UI(1



cos2



t)

Przebiegi napięcia i prądu oraz mocy chwilowej w

rezystorze idealnym przedstawia rysunek:

Wartość średnia mocy chwilowej w przypadku

rezystora dana jest wzorem:

P = UI

Moc w obwodach prądu sinusoidalnie zmiennego

Jest to moc czynna. W przypadku rezystora idealnego

moc czynna jest równa mocy pozornej, natomiast moc
bierna wynosi zero.

Równoważne wzory na moc czynną:

P = RI

2

P = GU

2

=

R

U

2

Moc w obwodach prądu sinusoidalnie zmiennego

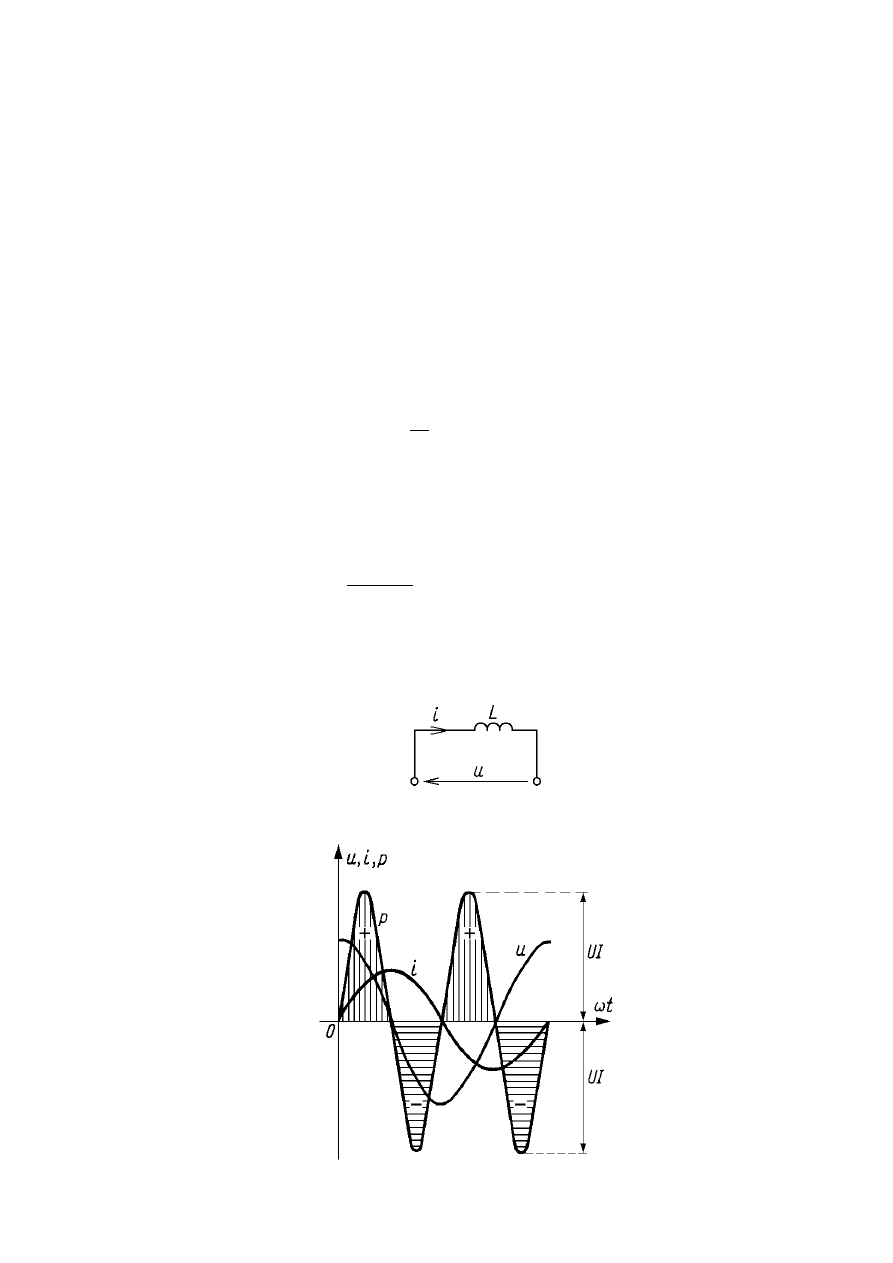
MOC W CEWCE IDEALNEJ O

INDUKCYJNOŚCI L

W przypadku cewki idealnej napięcie sinusoidalne

wyprzedza prąd o kąt fazowy



=

2

/



. Przyjmując, że prąd

posiada zerową fazę początkową i dany jest następującym
przebiegiem: i = I

m

sin



t, wówczas przebieg napięcia będzie

miał następującą postać: u = U

m

sin(



t +

2

/



). Moc

chwilowa:

p = ui = U

m

sin(



t +

2



)



I

m

sin



t = U

m

I

m

cos



tsin



t

Po uwzględnieniu zależności trygonometrycznych

(cos



sin



= ½ sin2



):

p =

2

m

m

I

U

sin2



t = UIsin2



t

Przebiegi napięcia i prądu oraz mocy chwilowej w

cewce idealnej przedstawia poniższy rysunek:

Moc w obwodach prądu sinusoidalnie zmiennego

Moc czynna P w tym przypadku wynosi zero, zaś moc

bierna dana jest wzorem:

Q = UI

i jest równa mocy pozornej S.
Podobnie jak w przypadku rezystancji, również i tu

możliwe jest obliczenie mocy biernej cewki w oparciu o
prawo Ohma (w myśl którego: U = X

L

I

2

):

Q = X

L

I

2

Q = B

L

U

2

Moc w obwodach prądu sinusoidalnie zmiennego

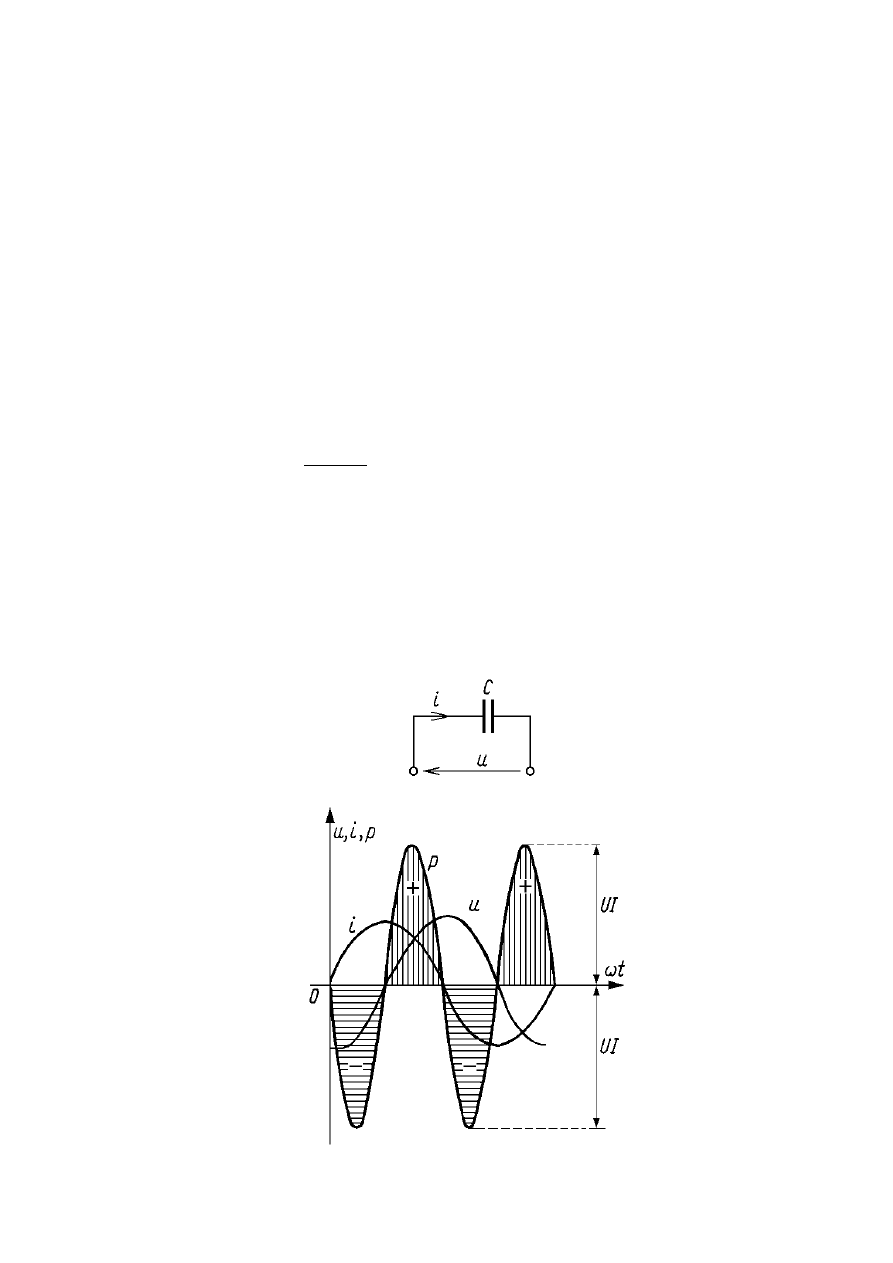
MOC W KONDENSATORZE IDEALNYM O

POJEMNOŚCI C.

W przypadku kondensatora idealnego przesunięcie

fazowe pomiędzy napięciem i prądem wynosi



=



2

/



.

Prąd posiada zerową fazę początkową, jest dany
przebiegiem czasowym: i = I

m

sin



t, natomiast napięcie

wyrażone jest następującym przebiegiem czasowym:
u = U

m

sin(



t



2

/



). Moc chwilowa:

p = ui = U

m

sin(



t



2

/



)



I

m

sin



t =



U

m

I

m

cos



tsin



t =



2

m

m

I

U

sin2



t =



UIsin2



t

Powyższy wzór jest taki sam jak dla cewki idealnej,

jedyną różnicą jest znak (moc indukcyjna jest dodatnia,
natomiast pojemnościowa ujemna).

Przebiegi napięcia, prądu i mocy chwilowej dla

kondensatora idealnego przedstawione są na rysunku:

Moc w obwodach prądu sinusoidalnie zmiennego

W układzie takim moc czynna P wynosi zero, natomiast

moc bierna Q obliczona przy danej wartości



:

Q =



UI

Moc bierna jest w przypadku kondensatora równa mocy

pozornej (co do wartości bezwzględnej).

Równoważne postacie zapisu mocy chwilowej:

Q =



X

C

I

2

Q =



B

C

U

2

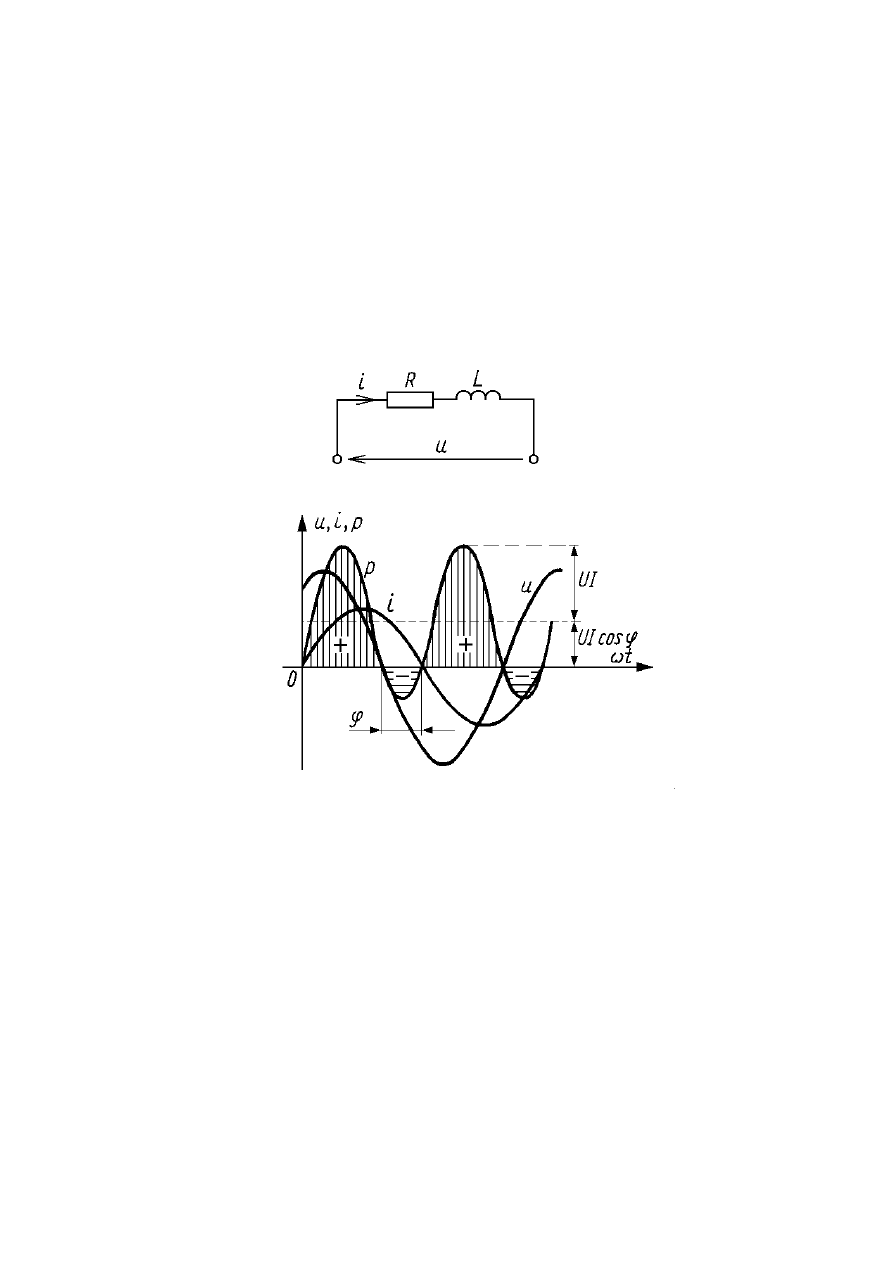
Moc w obwodach prądu sinusoidalnie zmiennego

MOC W CEWCE RZECZYWISTEJ.

Cewka rzeczywista to układ szeregowego połączenia

RL.

p = ui = U

m

sin(



t +



)



I

m

sin



t =

UI[cos





cos(2



t +



)]

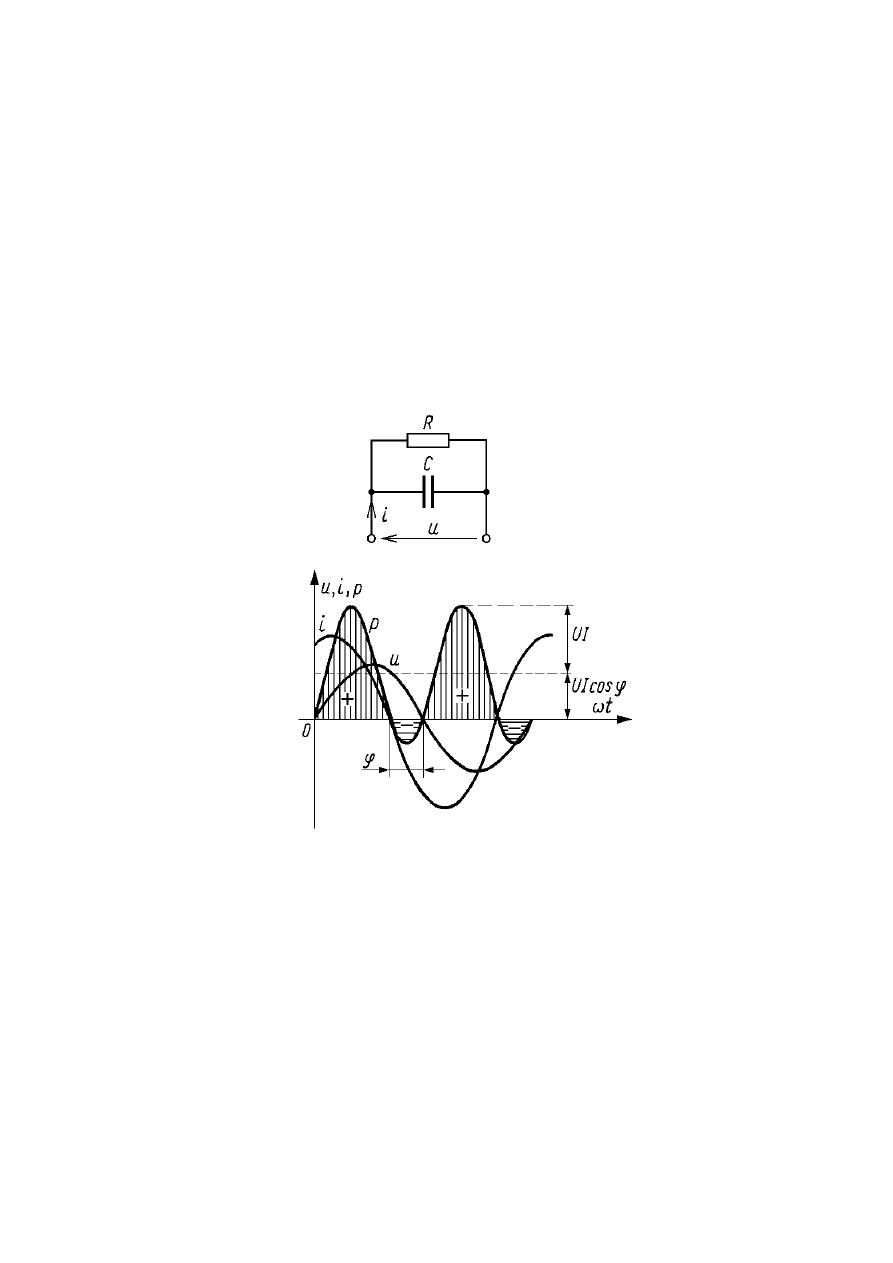
Przebiegi napięcia, prądu oraz mocy w układzie cewki

rzeczywistej przedstawia rysunek:

Moc czynna w przypadku przebiegu mocy chwilowej

jest równa średniej mocy chwilowej i wynosi:

P = UIcos



Z trójkąta napięć dla układu szeregowego RL wynika:

Ucos



= U

R

= RI

Równoważna zależność na moc czynną dwójnika

szeregowego RL:

P = RI

2

Moc bierna:

Moc w obwodach prądu sinusoidalnie zmiennego

Q = UIsin



Z trójkąta napięć dwójnika szeregowego RL wynika:

Usin



= U

L

= X

L

I

Równoważna zależność:

Q = X

L

I

2

Moc pozorna wyznaczana jest ze wzoru :

S = UI S = ZI

2

Z =

2

2

L

X

R



.

Moc w obwodach prądu sinusoidalnie zmiennego

MOC W KONDENSATORZE RZECZYWISTYM

Kondensator rzeczywisty może być przedstawiany za

pomocą dwóch różnych schematów: równoległego i
szeregowego. Dla układu równoległego:

p = ui = U

m

sin



t



I

m

sin(



t +



) =

UI[cos





cos(2



t +



)]

Przebieg mocy chwilowej w układzie równoległym RC

przedstawia rysunek:

Moc czynna w tym przypadku dana jest wzorem:

P = UIcos



Z trójkąta prądów dla dwójnika równoległego wynika:

Icos



= I

R

= GU

Równoważna zależność:

P = GU

2

Moc bierna wyznaczana ze wzoru definicyjnego:

Moc w obwodach prądu sinusoidalnie zmiennego

Q = UIsin



Z trójkąta prądów wynika, że:

Isin



=



I

C

=



B

C

U

Równoważna zależność

Q =



B

C

U

2

Moc pozorna:

S = UI

Równoważna zależność:

S = YU

2

gdzie: Y =

2

2

C

B

G



Współczynnik mocy i jego znaczenie techniczne i

ekonomiczne.

Współczynnik mocy cos



ma w eksploatacji urządzeń

znaczenie związane z efektywnością ich pracy. Większość
z odbiorników energii elektrycznej stosowanych na co
dzień odznacza się pewną indukcyjnością. Do urządzeń
tego typu zaliczyć można przede wszystkim silniki
elektryczne (zwłaszcza słabo obciążone), odbiorniki
przemysłowe, instalacje oświetleniowe z lampami
wyładowczymi, które są łączone w szereg z dławikami
ograniczającymi prąd i inne. Współczynnik mocy takich
urządzeń bez urządzeń kompensujących jego wartość
wynosiłby w granicach 0,55 do 0,60. Prąd dopływający do
odbiornika przy określonej mocy czynnej zależy odwrotnie
proporcjonalnie od wartości współczynnika mocy, stąd
dostarczenie do odbiornika określonej wartości mocy przy

Moc w obwodach prądu sinusoidalnie zmiennego

określonym napięciu wymaga większego prądu przy
mniejszym cos



niż przy większej jego wartości. Ponadto

straty w przewodach łączących zależą odwrotnie
proporcjonalnie od kwadratu współczynnika mocy, stąd jest
jak najbardziej pożądane, aby miał on wartość możliwie
największą, zbliżoną do jedności.

Metody poprawy współczynnika mocy dokonuje się

poprzez zmniejszenie mocy biernej indukcyjnej kosztem
mocy biernej pojemnościowej. Wykorzystuje się do tego
celu zwykle baterię kondensatorów włączoną równolegle z
odbiornikiem bądź ich grupą. Jako przykład można
rozpatrzyć kompensację mocy biernej przeprowadzoną dla
silnika elektrycznego o mocy P i współczynniku cos



1

włączonego do źródła napięcia U. Silnik elektryczny można
przedstawić

za

pomocą

schematu

zastępczego

równoległego RL. Prąd który pobiera silnik I

S

jest

opóźniony względem napięcia o kąt fazowy



1

, którego

wartość można wyznaczyć bezpośrednio z cos



1

. Prąd ten

posiada dwie składowe I

R

będącą w fazie z prądem I

S

, oraz

składową I

L

(składowa bierna) prostopadłą do napięcia

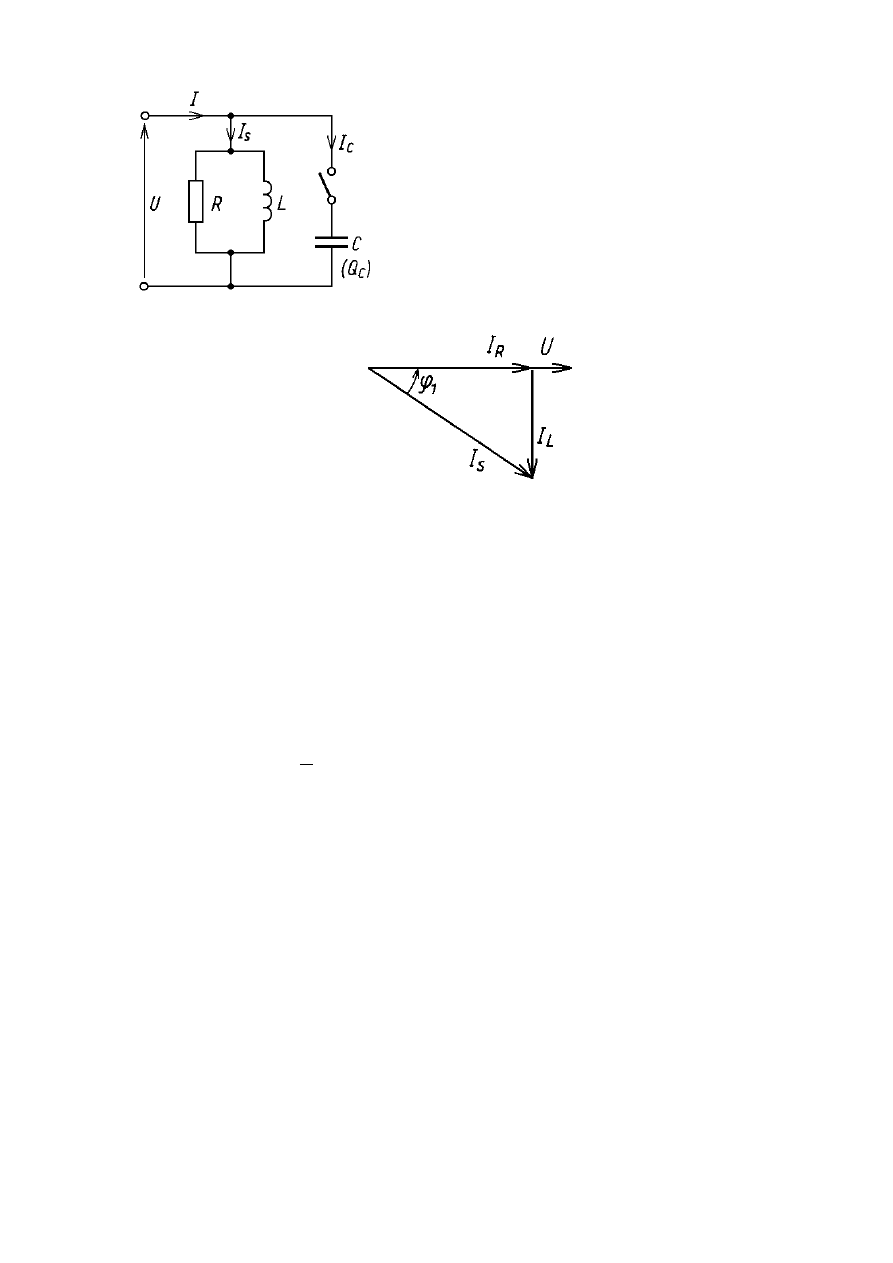
zasilania. Schemat układu zastępczego silnika oraz wykres
wektorowy dla układu nie skompensowanej mocy biernej
przedstawione są poniżej:

Moc w obwodach prądu sinusoidalnie zmiennego

Na podstawie wykresu wektorowego określamy wartość

prądu I

R

:

I

R

= I

S

cos



1

Dołączenie baterii kondensatorów powoduje pojawienie

się w układzie nowego prądu I

C

, przepływającego przez

gałąź z pojemnością. Prąd ten wyprzedza napięcie
zasilające o kąt

2



, posiada również przeciwny zwrot do

prądu I

L

. Możliwe jest takie dobranie układu

kondensatorów, aby prąd I

C

był równy prądowi I

L

(kompensacja idealna) lub mniejszy od niego.

W pierwszym ze wspomnianych przypadków oba

prądy posiadają wartości równe:

I

C

= I

L

= I

S

sin



1

W

przypadku

tym

moc

bierna

baterii

kondensatorów:

Q

C

= UI

C

= UI

S

sin



1

Sytuacji takiej odpowiada pojemność:

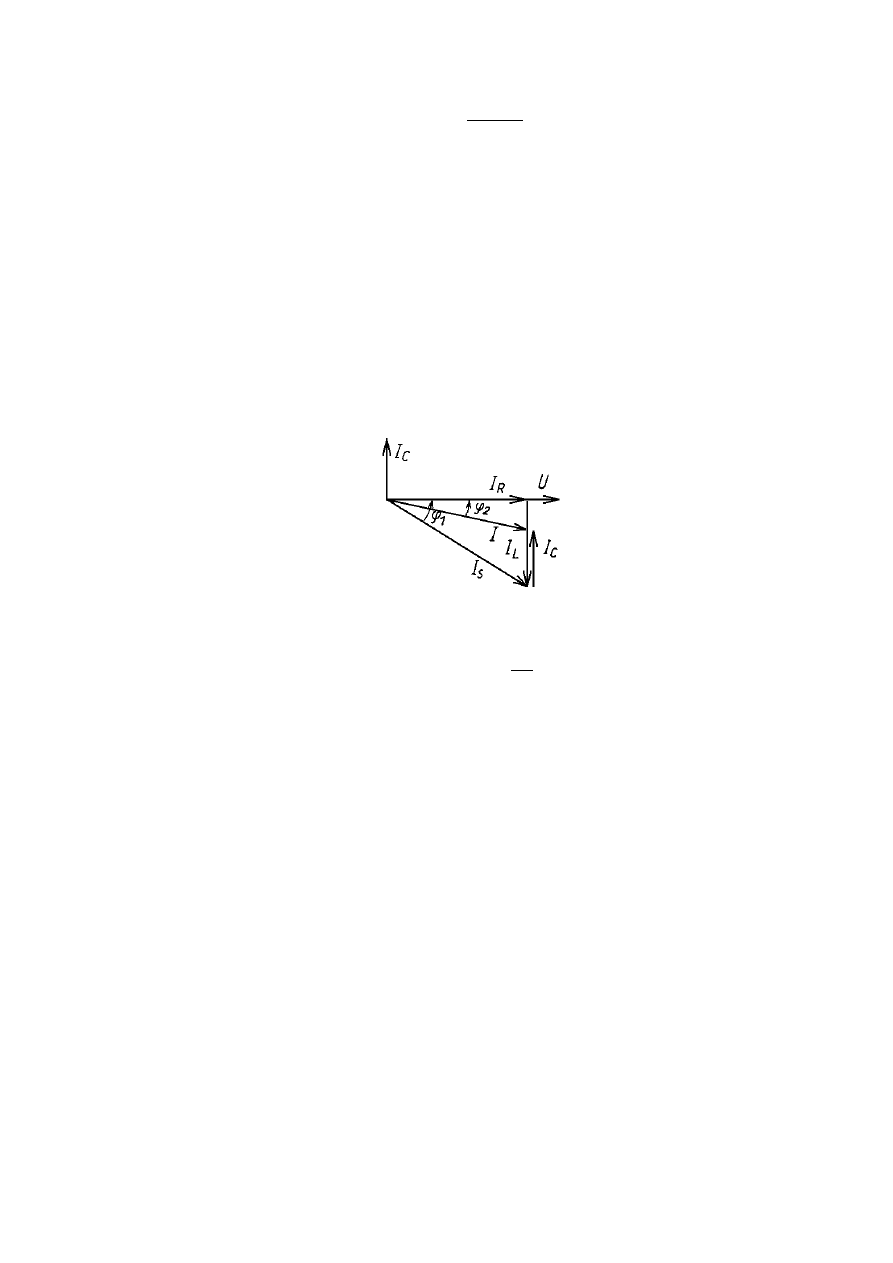
Moc w obwodach prądu sinusoidalnie zmiennego

C =

2

U

Q

C



Przy tak dobranej pojemności moc bierna indukcyjna

zostaje w całości skompensowana mocą bierną
pojemnościową i wypadkowy współczynnik mocy równy
jest jedności. Całkowity prąd dopływający do układu (silnik
i bateria) jest równy prądowi I

R

.

Druga z rozpatrywanych sytuacji opiera się na

założeniu, że prąd I

C

jest mniejszy od I

L

, co przedstawia

poniższy rysunek:

Na podstawie wykresu wektorowego można zapisać:

I

C

= I

R

tg



1



I

R

tg



2

=

U

P

( tg



1



tg



2

)

Dla prądu obliczonego powyżej moc baterii

kondensatorów:

Q

C

= UI

C

= P( tg



1



tg



2

)

Pojemność baterii kondensatorów jest obliczana z

tego samego wzoru, który stosowany był przy
kompensacji idealnej.