Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

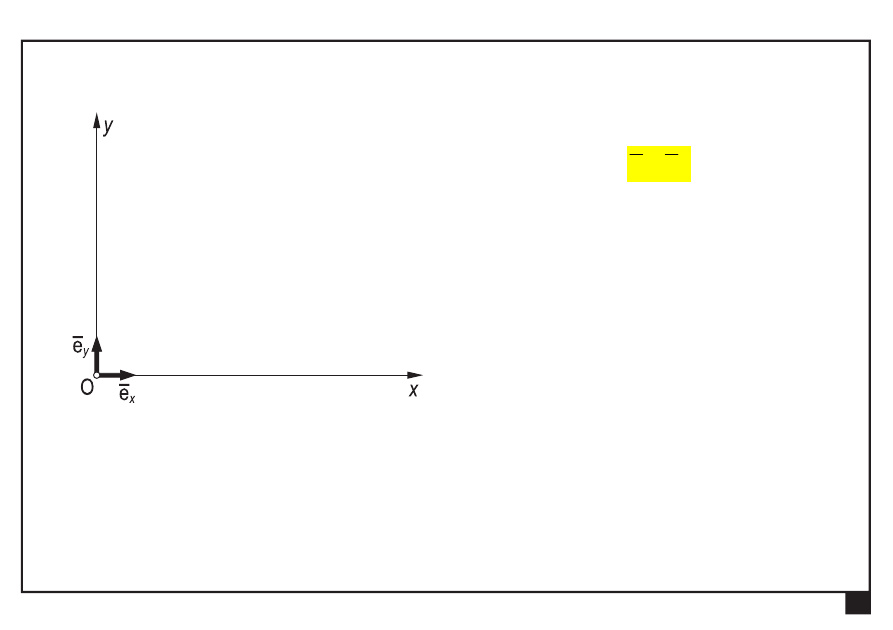
Opis analityczny wielkości podstawowych

wersory

y

x

e

,

e

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Opis analityczny wielkości podstawowych

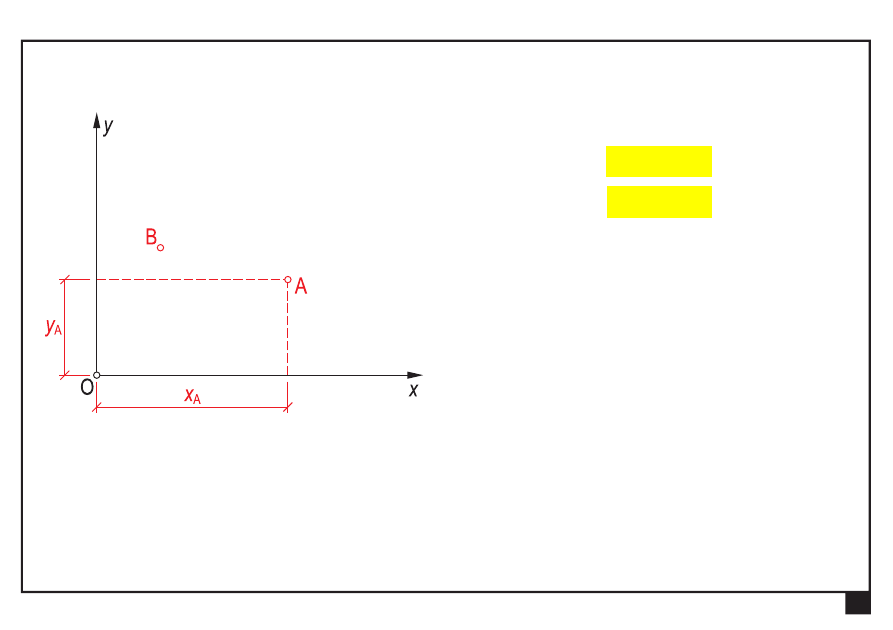
współrzędne punktów

)

,

(

A

A

A

y

x

)

,

(

B

B

B

y

x

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

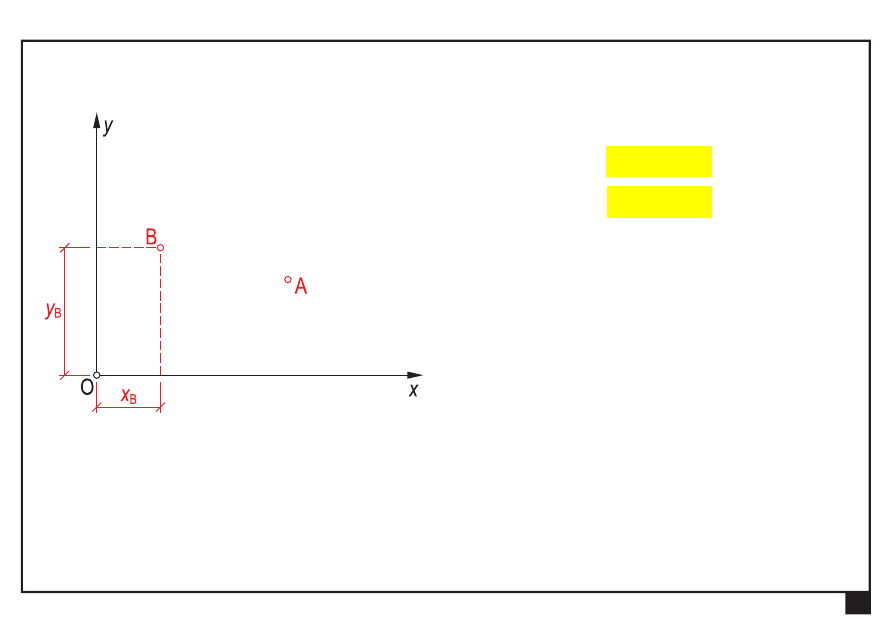
Opis analityczny wielkości podstawowych

współrzędne punktów

)

,

(

A

A

A

y

x

)

,

(

B

B

B

y

x

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Opis analityczny wielkości podstawowych

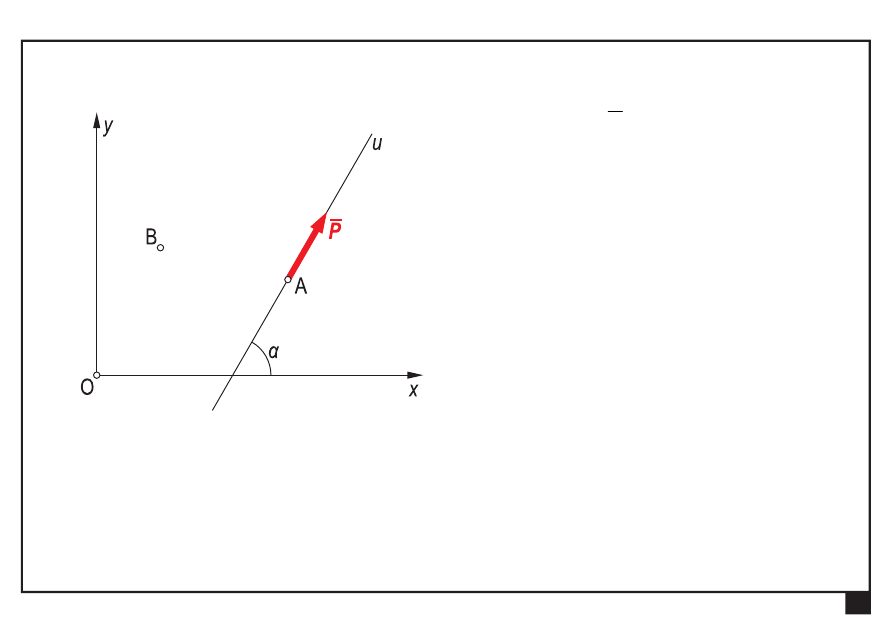
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Opis analityczny wielkości podstawowych

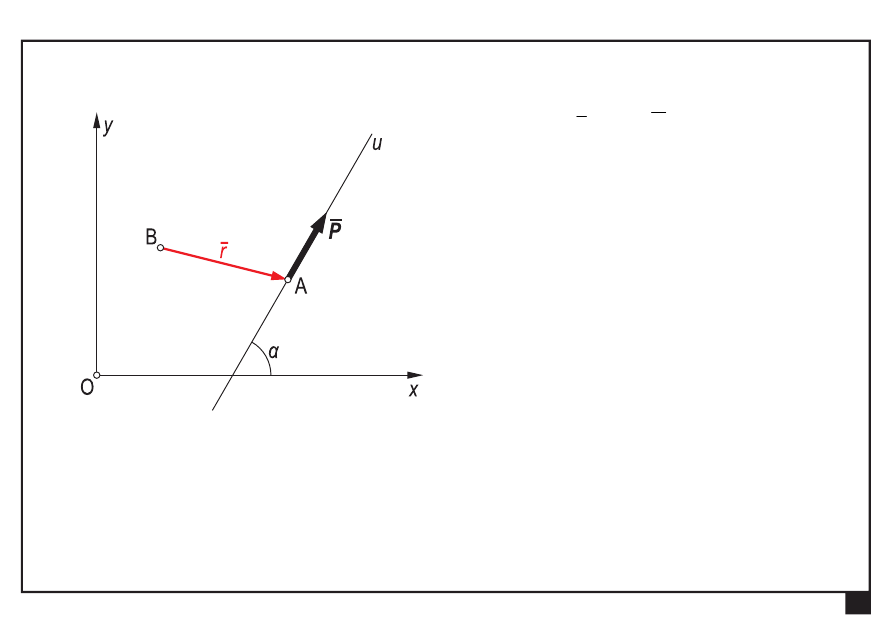
wektor siły

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Opis analityczny wielkości podstawowych

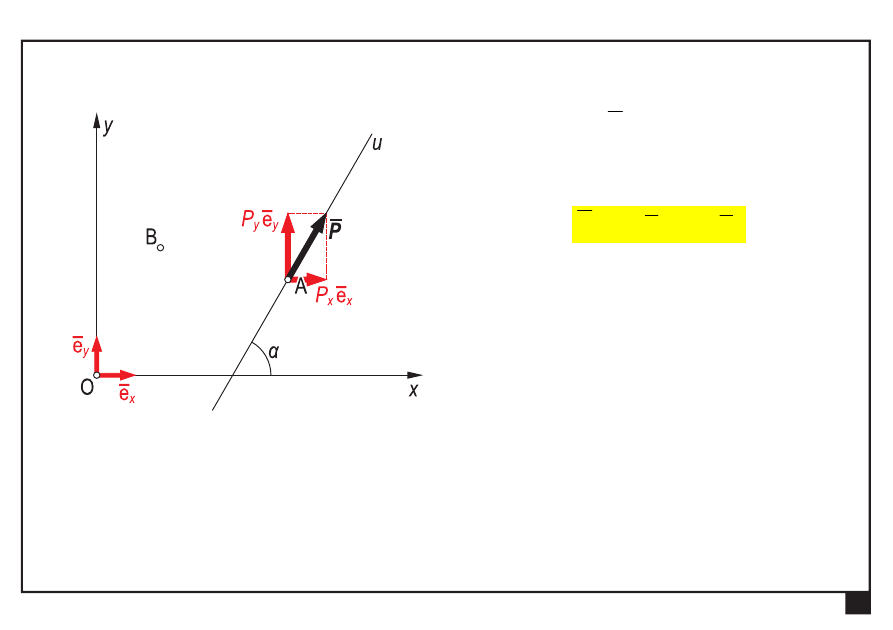
wektor siły

P

— zapis analityczny

y

y

x

x

P

P

P

e

e

+

=

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Opis analityczny wielkości podstawowych

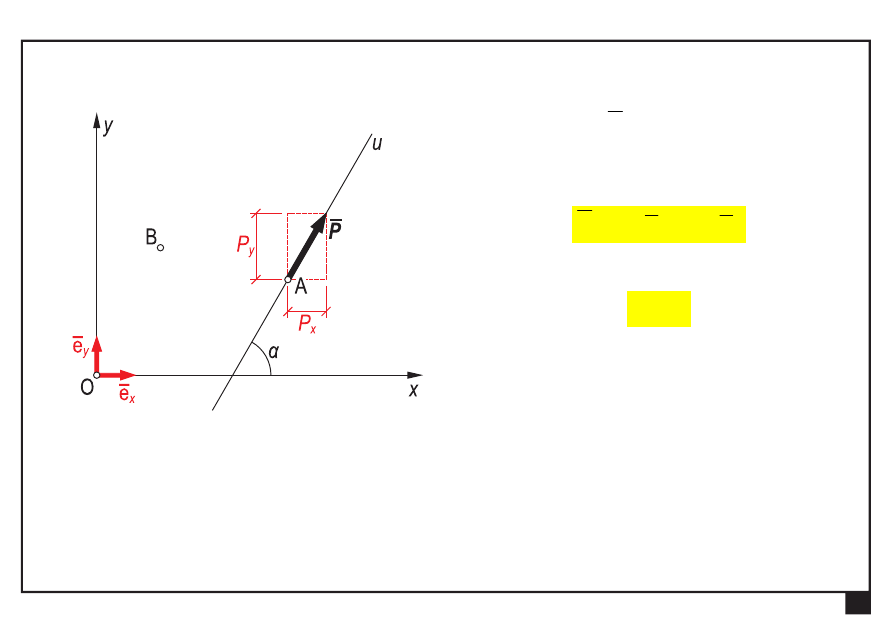
wektor siły

P

— zapis analityczny

y

y

x

x

P

P

P

e

e

+

=

— składowe siły [N]

y

x

P

P ,

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Opis analityczny wielkości podstawowych

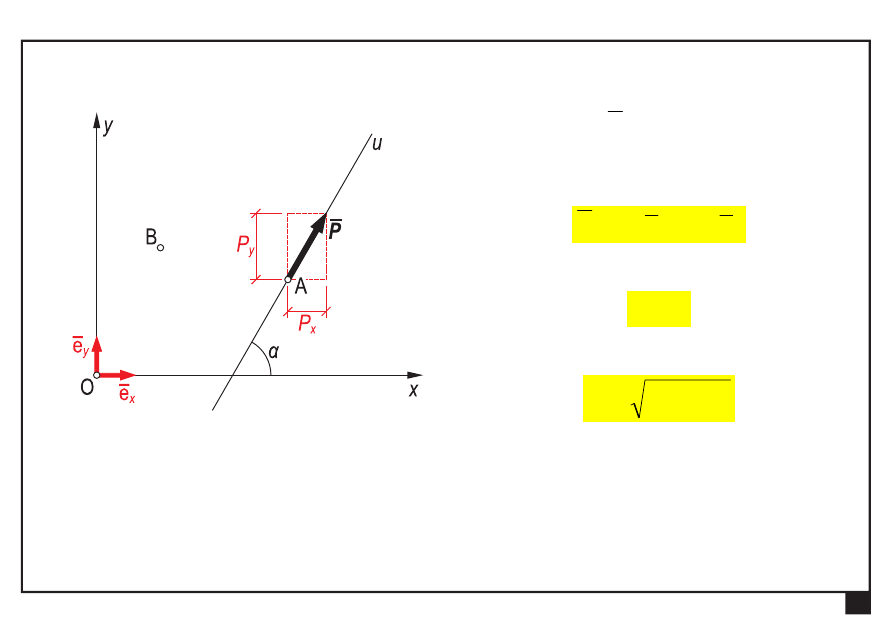
wektor siły

P

— zapis analityczny

y

y

x

x

P

P

P

e

e

+

=

— składowe siły [N]

y

x

P

P ,

— moduł (wartość) siły [N]

2

2

y

x

P

P

P

+

=

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Opis analityczny wielkości podstawowych

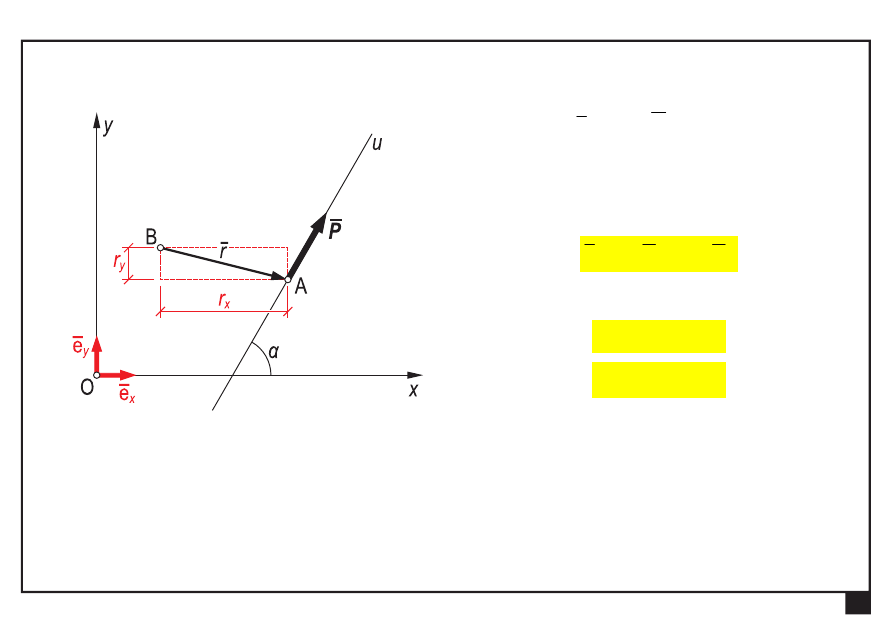
promień

r

siły

P

względem punktu B

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Opis analityczny wielkości podstawowych

promień

r

siły

P

względem punktu B

— zapis analityczny

y

y

x

x

r

r

r

e

e

+

=

— składowe promienia [m]

B

A

x

x

r

x

−

=

B

A

y

y

r

y

−

=

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Opis analityczny wielkości podstawowych

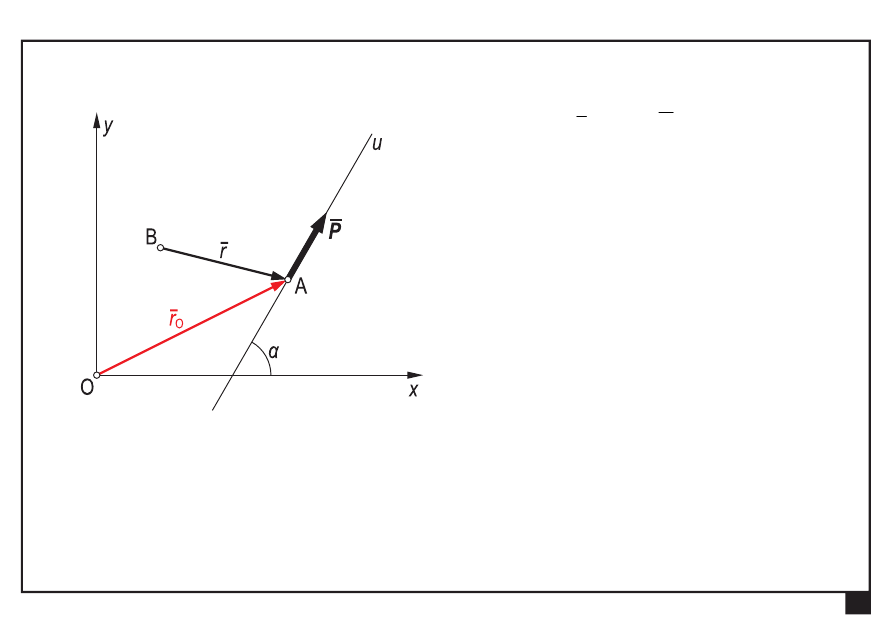
promień

O

r siły P

względem punktu O

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Opis analityczny wielkości podstawowych

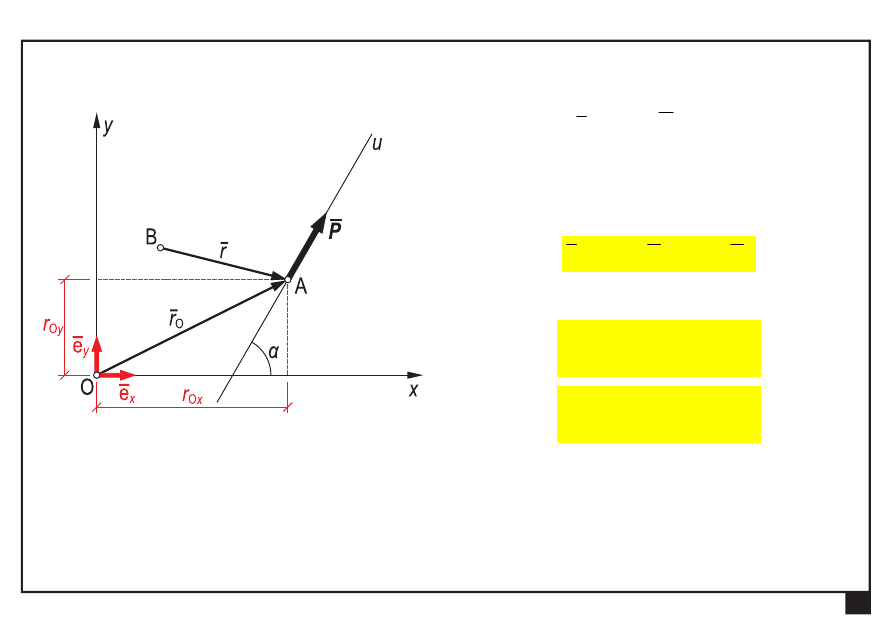
promień

O

r siły P

względem punktu O

— zapis analityczny

y

y

x

x

r

r

r

e

e

O

O

O

+

=

— składowe promienia [m]



A

0

O

A

O

x

x

x

r

x

=

−

=

=



A

0

O

A

O

y

y

y

r

y

=

−

=

=

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

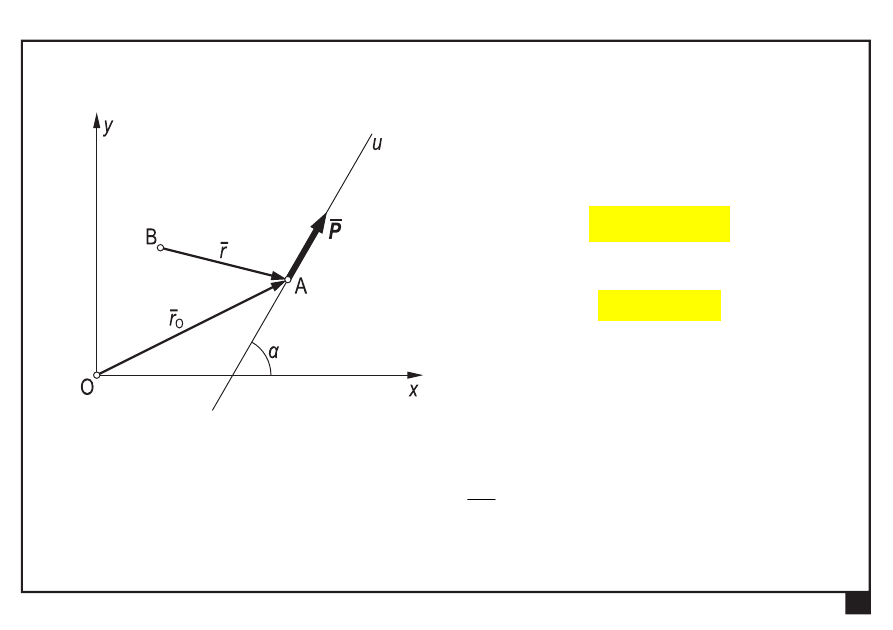
Opis analityczny wielkości podstawowych

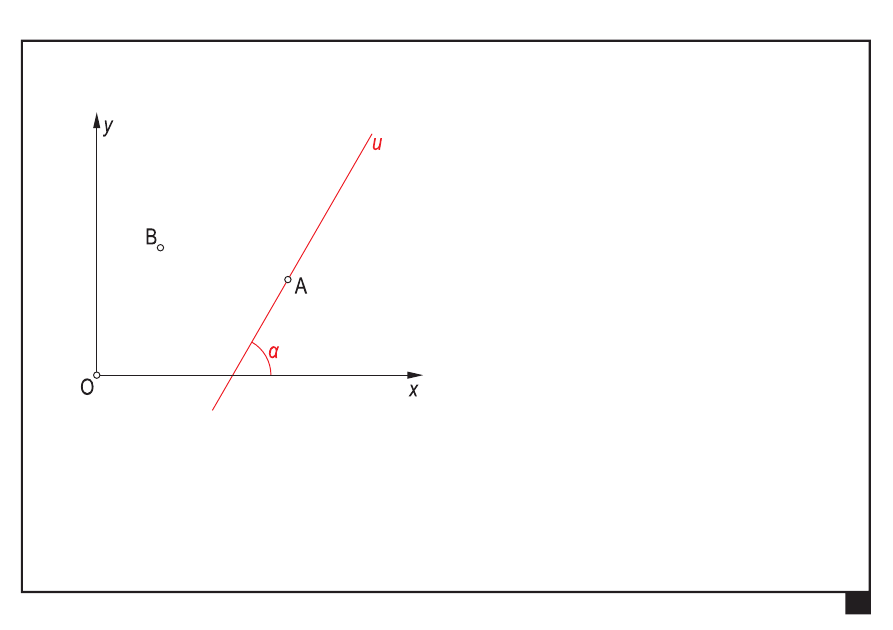
siła na płaszczyźnie opisana jest
przez

4 wielkości

A

A

,

,

,

y

x

P

P

y

x

lub

A

A

,

,

,

y

x

P

α

α

— kąt kierunkowy prostej działania siły

x

y

P

P

=

α

tg

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

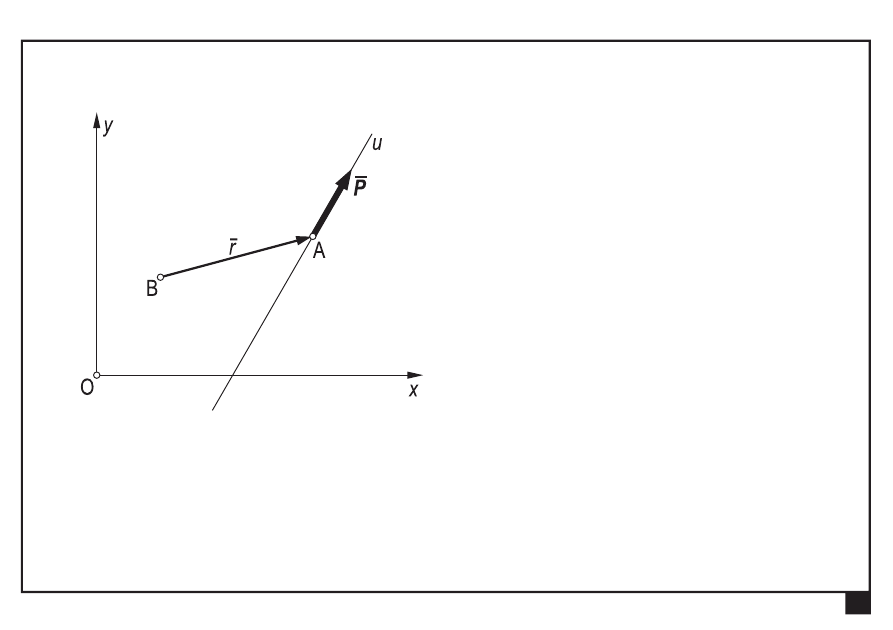
Moment siły względem punktu

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

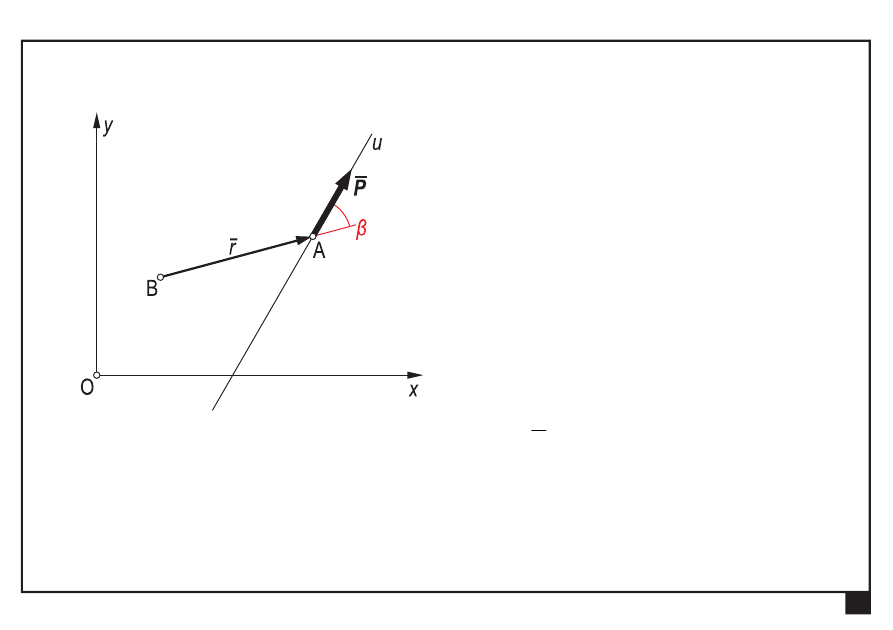
Moment siły względem punktu

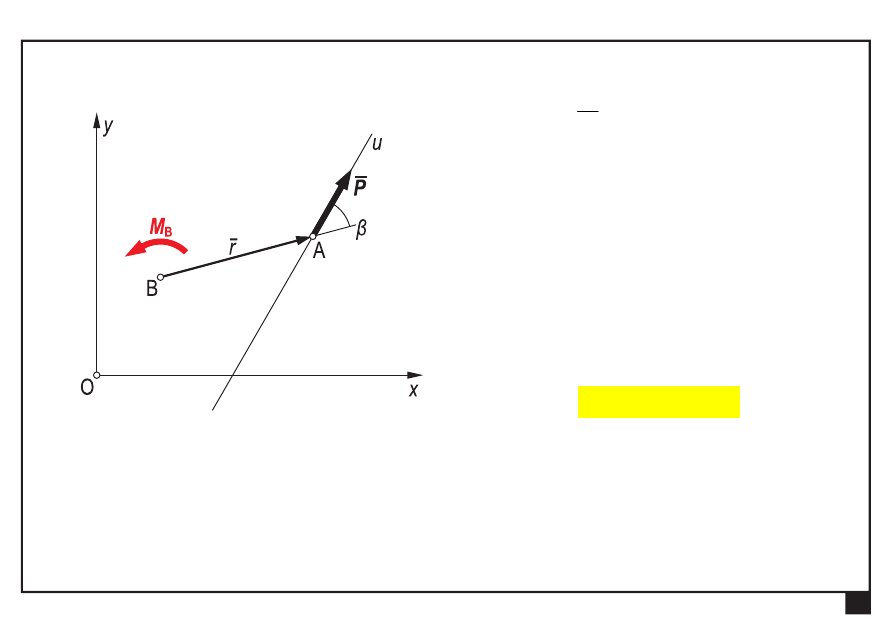
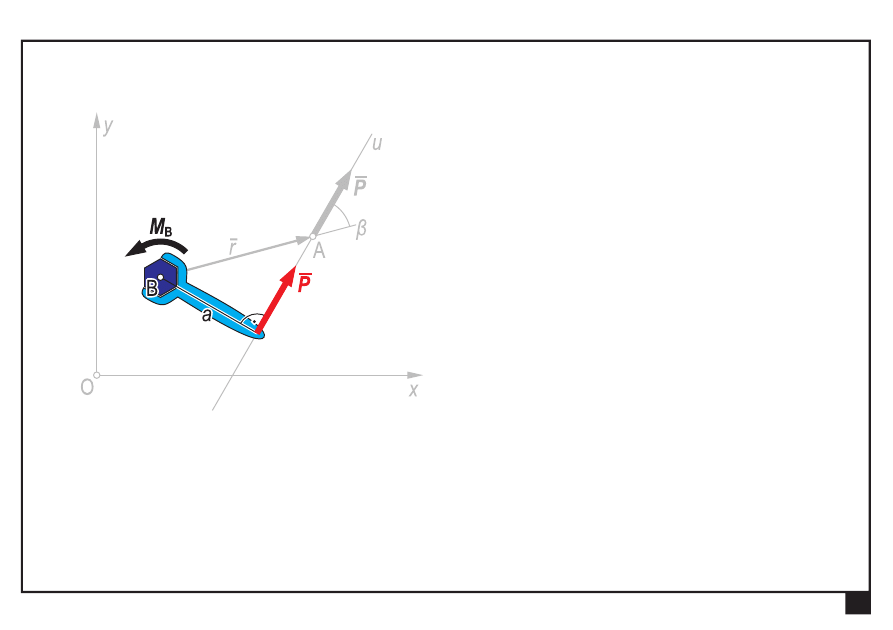
β

— kąt pomiędzy prostą działania siły P a promieniem siły

względem punktu B

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

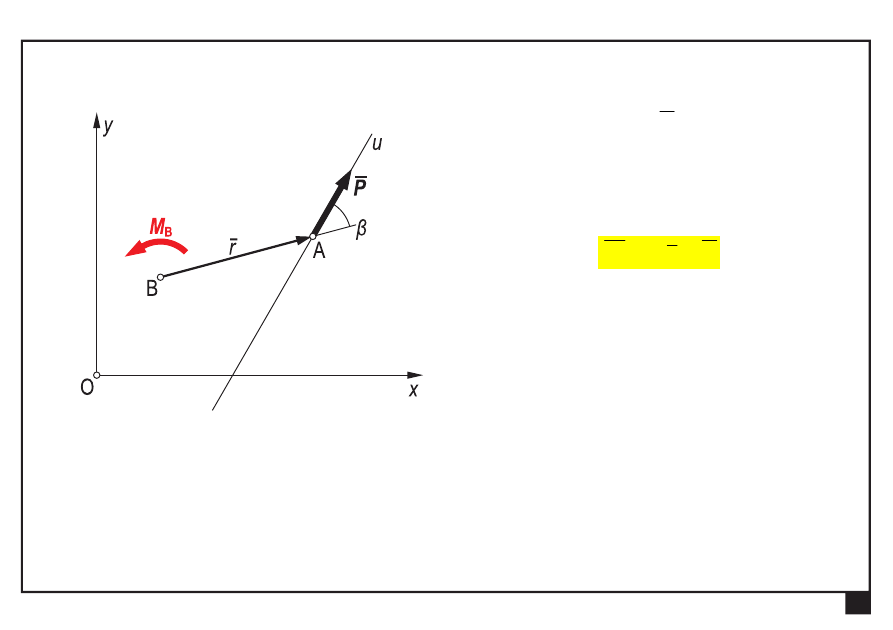
Moment siły względem punktu

momentem siły P
względem punktu B nazywamy

wektor

P

r

M

×

=

B

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Moment siły względem punktu

moment

B

M

— wektor prostopadły

do płaszczyzny y

x

— zwrot wektora zgodny

z regułą prawej dłoni

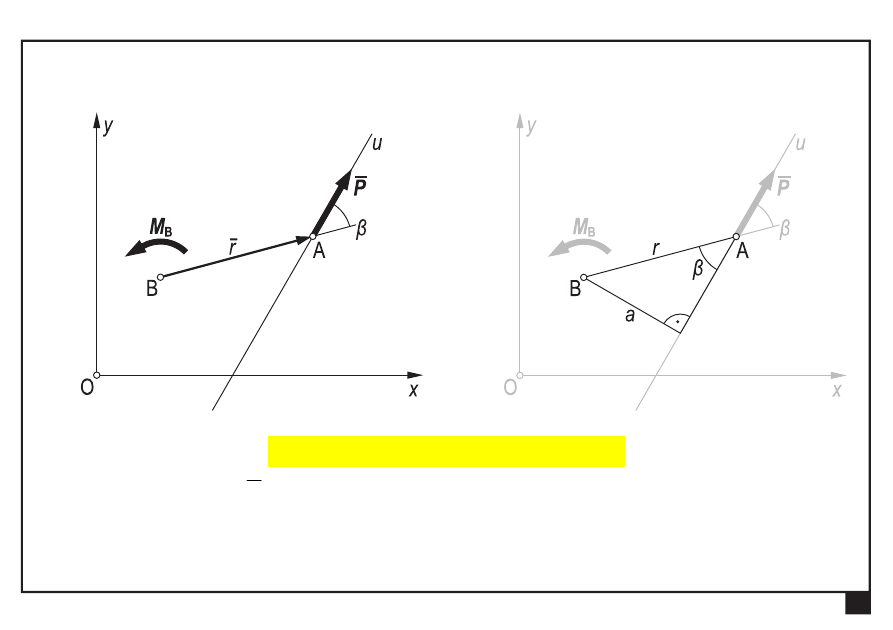
— wartość (moduł) wektora

β

P

r

M

sin

B

=

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Moment siły względem punktu

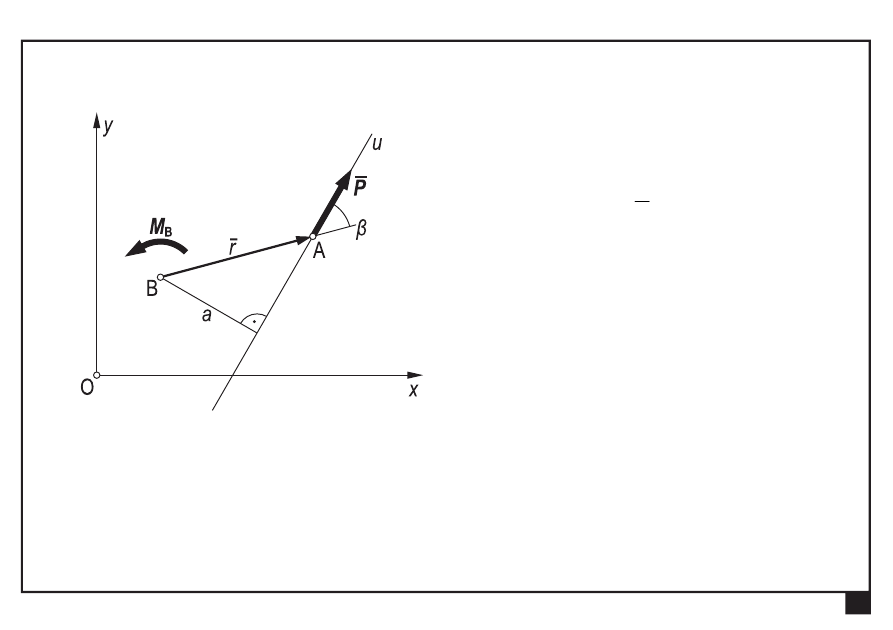
a

P

β

r

P

β

P

r

M

=

=

=

)

sin

(

sin

B

a — ramię siły P względem punktu B (

najmniejsza odległość

prostej działania siły od punktu B

)

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Moment siły względem punktu

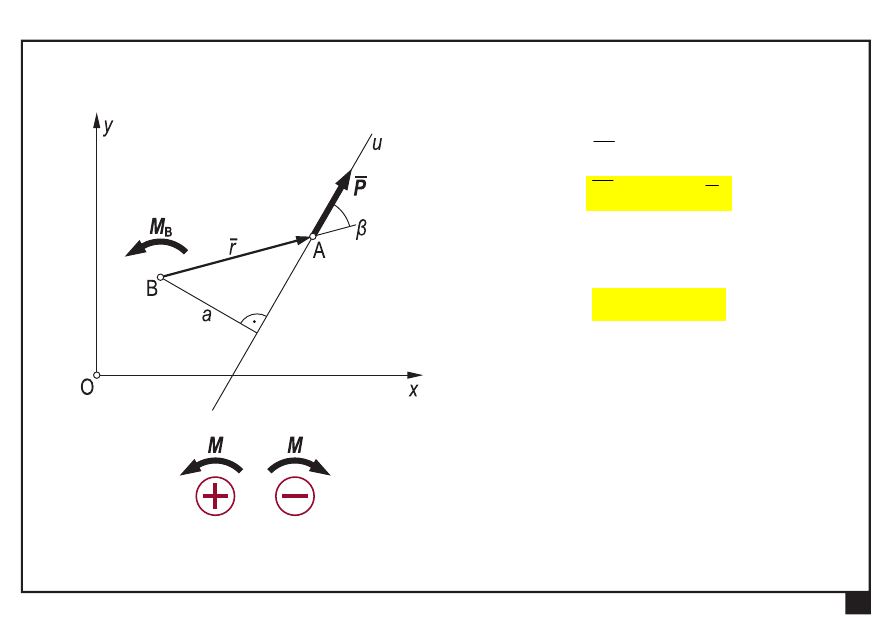
Wartość momentu

B

M

nie zależy

od wyboru

punktu A na prostej
działania siły P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Moment siły względem punktu

Zapis analityczny
momentu

B

M

z

z

M

M

e

B

B

=

— składowa momentu

a

P

M

z

±

=

B

—

znak (+)

odpowiada

momentowi działającemu
przeciwnie do obrotu
wskazówek zegara

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Moment siły względem punktu

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

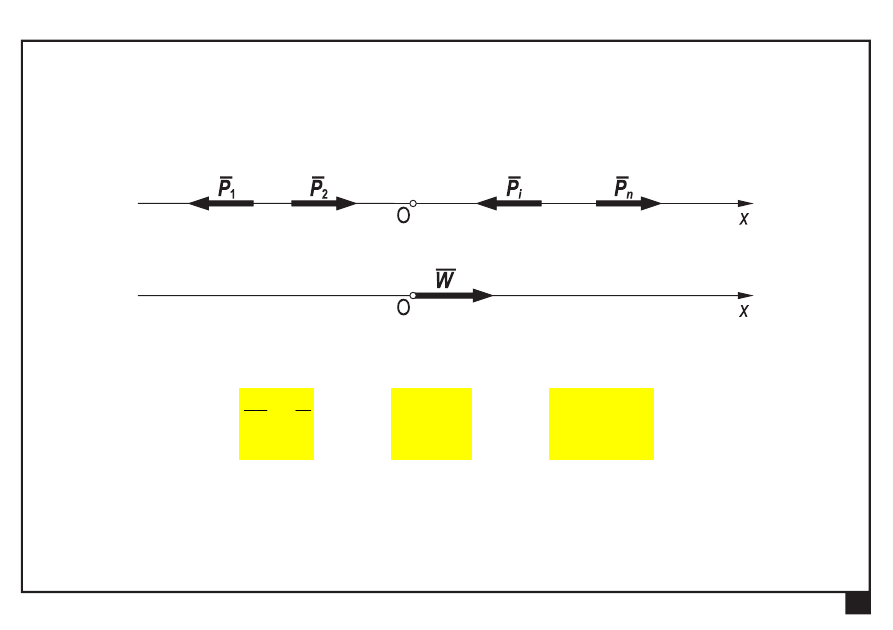
Kolinearny (współliniowy) układ sił

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Kolinearny (współliniowy) układ sił

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

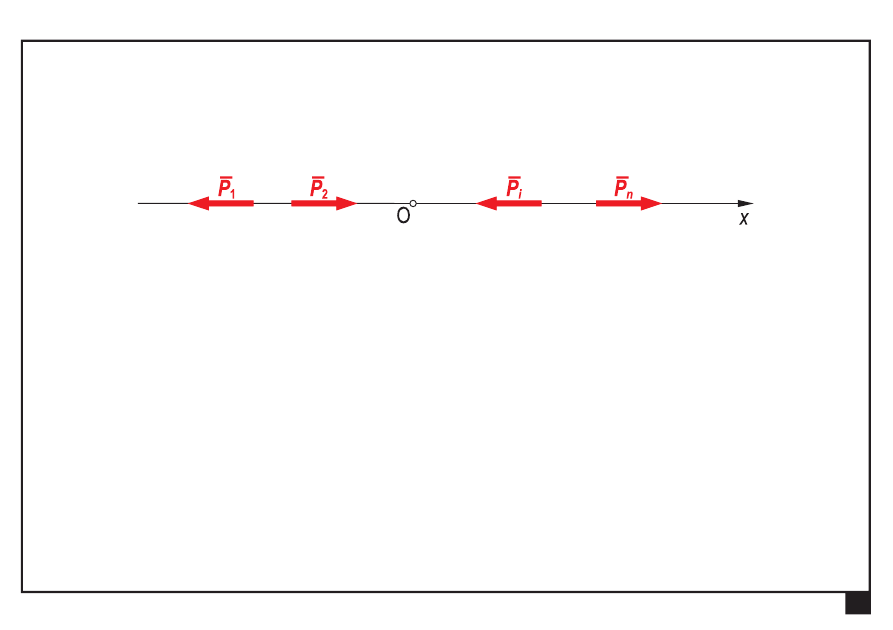
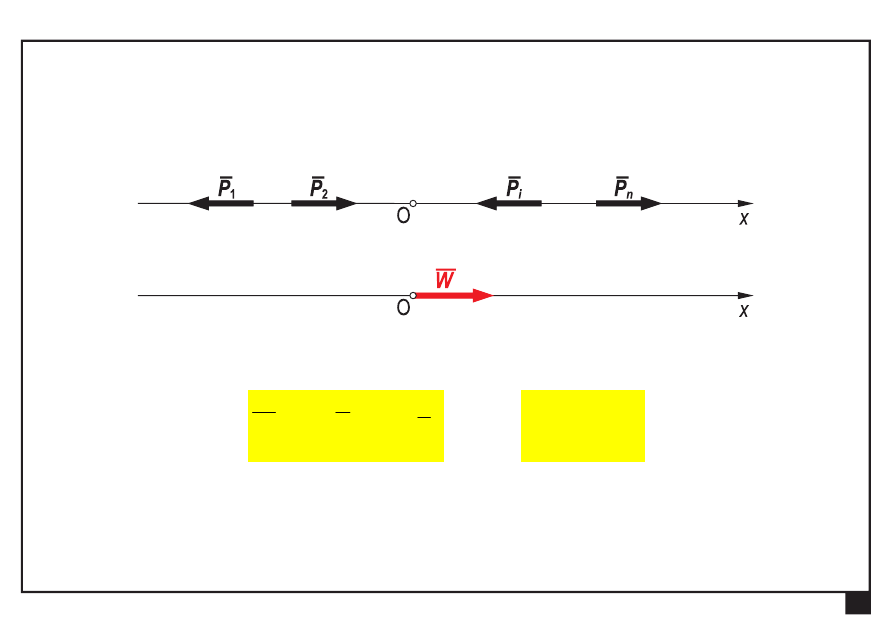
Kolinearny (współliniowy) układ sił



redukuje się do

wypadkowej

, kolinearnej z układem sił

x

x

n

i

i

W

P

W

e

1

=

=



=



=

=

n

i

ix

x

P

W

1

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

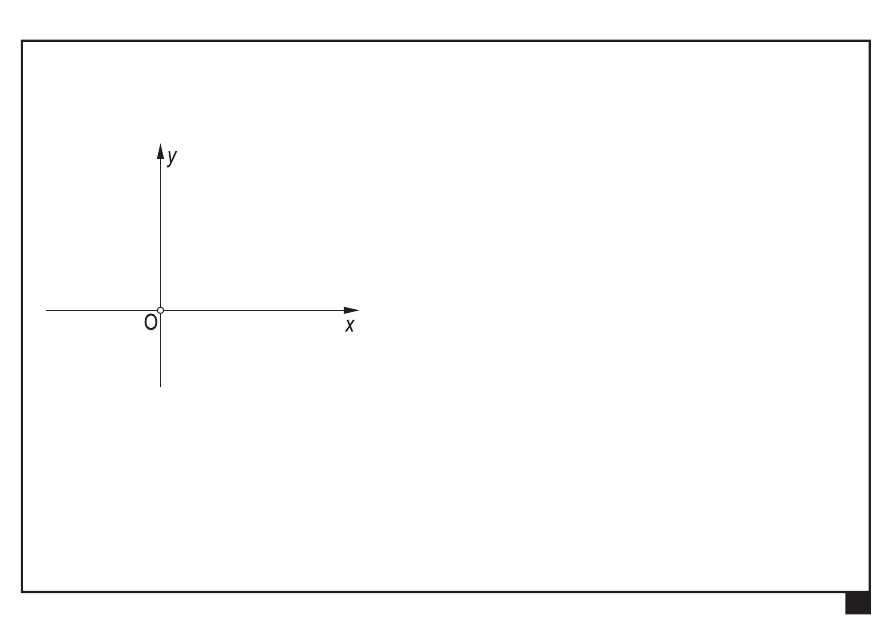
Kolinearny (współliniowy) układ sił



jest w równowadze, jeśli wypadkowa jest równa zeru

0

=

W

0

=

x

W

0

1

=



=

n

i

ix

P

Suma rzutów sił na oś x jest równa zeru

1 RRS (jedno równanie równowagi statycznej)

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

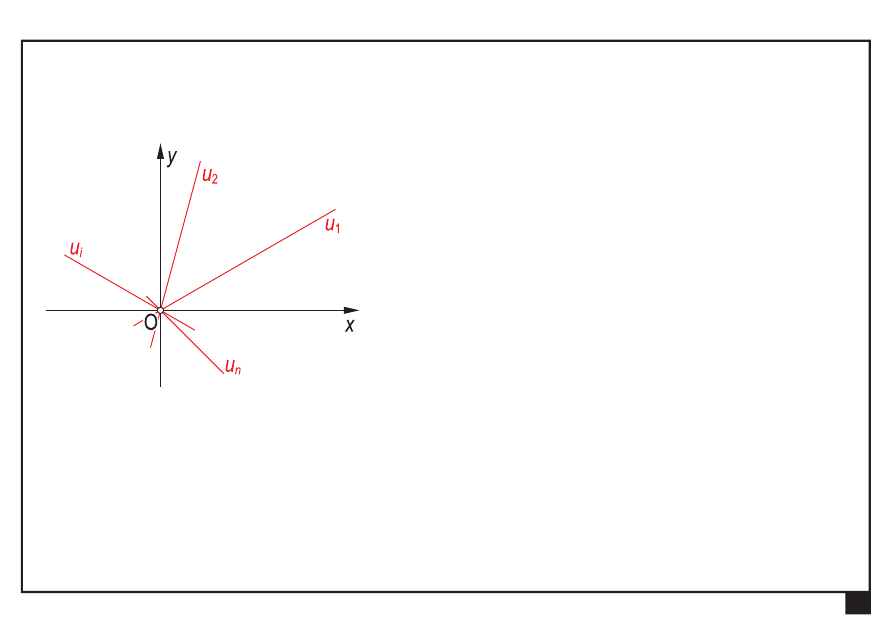
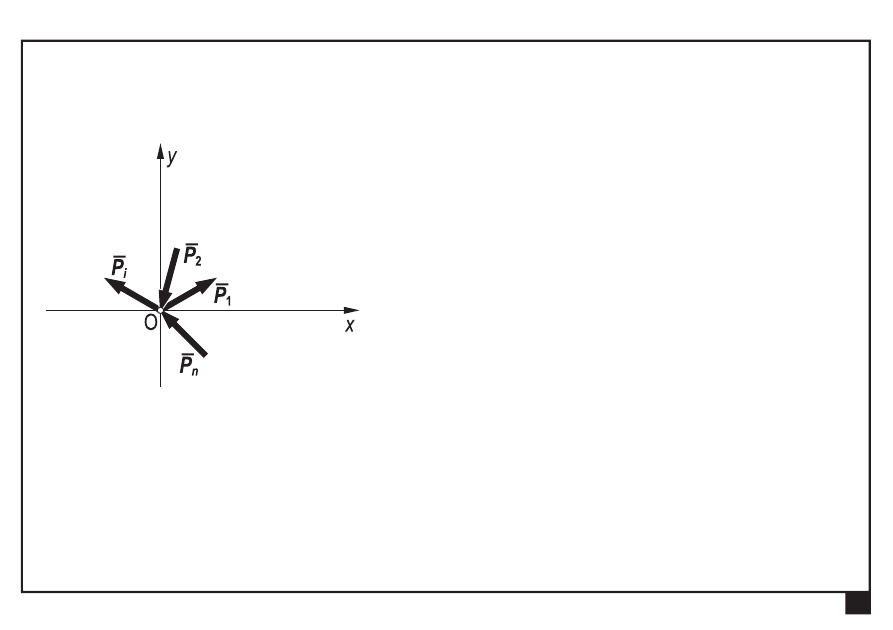
Zbieżny układ sił

linie działania sił przecinają się w jednym punkcie

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

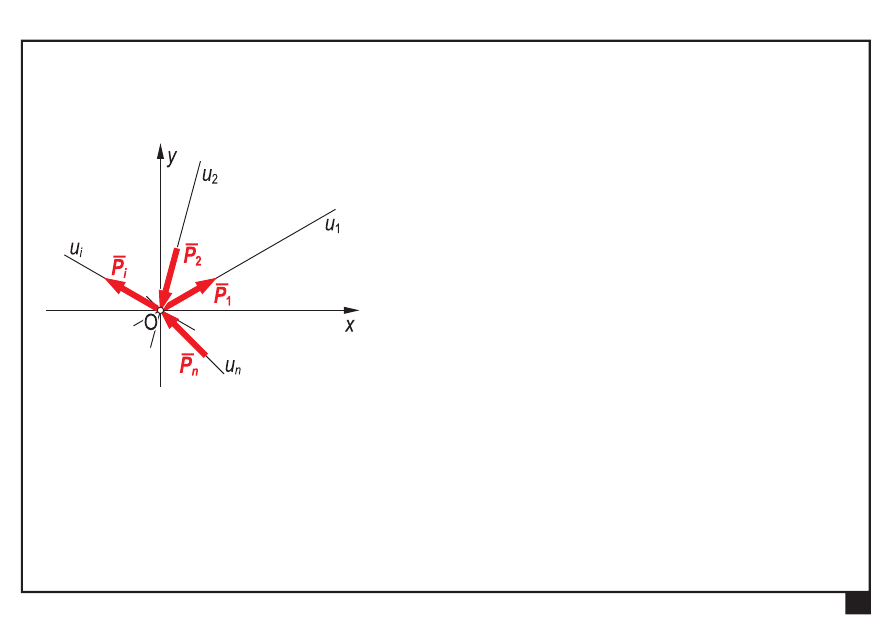
Zbieżny układ sił

linie działania sił przecinają się w jednym punkcie

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

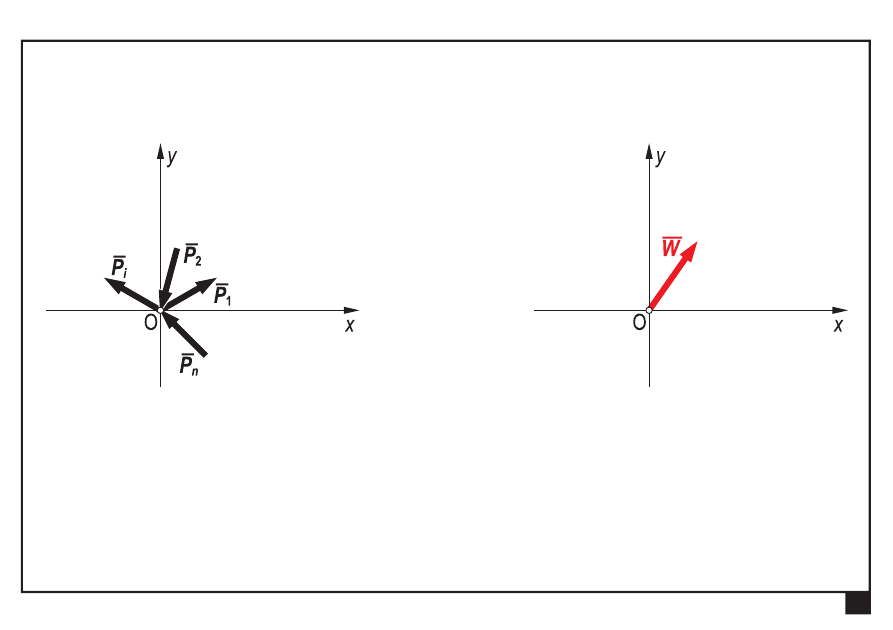
Zbieżny układ sił

rozpatruje się w początku układu współrzędnych xy

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił



redukuje się do

wypadkowej

o prostej działania

przechodzącej przez punkt zbieżności układu

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

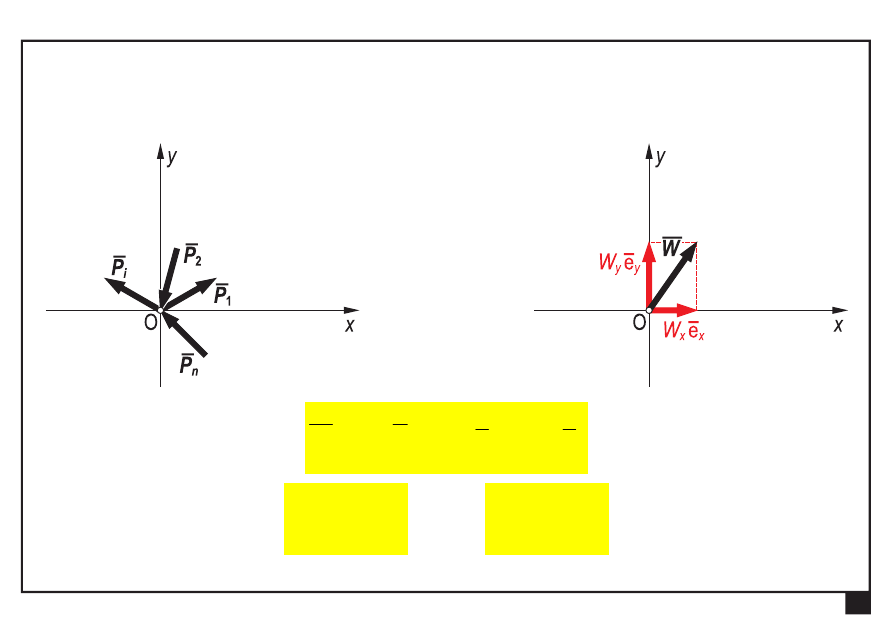
Zbieżny układ sił



y

y

x

x

n

i

i

W

W

P

W

e

e

1

+

=

=



=



=

=

n

i

ix

x

P

W

1



=

=

n

i

iy

y

P

W

1

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

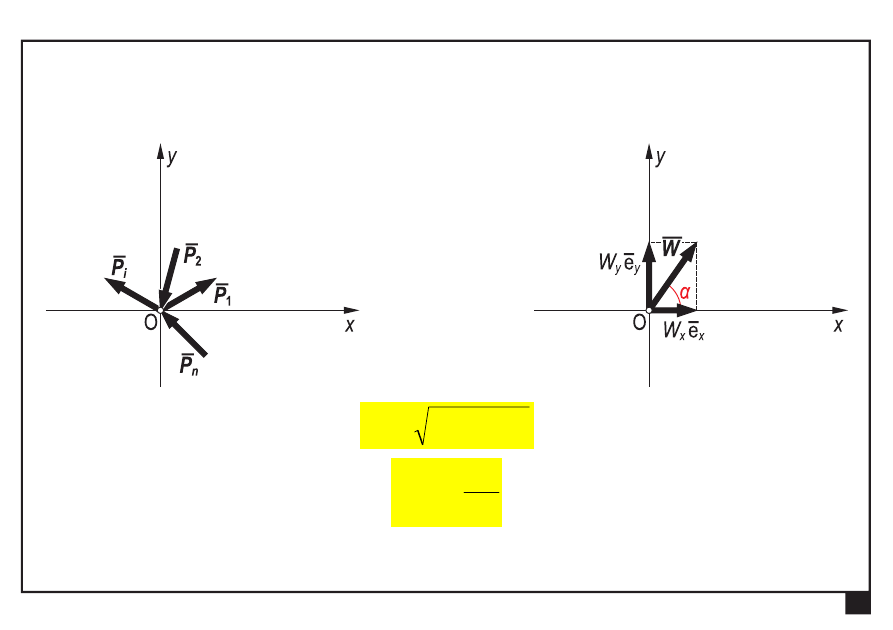
Zbieżny układ sił



2

2

y

x

W

W

W

+

=

x

y

W

W

=

α

tg

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
jest w równowadze, jeśli wypadkowa jest równa zeru

0

=

W

0

=

x

W



0

1

=



=

n

i

ix

P

Suma rzutów sił na oś x jest równa zeru

0

=

y

W



0

1

=



=

n

i

iy

P

Suma rzutów sił na oś y jest równa zeru

2 RRS (dwa równania równowagi statycznej)

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
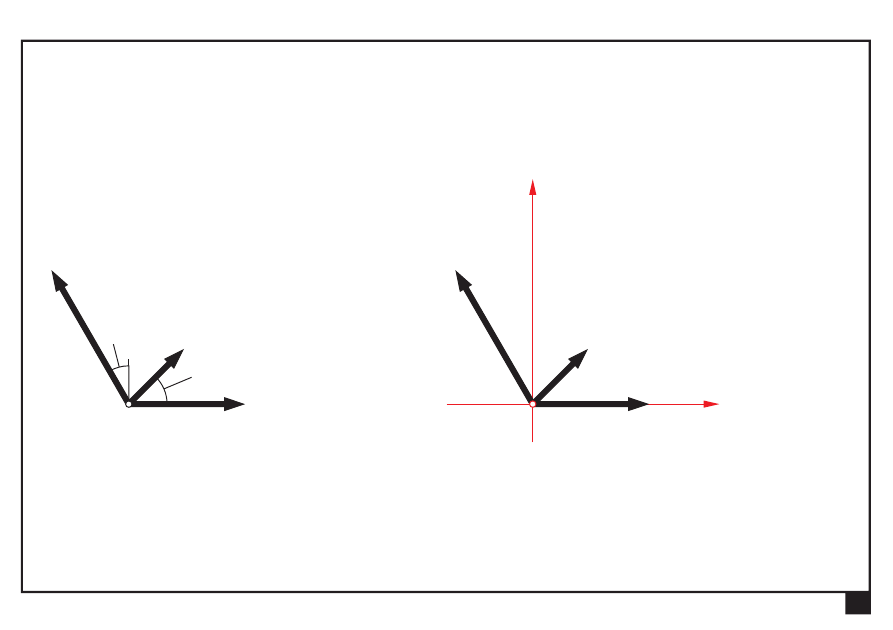
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
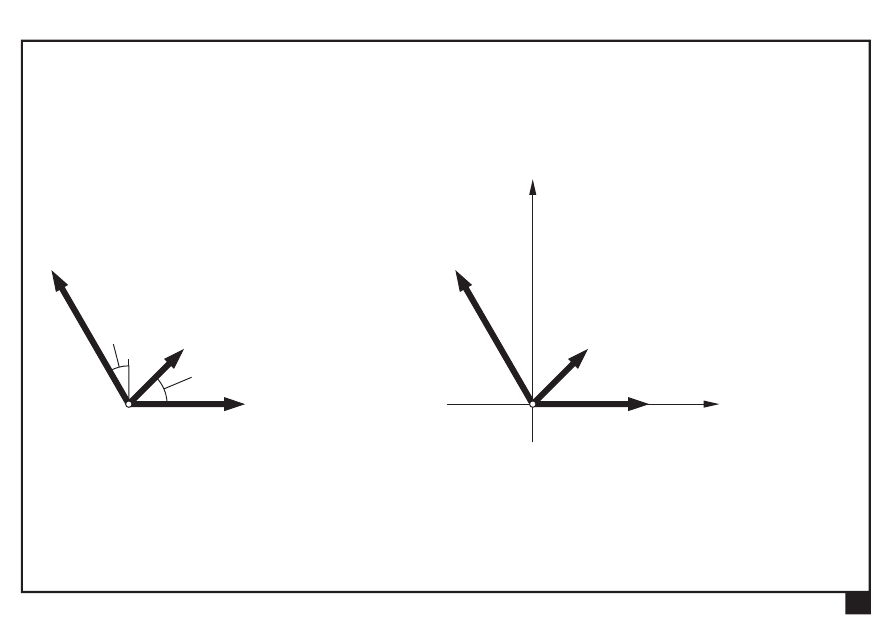
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

3P

4P

x

y

O

2P

Układ współrzędnych Oxy obieramy w punkcie zbieżności

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

3P

4P

x

y

O

2P

Wyznaczamy składowe W

x

, W

y

wypadkowej W:

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

3P

4P

x

y

O

2P

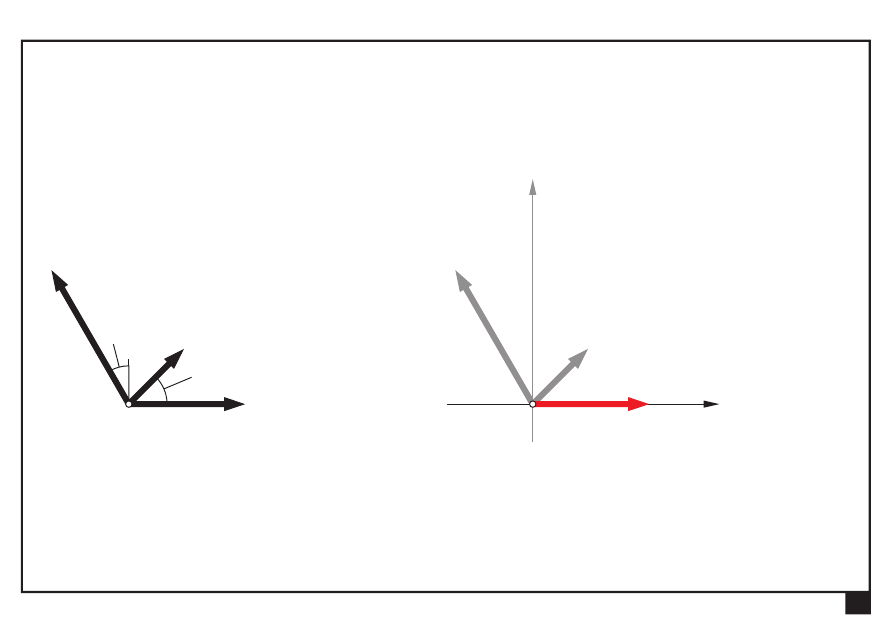
Wyznaczamy składowe W

x

, W

y

wypadkowej W:

= Σ

= 3

x

ix

W

P

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

3P

4P

45°

x

y

2 cos45°

P

O

2P

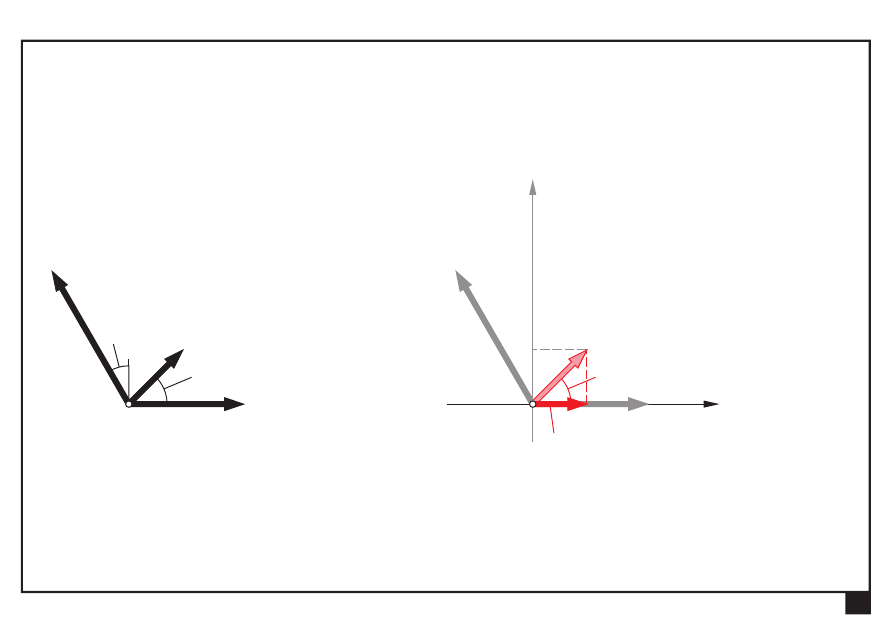
Wyznaczamy składowe W

x

, W

y

wypadkowej W:

= Σ

=

+

°

3

2 cos 45

x

ix

W

P

P

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
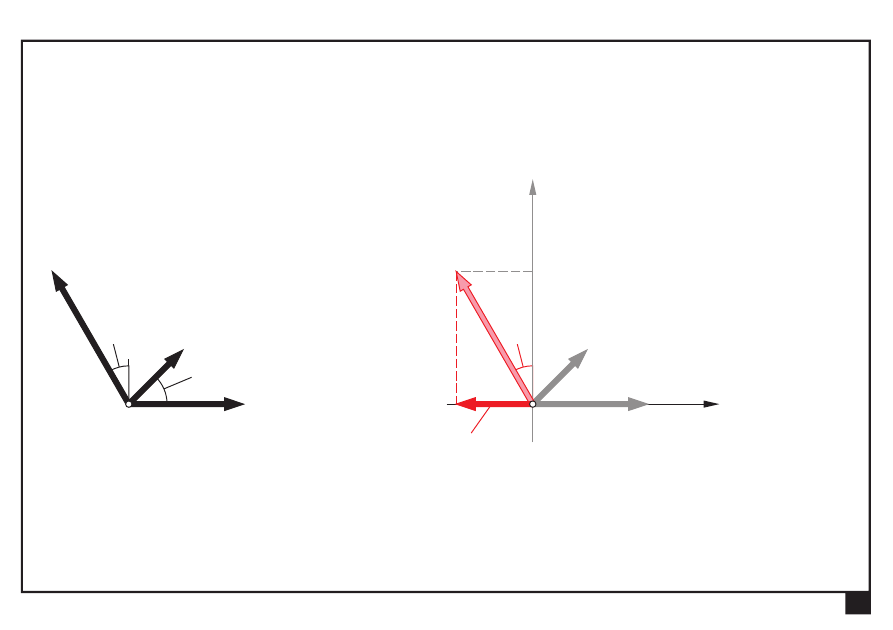
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

3P

4P

x

y

O

4 sin30°

P

30°

2P

Wyznaczamy składowe W

x

, W

y

wypadkowej W:

= Σ

=

+

° −

° =

3

2 cos 45

4 sin30

x

ix

W

P

P

P

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
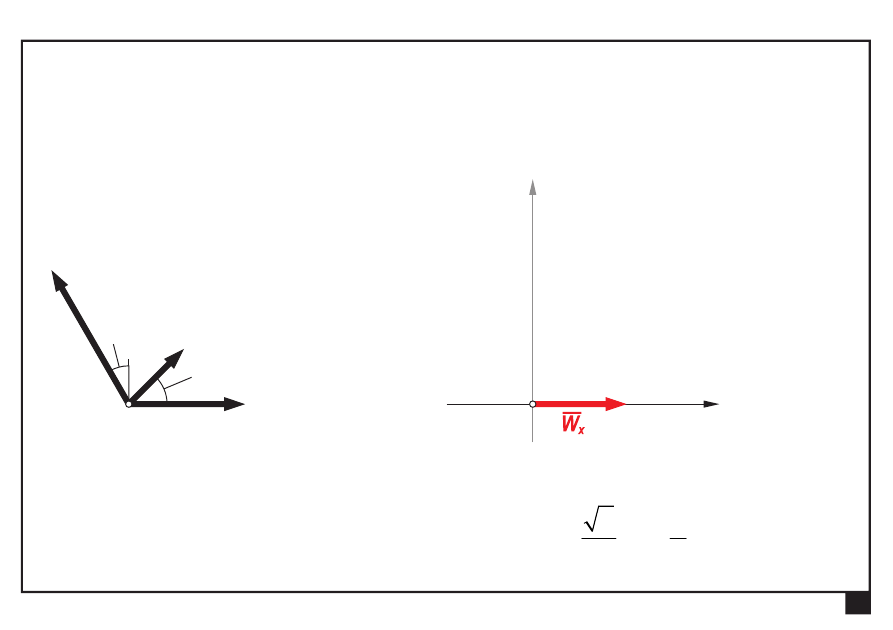
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

x

y

O

Wyznaczamy składowe W

x

, W

y

wypadkowej W:





= Σ

=

+

° −

° =

+ ⋅

− ⋅

=









2

1

3

2 cos 45

4 sin30

3 2

4

2

2

x

ix

W

P

P

P

P

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
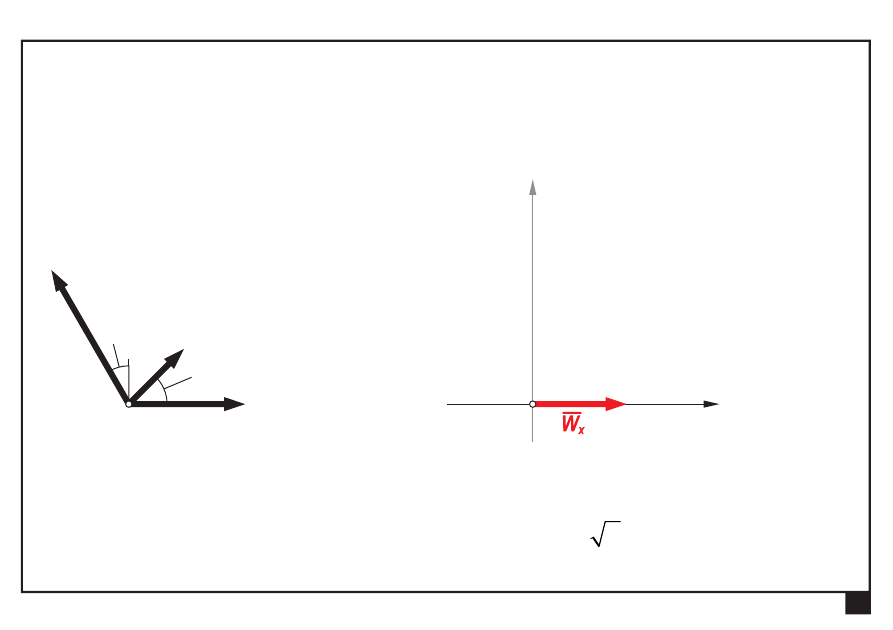
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

x

y

O

Wyznaczamy składowe W

x

, W

y

wypadkowej W:

= Σ

=

+

° −

° =

= +

≈

3

2 cos 45

4 sin30

... (1

2)

2,414

x

ix

W

P

P

P

P

P

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
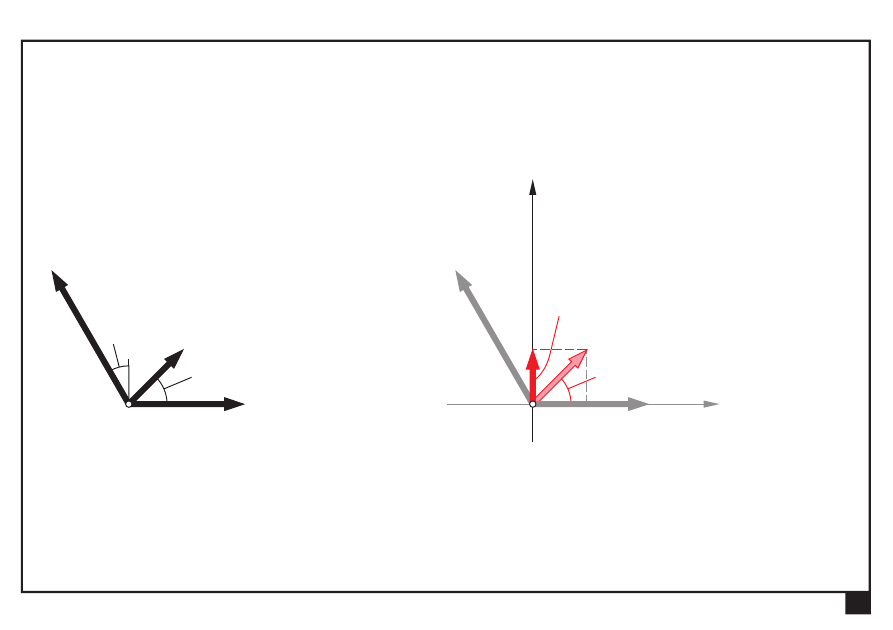
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

3P

4P

45°

x

y

2 sin45°

P

O

2P

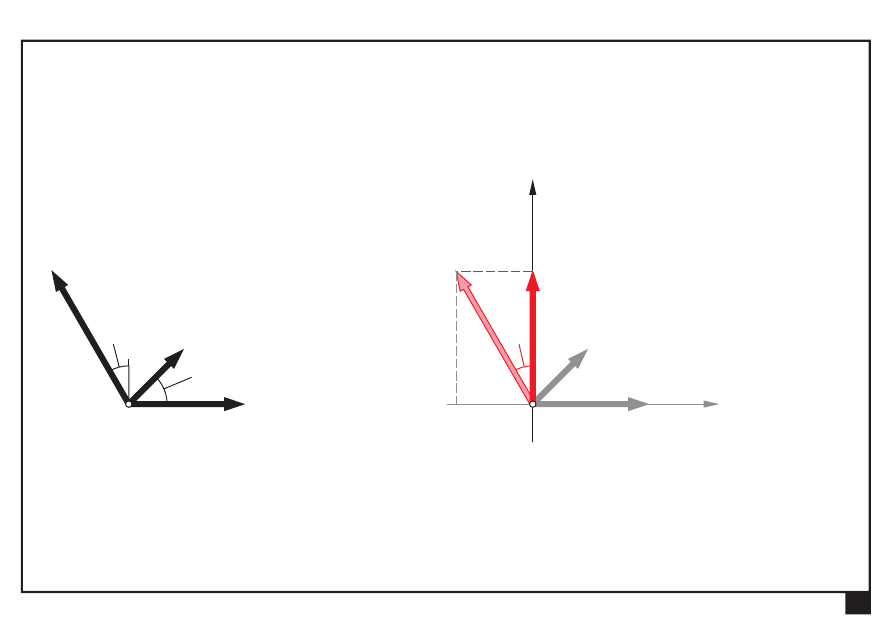
Wyznaczamy składowe W

x

, W

y

wypadkowej W:

= Σ

=

°

2 sin 45

y

iy

W

P

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

3P

4P

x

y

O

30°

2P

4 cos30°

P

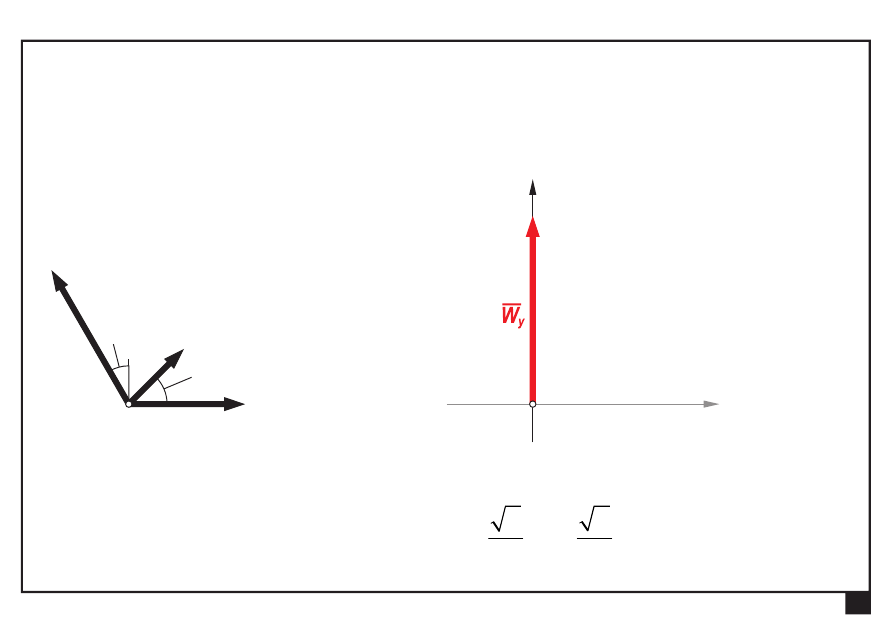
Wyznaczamy składowe W

x

, W

y

wypadkowej W:

= Σ

=

° +

° =

2 sin 45

4 cos 30

y

iy

W

P

P

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

x

y

O

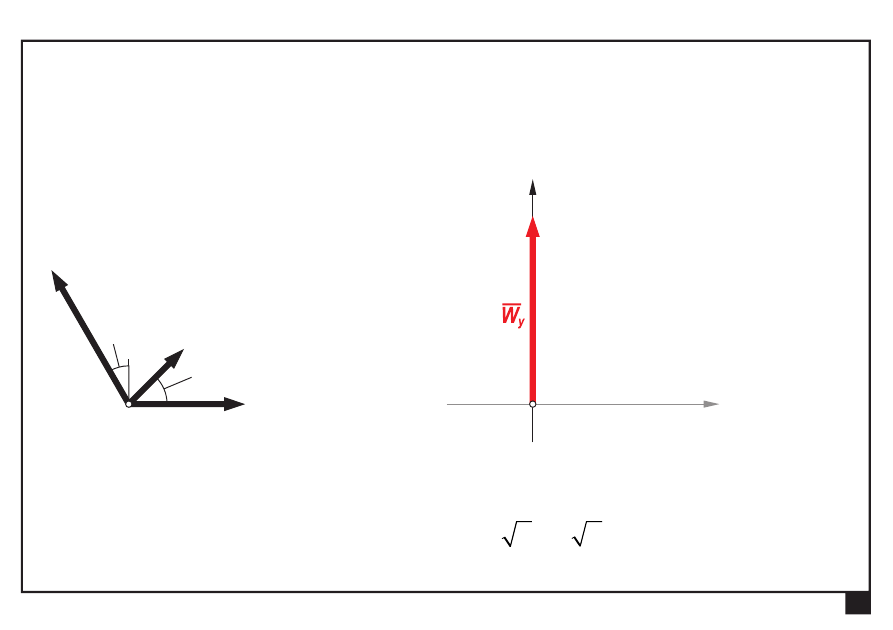
Wyznaczamy składowe W

x

, W

y

wypadkowej W:





= Σ

=

° +

° =

⋅

+ ⋅

=









2

3

2 sin 45

4 cos 30

2

4

2

2

y

iy

W

P

P

P

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

x

y

O

Wyznaczamy składowe W

x

, W

y

wypadkowej W:

= Σ

=

° +

° =

=

+

≈

2 sin 45

4 cos 30

... ( 2 2 3)

4,878

y

iy

W

P

P

P

P

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

x

y

O

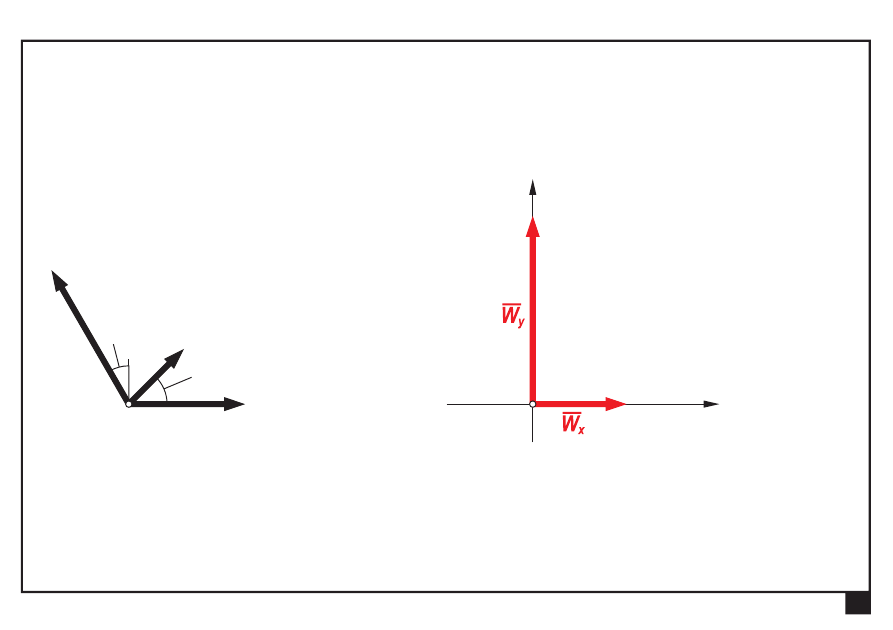
Wyznaczamy składowe W

x

, W

y

wypadkowej W:

≈2,414

x

W

P

,

≈ 4,878

y

W

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

x

y

O

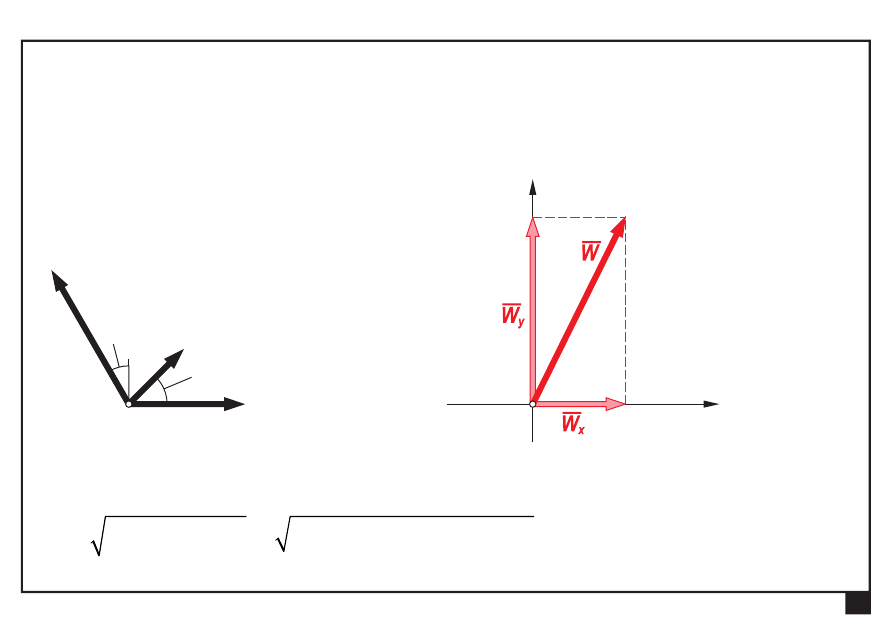
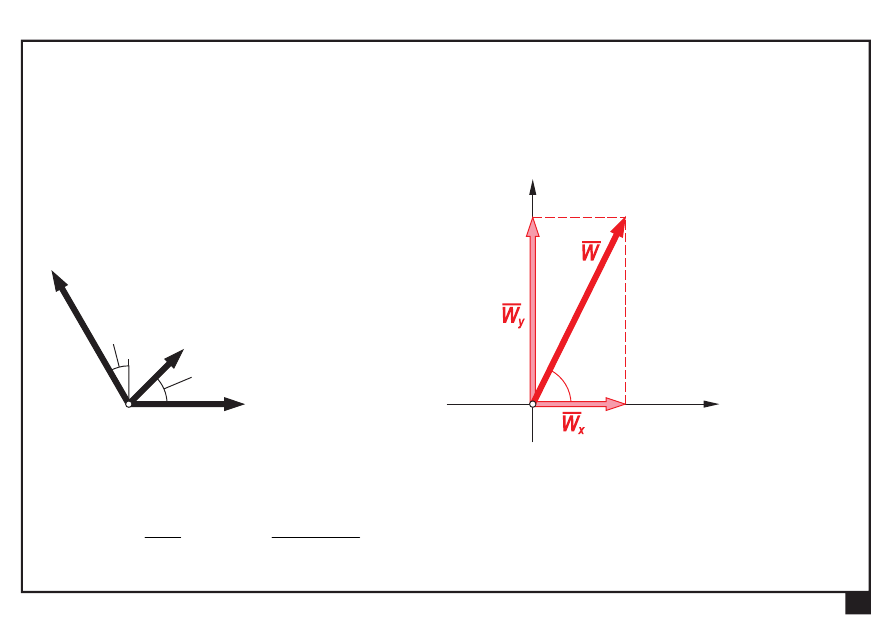
Wyznaczamy wartość (moduł) wypadkowej W:

=

+

=

+

≈

2

2

2

2

(

)

(

)

(2,414 )

(4,878 )

5,443

x

y

W

W

W

P

P

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

x

y

O

α

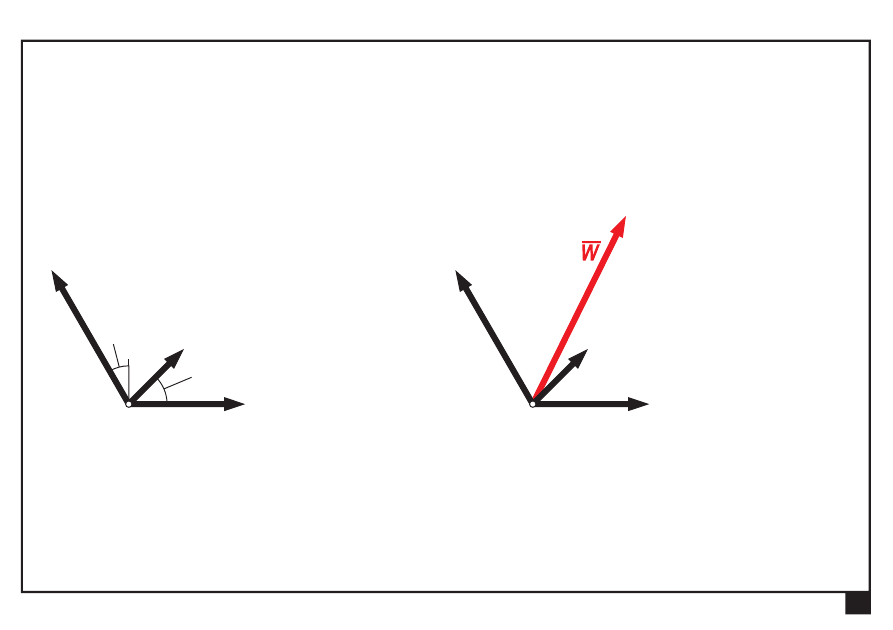
Wyznaczamy kąt nachylenia wypadkowej W:

α

=

=

≈

°

4,878

arctg

arctg

63,67

2,414

y

x

W

P

W

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

3P

4P

2P

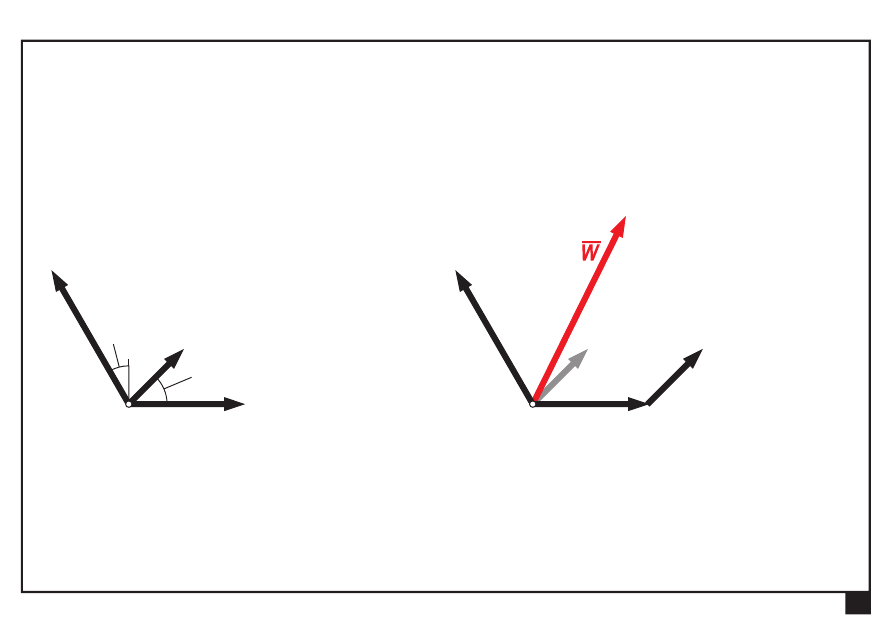
Rozwiązanie końcowe

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

3P

4P

2P

2P

Redukcji można także dokonać w sposób wykreślny

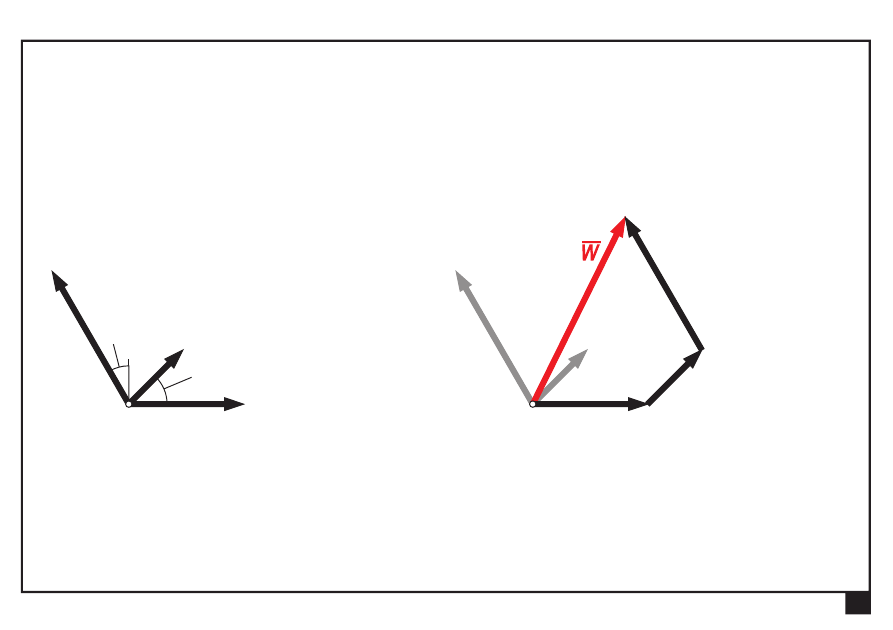
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Zbieżny układ sił
Dokonać redukcji płaskiego zbieżnego układu sił

3P

4P

45°

30°

2P

3P

4P

2P

4P

2P

Redukcji można także dokonać w sposób wykreślny

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił

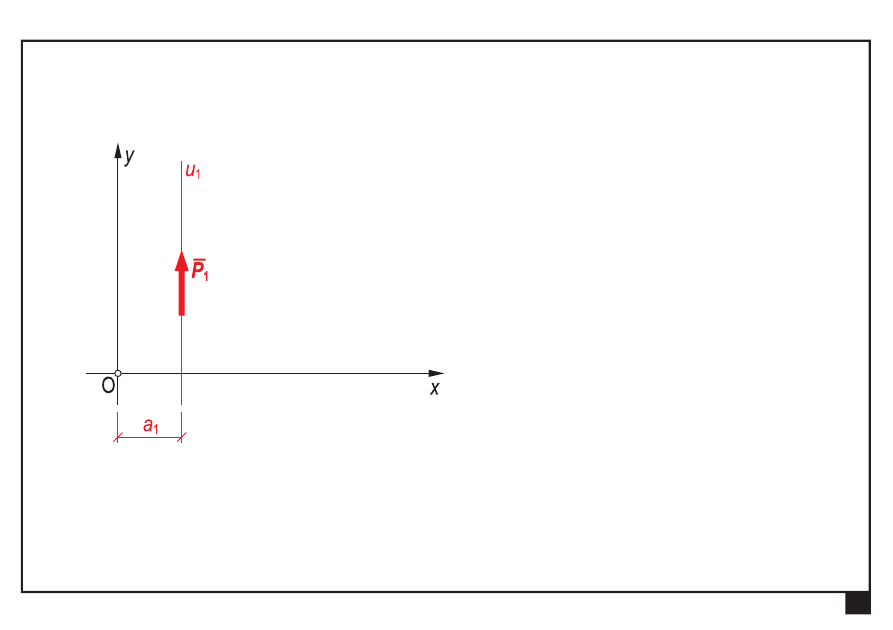
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił

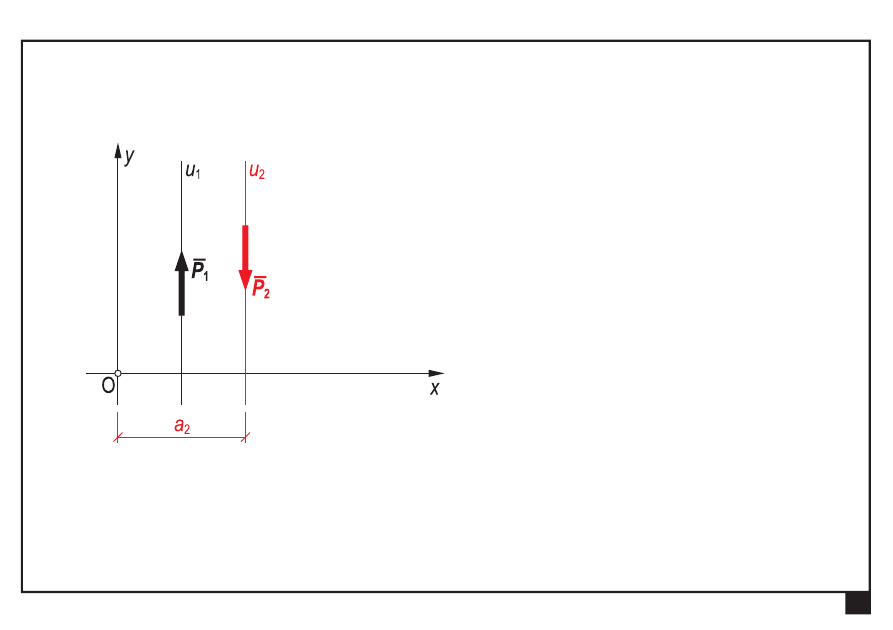
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

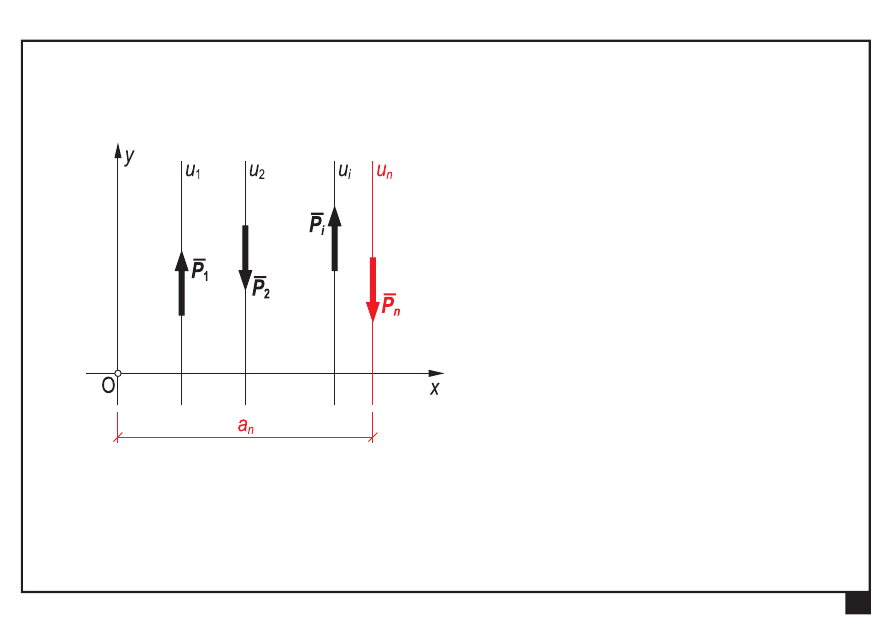
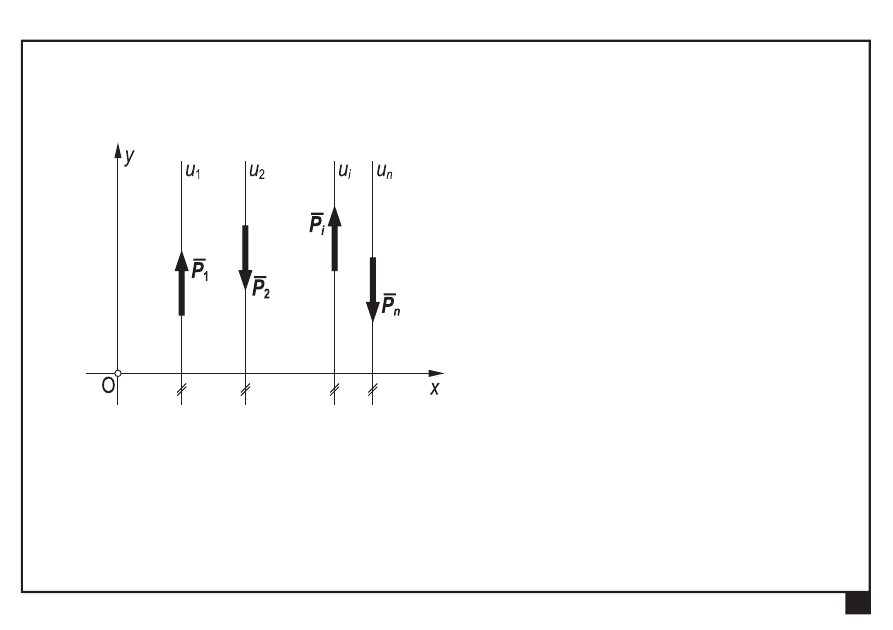
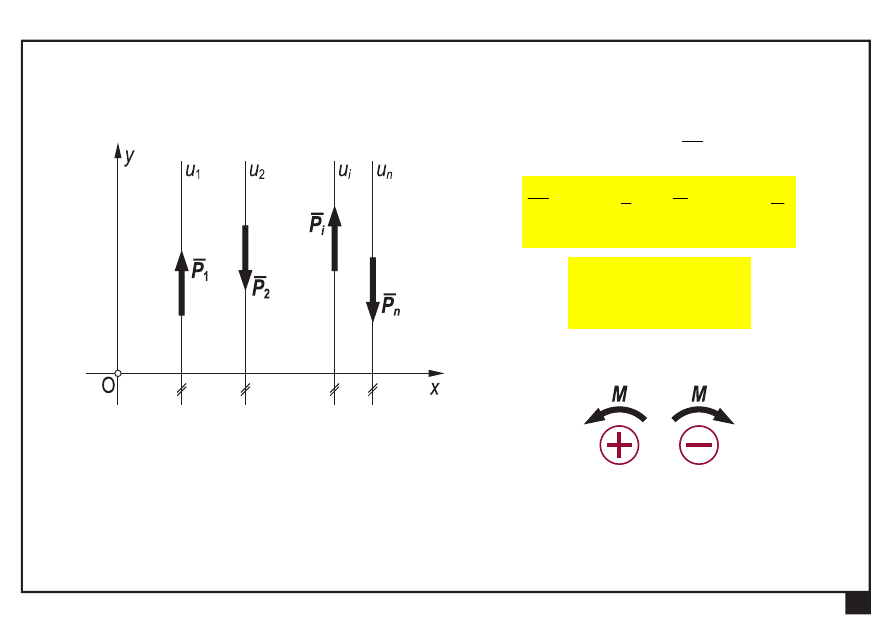
Równoległy układ sił

linie działania sił są równoległe

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

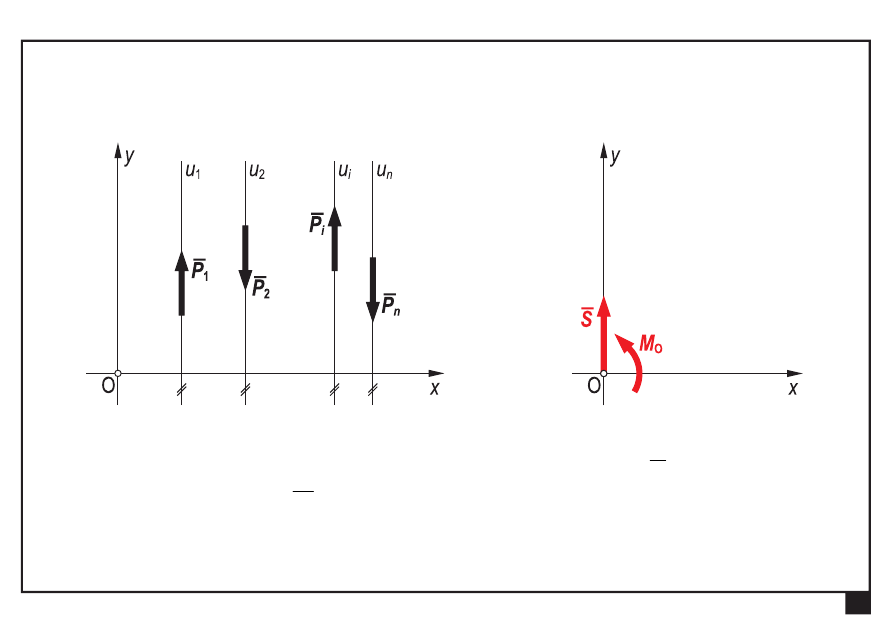
Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił



redukuje się wstępnie do punktu O, do siły ogólnej S
i momentu ogólnego

O

M

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił

siła ogólna S

y

y

n

i

i

S

P

S

e

1

=

=



=

)

(

1

1





=

=

±

=

=

n

i

i

n

i

iy

y

P

P

S

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił

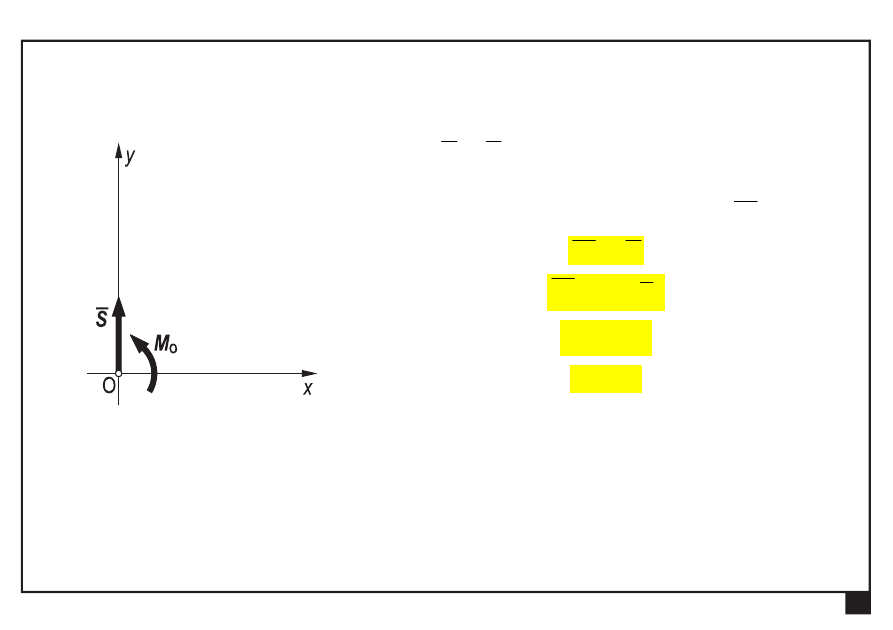
moment ogólny

O

M

z

z

n

i

i

i

M

P

r

M

e

O

1

O

O

=

×

=



=



=

±

=

n

i

i

i

z

a

P

M

1

O

)

(

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił

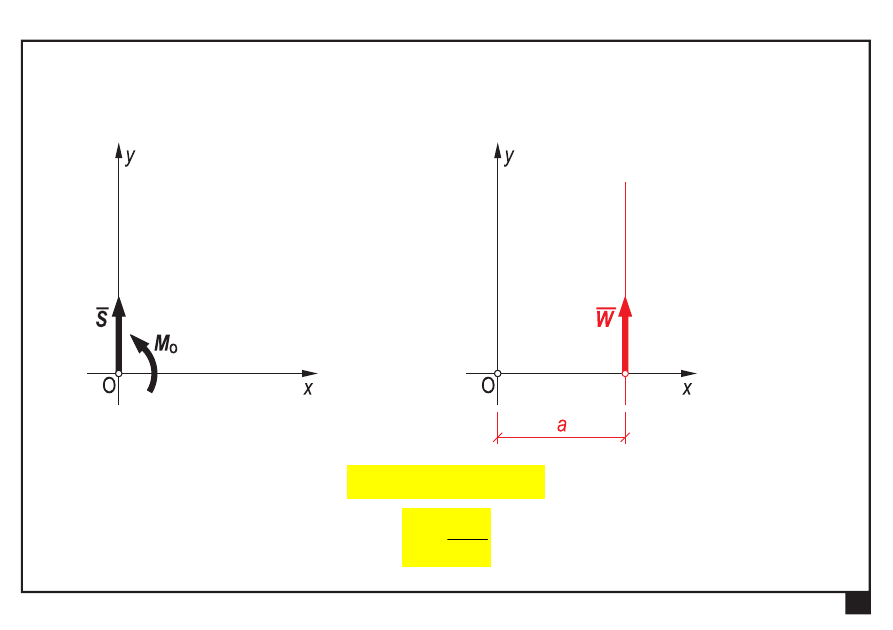
jeśli

0

≠

S

to możemy znaleźć taki

biegun redukcji A, że w wyniku
otrzymamy tylko wypadkową

W

S

W

=

y

y

W

W

e

=

y

y

S

W

=

S

W

=

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił



a

S

a

W

M

⋅

=

⋅

=

O

S

M

a

O

=

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
jest w równowadze, jeśli siła ogólna jest równa zeru
i moment ogólny jest równy zeru

0

=

S

,

0

O

=

M

0

=

y

S



0

1

=



=

n

i

iy

P

,

0

)

(

1

=

±



=

n

i

i

P

Suma rzutów sił na oś y jest równa zeru

0

O

=

z

M



0

1

O

=



=

n

i

i

M

,

0

)

(

1

=

±



=

n

i

i

i

a

P

Suma momentów względem punktu O jest równa zeru

2 RRS (dwa równania równowagi statycznej)

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
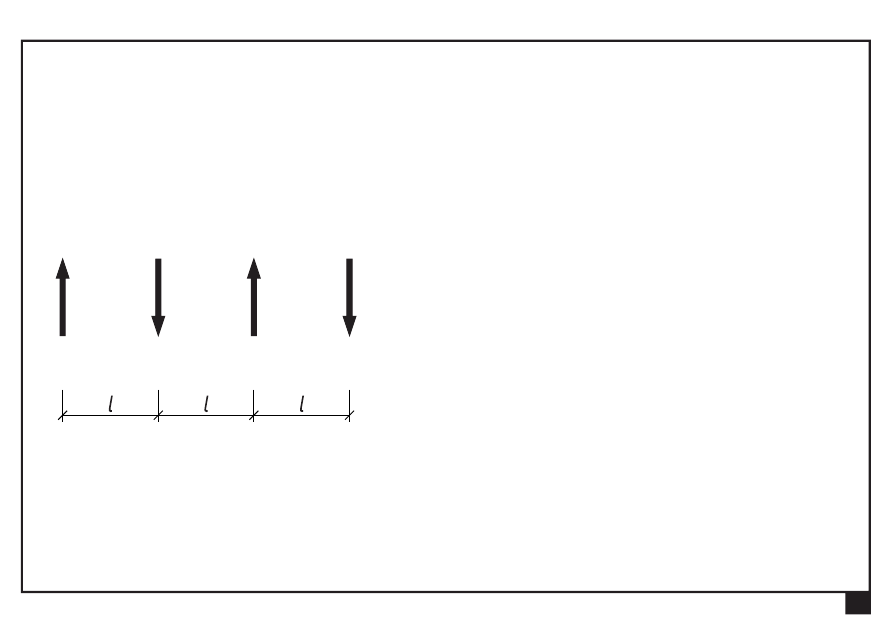
Dokonać redukcji płaskiego równoległego układu sił

3P

4P

P

2P

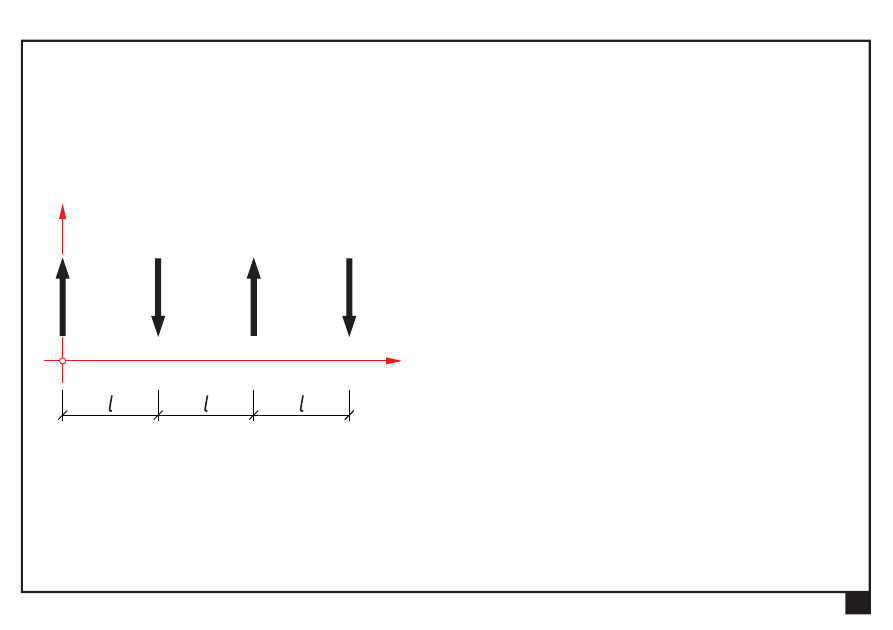
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

3P

4P

P

2P

x

O

y

Układ współrzędnych Oxy obieramy tak, aby oś y pokrywała się
z prostą działania jednej z sił

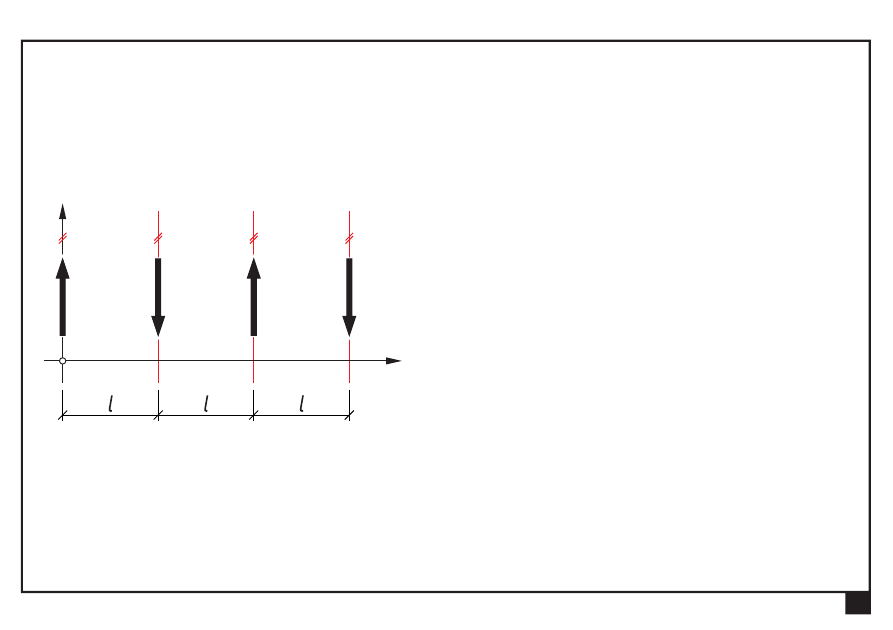
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

3P

4P

P

2P

x

O

y

Proste działania wszystkich sił w układzie są równoległe

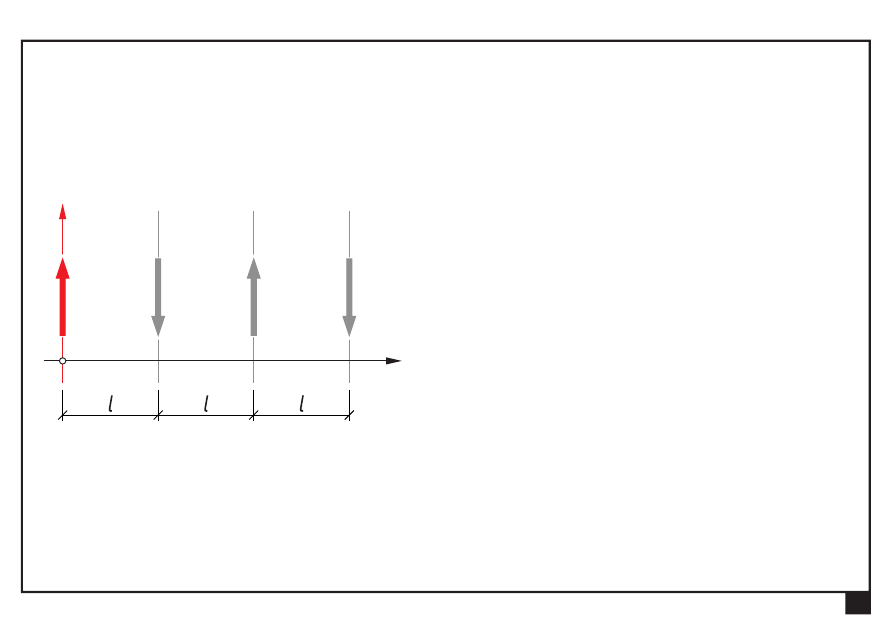
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

3P

4P

P

2P

x

O

y

Wyznaczamy siłę ogólną S = S

y

:

= Σ

=

3

y

iy

S

P

P

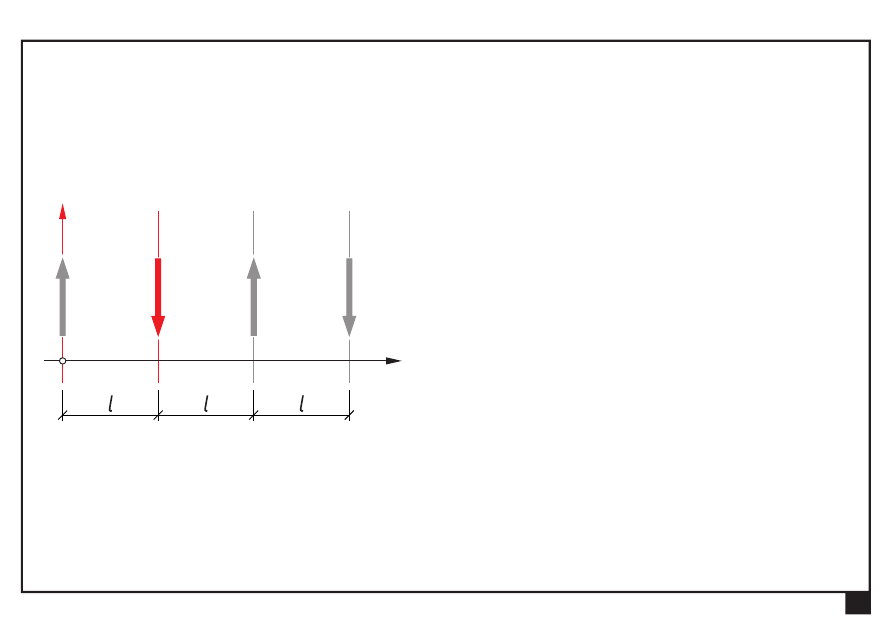
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

3P

4P

P

2P

x

O

y

Wyznaczamy siłę ogólną S = S

y

:

= Σ

=

−

3

4

y

iy

S

P

P

P

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

3P

4P

P

2P

x

O

y

Wyznaczamy siłę ogólną S = S

y

:

= Σ

=

−

+

3

4

y

iy

S

P

P

P P

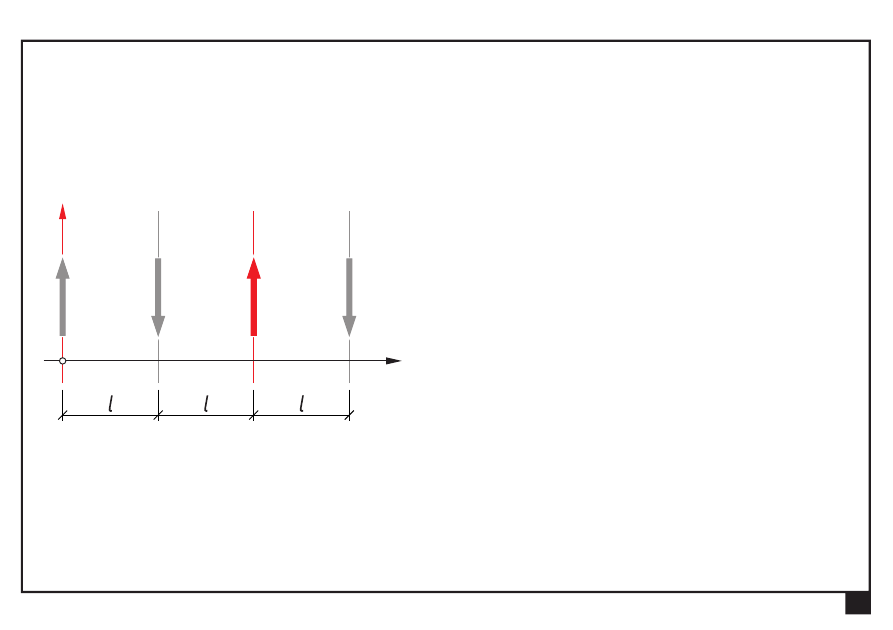
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

3P

4P

P

2P

x

O

y

Wyznaczamy siłę ogólną S = S

y

:

= Σ

=

−

+ −

=

3

4

2

y

iy

S

P

P

P P

P

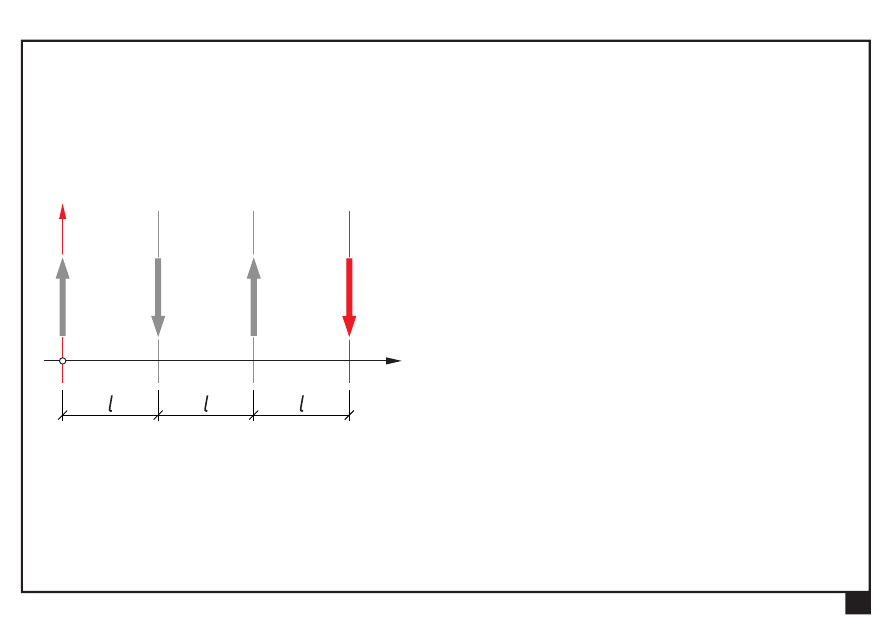
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

S

x

O

y

Wyznaczamy siłę ogólną S = S

y

:

= Σ

=

−

+ −

= −

3

4

2

2

y

iy

S

P

P

P P

P

P

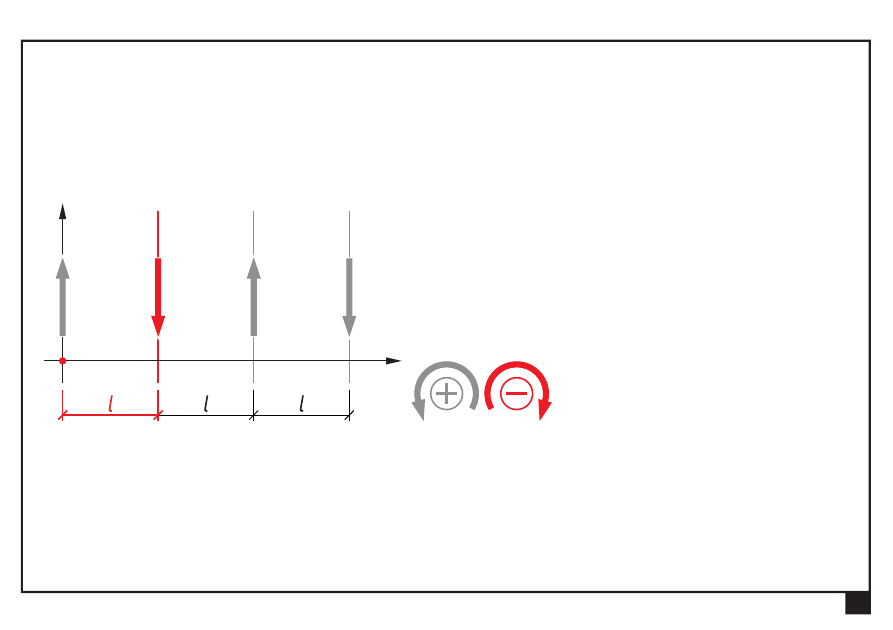
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

3P

4P

P

2P

x

O

y

Wyznaczamy moment ogólny M

O

:

= Σ

= −

⋅

O

O

4

i

M

M

P l

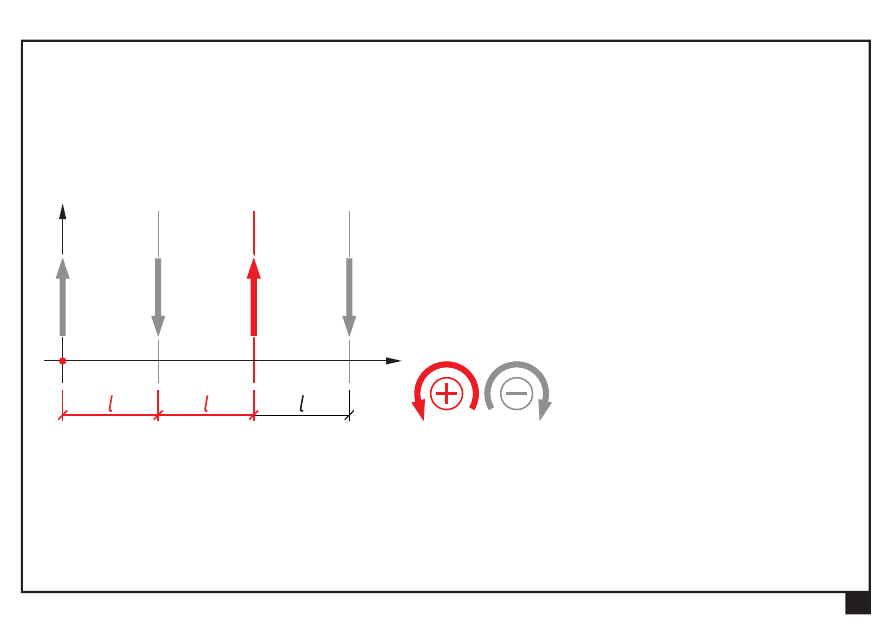
Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

3P

4P

P

2P

x

O

y

Wyznaczamy moment ogólny M

O

:

= Σ

= −

⋅ + ⋅

O

O

4

2

i

M

M

P l P

l

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

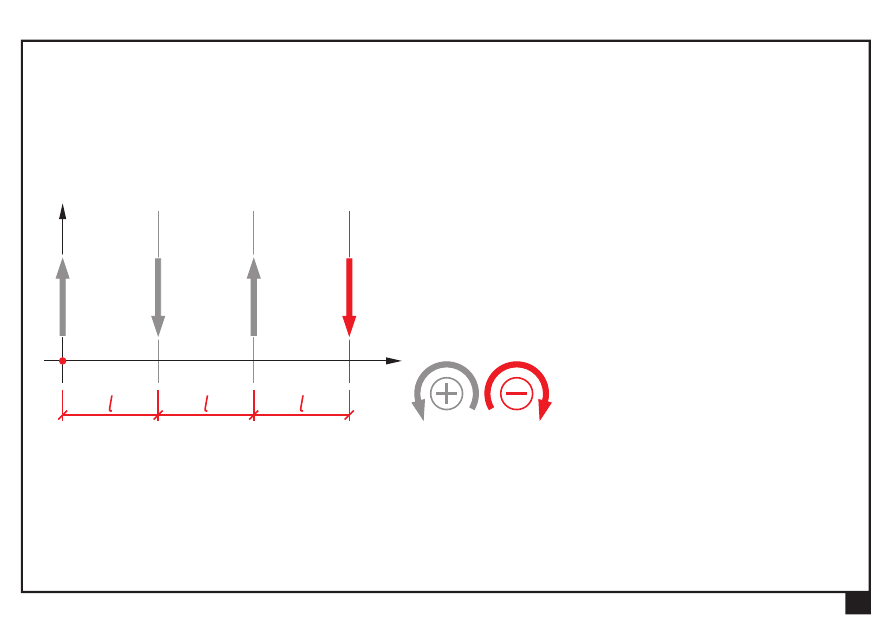
Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

3P

4P

P

2P

x

O

y

Wyznaczamy moment ogólny M

O

:

= Σ

= −

⋅ + ⋅ −

⋅

=

O

O

4

2

2

3

i

M

M

P l P

l

P

l

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

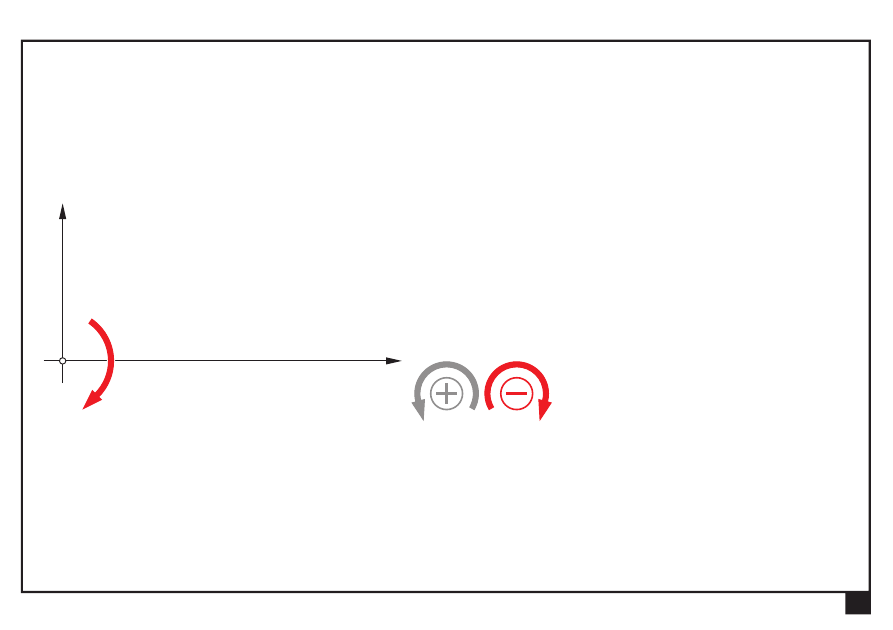
Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

x

O

y

M

O

Wyznaczamy moment ogólny M

O

:

= Σ

= −

⋅ + ⋅ −

⋅

= −

O

O

4

2

2

3

8

i

M

M

P l P

l

P

l

Pl

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

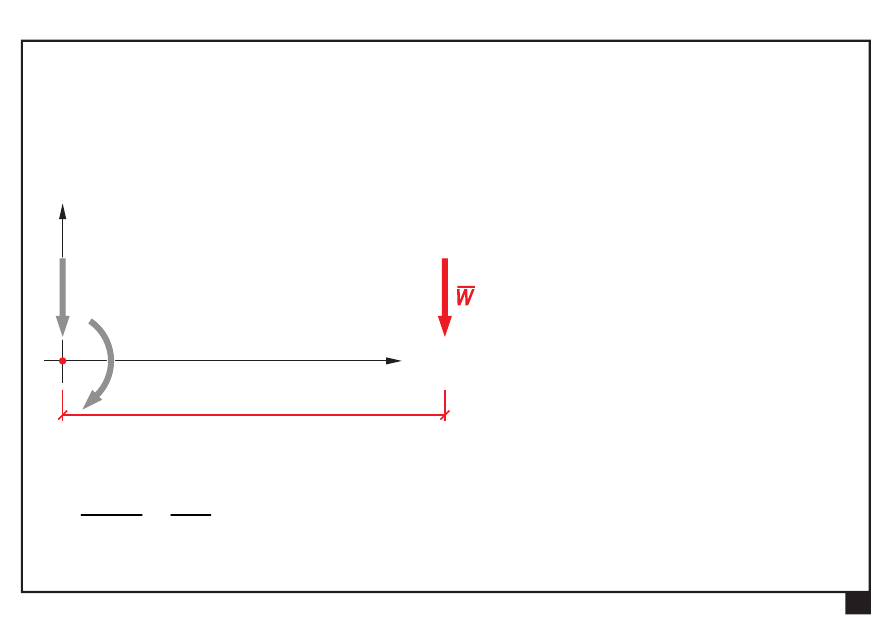
Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

S

x

O

y

M

O

Pośredni wynik redukcji do siły ogólnej S i momentu ogólnego M

O

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

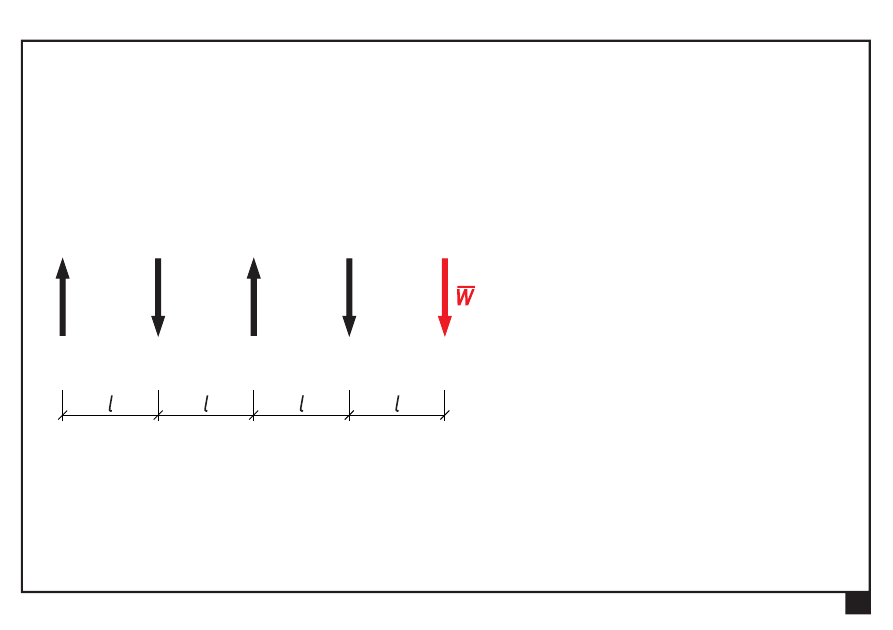
Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

x

O

y

a

Odsuwamy siłę ogólną od bieguna O na odległość a

=

=

=

O

|

| 8

4

| |

2

M

Pl

a

l

S

P

oraz

=

W

S

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Równoległy układ sił
Dokonać redukcji płaskiego równoległego układu sił

3P

4P

P

2P

Wynik końcowy redukcji

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

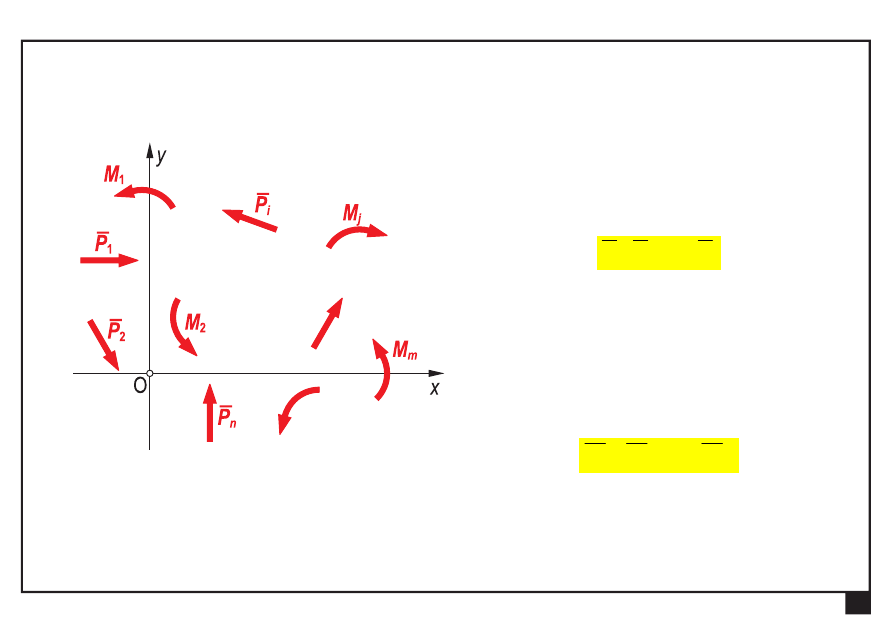
Dowolny układ obciążeń w płaszczyźnie xy

zbiór sił
(wektory liniowe)

n

P

P

P

...,

,

,

2

1

i/lub

momentów par sił
(wektory swobodne)

m

M

M

M

...,

,

,

2

1

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

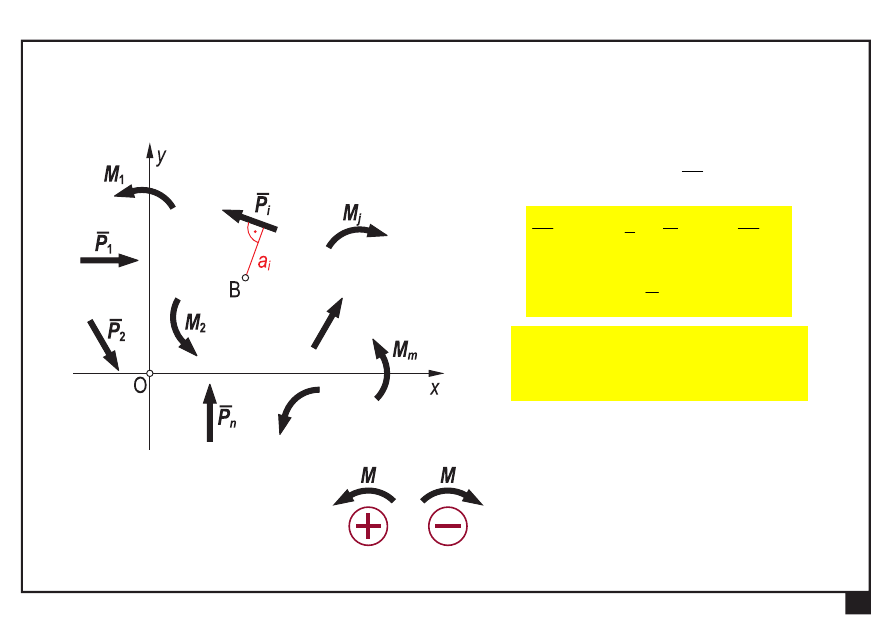
Dowolny układ obciążeń w płaszczyźnie xy

redukuje się wstępnie
do bieguna B,
do siły ogólnej S
i momentu ogólnego

O

M

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy

siła ogólna S

y

y

x

x

n

i

i

S

S

P

S

e

e

1

+

=

=



=



=

=

n

i

ix

x

P

S

1



=

=

n

i

iy

y

P

S

1

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy

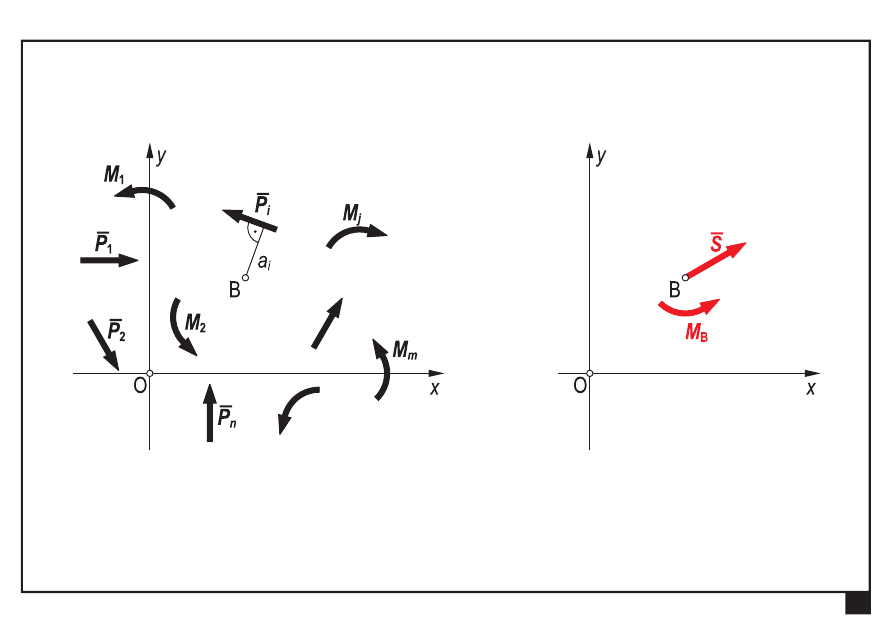
moment ogólny

B

M

z

z

m

j

j

n

i

i

i

M

M

P

r

M

e

B

1

1

B

=

=

+

×

=





=

=





=

=

±

+

±

=

m

j

j

n

i

i

i

z

M

a

P

M

1

1

B

)

(

)

(

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

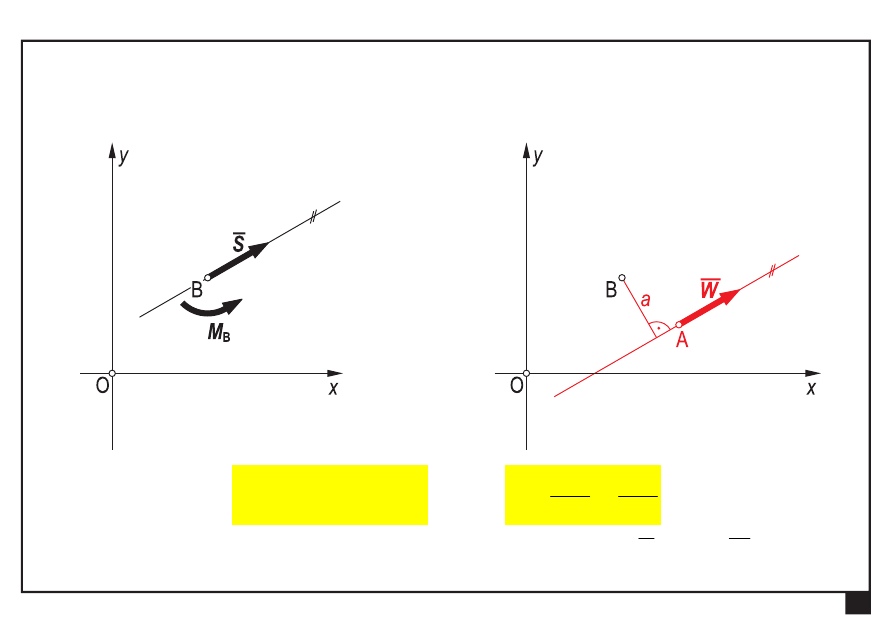
Dowolny układ obciążeń w płaszczyźnie xy



Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy

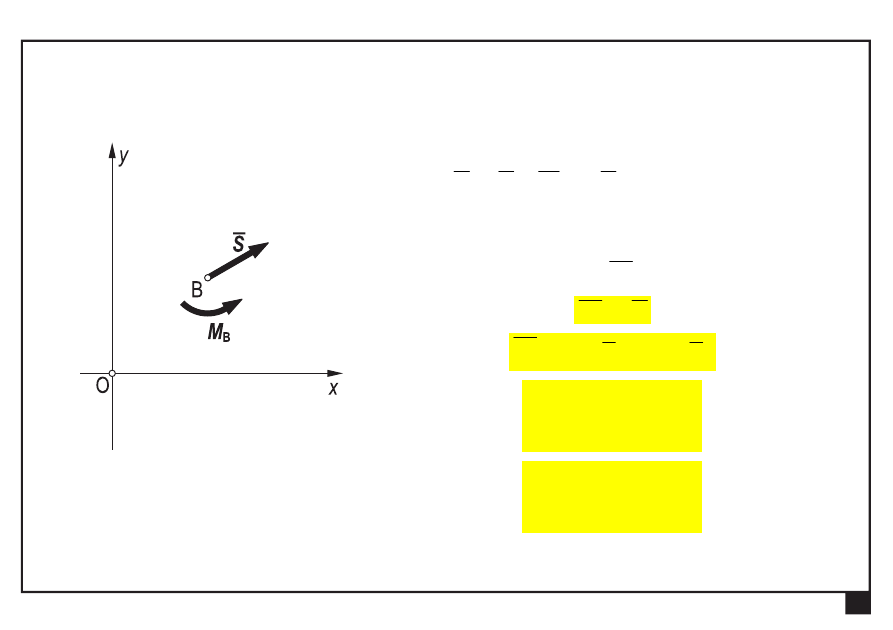
jeśli

0

≠

S

,

0

B

≠

M

to można

wyznaczyć taki biegun redukcji A,
że w wyniku otrzymamy
tylko wypadkową

W

S

W

=

y

y

x

x

W

W

W

e

e

+

=



=

=

=

n

i

ix

x

x

P

S

W

1



=

=

=

n

i

iy

y

y

P

S

W

1

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy



a

S

a

W

M

⋅

=

⋅

=

B

S

M

W

M

a

B

B

=

=

odległość a odkładamy z uwzględnieniem zwrotów S oraz

B

M

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
jest w równowadze, jeśli siła ogólna jest równa zeru
i moment ogólny jest równy zeru

0

=

S

,

0

B

=

M

0

=

x

S



0

1

=



=

n

i

ix

P

Suma rzutów sił na oś x jest równa zeru

0

=

y

S



0

1

=



=

n

i

iy

P

Suma rzutów sił na oś y jest równa zeru

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
jest w równowadze, jeśli siła ogólna jest równa zeru
i moment ogólny jest równy zeru

0

=

S

,

0

B

=

M

0

B

B

=

=

z

M

M



0

1

B

=



=

n

i

i

M

,

0

)

(

)

(

1

1

=

±

+

±





=

=

m

j

j

n

i

i

i

M

a

P

Suma momentów względem punktu B jest równa zeru

3 RRS (trzy równania równowagi statycznej)

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
jest w równowadze, jeśli

suma rzutów sił na oś x

jest równa zeru

suma rzutów sił na oś y

jest równa zeru

suma momentów względem

dowolnego punktu jest równa zeru

1

1

B

1

0

0

0

n

ix

i

n

iy

i

n

i

i

P

P

M

=

=

=



=







=







=











B

0

0

0

ix

iy

i

P

P

M



Σ

=







Σ

=







Σ

=





B

0

0

0

X

Y

M



Σ

=







Σ =







Σ

=





3 RRS (trzy równania równowagi statycznej)

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Do rozwiązywania dowolnych płaskich układów obciążeń
można wykorzystać różne kombinacje

3RRS

, np.:

B

0

0

0

ix

iy

i

P

P

M



Σ

=







Σ

=







Σ

=





A

B

0

0

0

ix

i

i

P

M

M



Σ

=







Σ

=







Σ

=





A

B

0

0

0

iy

i

i

P

M

M



Σ

=







Σ

=







Σ

=





A

B

C

0

0

0

i

i

i

M

M

M



Σ

=







Σ

=







Σ

=





przy czym punkty A, B i C nie mogą być współliniowe

Płaskie układy obciążeń, redukcja i równowaga.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Pamiętając

3RRS

można rozwiązać każdy z poznanych

płaskich układów sił lub obciążeń

kolinearny

układ sił

zbieżny

układ sił

równoległy

układ sił

dowolny

układ obciążeń

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

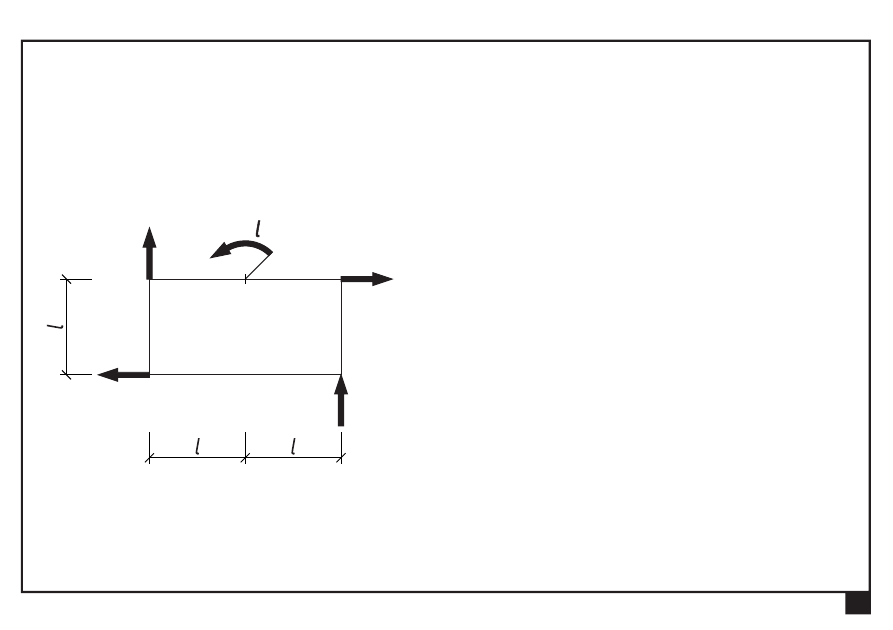
Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
Dokonać redukcji płaskiego dowolnego układu obciążeń

3P

4P

P

2P

P

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

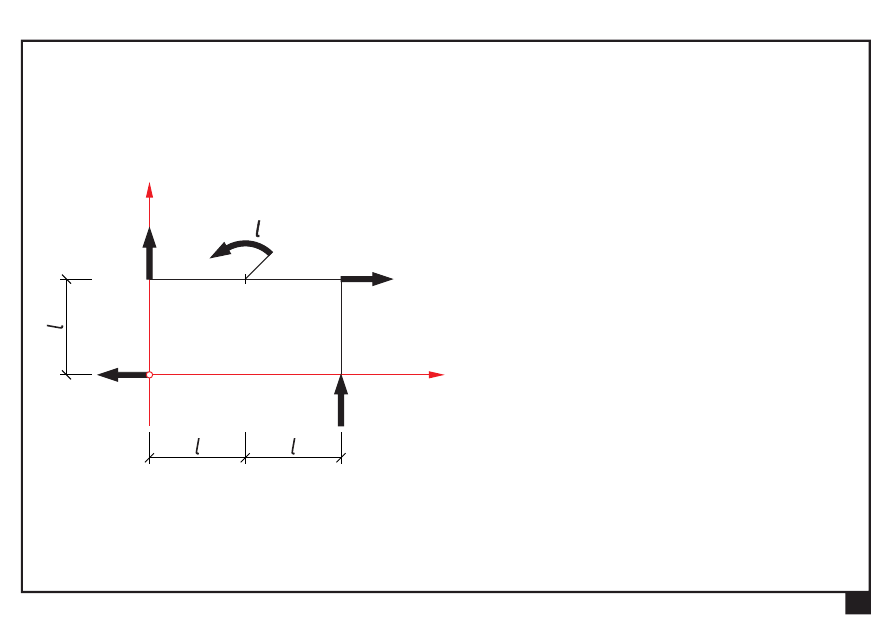
Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
Dokonać redukcji płaskiego dowolnego układu obciążeń

3P

4P

P

2P

x

y

O

P

Obieramy układ współrzędnych Oxy

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

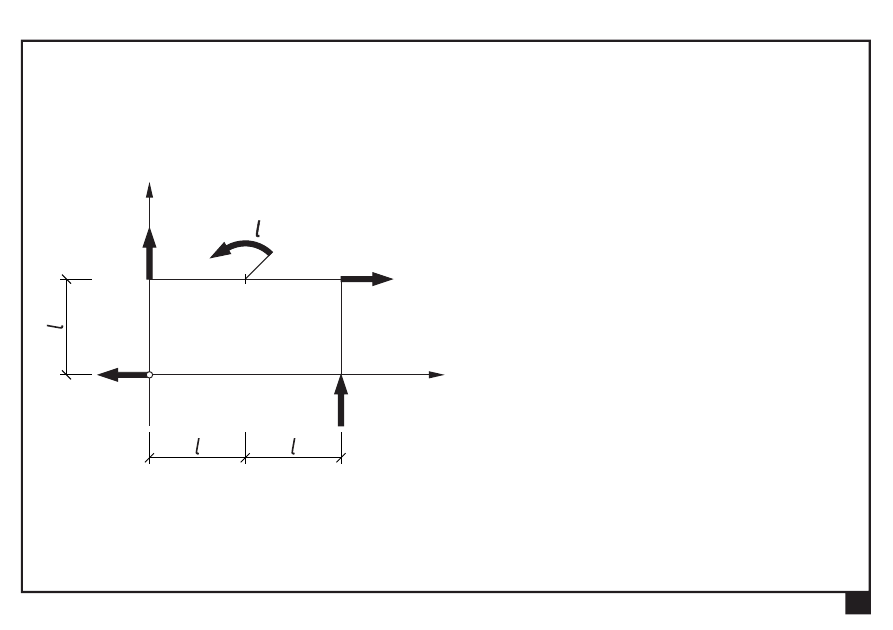
Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
Dokonać redukcji płaskiego dowolnego układu obciążeń

P

3P

4P

P

2P

x

y

O

Wyznaczamy składowe S

x

, S

y

siły ogólnej S:

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
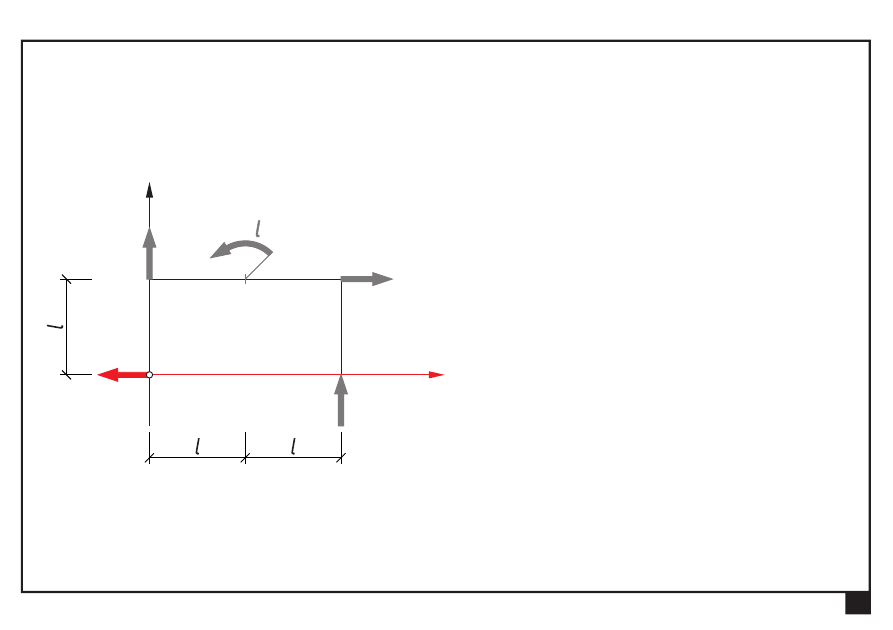
Dokonać redukcji płaskiego dowolnego układu obciążeń

P

3P

4P

P

2P

x

y

O

Wyznaczamy składowe S

x

, S

y

siły ogólnej S:

= Σ

= −

x

ix

S

P

P

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
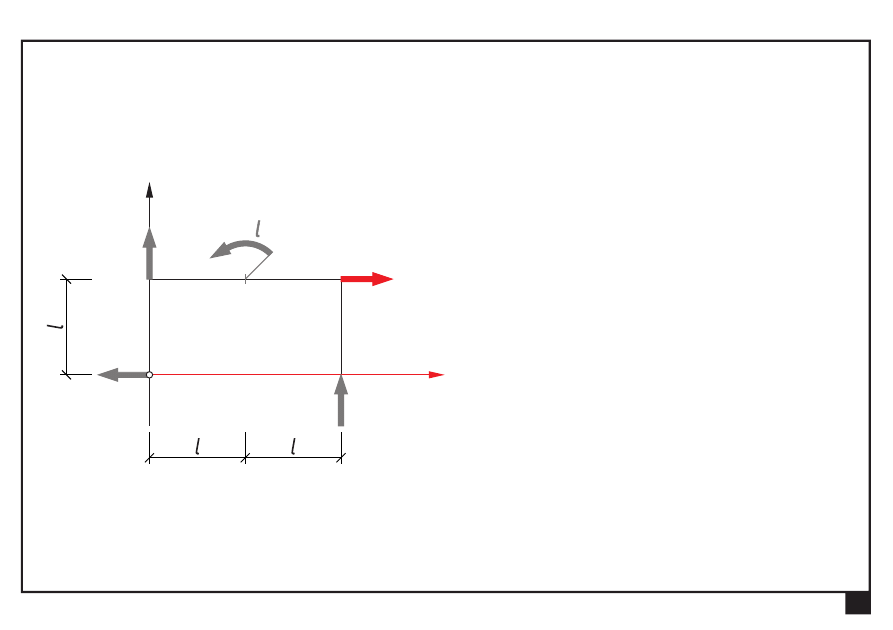
Dokonać redukcji płaskiego dowolnego układu obciążeń

P

3P

4P

P

2P

x

y

O

Wyznaczamy składowe S

x

, S

y

siły ogólnej S:

= Σ

= − +

=

4

3

x

ix

S

P

P

P

P

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
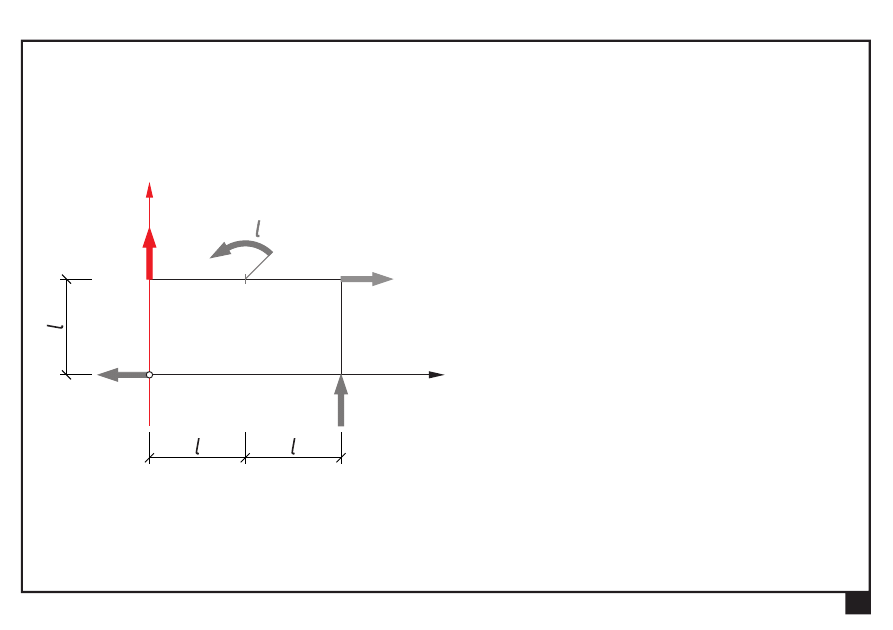
Dokonać redukcji płaskiego dowolnego układu obciążeń

P

3P

4P

P

2P

x

y

O

Wyznaczamy składowe S

x

, S

y

siły ogólnej S:

= Σ

=

y

iy

S

P

P

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
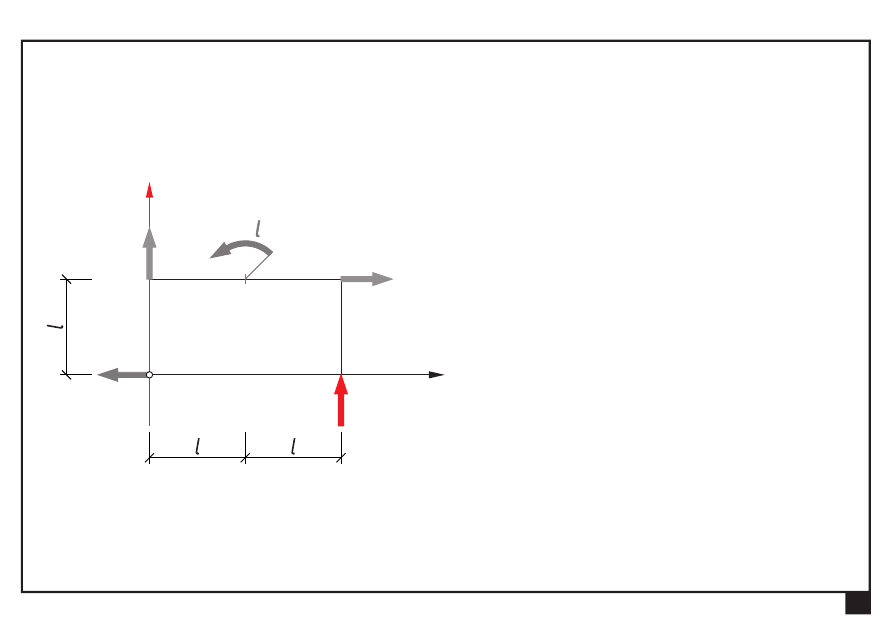
Dokonać redukcji płaskiego dowolnego układu obciążeń

P

3P

4P

P

2P

x

y

O

Wyznaczamy składowe S

x

, S

y

siły ogólnej S:

= Σ

= +

=

3

4

y

iy

S

P

P

P

P

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
Dokonać redukcji płaskiego dowolnego układu obciążeń

x

y

O

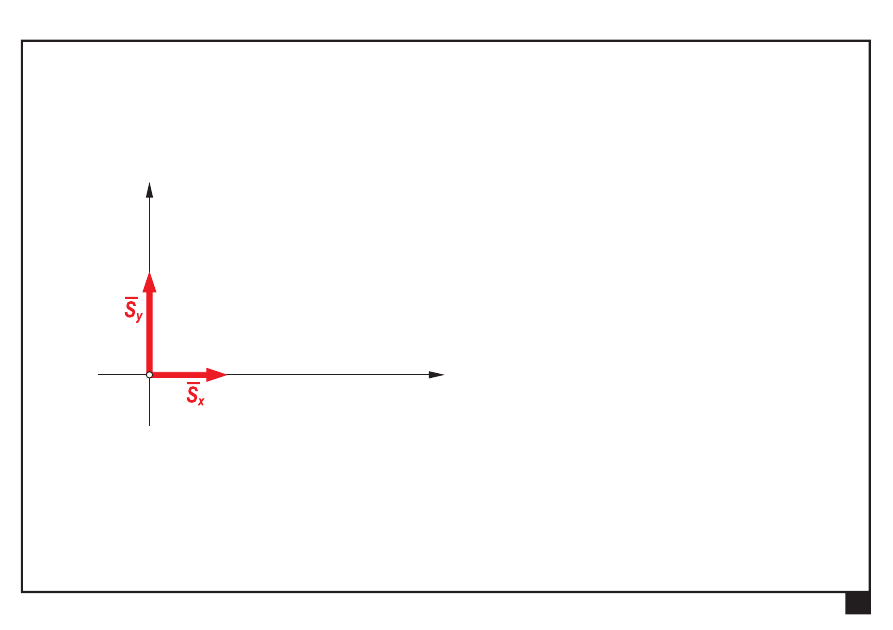
Składowe S

x

, S

y

siły ogólnej S są równe:

=3

x

S

P

,

= 4

y

S

P

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
Dokonać redukcji płaskiego dowolnego układu obciążeń

x

y

O

α

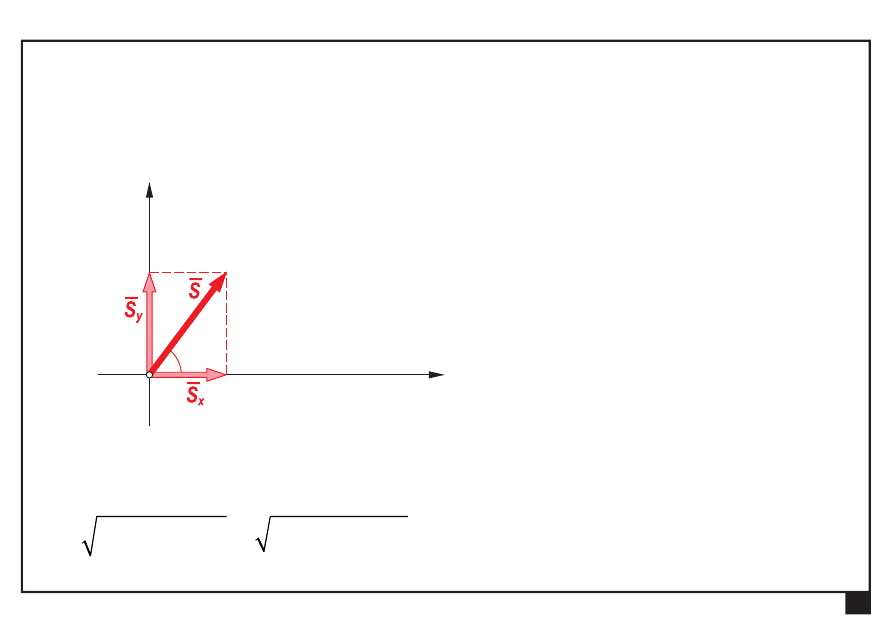
Wyznaczamy siłę ogólną S i kąt nachylenia:

=

+

=

+

=

2

2

2

2

(

)

( )

(3 )

(4 )

5

x

y

S

S

S

P

P

P

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
Dokonać redukcji płaskiego dowolnego układu obciążeń

x

y

O

α

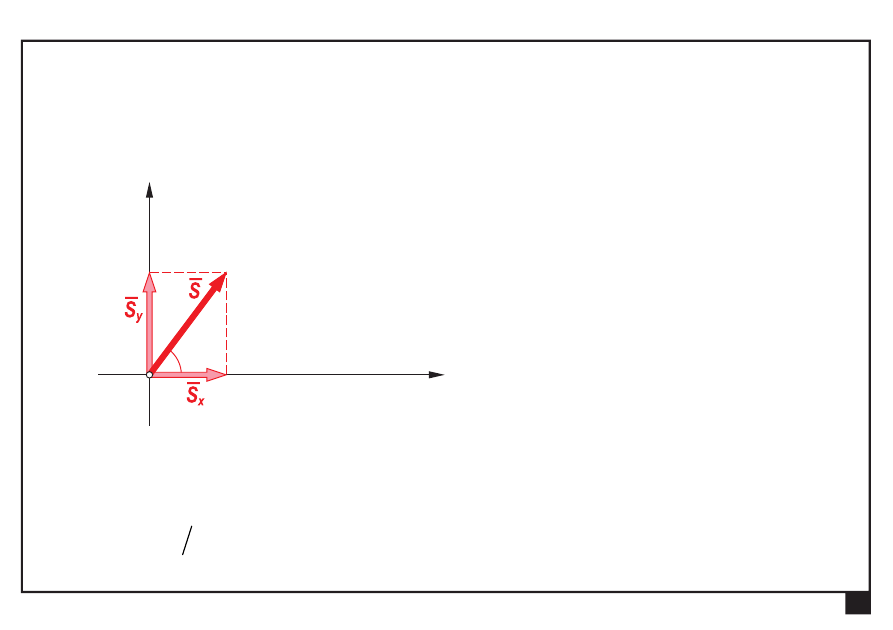
Wyznaczamy siłę ogólną S i kąt nachylenia:

α

=

=

≈

°

arctg (

) arctg (4 /3) 53,13

y

x

S S

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
Dokonać redukcji płaskiego dowolnego układu obciążeń

P

3P

4P

P

2P

x

y

O

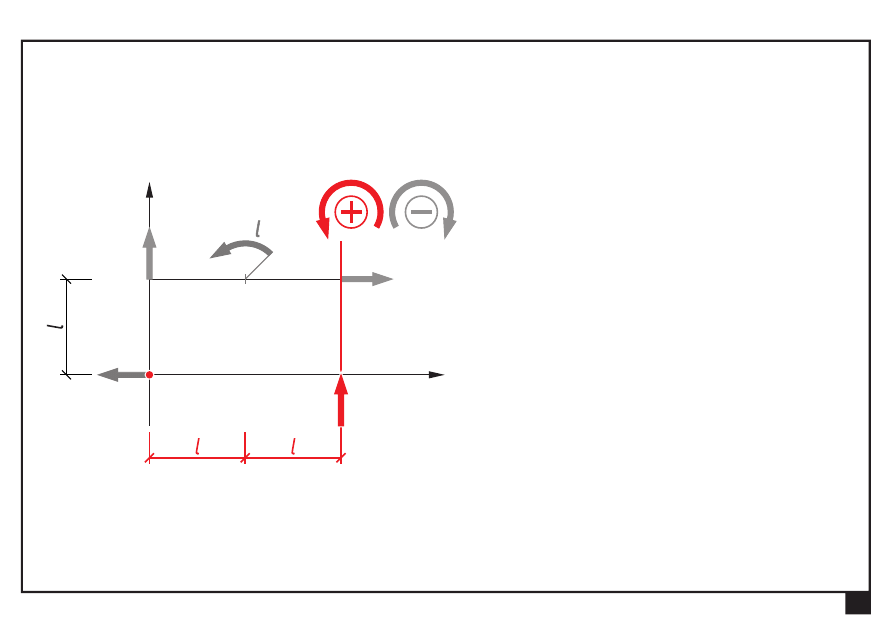
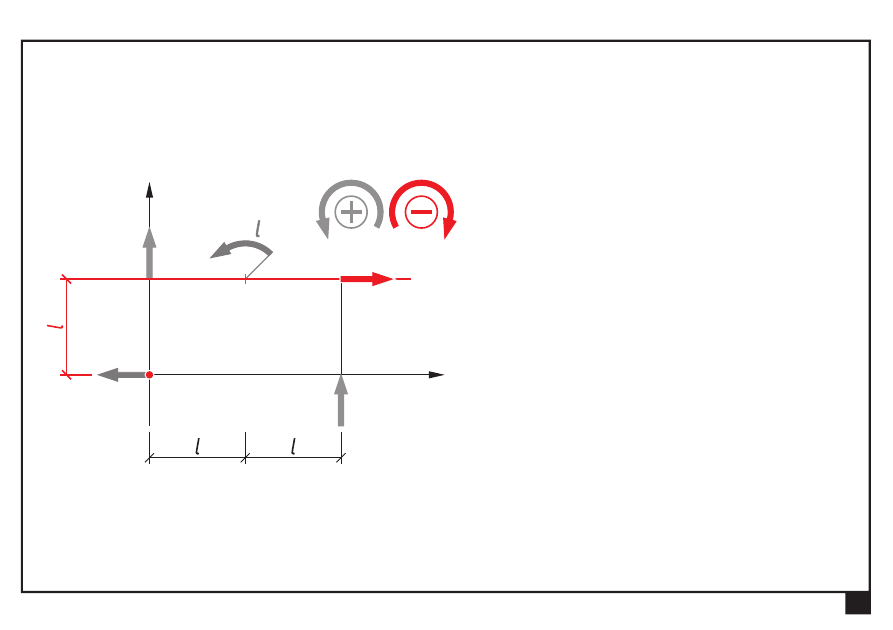
Wyznaczamy moment ogólny M

O

:

= Σ

=

⋅

O

O

3

2

i

M

M

P

l

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
Dokonać redukcji płaskiego dowolnego układu obciążeń

P

3P

4P

P

2P

x

y

O

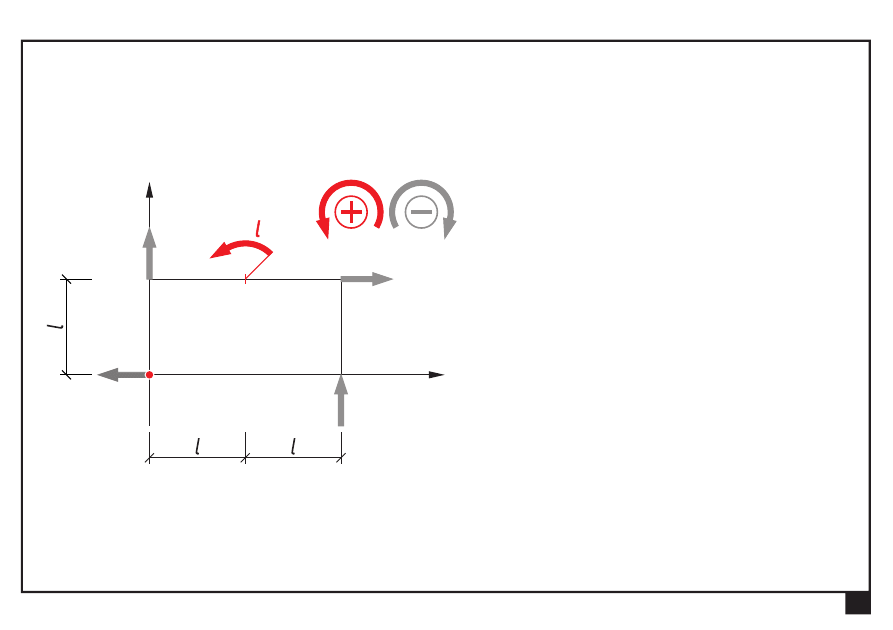
Wyznaczamy moment ogólny M

O

:

= Σ

=

⋅ −

⋅

O

O

3

2

4

i

M

M

P

l

P l

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
Dokonać redukcji płaskiego dowolnego układu obciążeń

P

3P

4P

P

2P

x

y

O

Wyznaczamy moment ogólny M

O

:

= Σ

=

⋅ −

⋅ +

=

O

O

3

2

4

2

4

i

M

M

P

l

P l

Pl

Pl

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
Dokonać redukcji płaskiego dowolnego układu obciążeń

x

y

O

M

O

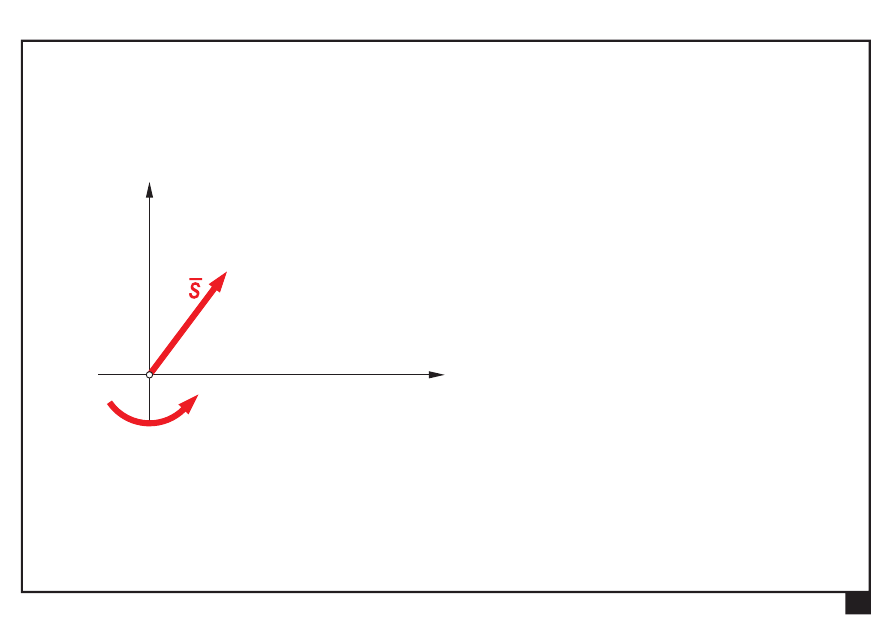
Pośredni wynik redukcji do siły ogólnej S i momentu ogólnego M

O

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
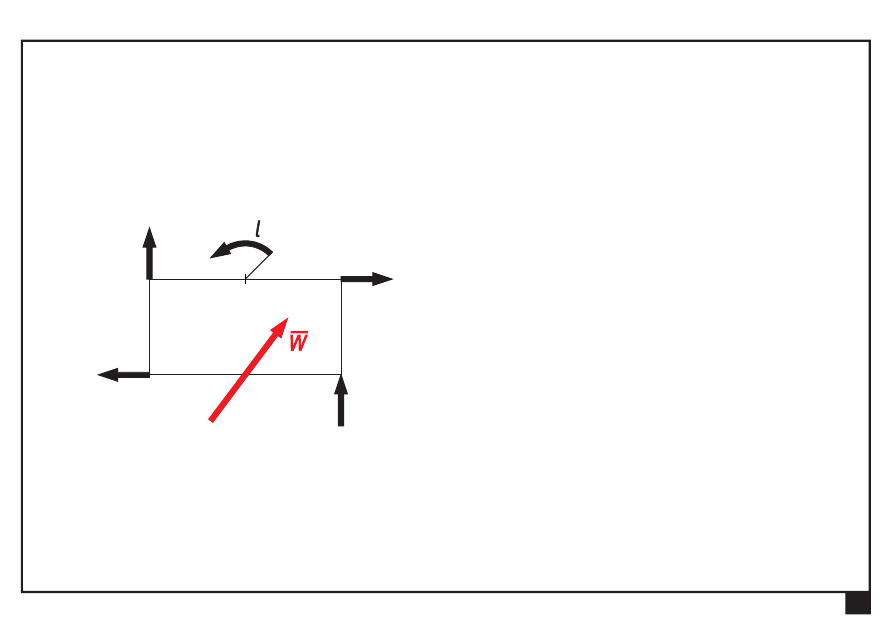
Dokonać redukcji płaskiego dowolnego układu obciążeń

x

y

O

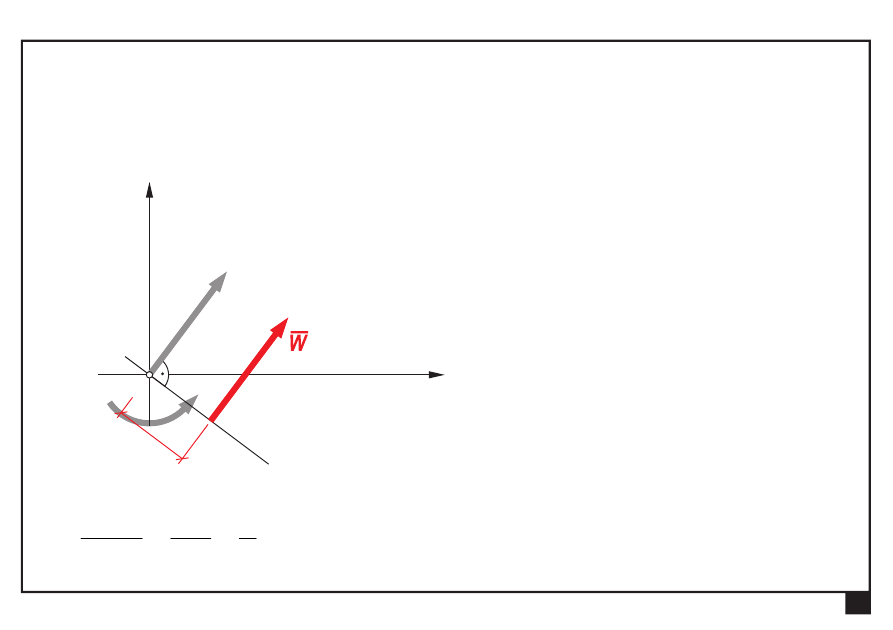
a

Odsuwamy siłę ogólną od bieguna O na odległość a

=

=

=

O

|

| 4

4

| |

5

5

M

Pl

a

l

S

P

oraz

=

W

S

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Redukcja i równowaga płaskich układów obciążeń

Dowolny układ obciążeń w płaszczyźnie xy
Dokonać redukcji płaskiego dowolnego układu obciążeń

3P

4P

P

2P

P

Końcowy wynik redukcji

Rachunek wektorowy. Pojęcia podstawowe. Aksjomaty statyki.

mechanika techniczna | statyka

2

Bibliografia

Klasztorny M., Niezgoda T., Mechanika ogólna. Podstawy teoretyczne,
zadania z rozwiązaniami

, OW PW, Warszawa 2006.

Klasztorny M., Mechanika ogólna, DWE, Wrocław 2005.