1. DANE:

Beton C30/37 (26)

fck

30MPa

:=

fcd

fck
1.4

21.429 MPa

⋅

=

:=

fctm

2.9MPa

:=

Ecm

32GPa

:=

STAL AIII 34GS

fyk

410MPa

:=

fyd

fyk

1.15

356.522 MPa

⋅

=

:=

ϕ

20mm

:=

Aϕ

π

ϕ

2









2

3.142

10

4

−

×

m

2

=

:=

ϕs

8mm

:=

Aϕ.s

π

ϕs

2













2

5.027

10

5

−

×

m

2

=

:=

KLASA EKPSPOZYCJI XC3 (43-44)

cnom

30mm

:=

2. STATYKA:

SŁUP

bsł

0.3m

:=

hsł

0.6m

:=

Lsł

4.0m

:=

PODCIĄG bw

0.3m

:=

bf

0.75m

:=

hp

0.45m

:=

hf

0.12m

:=

Lp

4.0m

:=

Ap

bf hf

⋅

bw hp hf

−

(

)

⋅

+

0.189m

2

=

:=

3. WYMIAROWANIE PODCIĄGU:

a1

cnom

ϕ

2

+

ϕs

+

0.048m

=

:=

a2

a1 0.048m

=

:=

d

hp a1

−

0.402m

=

:=

Obliczenie zbrojenia minimalnego(139, 112)

kc

0.4

:=

k

1

:=

Act

bw hp

⋅

2

0.068m

2

=

:=

σs

220MPa

:=

(112 tab. 7.2N)

fct.eff

fctm 2.9 MPa

⋅

=

:=

As.min

max 0.26

fctm

fyk

⋅

bw

⋅

d

⋅ 0.0013 b

w

⋅

d

⋅

,

kc k

⋅ f

ct.eff

⋅

Act

σs

⋅

,













3.559

10

4

−

×

m

2

⋅

=

:=

Obliczenie długości efektywnej i efektywnej szerokości półek (53)

l0

0.85 Lp

⋅

3.4 m

=

:=

(patrz rys. 5.2)

b1

22.5cm

:=

b2

22.5cm

:=

beff1

min b1 0.2b1 0.1l0

+

,

0.2l0

,

(

)

0.225 m

=

:=

beff2

min b2 0.2b2 0.1l0

+

,

0.2l0

,

(

)

0.225 m

=

:=

beff

beff1 beff2

+

bw

+

0.75 m

=

:=

Mf1

fcd beff

⋅

hf

⋅

d

0.5hf

−

(

)

⋅

659.571 kN m

⋅

⋅

=

:=

- nośność płyty

Mf2

fcd bw

⋅

hp hf

−

(

)

⋅

d

0.5 hp hf

−

(

)

−





⋅

502.779 kN m

⋅

⋅

=

:=

- nośność środnika

Mmax1

150kN m

⋅

:=

- moment przęsłowy

Mmax2

200kN m

⋅

:=

- moment podporowy

Mmax1 Mf1

<

1

=

- przekrój pozornie teowy, płyta nie współpracuje z ryglem

Mmax2 Mf2

<

1

=

- przekrój pozornie teowy, płyta nie współpracuje z ryglem

Wymiarowanie na moment przęsłowy

Scc.eff

Mmax1

fcd bw

⋅

d

2

⋅

0.144

=

:=

ξeff

1

1

2 Scc.eff

⋅

−

−

0.157

=

:=

εcm2

0.0035

:=

Es

200GPa

:=

εyd

fyd

−

Es

1.783

−

10

3

−

×

=

:=

ξeff.lim

0.8

εcm2

εcm2 εyd

−













⋅

0.53

=

:=

ξeff ξeff.lim

<

1

=

- przekrój pojedynczo zbrojony

xeff

ξeff d

⋅

0.063 m

=

:=

As1

max

fcd bw

⋅

xeff

⋅

fyd

As.min

,













1.136

10

3

−

×

m

2

=

:=

n

ceil

As1

Aϕ













4

=

:=

- ilość prętów

As1.prov1

n Aϕ

⋅

1.257

10

3

−

×

m

2

=

:=

- PRZYJĘTE ZBROJENIE DOŁEM

Wymiarowanie na moment podporowy

Scc.eff

Mmax2

fcd beff

⋅

d

2

⋅

0.077

=

:=

ξeff

1

1

2 Scc.eff

⋅

−

−

0.08

=

:=

εcm2

0.0035

:=

Es

200GPa

:=

εyd

fyd

−

Es

1.783

−

10

3

−

×

=

:=

ξeff.lim

0.8

εcm2

εcm2 εyd

−













⋅

0.53

=

:=

ξeff ξeff.lim

<

1

=

- przekrój pojedynczo zbrojony

xeff

ξeff d

⋅

0.032 m

=

:=

As1

max

fcd beff

⋅

xeff

⋅

fyd

As.min

,













1.454

10

3

−

×

m

2

=

:=

n

ceil

As1

Aϕ













5

=

:=

- ilość prętów

As1.prov2

n Aϕ

⋅

1.571

10

3

−

×

m

2

=

:=

- PRZYJĘTE ZBROJENIE DOŁEM

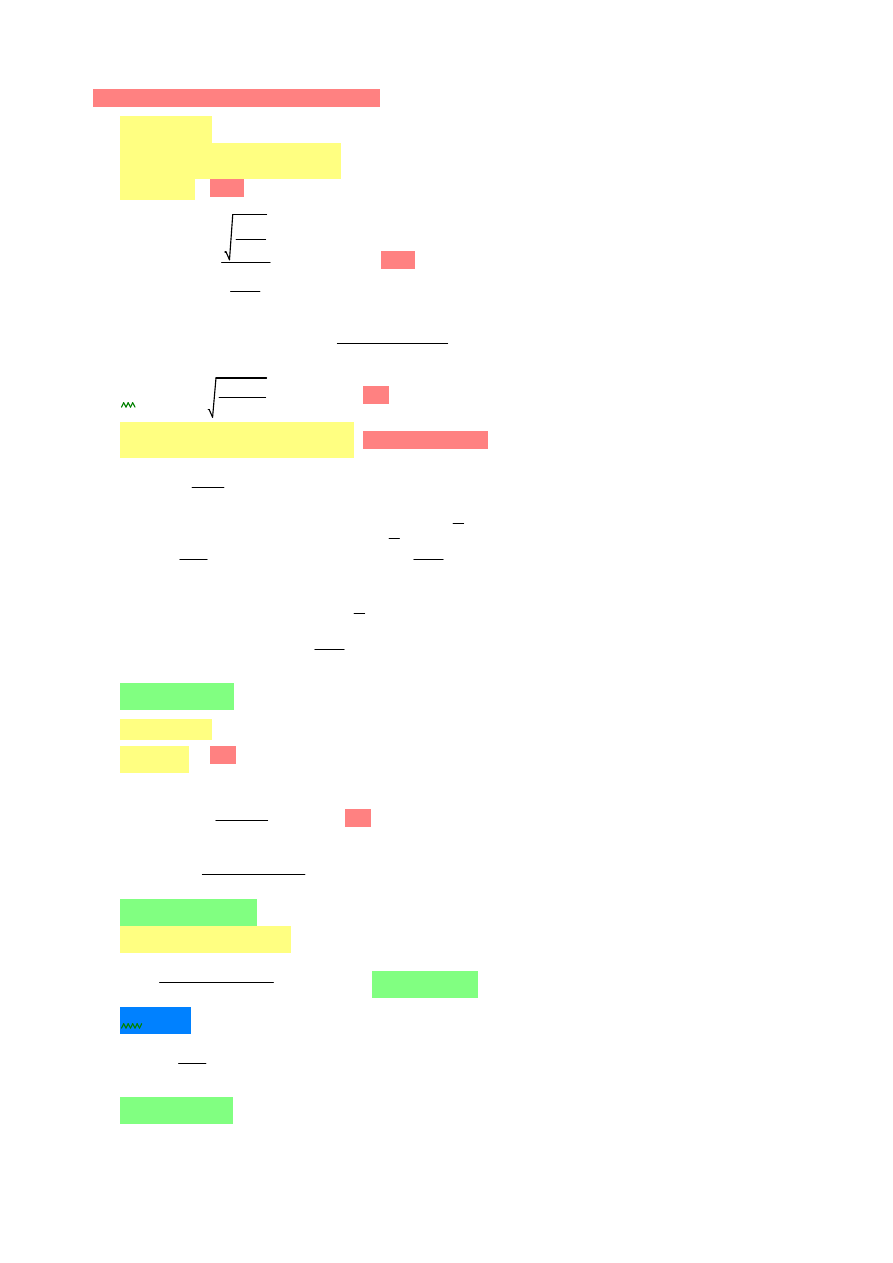
Wymiarowanie zbrojenia poprzecznego

VEd

175kN

:=

Asw

4 Aϕ.s

⋅

2.011

10

4

−

×

m

2

=

:=

- przyjęte zbrojenie czterocięte

α

90 deg

⋅

:=

(142)

ρw.min

0.08

fck

MPa

fyk

MPa

⋅

1.069

10

3

−

×

=

:=

(143)

sl.max

min 0.75 d

⋅

1

cot

α

( )

+

(

)

⋅

Asw

ρw.min bw

⋅

sin

α

( )

⋅

,













0.301 m

=

:=

k

min 1

200mm

d

+

2.0

,













1.705

=

:=

(78)

Asl

As1.prov2 1.571 10

3

−

×

m

2

=

:=

(79, patrz rys. 6.3)

ρ1

min

Asl

bw d

⋅

0.02

,













0.013

=

:=

CRdc

0.18

1.4

0.129

=

:=

vmin

0.035 k

2

3

⋅

fck

MPa













1

2

⋅

MPa

⋅

0.274 MPa

⋅

=

:=

VRdc

max CRdc k

⋅

100

ρ1

⋅

fck

MPa

⋅













1

3

⋅

bw

⋅

d

⋅ MPa

⋅

vmin bw

⋅

d

⋅

,

















89.73 kN

⋅

=

:=

VEd VRdc

>

1

=

- niezbędne zbrojenie obliczeniowe

θ

26.56 deg

⋅

:=

cot

θ

( )

2

=

tan

θ

( )

0.5

=

αcw

1.0

:=

(82)

z

0.9d

0.362 m

=

:=

v1

0.6 1

fck

250MPa

−













⋅

0.528

=

:=

(80)

VRd.max

αcw bw

⋅

z

⋅ v

1

⋅

fcd

⋅

cot

θ

( )

tan

θ

( )

+

491.156 kN

⋅

=

:=

VEd VRd.max

>

0

=

fywd

fyd 356.522 MPa

⋅

=

:=

s1

Asw z

⋅ f

ywd

⋅

cot

θ

( )

⋅

VEd

0.296 m

=

:=

s1 sl.max

≤

1

=

s1

29cm

:=

- przyjety rozstaw strzemion

VRds

Asw

s1

z

⋅ f

yd

⋅

cot

θ

( )

⋅

178.901 kN

⋅

=

:=

VRds VEd

≥

1

=

- warunek spełniony

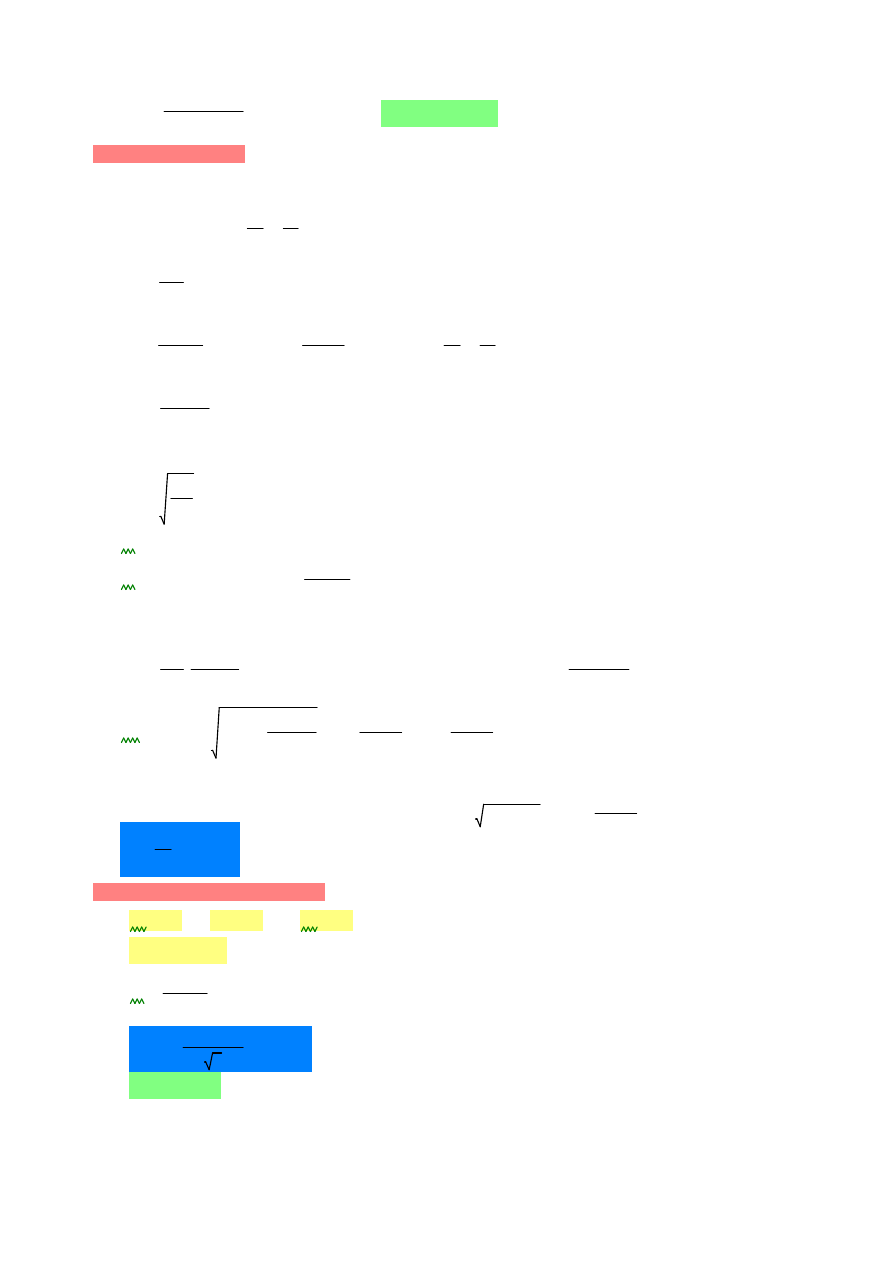
ρw

Asw

s1 bw

⋅

sin

α

( )

⋅

2.311

10

3

−

×

=

:=

ρw ρw.min

≥

1

=

- warunek spełniony

Obliczenie smukłości

hś

hp hf

−

0.33 m

=

:=

Sx0

hf bf

⋅

hp

hf

2

−

hś

2

−













⋅

2.025

10

4

×

cm

3

⋅

=

:=

yx

Sx0

Ap

0.107 m

=

:=

Ip

bw hś

3

⋅

12

bw hś

⋅

yx

2

⋅

+

bf hf

3

⋅

12

+

bf hf

⋅

hp

hf

2

−

hś

2

−

yx

−













2

⋅

+

3.393

10

3

−

×

m

4

=

:=

Isł

bsł hsł

3

⋅

12

5.4

10

3

−

×

m

4

=

:=

Asł

bsł hsł

⋅

0.18 m

2

=

:=

isł

Isł

Asł

0.173 m

=

:=

d

hsł a1

−

0.552 m

=

:=

θ

1.0

:=

Mp

0.5

θ

⋅ 3

⋅

Ecm Ip

⋅

Lp

⋅

4.072

10

4

×

kN m

⋅

⋅

=

:=

k1

∞

:=

- bo podpora przegubowa

k2

θ

Mp

Ecm Isł

⋅

Lsł

⋅

1.061

=

:=

- po przekształceniach

k2.

Isł Lp

⋅

1.5 Lsł

⋅

Ip

⋅

1.061

=

:=

l0

Lsł max 1 10

k1 k2

⋅

k1 k2

+

⋅

+

1

k1

1

k1

+

+













1

k2

1

k2

+

+













⋅

,









⋅

13.629 m

=

:=

Przy liczeniu ręcznym, należy policzyć granicę przy

k1

∞

→

Po przekształceniach otrzymujemy

l0.

Lsł max 1 10k2

+

2 1

k2

1

k2

+

+













⋅

,













⋅

13.629 m

=

:=

λ

l0

isł

78.689

=

:=

Obliczenie smukłości granicznej

A

0.7

:=

B

1.1

:=

C

0.7

:=

NEd

1500kN

:=

n

NEd

Asł fcd

⋅

0.389

=

:=

λlim

20 A

⋅ B

⋅ C

⋅

n

17.286

=

:=

λlim λ

>

0

=

- należy uwzględnić efekty drugiego rzędu

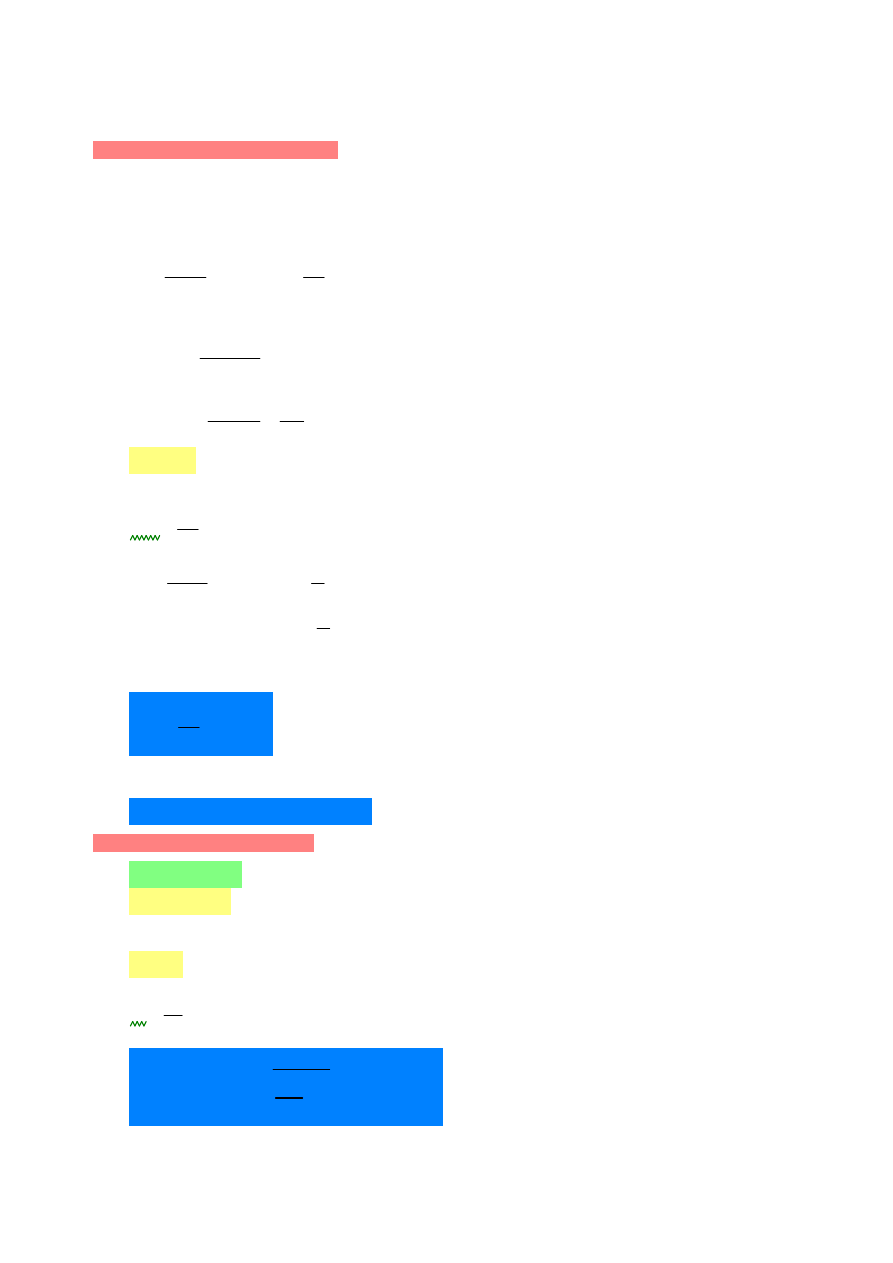
Metoda nominalnej krzywizny (66)

n

0.389

=

nbal

0.4

:=

ρzał

1.2%

0.012

=

:=

- założony stopień zbrojenia

ω

As fyd

⋅

Ac fcd

⋅

:=

As

ω

ρzał

fyd
fcd

⋅

0.2

=

:=

nu

1

ω

+

1.2

=

:=

Kr

min

nu n

−

nu nbal

−

1.0

,













1

=

:=

β

0.35

fck

200MPa

+

λ

150

−

0.025

−

=

:=

ϕef

2.9

:=

Kϕ

min 1

β ϕef

⋅

+

1.0

,

(

)

0.929

=

:=

εyd

fyd

Es

1.783

10

3

−

×

=

:=

r0

εyd

0.45 d

⋅

7.176

10

3

−

×

1

m

=

:=

- licząc ręcznie wstawiamy tu odwrotności

r

Kr Kϕ

⋅

r0

⋅

6.665

10

3

−

×

1

m

=

:=

- licząc ręcznie wstawiamy tu odwrotności

c

π

2

9.87

=

:=

e2

r

l0

2

c

⋅

0.125 m

=

:=

M2

NEd e2

⋅

188.153 kN m

⋅

⋅

=

:=

MEd

Mmax2 M2

+

388.153 kN m

⋅

⋅

=

:=

Metoda nominalnej sztywności

ρzał 0.002

≥

1

=

Ncrit

3000kN

:=

NB

Ncrit 3000 kN

⋅

=

:=

c0

10

:=

- patrz wzór 5.29!!!

β

π

2

c0

:=

MEd.

Mmax2 1

β

NB

NEd

1

−

+













⋅

397.392 kN m

⋅

⋅

=

:=

Wymiarowanie słupa

As.min

max

0.1 NEd

⋅

fyd

0.002Asł

,













4.207

10

4

−

×

m

2

=

:=

ee

MEd

NEd

0.259 m

=

:=

ei

l0

400

0.034 m

=

:=

e0

max ee ei

+

hsł

30

,

20mm

,













0.293 m

=

:=

etot

e0 0.293 m

=

:=

xeff

ξeff.lim d

⋅

0.293 m

=

:=

es1

etot

hsł

2

+

a1

−

0.545 m

=

:=

As2

NEd es1

⋅

fcd bsł

⋅

xeff

⋅

d

0.5 xeff

⋅

−

(

)

⋅

−

fyd d a2

−

(

)

⋅

3.015

10

4

−

×

m

2

=

:=

As2 0.5As.min

≤

0

=

As1

fcd bsł

⋅

xeff

⋅

fyd As2

⋅

+

NEd

−

fyd

1.37

10

3

−

×

m

2

=

:=

As1 0

>

1

=

As1 13.698 cm

2

⋅

=

n

max ceil

As1

Aϕ













2

,













5

=

:=

As1.prov

n Aϕ

⋅

15.708 cm

2

⋅

=

:=

As2 3.015 cm

2

⋅

=

n

max ceil

As2

Aϕ













2

,













2

=

:=

As2.prov

n Aϕ

⋅

6.283 cm

2

⋅

=

:=

ρobl

As1.prov As2.prov

+

bsł d

⋅

0.013

=

:=

ρzał 0.012

=

ρobl ρzał

−

ρzał

10.664 %

⋅

=

ρobl ρzał

−

ρzał

20%

≤

1

=

- prawidłowo przyjete zbrojenie