MaF

Ćwiczenia z geodezji II

1

TEMAT 1

Opracowanie wyników pomiarów kątów i kierunków wraz z oceną dokładności

4. Obliczenie kątów pomierzonych metodą wypełnienia horyzontu

4.1. Obliczenie kątów pomierzonych w poszczególnych seriach

(

)

2

"

,

'

,

,

i

s

i

s

i

s

α

α

α

+

=

;

;

'

,

'

1

,

'

'

i

s

i

s

i

s

K

K

−

=

+

α

"

,

"

1

,

"

'

i

s

i

s

i

s

K

K

−

=

+

α

gdzie

α’

si

– kąt obliczony z pierwszego położenia lunety

α”

si

– kąt obliczony z drugiego położenia lunety

4.2. Obliczenie kątów uzgodnionych

s

s

i

s

i

∑

=

1

,

α

α

, gdzie s – liczba serii

4.3. Sprawdzenie warunku zamknięcia horyzontu

∑

=

−

0

400

g

i

α

4.4. Ocena dokładności

a. Wyznaczenie poprawek V

s,i

V

s,i

= α

s,i

– α

i

gdzie

α

s,i

– kąt pomierzony w serii s

α

i

– kąt uzgodniony

b. Obliczenie średnich błędów kątów α

i

0i

i

m

m

s

α

= ±

( )

(

)

2

,

0,

1

s i

i

V

m

s

= ±

−

∑

gdzie m

0,i

– średni błąd jednostkowy kąta; m

αi

– średni błąd kąta

c. Obliczenie średniego błędu kąta na stanowisku

n

m

m

n

i

∑

±

=

1

2

α

α

, gdzie n – ilość kątów na stanowisku

4.5. Wykaz uzgodnionych kątów wraz z błędami

MaF

Ćwiczenia z geodezji II

2

Przykład tabeli ułatwiającej obliczenia

α

s,i

Poprawki V

s,i

[

cc

]

Kąt

Seria Seria

α

i

1

2

3

1

2

3

m

α,i

1

-

-

-

-

-

-

-

1

,

s

V

∑

∑

1

,

1

,

s

s

V

V

2

-

-

-

-

-

-

-

2

,

s

V

∑

,

2

,

s

s

V

V

∑

3

-

-

-

-

-

-

-

3

,

s

V

∑

∑

3

,

3

,

s

s

V

V

i

V

,

1

∑

i

V

,

2

∑

i

V

,

3

∑

∑

∑

i

i

V

V

,

1

,

1

i

i

V

V

,

2

,

2

∑

i

i

V

V

,

3

,

3

∑

∑

0,i

m

5. Wyrównanie stacyjne kierunków według Hausbrandta i Weigla

5.1. W dzienniku pomiarowym podczas pomiaru wykonujemy:

a. Obliczenie kierunków poprawionych o skręcenie limbusa

'

'

,

,

s i

'

,1

s i

K

K

K

=

−

s

dla I położenia lunety

"

"

,

,

s i

"

,1

s i

K

K

K

=

−

s

dla II położenia lunety

gdzie

K

s,i

’ – kierunek pomierzony w I położeniu lunety

K

s,i

” – kierunek pomierzony w II położeniu lunety

b. Obliczenie średnich wartości kierunków w seriach

'

"

,

,

,

2

s i

s

s i

K

K

K

+

=

i

c. Obliczenie kierunków poprawionych o odchyłkę niezamknięcia horyzontu

,

,

,

s i

s i

s

K

K

K

=

+ ∆

i

(

)

,

1

,

1

s n

s i

i

K

K

n

+

−

∆

=

−

gdzie

- poprawka ze względu na niezamknięcie horyzontu

i

s

K

,

∆

n – ilość mierzonych kierunków

d. Obliczenie kierunków uzgodnionych

s

K

K

s

i

s

i

∑

=

1

,

5.2. Ocena dokładności

a. Obliczenie średniego kierunku serii

n

K

K

n

i

s

s

∑

=

∨

1

,

MaF

Ćwiczenia z geodezji II

3

b. Obliczenie średniej ogólnej

s

K

K

s

s

∑

∨

=

1

kontrolnie

n

K

K

n

i

∑

=

1

c. Obliczenie przesunięcia poszczególnej serii

s

s

K

K

∨

−

=

δ

d. Obliczenie poprawek do spostrzeżeń K

s,i

(

)

s

i

s

i

i

s

K

K

V

δ

+

−

=

,

,

e. Obliczenie średniego błędu jednostkowego pojedynczego spostrzeżenia

( )

(

)(

)

2

,

1

0

1

1

ns

s i

V

m

n

s

= ±

−

−

∑

f. Obliczenie średniego błędu kierunku

s

m

m

k

0

±

=

5.3. Wykaz uzgodnionych kierunków wraz z błędami

7. Zestawienie otrzymanych wartości kątów wraz z błędami z obu metod pomiaru

Kąt

Metoda wyp.

horyzontu

m

α,i

Metoda

kierunkowa

m

k

m

α

α

∆

α

1

α

2

α

3

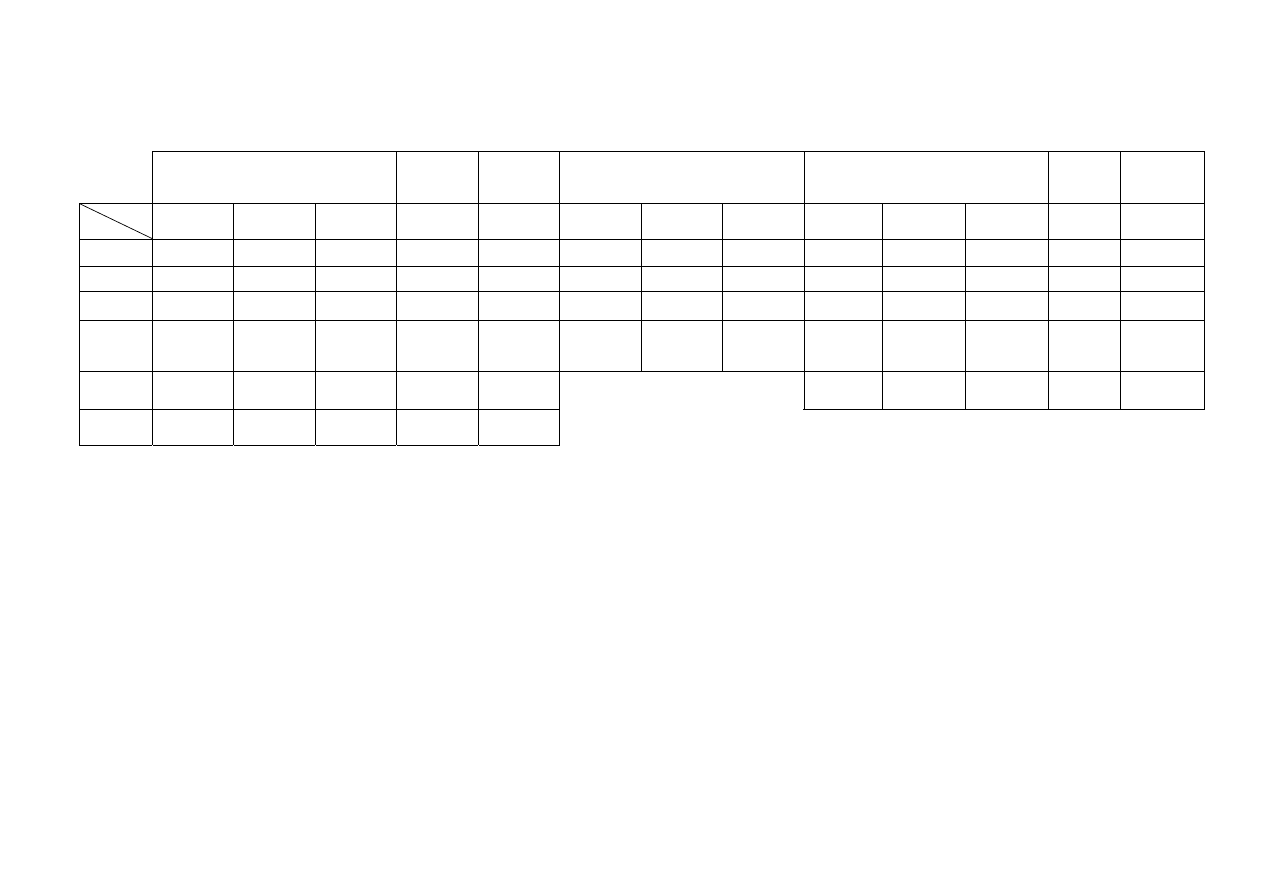
MaF

Ćwiczenia z geodezji II

5

K

V

Wyrównanie stacyjne kierunków według Hausbrandta i Weigla - przykład

s,i

∑

s

i

s

K

1

,

Ki

K

s,i

+δ

s

s,i

∑

s

i

s

V

1

,

∑

s

i

s

V

1

2

,

s

i

1

2

3

1

2

3

1

2

3

1

0,00000

0,00000

0,00000

0,00000

0,00000

0,00058

-0,00019

-0,00039

-5,8

1,9

3,9

0,0

52,1

2

97,12980

97,12960 97,12770 291,38710

97,12903

97,13038

97,12941 97,12731

-13,4

-3,8

17,2

0,0

491,6

3

185,69480 185,69730 185,69980 557,09190 185,69730 185,69538 185,69711 185,69941

19,2

1,9

-21,1

0,0

818,7

∑

n

i

s

K

1

,

282,82460 282,82690 282,82750 848,47900

0,0

0,0

0,0

0,0

1362,4

∨

s

K

94,27487

94,27563 94,27583 282,82633 282,82633

583,6

21,4

757,4

1362,4

δ

s

0,00058

-0,00019

-0,00039

94,27544

94,27544

m

0

= 18.5

cc

m

k

= 10

cc