dr inż. Mariusz Frukacz Ćwiczenia z geodezji II

Transformacja współrzędnych prostokątnych płaskich sposobem Helmerta Transformacja czteroparametrowa Helmerta wyrażona jest wzorami: X = c + bx − ay

i

i

i

Y = d + ax + by

(1)

i

i

i

gdzie

xi, yi – współrzędne i-tego punktu w układzie pierwotnym, Xi, Yi - współrzędne i-tego punktu w układzie wtórnym.

Wyznaczenie parametrów transformacji i ocena dokładności

1. Obliczenie wsp. środków ciężkości w obu układach (tylko z punktów dostosowania):

[ x ]

[ y ]

[ X ]

[ Y ]

i

= x ; i = y ; i = X ; i = Y

(2)

0

n

0

n

0

n

0

n

2. Centrowanie współrzędnych (obliczenie wsp. zredukowanych o środki ciężkości): ( y − y = y

∆ , ( x − x = x

∆ , (X − X = X

∆ , (Y − Y = Y

∆

(3)

i

0 )

i

0 )

i

0 )

i

0 )

i

i

i

i

3. Wyznaczenie parametrów transformacji: n

n

∑ (∆x Y

y X

∑ (∆x X

y Y

i∆

i + ∆ i∆

i )

i∆

i − ∆

i∆

i )

i =

a = 1

;

i =

b = 1

(4)

n

n

∑ (∆ 2

x + ∆ 2

y

∑ (∆ 2

x + ∆ 2

y

i

i )

i

i )

i =1

i =1

c = y a − x b + X ; d = − x a − y b + Y

(5)

0

0

0

0

0

0

Jeśli (5) podstawimy do (1) to otrzymamy drugą wersję wzorów na transformację: X = X + x − x b − y − y a i

0

( i 0) ( i 0)

Y = Y + x − x a + y − y b (6)

i

0

( i 0) ( i 0)

4. Obliczenie poprawek dla punktów dostosowania: t

V

= X − X ;

t

V = Y − Y

(7)

X

i

i

Y

i

i

i

i

5. Ocena dokładności

2

2

∑ V

∑ V

i

i

m =

⇒ m =

(8)

0

0

2 n − u

2 n − 4

Jako kryterium oceny dokładności transformacji, w formie zgeneralizowanej, możemy podać 1

warunek m ≤

m

, gdzie m

jest dopuszczalnym średnim błędem położenia punktu w 0

p dop.

p dop.

2

określonej klasie osnowy.

dr inż. Mariusz Frukacz

Ćwiczenia z geodezji II

6. Obliczenie korekt post-transformacyjnych Hausbrandta: n

n

∑ (r V

∑ (r V

ji

i

Y )

ji

Xi )

i =

V

;

i =

V

(9)

Y

= 1

X

= 1

j

n

j

n

∑ r

∑ r

ji

ji

i =1

i =1

gdzie

1

1

r =

=

(10)

ji

2

2

2

d

(X − X ) + (Y − Y )

i

j

i

j

ji

rji – waga (i = 1, 2, ... , n),

n – liczba punktów dostosowania.

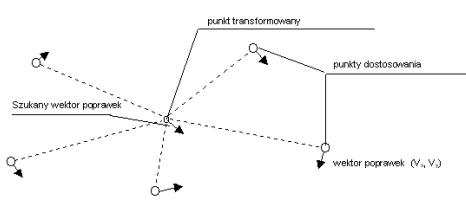
Elementy przyjęte do liczenia wag i ich oznaczenia zastosowane we wzorach (9) i (10) zilustrowano na rysunku.

7. Obliczenie ostatecznych wartości współrzędnych: X =

+

= +

j

X

V ;

Y

Y

V

(11)

j

X

j

j

Y

j

j

Wyznaczenie parametrów transformacji z zapisu macierzowego układu równań poprawek

1. Ułożenie równań poprawek (wprowadzając (1) do (7)): V

= y a − x b − c + X

X

1

1

i

1

V = − x a − y b − d + Y

Y

1

1

i

1

........................................

(12)

V

= y a − x b − c + X

X

n

n

n

n

V = − x a − y b − d + Y

Y

n

n

n

n

2. Zapis macierzowy wzorów (12) ma następującą postać: V = AX + L

(13)

dr inż. Mariusz Frukacz Ćwiczenia z geodezji II

gdzie



 y − x −1 0 

V



1

1





1

X

X









− x − y 0 −1



1

a 





V







1

1



Y

1

Y

 

 1 





 ................... 

b

⋮

= V



 =

  =

 ⋮  =





A

X

L (14)

 ...................

c









V



 

X

X





n





 y x 1 0

− −

d

n

n

n





V









Yn 

n

Y



− x − y 0 −1

n

n



3. Stosując warunek Φ = VTV = min obliczamy wektor parametrów 1

−

X = −(ATA) ATL

(15)

Punkty 4 –7 bez zmian.

Przykład:

Układ pierwotny:

Nr

X

Y

1

0.000

0.000

2

0.000

10.000

3

15.000

5.000

4

3.000

7.000

5

10.000

4.000

Układ wtórny:

Nr

X

Y

1

120.006

99.987

2

100.015

100.008

3

109.985

130.003