Przykłady
Przykład 1
Rozważmy przedziały na osi rzeczywistej A
= (1, 2] oraz B = [3, 5). Iloczynem kartezjańskim tych
zbiorów jest, zgodnie z definicją, zbiór wszystkich par uporządkowanych (x, y) takich, że x ∈ A oraz
y ∈ B. Iloczyn A × B jest zatem odpowiednim prostokątem na układzie współrzędnych zadanym przez
warunki: 1 < x ≤ 2 oraz 3 ≤ y < 5.
Przykład 2
Przedstawimy teraz dowód dla poniższej własności iloczynu kartezjańskiego (rozdzielność względem
iloczynu zbiorów):
A × (B ∩ C) = (A × B) ∩ (A × C)
Należy pokazać, że: ∀
x
(x ∈ A × (B ∪ C) ⇔ x ∈ (A × B) ∪ (A × C)).
Niech x będzie dowolne. Rozpatrzmy dwa przypadki: albo x nie jest parą uporządkowaną, albo x jest
parą uporządkowaną. W pierwszym przypadku równoważność oczywista (obie strony fałszywe, obiekt
niebędący parą uporządkowaną nie może należeć do iloczynu kartezjańskiego).
Jeśli zaś x = (a, b), to:
L : x ∈ A × (B ∩ C) ⇔
1
(a, b) ∈ A × (B ∩ C) ⇔
2
a ∈ A ∧ b ∈ (B ∩ C) ⇔
3
⇔
a ∈ A ∧ (b ∈ B ∧ b ∈ C) ⇔
4
a ∈ A ∧ a ∈ A ∧ b ∈ B ∧ b ∈ C ⇔
5
⇔
(a ∈ A ∧ b ∈ B) ∧ (a ∈ A ∧ b ∈ C) ⇔
⇔
(a, b) ∈ (A × B) ∧ (a, b) ∈ (A × C) ⇔
⇔
x ∈ (A × B) ∧ x ∈ (A × C) ⇔ x ∈ (A × B) ∩ (A × C) : P
Przykład 3
A × B ≠ ∅ ⇔ (A ≠ ∅ ∧ B ≠ ∅)
Powyższą równoważność udowodnimy, wykazując prawdziwość obu implikacji.
⇒
Załóżmy, że A × B ≠ ∅. Wtedy istnieje choć jeden element iloczynu kartezjańskiego A × B. Dla pewnej
pary (a, b) jest zatem: a ∈ A oraz b ∈ B. Oczywiście wtedy mamy: A ≠ ∅ oraz B ≠ ∅.
⇐
1
Ponieważ założyliśmy, że x = (a, b)
2
Z definicji iloczynu kartezjańskiego.
3
Definicja iloczynu zbiorów.
4
Własność łączności koniunkcji oraz prawo: α ⇔ α ∧ α.
5
Prawa łączności i przemienności koniunkcji.
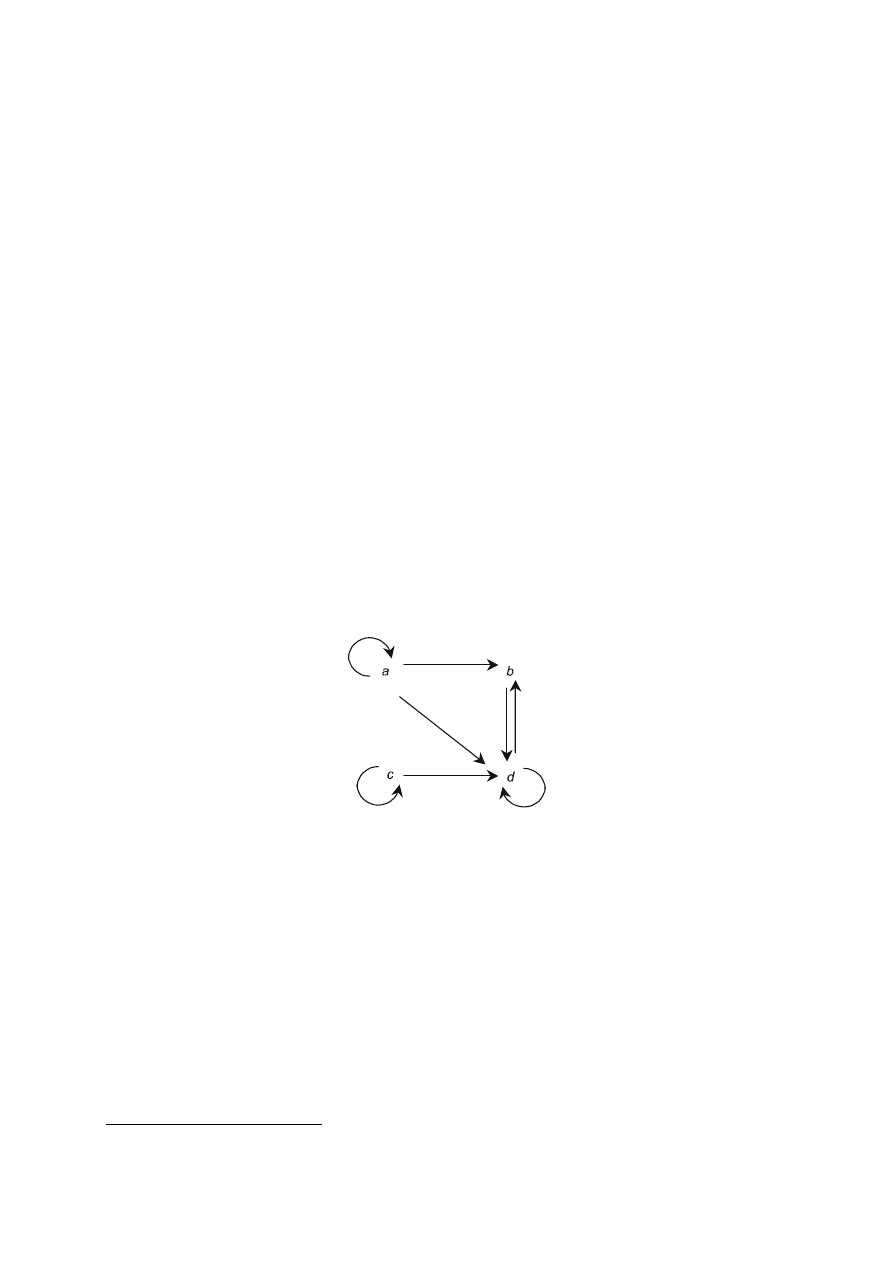
Załóżmy, że A
≠ ∅ ∧ B ≠ ∅. Wtedy istnieją elementy a oraz b takie, że a ∈ A oraz b ∈ B. Ale
oczywiście wtedy para uporządkowana (a, b) zgodnie z definicją iloczynu kartezjańskiego należy do
zbioru A
× B. Wtedy oczywiście A × B ≠ ∅.
Przykład 4
W ogólnym przypadku nie zachodzi równość: A – (B
× C) = (A – B) × (A – C). Poniżej pokażemy
przykład takich trzech zbiorów, dla których powyższa równość nie jest spełniona.
Niech A = B = C = R (zbiór liczb rzeczywistych).
Mamy wtedy:
L = A – (B
× C) = R – (R × R) = R
6
.
P = (A – B)
× (A – C) = (R – R) × (R – R) = ∅ × ∅ = ∅.
Oczywiście L
≠ P.
Przykład 5
Rozważmy zbiór A = {a, b, c, d} i określoną na nim relację
δ = {(a, a), (c, c), (a, b), (d, b), (c, d), (a, d), (b, d), (d, d) }.
Reprezentacja graficzna tej relacji jest przedstawiona na rysunku 1.
Rysunek 1
Reprezentacja macierzowa tej relacji jest następująca :
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
1
0
1
0
1
1
0
0
1
0
0
0
1
0
1
1
d
c
b
a
d
c
b
a
Rysunek 2
6
Zauważmy, że zbiory R oraz R
× R są rozłączne (nie mają części wspólnej).
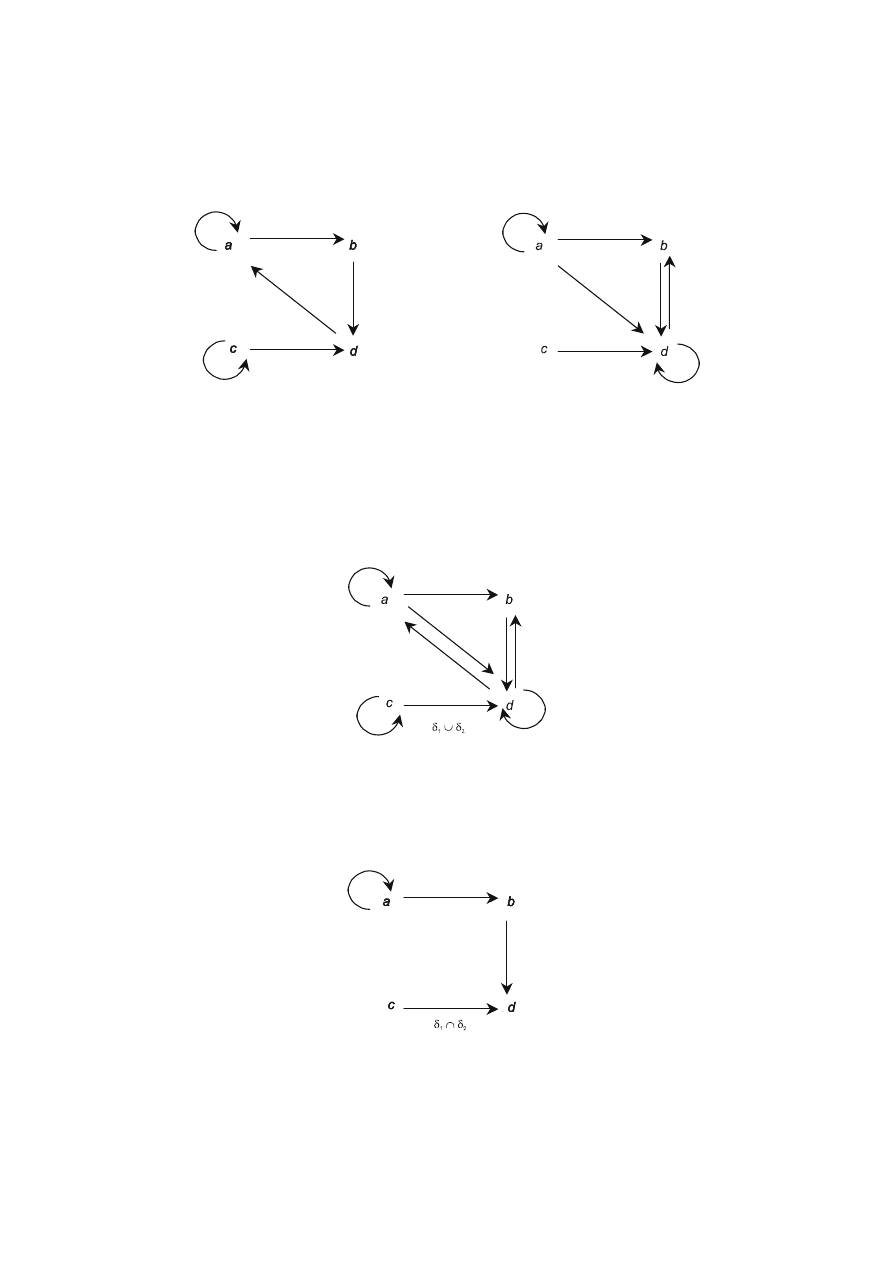
Przykład 6
Rozważmy dane niżej relacje określone na czteroelementowym zbiorze A = {a, b, c, d}:
Rysunek 3
Zgodnie z odpowiednimi definicjami mamy:
Suma relacji
δ
1
∪
δ
2
:
Rysunek 4
Iloczyn relacji
δ
1
∩
δ
2
:
Rysunek 5
δ
2
δ
1
Rysunek 6
Konwers relacji δ
2
:
Rysunek 7
Przykład 7
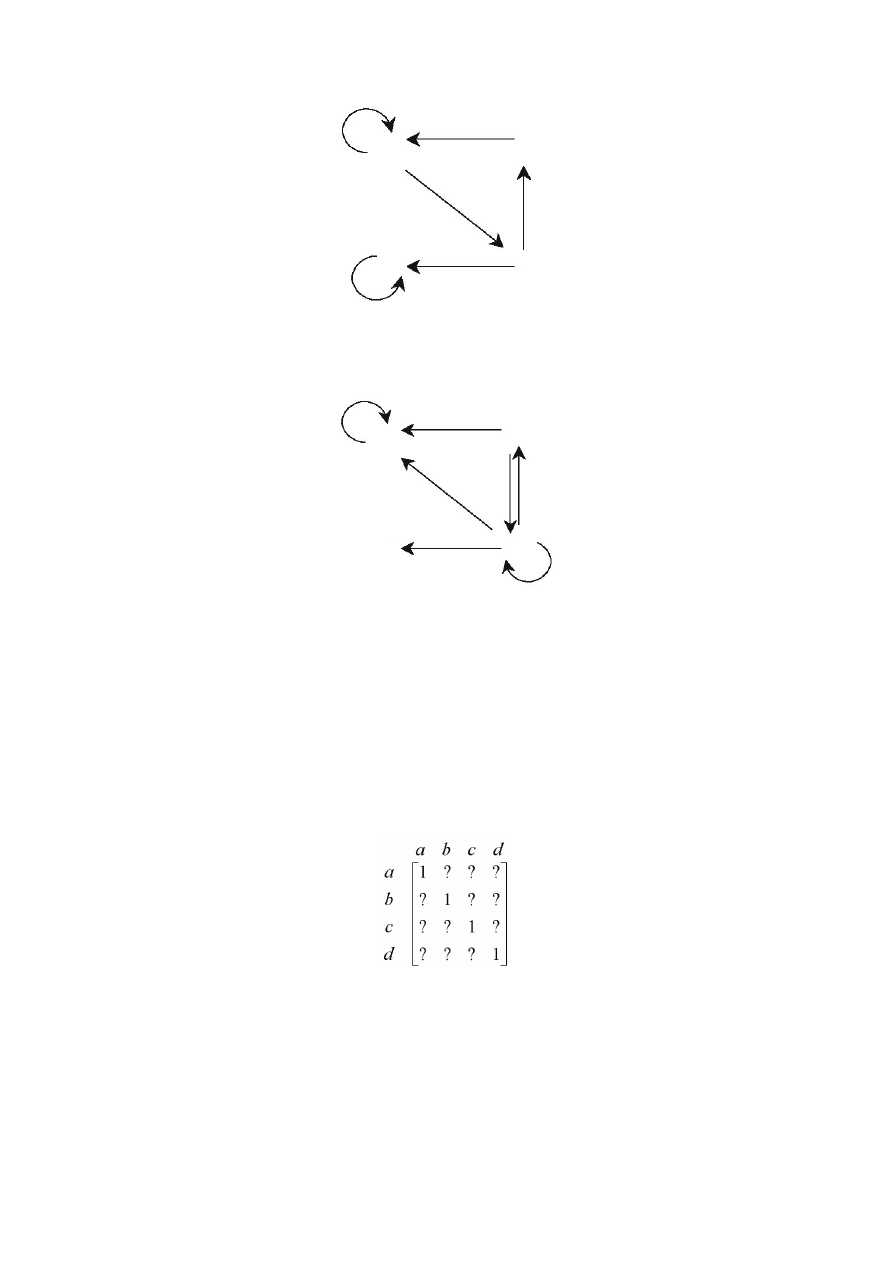
Jeżeli relacja jest zwrotna, to w reprezentującej ją macierzy na głównej przekątnej muszą być same
jedynki. Macierz dla powyższej relacji jest następująca (znaki zapytania oznaczają, że zwrotność od
zawartości tych komórek nie zależy):
Rysunek 8
Jeżeli relacja jest przeciwzwrotna, to w reprezentującej ją macierzy na głównej przekątnej muszą być
same zera. Macierz dla powyższej relacji jest następująca:
a
b
c
d
δ
1
–1
a
b
c
d
δ
1
–2
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
0
?
?
?
?
0
?
?
?
?
0
?
?
?
?
0
d
c
b
a
d
c
b
a
Rysunek 9
Jeżeli relacja jest symetryczna, to reprezentująca ją macierz musi być symetryczna względem głównej
przekątnej. Przykładowa macierz dla powyższej relacji jest następująca:
Rysunek 10
Jeżeli relacja jest asymetryczna, to reprezentująca ją macierz nie może zawierać żadnych
symetrycznych względem głównej przekątnej jedynek oraz nie może mieć jedynek na głównej
przekątnej. Przykładowa macierz dla powyższej relacji jest następująca:
Rysunek 11
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
0
1
0
1
1
0
0
0
0
0
1
1
1
0
1
0
d
c
b
a
d
c
b
a
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
0
1
0
1
0
0
0
1
0
1
0
0
0
0
1
0
d
c
b
a
d
c
b
a