Ćwiczenie 4: Energia sprężysta i hipotezy wytężeniowe,

wersja dla studentów

(opracowali: Z. Waszczyszyn i M. Kłos)

Wzory dla energii sprężystej

 Energia sprężysta U, złożona z energii odkształcenia objętościowego

V

U i postaciowego

f

U

















)

V

(

)

V

(

f

V

f

V

,

dV

dV

U

U

U

(1)

gdzie energia właściwa wynosi:













,

2

1

6

E

E

6

2

1

2

y

x

2

z

y

x

V

z



































(2a)



























































2
zx

2
yz

2
xy

x

z

z

y

y

x

2

z

2

y

2

x

f

3

E

3

1









.

4

3

1

3

E

2
zx

2
yz

2
xy

x

z

z

y

y

x

2

z

2

y

2

x























































(2b)

Przykład 1

(Krzyś i Życzkowski) [5], str. 94

Jak zmienia się stosunek energii:

U

/

U

f

i

U

/

U

v

dla pręta pryzmatycznego rozciąganego siłą P

w zależności od wartości współczynnika Poissona  .

Stan naprężenia jednoosiowego









A

/

P

x

generuje:





v

f





,

,







v

f







.

Energia sprężysta pręta ze względu na stan naprężenia jednorodnego:

V

E

2

V

V

dV

dV

U

U

U

2

)

v

(

v

f

v

)

v

(

f

v

f





























,

a więc stąd wynika:





V

V

U

v

f















.

Stosunek energii:





,

1

3

2

E

2

E

3

1

U

U

C

f

f

f

























.

2

1

3

1

E

2

E

6

2

1

C

v

v



















(3)

Na rys.1 podano zależności

 



f

C

i

 



v

C

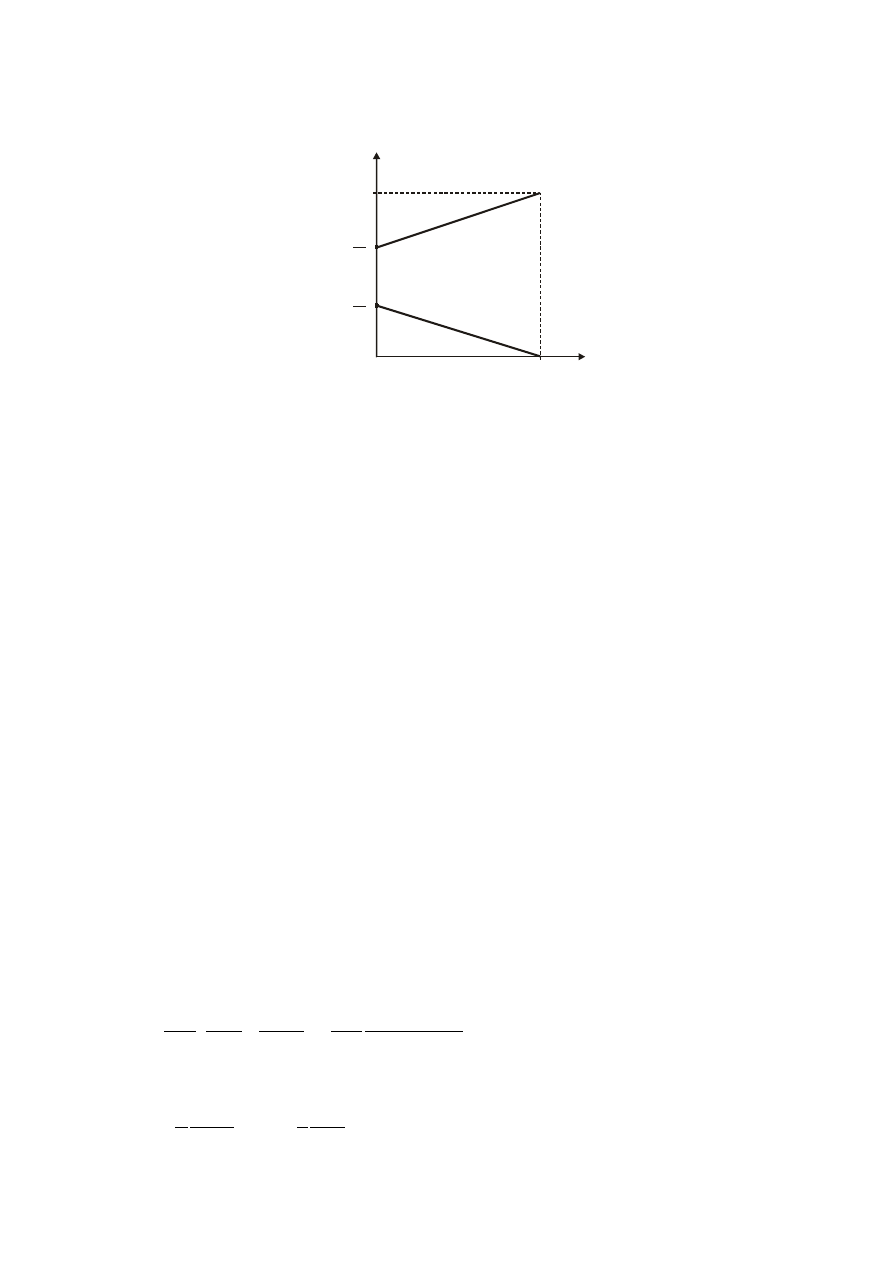
0 0 . 5

1 . 0

C

f

C

f

C



C





2
3

1
3

Rys.1. Współczynniki

f

C i

v

C jako funkcje współczynnika Poissona 

dla pręta swobodnie rozciąganego.

Widać, że dla

5

.

0





będzie

0

C

v

 , gdyż materiał jest nieściśliwy i w pręcie pojawi się tylko

energia odkształcenia postaciowego.

Przykład 2 (Krzyś i Życzkowski [5], str. 96

Pręt pryzmatyczny ściskany siłą P umieszczony w dopasowanej tuleji, idealnie gładkiej (nie
występują siły tarcia między prętami i tuleją). Zbadać jak się zmieniają współczynniki

 



f

C

oraz

 



v

C

.

W pręcie występuje jednoosiowy stan odkształcenia

0

,

0

,

0

zx

yz

xy

z

y

x

























,

(4)

oraz przestrzenny stan naprężeń, rys.2a

z

y

x









,



y



,

(5)

a, więc:





z

y





(6)

Zamiast prowadzić obliczenia w naprężeniach możemy obliczenia wykonać znacznie prościej
korzystając ze wzorów (2) wyrażonych przez odkształcenia:





v

f











,

2

1

1

1

2

E

2

1

1

1

2

6

E

2
x

2
x













































(7)

stąd wynikają współczynniki:

.

1

1

3

1

C

,

1

2

1

3

2

C

v

f





















(8)

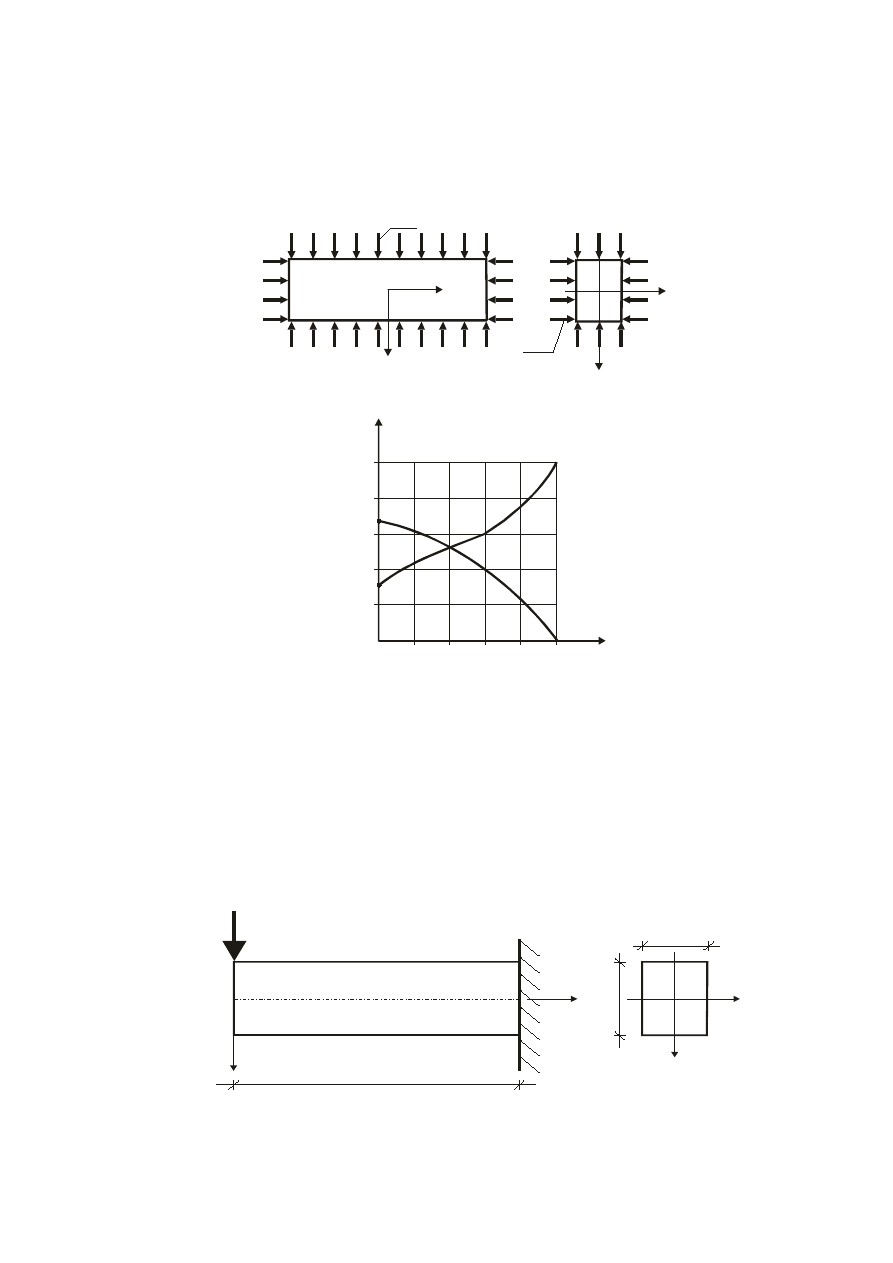
Na rys. 2b pokazano zależności

 



f

C

oraz

 



v

C

. W przeciwieństwie do pręta swobodnego, pręt

skrępowany tuleją dla

5

.

0





ma C

v

= 1.0 , gdyż nie może się odkształcić czysto postaciowo i

zachowuje się jak idealnie sztywny.

 

x

 

x



x

x

x

y

y

Rys. 2a

0 0 . 5

1 . 0

0 . 6 6 7

0 . 3 3 3

C

f

C

f

C



C





Rys. 2b

Rys.2:a) ściskanie pręta w dopasowanej tuleji, b) współczynniki

 



f

C

oraz

 



v

C

.

Przykład 3 (Krzyś i Życzkowski [ ], s. 99)

Obliczyć wartość energii odkształcenia postaciowego i objętościowego dla podanej belki,
przyjmując wzory z wytrzymałości materiałów i niżej podane dane.
b = 1 cm, h = 2 cm, l = 20 cm, P = 10KN, E = 210 GPa,  = 0.3 .

x

b

y

z

h

P

l

y

Rys. 3

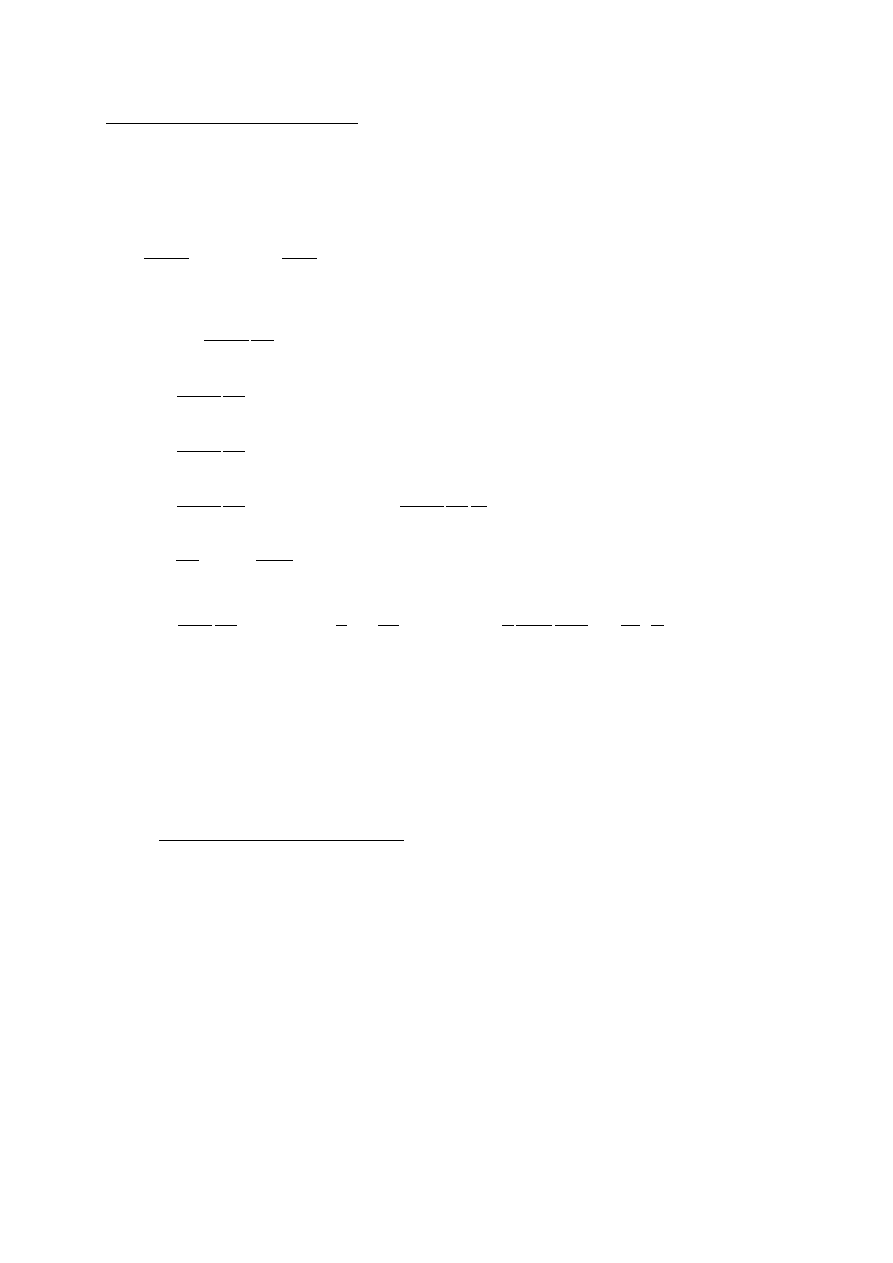
Wzory z wytrzymałości materiałów



x



,



xy



.

Z wzorów (2) na energię właściwą







2

6

2

1

x

v

E







,













2

2

3

3

1

xy

x

f

E









(9)

Podstawiamy (9) do wzoru (2):

3

l

I

P

E

6

2

1

dx

dy

y

x

b

I

P

E

6

2

1

dx

dy

dz

y

x

I

P

E

6

2

1

dz

y

x

dy

dx

I

P

E

6

2

1

dV

y

x

I

P

E

6

2

1

U

3

z

2

2

/

h

2

/

h

2

l

0

2

2
z

2

2

/

b

2

/

b

2

/

h

2

/

h

2

l

0

2

2
z

2

2

/

b

2

/

b

2

2

2

/

h

2

/

h

l

0

2
z

2

)

v

(

2

2

2
z

2

v





































































































(10)











3

3

2

2

1

3

2

bh

l

P

E

U

v



kNm

833

.

0

l

h

10

9

1

bh

l

P

E

1

3

4

dV

y

4

h

4

3

dV

y

x

I

P

E

3

1

U

2

3

3

2

)

V

(

2

2

2

)

V

(

2

2

2
z

2

f

















































































Całkowita energia i współczynniki

V

C i

f

C

U = 0.960 kNm ,

C

V

= 0.132, C

f

= 0.868 .

Wzory dla hipotez wytężeniowych

1). Hipotezy naprężeniowe:

G: Galileusza

r

1

k





,

(11)

TG: Tresci - Guesta

r

3

1

k









.

(12

2). Hipotezy odkształceniowe:

SV: Saint–Venanta





r

3

2

1

k















.

(13)

3). Hipotezy energetyczne

HMH: Hubera - Misesa – Hencky`ego





2
zx

2
yz

2
xy

x

z

z

y

y

x

2
z

2

y

2
x

1

3

3

2

2

1

2
3

2
2

2

1

2
0

3













































































(14)

B: Burzyńskiego





































































2
HMH

2

z

y

x

2

z

y

x

0

4

1

1

2

1

(15)

Przykład 4

(Krzyś i Życzkowski [5], str. 123)

Stan naprężenia w punkcie jest określony następującymi danymi:
a)

3

.

0

,

0

,

MPa

10

yz

zx

xy

z

y

x































b)

3

.

0

,

0

,

MPa

10

yz

zx

xy

z

y

x

































Przypadek a)

Dla hipotezy HMH możemy od razu obliczyć



HMH



Dla pozostałych hipotez najpierw liczymy naprężenia główne

MPa

1

.

4

,

MPa

10

,

MPa

1

.

24

3

2

1















Dalej liczymy:



G





TG





SV





HMH



Dla hipotezy Burzyńskiego przyjmujemy:

1





(stal):

MPa

5

.

24

HMH

B









6

.

3





(żeliwo):



B



Przypadek b)

MPa

1

.

24

,

MPa

10

,

MPa

1

.

4

3

1

2

















Wyniki dla różnych hipotez

Wyniki dla a)

MPa

G

1

.

4





24.1 MPa





MPa

1

.

28

1

.

24

1

.

4

TG











28.1 MPa





MPa

3

.

14

1

.

24

10

3

.

0

1

.

4

SV















22.3 MPa





1

MPa

5

.

24

B

HMH













24.5 MPa





MPa

6

.

27

6

.

3

B









6.02 MPa

Przykład 5

(Krzyś i Życzkowski [5], str. 128

Dla przypadku czystego ścinania określonego jednym naprężeniem  porównać naprężenia
zastępcze wynikające z hipotez.

Według hipotezy

max



:





2

0



Według hipotezy Hubera:

.

3

0



 

W porównaniu z hipotezą Hubera, która – jak wykazuje doświadczenie – najlepiej odpowiada
rzeczywistemu zachowaniu się materiałów elastoplastycznych, hipoteza

max



daje wynik o

6

.

15

3

3

2





% za wysoki (na korzyść pewności).

Przykład 6

(Krzyś i Życzkowski [5], str. 125

Dla stanu naprężenia o charakterystycznym stosunku

1

:

2

:

4

:

:

3

2

1









określić dopuszczalne

wartości naprężeń zastępczych za pomocą TG i HMH przyjmując:
a) stal o naprężeniach dopuszczalnych

,

3

.

0

,

MPa

0

.

120

k

k

c

r









b) żeliwo o naprężeniach dopuszczalnych

3

.

0

,

MPa

3

.

33

k

,

MPa

0

.

120

k

r

c









Według hipotezy TG (Coulomba – Guesta)

r

k





3

1





uwzględniając

,

4

1

1

3



 

otrzymujemy







3

2

1







zatem dla stali

,

MPa

160

1





,

MPa

80

2





,

MPa

40

3





dla żeliwa zaś

,

MPa

4

.

44

1





,

MPa

2

.

22

2





,

MPa

1

.

11

3





Według hipotezy HMH

r

k













1

3

3

2

2

1

2

3

2

2

2

1



















,

uwzględniając

1

2

2

1 





,

1

3

4

1 





otrzymujemy:

r

2

1

2

1

2

1

2

1

2

1

2

1

k

4

1

8

1

2

1

16

1

4

1

























,



1





2





3



czyli

,

51

.

1

1

r

k





,

76

.

0

2

r

k





,

38

.

0

3

r

k





a więc dla stali

MPa

2

.

181

1





,

,

MPa

6

.

90

2





,

MPa

3

.

45

3





dla żeliwa zaś

MPa

3

.

50

1





,

,

MPa

15

.

25

2





,

MPa

6

.

12

3





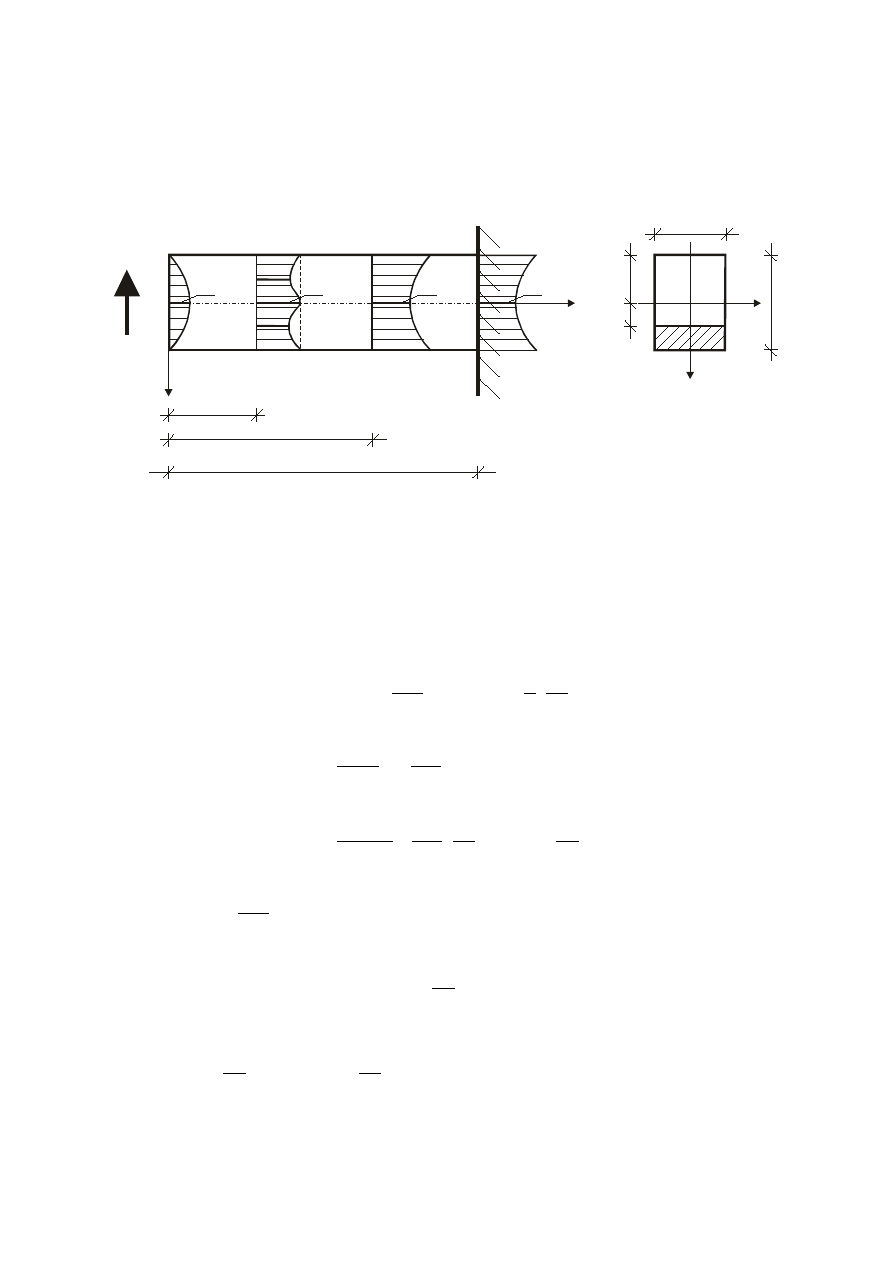
Przykład 7.

(wg Krzysia i Życzkowskiego [5], s. 130)

Dla belki wspornikowej o schemacie jak na rysunku wyznaczyć odległość x



, która rozróżnia

obszary dla których naprężenia zredukowane są maksymalnie na osi belki (y=0) lub we
włóknach skrajnych (y = h/2)

x

b

y

z

y

=

y

P

l

- y

d

y

d

y

0



0

0

1

y

2

y

y

3

3



0

0



0

g



0

d

y

=

1

y

=

2



0

g



0

0



0

g



0

0

x

*

x

* *

g

d

d

y

h

=

2

y

Rys. 4

L = 1.0 cm

E = 210 GPa

H = 20 cm

E = 2.10 - 10

3

MPa

B = 6 cm

- Pole sił wewnętrznych

 

 

P

x

Q

,

Px

x

M





- Charakterystyki przekroju





















2

2

z

2

2

z

y

4

h

2

b

)

y

(

S

,

1

bh

I

,

bh

A

(16)

- Pola naprężeń

Fxy

2

xy

bh

P

12

y

I

)

x

(

M

3

z

x













(17)









































2

2

2

2

3

z

z

xy

y

4

h

F

y

4

h

bh

P

6

b

I

)

y

(

QS

(18)

gdzie:

3

bh

P

6

F



a) Hipoteza HMH











































2

2

2

2

2

2

2

2
0

y

4

h

3

y

x

4

F

3

(19)

Stąd równania

ścinanie

2

2

2

zginanie

2

2

2

0

y

4

h

3

y

x

4

F





























 

(19.1)

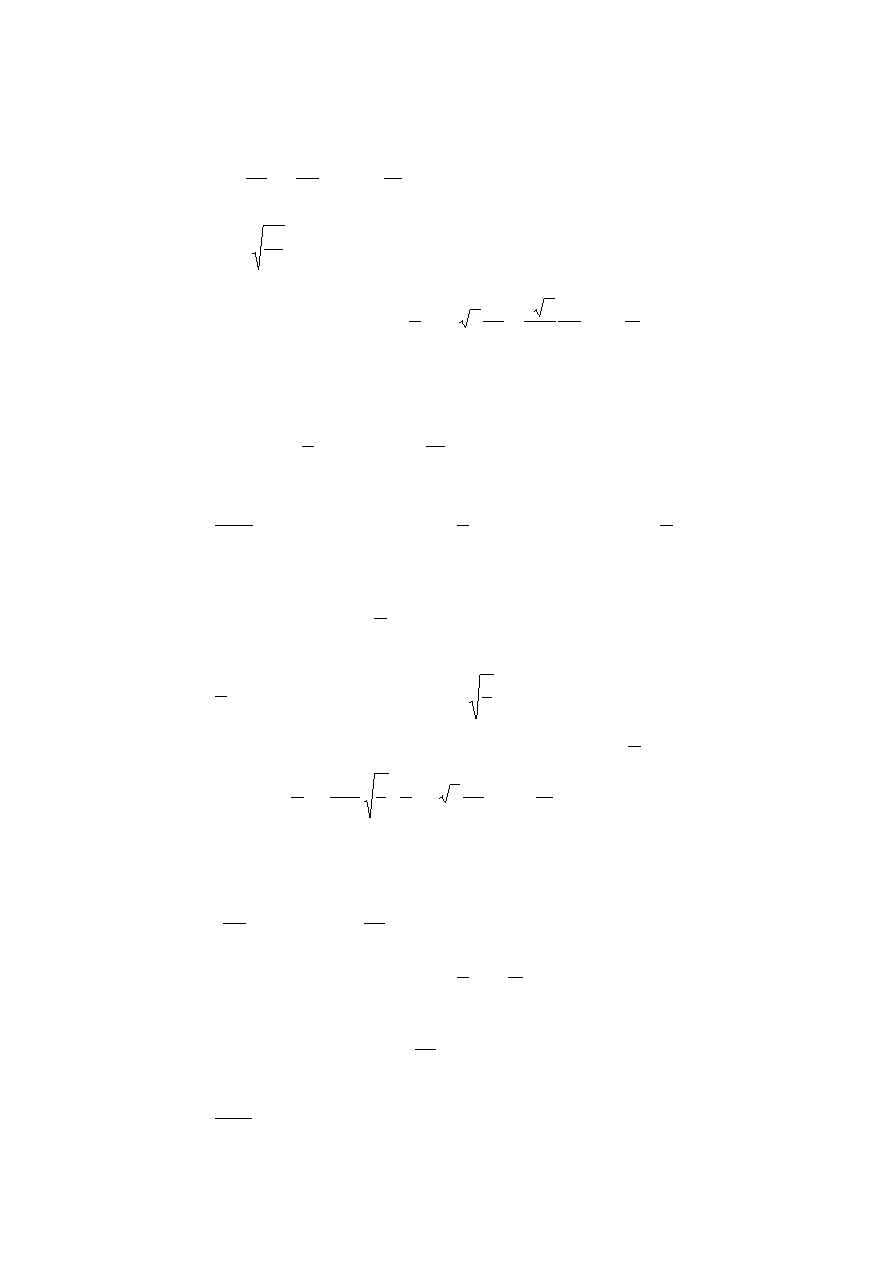
Rozumowanie: Szukamy takiego

*

x , dla którego naprężenie zredukowane od zginania we włóknach

skrajnych jest równe naprężeniu zredukowanemu od ścinania dla osi obojętnej, a więc:

,

h

16

3

x

16

h

3

4

h

x

4

2

2
*

4

2

2







(20)

stąd

h

433

.

0

h

16

3

x

*





(21)

Wartość naprężenia maksymalnego naprężenia zredukowanego wynika z (2) lub (1):





A

P

6

.

2

bh

P

2

3

3

4

h

3

F

2

h

y

,

x

0

y

,

x

2

*

0

*

0





























(22)

Obliczanie

*

*

x jest bardziej złożone, gdyż wymaga wyznaczenia położenia ekstremów

.

0

y

y

,

0

y

3

2

1







Równania (19.1) rozpisujemy do postaci

,

h

16

3

y

x

4

h

2

3

y

3

s

4

2

2

2

4

2





















(23)

gdzie:

.

F

/

s

0





Poszukujemy punktów istnienia ekstremów z równania

 









0

y

s

2

0

x

4

h

2

3

2

y

12

y

y

x

4

h

2

3

2

y

12

2

2

2

2

2

3

















































(24)
i stąd pierwiastki:

,

0

y

1



0

x

4

h

2

3

y

6

2

2

2



















(25)

Będziemy mieli

0

y

y

3

1





jeśli wyraz wolny będzie równy zeru, a więc:







0

x

4

h

2

3

2

2

h

612

.

0

h

8

3

x

*

*





(26)

Wartość maksymalnego naprężenia zredukowanego jest osiągana dla

2

h

y

 i zgodnie z (17) wynosi:

A

P

67

.

3

bh

P

3

3

2

h

h

8

3

bh

P

12

2

h

y

,

x

3

0























(27)

b) hipoteza TG

4

2

2
0

4











(28)

stąd:

2

2

2

2

2

2

0

y

4

h

4

y

x

4

F





























 

(29)





A

P

3

2

h

,

x

0

,

x

,

h

5

.

0

x

*

0

*

0

*























(30)

Zamiast równania (23) otrzymujemy:





4

h

y

x

2

h

2

y

4

s

2

2

2

2

4

2









(31)

stąd:

 





0

y

x

2

h

4

y

12

0

y

s

2

2

3

2















(32)

,

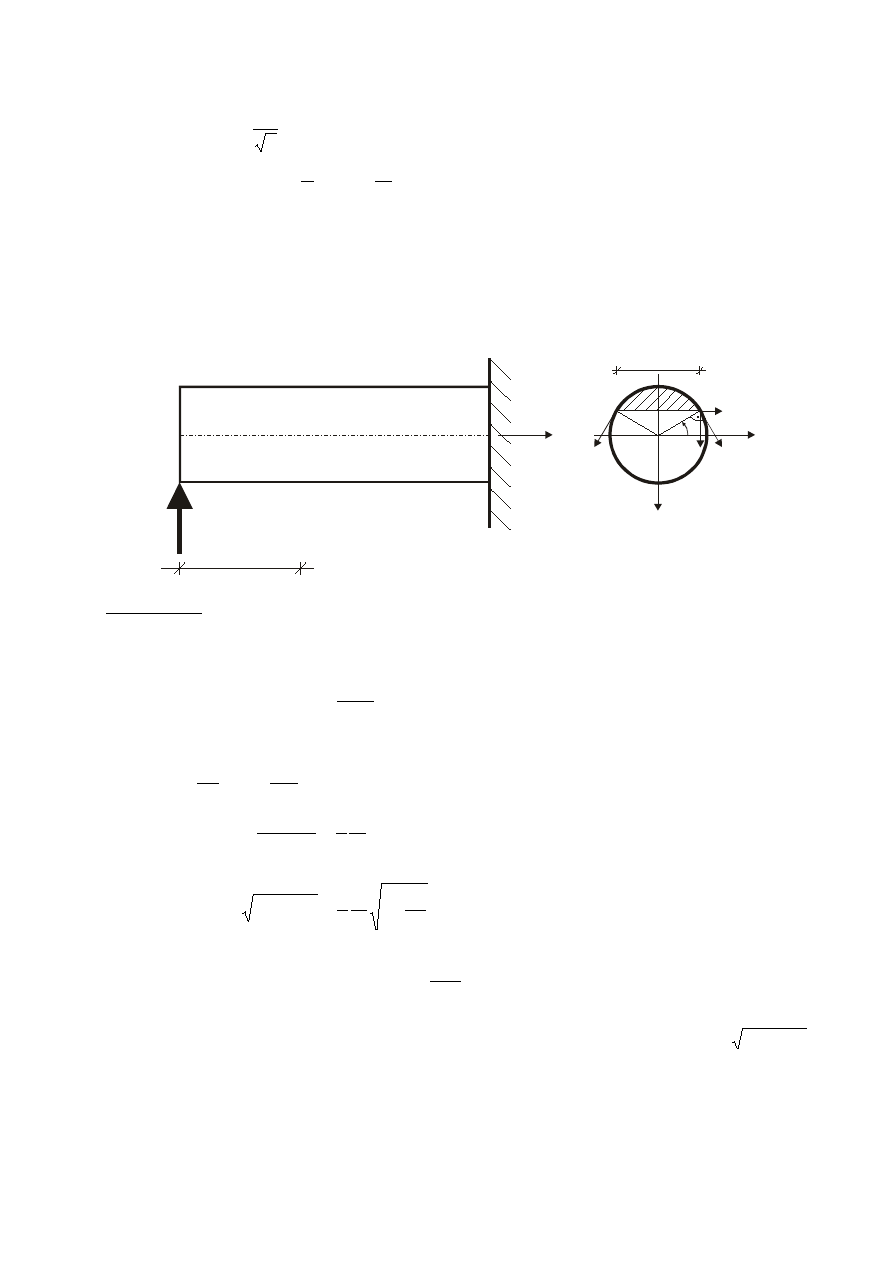
h

707

.

0

h

2

1

x





(33)

A

P

25

.

4

2

h

y

,

x

*

*

0



















(34)

Przykład 8

(wg Krzyś i Życzkowski [ 5 ], s.128

Belka stalowa o przekroju kołowym obciążona jest na swobodnym końcu siłą P jak na rys.2.

Wyznaczyć punkty, w których naprężenie zastępcze – według hipotezy energii odkształcenia
postaciowego – osiąga maksymalną wartość. Rozkład naprężeń przyjąć według teorii
elementarnej.

x

P

x

y

z

b ( y )



x z



x y



I





Rys. 5

Rozwiązanie:

Belka narażona jest na równoczesne zginanie i ścinanie. Zgodnie z teorią elementarną,

naprężenia od zginania wynoszą

z

z

x

I

y

M









(35)

od ścinania zaś (dla punktów na obwodzie koła) zgodnie z rys





cos

r

2

)

y

(

b

,











cos

xy

,

2

2

2

r

y

1

cos







,





3

3

I
z

cos

3

r

2

S

(patrz tablice)











2

z

I
z

xy

cos

A

Q

3

4

)

y

(

b

I

S

Q

,

r

y

1

A

Q

3

4

2

2

2
xz

2

xy















(36)

gdzie

.

r

A

,

4

r

I

,

P

Q

Px

M

2

4

z

z













Po podstawieniu obliczonych naprężeń do wzoru na naprężenie zredukowane

2

2

0

3











i

podnosząc stronami do kwadratu otrzymujemy:

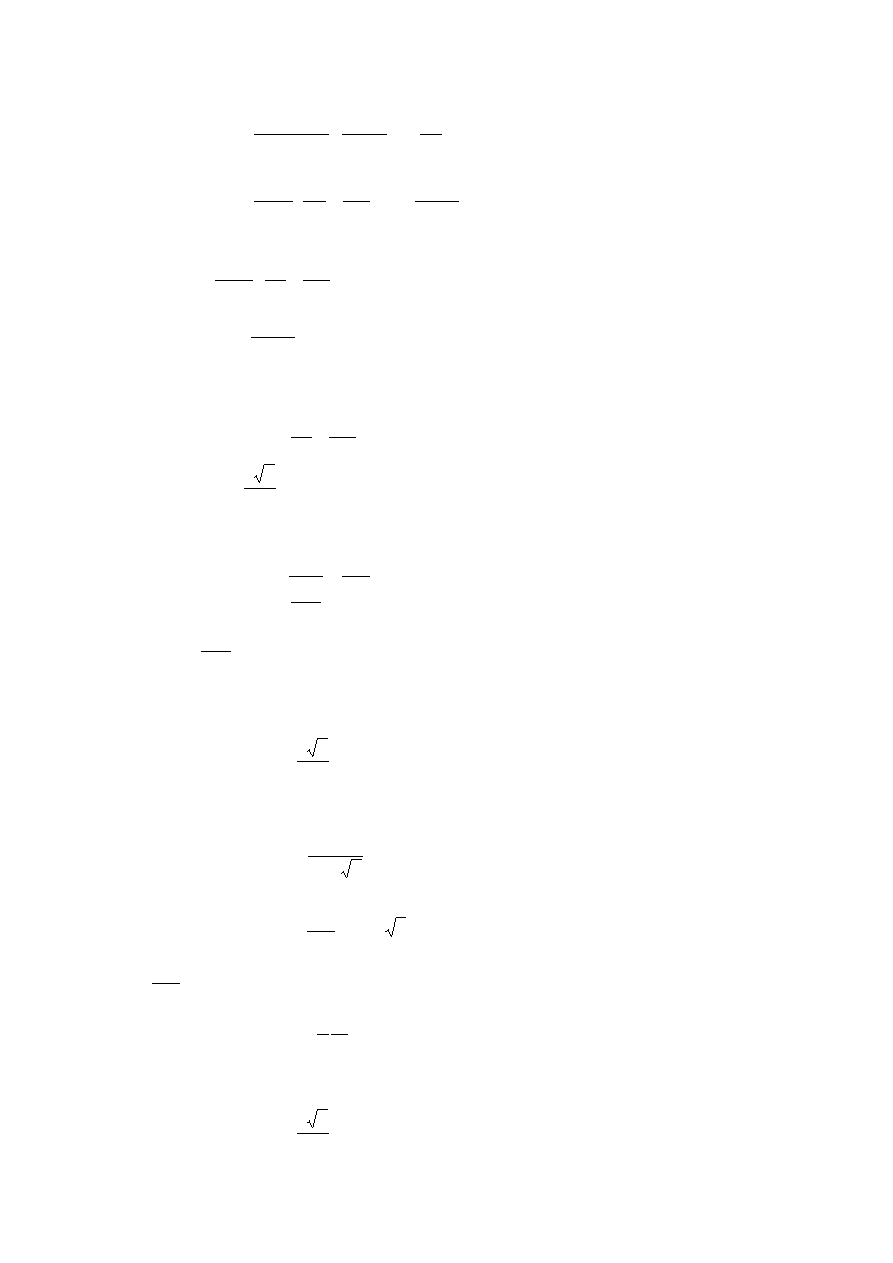
ścinanie

2

2

4

2

2

zginanie

8

2

2

2

2

2
0

r

y

1

r

3

P

16

r

y

x

P

16

























.

r

3

P

16

y

r

3

1

r

x

r

P

16

4

2

2

2

2

4

2

4

2

2

2
0

























(37)

Oznaczając



































C

r

3

P

16

B

r

3

1

r

x

r

P

16

4

2

2

2

4

2

4

2

2

(38)

możemy napisać

.

C

By

2

2
0







(39)

a) Gdy

,

0

B

 czyli

0

r

3

1

r

x

2

4

2





,

577

.

0

3

3

r

r

x





(40)

naprężenie zastępcze osiąga największą wartość we włóknach skrajnych, tj. dla

r

y

 i po

podstawieniu do wzoru (4) wynosi:

z

z

3

0

W

M

4

r

Px

)

r

,

x

(









(41)

gdzie

4

r

W

3

z





jest wskaźnikiem zginania. A zatem gdy

r

x

577

.

0



, dla wytężenia belki

rozstrzygający jest moment zginający.

b) Gdy B = 0, czyli

,

577

.

0

3

3

r

r

x





(42)

wówczas naprężenie zastępcze liczone ze wzoru (4) we wszystkich punktach na obwodzie przekroju
ma tę samą wartość

C

2
0





3

4

2

0

r

P



 

(43)

lub inaczej

,

3

W

M

max

z

z

0









(44)

gdzie

z

z

W

M

określa maksymalne naprężenie od zginania w rozpatrywanym przekroju, tj. dla

,

r

y

 a

A

Q

3

4

max





(45)

maksymalne naprężenie od ścinania w linii obojętnej, tj. dla

.

0

y



c) Gdy wreszcie

,

0



A

czyli

,

577

.

0

3

3

r

r

x





(46)

naprężenie zastępcze przyjmuje największą wartość dla

.

0

y

 , tj. w linii obojętnej, z uwagi na

zginanie i wynosi ze wzoru (4)

 

0

,

x

0



 

.

3

3

A

Q

3

4

3

r

P

4

0

,

x

max

2

0













(47)

Zatem jedynie gdy

,

577

.

0

r

x



o wytężeniu belki decyduje jej ścinanie.