
Iloraz inteligencji ma w populacji rozkład
normalny =100; =15. Znaleźć
prawdopodobieństwo, że z populacji
wylosujemy osobę z IQ:
a) nie większym niż 70
b) nie większym niż 120
c) większym niż 140
d) pomiędzy 70 i 130
Wejściówka
Wejściówka
x
z
Normalizacja

Iloraz inteligencji ma w populacji rozkład
normalny =100; =15. Znaleźć
prawdopodobieństwo, że z populacji
wylosujemy osobę z IQ:
a) nie większym niż 60
b) nie większym niż 110
c) większym niż 130
d) pomiędzy 70 i 120
Wejściówka
Wejściówka
x
z
Normalizacja

Iloraz inteligencji ma w populacji rozkład
normalny =110; =10. Znaleźć
prawdopodobieństwo, że z populacji
wylosujemy osobę z IQ:
a) nie większym niż 50
b) nie większym niż 120
c) większym niż 125
d) pomiędzy 60 i 110
Wejściówka
Wejściówka
x
z
Normalizacja

Wnioskowanie statystyczne i
Wnioskowanie statystyczne i
weryfikacja hipotez statystycznych
weryfikacja hipotez statystycznych
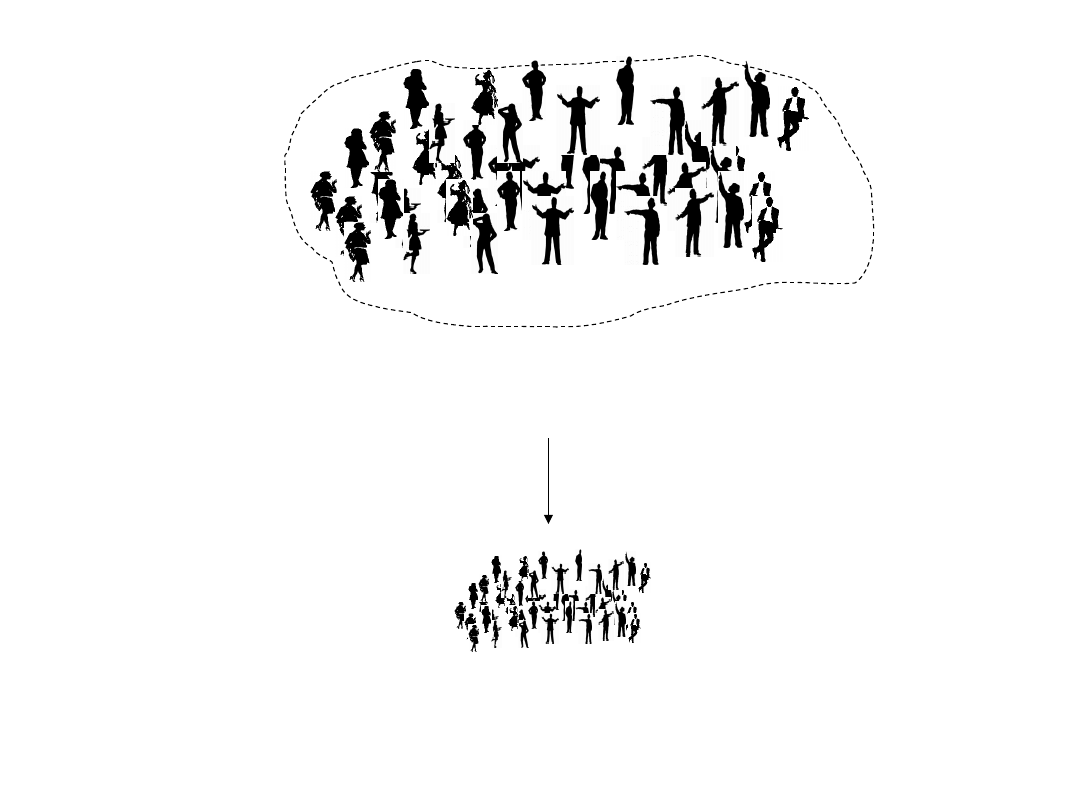
Populacja (N=∞)
Próba losowa
(losowość nie zależy od liczby
wylosowanych elementów)
Próba (n elemntowa)
Zmienna X w populacji ma E(X) i D(X), których nie znamy!
Zakładamy, że rozkład tej zmiennej jest normalny

Wnioskowanie statystyczne
Wnioskowanie statystyczne
Wnioskowanie statystyczne obejmuje następujące czynności:
• Sformułowanie hipotezy zerowej i hipotezy alternatywnej.
• Ustalenie poziomu istotności .
• Wybór statystyki do weryfikacji hipotezy H0 i ustalenie
obszaru
krytycznego (wartości krytycznych).
• Obliczenie wartości statystyki w próbie.
• Sformułowanie wniosków (weryfikacja hipotezy H0) przez
porównanie
wartości obliczonej statystyki z wartościami
krytycznymi; będzie to jeden z dwóch wniosków:
– odrzuca się hipotezę zerową i za prawdziwą uznaje się
hipotezę
alternatywną,
– nie ma podstaw do odrzucenia H0 (co nie oznacza jej
przyjęcia).

Definicje
Definicje
Hipotezą statystyczną – nazywamy każdy sąd o zbiorowości generalnej, wydany bez
przeprowadzenia badania całkowitego, prawdziwość hipotezy statystycznej orzeka się na
podstawie próby losowej.
Hipoteza zerowa H
0
– hipoteza sprawdzana (testowana, weryfikowana).
Hipoteza alternatywna H
1
– hipoteza, którą można przyjąć, gdy zostanie odrzucona hipoteza
zerowa H
0
.
Sprawdzianem hipotezy – (zwanym też statystyką testową) jest taka zmienna losowa T, o
znanym rozkładzie, której wartość empiryczna t
emp.
, policzona na podstawie próby losowej,
pozwala na podjęcie decyzji, czy przyjąć, czy też odrzucić hipotezę H
0
.
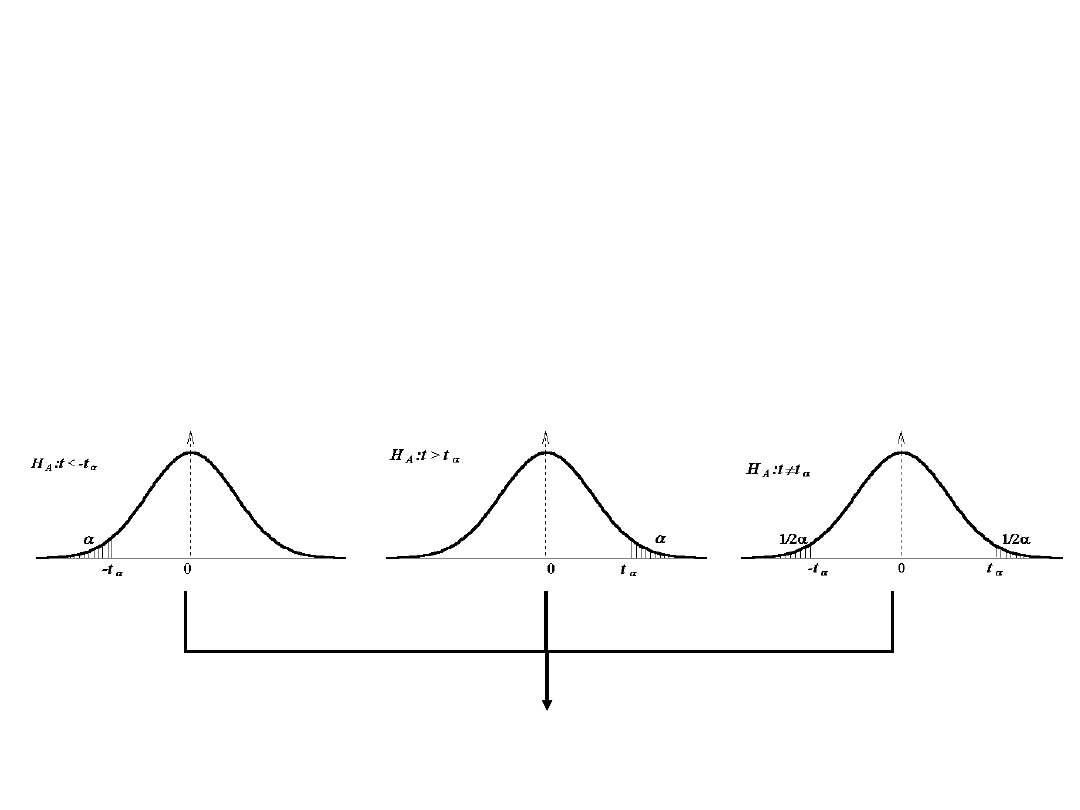
Zbiór krytyczny Z – jest to zbiór tych wartości sprawdzianu hipotezy, które przemawiają za
odrzuceniem hipotezy H
0
. W zależności od hipotezy może być zbiorem jednostronnym
(prawostronnym lub lewostronnym) albo zbiorem dwustronnym.
Przedziałem ufności – nazywamy taki przedział, który z zadanym z góry
prawdopodobieństwem zwanym poziomem ufności lub współczynnikiem ufności, pokrywa
nieznaną wartość szacowanego parametru.
to poziom istotności
1

Konstruowanie przedziału ufności dla wartości
Konstruowanie przedziału ufności dla wartości
przeciętnej m
przeciętnej m
Jeżeli mamy dużą próbę (n>30) oraz cecha X ma rozkład normalny X ~ N(m, ) , wówczas
przedział ufności dla parametru m ma postać:
n
t
x
m
n
t
x
gdzie:
- średnia arytmetyczna
- odchylenie standardowe, założenie ( )
- liczebność próby
- wartość oczekiwana (przeciętna),
- wartość krytyczna odczytana z tablic rozkładu normalnego, gdzie:
x
S
n
m
t
2
1
t
Przykład 1 krok po kroku
Przykład 1 krok po kroku
Przypuśćmy, że interesuje nas populacja krów i na podstawie
jakichś informacji spodziewamy się, że średnia wydajność
mleka w tej populacji jest równa
0
= 200 litrów mleka.
Gdybyśmy chcieli na podstawie jakieś próby sprawdzić czy
rzeczywiście wartość średnia populacji jest równa 200,
przyjęlibyśmy hipotezę zerową H0:
= 200.
Moglibyśmy sformułować wiele hipotez alternatywnych np.
H
A
:
= 384 litrów mleka, jednak sens mają tylko trzy:
H
1
:
< 200 hipoteza jednostronna <
0
stosujemy test
jednostronny
H
2
:
> 200 hipoteza jednostronna >
0
stosujemy test
jednostronny
H
3
:
200 hipoteza dwustronna
0
stosujemy test
dwustronny
Przystępując do testowania hipotezy zerowej zakładamy, że jest ona prawdziwa

Przykład 1
Przykład 1
Przykład krok po kroku – wersja 1 – test
Przykład krok po kroku – wersja 1 – test
dwustronny
dwustronny
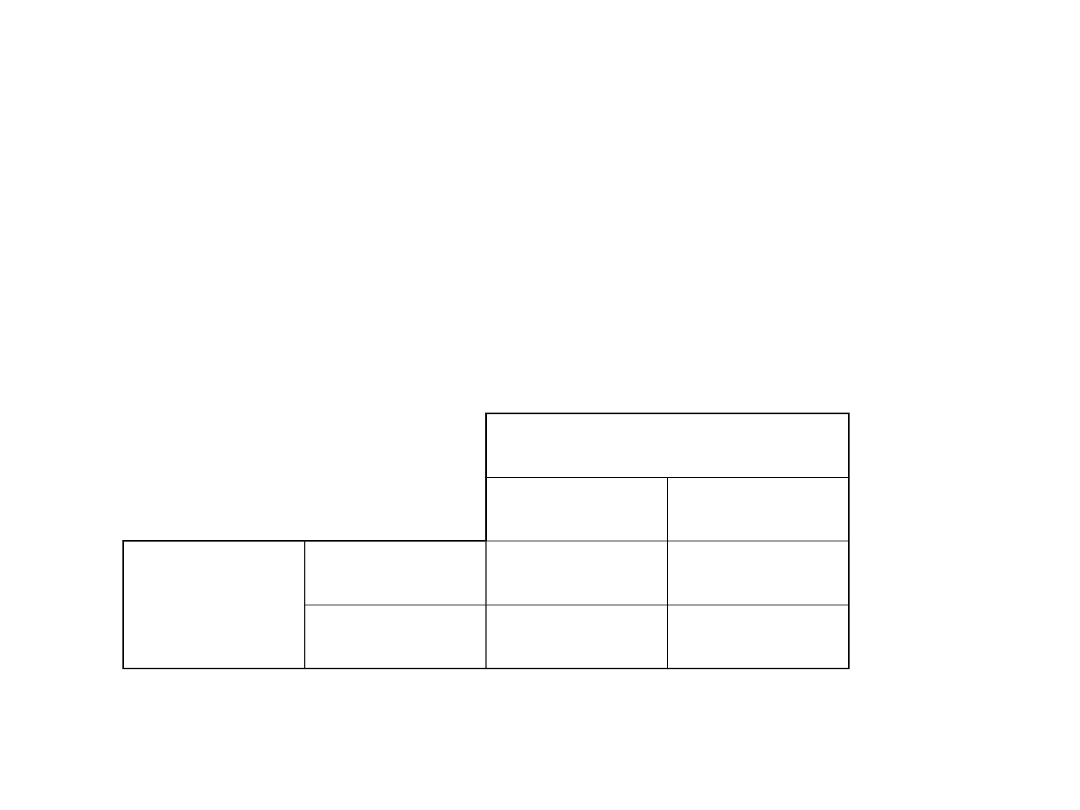
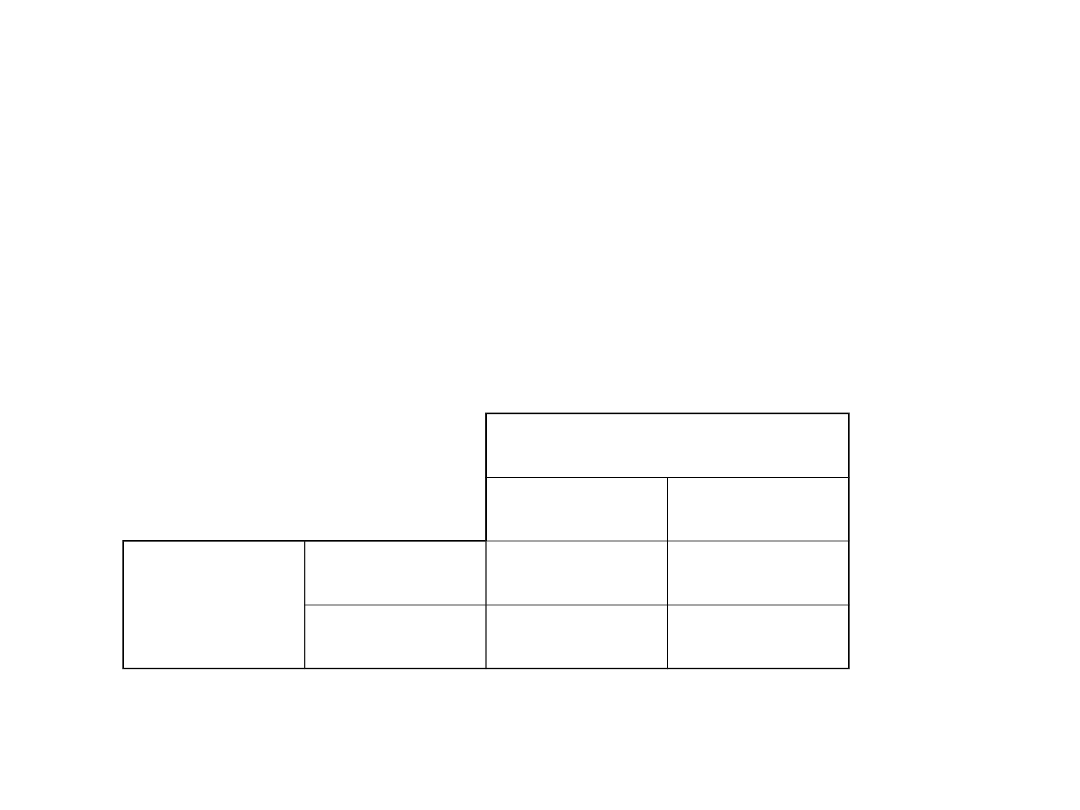
Hipoteza H0
prawdziwa
fałszywa
Decyzja
Przyjmujemy
H0
1-
Błąd II rodzaju
Odrzucamy H0
Błąd I rodzaju
1-
Agronom twierdzi: „średnia ilość mleka to 200 litrów”
Pastuch Kazio mówi: „a wcale bo nieprawda!”
Agronom: zatrudnijmy socjologa i niech zrobi nam badanie
Socjolog: Przeprowadzono badanie na n=324 krowach i
uzyskano następujące wyniki: E(X)=198 litrów D(X)=20
Agronom: „to kto qrde… ma rację i o co w tym chodzi?”
Socjolog: Przeprowadzono badanie na n=324 krowach i
uzyskano następujące wyniki: E(X)=198 litrów, D(X)=20
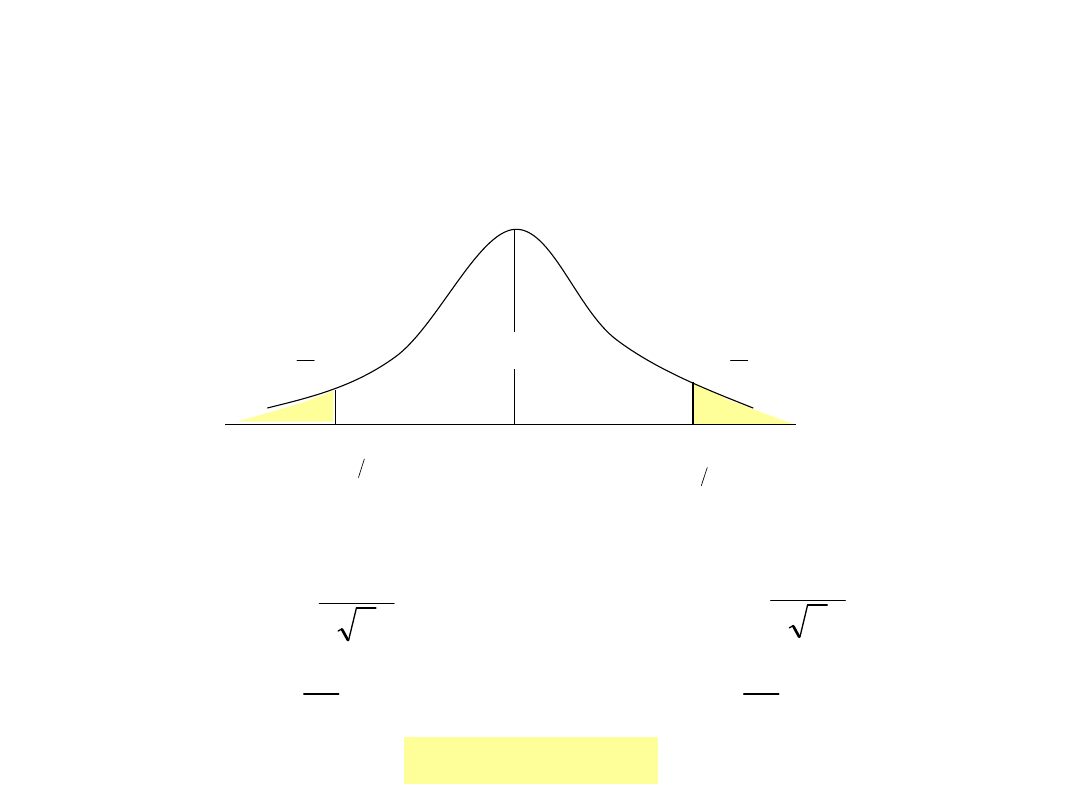
- Ustalamy poziom
0
2
2
1
96
1,
96
1,
05
0,
Obszar akceptacji
hipotezy zerowej
2
2
n
X
D
,
X
E
96
1
n
X
D
,
X
E
96
1
196
18
20
96
,
1
198
200
18
20
96
,
1
198
0
0
200
;
196
a
h
Przykład krok po kroku – wersja 1 – test
Przykład krok po kroku – wersja 1 – test
dwustronny
dwustronny
Przykład krok po kroku – wersja 2 – test
Przykład krok po kroku – wersja 2 – test
lewostronny
lewostronny
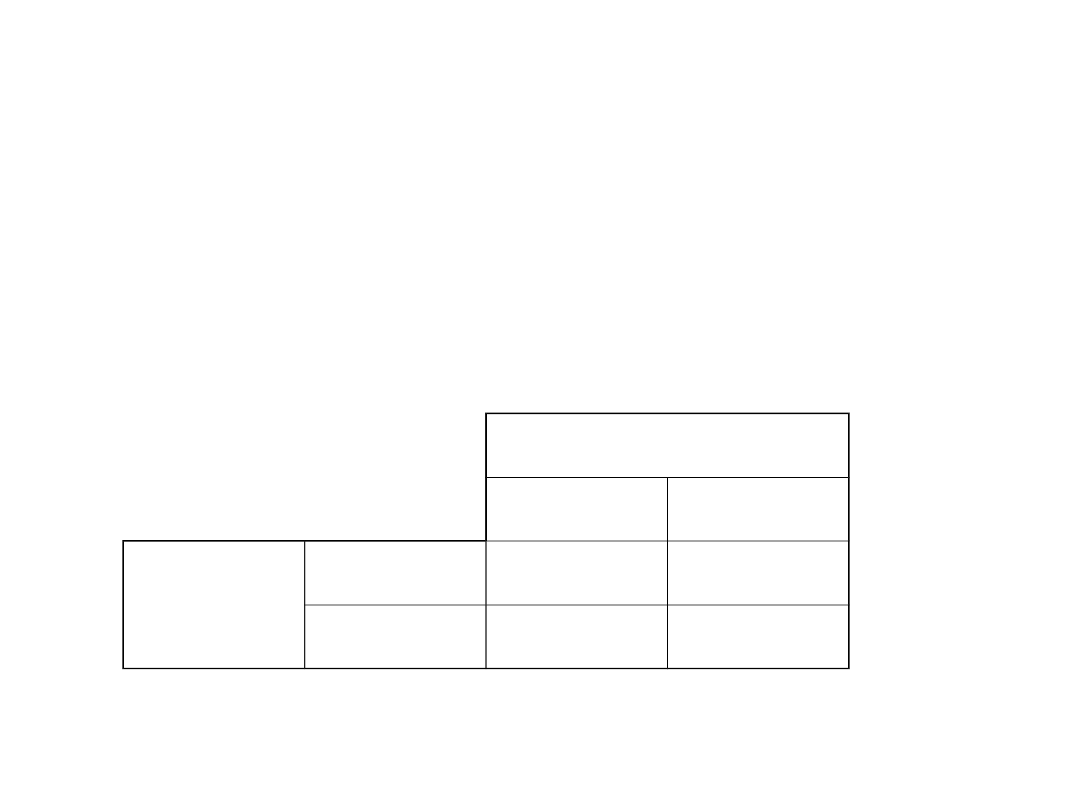
Hipoteza H0
prawdziwa
fałszywa
Decyzja
Przyjmujemy
H0
1-
Błąd II rodzaju
Odrzucamy H0
Błąd I rodzaju
1-
Agronom twierdzi: „średnia ilość mleka to 200 litrów”
Pastuch Kazio mówi: „jak doiłem ostatnio to wyszło mi mniej”
Agronom: zatrudnijmy socjologa i niech zrobi nam badanie
Socjolog: Przeprowadzono badanie na n=324 krowach i
uzyskano następujące wyniki: E(X)=198 litrów D(X)=20
Agronom: „to kto qrde… ma rację i o co w tym chodzi?”
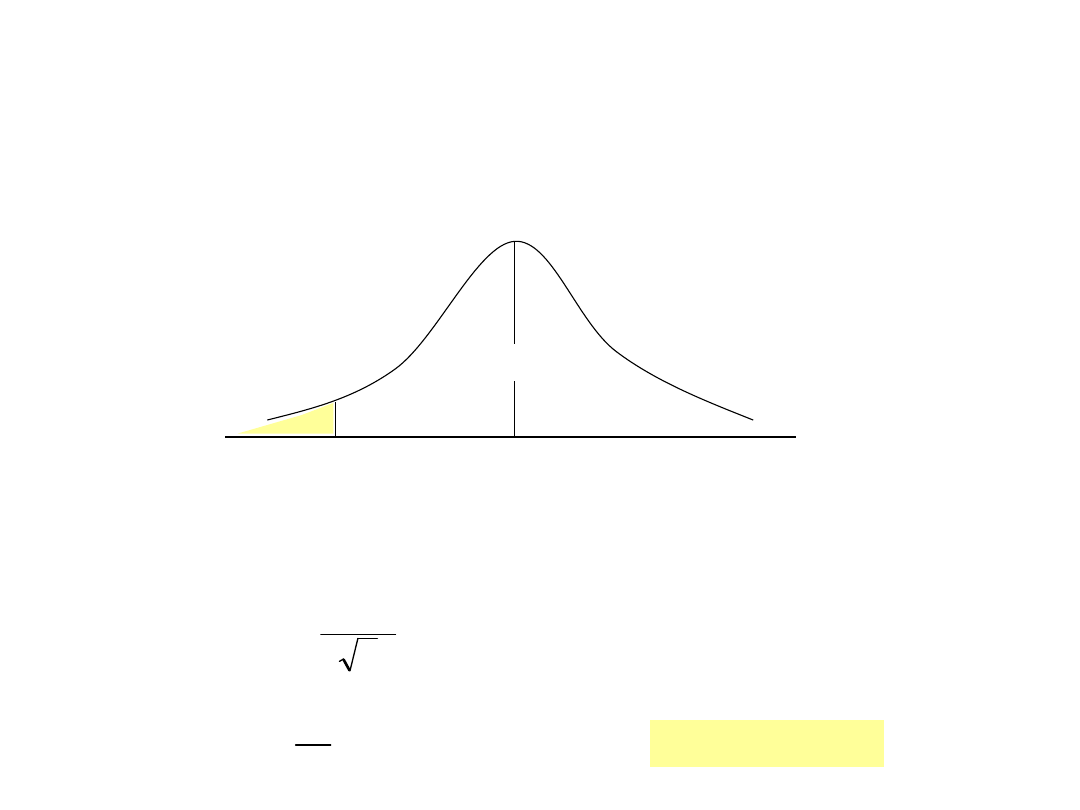
0
1
64
1,
05
0,
E(X)
n
X
D
X
E
64
,
1
196
18
20
64
,
1
198
Obszar akceptacji
hipotezy zerowej
Hipoteza „zerowa, testowana” h
0
Hipoteza „alternatywna, konkurencyjna” h
1
200
200
Wynik w próbie n=324
E(X)=198
D(X)=20
0
0
;
196
a
h
Przykład krok po kroku – wersja 2 – test
Przykład krok po kroku – wersja 2 – test
lewostronny
lewostronny
Przykład krok po kroku – wersja 3 – test
Przykład krok po kroku – wersja 3 – test
prawostronny
prawostronny
Hipoteza H0
prawdziwa
fałszywa
Decyzja
Przyjmujemy
H0
1-
Błąd II rodzaju
Odrzucamy H0
Błąd I rodzaju
1-
Agronom twierdzi: „średnia ilość mleka to 200 litrów”
Pastuch Kazio mówi: „jak doiłem ostatnio to wyszło mi
więcej”
Agronom: zatrudnijmy socjologa i niech zrobi nam badanie
Socjolog: Przeprowadzono badanie na n=324 krowach i
uzyskano następujące wyniki: E(X)=198 litrów D(X)=20
Agronom: „to kto qrde… ma rację i o co w tym chodzi?”
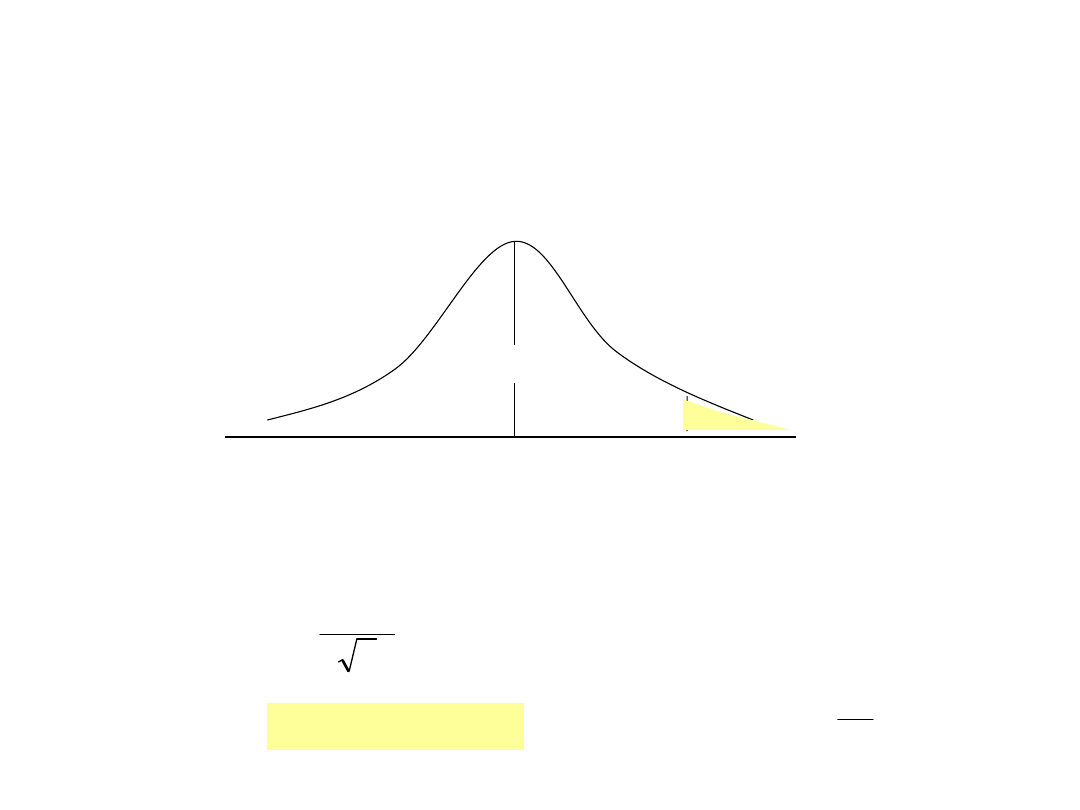
0
1
64
1,
05
0,
E(X)
n
X
D
,
X
E
64
1
200
18
20
64
,
1
198
Obszar akceptacji
hipotezy zerowej
Hipoteza „zerowa, testowana” h
0
Hipoteza „alternatywna, konkurencyjna” h
1
200
200
Wynik w próbie n=324
E(X)=198
D(X)=20
0
0
200
;
a
h
Przykład krok po kroku – wersja 3 – test
Przykład krok po kroku – wersja 3 – test
prawostronny
prawostronny

Przykład 2
Przykład 2

Amerykanie chcą ulokować bazę F16 w Krzesinach. Uzależnione jest to od poziomu hałasu,
który przeszkadza mieszkańcom. Jeśli przekroczy on ustaloną normę, inwestycja nie będzie
mogła mieć miejsca. Przeprowadzone w przeszłości szczegółowe badania poziomu hałasu na
lotnisku doprowadziły do wartości średniej 63 dB z odchyleniem standardowym 8 dB, co mieści
się normach UE. Jednak mieszkańcy postanowili sami zmierzyć poziom hałasu emitowany
przez odrzutowce. Po pewnym czasie 24‐krotne pomiary kontrolne dały wartość średniej 68 dB.
Pytamy, czy upoważnia nas to do rewizji wyznaczonej uprzednio wartości?
1. Hipoteza zerowa
H
0
:
= 63dB
Hipoteza alternatywna
H
0
:
63dB
2. Jako sprawdzian hipotezy zerowej wybieramy statystykę
Która ma rozkład normalny standaryzowany, jeśli słuszna jest hipoteza
H
0
n
x
Z
/
dB
63
dB
8
3. Przyjmujemy poziom istotności, np.
05
0,
4. Określamy zbiór krytyczny:
(test
dwustronny)
z tablic odczytujemy: .
))
(
)
((
2
/
1
2
/
0
z
Z
z
Z
P
H
5. Obliczamy wartość statystyki testowej: .
06
,
3
24
/
8
63
68
z
Ponieważ z> ,tj. należy do zbioru krytycznego, zatem na wybranym poziomie istotności
hipotezę zerową należy odrzucić
96
,
1
025
,
0
z
96
,
1
975
,
0
z
975
,
0
z
Przykład2
Przykład2

ZADANIA
ZADANIA

Zadanie1
Zadanie1
Zbadano w 81 wylosowanych polmosach produkujących wino
koszty butelek przy produkcji 100 skrzynek i otrzymano średnią
zł oraz zł. Na poziomie istotności zweryfikować
hipotezę, że średnie koszty produkcji butelek wynoszą 600 zł.
540
x
150
D
05
,
0
Postępowanie:
1. Wypisujemy dane które mamy
2. Formułujemy hipotezę zerową i hipotezę alternatywną
3. Ustalamy poziom istotności
4. Ustalamy zbiór krytyczny
5. Podstawiamy dane do wzoru
6. Interpretujemy wynik
n
m
x
t
emp
.

Zadanie2
Zadanie2
Średnia życia mężczyzn w Polsce wynosi 67,5 lat. Interesuje nas
obszar zagłębia legnicko-głogowskiego. Podejrzewamy, że z uwagi
na duże zagrożenie ekologiczne, średnia życia jest tutaj niższa niż
średnia krajowa. Wybrano losowo 238 mężczyzn i obliczono, że
oraz S=12,9. Na poziomie istotności 0,05 zweryfikować
powyższą hipotezę.
Postępowanie:
1. Wypisujemy dane które mamy
2. Formułujemy hipotezę zerową i hipotezę alternatywną
3. Ustalamy poziom istotności
4. Ustalamy zbiór krytyczny
5. Podstawiamy dane do wzoru
6. Interpretujemy wynik
n
m
x
t
emp
.
4
,
65
x
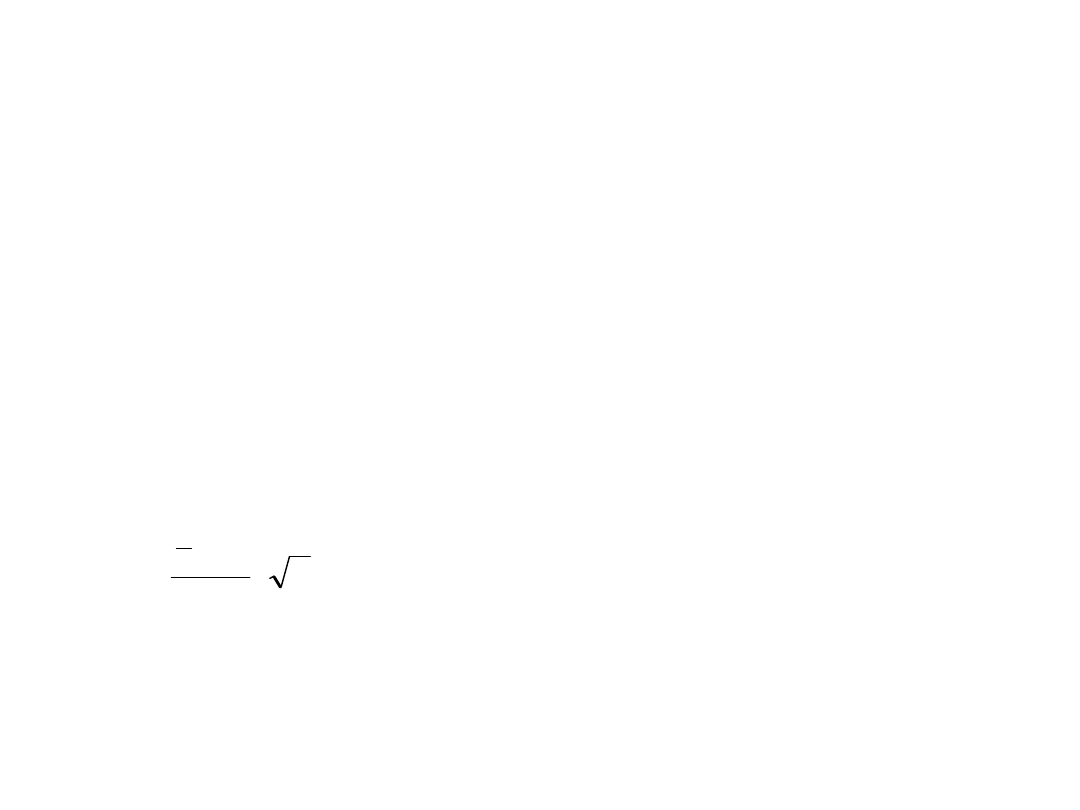
Zadanie3
Zadanie3
Na losowo dobranej próbie 150 samochodów marki X zbadano zużycie
benzyny po przejechaniu trasy 100 km. Średnie zużycie benzyny dla tej
próby wyniosło 7,5 litra przy odchyleniu standardowym 0,9 litra. Norma
fabryczna wynosi 7,01 litra na 100 km. Czy rzeczywiste zużycie benzyny
różni sie istotnie od normy fabrycznej na poziomie istotności 0,03 (zużycie
benzyny ma rozkład normalny)?
Postępowanie:
1. Wypisujemy dane które mamy
2. Formułujemy hipotezę zerową i hipotezę alternatywną
3. Ustalamy poziom istotności
4. Ustalamy zbiór krytyczny
5. Podstawiamy dane do wzoru
6. Interpretujemy wynik
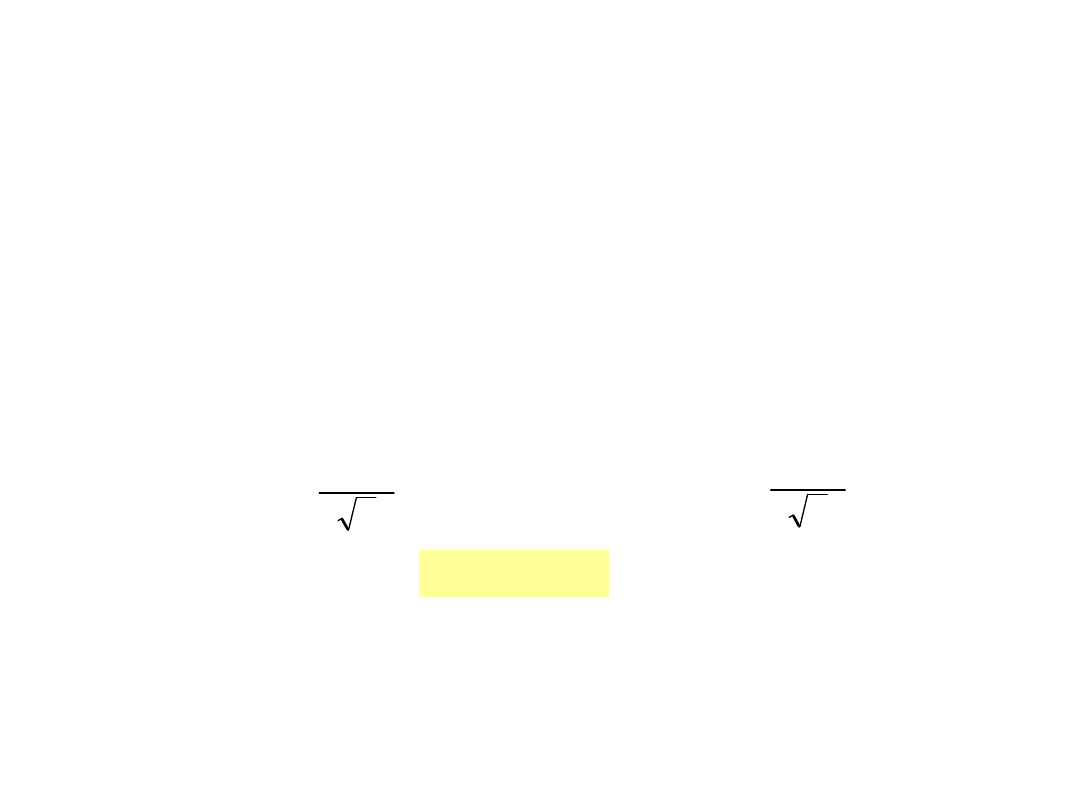
n
m
x
t
emp
.
Zadanie3
Zadanie3
W pewnym doświadczeniu medycznym bada się czas snu
pacjentów po zastosowaniu pewnego leku. Zmierzono czas snu (w
minutach) u 17 losowo wybranych pacjentów i otrzymano: 435,
533, 393, 458, 525, 481, 324, 433, 515, 348, 503, 383, 395, 416,
555, 500, 488. Na poziomie istotności 0,05 sprawdzić hipotezę, że
średni czas snu pacjentów wynosi 7 godz.
Postępowanie:
1. Wypisujemy dane które mamy
2. Formułujemy hipotezę zerową i hipotezę alternatywną
3. Ustalamy poziom istotności
4. Ustalamy zbiór krytyczny
5. Podstawiamy dane do wzoru
6. Interpretujemy wynik
E(X)
n
X
D
,
X
E
96
1
n
X
D
,
X
E
96
1
0
0
?
?;
a
h
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
Wyszukiwarka
Podobne podstrony:
Weryfikacja hipotez statystycznych
w7i8, Weryfikacja hipotez statystycznych
Testowanie, WERYFIKACJA HIPOTEZ STATYSTYCZNYCH
5 Weryfikacja hipotez statystycznych z wykorzystaniem testˇw parametrycznych
3 zadania, zadania weryfikacja hipotez statystycznych
Weryfikacja hipotez statystycznych 2, SQL, Statystyka matematyczna
w5 weryfikacja hipotez statystycznych
weryfikacja hipotez statystycznych - wzory (1 str), Weryfikacja hipotez statystycznych
WERYFIKACJA HIPOTEZ STATYSTYCZNYCH
WERYFIKACJA HIPOTEZ STATYSTYCZNYCH
Weryfikacja hipotez statystycznych
Weryfikacja hipotez statystycznych
Weryfikacja hipotez 3 (2 średnie), Semestr II, Statystyka matematyczna
Weryfikacja hipotez- Średnia Duża próba, Semestr II, Statystyka matematyczna
04 Statystyka Matematyczna Weryfikacja hipotez parametrycznychid 5193
Weryfikacja hipotez 4 (2 średnie), Semestr II, Statystyka matematyczna
więcej podobnych podstron