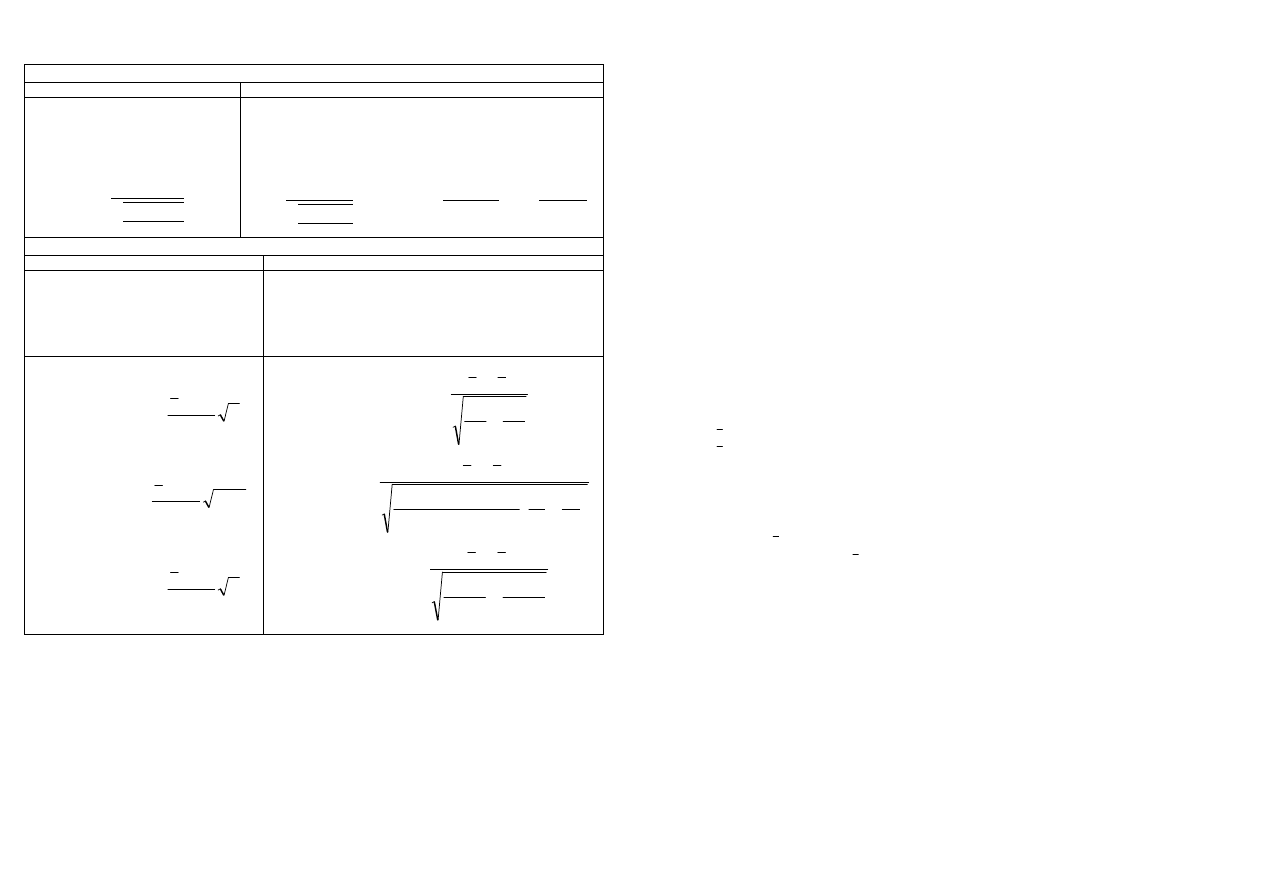
WERYFIKACJA HIPOTEZ PARAMETRYCZNYCH

FRAKCJA / TEST DLA PROPORCJI

1 próba

2 próby

Hipotezy:
H

0

: p=p

0

H

1

: p≠p

0

lub p>p

0

lub p<p

0

Statystyka testowa:

=

−

(1 − )

Hipotezy:
H

0

: p

1

=p

2

H

1

: p

1

≠

p

2

lub p

1

>p

2

lub p

1

<p

2

Statystyka testowa:

=

̅(1 − )

̅ =

+

+

=

+

Ś

REDNIA

1 próba

2 próby

Hipotezy:
H

0

: m=m

0

H

1

: m≠m

0

lub m>m

0

lub m<m

0

Statystyka testowa:

Hipotezy:
H

0

: m

1

=m

2

H

1

: m

1

≠

m

2

lub m

1

>m

2

lub m

1

<m

2

Statystyka testowa:

- rozkład

Normalny,

- znane σ

-liczebność

dowolna

n

m

x

U

σ

0

−

=

- rozkład

Normalny,

- nieznane σ

-mała próba

(n<30)

1

)

(

0

−

−

=

n

x

S

m

x

t

- rozkład

dowolny

- nieznane σ

-duża

próba(n≥30)

n

x

S

m

x

U

)

(

0

−

=

- rozkład

Normalny,

- znane σ

-liczebność

dowolna

2

2

2

1

2

1

2

1

n

n

x

x

U

σ

σ

+

−

=

- rozkład

Normalny,

- nieznane σ

-małe próby

(n

1

,n

2

<30)

)

1

1

(

2

)

(

)

(

2

1

2

1

2
2

2

2

1

1

2

1

n

n

n

n

x

S

n

x

S

n

x

x

t

+

−

+

+

−

=

- rozkład

dowolny

- nieznane σ

-duże próby

(n

1

,n

2

≥

30)

2

2
2

1

2

1

2

1

)

(

)

(

n

x

S

n

x

S

x

x

U

+

−

=

Zadanie 1.
Istnieje opinia, że pasażerowie linii lotniczych mają tendencję do zabierania coraz większego bagażu
podręcznego. Kabiny w samolotach pewnej linii umożliwiają przechowywanie bagażu podręcznego o
nominalnej wadze 20 kg.
Aby właściwie przeprojektować kabiny, zbadano wagę bagażu podręcznego dla losowej próby 150 pasażerów,
uzyskując średnią wagę bagażu równą 22 kg, przy odchyleniu standardowym 6 kg.
Czy przyjmując poziom istotności 0,05 możemy twierdzić, że:

a)

Ś

rednia waga bagażu podręcznego pasażerów nie różni się od wagi nominalnej?

b)

Ś

rednia waga bagażu podręcznego pasażerów jest większa od wagi nominalnej?

Zadanie 2.
Na opakowaniu pewnego towaru widnieje napis „przeciętna waga wynosi 200 gram”. Do Stowarzyszenia
konsumentów napływają jednak skargi, że producent zaniża wagę produktu. W celu sprawdzenia prawdziwości
informacji podanej przez producenta, zważono 100 losowo wybranych opakowań danego produktu. Uzyskano

ś

rednią wagę 199,5 gram oraz odchylenie standardowe 6 gram. Czy przyjmując poziom istotności 0,05 można

uznać, że:

a)

Informacja na opakowaniu jest prawdziwa?

b)

Rację mają konsumenci?

Zadanie 3.
Kierownictwo pewnej firmy ubezpieczeniowej wysunęło przypuszczenie, że średnie wypłaty ponoszone z
tytułu odszkodowań powodziowych przekraczają kwotę 2 mln zł. Przeanalizowano dane dotyczące wysokości
odszkodowań poniesionych przez tę firmę podczas 5 kolejnych powodzi. Ustalono, że łączne kwoty
odszkodowań powodziowych wypłaconych w rozważanych okresach wynosiły odpowiednio (w mln zł): 1,9;
3,7; 2,9; 2,0; 3,3.
Czy można przyjąć że kierownictwo firmy ma rację? Zweryfikować odpowiednią hipotezę na poziomie
istotności 0,05, zakładając, że rozkład wysokości odszkodowań powodziowych ma rozkład normalny.
Zadanie 4.
Miesięczne wydatki na żywność w przeliczeniu na jedną osobę w gospodarstwach pracowniczych (w PLN)
mają rozkład normalny z odchyleniem standardowym 100 PLN. Na podstawie badania 400 losowo wybranych
gospodarstw stwierdzono, że średnie wydatki w tej grupie wynoszą 250 PLN. Czy na podstawie powyższych
danych, zakładając poziom istotności 0,05, można uznać, że średnie wydatki na żywność ogółu gospodarstw
nie przekraczają 240 PLN?
Zadanie 5.
Rozkład tygodniowego czasu poświęconego na naukę poza uczelnią studentów I roku studiów dziennych SGH
jest rozkładem N(m; 5),natomiast w rozkładzie normalnym tygodniowego czasu studentów II roku odchylenie
standardowe wynosi 6 godz. Pobrano niezależnie 10-elementową próbę studentów I roku oraz 24-elementową
studentów II roku. Średnie w tych próbach wynosiły odpowiednio: 20 godz. i 15 godz. Czy na poziomie 0,1
można przyjąć, iż średni czas nauki poza uczelnią ogółu studentów I roku jest wyższy niż na roku II?
Zadanie 6.
W wyniku badania zmian poziomu płac pracowników firmy Intraco w Warszawie w latach 1993-1994
otrzymano następujące dane dla 50 losowo wybranych pracowników w każdym roku:
1993 rok:

50

7

,

118

)

(

398

=

=

=

n

PLN

x

s

PLN

x

1994 rok:

50

5

,

213

)

(

654

=

=

=

n

PLN

x

s

PLN

x

Czy na podstawie powyższych wyników można mówić o wzroście poziomu płac ogółu pracowników Intraco w
1994 roku w stosunku do 1993 roku?
Zadanie 7.
W wyniku ewidencji dziennej sprzedaży dwóch rodzajów zegarków na rękę szwajcarskiej firmy Swatch w
wybranych 20 dniach roboczych ustalono, co następuje:
- zegarki tradycyjne:

5

,

7

)

(

37

=

=

x

s

x

- zegarki z dodatkowymi funkcjami:

2

,

8

)

(

30

=

=

x

s

x

Czy na podstawie powyższych wyników, wiedząc że sprzedaż obu zegarków ma rozkład normalny, można
stwierdzić, że:

a)

ś

rednia dzienna sprzedaż zegarków tradycyjnych i z dodatkowymi funkcjami jest taka sama?

b)

ś

rednia dzienna sprzedaż zegarków tradycyjnych jest większa niż zegarków z dodatkowymi funkcjami?

Zadanie 8.
Wśród losowo wybranych 5032 dorosłych osób, 566 osób stwierdziło, że rzadko uczestniczy w praktykach
religijnych. Czy przyjmując założenie o popełnieniu nie mniej niż 1 pomyłki na 100 przy podejmowaniu
odpowiedniej decyzji weryfikacyjnej, można uznać, że nie więcej niż 10% ogółu dorosłych mieszkańców
Polski rzadko uczestniczy w praktykach religijnych?
Zadanie 9.
Wysunięto hipotezę, że studenci Akademii Medycznej pala papierosy rzadziej niż studenci SGH. W celu jej
sprawdzenia wylosowano po 200 studentów z każdej uczelni i zapytano ich, czy palą. W grupie studentów AM
papierosy paliło 68 osób, w grupie studentów SGH – 76 osób. Na poziomie istotności równym 0,05
zweryfikować prawdziwość postawionej hipotezy.
Zadanie 10.
Badanie skuteczności działania dwóch leków obniżających ciśnienie krwi dostarczyło następujących
informacji: w 100-osobowej grupie pacjentów, którym przez rok podawano pierwszy lek, u 50 stwierdzono
obniżenie ciśnienia krwi do poziomu normalnego; wśród 200 pacjentów, którzy stosowali w ciągu roku drugi
lek, stwierdzono to samo u 72 osób. Na poziomie istotności 0,05 sprawdzić hipotezę, że pierwszy lek jest
skuteczniejszy niż drugi.