TESTY PARAMETRYCZNE 2

Średnia waga torebek cukru w hurtowni ma wynosić 1000 gr. W celu zbadania, czy torebki cukru spełniają warunki normy wylosowano 17 torebek i uzyskano następujące wyniki w próbie:
= 998gr. S=3gr.

1. Jaki test zastosujemy do analizy.

2. Postaw hipotezę zerową i alternatywną.

3. Od czego zależy rodzaj obszaru krytycznego testu.

4. Jaki obszar krytyczny zastosujemy w tym teście.

5. Jaką statystykę zastosujemy w tym teście.

6. Jaki rozkład ma ta statystyka.

7. Załóż poziom istotności α=0,05 i podaj interpretację.

8. Przy poziomie istotności α=0,05 wyznacz obszar krytyczny testu.

9. Oblicz statystykę testową.

10. Podaj wniosek weryfikacyjny.

ODPOWIEDZI

1. Zastosujemy test dla jednej średniej (porównanie ze wzorcem) dla dużej próby.

2. H₀: µ=(µ₀ =1000g. )

H₁: µ<(µ₀=1000g.)

3. Rodzaj obszaru krytycznego zależy od postaci H₁

4. Zastosujemy obszar krytyczny jednostronny (lewostronny)

5. 
   

6. Ponieważ próba jest mała (n<30), więc zastosujemy statystykę t-Studenta o n-1 stopniach swobody.

7. Poziom istotności α=0,05 oznacza, że zakładamy możliwość popełnienia w 5 przypadkach na 100 błąd 1-go rodzaju, czyli odrzucenia H_0, gdy w rzeczywistości jest ona prawdziwa.

8. Obszar krytyczny odczytujemy z tablic dystrybuanty t-Studenta dla α=0,05 i n-1 stopni swobody dla jednostronnego (lewostronnego) obszaru krytycznego. Otrzymujemy wartość t_α=1,746. Zmieniamy znak na przeciwny, czyli obszar krytyczny będzie w przedziale

-∞≤t≤-1.746 Jeżeli wartość wyliczona t znajdzie się w tym obszarze, to hipotezę zerową odrzucamy i przyjmujemy alternatywną, że waga torebek cukru jest istotnie poniżej normy.

9. 
   

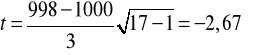
10. Wartość wyliczona t znalazła się w obszarze krytycznym, więc hipotezę zerową odrzucamy i przyjmujemy alternatywną, czyli torebki cukru ważą istotnie poniżej normy.

---