Weryfikacja hipotez 4

W celu sprawdzenia hipotezy stwierdzającej, że wyniki egzaminu na kierunkach Z i F różnią się istotnie, wylosowano z obu kierunków po 36 prac egzaminacyjnych i uzyskano następujące informacje.
,
, Sz=16pkt, Sf= 9pkt. Przy poziomie istotności α=0,05 sprawdź hipotezę o różnym poziomie wyników na badanych kierunkach.

1. Jakich parametrów dotyczy weryfikacja?

2. Postaw hipotezę zerową i alternatywną.

3. Czy można w tym miejscu określić statystykę testową?

4. Postaw hipotezę zerową i alternatywną dotyczącą wielkości zróżnicowania ocen na obu kierunkach.

5. Określ statystykę testową dla dwóch wariancji.

6. Jaki rozkład ma ta statystyka?

7. Określ na podstawie tablic obszar krytyczny testu.

8. Oblicz wartość powyższej statystyki na podstawie wylosowanych prób.

9. Wyciągnij wniosek weryfikacyjny.

10.Określ statystykę testową dla dwóch średnich.

11.Jaki rozkład ma ta statystyka?

12.Określ na podstawie tablic obszar krytyczny testu.

13.Oblicz wartość powyższej statystyki na podstawie

wylosowanych prób.

14.Wyciągnij wniosek weryfikacyjny.

1. Weryfikacja dotyczy badania różnicy między średnimi wynikami na dwóch kierunkach.

2. 
   

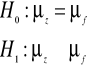
3. W tym miejscu można stwierdzić, że statystyka będzie mieć rozkład asymptotycznie normalny, ale nie wiemy, czy wariancje w populacji są równe.

4. 
   
   

5.

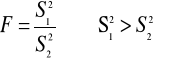
6. Powyższa statystyka ma rozkład F-Snedecora o

n₁-1 i n₂-1 stopniach swobody.

7. Dla α=0,05 oraz n₁-1=35 i n₂-1=35 stopni swobody wartość krytyczna testu odczytana z tablic rozkładu

F-Snedecora wynosi 1,76.

8.

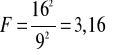
9. Obszar krytyczny testu (prawostronny) odczytany z tablic [1,76;+∞]. Wartość wyliczona statystyki F=3,16 znalazła się w obszarze krytycznym, więc hipotezę zerową o jednakowych wariancjach w obu populacjach odrzucamy i przyjmujemy hipotezę alternatywną, że wariancja na kierunku Z jest większa.

10. Zastosujemy statystykę testową dla dwóch średnich o rozkładzie normalnym przy różnych wariancjach w populacjach generalnych.

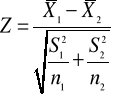
11. Statystyka powyższa ma rozkład normalny.

12. Wartość statystyki przy dwustronnym obszarze krytycznym oraz poziomie istotności α=0,05 wynosi 1,96. Czyli obszar krytyczny wynosi [-∞;-1,96] lub [1,96;+∞].

13.

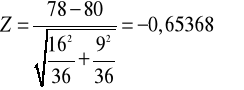
14. Wartość wyliczona Z=-0,65368 nie znalazła się w obszarze krytycznym, więc nie ma podstaw do odrzucenia hipotezy zerowej o jednakowym poziomie średnich wyników na obu kierunkach.

---