NAZWISKO I IMIĘ ……………………………… …………. GRUPA ……..

STATYSTYKA MATEMATYCZNA B

W firmie ubezpieczeniowej Z wylosowano 19 ubezpieczonych w wieku poniżej 30 lat (X₁) i 29 w wieku 30lat i starszych (X₂) w celu zbadania wysokości sumy ubezpieczenia na życie.

Uzyskano następujące informacje:
S₁=8tyś zł

S₂=7 tyś zł

1. Oszacuj metodą punktową średnią wysokość sumy ubezpieczenia osób poniżej 30 roku życia.

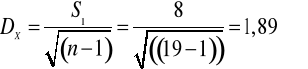
tyś zł

2. Przy współczynniku ufności 1-α=0,95 oszacuj metodą przedziałową średnią wysokość sumy ubezpieczenia osób poniżej 30 roku życia.

d_(x)=2,101*1,89=3,97 tyś zł

Przedział ufności ma następującą postać:

64-3,97≤μ≤64+3,97

60,029≤μ≤67,97

3. Zakładając, że powyższa próba jest próbą pilotażową oblicz minimalną liczebność próby, przy której maksymalny błąd szacunku będzie niewiększy niż 2 tyś. zł.

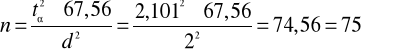
4. Na podstawie powyższych prób sprawdź hipotezy o jednakowym zróżnicowaniu i jednakowym średnim poziomie sumy ubezpieczenia w obu zbiorowościach ubezpieczonych przy poziomie istotności α=0,05.

H₀:

H_!:

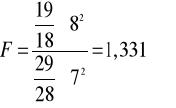
F_α=1,99 (1,96)

Wniosek: Nie podstaw do odrzucenia hipotezy zerowej.

H₀:

H_!:

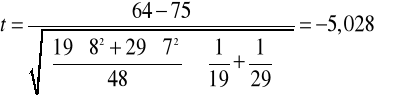
t_α=2,021 (2,000)

Wniosek: Hipotezę zerową odrzucamy.

5. Co oznacza zapis: „N( 0;1)” Rozkład normalny standaryzowany o średniej 0 i odchyleniu standardowym 1.

6. Co to jest „współczynnik ufności” Założone prawdopodobieństwo, że zbudowany przedział obejmie szacowany parametr.

7. Co zawierają kolumny rozkładu zmiennej losowej skokowej . Wartości zmiennej i prawdopodobieństwa wystąpienia tych wartości.

8. Czym charakteryzuje się estymator zgodny. Im większa próba, tym dokładniejsze oszacowanie.

---