Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
1
MPiS30 W11: WERYFIKACJA HIPOTEZ
PARAMETRYCZNYCH
1. Hipoteza statystyczna
2. Podział hipotez statystycznych
3. Procedura weryfikacji hipotezy
4. Testy parametryczne
5. Testy dla wartości oczekiwanej
Przykład 1
6. Test dla wariancji
7. Test dla wskaźnika struktury
Przykład 2
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
2
Klasyczna teoria J. Neymana i E. Pearsona dotyczy testów
istotności (test of significance). Metody dostosowane do norm
PN-ISO 3494, PN-ISO 3534.
1. Hipoteza statystyczna
(Statistical hypothesis) to dowolne przypuszczenia dotyczące
rozkładu badanych cech w populacji
postaci funkcyjnej lub
wartości parametrów rozkładu.
Przykłady hipotez statystycznych:
trwałość akumulatora ma rozkład N(70, 5) [m-cy],
zawartość szkodliwych związków w spalinach samochodów
z katalizatorem i bez katalizatora różni się,
wynik egzaminu zależy od czasu uczenia się studenta.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
3
Na podstawie wiedzy o populacji i badanych cechach formu-
łujemy zbiór hipotez dopuszczalnych
, czyli zbiór rozkładów,
które mogą charakteryzować badane cechy w populacji. Hipote-
zą statystyczną nazywamy podzbiór H zbioru
.
2. Podział hipotez statystycznych:
A. Ze względu na metody:
parametryczne (parametric hypothesis)
hipotezy dotyczące
nieznanych wartości parametrów,
nieparametryczne
hipotezy dotyczące postaci funkcyjnej
rozkładu, losowości próby, niezależności badanych cech, i in.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
4
B. Ze względu na liczebność podzbioru H zbioru
:
proste (simple hypothesis)
hipotezy, które jednoznacznie
określają rozkład danej populacji, odpowiadające im podzbiory
H zbioru
zawierają dokładnie jeden element (jeden rozkład),
złożone (composite hypothesis)
hipotezy, które nie określają
w pełni rozkładu populacji. Podzbiory H zbioru
zawierają
więcej niż jeden element (rodzina rozkładów).
C. Ze względu na liczbę populacji:
dotyczące jednej, dwóch lub wielu populacji.
D. Ze względu na liczbę badanych cech:
dotyczące jednej, dwóch lub wielu cech.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
5
Stwierdzenie: wzrost pewnej populacji ludzi jest określony roz-
kładem normalnym o parametrach m
1,75m i σ
10cm jest
prostą hipotezą parametryczną, ponieważ określa wartość para-
metrów rozkładu i jednoznacznie definiuje rozkład.
Stwierdzenie „wzrost badanej populacji jest określony rozkła-
dem normalnym” jest hipotezą nieparametryczną
nie dotyczy
wartości parametrów rozkładu i złożoną
określa rodzinę roz-
kładów.
3. Procedura weryfikacji hipotezy
Weryfikacją hipotezy (hypothesis testing) nazywamy
sprawdzanie przypuszczeń o rozkładzie badanej cechy lub cech
w populacji, sformułowanych bez zbadania jej całości.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
6
Procedurą weryfikacji hipotezy nazywamy sformalizowane
postępowanie badawcze, przebiegające w kilku krokach, prze-
prowadzone na podstawie prób losowych pobranych z populacji.
Krok 1: Sformułowanie hipotez: zerowej i alternatywnej
Hipoteza zerowa H
0
(null hypothesis)
hipoteza poddana pro-
cedurze weryfikacyjnej. Przykładowo porównując parametry θ
1
,
θ
2
R, (na przykład wartości oczekiwane lub wskaźniki struktu-
ry badanej cechy w dwóch populacjach), hipotezę zerową mo-
żemy zapisać na trzy sposoby:
a) H
0
: θ
1
θ
2
.
0
, b) H
0
: θ
1
θ
2
.
0
, c) H
0
: θ
1
θ
2
.
0
,
gdzie
0
jest wielkością stałą,.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
7
Hipoteza alternatywna H
1
(alternative hypothesis)
hipote-
za przeciwstawna do hipotezy zerowej. Dotyczy ona przypusz-
czenia, które zostanie przyjęte w przypadku odrzucenia hipotezy
zerowej. Przy porównywaniu parametrów θ
1
, θ
2
możemy ją zapi-
sać na trzy sposoby, w zależności od hipotezy zerowej:
a) H
1
: θ
1
θ
2
0
(hipoteza dwustronna),
b) H
1
: θ
1
θ
2
. >
0
(hipoteza prawostronna),
c) H
1
: θ
1
θ
2
.<
0
(hipoteza lewostronna).
Np. założeniu symetryczności monety odpowiada prosta hipote-
za zerowa H
0
: p = 1/2, natomiast hipoteza o braku symetryczno-
ści H
1
: p
½ jest dwustronną hipotezą złożoną.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
8
Krok 2: Określenie poziomu istotności α
Poziom istotności (significance level) testu jest to arbitralnie
przyjęte prawdop.
, które jest górną granicą popełnienia błędu I
rodzaju (error of first kind), który polega na odrzuceniu hipotezy
H
0
wtedy, gdy jest ona prawdziwa. Ponieważ chcemy, aby ryzy-
ko popełnienia błędu
było jak najmniejsze, więc z praktycz-
nych aspektów przyjmujemy, że α ≤ 0,1 (domyślnie α = 0,05).
Nie odrzucenie fałszywej hipotezy H
0
nazywamy błędem II
rodzaju. Prawdopod. popełnienia tego błędu oznaczamy
.
Prawdop. (1
) nazywamy mocą testu.
Krok 3: Wybór statystyki testowej i obliczenia z próby
Testem hipotezy H
0
nazywam regułę, która precyzuje dla ja-
kich wartości próby powinniśmy ją przyjąć albo odrzucić. Na
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
9
podstawie informacji i założeń o rozkładzie populacji, parame-
trach i liczności próby konstruujemy lub wybieramy spośród
znanych statystyk taką statystykę U = h(X), której rozkład
prawd. (dokładny lub asymptotyczny) jest całkowicie znany (np.
normalny, t-Studenta, chi-kwadrat) przy założeniu prawdziwości
hipotezy H
0
. Statystykę U zastosowaną do sprawdzenia hipotezy
H
0
nazywamy statystyką testową lub jej testem.
Wyniki próby opracowujemy zgodnie z procedurą wybrane-
go testu. Są one podstawą do obliczenia oceny u
0
testu U.
Krok 4: Wyznaczenie obszaru krytycznego
Obszar krytyczny (critical region)
podzbiór R
zbioru
wartości statystyki testowej U dla których hipoteza H
0
jest od-
rzucana. Obszar R
spełnia warunek: P(U
R
H
0
)
.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
10
Obszar ten znajduje się zawsze na krańcach rozkładu staty-
styki U i zależy od poziomu istotności α, natomiast jego położe-
nie określone jest przez hipotezę H
1
.
Wartości graniczne obszaru krytycznego nazywamy warto-
ściami krytycznymi. Przy danym α wartości krytyczne są wy-
znaczane za pomocą tablic, tak aby spełniona była relacja zależ-
na od sposobu sformułowania hipotezy H
1
:
gdy H
1
typu ≠, to obszar krytyczny dwustronny
R
{u
R: u < u
/2
u > u
1
/2
}, ,
gdy H
1
typu >, to obszar krytyczny prawostronny
R
{u
R: u > u
1
},
gdy H
1
typu <, to obszar krytyczny lewostronny
R
{u
R: u < u
}, ,
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
11
gdzie u
p
jest kwantylem rzędu p rozkładu statystyki U.
Krok 5: Podjęcie decyzji
Sprawdzamy, czy obliczona z próby wartość statystyki u
0
należy
do obszaru krytycznego R
. Reguła decyzyjna:
jeśli u
0
R
, to na przyjętym poziomie istotności
odrzuca-
my hipotezę H
0
, jako mało prawd., na rzecz hipotezy H
1
,
jeśli u
0
R
, to stwierdzamy brak podstaw do odrzucenia
hipotezy H
0
(jako bardzo prawdop.). Nie odrzucenie hipote-
zy zerowej nie oznacza, że jest ona prawdziwa.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
12
4. Testy parametryczne
Służą do weryfikacji hipotez odnoszących się do parametrów
rozkładu badanych cech w jednej, dwóch lub kilku populacjach
generalnych. Najczęściej weryfikowane są sądy dotyczące pod-
stawowych parametrów rozkładu cech, tj. wartości oczekiwanej,
wariancji, wskaźnika struktury, czy współczynnika korelacji.
W testach tych oceny parametrów uzyskane z próby losowej są
porównywane z hipotetycznymi wielkościami parametrów, trak-
towanymi jako pewien wzorzec.
W praktyce, testy te często służą do porównywania parame-
trów na podstawie ocen uzyskanych z kilku prób losowych.
Testy te można stosować tylko wówczas, gdy spełnione są od-
powiednie założenia, które należy wcześniej sprawdzić.
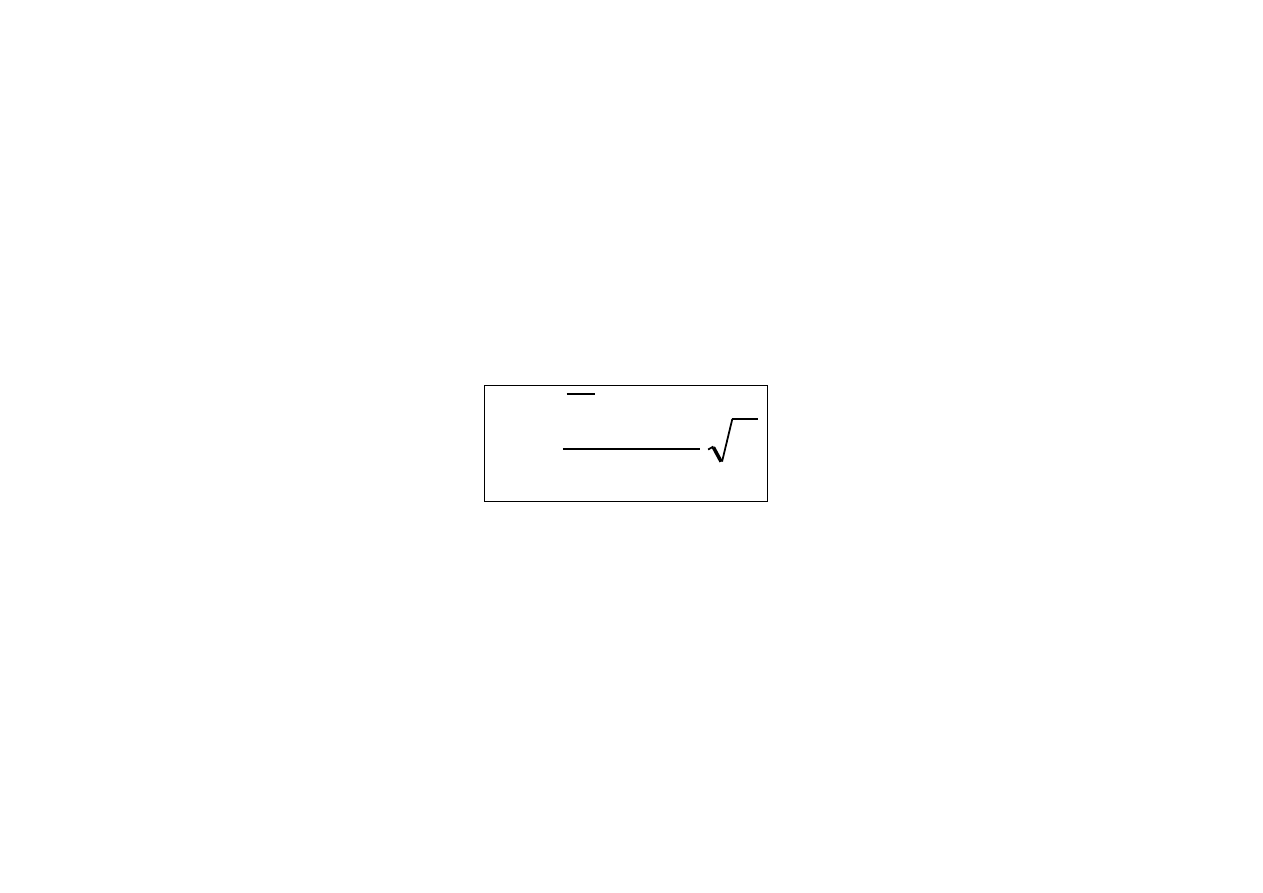
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
13
5. Testy dla wartości oczekiwanej
Zm. l. X jest modelem badanej cechy w populacji. Hipoteza
zerowa dotyczy nieznanej wartości oczekiwanej.
Model 1. X~N(m
?,
) oraz odchylenie standardowe jest znane.
Statystyka służąca do weryfikacji hipotezy H
0
dana jest wzorem
n
m
Z
n
0
X
.
Przy założeniu prawdziwości H
0
, na mocy tw. o rozkładzie śred-
niej arytmetycznej Z~N(0, 1).
Z tablicy kwantyli rozkładu N(0, 1) wyznaczamy stosownie do
H
1
obszar krytyczny, obliczamy wartość statystyki i, na przyję-
tym poziomie istotności
, podejmujemy decyzję dotyczącą H
0
.
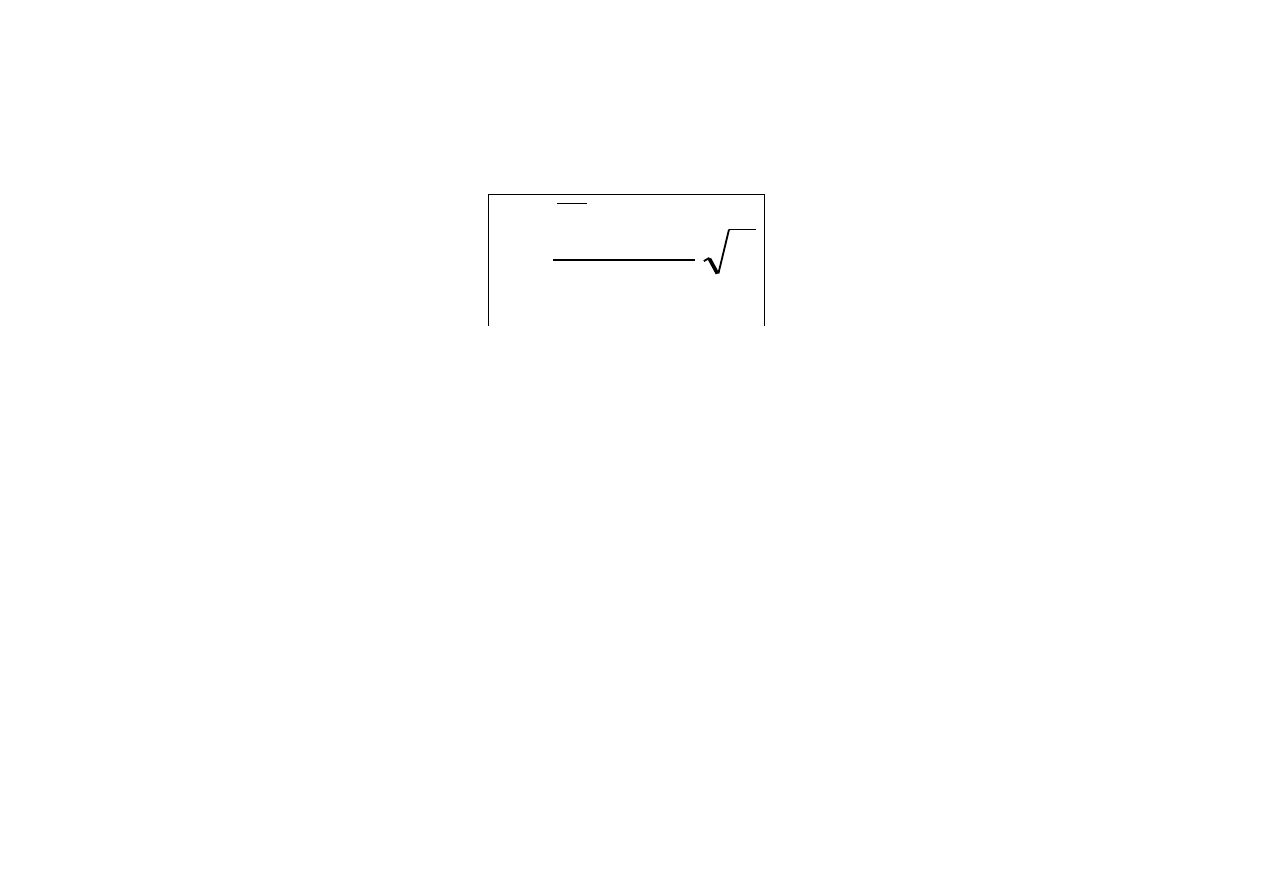
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
14
Model 2. X~N(m
?,
?), odchylenie standardowe jest niezna-
ne. Do sprawdzenia hipotezy H
0
stosujemy statystykę t-Studenta
n
S
m
t
n
n
0
X
.
Jeżeli hipoteza H
0
: m
m
0
jest prawdziwa, to na mocy tw. o
rozkładzie średniej arytmetycznej, przy nieznanej wariancji
2
wiadomo, że t~t(n
1).
Korzystając z kwantyli rozkładu t-Studenta, wyznaczamy ob-
szar R
stosownie do H
1
i danego
.
Obliczamy wartość t
0
statystyki i podejmujemy decyzję doty-
czącą H
0
.
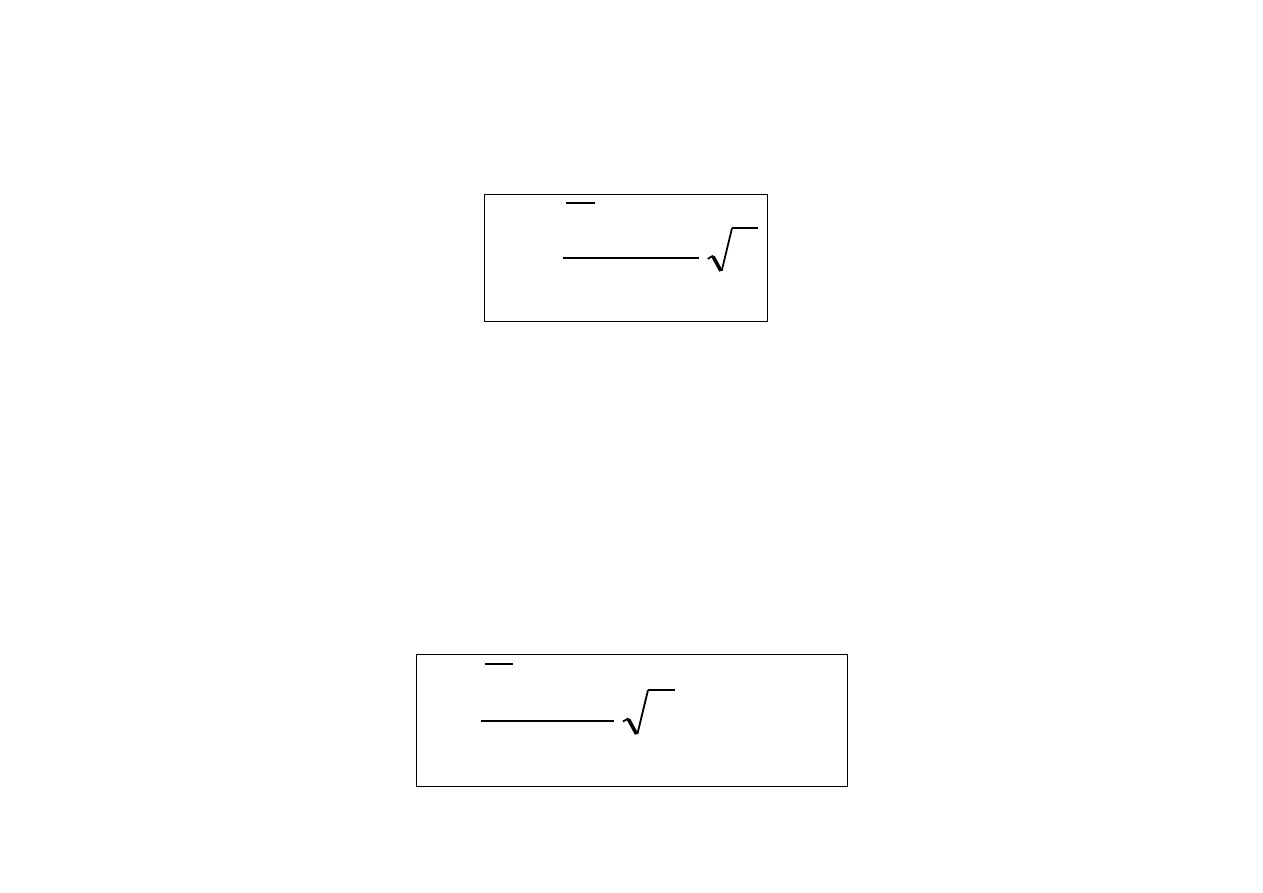
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
15
Model 3. X~dowolny (m
?,
?). Do sprawdzenia hipotezy H
0
stosujemy asymptotyczną statystykę Z
n
S
m
Z
n
n
0
X
.
Przy założeniu prawdziwości hipotezy H
0
: m
m
0
, na mocy CTG
statystyka Z ma graniczny rozkład N(0, 1). Stosowana jest więc
dla dostatecznie dużej próby (n
30).
Model 4. Niech (X
i
, Y
i
), i
1,…, n będzie próbą powiązaną (ma-
thed pairs) z populacji (X, Y) oraz różnica D
X−Y ma rozkład
N(m
D
?,
D
?). Jeśli hipoteza H
0
: d
d
0
jest prawdziwa, to
)
1
(
~
0
n
t
n
S
d
t
D
n
D
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
16
Przykład 1. Przed wykonaniem określonego zabiegu na n ele-
mentach próby dokonujemy pomiarów X
1
,…, X
n
pewnej cechy
X. Następnie po dokonanym zabiegu mierzymy tę samą cechę
otrzymując, w tej samej kolejności elementów, wyniki Y
1
,…, Y
n
.
Sprawdzić hipotezę zerową H
0
: m
X
− m
Y
0 określającą równość
wartości oczekiwanych badanej cechy populacji przed i po za-
biegu.
Wskazówka. Zastosować model 4.
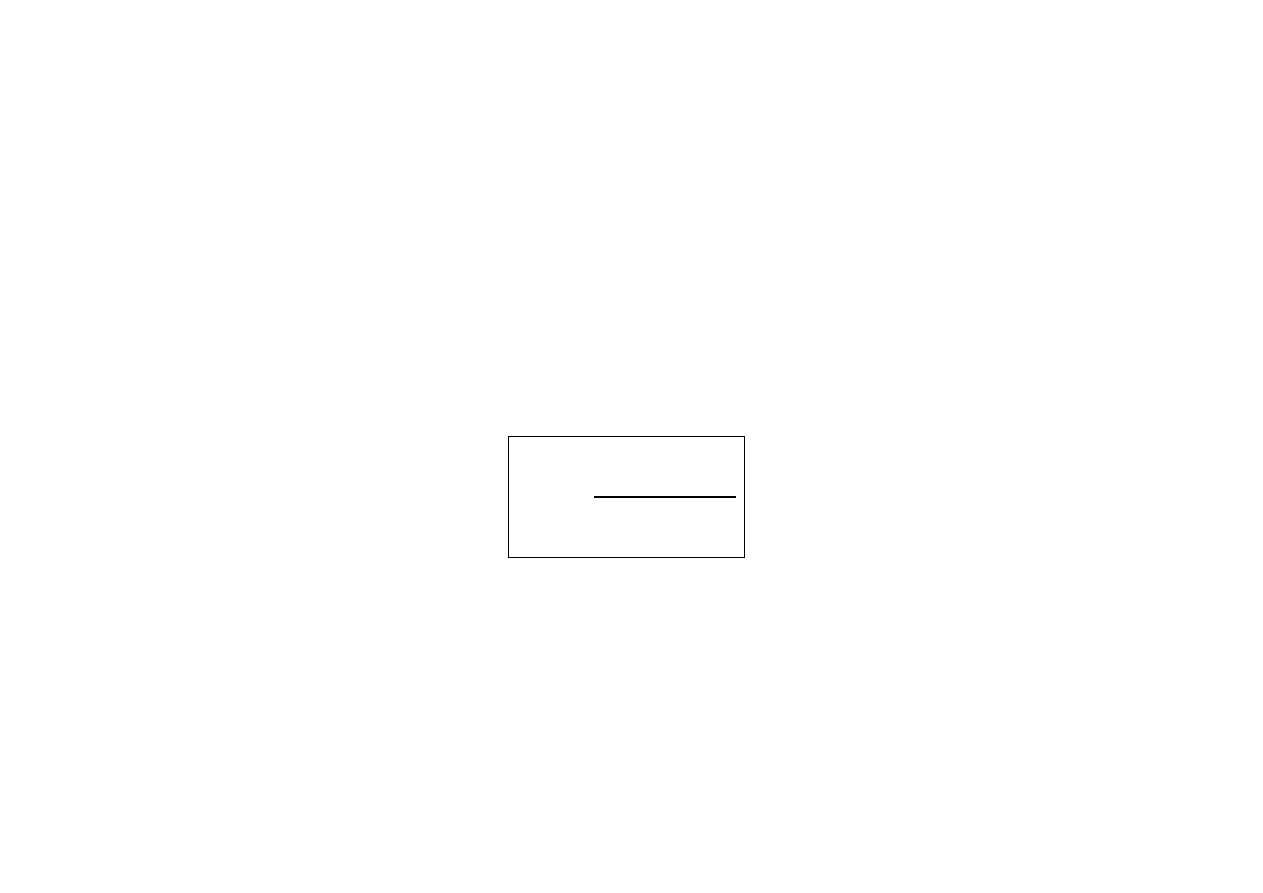
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
17
6. Test dla wariancji
Testujemy hipotezę dla wariancji
H
0
:
2
0
2
,
(lub dla odchylenia standardowego H
0
:
0
).
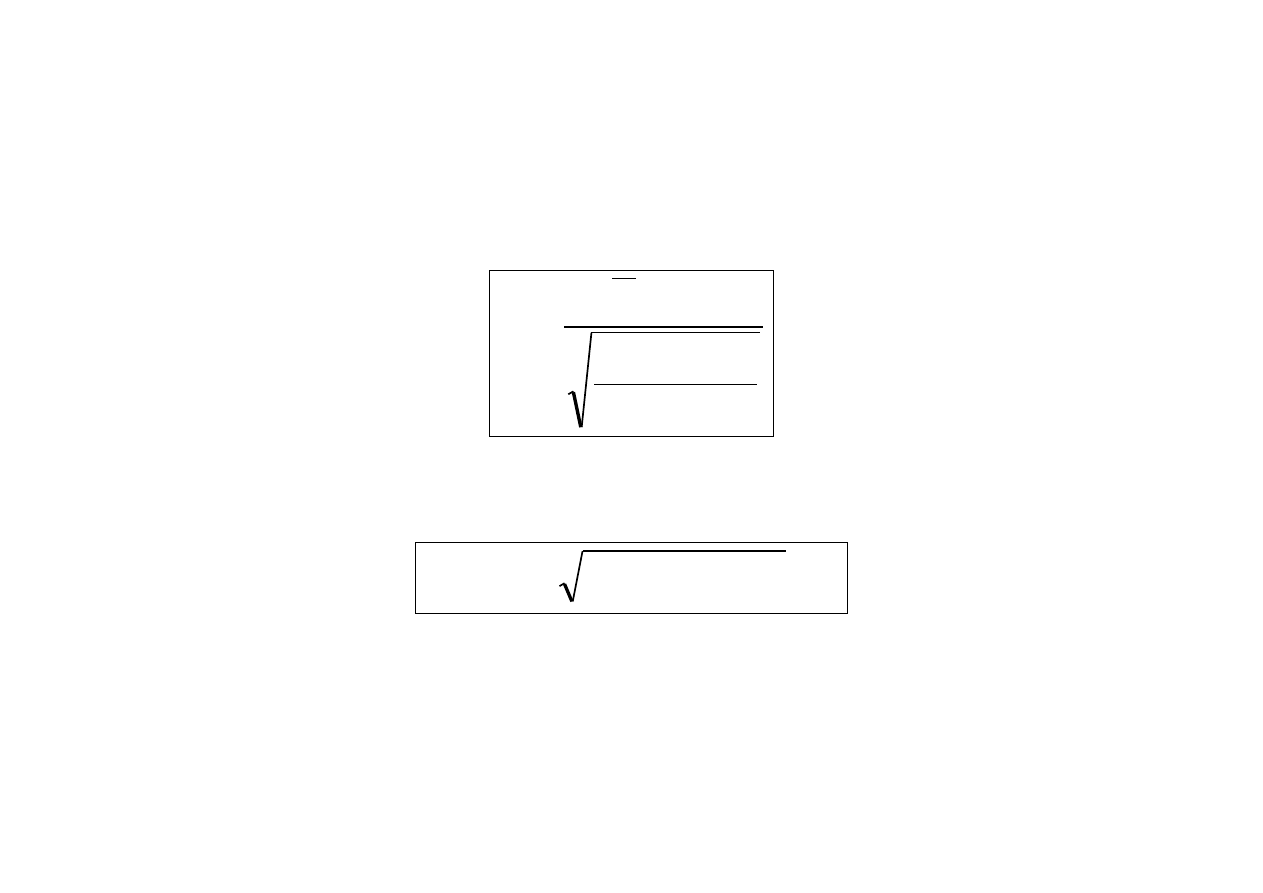
Jeśli cecha w populacji generalnej ma rozkład normalny z
nieznanymi parametrami, to statystyka
2
0
2
2
)
1
(
n
S
n
,
obliczona z próby n-elementowej, ma rozkład chi-kwadrat o n
1
stopniach swobody. Z tablic odczytujemy kwantyle
2
, n
1
rzędu
rozkładu chi-kwadrat dla n
1 stopni swobody i ustalamy ob-
szar krytyczny R
.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
18
7. Test dla wskaźnika struktury
Sprawdzamy hipotezę H
0
: p
p
0
. Jeśli cecha w populacji gene-
ralnej ma rozkład B(p) z nieznanym parametrem p, to statystyka
n
p
p
p
P
Z
n
)
1
(
0
0
0
ma rozkład asymptotycznie normalny N(0, 1). W praktyce staty-
stykę tę możemy stosować dla prób spełniających warunek.
1
/
)
1
(
0
0
0
0
n
p
p
p
UWAGA. W przypadku jednostronnych alternatywnych hipotez
parametrycznych H
1
typu > lub <, jako hipotezę H
0
przyjmujemy
zgodnie z normami hipotezę złożoną typu
lub
.
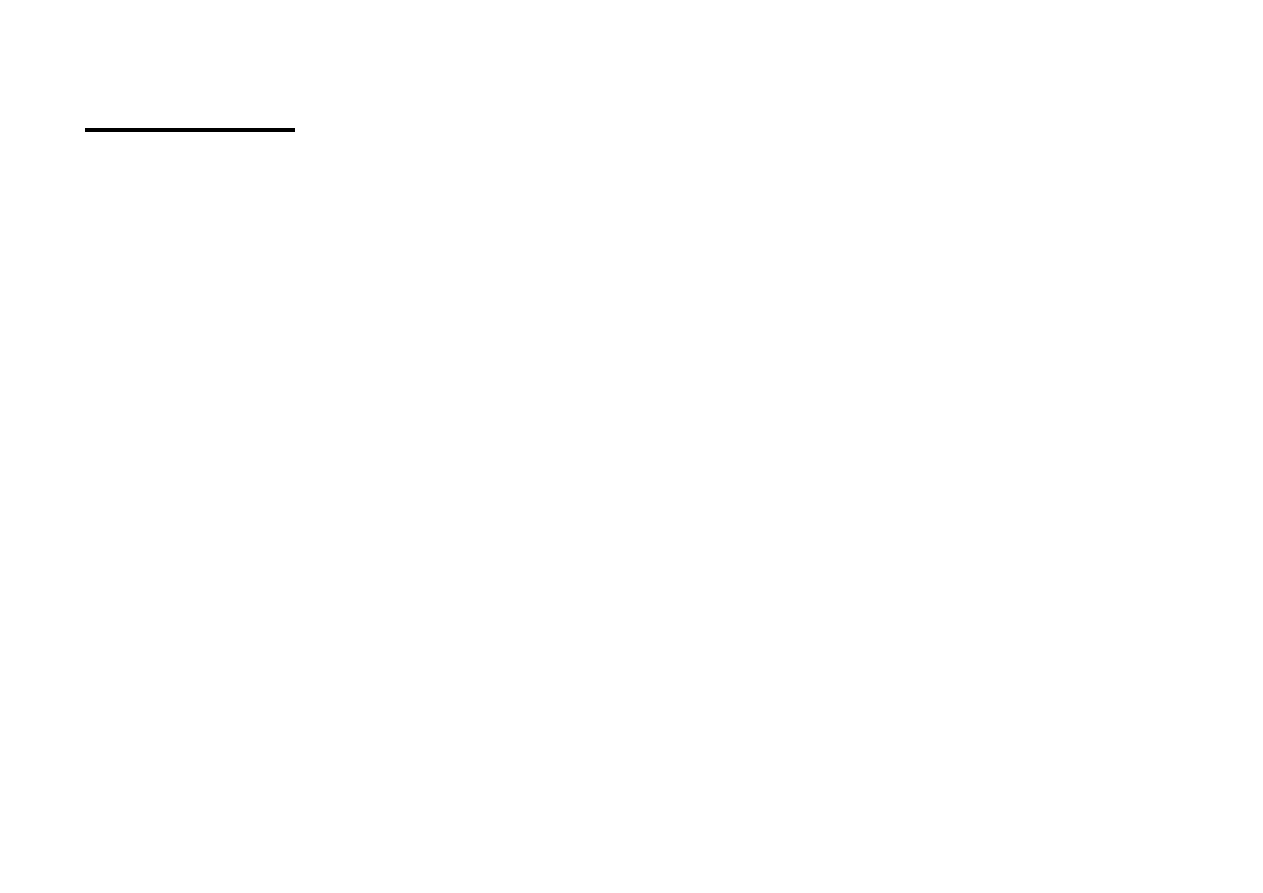
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
19
Przykład 2. Dla danych z przykładu 4 W10 (Estymacja para-
metrów) dotyczących liczby usterek w produkowanych urządze-
niach (populacja X), zweryfikować hipotezy parametryczne, na
poziomie istotności
= 0,05.
a) przeciętna liczba usterek wynosi 2,
b) przeciętna liczba usterek jest większa od 1,
c) wariancja liczby usterek wynosi 2,
d) odch. standardowe liczby usterek jest większe od 1,2,
e) wskaźnik urządzeń bezusterkowych jest większy od 20%.
Rozwiązanie. Rozkład usterkowości X w populacji jest niezna-
ny, ale próba jest bardzo duża (n
500) i możemy skorzystać
z twierdzeń granicznych.
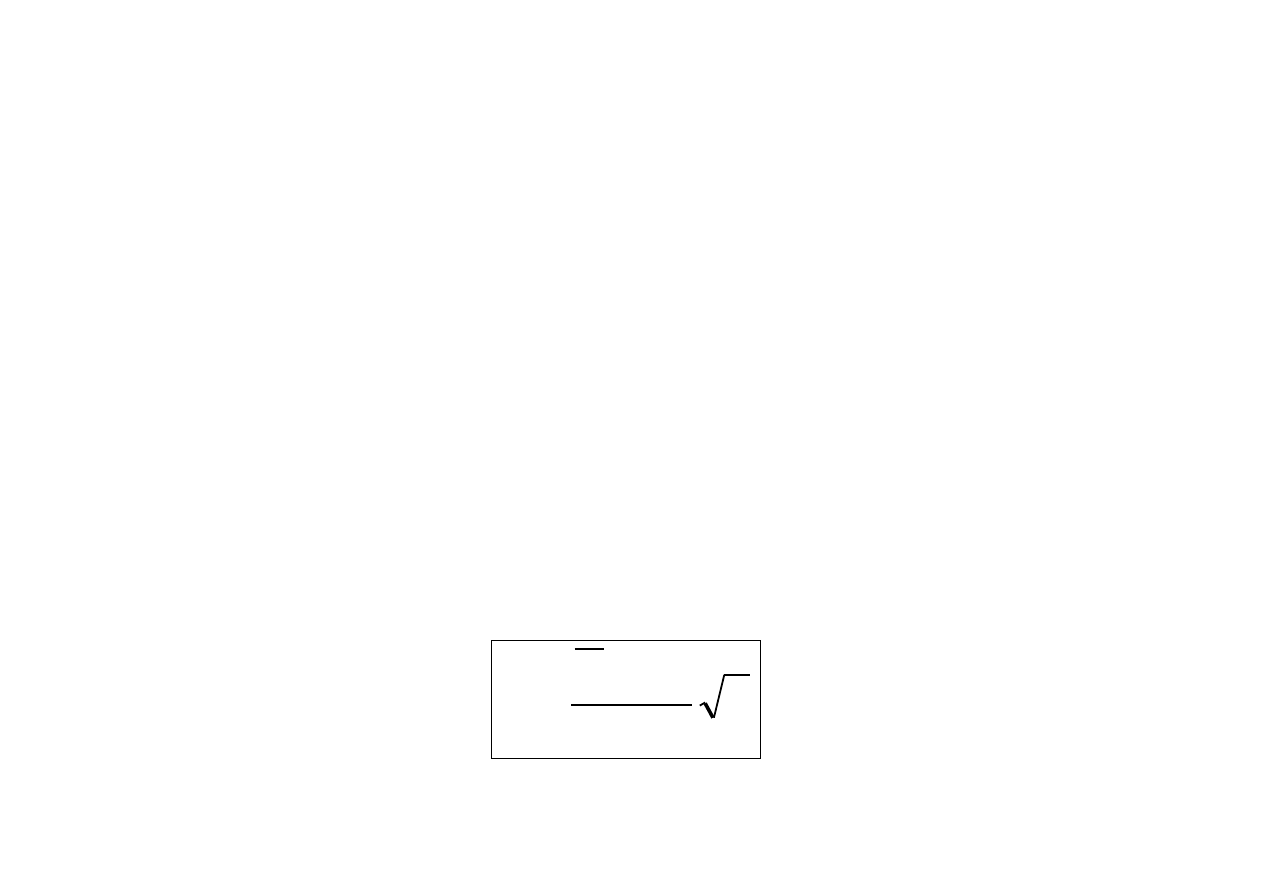
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
20
Wszystkie hipotezy dotyczą parametrów jednej cechy w popula-
cji. Parametrami tymi są: m,
, p.
a) Hipoteza „przeciętna liczba usterek wynosi 2” jest parame-
tryczną hipotezą prostą, dotyczącą populacji X
liczby usterek
w produkowanych urządzeniach. Hipotezę tę ustawiamy jako
hipotezę zerową:
H
0
: m = 2,
jako hipotezę H
1
przyjmujemy hipotezę złożoną:
H
1
: m
2.
Do sprawdzenia hipotezy zerowej zastosujemy statystykę
n
S
m
Z
0
X
.
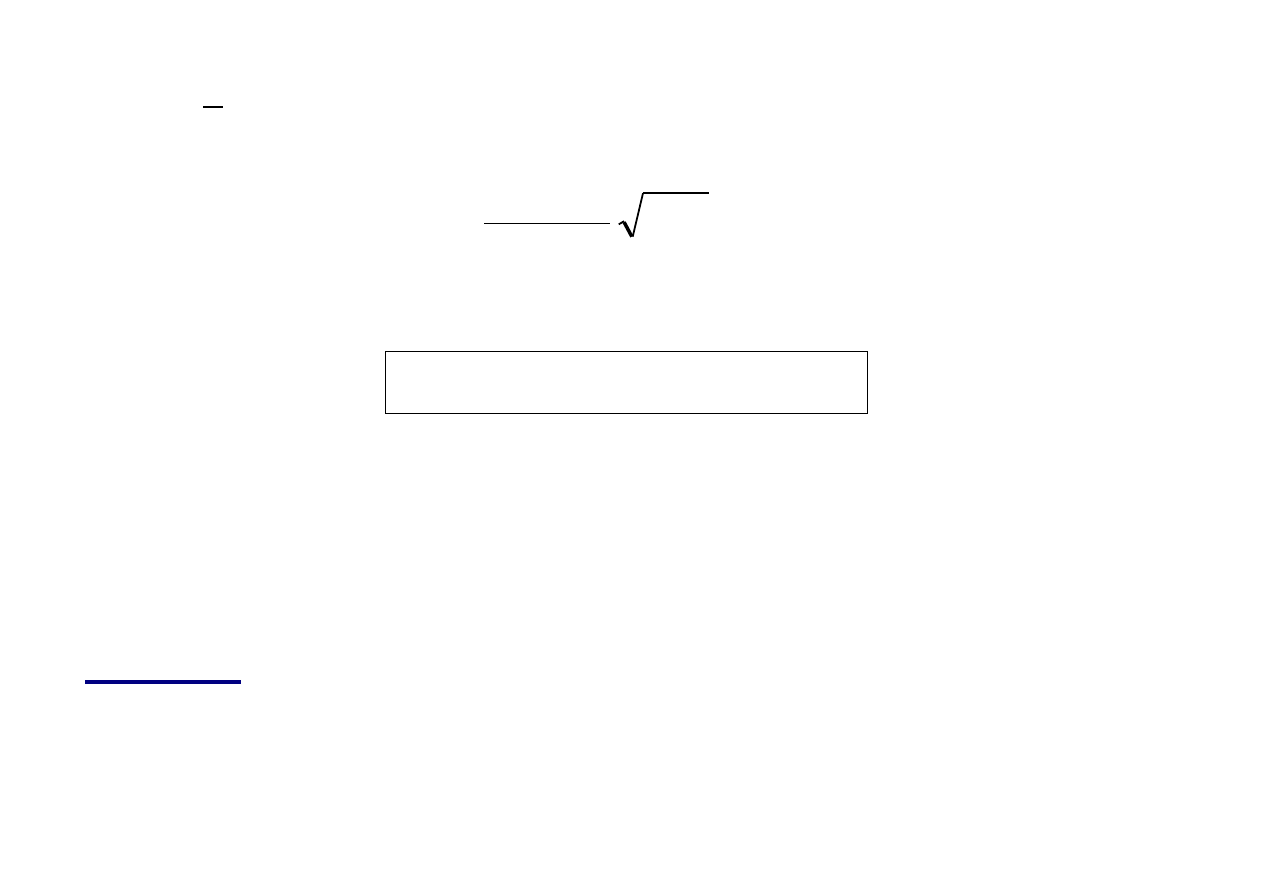
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
21
Dane:
52
1,
n
x
, m
0
= 2, s
n
= 1,24, n = 500,
= 0,05.
66
,
8
500
24
,
1
2
52
,
1
0
z
.
Hipoteza H
1
jest dwustronna, więc obszar krytyczny ma postać
)
,
(
)
,
(
2
/
1
2
/
z
z
R
,
gdzie z
p
jest kwantylem p-tego rzędu rozkładu N(0, 1). W tym
przykładzie p = 0,025 i p = 0,975. Odczytane z tablic kwantyle
wynoszą: z
0,025
=
1,960, z
0,975
= 1,960. Stąd
)
,
96
,
1
(
)
96
,
1
,
(
05
,
0
R
.
Decyzja:
Ponieważ z
0
8,66
R
0,05
, więc na poziomie istot-
ności 0,05, odrzucamy hipotezę H
0
na rzecz hipotezy H
1
i
stwierdzamy, że przeciętna liczba usterek istotnie różni się od 2.
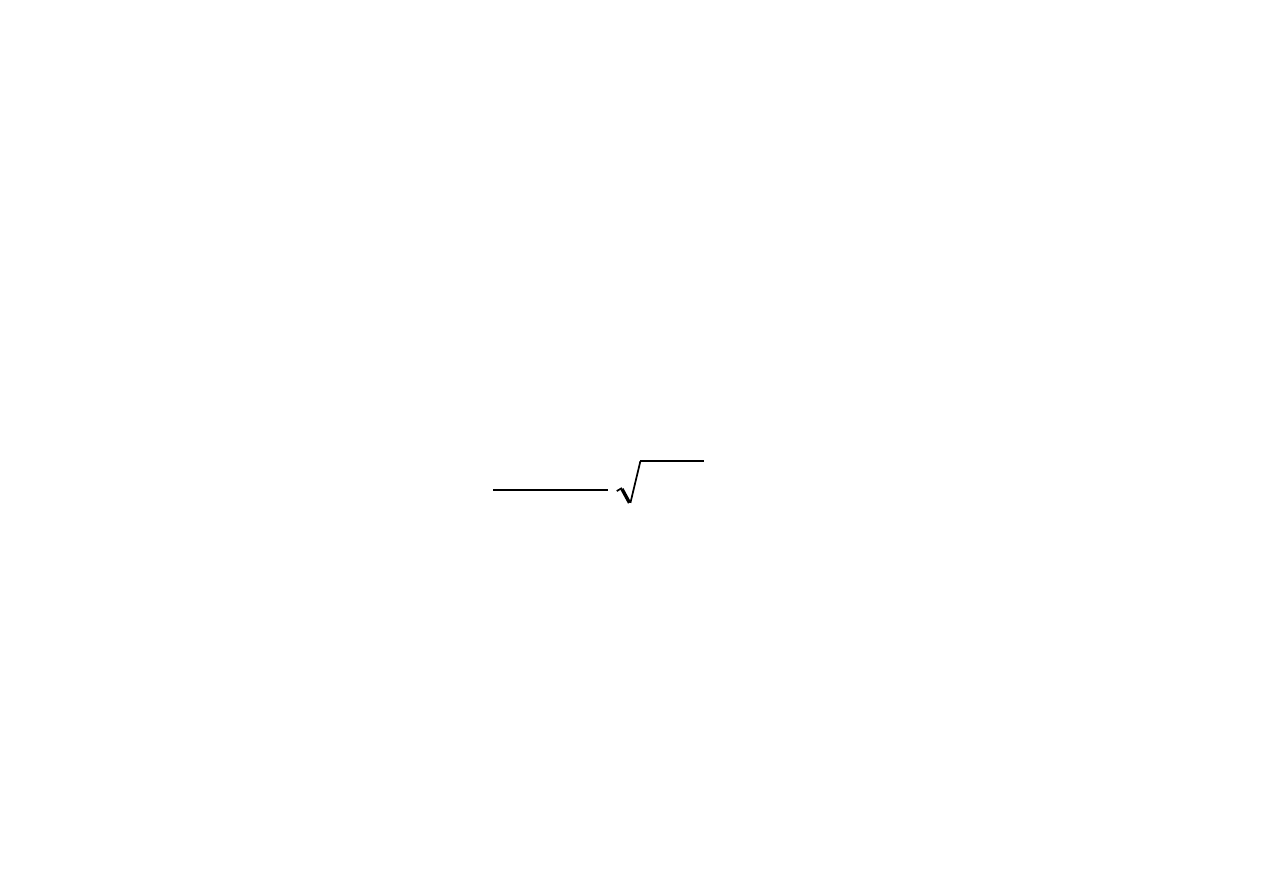
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
22
b) Hipoteza
„przeciętna liczba usterek jest wieksza od 1”
jest
parametryczną hipotezą złożoną ustawianą jako hipoteza H
1
.
Uzupełniamy jednostronną hipotezę zerową i poddajemy ją
sprawdzeniu. Czyli
H
0
: m
1, H
1
: m > 1.
Statystyka jest ta sama co w punkcie a). Wśród danych zmienia
się wartość m
0
. Teraz m
0
= 1. Obliczamy statystykę
377
,
9
500
24
,
1
1
52
,
1
0
z
.
Hipoteza H
1
jest prawostronna, więc obszar krytyczny dla
=
0,05 ma postać:
)
,
65
,
1
(
)
,
(
05
,
0
05
,
0
z
R
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
23
Decyzja.
Ponieważ z
0
R
0,05
,
więc odrzucamy hipotezę H
0
na
rzecz hipotezy H
1
i twierdzimy, że przeciętna usterkowość jest
istotnie większa od 1.
c) Hipoteza
„wariancja liczby usterek wynosi 2”
jest parame-
tryczną hipotezą prostą dotyczącą wariancji badanej populacji.
Ustawiamy ja jako hipotezę zerową
H
0
:
2
= 2.
Jako przeciwstawną przyjmujemy dwustronną hipotezę alt.
H
1
:
2
2.
Stosujemy test chi-kwadrat
2
0
2
2
)
1
(
S
n
.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
24
Dane: n = 500,
2
2
0
, s = 1,24,
= 0,05, stąd
63
,
383
2
5376
,
1
499
2
0
.
Obszar krytyczny:
)
,
(
)
,
0
(
2
1
,
2
/
1
2
1
,
2
/
n
n
R
.
Wielkości
2
499
;
025
,
0
2
499
;
975
,
0
są kwantylami rzędu 0,025 i 0,975
rozkładu chi-kwadrat z 499 stopniami swobody.
Uwaga.
Tablice kwantyli rozkładu chi-kwadrat są sporządzane
zwykle od 1 do 30 stopni swobody. Jeżeli nie możemy skorzy-
stać z komputerowego obliczenia, to korzystamy z przybliżenia
(*)
)
)
1
(
2
,
1
(
~
)
1
(
2
0
2
2
n
n
N
S
n
n
,
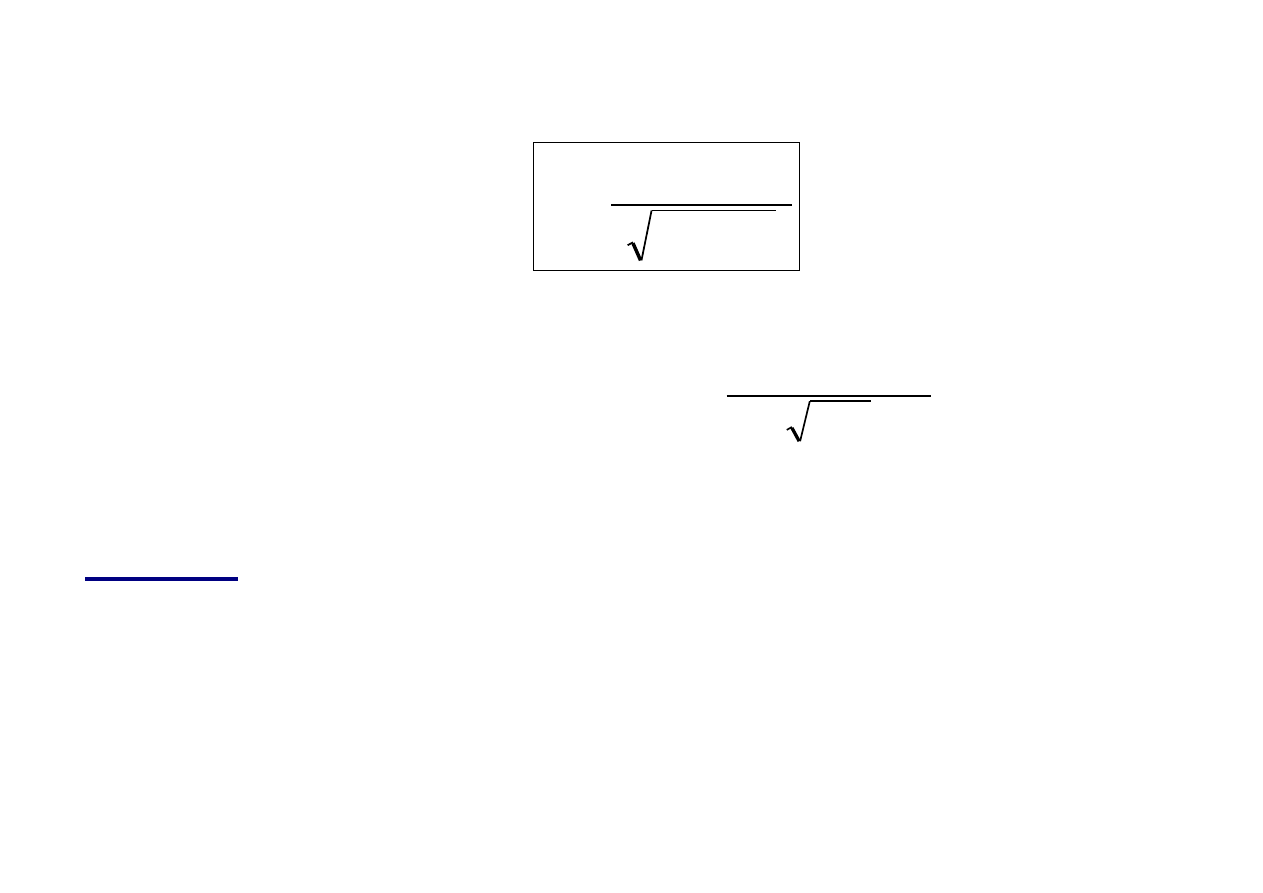
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
25
a po standaryzacji statystyki (*) otrzymujemy statystykę
(**)
)
1
(
2
)
1
(
2
n
n
Z
,
która dla dużych n ma w przybliżeniu rozkład N(0, 1).
Obliczamy wartość statystyki:
65
,
3
998
499
63
,
383
0
z
.
Obszar krytyczny:
)
,
96
,
1
(
)
96
,
1
,
(
05
,
0
R
.
Decyzja.
Ponieważ z
0
R
0,05
, więc na poziomie istotności 0,05
odrzucamy hipotezę H
0
i twierdzimy, że wariancja usterkowości
istotnie różni się od 2.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
26
d) Hipoteza
„odchylenie standardowe liczby usterek jest więk-
sze od 1,2”
jest hipotezą złożoną. ustawiamy ją jako hipotezę
alt. Uzupełniamy hipotezę zerową jako zaprzeczenie H
1
. Czyli
H
0
:
1,2 oraz H
1
:
> 1,2.
Powyższe hipotezy przekształcamy na równoważne hipotezy do-
tyczące wariancji. Stąd
H
0
:
2
1,44 oraz H
1
:
2
> 1,44.
Ponieważ n
500, więc stosujemy statystykę (**)
07
,
1
0
z
.
Prawostronny obszar krytyczny:
)
,
65
,
1
(
05
,
0
R
.
Decyzja.
Obliczona statystyka
nie należy do tego obszaru
, więc
nie mamy podstaw do odrzucenia hipotezy zerowej, że odchyle-
nie standardowe liczby usterek wynosi co najwyżej 1,2.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
27
e) Hipoteza „wskaźnik urządzeń bez usterek jest większy od
20%” jest hipotezą złożoną. Ustawiamy ją jako prawostronną
hipotezę alternatywną. Uzupełniamy hipotezę H
0
jako zaprze-
czenie hipotezy H
1
. Czyli
H
0
: p
0,2,
H
1
: p > 0,2.
Badana cecha ma rozkład zero-jedynkowy. Próba jest bardzo
duża, więc korzystamy z
n
p
p
p
p
z
n
)
1
(
0
0
0
.
Karol J. Andrzejczak, MPiS2 W11: Weryfikacja hipotez parametrycznych
28
Dane: p
0
= 0,2, n = 500,
224
,
0
n
p
.
Obliczona statystyka: z
0
1,34.
Obszar krytyczny prawostronny:
)
,
65
,
1
(
)
,
(
95
,
0
05
,
0
tabl
z
R
.
Decyzja.
Ponieważ obliczona statystyka z
0
nie należy do obsza-
ru R
, więc na poziomie istotności 0,05 nie mamy podstaw do
odrzucenia hipotezy H
0
, że wskaźnik urządzeń bez usterek wy-
nosi co najwyżej 20%.