1

Wykłady ze statystyki matematycznej

5. Weryfikacja hipotez statystycznych z

wykorzystaniem testów parametrycznych

2

Procedura weryfikacji hipotez statystycznych

z wykorzystaniem testu istotno

ś

ci

1. Sformułowanie hipotez H

0

i H

1

(H

0

jest zawsze formułowana w

postaci równości)

2. Określenie poziomu istotności 1-

α

3. Ustalenie wartości statystyki empirycznej t

emp

na podstawie

obserwacji z próby

4. Odczytanie statystyki teoretycznej t

t

z tablic statystycznych

5. Porównanie wartości statystyki empirycznej t

emp

z wartościami

statystyki teoretycznej t

t

i podjęcie decyzji o odrzuceniu lub

braku podstaw do odrzucenia H

0

3

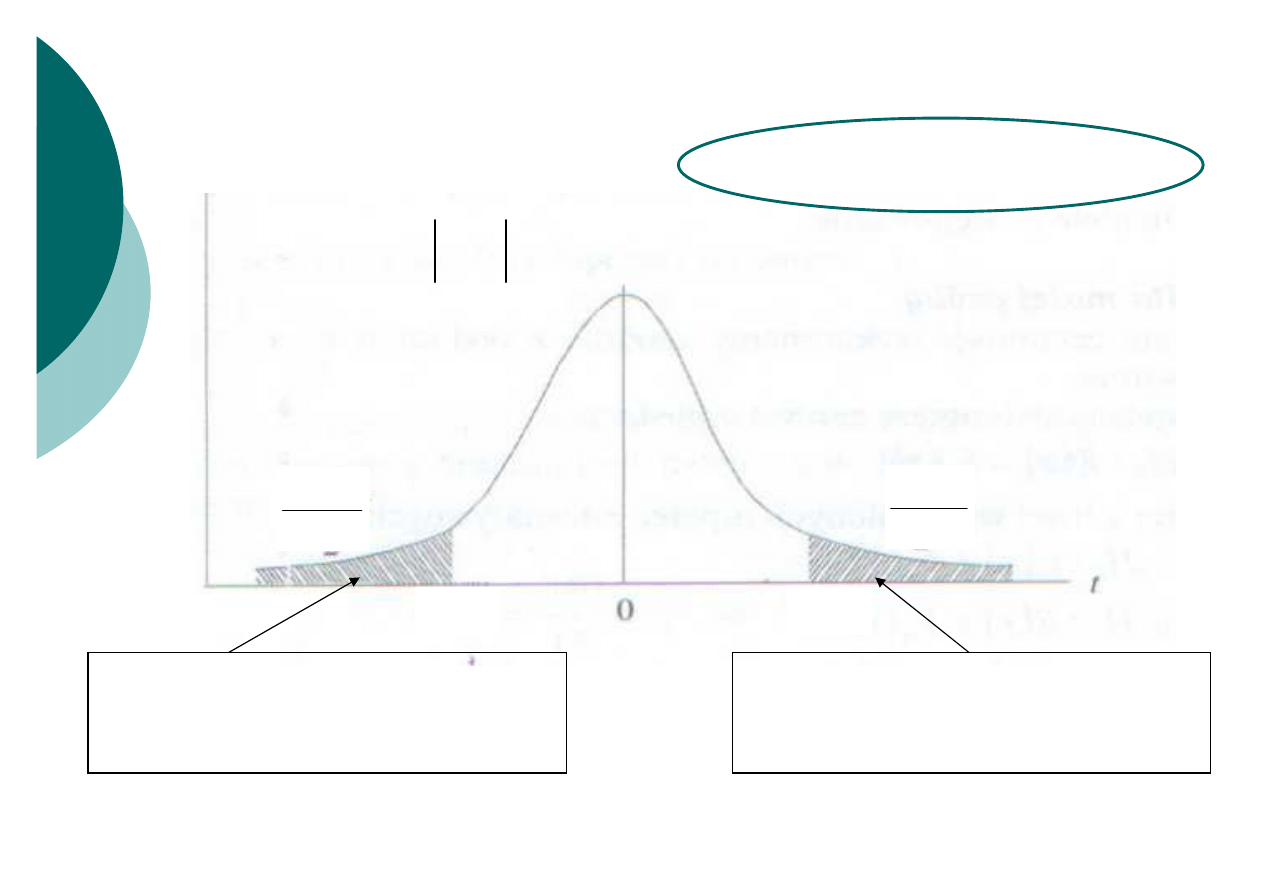
Test dwustronny

2

1

α

−

2

1

α

−

H

0

: E(x) = E

0

(x)

H

1

: E(x) ≠ E

0

(x)

2

1

α

−

obszar krytyczny
(obszar odrzucenia)
dla danego poziomu istotności

obszar krytyczny
(obszar odrzucenia)
dla danego poziomu istotności

-t

t

t

t

t

emp

t

t

<

brak podstaw do odrzucenia H

0

2

1

α

−

Jeżeli wartość

t

emp

wpada w obszar krytyczny należy odrzucić H

0

E

(x) – wartość średnia dla populacji

E

0

(x) – założona wartość średnia

4

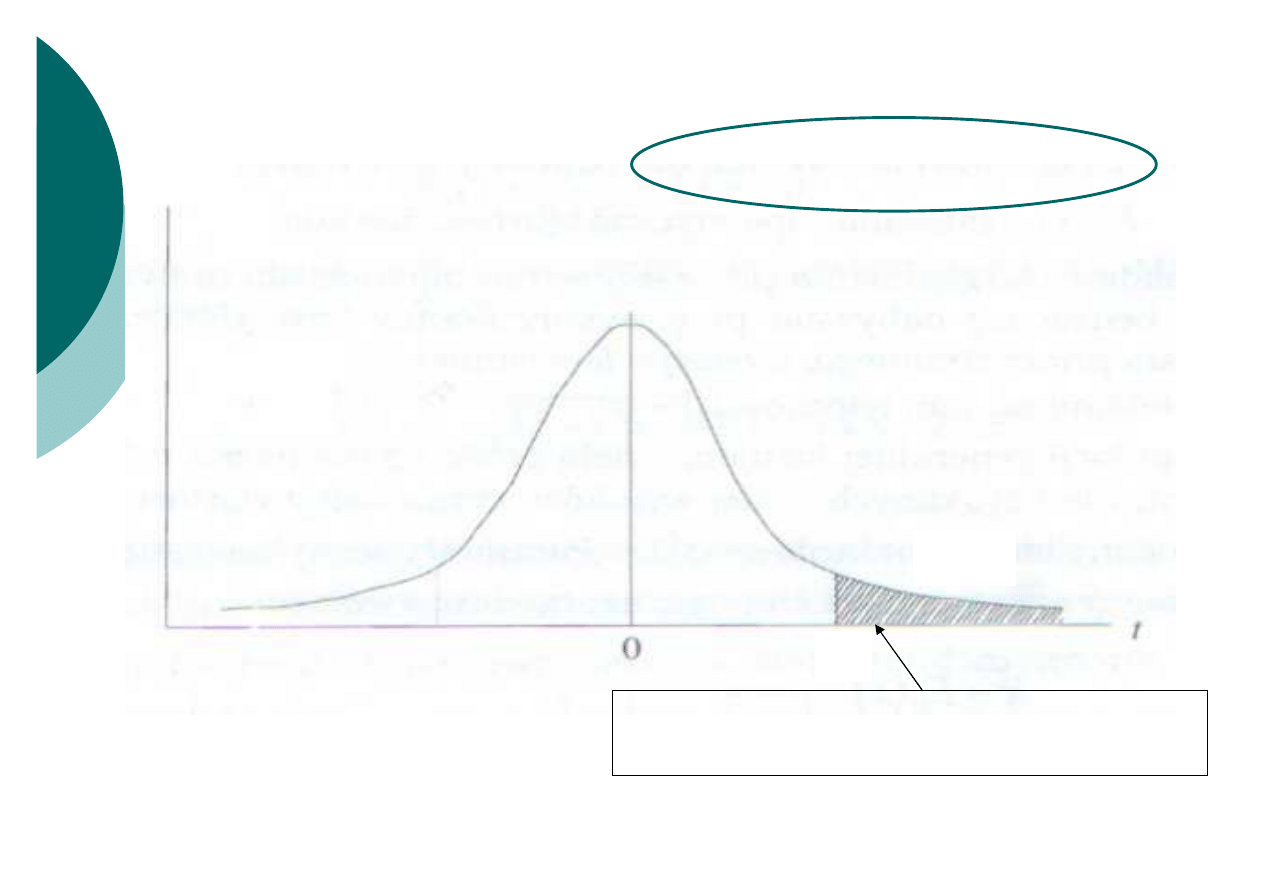
Test prawostronny

obszar krytyczny (obszar odrzucenia)

dla danego poziomu istotności

α

−

1

H

0

: E(x) = E

0

(x)

H

1

: E(x) > E

0

(x)

t

t

t

emp

t

t

<

brak podstaw do odrzucenia H

0

Jeżeli wartość

t

emp

wpada w obszar krytyczny należy odrzucić H

0

E

(x) – wartość średnia dla populacji

E

0

(x) – założona wartość średnia

5

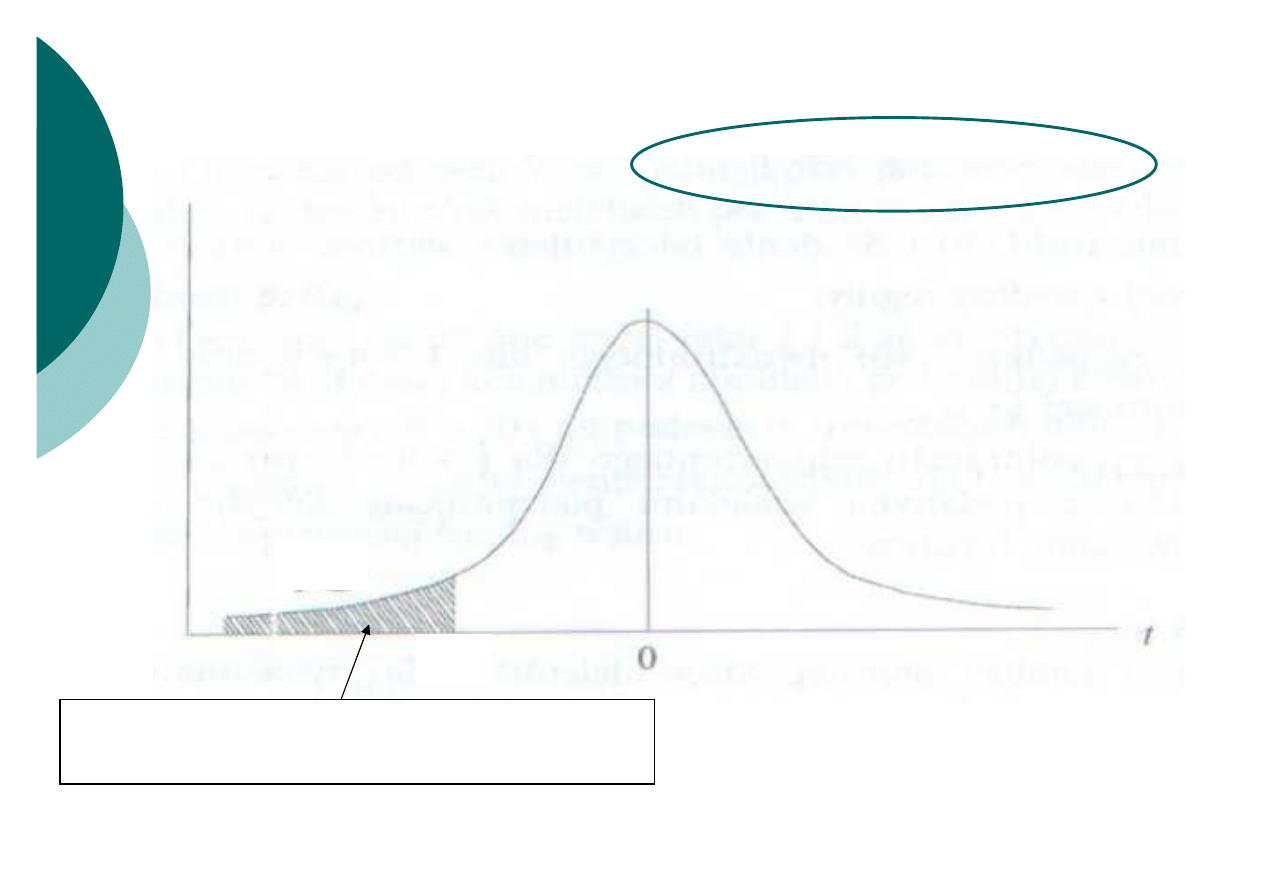
Test lewostronny

obszar krytyczny (obszar odrzucenia)

dla danego poziomu istotności

α

−

1

H

0

: E(x) = E

0

(x)

H

1

: E(x) < E

0

(x)

t

emp

t

t

−

>

-t

t

brak podstaw do odrzucenia H

0

Jeżeli wartość

t

emp

wpada w obszar krytyczny należy odrzucić H

0

E

(x) – wartość średnia dla populacji

E

0

(x) – założona wartość średnia

6

Weryfikacja hipotezy statystycznej

dla warto

ś

ci

ś

redniej

Założenie: rozkład badanej zmiennej w populacji
generalnej ma charakter rozkładu normalnego
o nieznanej średniej i odchyleniu standardowym

H

0

zawsze przyjmuje postać równości:

H

0

: E(x) = E

0

(x)

H

1

może przyjąć jedną z postaci:

H

1

: E(x) ≠ E

0

(x) test dwustronny

H

1

: E(x) > E

0

(x) test prawostronny (jednostronny)

H

1

: E(x) < E

0

(x) test lewostronny (jednostronny)

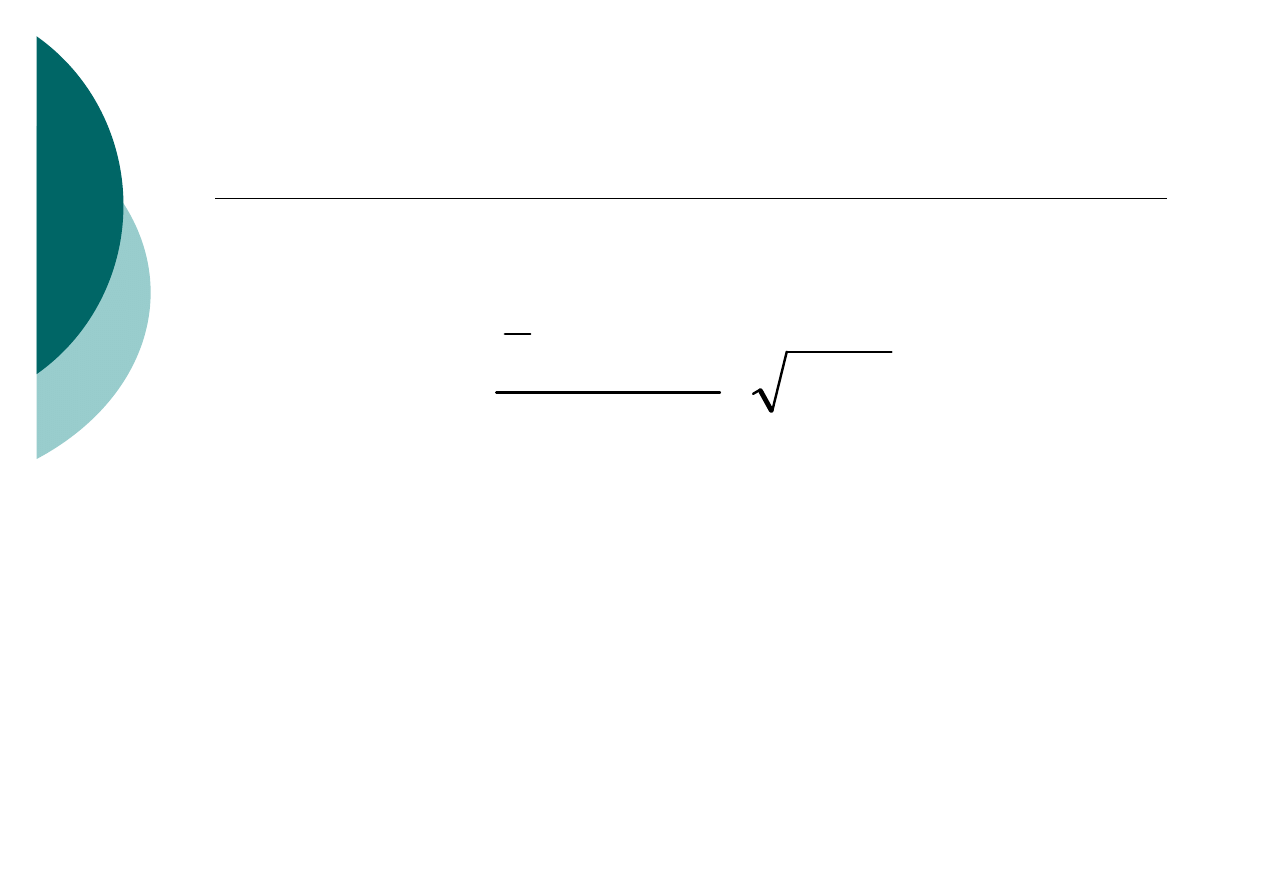
7

Weryfikacja hipotezy statystycznej

dla warto

ś

ci

ś

redniej

Model dla małej próby (n ≤ 30)

1

)

(

)

(

0

−

⋅

−

=

n

x

s

x

E

x

t

emp

Wartość statystyki teoretycznej t

t

należy odczytać z tablic rozkładu

t

Studenta:

• test dwustronny – dla k = n -1 oraz poziomu istotności 1-

α

• test jednostronny - dla k = n -1 oraz poziomu istotności 2(1-

α

)

8

Zad. 8

Wiadomo, że w minionych latach turysta korzystał średnio z 4

noclegów w hotelu w Hongkongu. Analityk przemysłu turystycznego

chce wiedzieć, czy ostatnie zmiany w uprawianiu turystyki w

Hongkongu zmieniły tę średnią. Zebrano informacje dla losowo

wybranych 26 turystów i otrzymano średnią liczbę noclegów 3,5 i

odchylenie standardowe 2 noclegi. Zakładając, że rozkład noclegów

turystów przebywających w Hongkongu ma charakter rozkładu

normalnego, czy można uważać, że średnia liczba noclegów dla

całej populacji turystów zmieniła się? Przeprowadź test przyjmując

poziom istotności 0,05.

9

Zad. 9

W pewnej korporacji międzynarodowej dla losowo wybranych 17

pracowników otrzymano średni wiek 43 lata i odchylenie

standardowe 3 lata. Zakładając, że wiek pracowników ma rozkład

normalny, czy można uważać, że przeciętny wiek pracownika w tej

korporacji jest istotnie wyższy niż 40 lat? Poziom istotności wynosi

0,01.

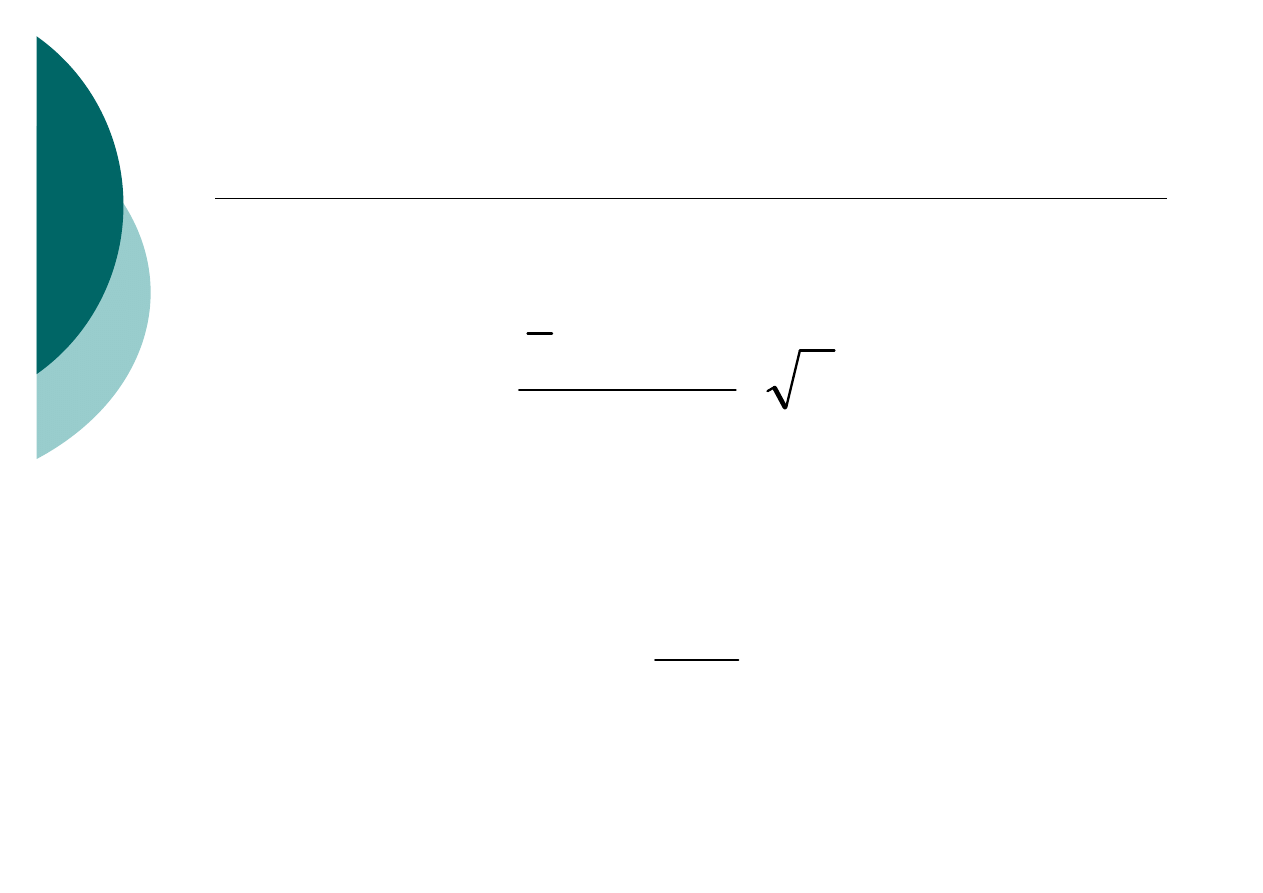
10

Weryfikacja hipotezy statystycznej

dla warto

ś

ci

ś

redniej

n

x

s

x

E

x

t

emp

⋅

−

=

)

(

)

(

0

Model dla dużej próby (n > 30)

Wartość statystyki teoretycznej t

t

należy odczytać z tablic

dystrybuanty rozkładu normalnego:

• test dwustronny – dla

• test jednostronny – dla

)

1

(

5

,

0

α

−

−

2

1

5

,

0

α

−

−

11

Zad. 10

Zakłada się, że „długość życia” opon samochodowych ma rozkład

normalny.

Producent

twierdzi,

że

wartość

przeciętna

tej

charakterystyki jest równa 50 tys. km. Na podstawie 100 losowo

wybranych opon otrzymano średnią 45 tys. km i odchylenie

standardowe 8 tys. km. Czy na poziomie istotności 0,05 można

uważać, że producent ma rację?

12

Weryfikacja hipotezy statystycznej

dla dwóch

ś

rednich

Założenie: rozkłady obu populacji są normalne
o nieznanych wartościach średnich i nieznanych,
ale jednakowych odchyleniach standardowych

H

0

zawsze przyjmuje postać równości:

H

0

: E

1

(x) = E

2

(x)

H

1

może przyjąć jedną z postaci:

H

1

: E

1

(x) ≠ E

2

(x) test dwustronny

H

1

: E

1

(x) > E

2

(x) test prawostronny (jednostronny)

H

1

: E

1

(x) < E

2

(x) test lewostronny (jednostronny)

E

1

(x) i E

2

(x) hipotetyczne wartości średnie dla pierwszej i drugiej

populacji

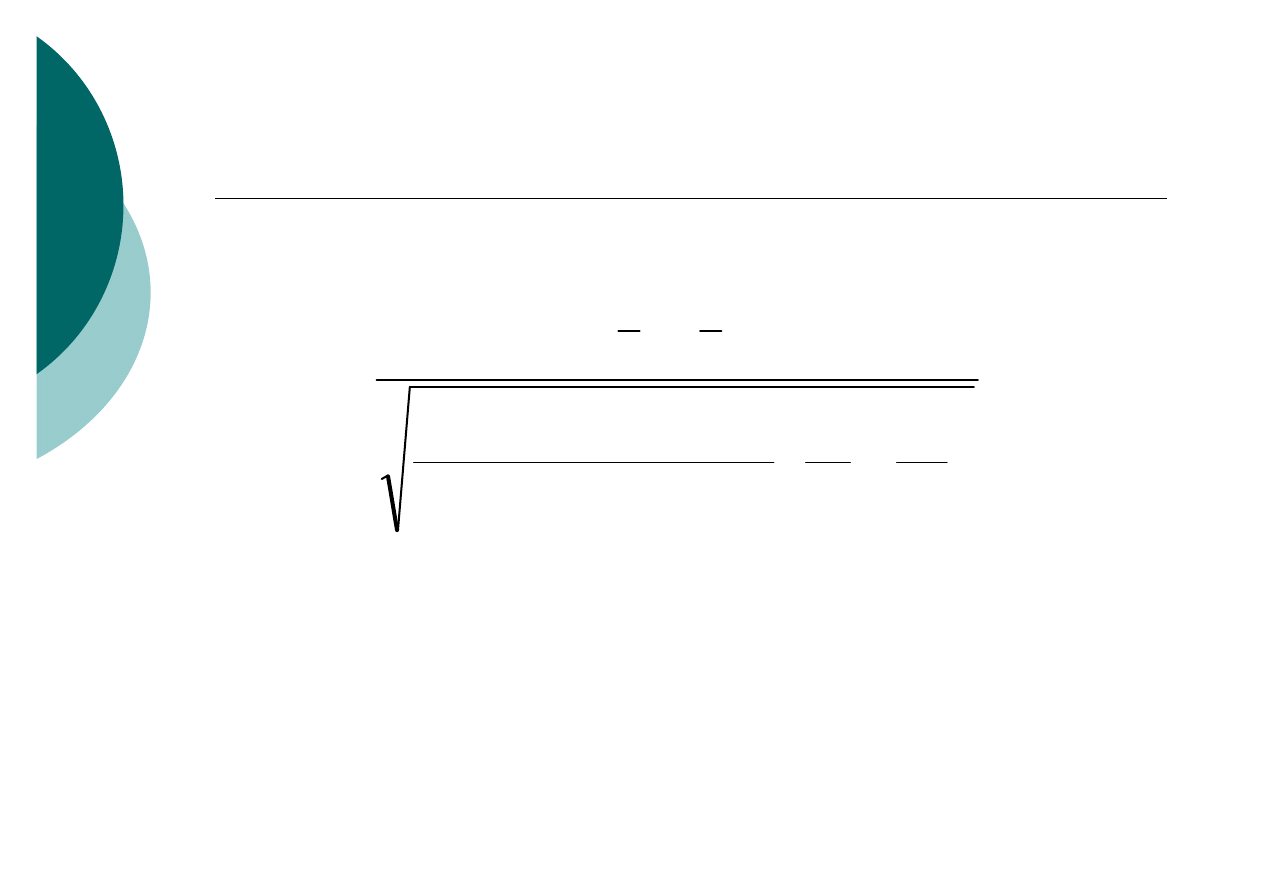
13

Weryfikacja hipotezy statystycznej

dla dwóch

ś

rednich

Model dla dwóch małych prób (n

1

i n

2

≤ 30)













+

−

+

+

−

=

2

1

2

1

2

2

2

2

1

1

2

1

1

1

2

)

(

)

(

n

n

n

n

x

s

n

x

s

n

x

x

t

emp

Wartość statystyki teoretycznej t

t

należy odczytać z tablic rozkładu

t

Studenta:

• test dwustronny – dla k = n

1

+n

2

-2 oraz poziomu istotności 1-

α

• test jednostronny – dla k = n

1

+n

2

-2 oraz poziomu istotności 2(1-

α

)

14

Zad. 11

Rodzina Nowaków jeździ do hotelu „Sandra” grać w kręgle. Ma do

wyboru dwie trasy dojazdu. Nowakowie postanowili sprawdzić, czy

przeciętne czasy przejazdu na obu trasach są takie same. W tym

celu notowali losowo czas podróży alternatywnymi drogami i

otrzymali następujące wyniki.

Dla pierwszej trasy: liczebność zanotowanych przejazdów 13,

średni czas przejazdu 32 minuty, odchylenie standardowe czasu

przejazdu 7 minut.

Dla drugiej trasy: liczebność zanotowanych przejazdów 11, średni

czas przejazdu 30 minut, odchylenie standardowe czasu przejazdu

9 minut.

Przyjmij, że poziom istotności wynosi 0,01.

15

Weryfikacja hipotezy statystycznej

dla dwóch

ś

rednich

2

2

2

1

2

1

2

1

)

(

)

(

n

x

s

n

x

s

x

x

t

emp

+

−

=

Model dla dwóch dużych prób (n

1

i n

2

> 30)

Wartość statystyki teoretycznej t

t

należy odczytać z tablic

dystrybuanty rozkładu normalnego:

• test dwustronny – dla

• test jednostronny – dla

)

1

(

5

,

0

α

−

−

2

1

5

,

0

α

−

−

16

Zad. 12

Studenci zarządzania i finansów dwóch równoległych lat studiów

uzyskali następujące średnie ocen.

Zarządzanie: średnia ocen 3,6; odchylenie standardowe ocen 2.

Finanse: średnia ocen 4,1; odchylenie standardowe ocen 1,8.

Przy obliczaniu średnich uwzględniono wszystkie stopnie uzyskane

przez studentów w ostatnim roku akademickim. Zbadano 200

studentów na kierunku Zarządzanie i 280 studentów na kierunku

Finanse. Zakładając, że w całej populacji studentów średnia ocen

ma rozkład zbliżony do normalnego, przy poziomie istotności 0,05

zweryfikuj hipotezę, że studenci kierunku Zarządzanie mają gorsze

wyniki w nauce niż studenci kierunku Finanse.

17

Weryfikacja hipotezy statystycznej

dla wska

ź

nika struktury

Odnosi si

ę

zazwyczaj do cech opisowych

Założenie: populacja ma rozkład dwupunktowy o
parametrach p i q, gdzie p jest wskaźnikiem struktury
dla wyróżnionych elementów populacji

H

0

zawsze przyjmuje postać równości:

H

0

: p = p

0

H

1

może przyjąć jedną z postaci:

H

1

: p ≠ p

0

test dwustronny

H

1

: p > p

0

test prawostronny (jednostronny)

H

1

: p < p

0

test lewostronny (jednostronny)

p

0

hipotetyczna wartość wskaźnika struktury w populacji

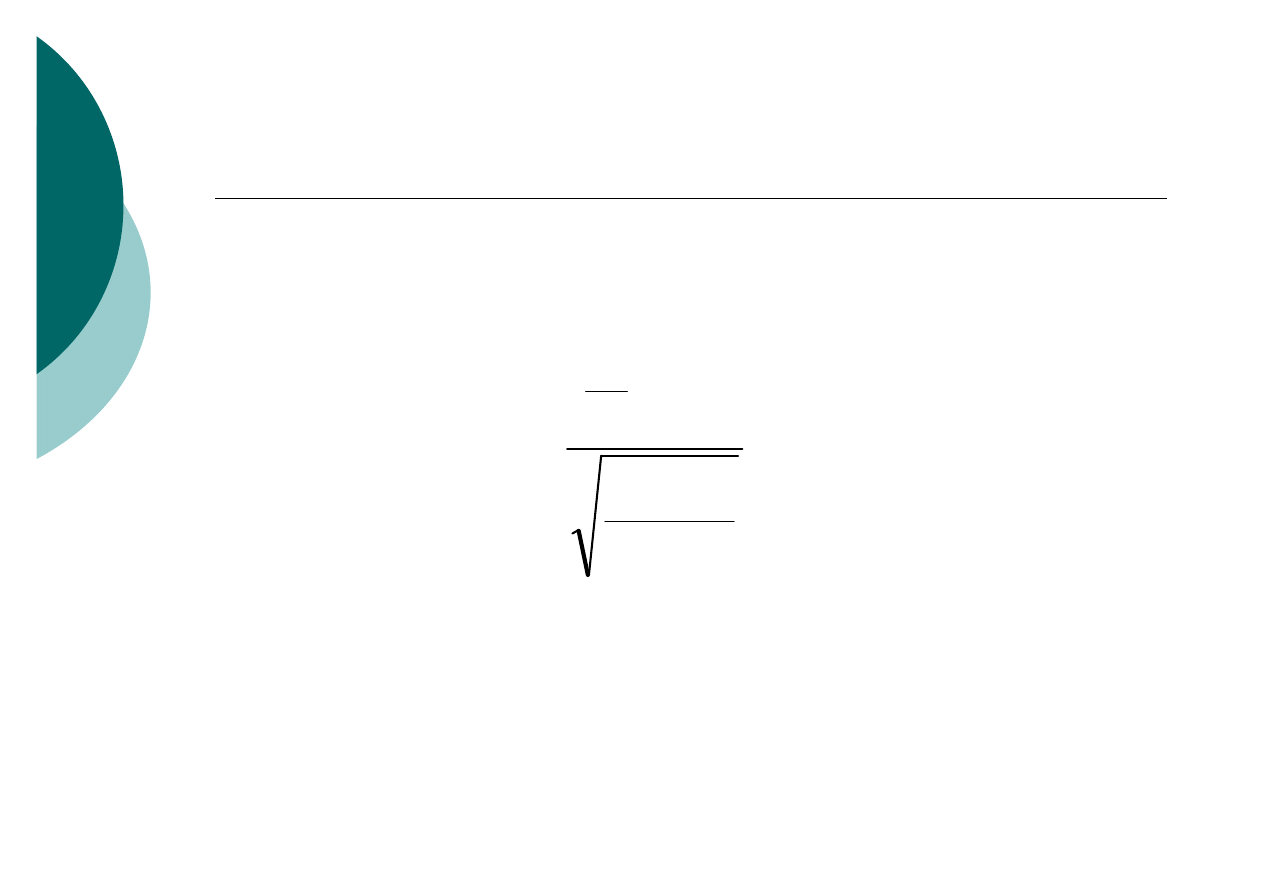
18

Weryfikacja hipotezy statystycznej

dla wska

ź

nika struktury

Dla dużej próby o liczebności n > 100

zakładany jest poziom istotności 1-

α

gdzie:

n

– liczebność próby

m

– liczba wyróżnionych elementów w próbie

P

0

–

hipotetyczny wskaźnik struktury dla wyróżnionych

elementów

q

0

=

1-p

0

n

q

p

p

n

m

t

emp

0

0

0

⋅

−

=

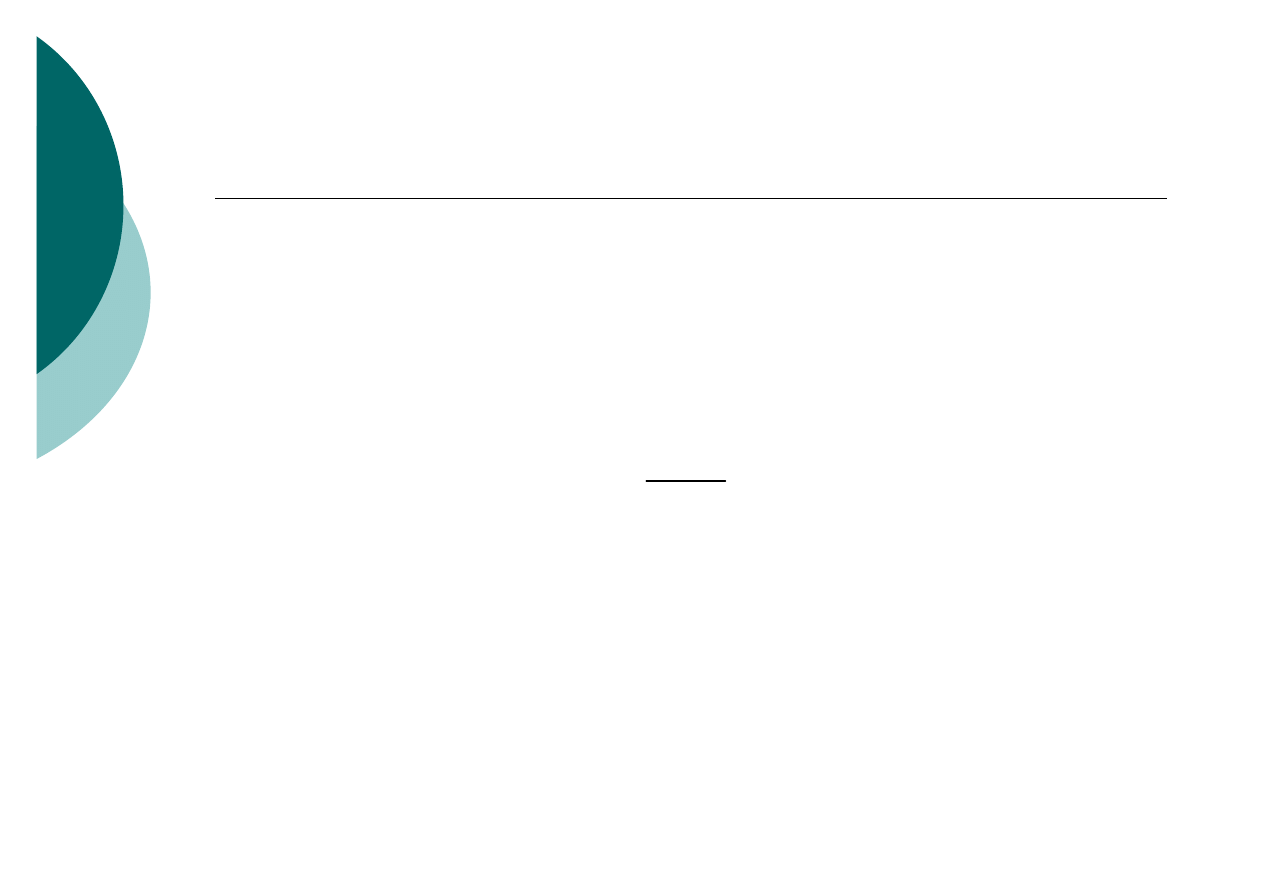
19

Weryfikacja hipotezy statystycznej

dla wska

ź

nika struktury

Wartość statystyki teoretycznej t

t

należy odczytać z tablic

dystrybuanty rozkładu normalnego:

• test dwustronny – dla

• test jednostronny – dla

)

1

(

5

,

0

α

−

−

2

1

5

,

0

α

−

−

20

Zad. 13

Wysunięto hipotezę, że 60% Polaków jest w wieku produkcyjnym.

W celu sprawdzenia tej hipotezy zbadano wiek 6000 mieszkańców

pewnego kompleksu budynków i stwierdzono wśród nich 4220 osób

w wieku produkcyjnym. Przy poziomie istotności 0,05 zweryfikuj

założoną hipotezę.

21

Weryfikacja hipotezy statystycznej

dla współczynnika korelacji

Założenie: cechy mają charakter liczbowy a związek
między nimi jest liniowy

H

0

zawsze przyjmuje postać równości:

H

0

: ρ = 0

H

1

może przyjąć jedną z postaci:

H

1

:

ρ

≠ 0 test dwustronny (

występuje zależność w sensie

parametrycznym

)

H

1

:

ρ

> 0 test prawostronny (

występuje zależność o

kierunku dodatnim)

H

1

:

ρ

< 0 test lewostronny (

występuje zależność o kierunku

ujemnym

)

22

Weryfikacja hipotezy statystycznej

dla współczynnika korelacji

Dla małej próby o liczebności

n ≤ 30

zakładany jest poziom istotności 1-

α

gdzie:

n

– liczebność próby

r

p

– współczynnik korelacji liniowej Pearsona z próby

2

)

(

1

2

−

⋅

−

=

n

r

r

t

p

p

emp

23

Weryfikacja hipotezy statystycznej

dla współczynnika korelacji

Wartość statystyki teoretycznej t

t

należy odczytać z tablic

rozkładu t Studenta:

• test dwustronny – dla k = n-2 oraz poziomu istotności 1-

α

• test jednostronny – dla k = n-2 oraz poziomu istotności 2(1-

α

)

24

Zad. 14

Sformułowano przypuszczenie, że spożycie ziemniaków jest tym

mniejsze im wyższe są dochody konsumentów. W celu sprawdzenia

tego przypuszczenia wylosowano 10 gospodarstw domowych, dla

których określono roczny dochód na osobę i roczne spożycie

ziemniaków. Współczynnik korelacji liniowej Pearsona wyniósł

-0,93. Przyjmując poziom istotności 0,01 zweryfikuj sformułowane

przypuszczenie.