Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 1

Tematy projektów z przedmiotu "Mechanika analityczna i drgania"

1. Wyprowadzić równania ruchu metodą równań Lagrange'a II rodzaju.

a)

określić współrzędne wyjściowe oraz zapisać równania więzów

b)

określić liczbę stopni swobody i współrzędne uogólnione

c)

zapisać energie kinetyczną, potencjalną oraz funkcję dyssypacji energii we współrzędnych

uogólnionych

d)

zapisać pracę wirtualną sił niepotencjalnych oraz siły uogólnione

e)

obliczyć pochodne z równań Lagrange'a

f)

zapisać układ różniczkowych równań ruchu.

2. Korzystając z metod numerycznych przedstawić przebiegi czasowe w wybranych współrzędnych
uogólnionych:

a) drgań swobodnych

b) drgań wymuszonych

Uwaga: Przebiegi czasowe mają być czytelne. Tzn. jeżeli układ ustala się po 3s, to proszę nie
zamieszczać 30s przebiegów czasowych. Na wszystkich wykresach osie mają być podpisane z
zaznaczonymi jednostkami.

3. Wykonać indywidualne polecenia przedstawione w wybranym projekcie.

dod. 4. Wykonać prostą animację ruchu układu w programie MATLAB* lub innym. Krążki, szpule,
walce oraz kule należy zamarkować na obwodzie, aby można było dostrzec ruch obrotowy tych brył.
(nieobowiązkowe)

*animacje można wykonać np. w oparciu o rysowanie figur geometrycznych (plot) w pętli for przy
użyciu instrukcji: rsmak(), fnplt(), drawnow, pause(), line(), patch(),fill(), VideoWriter(),
VideoReader().
Zostaną załączone pliki z przykładową animacją i użyciem tych funkcji.

Wskazówki:

•

Zakładamy: niewielką amplitudę drgań, wszystkie sprężyny narysowane na schematach są w
stanie nierozciągniętym, chyba że opisano inaczej.

•

Przyjąć tak czas symulacji, aby pokazać stan ustalony ( jeśli istnieje )

•

Rozwiązując równania numerycznie, podczas zapisywania sił tarcia, należy użyć funkcji
signum sgn(x) (w matlabie sign(x)), aby uwzględnić odpowiedni zwrot siły tarcia. W
argumencie należy podać różnicę prędkości (prędkość względną) trących o siebie powierzchni

np.

(

)

1

2

sgn x

x

−

ɺ

ɺ

.

( )

1 dla

0

sgn

0 dla

0

1 dla

0

x

x

x

x

>





=

=



−

<



•

starać się indeksować współrzędne poszczególnych brył zgodnie z przyporządkowanym
indeksem masy

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 2

•

Przy wklejaniu przebiegów czasowych z okna 'figure' należy skorzystać z opcji EDIT->Copy
Figure. Wklejamy wówczas grafikę wektorową, a nie raster. (lepsza jakość).

•

pręty bezmasowe

•

pręty masowe

•

wymuszenie siłowe

•

wymuszenie kinematyczne

•

wszystkie podane wielkości fizyczne, przedstawiono w jednostkach z układu SI

•

gdy wartości określone są przedziałowo np.

10 100

ω

=

÷

należy wybrać dowolną wartość w

podanym przedziale lub zbadać wpływ parametru w granicach tego przedziału.

•

W uzasadnionych przypadkach można zmienić wartości parametrów podane w projektach

Projekt należy oddać w formie wydrukowanej (D-1 s. 310) i elektronicznej ( [e-mail] )
do 23 czerwca, aby uzyskać zaliczenie w pierwszym terminie. Projekt należy rozpocząć uzupełnioną
tabelka przedstawioną poniżej. W polu "Uwagi" proszę wpisać termin odbywania zajęć, jeżeli nie
uczęszczano na zajęcia w swojej grupie (np. pon. 11:00).

Temat nr:

Nazwisko i Imię:

Grupa (spec.):

Uwagi:

Ocena:

Konsultacje: D-A s.310
Pon: 16:00 - 17:00
Czw: 10:30 - 11:30

Możliwe, że w niektórych projektach znajdą się pewne niespójności wynikające z geometrii
mechanizmów. Proszę wszelkie błędy i braki na bieżąco zgłaszać mailowo.

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 3

1

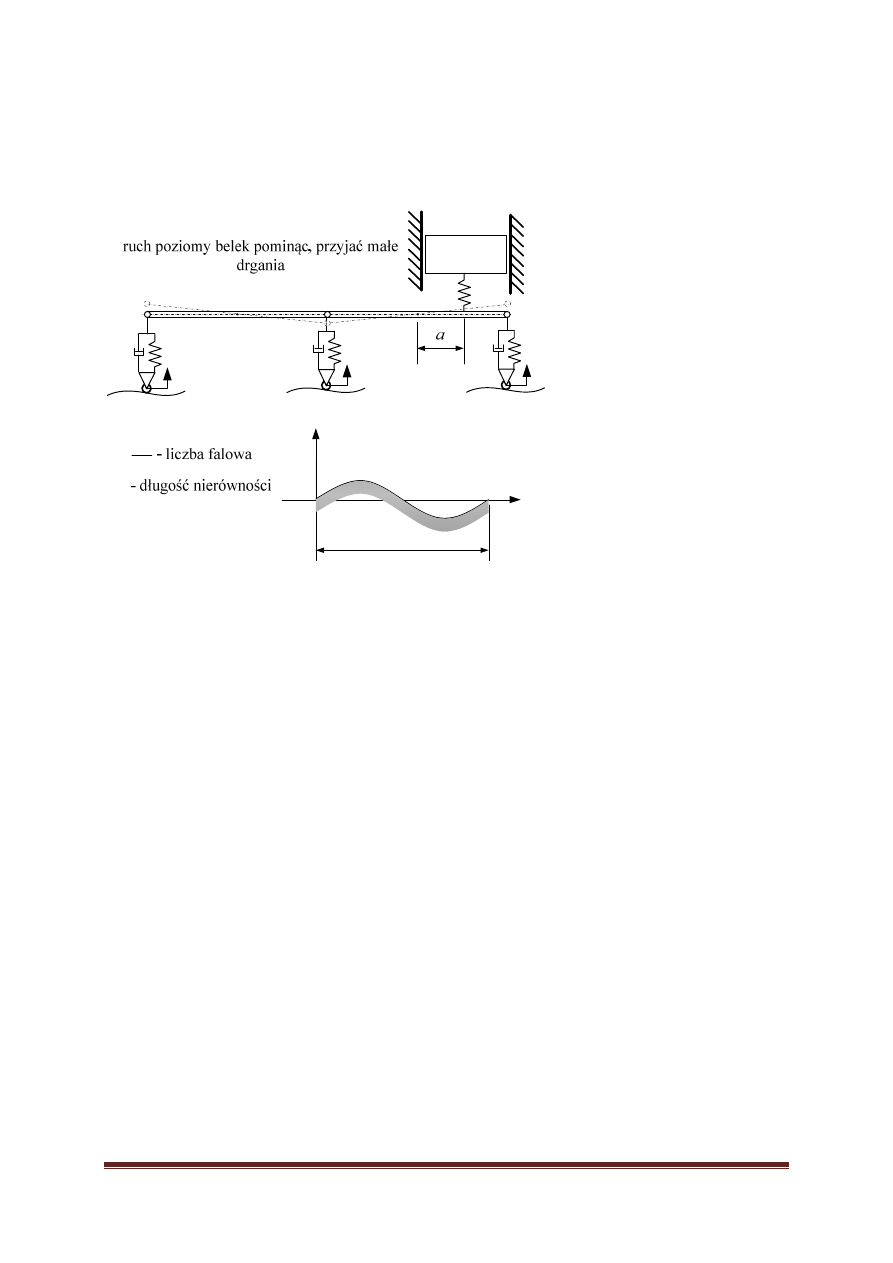
Model autobusu przegubowego. Należy zbadać komfort jazdy kierowcy o
masie M ( komfort wyrażony jako amplituda drgań i siła wywierana na
kierowcę) w zależności od:
a) prędkości pojazdu v, w przedziale od 20km/h do 120km/h.
b) długości nierówności L w przedziale od 50cm do 3m
c) ocenić w którym miejscu należy optymalnie zainstalować siedzenie
kierowcy? (a=?)

b

( )

(

)

3

sin

4

u

t

A

vt

l

λ

=

−









1

k

b

( )

(

)

2

sin

2

u

t

A

vt

l

λ

=

−









1

k

b

( )

(

)

1

sin

u

t

A

vt

λ

=

1

k

, 2

m

l

, 2

m

l

M

2

k

2

L

L

π

λ =

x

u

L

90

M =

1000

m =

5

1

2 10

k = ⋅

4

2

7 10

k

=

⋅

255

b =

10

250

ω

=

÷

0,1

A =

3

l =

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 4

2

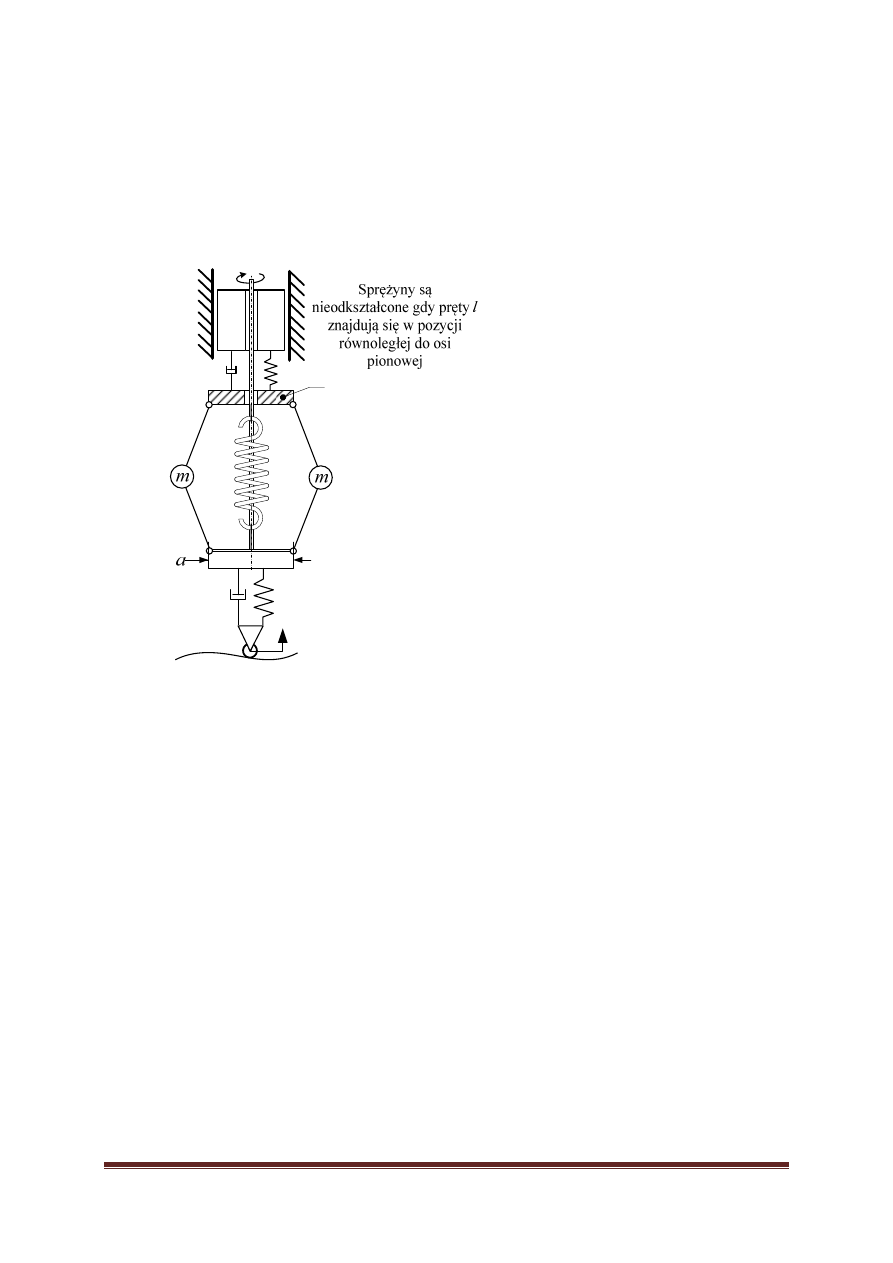
Amortyzator aktywny.
a) zbadać wpływ zmiany prędkości

s

ω

na częstość drgań własnych

układu
b) dobrać optymalną wartość

s

ω

, aby zminimalizować siłę oddziaływania

sprężyny k

3

na masę chronioną M w stanie ustalonym.

c) dla jakiej wartości

s

ω

, siła oddziaływania sprężyny k

3

na masę

chronioną M jest największa?

s

ω

b

( )

( )

1

sin

u

t

A

t

ω

=

1

k

b

3

k

4x l

M

1

m

2

k

2

m

400

M =

10

m =

1

5

m

=

2

1

m

=

5

1

10

k =

5

2

2 10

k

=

⋅

4

3

5 10

k

=

⋅

40

b =

0, 5

l =

0,1

a =

30

ω =

0

1200

s

ω

=

÷

0,1

A =

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 5

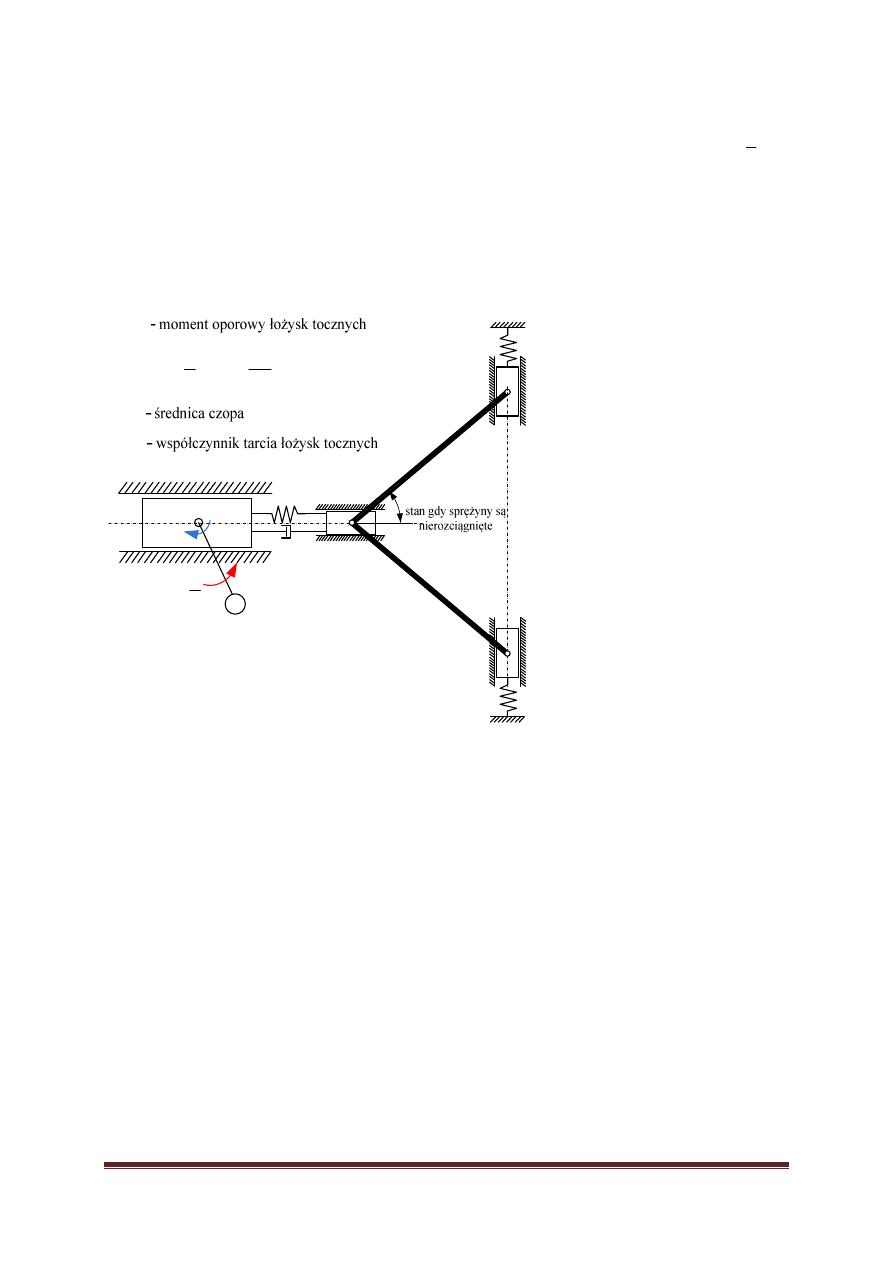
3

Wibrator inercyjny. Na skutek wirującej masy m

k

w układzie wzbudzane

są drgania.
a) przy jakim momencie M

n

wahadło zacznie wirować?

b) zarejestrować drgania swobodne masy M przy wychyleniu wahadła o
90st. od położenia równowagi

c) oblicz prędkość kątową wahadła

kr

ω

,dla której układ ulegnie

uszkodzeniu, zakładając, że dopuszczalna siła w sprężynach nie może
przekroczyć 120kN. Przyjąć moment napędowy dwukrotnie większy od
wyliczonego w punkcie a).
d) wykonać następujący eksperyment: W czasie gdy wahadło osiągnie

kr

ω

, wyłączyć silnik i obliczyć czas do momentu zatrzymania układu.

2

k

b

1

k

1

k

m

m

m

l

l

M

k

m

n

M

α

2

l

0

M

0

M

( )

2

0

2

2

cz

k

l

d

M

m

sign

ω

µ

ω

=

⋅

⋅

cz

d

µ

200

M =

10

k

m

=

15

m =

1

70000

k =

6

2

10

k

=

40

b =

0, 003

µ =

?

n

M =

0, 5

l =

1

3

α

π

=

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 6

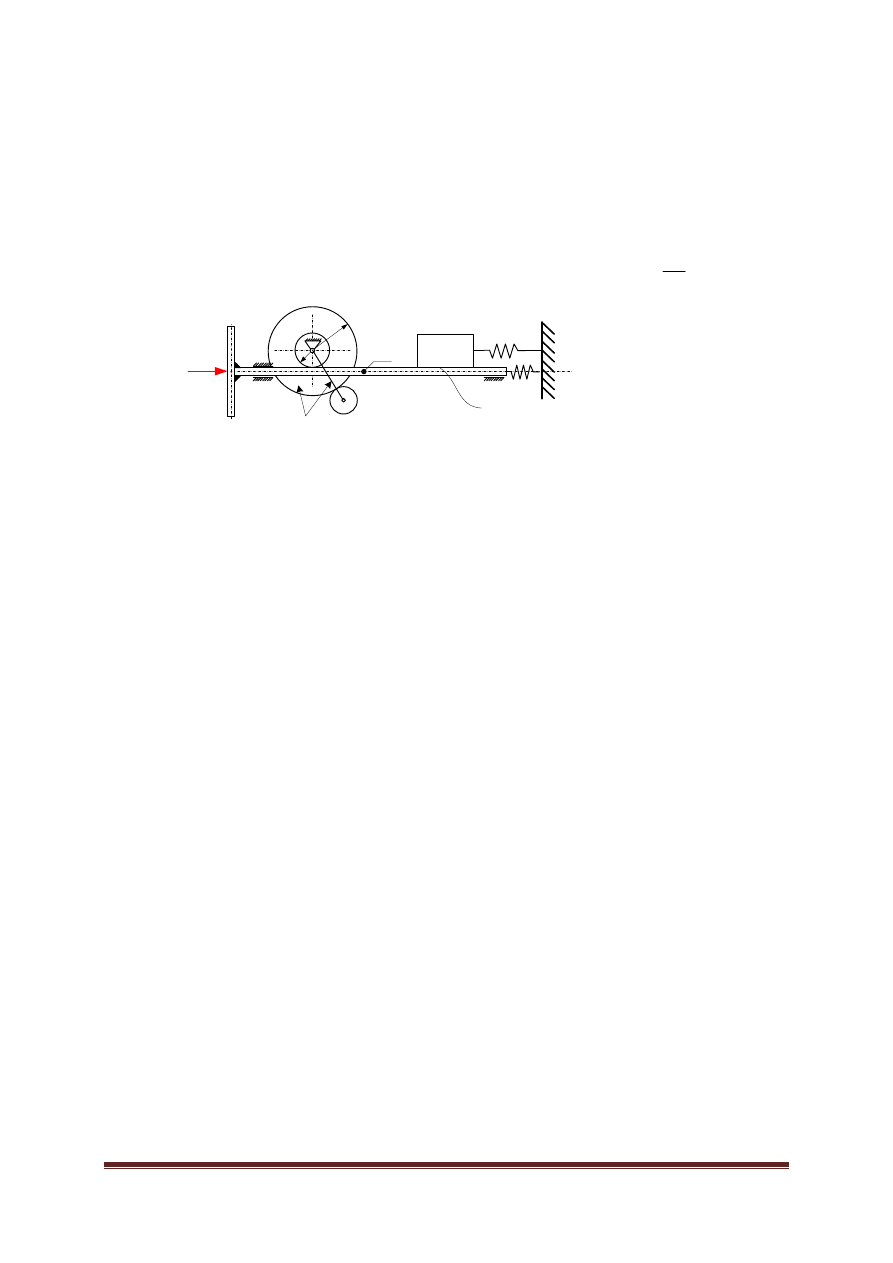
4

Zderzak
- zbadać wpływ czasu trwania impulsu i wartość siły F na ruch masy
chronionej M.
- dobrać parametry układu (J,k

2

,r) tak, aby masa chroniona M

,

najłagodniej odczuła uderzenie (minimalizacja siły) oraz określić wpływ
tych parametrów.
- dla jakiej wartości siły F

0

(przy ustalonym czasie t

1

=1s) nastąpi poślizg

masy M po prowadnicy o masie m

2

.

- zbadać jaki wpływ mają parametry geometryczne krążków na
maksymalną siłę w sprężynie k

1

(przy stałej F

0

). Krążki wykonane są ze

stali o gęstości

ρ

oraz mają grubość g.

R

r

2

k

1

1

,

m

r

J

1

k

2

m

µ

niezależne

ruchy

M

( )

0

1

1

dla

0 dla

F

t

F t

t

t

≤



= 

>



150

M

kg

=

2

55

m

kg

=

?

J =

5

1

10

k =

2

?

k

=

5

?

R

r

r

=

=

3

7850

kg

m

ρ =

5

g

cm

=

( )

1

?

m

r

=

4

5

0

10

10

F =

÷

1

0,1 1

t

s

=

÷

0,3

µ =

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 7

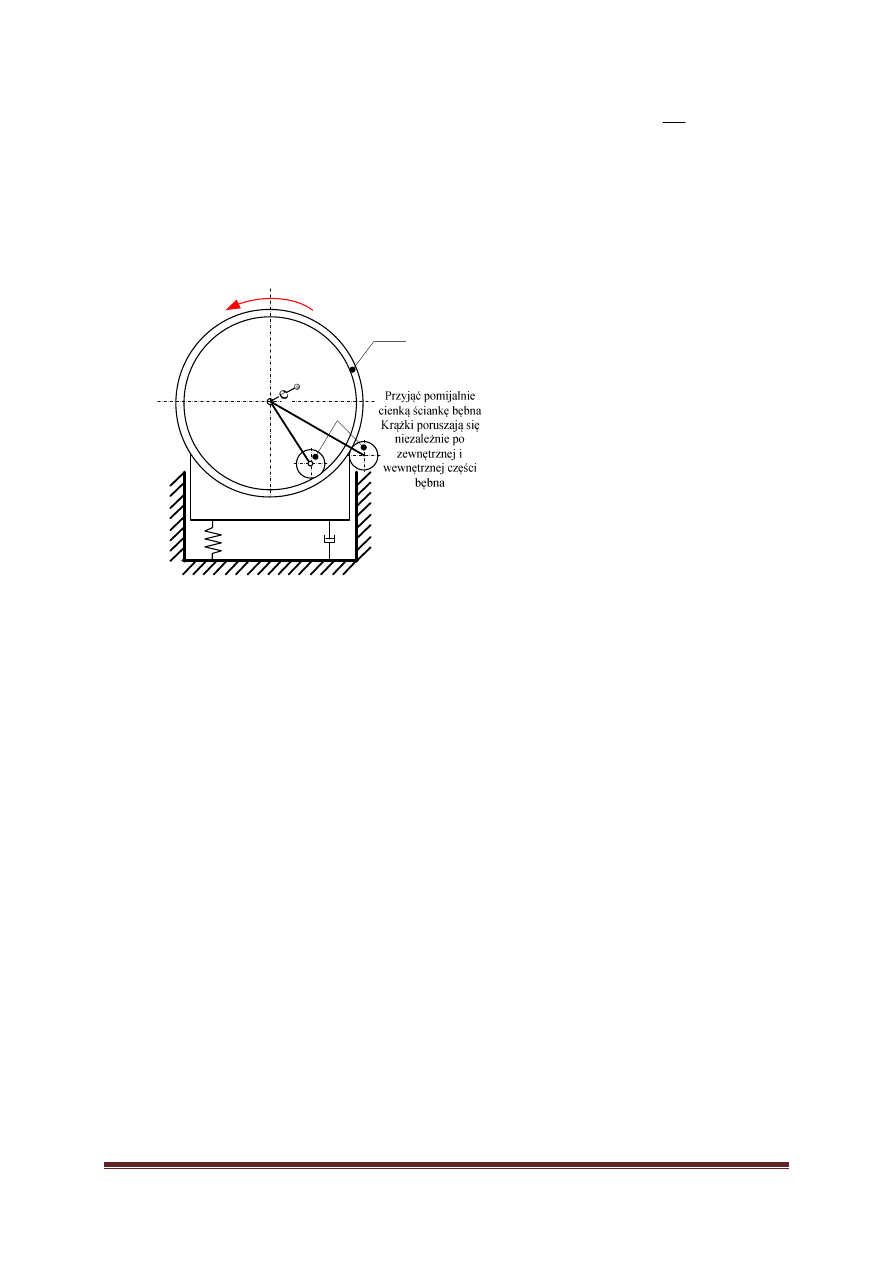
5

Maszyna wirnikowa jest napędzana stałym momentem M

n

przez silnik

elektryczny. Wirnik maszyny jest niewyważony i jego mimośród wynosi
e.
- określić minimalny/maksymalny moment napędowy, dla którego krążki
zaczną toczyć się po obwodzie bębna przy założonych promieniach r.
- jak zmieni się ten moment, gdy zmienimy promienie krążków
- zbadać wpływ promieni krążków na amplitudę drgań masy chronionej
M, przy założeniu że krążki toczą się dookoła bębna.

Krążki wykonane są ze stali o gęstości

ρ

oraz mają grubość g.

k

b

M

,

m r

n

M

,

J R

w

m

150

M

kg

=

3

7850

kg

m

ρ =

15

w

m

kg

=

30000

k =

20

b =

3

J =

5

g

cm

=

?

n

M =

( )

?

m

r

=

?

r =

0, 4

R =

0, 02

e =

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 8

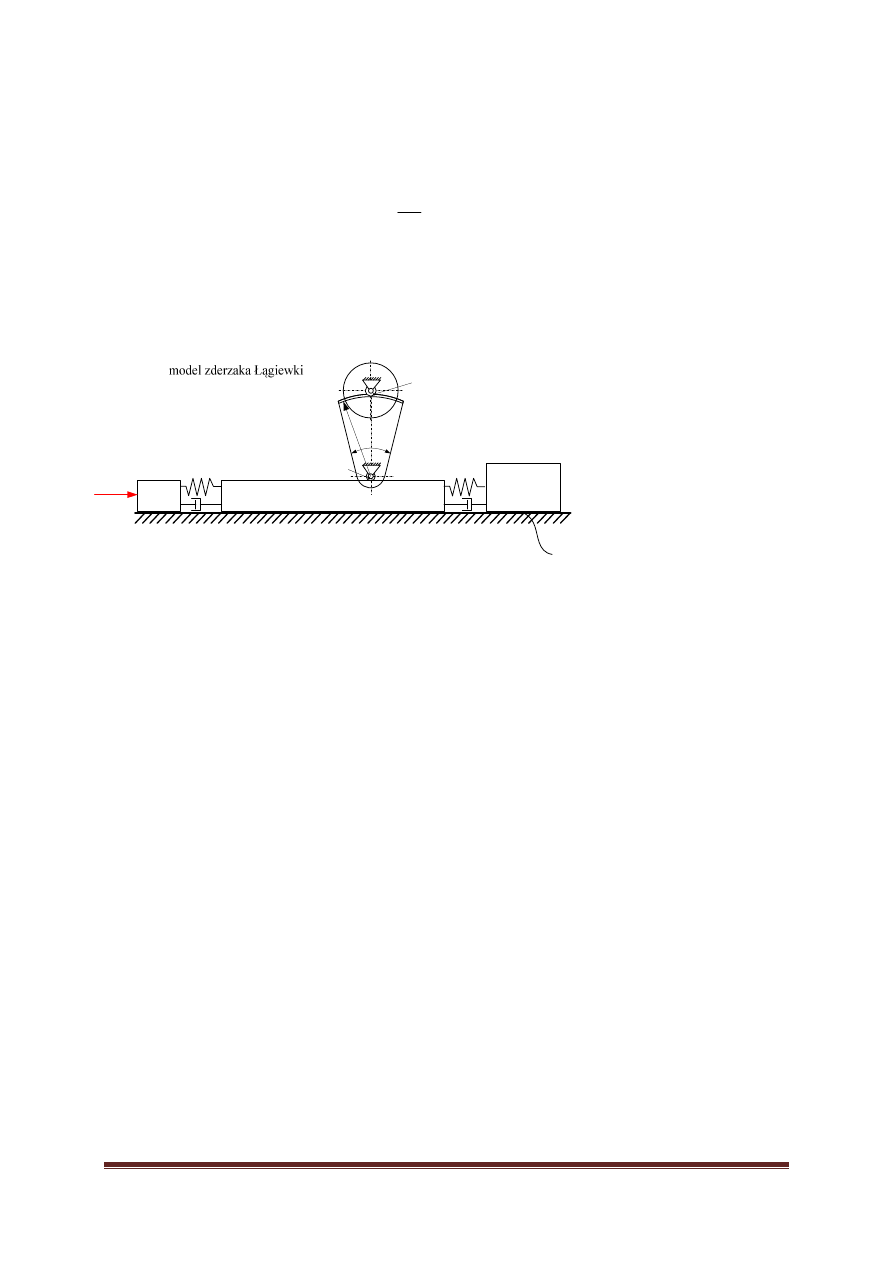
6

Model zderzaka Lucjana Łągiewki
a) zbadać wpływ czasu trwania impulsu i wartość siły F na ruch masy
pojazdu M ( gdy pojazd znajduje się w spoczynku).
b) jak zmieni się siła oddziaływania sprężyny k

2

oraz tłumika b

2

przy

zmianie momentu bezwładności pochłaniacza energii J

2

.

c) przeprowadzić eksperyment, kiedy pojazd uderza w nieodkształcalną

ścianę z prędkością w przedziale

30

120

km

v

h

=

÷

. Przedstawić przebieg

czasowy oraz wykres wypadkowej siły działającej na pojazd M.
Podpowiedź: przyjąć warunki, że m

1

ma stale zerową prędkość, natomiast

pozostałe masy mają prędkość v. W tabeli przedstawić wartości
maksymalnych sił w sprężynach k

1

,k

2

dla rozpatrywanych prędkości.

Wskazówki: (zaniedbać energie potencjalną przekładni 1)

α

M

1

k

1

b

2

b

2

k

2

m

1

m

1

J

2

J

( )

0

1

1

dla

0 dla

F

t

F t

t

t

≤



= 

>



( )

F t

1

R

1

r

2

r

µ

1200

M =

1

5

m

=

2

15

m

=

1

3

J =

2

?

J

=

7

1

10

k =

6

2

2 10

k

=

⋅

1

12700

b =

2

2500

b =

5

6

10

10

F =

÷

1

0,1

t

=

1

1

2

0, 05

0, 4

0, 04

r

R

r

=

=

=

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 9

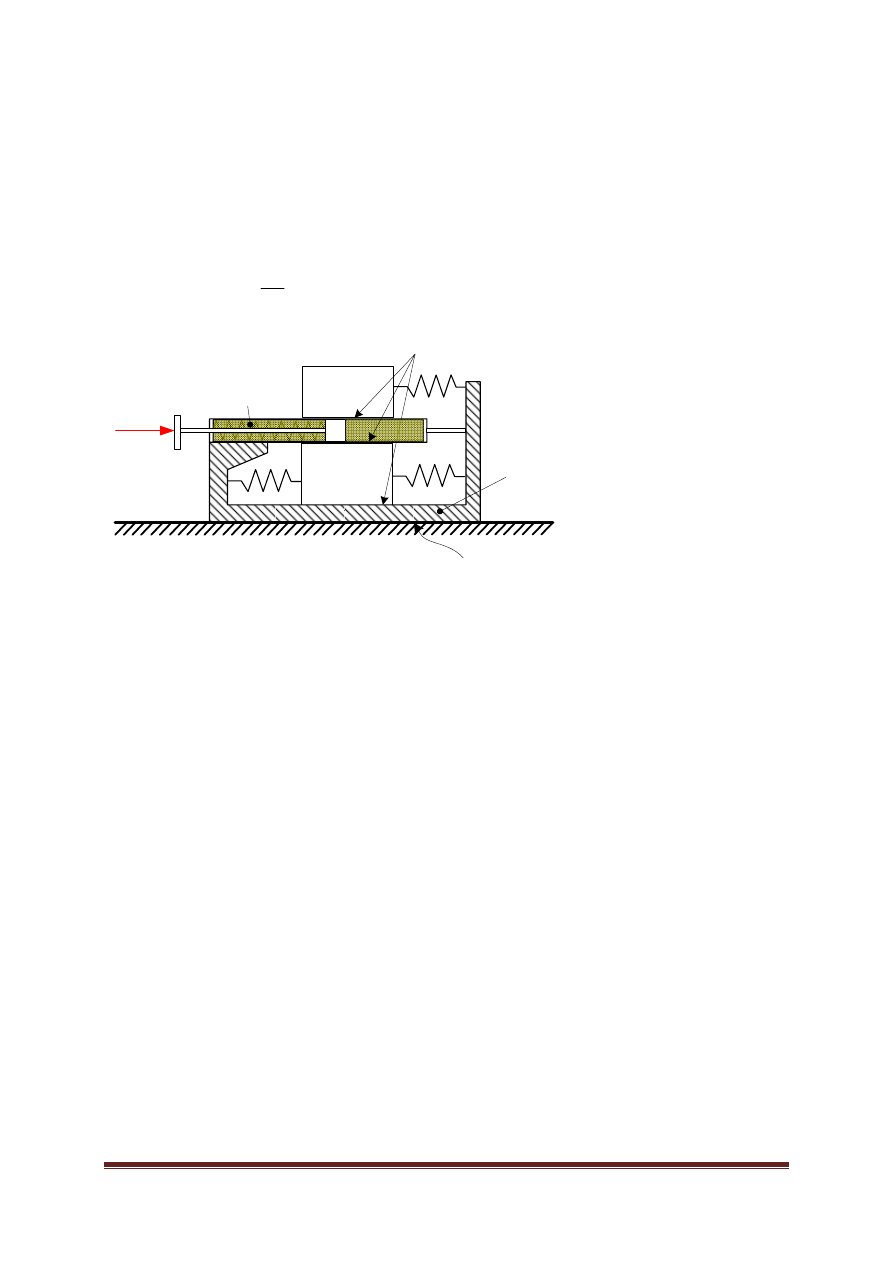
7

Zderzak
a) zbadać wpływ czasu trwania impulsu i wartość siły F na ruch masy
pojazdu M ( gdy pojazd znajduje się w spoczynku).
b) Dobrać parametry układu tak, aby kierowca o masie m

1,

najłagodniej

odczuł uderzenie oraz określić wpływ tych parametrów.
c) przeprowadzić eksperyment, kiedy pojazd uderza w nieodkształcalną
ścianę z różną prędkością v. Przedstawić przebieg czasowy oraz wykres
wypadkowej siły (tarcie i siła w sprężynie) działającej na człowieka o
masie m

1

. Podpowiedź: przyjąć warunki, że tłok m

2

ma stale zerową

prędkość, natomiast pozostałe masy mają prędkość v. Zbadać przedział

prędkości

30

120

km

v

h

=

÷

.

W

tabeli

przedstawić

wartości

maksymalnych sił w sprężynach k

1

,k

2

i k

3

dla rozpatrywanych prędkości.

2

k

3

m

M

µ

3

k

2

m

b

1

m

2

µ

1

k

1

k

( )

0

1

1

dla

0 dla

F

t

F t

t

t

≤



= 

>



1500

M

kg

=

1

90

m

kg

=

2

55

m

kg

=

1

?

k =

5

2

10

k

=

3

?

k

=

?

b =

4

5

0

10

10

F =

÷

1

0,1 1

t

s

=

÷

0,3

µ =

2

0,5

µ =

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 10

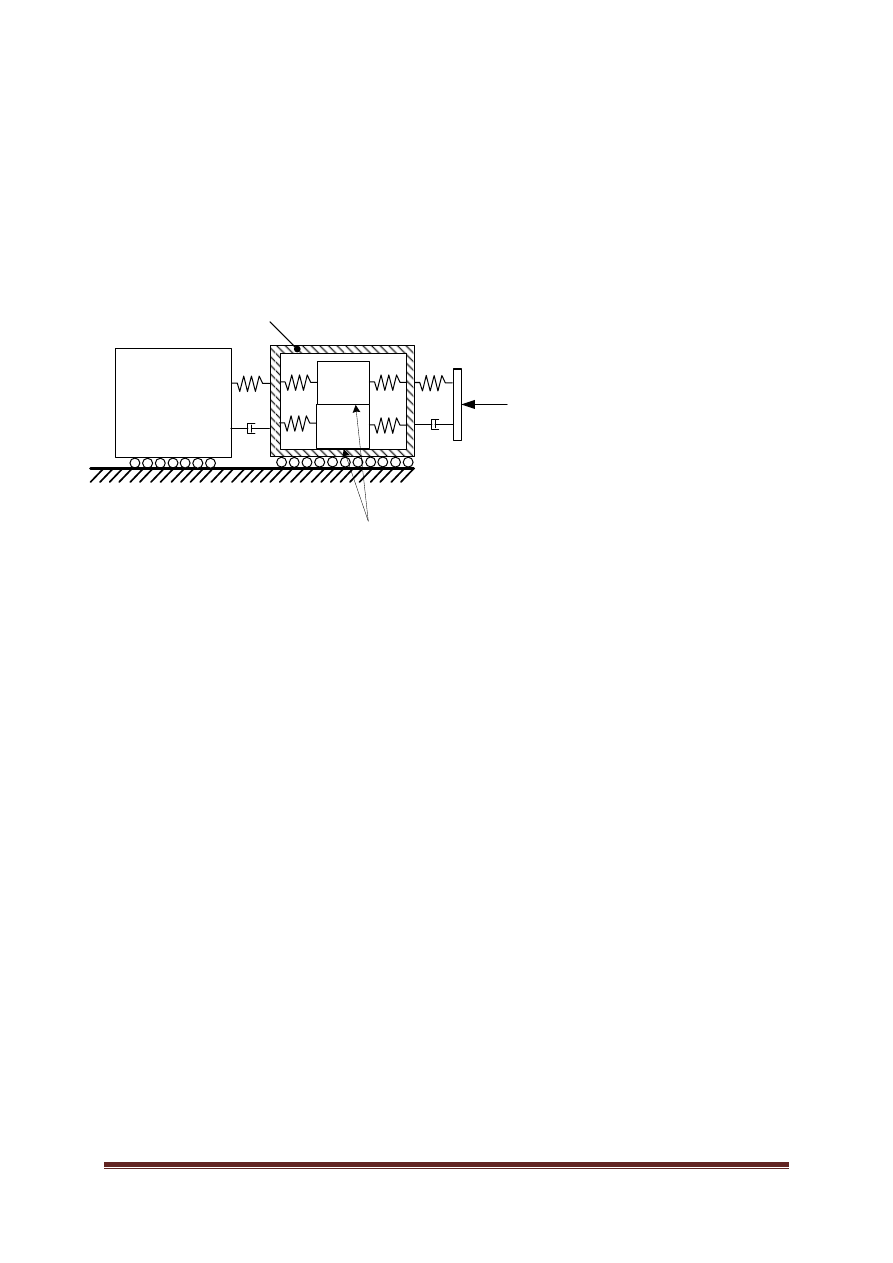
8

Zderzak
a) dla jakich częstości

ω

masy m

1

i m

2

poruszają się w:

- przeciwnym kierunku?

- jednakowym kierunku?

b) dla jakiej częstości

ω

siła w sprężynie k

3

jest maksymalna (w stanie

ustalonym)?
c) dobrać sprężynę k

2

w taki sposób aby masy m

1

, m

2

poruszały się w

przeciwnych kierunkach przy

10

ω =

i dla takich warunków obliczyć

maksymalną siłę w sprężynie k

3

.

d) przedstawić przebiegi czasowe we współrzędnych uogólnionych gdy

( )

0,1

u t

=

(impuls)

1

m

2

m

2

4xk

µ

( )

sin

u t

A

t

ω

=

1

k

1

b

3

k

M

2

b

3

m

100

M =

1

10

m

=

2

5

m

=

3

40

m

=

5

1

2 10

k = ⋅

4

2

2 10

k

=

⋅

5

3

10

k

=

1

255

b =

2

15

b =

10

250

ω

=

÷

0, 05

A =

0,1

µ =

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 11

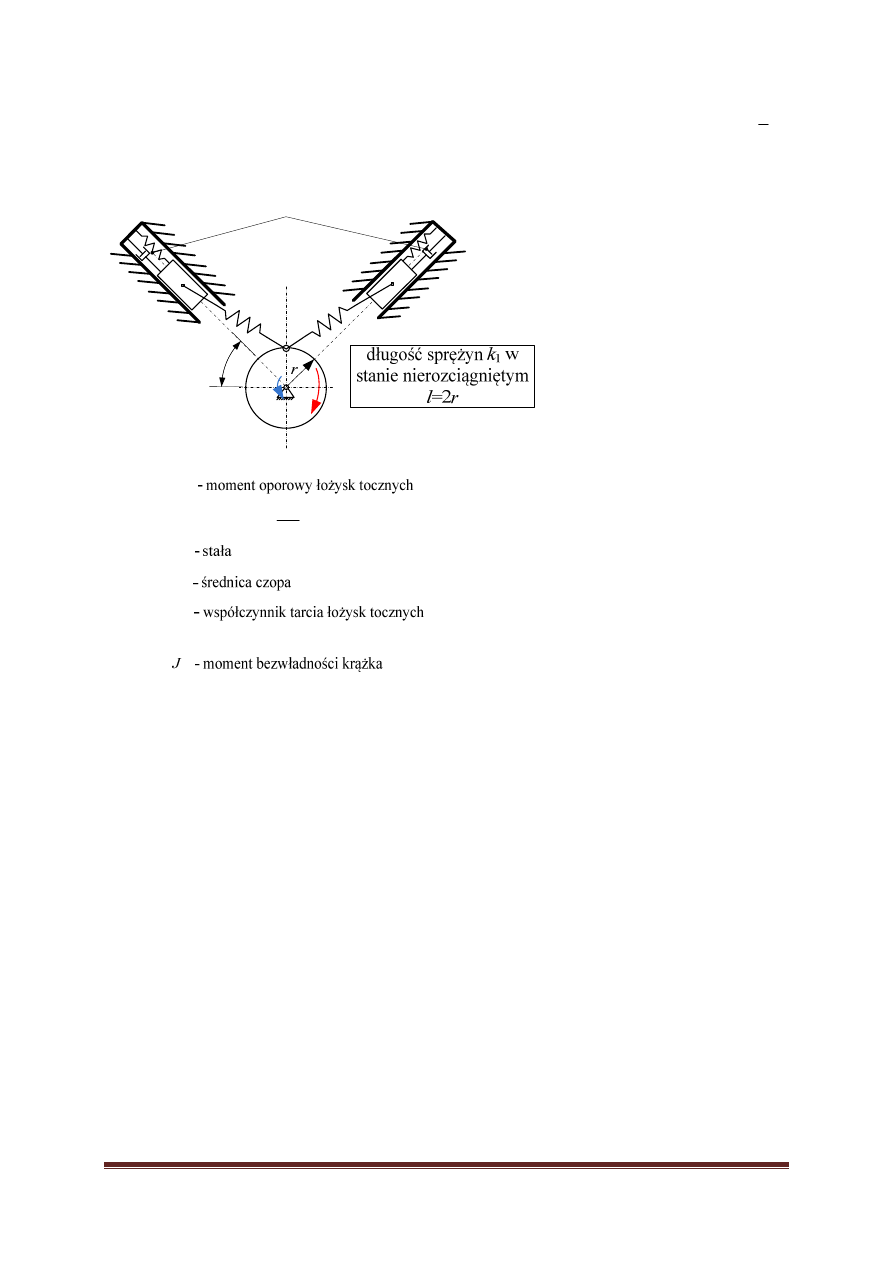
9

a) zbadać minimalną wartość momentu sił M

n

, dla którego koło zacznie

się obracać.
b) zakładając moment napędowy jako 2M

n

(obliczonego w punkcie a),

wyznacz maksymalne siły w sprężynach k

1,2

.

c) gdy układ znajduje się w stanie ustalonym, należy wyłączyć silnik
(M

n

=0) i obliczyć czas wyhamowania koła.

α

1

k

(

)

2

,

k

b

1

k

n

M

- masa suwaków

m

0

M

( )

2

0

2

cz

d

M

sign

λ ω

µ

ω

=

⋅

⋅

⋅

cz

d

µ

o

M

λ

1

m =

0, 05

J =

1

7000

k =

4

2

10

k

=

15

b =

100

λ =

?

n

M =

1

3

α

π

=

0, 2

r =

0, 05

cz

d

=

0, 003

µ =

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 12

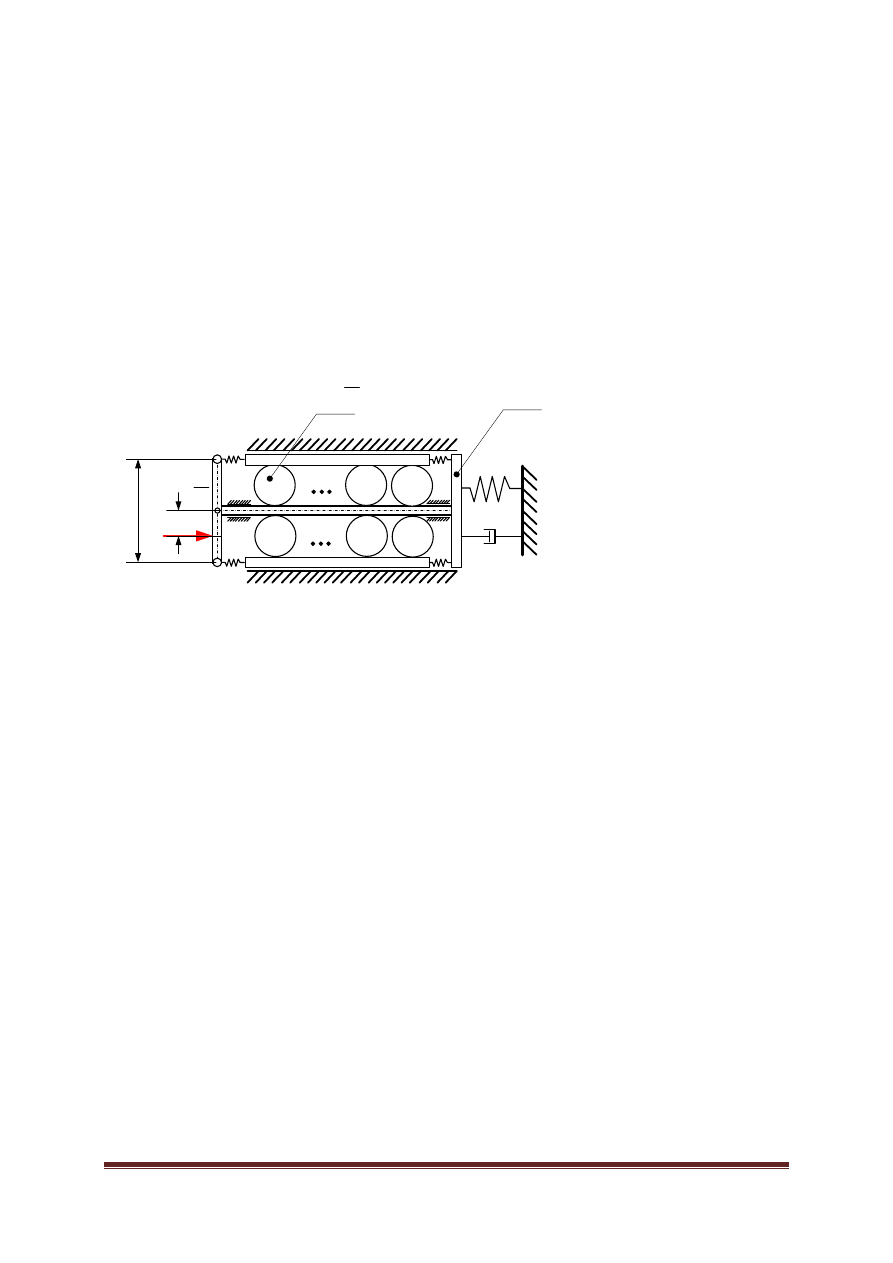
10

Model zderzaka. Zbadać wpływ parametru a ( miejsca przyłożenia siły )
oraz liczbe kul (pochłaniaczy energi) N (parzysta liczba):
a) zbadać wpływ czasu trwania impulsu i wartość siły F na ruch masy
pojazdu M (wnioski)
b) przy ustalonym czasie trwania impulsu t

1,

ocenić wpływ liczby kul w

urządzeniu na ruch masy M.
c) przy ustalym czasie trwania impulsu t

1

, oraz liczbie kul N zbadać jaki

wpływ ma miejsce przyłożenia siły a.
d) przeprowadzić eksperyment, gdy zamiast siłowego wymuszenia F(t)
jest wymuszenie kinematyczne u(t), takie że przemieszczenie belki w
miejscu

przyłożenia

siły

wynosi

u(t)=0,05

m.

Wskazówka:

należy

obliczyć

jaki

obrót

wykona

belka

gdy

przemieszczenie odpowiedniego miejsca belki wyniesie u(t), następnie
wstawić to w warunkach początkowych, zakładając że siła F(t) =0.

2

4x k

m

m

1

k

b

M

2

m

,

4

m

N

r





× 







a

2l

( )

0

1

1

dla

0 dla

F

t

F t

t

t

≤



= 

>



( )

F t

80

M =

5

m =

0,15

r =

1

4000

k =

2

3000

k

=

10

b =

0

10000

F =

1

0,5 2

t

s

=

÷

0, 5

l =

4

20

.

N

szt

=

÷

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 13

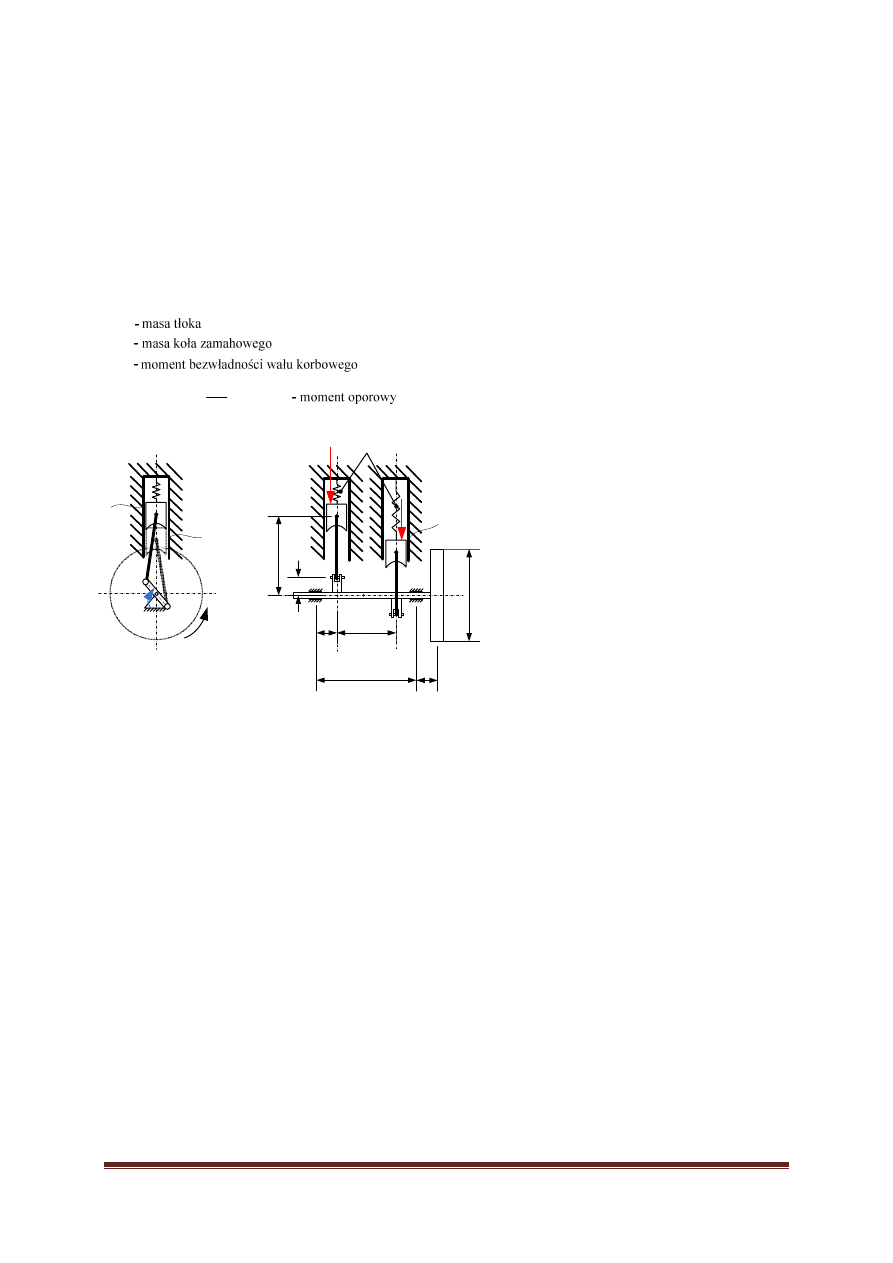
11

Model silnika dwucylindrowego.
a) zbadać przy jakich warunkach początkowych nastąpi rozruch silnika, a
dla jakich nie. (zarejestrować przebiegi czasowe, jeżeli rozruch silnika nie
wystąpi dla żadnych warunków początkowych to zmienić parametry
układu, przede wszystkim k i zapisać wnioski)
b) obliczyć prędkość nominalną silnika oraz czas rozpędzania przy
zadanych warunkach pracy.
c) Po osiągnięciu prędkości nominalnej wyłączyć silnik (F

0

=0) i obliczyć

czas do chwili zatrzymania się wału ( zarejestrować przebiegi czasowe)
d) wyznaczyć maksymalne siły reakcji w łożyskach A i B
e) optymalnie dobrać wymiar b, aby zminimalizować siłę reakcji w
łożyskach.

m

µ

µ

k

a

D

M

µ

l

A

B

b

c

d

a

( )

( )

(

)

0

sin

1

F t

F

t

ϕ

=

+

ɺ

( )

( )

(

)

0

cos

1

F t

F

t

ϕ

=

+

ɺ

J

o

M

ϕ

( )

2

0

2

cz

d

M

sign

λ ϕ

µ

ϕ

=

⋅

⋅

⋅

ɺ

ɺ

60

M =

0, 4

m =

3

J =

4000

k =

8 0 0

λ =

0, 5

l =

0,1

a =

0, 4

b =

0,8

c =

0,1

d =

0, 4

D =

0, 05

cz

d

=

0

1000

F =

0, 03

µ =

Tematy projektów z Mechaniki analitycznej i drgań - mgr inż. Sebastian Pakuła

Strona 14

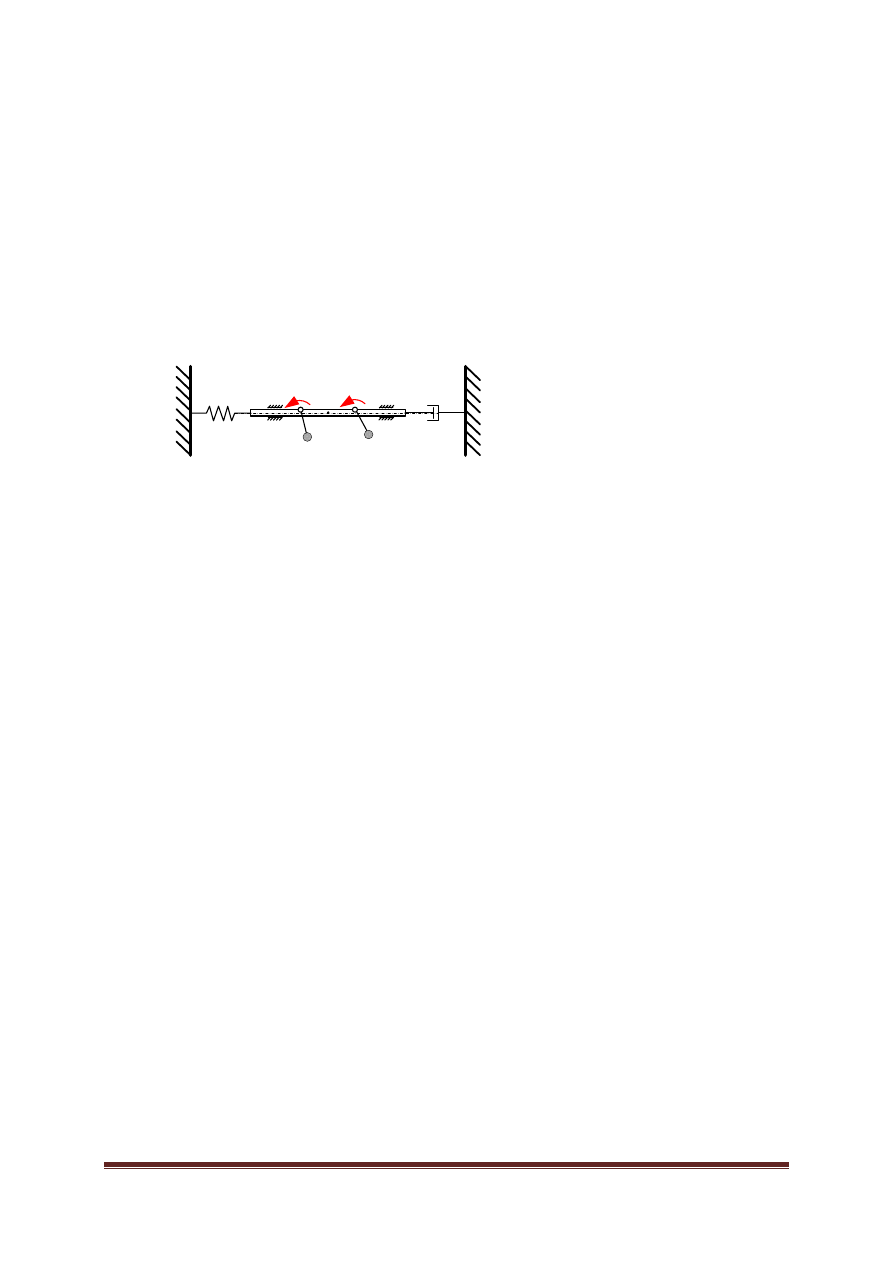
12

Projekt dla jednej osoby:
Należy zbadać wpływ warunków początkowych i długości cięgien
wahadeł matematycznych ( e

1

i e

2

) na ruch układu. Należy

przeanalizować ruch osi o masie M oraz wahadeł.
a) zarejestrować przebiegi drgań swobodnych (M

n

=0) gdy e

1

=

e

2

oraz:

- wahadła wychylono o tą samą wartość w tym samym kierunku

- wahadła wychylono o tą samo wartość w przeciwnym kierunku

- wychylono tylko jedno wahadło

b) zarejestrować przebiegi drgań wymuszonych gdy:

- e

1

=

e

2 (przy zerowych warunkach początkowych)

- e

1

=

e

2 (gdy jedno z wahadeł wychylono o π/20)

- e

1

=

e

2 (gdy wahadła ustawiono przeciwlegle)

- e

1

≅ e

2

(gdy różnią się niewiele ok. 1%)

- e

1

> e

2

k

b

1

e

2

e

m

m

M

n

M

n

M

2

M =

0, 4

m =

2000

k =

10

b =

1

n

M =

1

0, 04

0,5

e

=

÷

2

0,04

0,5

e

=

÷