Akademia Górniczo-Hutnicza im. Stanisława Staszica

w Krakowie

Wydział Inżynierii Mechanicznej i Robotyki

Podstawy Konstrukcji Maszyn 2

Projekt nr 4 – Przekładnia

Wykonał:
Tomasz Siudak
Grupa 5

1

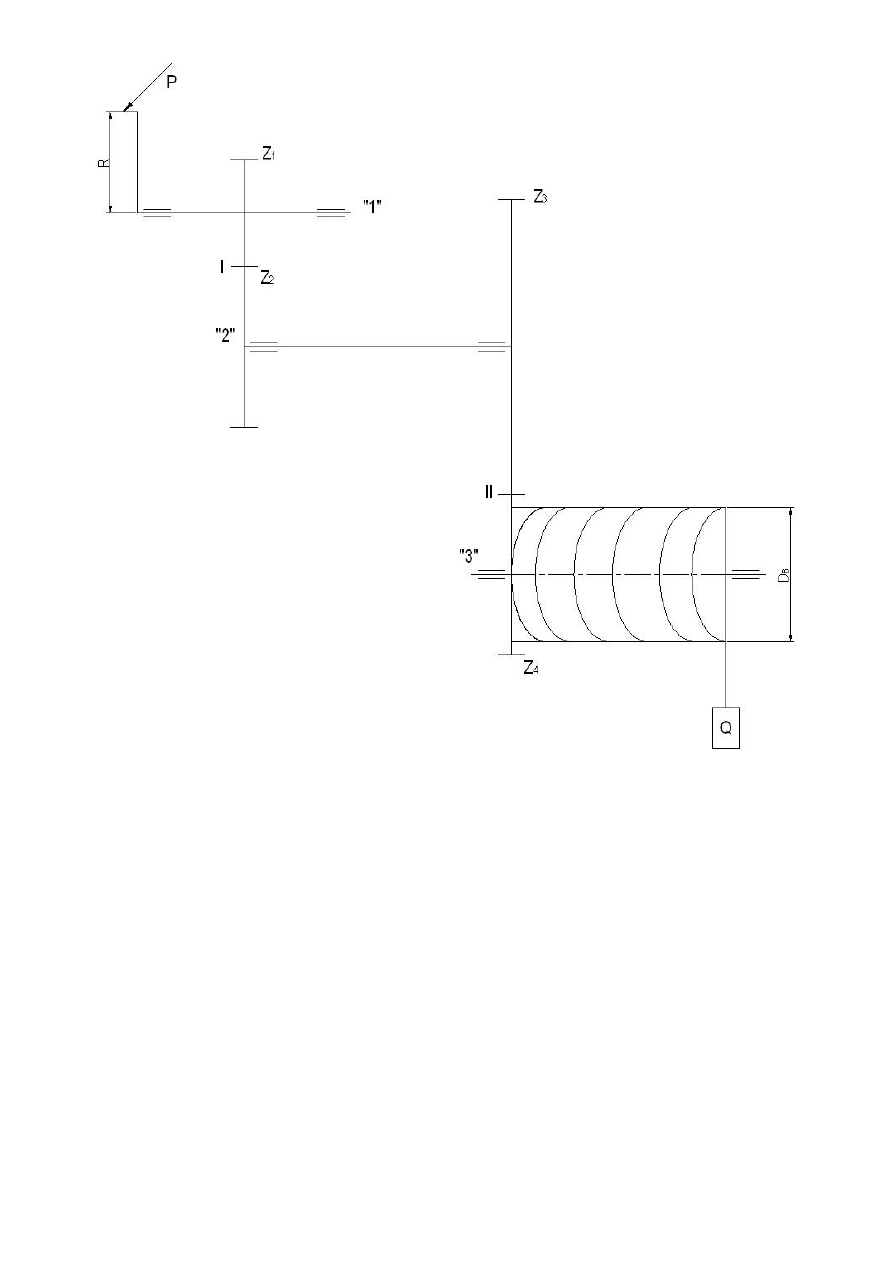
Temat: Obliczyć parametry kół zębatych przekładni zębatej otwartej dla danych wg
podanego schematu przekładni:

250

P

N

=

,

380

R

mm

=

,

14

Q

kN

=

,

440

B

D

mm

=

6

I

i

≤

,

,

6

II

i

≤

1

14

z

≤

2

Dane Obliczenia Wynik

1. Założenia projektowe

Projektowana przekładnia, jest przekładnią zębatą otwartą

- liczba cykli nie jest duża

- przekładnia jest napędzana siłą rąk ludzkich w związku z czym,

prędkości obrotowe są niskie stosuje koła zębate o zębach prostych

- produkcja przekładni jednostkowa

20

α

=

D

0

β

=

D

Wał z kołami zębatymi będzie ułożyskowany symetrycznie, w związku

z czym względną szerokość przekładni w odniesieniu do średnicy

podziałowej

1

d

b

d

ϕ

=

zaleca się przyjmować w granicach

(

)

0,8 1,6

÷

Zbyt dużo niewiadomych we wstępnej fazie obliczeń zmusza nas do

przyjęcia wartości przybliżonych, empirycznie sprawdzonych, a

mianowicie:

- względną długość zęba

λ przyjmuje się zwykle w granicach

6 15

b

m

λ

=

= ÷ w przekładniach ogólnego zastosowania, chociaż w

zastosowaniach specjalnych zdarzają się wyjątki.

Przyjmuję:

10

b

m

λ

=

=

2. Mechanika obciążeń
2.1 Obliczanie momentów obrotowych na wałach „1” i „3”

1

M

P R

= ⋅

1

250

0,38

95

M

N

m

N

=

⋅

=

m

3

14

0,22

3,08

2

B

D

M

Q

kN

m

k

= ⋅

=

⋅

=

Nm

2.2 Całkowite przełożenie przekładni

3

1

c

c

M

M i

η

=

⋅ ⋅ gdzie:

c

i - całkowite przełożenie przekładni

c

η

- sprawność przekładni (dla przekładni zębatych przyjmuje się

95%

c

η

=

)

3

1

3080

95 0,95

c

c

c

M

i

i

M

η

=

⇒ =

⋅

⋅

34,13

c

i

=

2.3 Przełożenia poszczególne

c

I

I

i

i i

I

= ⋅

przyjmuję

6

I

i

=

34,13

6

c

II

II

I

i

i

i

i

= ⇒

=

5,69

II

i

=

2.4 Dobór ilości zębów dla kół zębatych pierwszego stopnia przełożenia

3

Przyjmuję

1

14

z

=

wobec, czego

2

1

I

z

z i

= ⋅

2

14 6 84

z

=

⋅ =

2.5 Dobór ilości zębów dla kół zębatych drugiego stopnia przełożenia

Przyjmuje

3

17

z

=

4

3

II

z

z i

= ⋅

4

17 5,69 96,73

z

=

⋅

=

Przyjmuję

4

97

z

=

2.4 Graniczna liczba zębów

Teoretyczna graniczna liczba zębów

g

z - najmniejsza liczba zębów,

przy której nie wystąpi jeszcze podczas nacinania koła zębatego,

podcięcie zęba oblicza się z zależności:

2

0

2

sin

g

z

α

=

Dla

20

α

=

D

17

g

z

=

Przy

g

z

z

< występuje podcięcie zęba u podstawy. Ponieważ w praktyce

dopuszcza się nieznaczne podcięcie niepowodujące jeszcze ujemnych

skutków, wprowadza się tzw. praktyczną graniczną liczbę zębów

,
g

z

określoną zależnością:

,

5
6

g

g

z

=

4

z , dla

20

α

=

D

,

14

g

z

=

2.5 Współczynnik przesunięcia zarysu

Pomimo tego że liczba zębów

14

z

=

jest jeszcze dopuszczalna to

jednak zakładam że nawet minimalne podcięcie zarysu jest

niedopuszczalne, w związku z powyższym należy zastosować

przesunięcie zarysu zęba dla pierwszego koła zębatego.

Współczynnik granicznego przesunięcia zarysu

x

jest równy:

1

1

1

17 14

17

g

g

g

g

z

z

x

x

z

−

−

=

⇒

=

1

0,18

g

x

=

- powyżej tej wielkości następuje niedopuszczalne

zaostrzenie zębów.

Przyjmuję

1

0,18

x

=

3. Dobór materiałów
3.1 Materiał zębnika

Na materiał zębnika dobieram stal C55 wg PN-EN 10083-2+11:1999 w

stanie ulepszonym cieplnie (QT)

550

e

R

MPa

=

800 950

m

R

MPa

=

÷

Twardość:

260

HB

1

0,8

440

FP

e

R

MPa

σ

=

⋅

=

3.2 Materiał koła zębatego

Na koło zębate dobieram stal C45 wg PN-EN 10083-2+11:1999 w

stanie ulepszonym cieplnie (QT)

490

e

R

MPa

=

700 850

m

R

MPa

=

÷

Twardość

240HB

2

0,8

390

FP

e

R

MPa

σ

=

⋅

=

4. Wstępne obliczenia modułu

Dominujące niebezpieczeństwo zniszczenia przekładni pochodzi od

złamania zębów, w związku z powyższym należy zastosować

odpowiednio duży moduł, aby zmniejszyć naprężenia zginające u

podstawy zęba.

g

F

FS

F

Y

b m

FP

σ

σ

=

⋅

≤

⋅

Znam moment skręcający na kole czynnym, więc przyjmuję:

1

1

n

d

m

z

=

⋅ oraz

n

b

m

λ

= ⋅

Zależność na moduł przybiera postać:

1

3

1

1

1

2

F

FS

FP

M K

m

Y

z

Y Y

ε

β

λ

σ

⋅

⋅

≥

⋅

⋅

⋅ ⋅

⋅

, gdzie:

1

M - moment obrotowy na wale „1”

F

σ

- rzeczywiste naprężenia od zginania

FP

σ

- dopuszczalne naprężenia na zginanie nie powodujące

odkształcenia zęba

g

F - nominalna siła obwodowa – zginająca, działająca na okręgu

podziałowym w przekroju czołowym

b

- szerokość wieńca koła

m

- moduł zęba

λ - względna długość zęba

z

- liczba zębów

4.1 Współczynniki eksploatacyjne

F

A

V

F

F

K

K

K

K

K

α

β

=

⋅

⋅

⋅

F

K - współczynnik eksploatacyjny – ujmuje on wpływ różnych

oddziaływań w warunkach eksploatacji na rzeczywiste naprężenia w

podstawie zębów.

A

K - współczynnik zastosowania. Uwzględnia nadwyżki dynamiczne

zewnętrzne (przeciążenia układu roboczego, charakterystyka silnika

napędowego, rozkład mas za i przed przekładnią oraz sprężystość

wałów i sprzęgieł) W obliczeniach wstępnych współczynnik

A

K

przyjmuję się: 1,1 1,4

A

K

=

÷

.

Przyjmuję 1,2

A

K

=

V

K - współczynnik dynamiczny zależny od wielu czynników, z których

prędkość obwodowa kół ma decydujące znaczenie. Ponadto istotny

wpływ ma dokładność wykonania przekładni i sztywność zazębienia.

W obliczeniach wstępnych można przyjąć empiryczny wzór Merita:

5

1

V

K

ϑ

=

≥

, jeśli w dalszych obliczeniach należy przyjąć

, ponieważ w temacie zadania nie ma zdefiniowanej wymaganej

prędkości wyciągania ciężaru Q toteż przyjmuję, że prędkość

obwodowa

1

V

K

<

1

V

K

=

ϑ jest mała i co za tym idzie

1

V

K

= .

F

K

β

- współczynnik rozkładu obciążenia gnącego na długości zęba

(szerokości wieńca zębatego) uwzględnia wzrost naprężeń gnących

wskutek nierównomiernego przylegania zębów pod obciążeniem.

Współczynnik

H

K

β

w zależności od układu kół zębatych w przekładni,

5

oraz dla kół „miękkich” w przybliżeniu jest równy:

1,025

H

K

β

=

Współczynnik

F

K

β

jest około 15-20% mniejszy od

H

K

β

i można go

oszacować z zależności:

F

N

F

H

K

K

β

β

=

Przy czym wykładnik

dla zębów prostych, oraz względnej długości

zębów równej:

F

N

10

b

m

λ

=

=

jest równy:

0,85

F

N

=

, zatem

0,85

1,025

F

K

β

=

1,021

F

K

β

=

F

K

α

- współczynnik rozkładu obciążenia wzdłuż odcinka przyporu na

poszczególne pary zębów znajdujących się w danej chwili w przyporze.

W określonych granicach stosowania współczynnik

F

K

α

jest równy

H

K

α

, wstępnie można je wyznaczyć w zależności od klasy dokładności

wykonania kół:

(

)

2

1

1 0,25

5

1

H

F

K

K

n

Z

α

α

ε

⎛

⎞

=

= +

−

−

⎜

⎝

⎠

⎟

, gdzie - klasa dokładności 5…9.

n

Z

ε

- współczynnik stopnia pokrycia

Dla kół wykonanych w klasie 6…8, o zębach prostych w przybliżeniu

przyjmuje się

1,00 1,18

H

F

K

K

α

α

=

=

÷

Przyjmuję 1,1

F

K

α

=

1,2 1 1,021 1,1

F

K

=

⋅ ⋅

⋅

1,35

F

K

=

4.2 Współczynniki konstrukcyjne

Ujmują one wpływ niektórych podstawowych parametrów

konstrukcyjnych.

FS

Y - współczynnik kształtu zęba

FS

Fa

Sa

Y

Y

Y

=

⋅

Fa

Y - współczynnik uwzględniający stereomechaniczny układ

przyłożenia siły zginającej do wierzchołka zęba.

Sa

Y - współczynnik uwzględniający działanie karbu oraz wpływ

naprężeń tnących i ściskających w podstawie zęba.

Dla zębów o kącie przyporu

i względnego promienia zaokrąglenia

narzędzia

20

D

0

0,2

a

n

m

ρ

=

przybliżony wzór na współczynnik kształtu

ma postać:

FS

Y

2

7,63 15,94

4,08 0,18

FS

v

v

x

Y

x

z

z

=

+

+

−

Po podstawieniu danych otrzymuję:

(

)

2

7,63 15,94 0,176

4,08 0,18 0,176

14

14

FS

Y

⋅

=

+

⋅

+

−

6

4,43

FS

Y

=

Y

ε

- współczynnik liczby przyporu, uwzględniający to, że w strefie

jednoparowego przyporu pełne obciążenie

nie działa na wierzchołku

zęba, lecz na mniejszym ramieniu, dlatego współczynnik ten zwykle

przyjmuje wartość mniejszą od jedności:

bn

F

0,8

0,2

Y

ε

α

ε

=

+

W obliczeniach wstępnych można przyjąć z korzyścią dla obliczeń

0,8 1

Y

ε

=

÷

Przyjmuję 0,8

Y

ε

=

Y

β

- współczynnik pochylenia linii zęba, uwzględniający korzystniejszy

rozkład naprężeń u podstawy zęba w rzeczywistości niż w zastępczym

modelu obliczeniowym.

min

1

120

Y

Y

β

β

β

β

ε

= −

≥

min

1 0,25

0,75

Y

β

β

ε

= −

≥

W obliczeniach wstępnych można przyjąć Y

1

β

=

4.3 Obliczenia modułu

3

1

6

2 95 1,35

4,43 0,8 1

10 14 440 10

m

⋅ ⋅

≥

⋅

⋅ ⋅

⋅

⋅

⋅

3

1

10

909,036

6,16 10

m

≥

⋅

1

1

0,00245

2,45

m

m

m

≥

⇒

≥

mm

m

Dobieram najbliższy znormalizowany moduł

1

2,5

m

m

=

1

2

m

m

=

5. Obliczenia odległości i współczynników korekcji

Teoretyczna odległość osi kół jest równa

1

2

0

1

2

z

z

a

m

+

=

⋅

0

14 84

2,5

122,5

2

a

mm

+

=

⋅

=

mm

m

Przyjmuję znormalizowaną rzeczywistą nominalną odległość osi kół:

125

r

a

m

=

Różnicę między nominalną i rzeczywistą odległością osi usuwam za

pomocą korekcji P

Obliczam wartość współczynnika

r

B

0

0

125 122,5

122,5

r

r

r

a

a

B

B

a

−

−

=

⇒

=

0,02041

r

B

=

1 7

0,02041 1 7 0,02041

p

r

r

B

B

B

=

+

=

+ ⋅

0,02182

p

B

=

Obliczam pozorną odległość osi

(

)

(

)

0

1

122,5 1 0,02182

p

p

a

a

B

= ⋅ +

=

⋅ +

125,17295

p

a

mm

=

7

Ponieważ istnieje konieczność zmniejszenie nadmiernego luzu

obwodowego, sprawdzam wartość zbliżenia osi K

p

r

K

a

a

=

−

125,173 125 0,173

K

=

−

=

Zbliżenie osi o wielkość K powoduje zmniejszenie luzu

wierzchołkowego, który wyniesie:

0,25

c

m

K

=

⋅ −

0,25 2,5 0,173 0,452

c

m

=

⋅

−

=

m

m

Wartość otrzymanego luzu wierzchołkowego będzie większa od

wartości minimalnej

(

)

, a

więc można nie ścinać głów zębów – wynika to również z zależności:

min

min

0,1

0,1 2,5

0,25

c

m

c

mm

m

=

⋅ ⇒

=

⋅

=

0,173

0,0692 1

2,5

K

k

m

=

=

=

< .

Obliczam sumę przesunięć zarysu w obu kołach

1

2

p

0

X

X

a

a

+

=

−

1

2

125,173 122,5 2,673

X

X

m

+

=

−

=

m

1

2

1

2

1

2

1,0692

X

X

x

x

x

x

m

+

+

=

⇒ +

=

2

1

1,0692

x

x

=

−

2

1,0692 0,18 0,89

x

=

−

=

W wyniku dokonania korekcji otrzymuje się zmienioną odległość osi a

co za tym idzie zmianie ulega również toczny kąt przyporu

0

cos

cos

w

r

a

a

α

α

=

122,5

cos

cos 20

0,920898768

125

w

α

=

=

D

'

22 56

w

α

=

D

6. Wymiary zębów i kół:
6.1 Wymiary zębnika

1

d

Wartość przesunięcia zarysu

1

1

1

X

x m

= ⋅

1

0,176 2,5

0,44

X

mm

mm

=

⋅

=

Średnica podziałowa

1

1

d

z m

1

= ⋅

1

14 2,5

35

d

mm

=

⋅

= mm

Średnica wierzchołków

(

)

1

1

1

2

2

a

d

m z

X

=

+

+

1

mm

(

)

1

2,5 14 2

2 0,44

40,88

a

d

mm

=

+

+ ⋅

=

Średnica podstaw

(

)

1

1

1

2,5

2

f

d

m

z

X

=

⋅

−

+

1

m

1

(

)

1

2,5 14 2,5

2 0,44 29,63

f

d

m

=

⋅

−

+ ⋅

=

Wysokość głowy zęba

1

1

a

h

m

X

=

+

1

2,5 0,44 2,94

a

h

m

=

+

=

m

Wysokość stopy zęba

8

9

1

X

1

1

1,25

f

h

m

=

⋅

+

1

1,25 2,5 0,44 3,57

f

h

=

⋅

+

=

Luz wierzchołkowy

1

1

3,57 2,94 0,63

f

a

c

h

h

c

=

−

⇒ =

−

=

6.2 Wymiary koła

2

d

Wartość przesunięcia zarysu

2

2

2

X

x m

= ⋅

2

0,89 2,5

2,26

X

mm

mm

=

⋅

=

Średnica podziałowa

2

2

d

z m

2

= ⋅

1

84 2,5

210

d

mm

=

⋅

=

mm

Średnica wierzchołków

(

)

2

2

2

2

2

a

d

m

z

X

=

+ +

2

mm

(

)

2

2,5 84 2

2 2,26

219,52

a

d

mm

=

+ + ⋅

=

Średnica podstaw

(

)

2

2

2

2,5

2

f

d

m

z

X

=

⋅

−

+

2

m

2

(

)

2

2,5 84 2,5

2 2,26 208,27

f

d

m

=

⋅

−

+ ⋅

=

Wysokość głowy zęba

2

2

a

h

m

X

=

+

2

2,5 2,26 4,76

a

h

m

=

+

=

m

2

X

Wysokość stopy zęba

2

2

1,25

f

h

m

=

⋅

+

2

1,25 2,5 2,26 5,385

f

h

=

⋅

+

=

Luz wierzchołkowy

2

2

2

2

5,39 4,76 0,63

f

a

c

h

h

c

=

−

⇒

=

−

=

Szerokość wieńca koła

2

2

2

10 2,5

25

b

m

b

mm

mm

λ

= ⋅

⇒

=

⋅

=

Szerokość wieńca zębnika

1

2

b

b

m

1

= +

1

25

2,5

27,5

b

mm

mm

m

=

+

=

m

1

7. Obliczenia konstrukcyjne kół 3 i 4

Materiał jak dla koła nr 2

2

1

M

M i

=

⋅

2

95

6 570

M

Nm

Nm

=

⋅ =

2

3

3

3

3

2

F

FS

FP

M

K

m

Y

z

Y Y

ε

β

λ

σ

⋅

⋅

≥

⋅

⋅

⋅ ⋅

⋅

3

3

6

2 570 1,35

4, 43 0,8 1

10 17 390 10

m

⋅

⋅

≥

⋅

⋅ ⋅

⋅

⋅

⋅

3

3

3

10

5454,22

4,35

6,63 10

m

m

≥

⇒

≥

⋅

Dobieram znormalizowany moduł:

3

4,6

m

=

3

4

m

m

=

7.1 Obliczenia odległości i współczynników korekcji

Teoretyczna odległość osi kół jest równa

3

4

0(3 4)

3

2

z

z

a

m

−

+

=

⋅

0(3 4)

17 97

4,6

262,2

2

a

mm

−

mm

+

=

⋅

=

Ponieważ w temacie zadania nie ma wymaganego przyjmowania

znormalizowanych odległości osi przyjmuję rzeczywistą odległość osi

kół:

262

r

a

mm

=

Różnicę między nominalną i rzeczywistą odległością osi usuwam za

pomocą korekcji P

Obliczam wartość współczynnika

r

B

(3 4)

0(3 4)

0(3 4)

262 262,2

262,2

r

r

r

a

a

B

B

a

−

−

−

−

−

=

⇒

=

0,00076

r

B

= −

1 7

0,00076 1 7 0,00076

p

r

r

B

B

B

=

+

= −

− ⋅

0,00076

p

B

= −

Obliczam pozorną odległość osi

(

)

(

)

(3 4)

0(3 4)

1

262,2 1 0,00076

p

p

a

a

B

−

−

=

⋅ +

=

⋅ −

(3 4)

262

p

a

m

−

m

=

Ponieważ odchyłki wymiarów są bardzo małe nie spowodują

znaczącego zmniejszenia luzu wierzchołkowego

p

r

K

a

a

=

−

0

K

=

Luzu wierzchołkowy wyniesie:

0,25

c

m

K

=

⋅ −

0,25 4,6 1,15

c

m

=

⋅

=

m

4)

Obliczam sumę przesunięć zarysu w obu kołach

3

4

(3 4)

0(3

p

X

X

a

a

−

−

+

=

−

3

4

3

4

3

4

3

262 262,2

0,04

4,6

X

X

x

x

x

x

m

+

−

+

=

⇒ +

=

= −

Przyjmuję:

3

0

x

=

4

0,04

x

= −

W wyniku dokonania korekcji otrzymuje się zmienioną odległość osi a

co za tym idzie zmianie ulega również toczny kąt przyporu

0

cos

cos

w

r

a

a

α

α

=

262,2

cos

cos 20

0,947643866

260

w

α

=

=

D

'

18 37

w

α

=

D

7.2 Wymiary zębów i kół:

10

11

3

7.2.1 Wymiary koła

3

d

Średnica podziałowa

3

3

d

z m

= ⋅

3

17 4,6

78,2

d

mm

=

⋅

=

mm

Średnica wierzchołków

(

)

2

3

3

2

a

d

m z

=

+

(

)

1

4,6 17 2

87, 4

a

d

m

=

+

=

m

Średnica podstaw

(

)

3

3

3

2,5

f

d

m

z

=

⋅

−

(

)

3

4,6 17 2,5

66,7

f

d

m

=

⋅

−

=

m

Wysokość głowy zęba

3

3

a

h

m

=

3

4,6

a

h

mm

=

Wysokość stopy zęba

3

3

1,25

f

h

m

=

⋅

3

1,25 4,6 5,75

f

h

=

⋅

=

Luz wierzchołkowy

3

3

5,75 4,6 1,15

f

a

c

h

h

c

=

−

⇒ =

−

=

Szerokość wieńca koła

3

3

3

10 4,6

46

b

m

b

mm

mm

λ

= ⋅

⇒ =

⋅

=

7.2.2 Wymiary koła

4

d

Wartość przesunięcia zarysu

4

4

4

X

x m

= ⋅

4

0,04 4,6

0,184

X

mm

mm

= −

⋅

= −

Średnica podziałowa

4

4

d

z m

4

= ⋅

4

97 4,6

446,2

d

mm

=

⋅

=

mm

Średnica wierzchołków

(

)

4

4

4

2

2

a

d

m

z

X

=

+

+

4

m

mm

(

)

4

4,6 97 2

2 0,184

455

a

d

m

=

+

− ⋅

=

Średnica podstaw

(

)

4

4

4

2,5

2

f

d

m

z

X

=

⋅

−

+

4

m

4

(

)

4

4,6 97 2,5

2 0,184 434,332

f

d

m

=

⋅

−

− ⋅

=

Wysokość głowy zęba

4

4

a

h

m

X

=

+

4

4,6 0,184 4,416

a

h

m

=

−

=

m

4

X

Wysokość stopy zęba

4

4

1,25

f

h

m

=

⋅

+

4

1,25 4,6 0,184 5,566

f

h

=

⋅

−

=

Luz wierzchołkowy

4

4

4

4

5,566 4,416 1,15

f

a

c

h

h

c

=

−

⇒

=

−

=

Szerokość wieńca koła

3

3

3

10 4,6

46

b

m

b

mm

mm

λ

= ⋅

⇒ =

⋅

=

12

Literatura

:

1. Osiński Z., Bajon W., Szucki T.: Podstawy Konstrukcji Maszyn, PWN, Warszawa 1986
2. Orlik Z., Surowiak W., Rutkowski A.: Części maszyn cz. I i II, WSiP, Warszawa 1985
3. Przykłady obliczeń z Podstaw Konstrukcji Maszyn, pod redakcją Eugeniusza Mazanka, WNT,

Warszawa 2005