Układy przeniesienia

Układy przeniesienia

napędu

napędu

Prof. dr hab. inż. Bogusław Łazarz

Politechnika

Politechnika

Ś

Ś

l

l

ą

ą

ska, Wydzia

ska, Wydzia

ł

ł

Transportu

Transportu

Katedra Budowy Pojazd

Katedra Budowy Pojazd

ó

ó

w

w

Samochodowych

Samochodowych

Wstęp

Wstęp

Liczba

parametrów

geometrycznych

występujących w obliczeniach przekładni

znacznie przekracza liczbę warunków

wytrzymałościowych, co daje możliwość

rozwiązania niemal dla każdej kombinacji

założonych

wielkości.

Równocześnie

umożliwia to postawienie dodatkowych

warunków technicznych i ekonomicznych.

Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

Całkowite

przełożenie

przekładni

jest

dane

w założeniach projektowych, przy czym jest dana

także tolerancja zachowania założonej wielkości. Ze

względów wytrzymałościowych korzystnie jest, aby

liczby zębów współpracujących kół, były względem

siebie liczbami pierwszymi, tj. nie miały wspólnych

podzielników.
Konstruktor określa optymalną liczbę stopni oraz

optymalny rozkład przełożenia na poszczególne

stopnie. Najczęściej stawiane są następujące

dodatkowe

warunki

umożliwiające

dokonanie

wyboru najlepszego rozwiązania:
- całkowity koszt produkcji przekładni powinien być

możliwie mały,

Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

- całkowita masa przekładni, a zwłaszcza

elementów wirujących, powinna być możliwie

mała,
- całkowity moment bezwładności elementów

wirujących powinien być jak najmniejszy,
- duże koła poszczególnych stopni powinny

mieć w przybliżeniu równe średnice, aby

jednakowo zanurzały się w oleju,
- całkowita długość przekładni, lub długość

zajęta przez elementy wirujące powinna być

mała.

Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

Objętość zębnika zależy od:
- momentu obrotowego M

1

,

- przełożenia danego stopnia u

1

przy czym dla u

1

=

1 objętość jest dwa razy większa niż dla u = ,
- wytrzymałości materiału na naciski k

z

(materiału

o mniejszej wytrzymałości),
-

dokładności

wykonania

wpływającej

na

współczynniki K

d

, K

rw

oraz w pewnym stopniu na y

h

,

-

geometrii

zazębienia,

mającej

wpływ

na

współczynniki K

s

, y

c

, y



,

- dziedziny zastosowań przekładni rzutującej na K

p

oraz X

pwym

.

Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

W przypadku przekładni jednostopniowej

objętość zębnika zależy przy określonym

wytwarzaniu i konstrukcji od momentu

obrotowego i w pewnym stopniu od

przełożenia. Można więc uważać, że

objętość zębnika V

1

jest określona niemal

w założeniach projektowych i wynikających

stąd

ograniczeniach

dotyczących

dokładności

wykonania,

własności

materiałowych itd.

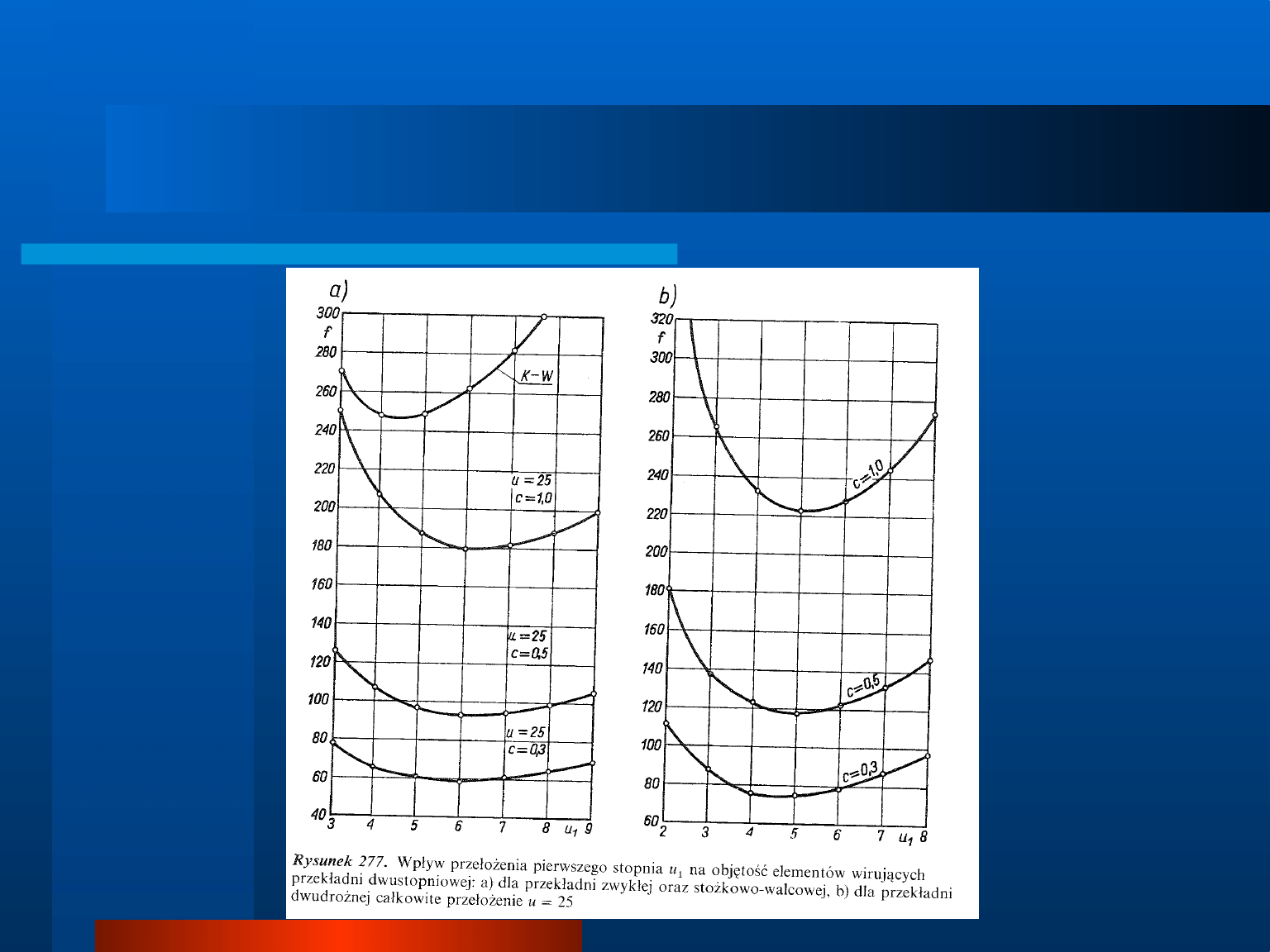
Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

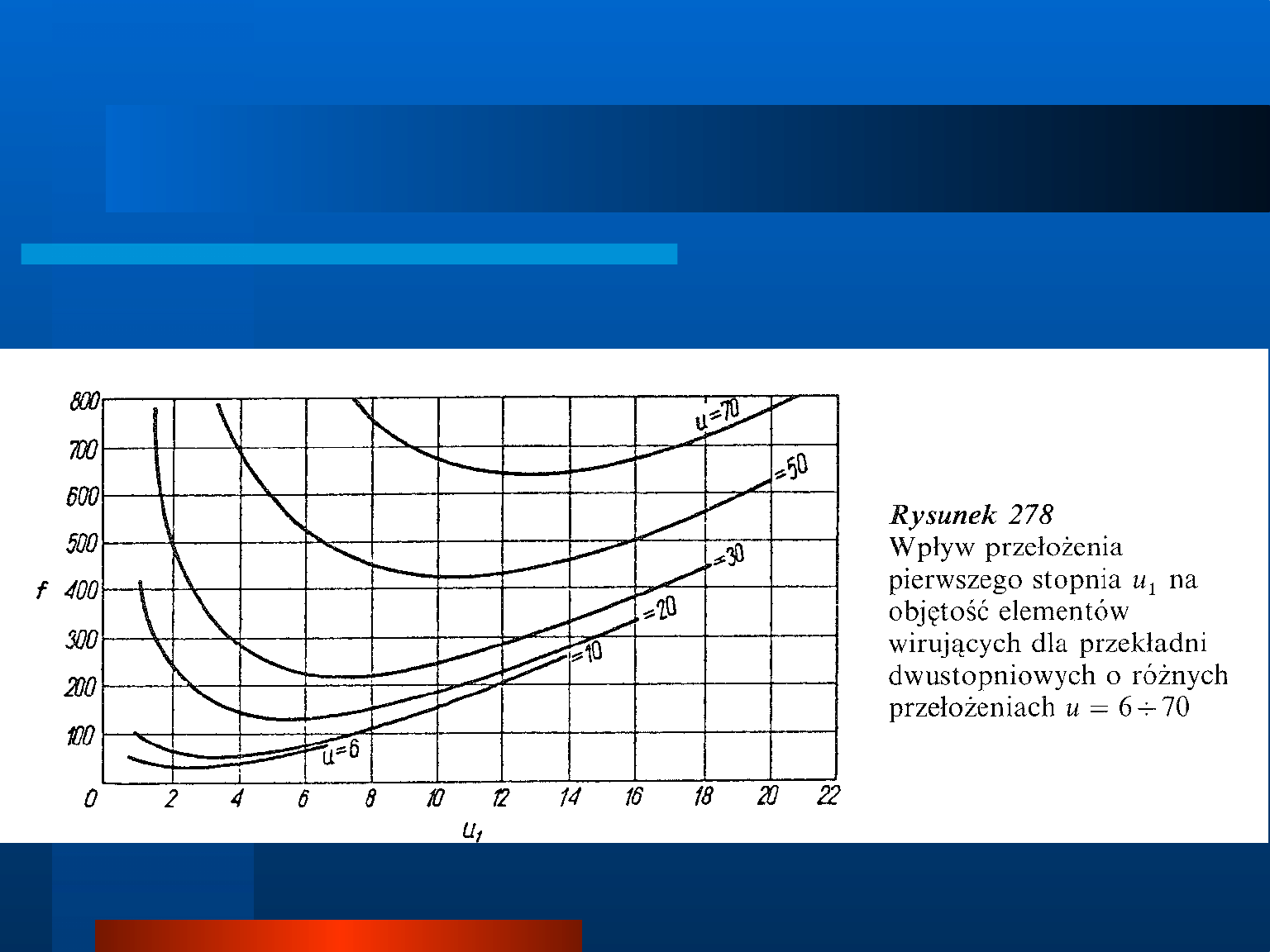
Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

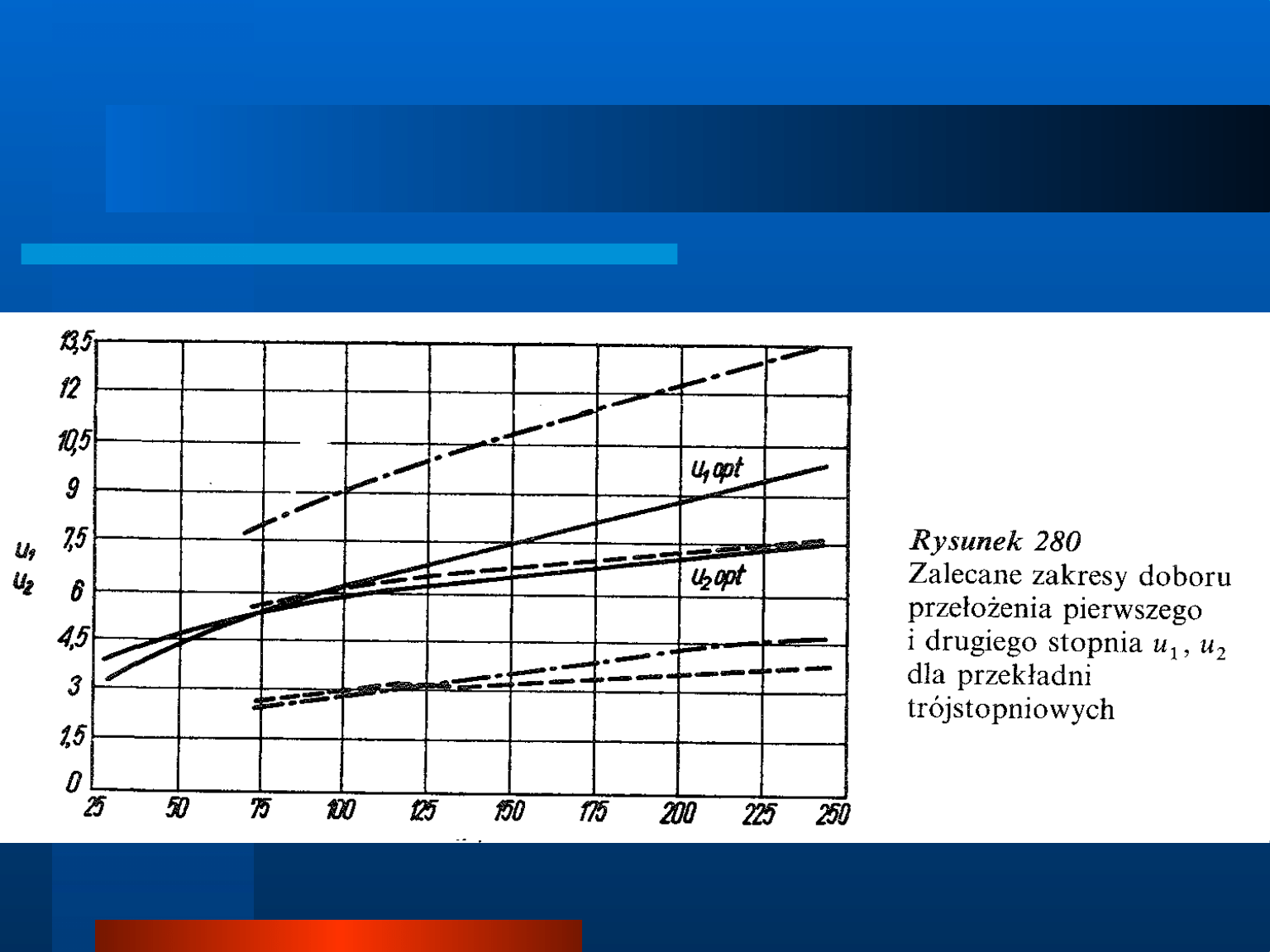
Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

u

Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

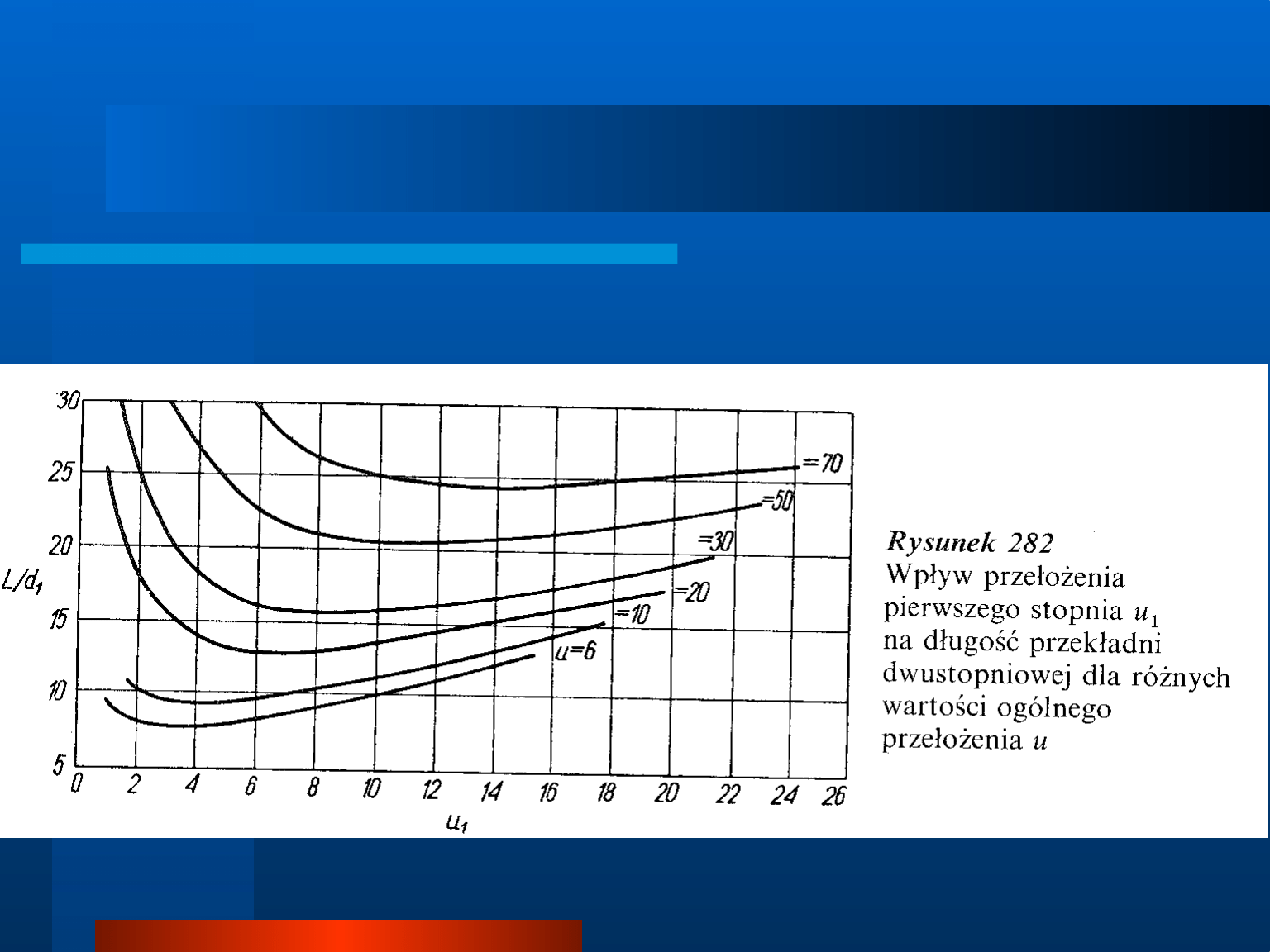
Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

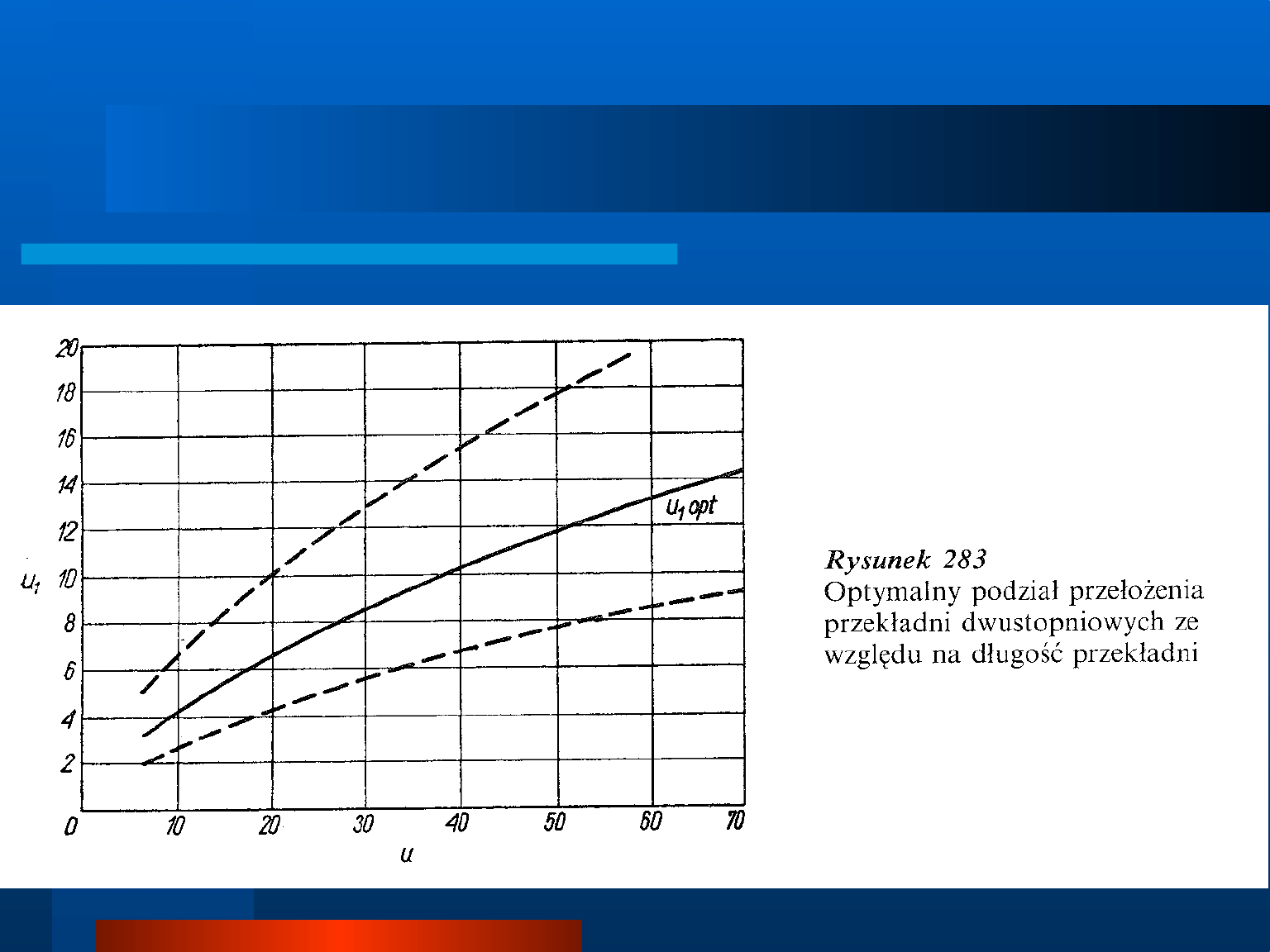
Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

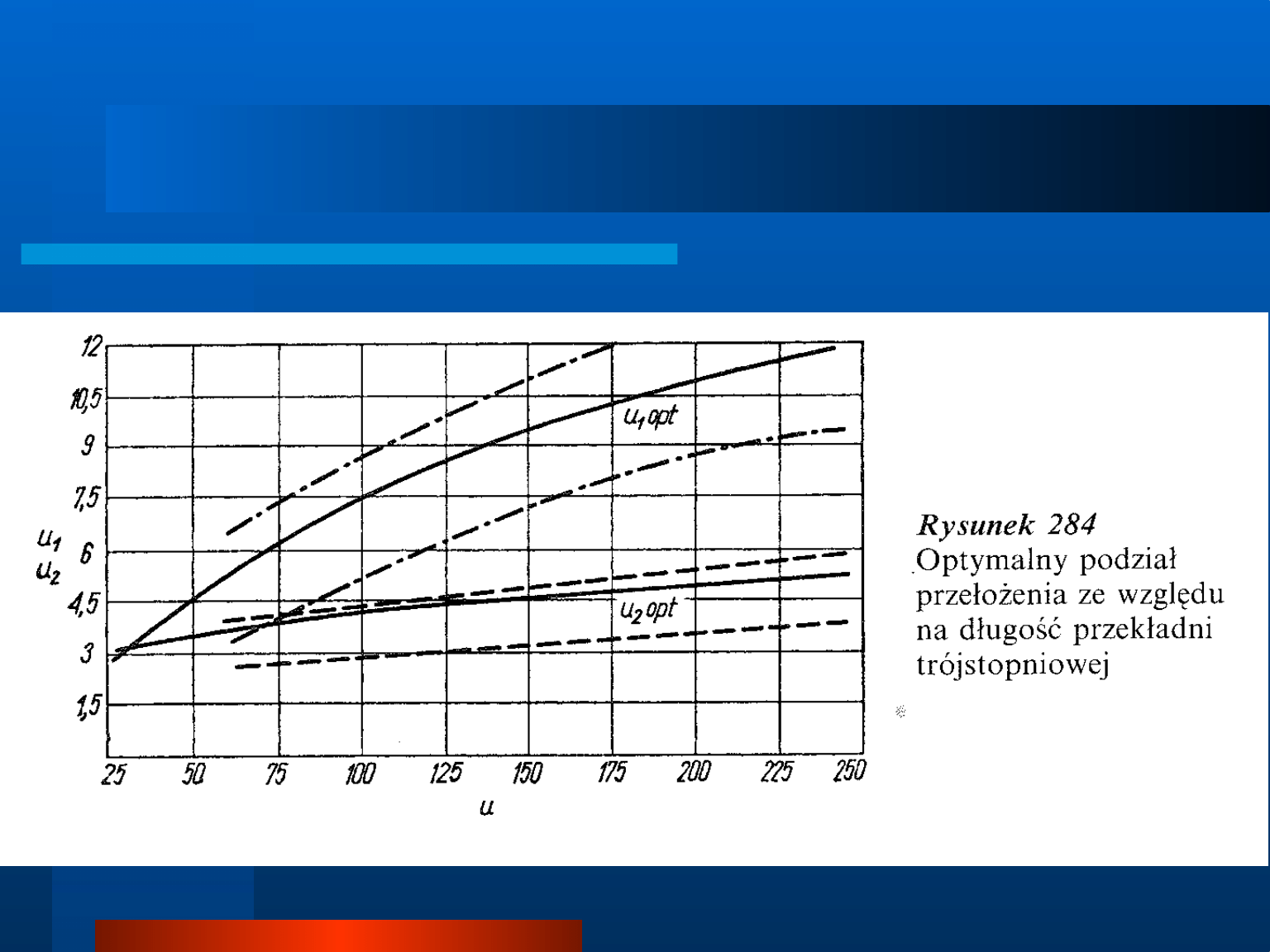
Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

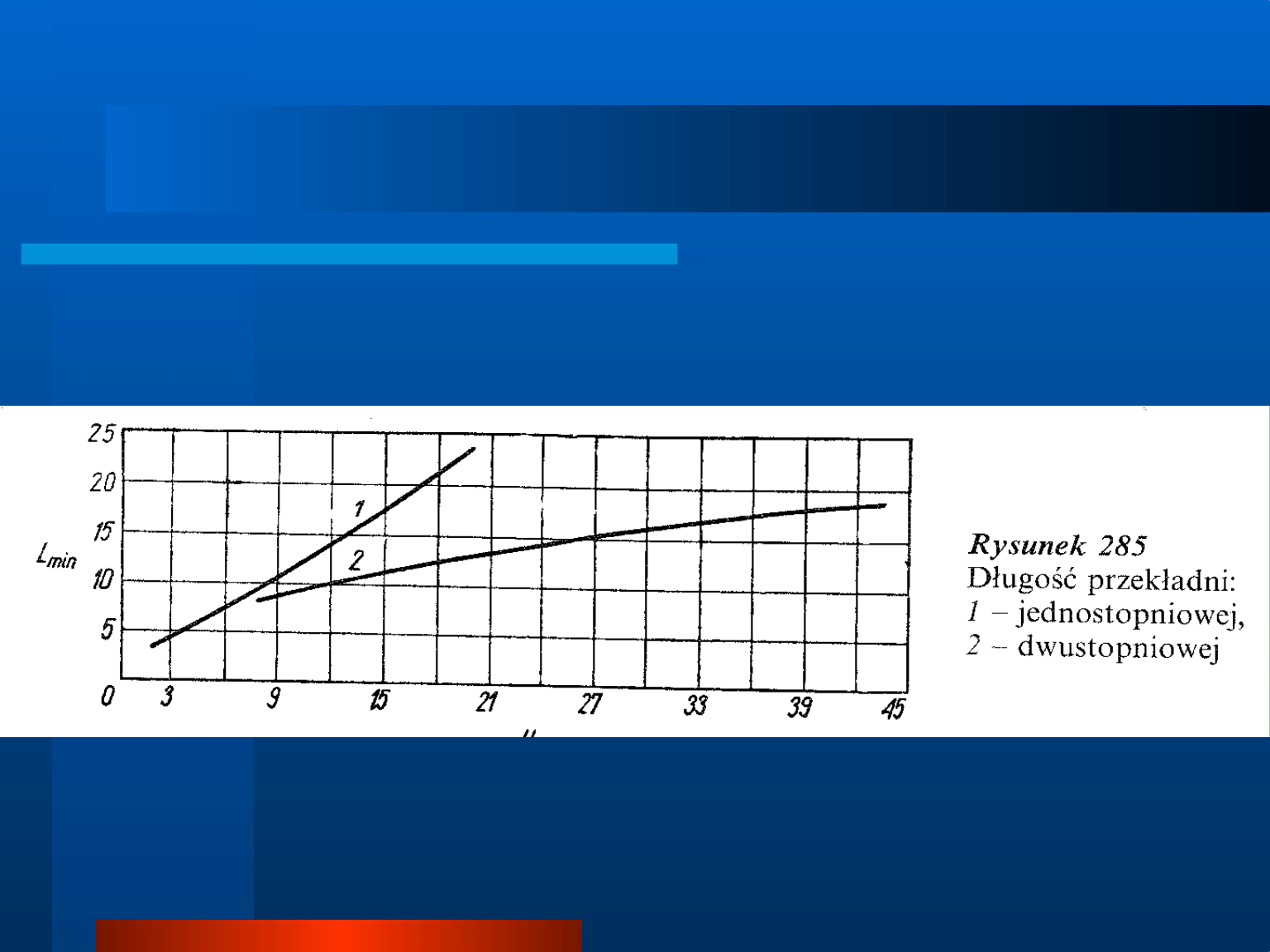
Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

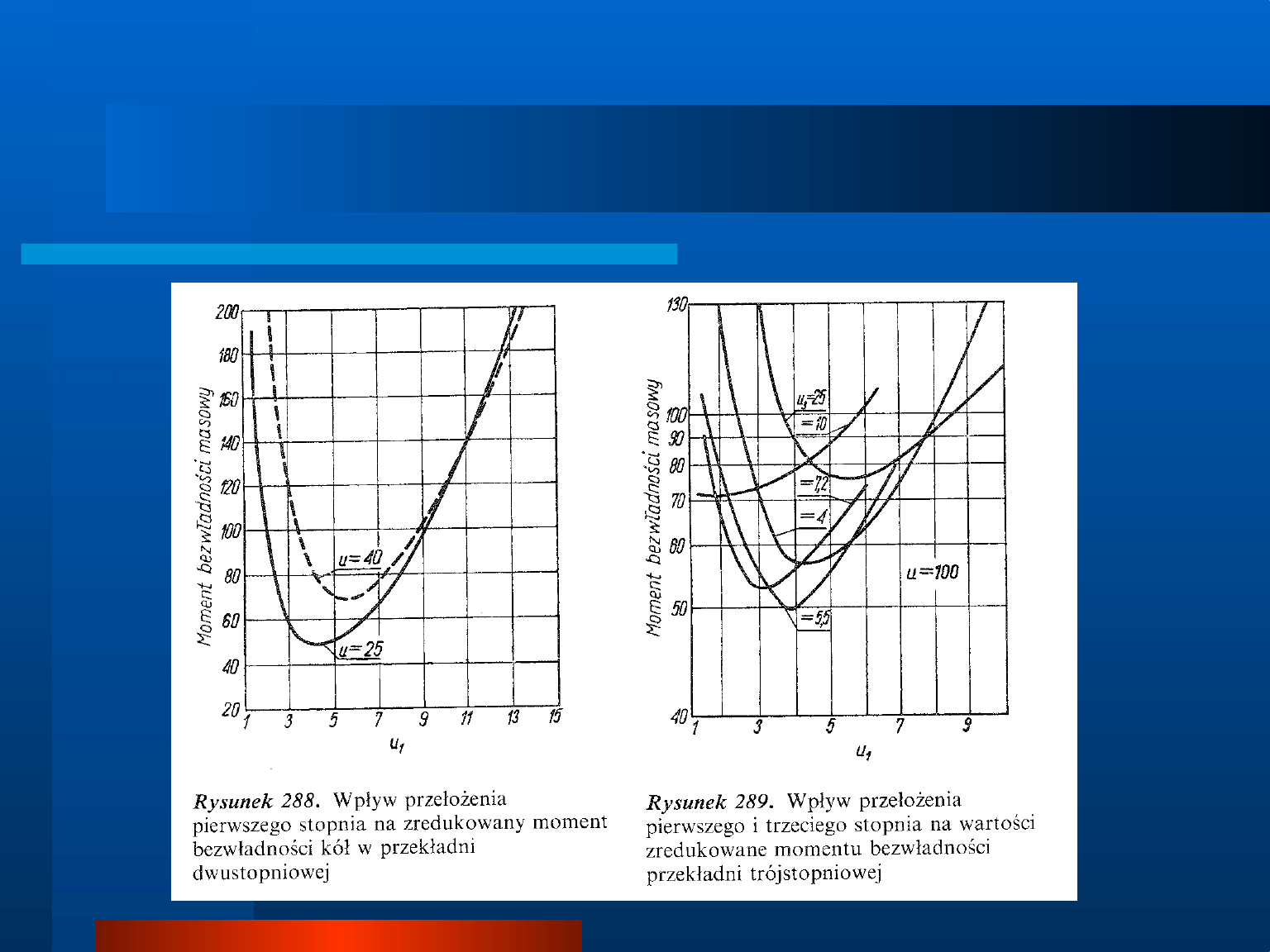
Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

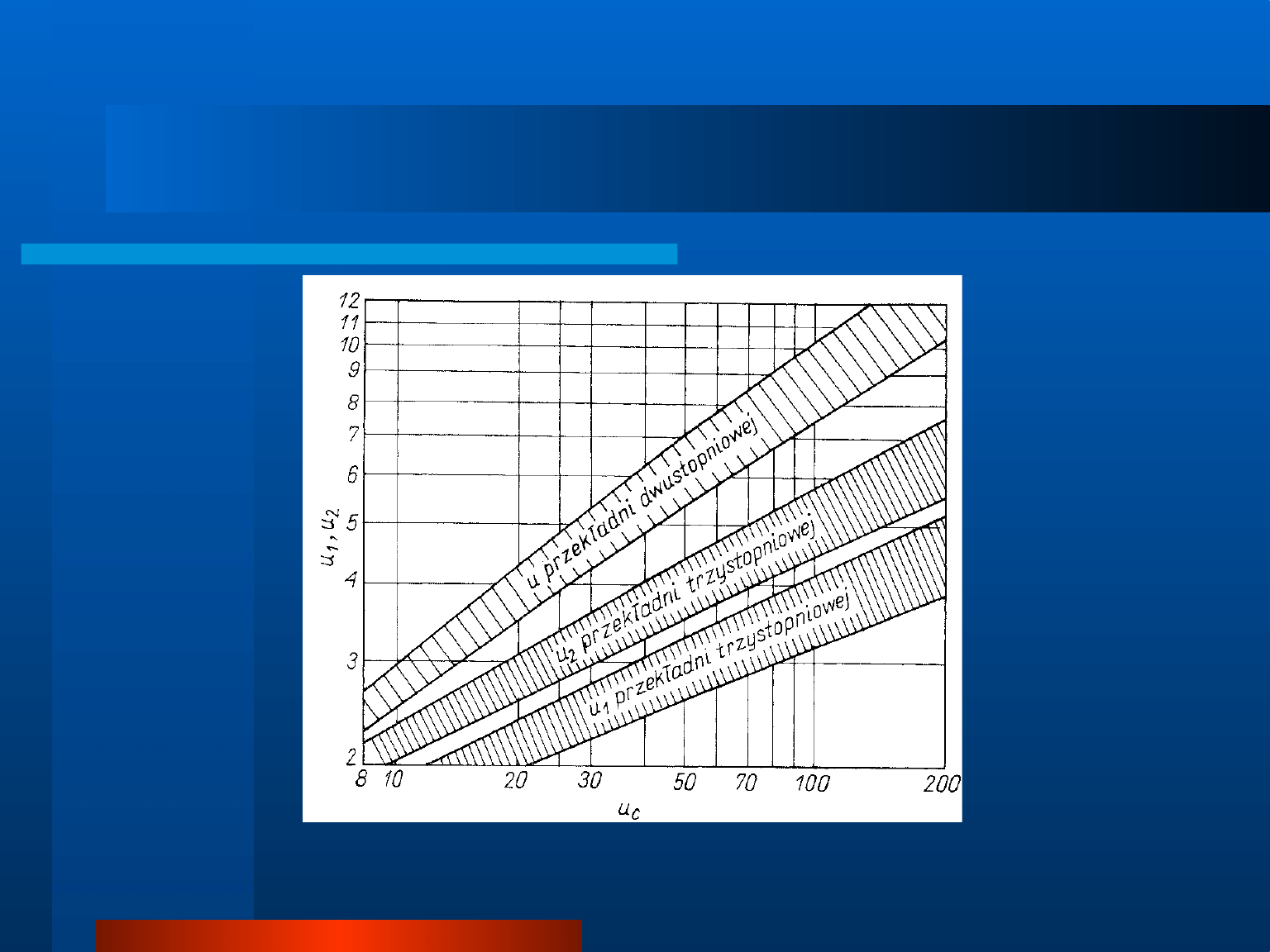
Rozkład przełożenia na poszczególne stopnie

Rozkład przełożenia na poszczególne stopnie

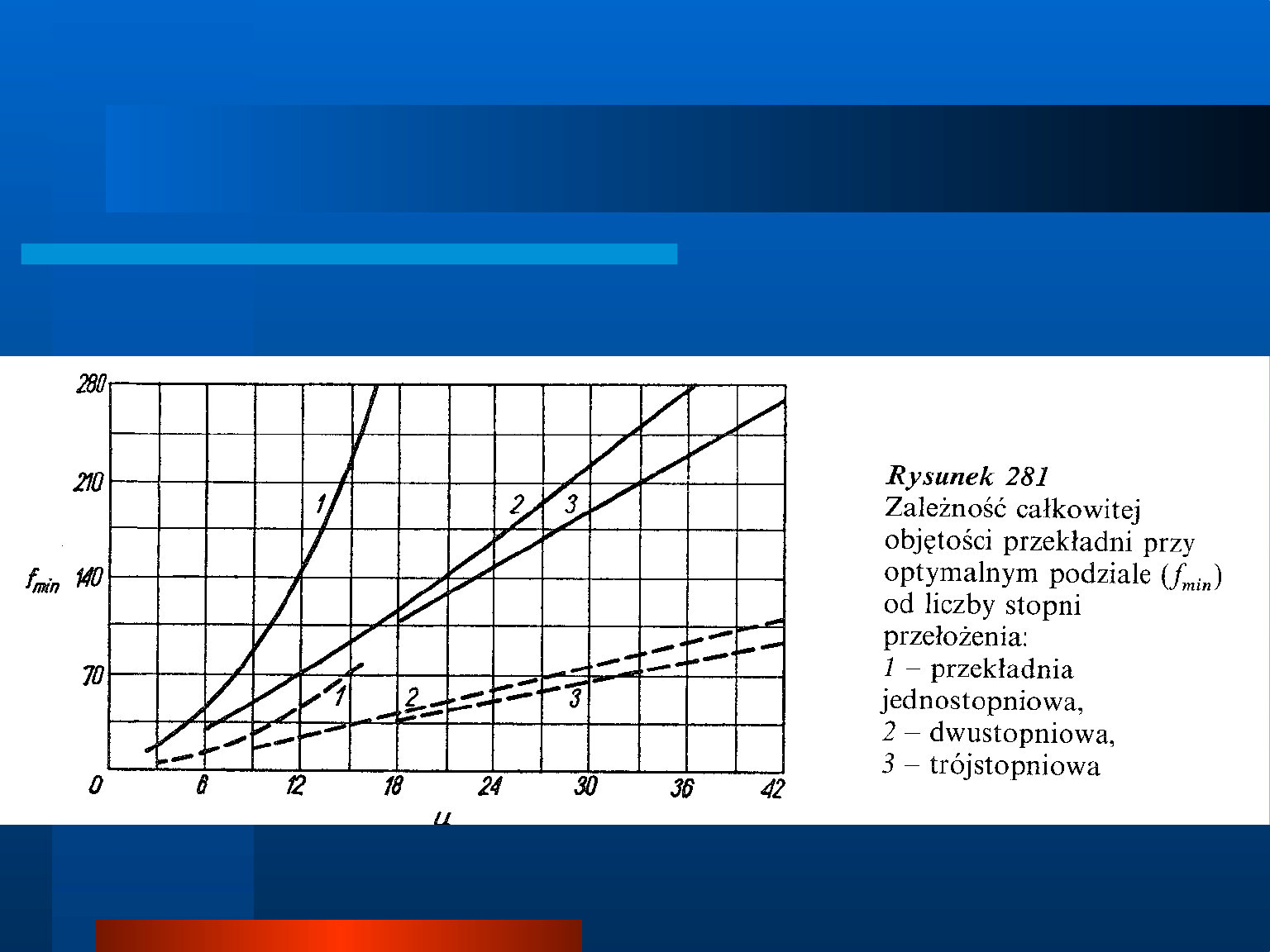
Rozkład przełożenia na poszczególne stopnie ze

względu na minimum momentu bezwładności

Dobór stosunku

Dobór stosunku

b

b

/

/

d

d

1

1

Ustalenie przełożenia obliczanego stopnia określa

jednoznacznie

objętość

zębnika

zarówno

w

przypadku,

gdy

o rozmiarach

koła

decyduje

złamanie zęba, jak też w przypadku nacisków czy

zatarcia

gdzie



= b/d

1

- względna szerokość koła.

Im większe jest



, tym mniejsze średnice kół i tym

mniejsza całkowita długość przekładni, a także tym

mniejszy moment bezwładności.

Dobór stosunku

Dobór stosunku

b

b

/

/

d

d

1

1

Przy stałej objętości V, wynikającej z warunków

wytrzymałościowych, moment bezwładności będzie

tym mniejszy, im mniejsza będzie średnica koła, co

oczywiście prowadzi do odpowiedniej szerokości b.
Tak więc wzrost stosunku b/d

1

wpływa korzystnie

na:
- ogólną długość przekładni,
- zredukowany moment bezwładności kół,
- cichobieżność przekładni,
natomiast wpływa niekorzystnie na rozkład

obciążenia wzdłuż zęba, zarówno z powodu błędów

wykonawczych, jak też ze względu na ugięcia

wałów i ich skręcenie.

Dobór stosunku

Dobór stosunku

b

b

/

/

d

d

1

1

Przez wprowadzenie modyfikacji linii zęba

można uniknąć skutków odkształceń. W

takim przypadku szerokość koła b albo

stosunek b/d

1

są ograniczone względami

wytrzymałościowymi. Im większa jest

szerokość koła b, tym mniejsza jego

średnica d

1

co prowadzi do zwiększenia

naprężeń w wałku od strony sprzęgła, a

tym

samym

ogranicza

wielkość

przenoszonego momentu obrotowego.

Dobór kąta pochylenia linii zęba

Dobór kąta pochylenia linii zęba

Kąt pochylenia linii zęba, mierzony na kole

podziałowym, dobiera się dla kół o zębach

śrubowych,

w granicach

8°-15°,

a dla

kół

daszkowych 25°-45°. Korzystnie jest tak dobierać

kąt

pochylenia,

aby

poskokowy

wskaźnik

zazębienia) był liczbą całkowitą:

Ze wzrostem kąta pochylenia linii zęba rośnie siła

osiowa, a tym samym rośnie dodatkowe obciążenie.

W przypadku zębów daszkowych siły osiowe

wzajemnie się znoszą, stąd można stosować

znacznie większe kąty. Wpływa to korzystnie na

wytrzymałość zęba i poprawia także poskokowy

wskaźnik zazębienia.

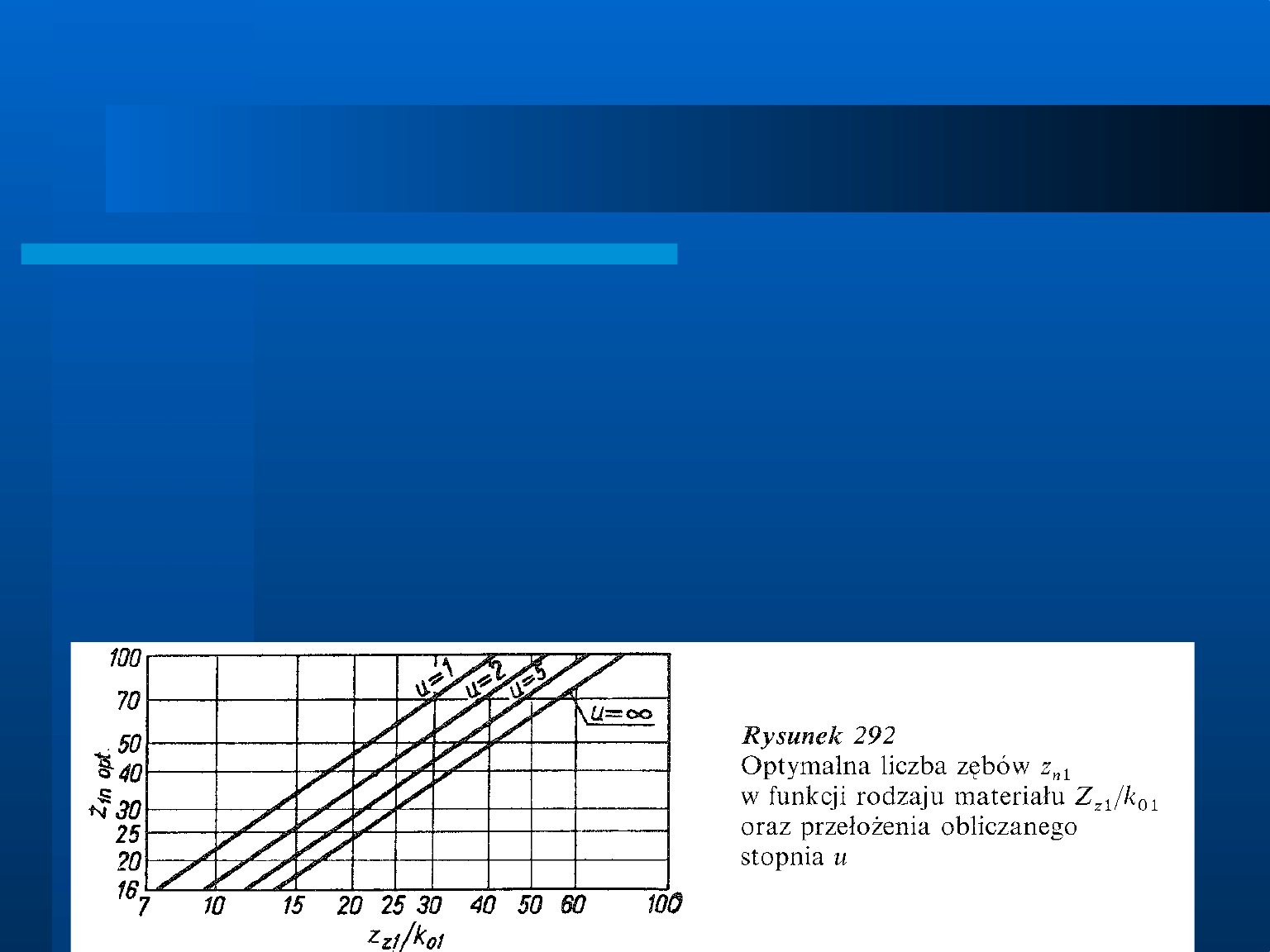
Dobór liczby zębów zębnika

Dobór liczby zębów zębnika

z

z

1

1

Liczba zębów wpływa w istotny sposób na wskaźniki

wytrzymałościowe zarówno na zginanie, jak też na naciski. Ma

ona także wpływ na inne wskaźniki i dlatego musi być

starannie dobierana. Na rysunku przedstawiono zależność

między optymalną liczbą zębów w przekroju normalnym z

n

a właściwościami materiału wyrażającymi się stosunkiem

wytrzymałości zęba przy zginaniu Z

z

do wytrzymałości zęba na

naciski k

z

. Wpływ na wybór liczby zębów ma też przełożenie u.

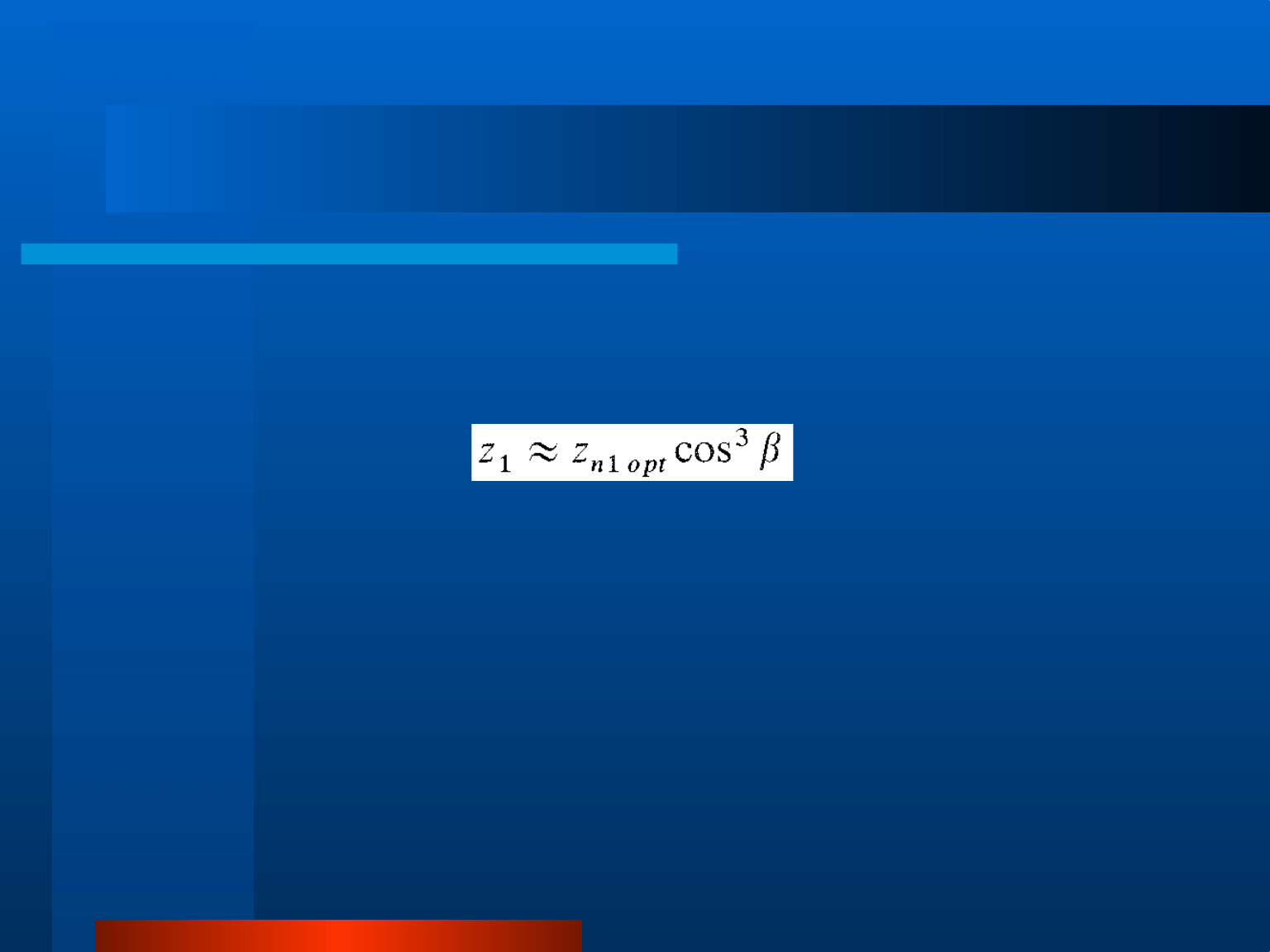
Dobór liczby zębów zębnika

Dobór liczby zębów zębnika

z

z

1

1

i koła

i koła

z

z

2

2

Wyznaczone z rysunku wartości należy traktować

jako orientacyjne. Rzeczywista liczba zębów może być

wyznaczoną za pomocą przybliżonego wzoru

Liczba zębów koła z

2

wynika w szczególności z

obliczonej liczby zębów zębnika z

1

oraz obranego

przełożenia

u

1

rozpatrywanego

stopnia.

Dla

zwiększenia wytrzymałości zęba na naciski korzystnie

jest tak dobrać liczbę zębów z

2

aby była bliska

iloczynowi z

1

u

1

i była przy tym liczbą pierwszą

względem z

1

tj. aby liczby z

1

oraz z

2

nie miały

wspólnych podzielników. W ten sposób ustala się

ostatecznie wartość przełożenia danego stopnia u =

z

2

/ z

1

.

Dobór liczby zębów koła

Dobór liczby zębów koła

z

z

2

2

W przekładniach wykonanych w najniższych

klasach dokładności, np. w przypadku zębów nie

obrabianych

mechanicznie,

lepiej

jest

tak

dobierać liczby zębów, aby miały jak najwięcej

wspólnych podzielników, tj. aby przełożenie u

(jeżeli to tylko możliwe) było liczbą całkowitą.

Wtedy bowiem często następuje współpraca tych

samych zębów, co ułatwia ich dotarcie się

i powoduje

znaczne

zmniejszenie

błędów

kinematycznych. Natomiast w przekładniach

precyzyjnie wykonanych korzystniej jest, gdy

ewentualne nierówności powierzchni spotykają się

ze sobą jak najrzadziej, co przedłuża ich czas

pracy.

Dobór przesunięcia zarysów zazębienia

Dobór przesunięcia zarysów zazębienia

W przypadku przekładni bez przesunięć upraszczają się

znacznie obliczenia geometryczne i wytrzymałościowe,

stąd konstruktorzy chętnie stosują tego rodzaju

zazębienie. Podkreśla się często zaletę polegającą na

możliwości kojarzenia kół o jednakowych modułach w

dowolne pary, bez względu na liczbę zębów itp.

Natomiast

pomija

się

zalety

zazębienia

z

przesunięciem, wykazującego wyższą wytrzymałość przy

tych samych gabarytach i szereg innych cennych

właściwości.
Konstruktorzy najczęściej ograniczają zastosowanie

przesunięcia tylko do przypadku, gdy ze względu na

małą liczbę zębów w kole zachodzi obawa ich

podcinania oraz w przypadku zębów prostych, gdy

zależy na uzyskaniu założonej odległości osi, różnej od

odległości podziałowej.

Przekładnie o równej sumie przesuni

Przekładnie o równej sumie przesuni

ęć zarysów

ęć zarysów

zazębienia

zazębienia

Charakterystyczną

cechą

tych

przekładni

jest

zachowanie zależności x

1

= -x

2

. Odległość osi jest taka

sama jak w przypadku przekładni bez przesunięć, a

średnice toczne kół pokrywają się ze średnicami

podziałowymi, kąt zarysu na średnicy tocznej nie ulega

więc

zmianie.

Istnieje

możliwość

znacznego

zwiększenia wartości współczynnika X

z1

kosztem

nieznacznego

zmniejszenia

współczynnika

X

z2

.

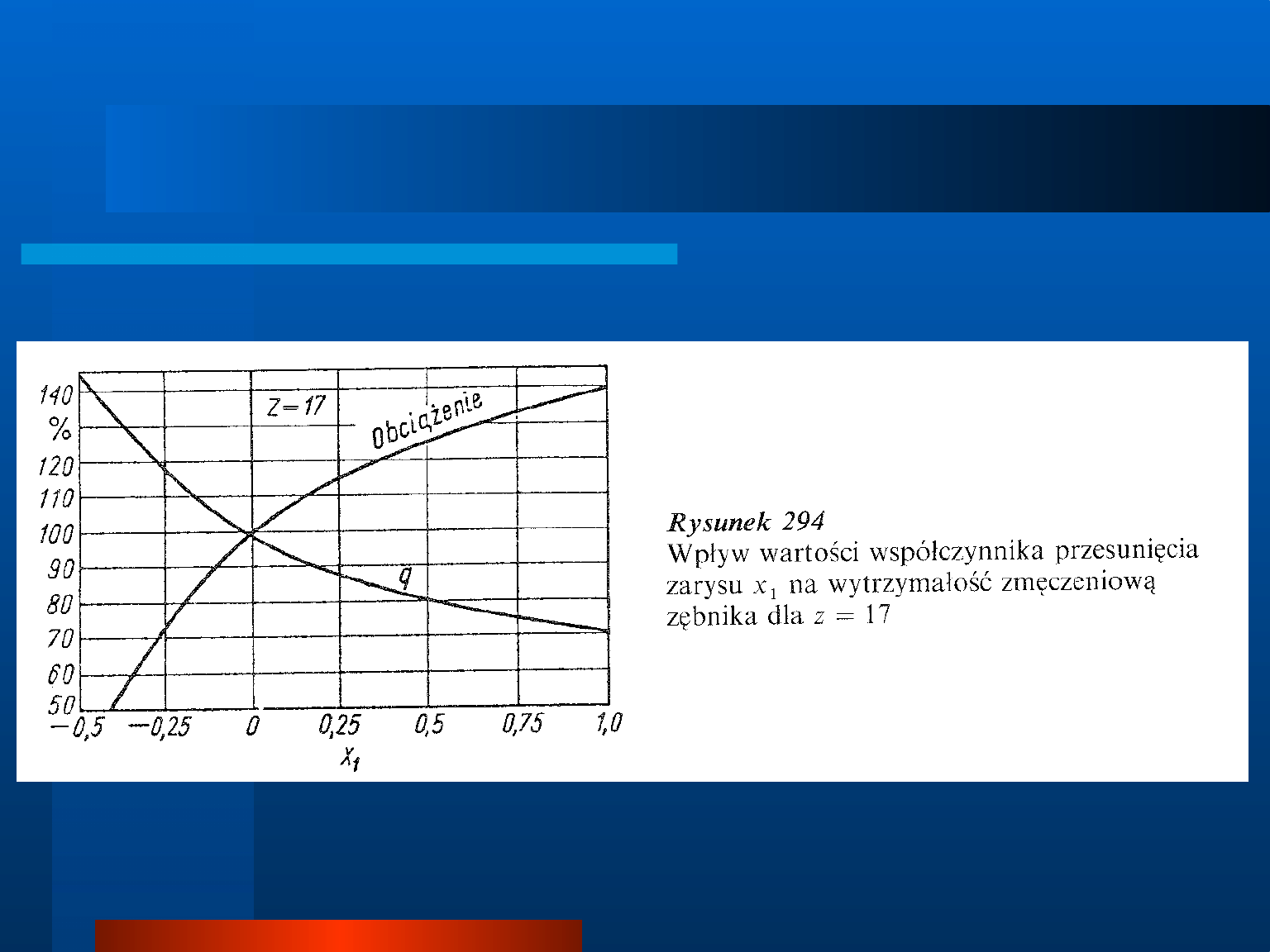
Zastosowanie

w przypadku

zębnika

dodatniego

przesunięcia x

1

zmniejsza wartość współczynnika q,

proporcjonalnego do naprężeń u podstawy zęba,

natomiast przy dużej liczbie zębów z

2

wprowadzenie

wartości ujemnej x

2

= -x

1

nie wywołuje znacznych

zmian wartości współczynnika q, który i tak jest dla

koła mniejszy niż dla zębnika.

Przekładnie o równej sumie przesuni

Przekładnie o równej sumie przesuni

ęć zarysów

ęć zarysów

zazębienia

zazębienia

Przekładnie o

Przekładnie o

dodatniej lub ujemnej sumie

dodatniej lub ujemnej sumie

przesuni

przesuni

ęć zarysów zazębienia

ęć zarysów zazębienia

Przypadek ten charakteryzujący się tym, że x

1

+x

2

 0 pozwala nie tylko na uzyskanie dowolnej

odległości

osi,

mimo

stosowania

znormalizowanych modułów, ale także daje
możność niezależnego wzmocnienia zarówno
zębów zębnika, jak też i koła.
Konstruktorzy nie stosują wartości skrajnych
przesunięć, lecz tylko takie, które w sposób
istotny wpłyną na poprawę pracy przekładni
niemal pod każdym względem. Rezygnuje się
więc z jednocelowej optymalizacji, na rzecz
optymalizacji wielocelowej.

Przekładnie o

Przekładnie o

dodatniej lub ujemnej sumie

dodatniej lub ujemnej sumie

przesuni

przesuni

ęć zarysów zazębienia

ęć zarysów zazębienia

Polega ona na tym, że dobiera się takie wartości

współczynników przesunięcia zarysu, aby: 
a) znaleźć się wewnątrz pola dozwolonych rozwiązań,

określonych za pomocą wykresów konturowych,

możliwie daleko od brzegów wykresu,
b) nie wykraczając poza wykres uzyskać jednocześnie

znaczną poprawę wszystkich wskaźników.
W przypadku:
a) stosuje się między innymi przesunięcie o stałej

wartości współczynników x

1

=x

2

= 0,5 lub x

1

+x

2

= 0,6,

b) korzysta się z wykresów ułatwiających wielocelową

optymalizację zazębienia.

Przekładnie o

Przekładnie o

dodatniej lub ujemnej sumie

dodatniej lub ujemnej sumie

przesuni

przesuni

ęć zarysów zazębienia

ęć zarysów zazębienia

Dobór lepkości oleju

Dobór lepkości oleju

Lepkość oleju jest uzależniona głównie od

prędkości

obwodowej,

która

zostaje

określona dopiero po wstępnym obliczeniu

średnicy. Zwykle do obliczeń przyjmuje się

lepkość

w

temperaturze

50°,

w wyjątkowych przypadkach w rzeczywistej

temperaturze pracy.

Dobór klasy dokładności wykonania kół

Dobór klasy dokładności wykonania kół

Norma PN- 79/M-88521.1 określa dla klas

dokładności 3 12 dopuszczalne odchyłki:
- dokładności kinematycznej,
- płynności pracy,
- przylegania zębów.
Zadaniem konstruktora jest na podstawie

analizy warunków pracy przekładni wybrać

odpowiednią klasę dokładności wykonania,

tym samym ustalić zgodnie z normą

dopuszczalne odchyłki.

Dobór klasy dokładności wykonania kół

Dobór klasy dokładności wykonania kół

Norma dopuszcza przyjmowanie różnych klas

dokładności kinematycznej, płynności pracy i

przylegania zębów z następującymi ograniczeniami:
- klasa płynności pracy może być wyższa najwyżej o

dwie klasy od klasy dokładności kinematycznej,
- klasa płynności pracy może być niższa o jedną

klasę od klasy dokładności kinematycznej,
- klasa przylegania zębów może być niższa o jedną

klasę od klasy płynności pracy.
Symbol

oznaczenia

dokładności

wykonania

przekładni powinien zawierać klasę dokładności

kinematycznej, płynności pracy, przylegania zębów

oraz rodzaj pasowania współpracujących kół w

przekładni.

Wstępne obliczenie wymiarów przekładni

Wstępne obliczenie wymiarów przekładni

W I etapie oblicza się wstępnie wymiary kół na

poszczególnych stopniach, a w szczególności

ich średnice i szerokości, a tym samym

odległości osi kół.
W II etapie przeprowadza się częściowe

obliczenia geometryczne w celu spełnienia

podstawowych zależności dotyczących liczby

zębów, modułów, odległości osi, współczynników

przesunięcia zarysu. Na ogół obliczenia te

ogranicza się do zakresu wymaganego w

obliczeniach wytrzymałościowych.

Wstępne obliczenie wymiarów przekładni

Wstępne obliczenie wymiarów przekładni

W

III

etapie

przeprowadza

się

obliczenia

wytrzymałościowe, a więc sprawdza się współczynniki

bezpieczeństwa na złamanie, naciski oraz zatarcie. Na

podstawie uzyskanych wyników wprowadza się zmiany w

założeniach geometrycznych lub materiałowych, a także

ostatecznie ustala klasy dokładności wykonania. Zwykle

drugie przybliżenie, oparte na schematach II i III

etapu, daje zadowalające wyniki, tj. otrzymuje się koła o

takich parametrach, które nie tylko spełniają warunki

geometryczne i wytrzymałościowe, ale także warunki

konstrukcyjne, w tym także wymogi normalizacji itd.
W IV etapie przeprowadza się ostateczne obliczenia

geometryczne, potrzebne do celów wykonawczych oraz

w uzasadnionych przypadkach warunki nieinterferencji

itd.

Wstępne obliczenie wymiarów przekładni

Wstępne obliczenie wymiarów przekładni

Przełożenie rozpatrywanego stopnia jest

określane jako

Obliczenie średnicy zębnika d

1

Obliczenie odległości osi kół a

Wstępne obliczenie wymiarów przekładni

Wstępne obliczenie wymiarów przekładni

Obliczenie szerokości koła b

Obliczenie modułu w przekroju normalnym m

n

Do dalszych obliczeń wprowadza się wartość

znormalizowaną.

Wywoła

to

konieczność

wprowadzenia drobnych zmian w przyjętych

parametrach,

których

wartości

ustalone

zostaną w II etapie obliczeń dotyczących

geometrii zazębienia.

Sprawdzenie warunków geometrycznych

Sprawdzenie warunków geometrycznych

i

i

 

 

wytrzymałościowych

wytrzymałościowych

W przypadku zazębienia bez przesunięcia obliczenia

drugiego etapu można ograniczyć do spełnienia

zależności

Ostatecznym celem obliczeń jest określenie wartości

współczynników bezpieczeństwa na złamanie i

naciski. Po uzyskaniu zadowalających ich wartości

można przystąpić do ostatniego etapu - obliczeń

geometrycznych. Wielkości geometryczne stanowiące

podstawę

ustawiania

obrabiarki

lub

kontroli

dokładności wykonania powinny być obliczane

z dokładnością do 1 m.

Modyfikacja zarysu zęba

Modyfikacja zarysu zęba

W warunkach pracy pod obciążeniem ząb zmienia

swoje kształty geometryczne, co wywołuje między

innymi

siły

dynamiczne.

Przez

odpowiednią

modyfikację zarysu zęba można uzyskać takie kształty,

które dopiero w warunkach pracy pod obciążeniem

zapewnią optymalne parametry dynamiczne.
W przekładniach szybkobieżnych występuje znaczna

różnica między temperaturą zębnika i koła. Stąd

zębnik jako cieplejszy wykazuje w stosunku do koła

powiększony promień okręgu zasadniczego, co

prowadzi do znacznych sił dynamicznych.
W przypadku większych różnic temperatur zmiany są

tak duże, że wymagają wprowadzenia odpowiednich

poprawek.

Modyfikacja zarysu zęba

Modyfikacja zarysu zęba

Zębnik wykonuje się przy nieco większym kącie

zarysu niż koło, tak aby uzyskać podczas pomiarów

kontrolnych

zmniejszenie

promienia

okręgu

zasadniczego, a tym samym zmniejszenie podziałki

zasadniczej. Pod wpływem temperatury promień

okręgu zasadniczego i podziałka uzyskują pożądaną

wartość. Różnica temperatur zębnika i koła zależy od

prędkości obwodowej, a także od przełożenia, im

większa jest prędkość oraz im większe jest

przełożenie, tym większa jest różnica temperatur i

tym większe zmiany podziałki. Ponieważ dokładne

ustalenie temperatury jest trudne, to do obliczeń

przyjmuje się zwykle zawyżoną wartość, zapewniającą

raczej pewien luz, niż przedwczesne krawędziowe

uderzenie.

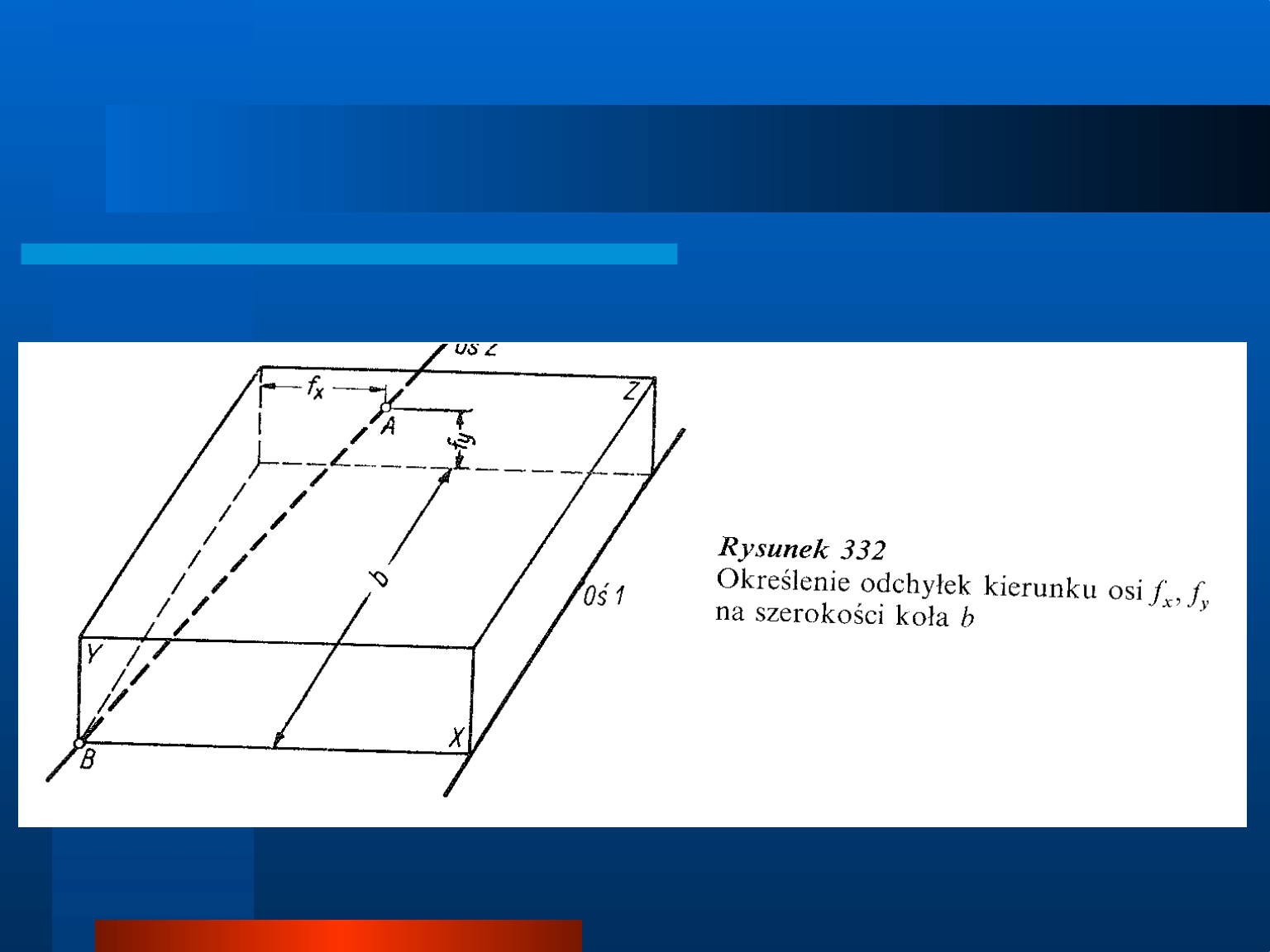
Modyfikacja linii zęba

Modyfikacja linii zęba

Odchyłki równoległości osi f

x

, f

y

, a także

odchyłka kierunku linii zęba są przyczyną

nierównomiernego rozkładu obciążenia na

szerokości koła. Szczególnie niekorzystny jest

liniowy rozkład tych odchyłek, dający wysokie

wartości

współczynnika

K

r

.

Rozkład

taki

utrzymuje się przez długi czas w przypadku

zębów utwardzanych, kiedy zużycie jest małe w

porównaniu

z wielkością

występujących

odchyłek. Dlatego często w praktyce nadaje się

łukowy

kształt

linii

zęba,

zapewniający

korzystniejszy rozkład obciążenia.

Modyfikacja linii zęba

Modyfikacja linii zęba

Modyfikacja linii zęba

Modyfikacja linii zęba

W kołach dokładnie wykonanych współczynnik K

r

jest bliski jedności, ale w przypadku znacznych

wartości współczynnika b/d

1

pojawia się silny wpływ

odkształceń. W wielu przypadkach konstrukcyjnych

dąży się do dużych wartości stosunku b/d

1

, co

wymaga zastosowania modyfikacji linii zęba w ten

sposób

zaprojektowanej,

aby

dopiero

po

wystąpieniu

obciążenia

i

odkształceń

zęby

przylegały równomiernie na całej szerokości koła.
Podstawą projektowania modyfikacji linii zęba w

przypadku dokładnego wykonania zazębienia jest

znajomość odkształceń giętnych i skrętnych wałka,

szczególnie w miejscu gdzie znajduje się zębnik.

Modyfikacja linii zęba

Modyfikacja linii zęba

W ogólnym przypadku gdy zębnik jest

usytuowany

asymetrycznie

względem

podpór, oraz gdy na wałek działają jeszcze

siły od innych kół, tok obliczeń modyfikacji

jest następujący:
1. Należy wyznaczyć linię ugięcia wału,

zwykle z pominięciem sił promieniowych i

osiowych,

a obliczeniu

wyłącznie

sił

obwodowych działających na wałek i

wywołanych przez nie reakcji.

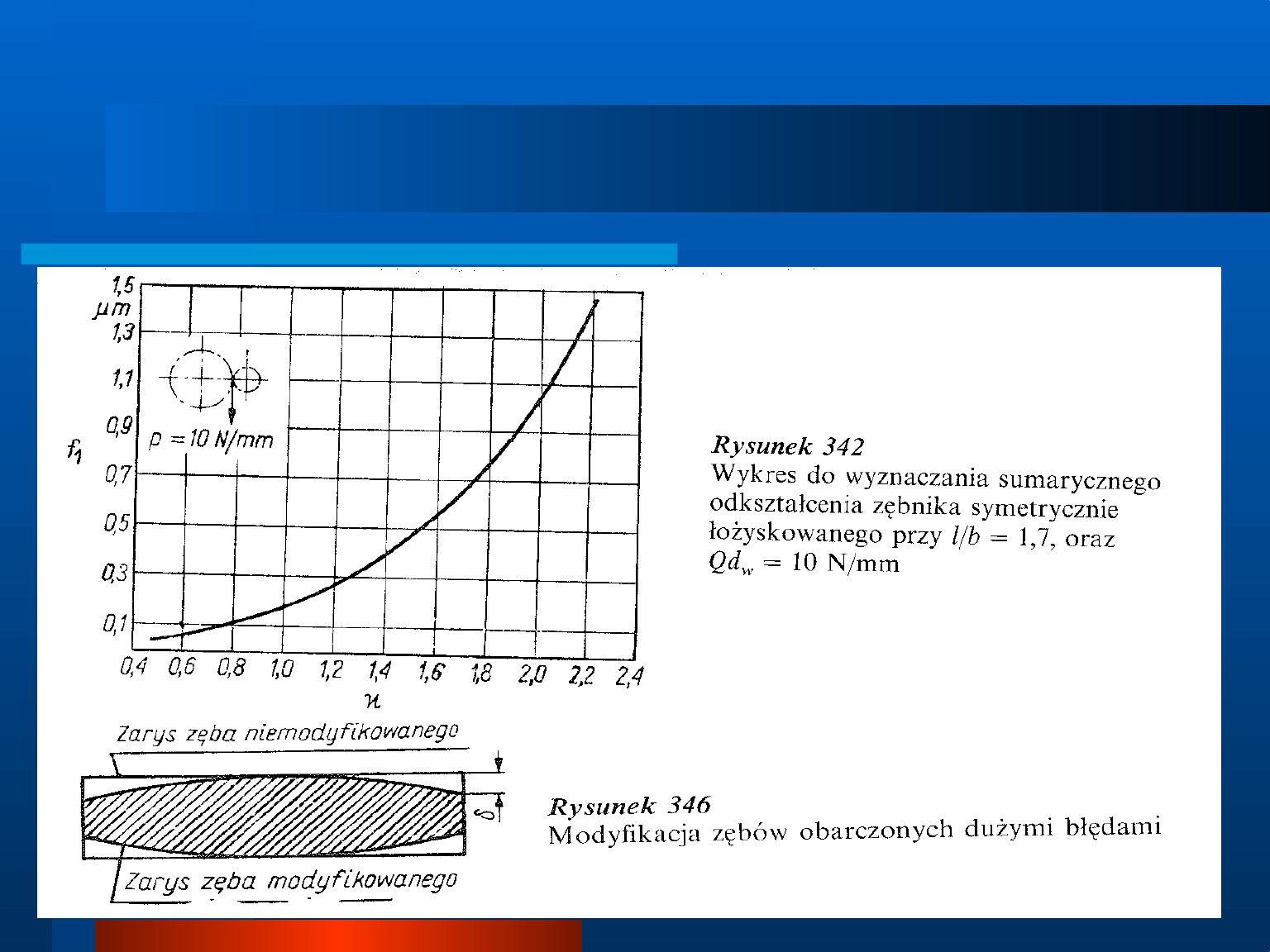
Modyfikacja linii zęba

Modyfikacja linii zęba

2. Wykonuje się wykres momentów gnących metodą

wykreślną

lub

po

analitycznym

wyznaczeniu,

momentów w kilku charakterystycznych punktach

wału; wykres momentów dzieli się na przedziały o

stałej średnicy wałka albo stałej wartości momentu

bezwładności J; wykonuje się wykres momentów

zredukowanych

M/J

i

oblicza

powierzchnię

poszczególnych przedziałów.
3. Wałek o stałym przekroju obciąża się siłami

proporcjonalnymi

do

wielkości

powierzchni

poszczególnych przedziałów, uwzględniając znaki sił

wg znaków pól; wyznacza się reakcje i wykreśla linię

momentów gnących, która w odpowiedniej skali

określa jednocześnie linię ugięcia pierwotnego wałka.

Modyfikacja linii zęba

Modyfikacja linii zęba