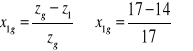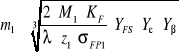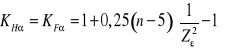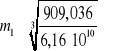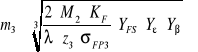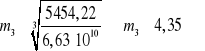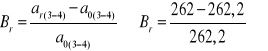Akademia Górniczo-Hutnicza im. Stanisława Staszica w Krakowie

Wydział Inżynierii Mechanicznej i Robotyki

Podstawy Konstrukcji Maszyn 2

Projekt nr 4 - Przekładnia

Wykonał:

Tomasz Siudak

Grupa 5

Temat: Obliczyć parametry kół zębatych przekładni zębatej otwartej dla danych wg podanego schematu przekładni:
,
,
,

,
,

Dane	Obliczenia	Wynik
	1. Założenia projektowe Projektowana przekładnia, jest przekładnią zębatą otwartą - liczba cykli nie jest duża - przekładnia jest napędzana siłą rąk ludzkich w związku z czym, prędkości obrotowe są niskie stosuje koła zębate o zębach prostych - produkcja przekładni jednostkowa Wał z kołami zębatymi będzie ułożyskowany symetrycznie, w związku z czym względną szerokość przekładni w odniesieniu do średnicy podziałowej zaleca się przyjmować w granicach Zbyt dużo niewiadomych we wstępnej fazie obliczeń zmusza nas do przyjęcia wartości przybliżonych, empirycznie sprawdzonych, a mianowicie: - względną długość zęba przyjmuje się zwykle w granicach w przekładniach ogólnego zastosowania, chociaż w zastosowaniach specjalnych zdarzają się wyjątki. Przyjmuję: 2. Mechanika obciążeń 2.1 Obliczanie momentów obrotowych na wałach „1” i „3” 2.2 Całkowite przełożenie przekładni gdzie: - całkowite przełożenie przekładni - sprawność przekładni (dla przekładni zębatych przyjmuje się ) 2.3 Przełożenia poszczególne przyjmuję 2.4 Dobór ilości zębów dla kół zębatych pierwszego stopnia przełożenia Przyjmuję wobec, czego 2.5 Dobór ilości zębów dla kół zębatych drugiego stopnia przełożenia Przyjmuje Przyjmuję 2.4 Graniczna liczba zębów Teoretyczna graniczna liczba zębów - najmniejsza liczba zębów, przy której nie wystąpi jeszcze podczas nacinania koła zębatego, podcięcie zęba oblicza się z zależności: Dla Przy występuje podcięcie zęba u podstawy. Ponieważ w praktyce dopuszcza się nieznaczne podcięcie niepowodujące jeszcze ujemnych skutków, wprowadza się tzw. praktyczną graniczną liczbę zębów określoną zależnością: , dla 2.5 Współczynnik przesunięcia zarysu Pomimo tego że liczba zębów jest jeszcze dopuszczalna to jednak zakładam że nawet minimalne podcięcie zarysu jest niedopuszczalne, w związku z powyższym należy zastosować przesunięcie zarysu zęba dla pierwszego koła zębatego. Współczynnik granicznego przesunięcia zarysu jest równy: - powyżej tej wielkości następuje niedopuszczalne zaostrzenie zębów. Przyjmuję 3. Dobór materiałów 3.1 Materiał zębnika Na materiał zębnika dobieram stal C55 wg PN-EN 10083-2+11:1999 w stanie ulepszonym cieplnie (QT) Twardość: 3.2 Materiał koła zębatego Na koło zębate dobieram stal C45 wg PN-EN 10083-2+11:1999 w stanie ulepszonym cieplnie (QT) Twardość 4. Wstępne obliczenia modułu Dominujące niebezpieczeństwo zniszczenia przekładni pochodzi od złamania zębów, w związku z powyższym należy zastosować odpowiednio duży moduł, aby zmniejszyć naprężenia zginające u podstawy zęba. Znam moment skręcający na kole czynnym, więc przyjmuję: oraz Zależność na moduł przybiera postać: , gdzie: - moment obrotowy na wale „1” - rzeczywiste naprężenia od zginania - dopuszczalne naprężenia na zginanie nie powodujące odkształcenia zęba - nominalna siła obwodowa - zginająca, działająca na okręgu podziałowym w przekroju czołowym - szerokość wieńca koła - moduł zęba - względna długość zęba - liczba zębów 4.1 Współczynniki eksploatacyjne - współczynnik eksploatacyjny - ujmuje on wpływ różnych oddziaływań w warunkach eksploatacji na rzeczywiste naprężenia w podstawie zębów. - współczynnik zastosowania. Uwzględnia nadwyżki dynamiczne zewnętrzne (przeciążenia układu roboczego, charakterystyka silnika napędowego, rozkład mas za i przed przekładnią oraz sprężystość wałów i sprzęgieł) W obliczeniach wstępnych współczynnik przyjmuję się: . Przyjmuję - współczynnik dynamiczny zależny od wielu czynników, z których prędkość obwodowa kół ma decydujące znaczenie. Ponadto istotny wpływ ma dokładność wykonania przekładni i sztywność zazębienia. W obliczeniach wstępnych można przyjąć empiryczny wzór Merita: , jeśli w dalszych obliczeniach należy przyjąć , ponieważ w temacie zadania nie ma zdefiniowanej wymaganej prędkości wyciągania ciężaru Q toteż przyjmuję, że prędkość obwodowa jest mała i co za tym idzie . - współczynnik rozkładu obciążenia gnącego na długości zęba (szerokości wieńca zębatego) uwzględnia wzrost naprężeń gnących wskutek nierównomiernego przylegania zębów pod obciążeniem. Współczynnik w zależności od układu kół zębatych w przekładni, oraz dla kół „miękkich” w przybliżeniu jest równy: Współczynnik jest około 15-20% mniejszy od i można go oszacować z zależności: Przy czym wykładnik dla zębów prostych, oraz względnej długości zębów równej: jest równy: , zatem - współczynnik rozkładu obciążenia wzdłuż odcinka przyporu na poszczególne pary zębów znajdujących się w danej chwili w przyporze. W określonych granicach stosowania współczynnik jest równy , wstępnie można je wyznaczyć w zależności od klasy dokładności wykonania kół: , gdzie - klasa dokładności 5…9. - współczynnik stopnia pokrycia Dla kół wykonanych w klasie 6…8, o zębach prostych w przybliżeniu przyjmuje się Przyjmuję 4.2 Współczynniki konstrukcyjne Ujmują one wpływ niektórych podstawowych parametrów konstrukcyjnych. - współczynnik kształtu zęba - współczynnik uwzględniający stereomechaniczny układ przyłożenia siły zginającej do wierzchołka zęba. - współczynnik uwzględniający działanie karbu oraz wpływ naprężeń tnących i ściskających w podstawie zęba. Dla zębów o kącie przyporu i względnego promienia zaokrąglenia narzędzia przybliżony wzór na współczynnik kształtu ma postać: Po podstawieniu danych otrzymuję: - współczynnik liczby przyporu, uwzględniający to, że w strefie jednoparowego przyporu pełne obciążenie nie działa na wierzchołku zęba, lecz na mniejszym ramieniu, dlatego współczynnik ten zwykle przyjmuje wartość mniejszą od jedności: W obliczeniach wstępnych można przyjąć z korzyścią dla obliczeń Przyjmuję - współczynnik pochylenia linii zęba, uwzględniający korzystniejszy rozkład naprężeń u podstawy zęba w rzeczywistości niż w zastępczym modelu obliczeniowym. W obliczeniach wstępnych można przyjąć 4.3 Obliczenia modułu Dobieram najbliższy znormalizowany moduł 5. Obliczenia odległości i współczynników korekcji Teoretyczna odległość osi kół jest równa Przyjmuję znormalizowaną rzeczywistą nominalną odległość osi kół: Różnicę między nominalną i rzeczywistą odległością osi usuwam za pomocą korekcji P Obliczam wartość współczynnika Obliczam pozorną odległość osi Ponieważ istnieje konieczność zmniejszenie nadmiernego luzu obwodowego, sprawdzam wartość zbliżenia osi K Zbliżenie osi o wielkość K powoduje zmniejszenie luzu wierzchołkowego, który wyniesie: Wartość otrzymanego luzu wierzchołkowego będzie większa od wartości minimalnej , a więc można nie ścinać głów zębów - wynika to również z zależności: . Obliczam sumę przesunięć zarysu w obu kołach W wyniku dokonania korekcji otrzymuje się zmienioną odległość osi a co za tym idzie zmianie ulega również toczny kąt przyporu 6. Wymiary zębów i kół: 6.1 Wymiary zębnika Wartość przesunięcia zarysu Średnica podziałowa Średnica wierzchołków Średnica podstaw Wysokość głowy zęba Wysokość stopy zęba Luz wierzchołkowy 6.2 Wymiary koła Wartość przesunięcia zarysu Średnica podziałowa Średnica wierzchołków Średnica podstaw Wysokość głowy zęba Wysokość stopy zęba Luz wierzchołkowy Szerokość wieńca koła Szerokość wieńca zębnika 7. Obliczenia konstrukcyjne kół 3 i 4 Materiał jak dla koła nr 2 Dobieram znormalizowany moduł: 7.1 Obliczenia odległości i współczynników korekcji Teoretyczna odległość osi kół jest równa Ponieważ w temacie zadania nie ma wymaganego przyjmowania znormalizowanych odległości osi przyjmuję rzeczywistą odległość osi kół: Różnicę między nominalną i rzeczywistą odległością osi usuwam za pomocą korekcji P Obliczam wartość współczynnika Obliczam pozorną odległość osi Ponieważ odchyłki wymiarów są bardzo małe nie spowodują znaczącego zmniejszenia luzu wierzchołkowego Luzu wierzchołkowy wyniesie: Obliczam sumę przesunięć zarysu w obu kołach Przyjmuję: W wyniku dokonania korekcji otrzymuje się zmienioną odległość osi a co za tym idzie zmianie ulega również toczny kąt przyporu 7.2 Wymiary zębów i kół: 7.2.1 Wymiary koła Średnica podziałowa Średnica wierzchołków Średnica podstaw Wysokość głowy zęba Wysokość stopy zęba Luz wierzchołkowy Szerokość wieńca koła 7.2.2 Wymiary koła Wartość przesunięcia zarysu Średnica podziałowa Średnica wierzchołków Średnica podstaw Wysokość głowy zęba Wysokość stopy zęba Luz wierzchołkowy Szerokość wieńca koła

12

---