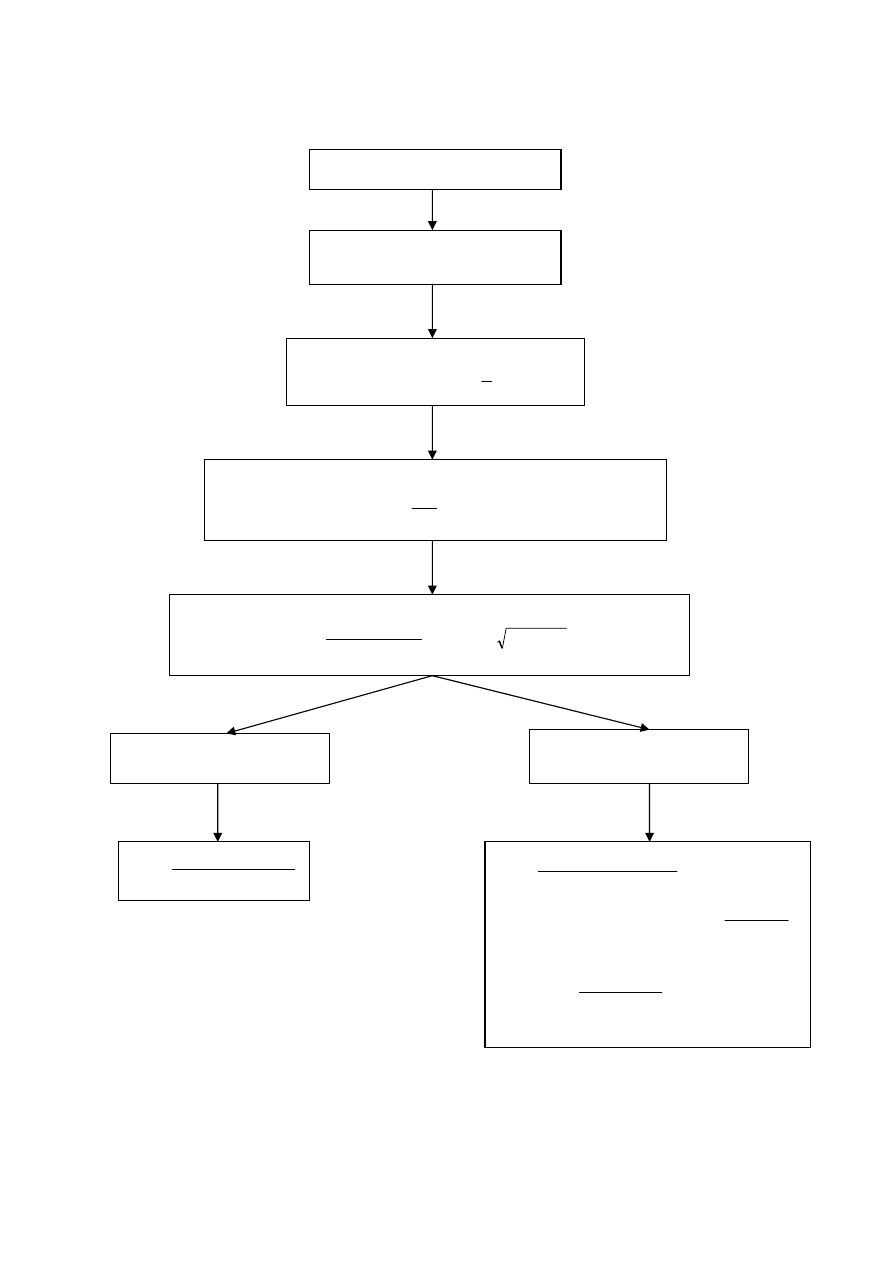
Algorytm dla zginania przekroju prostokątnego 

 
 
 

Zakładamy średnice zbrojenia 

głównego i strzemion:    Φ    Φ

s

 

Wysokość użyteczna przekroju:

  

2

φ

φ

−

−

−

=

s

c

h

d

 

Minimalne pole zbrojenia: 















=

d

b

d

b

f

f

A

yk

ctm

s

*

*

0013

.

0

*

*

*

26

.

0

max

min

,

 

Sprawdzenie czy przekrój ma być pojedynczo czy podwójnie zbrojony: 

2

*

*

*

d

b

f

M

S

cd

sd

c

α

=

; 

c

eff

S

*

2

1

1

−

−

=

ξ

 

Przekrój pojedynczo zbrojony 

lim

,

eff

eff

ξ

ξ

≤

 

yd

eff

cd

I

s

f

d

b

f

A

*

*

*

*

lim

,

1

ξ

α

=

 













−

=

2

*

*

*

*

*

*

lim

,

lim

,

d

d

d

b

f

M

eff

eff

cd

I

sd

ξ

ξ

α

I

sd

sd

sd

M

M

M

−

=

∆

 

(

)

2

2

1

*

a

d

f

M

A

A

yd

sd

s

II

s

−

∆

=

=

 

II

s

I

s

s

A

A

A

1

1

1

+

=

 

yd

eff

cd

s

f

d

b

f

A

*

*

*

*

1

ξ

α

=

 

Przekrój podwójnie zbrojony 

lim

,

eff

eff

ξ

ξ

>

 

Dane: b h M

sd

 f

cd

 f

yd

 ξ

eff,Lim

 α f

ctm

 f

yk