2014-05-20
1
Bezpieczeństwo i ochrona
danych
Podpisy elektroniczne
Grzegorz Kołaczek, Ph.D., Eng.
Agenda
1. Podpis elektroniczny - cele
2. Klasyczne metody uwierzytelnienia
użytkownika
3. Mechanizmy tworzenia podpisu elektronicznego
Podpis elektroniczny
Ustawa o podpisie elektronicznym z 18 września 2001 r.
„Bezpieczny podpis, to podpis, który:
- Jest przyporządkowany wyłącznie do osoby
składającej ten podpis,
- Jest sporządzony za pomocą podlegających wyłącznej
kontroli osoby składającej podpis elektroniczny
bezpiecznych urządzeń służących do składania podpisu
elektronicznego i danych służących do składania
podpisu elektronicznego,
- Jest powiązany z danymi, do których został
dołączony, w taki sposób, że jakakolwiek późniejsza
zmiana tych danych jest rozpoznawalna.”
Funkcje podpisu cyfrowego
Podpis tradycyjny
Podpis cyfrowy
Cechy wspólne
1. przypisany jednej osobie
2.
niemożliwy do podrobienia
3.
uniemożliwiający wyparcie się go przez autora
4.
łatwy do weryfikacji przez osobę niezależną
5.
łatwy do wygenerowania
Różnice
6.
związany nierozłącznie z dokumentem 6. może być składowany i transmitowany
niezależnie od dokumentu
7.
taki sam dla wszystkich dokumentów
7. będący funkcją dokumentu
8. stawiany na ostatniej stronie
dokumentu
8. obejmuje cały dokument
Funkcje podpisu cyfrowego
• Uwierzytelnienie
• Niezaprzeczalność
• Integralność
• Identyfikacja
Dystrybucja klucza
• Znajomość klucza publicznego -> pewność
autorstwa
• Certyfikat to klucz publiczny podpisany
przez osobę godną zaufania
2014-05-20
2
STANDARD X509
• Organ certyfikujący – Certification
Authority (CA)
STANDARD X509
• Struktura certyfikatu
– Certyfikat zgodny ze standardem X.509 wersji
3 składa się, najczęściej, z:
• Tematu (subject) – Jednoznacznie
identyfikującego właściciela (np. użytkownika,
komputer, urządzenie sieciowe…) klucza
prywatnego powiązanego z danym certyfikatem,
• Dodatkowych informacji o właścicielu (np. adres,
itp.),
• Informacji o podpisującym CA,
STANDARD X509
• Struktura certyfikatu
– Certyfikat zgodny ze standardem X.509 wersji
3 składa się, najczęściej, z:
• Klucza publicznego,
• Nazw algorytmów kryptograficznych używanych
do stworzenia danego certyfikatu (np. do
wygenerowania podpisu CA),
• Listy rozszerzeń (extensions) zawartych w
certyfikacie,
• Informacji o sposobie uzyskiwania informacji o
ewentualnym odwołaniu certyfikatu (np. adres
www z którego można pobrać listę CRL).
Modele zaufania
Model ze ścisłą hierarchią centrów certyfikacji
Modele zaufania
Model zaufania skoncentrowany na użytkowniku
Schematy podpisu elektronicznego
• Z algorytmem symetrycznym i arbitrem
• Tradycyjne czyli z załącznikiem (ang. appendix)
– RSA, ElGamal, DSA, Shnorr,
• Jednorazowe (ang. one-time)
– Rabin, Merkle,
• Ślepe (ang. blind )
– Chaum,
• Niezaprzeczalne (ang. undeniable)
– Chaum-van Antwerpen,
• Grupowe (ang. group) i pierscieniowe (ang. ring )
– Rivest-Shamir-Tauman,
2014-05-20
3
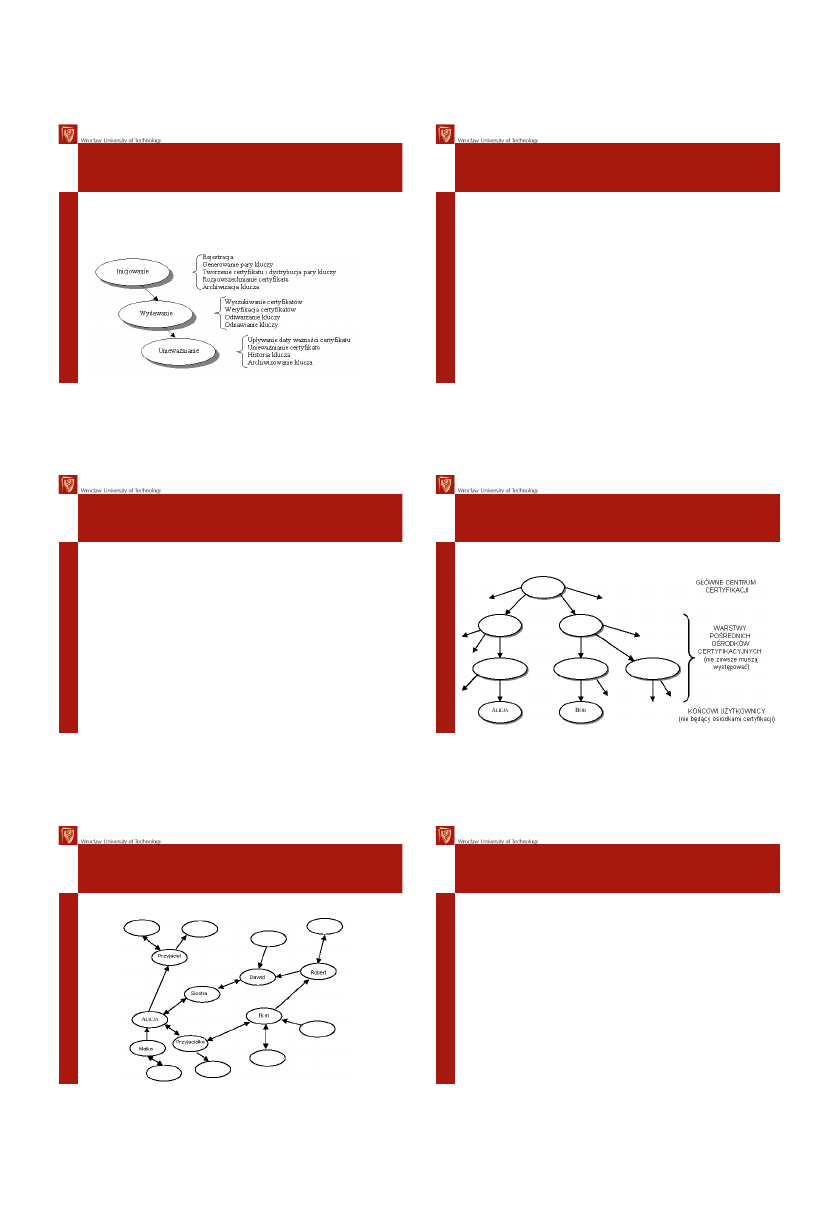
Podpis z symetrycznym algorytmem
kryptograficznym
1.
„A” szyfruje wiadomość dla „B”
kluczem KA (do arbitra)
2.
Arbiter deszyfruje wiadomość
KA i stwierdza, że pochodzi ona
od „A”
3.
Arbiter szyfruje wiadomość KB i
wysyła do „B”
4.
„B” odszyfrowuje KB i
porównuje z informacją od „A”
Informacje te same - wiadomość
została wysłana przez „A”
Podpis z załącznikiem
• Podpis z załącznikiem wymaga aby w
czasie weryfikacji podpisu użyta została
wiadomość pod którą podpis został złożony
Podpis z asymetrycznym algorytmem
kryptograficznym (RSA)
• Protokół:
– Alicja szyfruje dokument przy użyciu własnego klucza
prywatnego, tym samym go podpisuje
– Alicja przesyła podpisany dokument Bobowi
– W celu sprawdzenia podpisu Bob deszyfruje dokument
za pomocą klucza publicznego Alicji
Podpis z asymetrycznym algorytmem
kryptograficznym (RSA)
Protokół ten spełnia następujące wymagania:
• Podpis jest autentyczny, kiedy odbiorca weryfikuje wiadomość za
pomocą klucza publicznego nadawcy wie, że to on ją podpisał.
• Podpis jest niepodrabialny, gdyż jedynie nadawca zna odpowiedni
klucz prywatny.
• Podpis nie jest ponownie używany; podpis funkcjonuje razem z
dokumentem i nie może być przeniesiony do dowolnego innego
dokumentu.
• Podpisany dokument jest niezmienialny; jeśli wystąpi najmniejsza
modyfikacja dokumentu, to nie może on być nadal sprawdzany przy
użyciu klucza publicznego nadawcy.
• Nie można wyprzeć się podpisu.
Odbiorca nie potrzebuje pomocy ze strony nadawcy, aby sprawdzić
jego podpis.
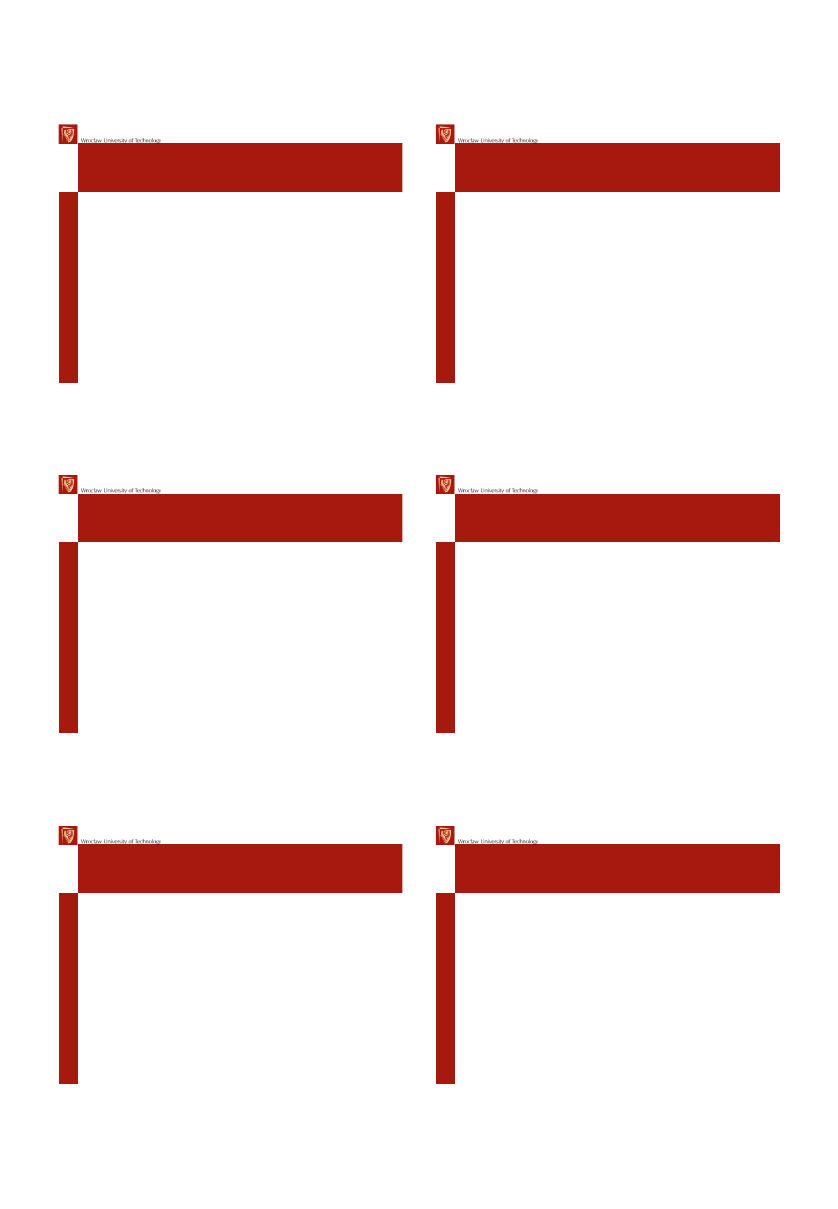
Tworzenie podpisu cyfrowego
• Jednokierunkowa funkcja skrótu
– Bardzo łatwo obliczyć skrót na podstawie
ciągu wejściowego,
– Bardzo trudno wygenerować ciąg wejściowy
znając funkcję skrótu
– MD-5, SHA, MD-2 128-160 bitów
Tworzenie podpisu cyfrowego
2014-05-20
4
Weryfikacja podpisu cyfrowego
Podpis Shnorra
• Podmiot A podpisuje binarną wiadomość m o
dowolnej długości.
• Dowolny podmiot B może zweryfikować podpis
podmiotu A, stosując jego klucz publiczny
• Jego bezpieczeństwo opiera się na trudności w
rozwiązaniu logarytmu dyskretnego.
• Algorytm jest wydajny i tworzy krótkie podpisy.
Podpis Shnorra
• Klucz publiczny
– (p,q,g,y)
– q – liczba pierwsza (≥ 2^160)
– p – liczba pierwsza taka, że q dzieli (p-1) (≈ 2^1024)
– g - generator
– y=g
a
mod p
• Klucz prywatny
– losowa liczba a, taka że 1
a
p-2
Podpis Shnorra
• Podpisywanie (podmiot A)
– wybierz losowe (tajne) k,
• 1
k
q -1,
– oblicz:
• r = g
k
mod p
• e = h(m||r ),
• s = (ae + k) mod q,
– podpisem pod m jest para (e,s).
Podpis Shnorra
• Weryfikacja
– sprawdź czy 0 < s < q,
• jeśli nie, to odrzuć podpis,
– oblicz v
1
= g
s
y
-e
mod p,
– oblicz v
2
= h(m|| v
1
),
– sprawdź czy v
2
= e
– jeśli tak, to podpis jest poprawny.
Podpis Nyber-Rueppel
z odtwarzaniem wiadomości
• Podmiot A podpisuje binarną wiadomość
m
M.
• Dowolny podmiot B może zweryfikować
podpis podmiotu A i odtworzyć z podpisu
wiadomość m
2014-05-20
5
Idea podpisów jednorazowych
• Mechanizm podpisów, który w sposób bezpieczny
może być użyty dokładnie raz
• Każde użycie schematu wymaga generowania
nowej pary informacji prywatna-publiczna,
• Większość schematów może być bardzo
efektywnie zaimplementowana.
Podpisy jednorazowe Rabina
• Przygotowanie
– wybierz bezpieczny schemat szyfrowania
symetrycznego,
– wylosuj 2n kluczy szyfrujących k
1
; k
2
; …; k
2n
,
– oblicz y
i
= E
ki
(i) dla 1
i
2n,
– publicznym kluczem jest (y
1
; y
2
; …; y
2n
),
– kluczem prywatnym (k
1
; k
2
; …; k
2n
)
Podpisy jednorazowe Rabina
• Podpis
– oblicz h(m),
– oblicz s
i
= E
ki
(h(m)) dla 1
i
2n
– podpisem jest (s
1
; s
2
; …; s
2n
).
Podpisy jednorazowe Rabina
• Weryfikacja podpisu
– weź m, (s
1
; s
2
; …; s
2n
) i klucz publiczny (y
1
; y
2
; …; y
2n
).
– oblicz h(m),
– wylosuj n liczb 1
r
j
2n,
– zażądaj od podpisującego kluczy k
rj
dla 1
j
n,
– sprawdź czy y
rj
= E
k(rj)
(r
j
) dla 1
j
n,
• jeśli NIE, to odrzuć podpis,
– sprawdź czy s
rj
= E
k(rj)
(h(m)) dla 1
j
n,
• jeśli TAK, to zaakceptuj podpis.
Podpisy jednorazowe Rabina
• Klucz publiczny jest zobowiązaniem podpisującego co do
wyboru kluczy k
i
,
• podpisywanie
– 2n szyfrogramów wiadomości (h(m))z użyciem różnych kluczy,
• weryfikacja
– losowe sprawdzenie poprawności n szyfrogramów poprzez
ujawnienie n kluczy k
i
,
• Wady:
– rozmiar podpisu,
– weryfikacja podpisu wymaga interakcji podpisującego i
weryfikującego.
Podpisy jednorazowe Merkle
• Przygotowanie
– Aby podpisać n-bitową wiadomość:
• wylosuj t = n +
log
2
n
+ 1
losowych, tajnych l -bitowych liczb k
i
,
• oblicz v
i
=h(k
i
), 1
i
t,
• publicznym kluczem jest (v
1
,v
2
,...v
2n
),
• prywatnym (k
1
,k
2
,...k
2n
)
2014-05-20
6
Podpisy jednorazowe Merkle
• Podpis wiadomości ‚m’ długości ‚n’ bitów
– oblicz w,
gdzie c jest binarną reprezentacja liczebności ‚0’ w
liczbie m;
w=m||c =(a
1
a
2
...a
t
)
– ustal pozycje ‚1’
i
1
<i
2
...<i
u
w liczbie w, a
ij
=1
– Niech s
j
=k
ij
, 1
j
u.
– Podpisem jest (s
1
,...s
u
)
Podpisy jednorazowe Merkle
• Weryfikacja podpisu
– weź m oraz klucz publiczny(v
1
; v
2
; …; v
2n
).
– oblicz c,
– wyszukaj wszystkie bity i
j
liczby w = m||c, takie że
w
ij
= 1,
– sprawdź czy v
ij
= h(k
ij
) dla 1
j
u, jeśli TAK, to
zaakceptuj podpis,
Podpisy jednorazowe Merkle
• Mniejszy rozmiar podpisu – podpisujemy tylko
jedynki w bitowym zapisie h(m),
• Większa efektywność – funkcja skrótu zamiast
szyfrowania,
• Kolejne wykorzystanie protokołu z tymi samymi
parametrami zwiększa prawdopodobieństwo
podrobienia podpisu (ujawnia coraz więcej
sekretów).
Ślepe podpisy
• Protokół realizowany przez dwie strony (A i B), w których
A wysyła do B pewną informację m’, która B podpisuje.
• Na podstawie uzyskanego podpisu A jest w stanie
wygenerować podpis pod wybraną wcześniej
wiadomością m, tym razem już bez udziału B.
– B nie wie co podpisuje – nie zna m,
– B nie potrafi powiązać m’ z podpisem pod m,
– B widząc swój podpis pod m nie potrafi powiedzieć dla kogo ją
wygenerował.
• Potrzebne np.:
– przy elektronicznych wyborach, systemach elektronicznych
płatności
Ślepe podpisy Chauma
• Przygotowanie
– Analogiczne jak w schemacie RSA, przy czym B
posiada swoją parę kluczy
• prywatny (d; n)
• publiczny (e; n).
– Druga strona – A, musi tylko znać klucz
publiczny B.
Ślepe podpisy Chauma
• Podpisywanie
– A losuje 1 < k < n-1, takie, ze NWD(k, n) = 1,
– A oblicza m’ = mk
e
mod n i wysyła do B,
– B podpisuje s’ = (m’)
d
mod n i odsyła s’ do A,
– A oblicza s = s’k
-1
mod n, które jest podpisem
B pod m.
• Weryfikacja
– Analogicznie jak w przypadku RSA
2014-05-20
7
Podpisy niezaprzeczalne
• Podpis, którego użytkownik nie może się wyprzeć
– można pokazać, że podpis został wygenerowany z
użyciem klucza prywatnego użytkownika,
– weryfikacja zawsze przeprowadzana on-line,
– wymagają dodatkowej procedury odrzucenie podpisu,
która jest wykonywana zawsze jeśli weryfikacja
zakończyła się brakiem akceptacji podpisu
– procedura ma za zadanie ustalić, czy oszukuje
podpisujący czy rzeczywiście podpis nie jest jego,
Schemat Chaum-van Antwerpen
• Przygotowanie
– wybierz losową liczbę pierwszą p = 2q + 1
gdzie q jest pierwsze,
– wybierz generator g podgrupy Z
q
,
– wybierz losowa liczbę 1
a < q,
oblicz y = g
a
mod p,
– kluczem publicznym jest (y; g; p),
– prywatnym a.
Schemat Chaum-van Antwerpen
• Podpis
– oblicz s = m
a
mod p,
– podpisem pod m jest s.
• Weryfikacja
– weryfikujący (B) wybiera losowe liczby 1
x
1
; x
2
< q,
– B oblicza z = s
x1
y
x2
mod p i wysyła do A,
– A oblicza w = z
a-1
mod p i odsyła w do B,
– B sprawdza czy m
x1
g
x2
= w,
• jeśli TAK to akceptuje podpis,
• jeśli NIE to wykonuje procedurę odrzucenia podpisu.
Schemat Chaum-van Antwerpen
• Procedura odrzucenia podpisu
–
weryfikujący (B) wybiera losowe liczby 1
x
1
; x
2
< q,
–
B oblicza z = s
x1
y
x2
mod p i wysyła do A,
–
A oblicza w = z
a-1
mod p i odsyła w do B,
–
B sprawdza czy m
x1
g
x2
= w, jeśli TAK to akceptuje podpis i kończy,
– jeśli NIE, to B losuje liczby 1
x
1
’, x
2
’ < q
– B oblicza z’ = s
x1’
y
x2’
mod p i wysyła do A,
– A oblicza w’ = z’
a-1
mod p i odsyła w’ do B,
– B sprawdza czy m
x1’
g
x2’
= w’,
• jeśli TAK to akceptuje podpis i kończy,
• jeśli NIE to sprawdza czy: (wg
-x2
)
x1’
= (w’g
-x2’
)
x1
– jeśli TAK to s jest fałszywe,
– jeśli NIE to A oszukuje.
Podpisy grupowe
• Podpis, który został złożony przez jednego
z użytkowników należących do pewnej
grupy.
• Weryfikujący może jedynie stwierdzić, że
podpis złożył członek grupy, ale nie jest w
stanie powiedzieć który.
Podpisy pierścieniowe
• Przygotowanie
– każdy użytkownik 1
i
t posiada parę kluczy
(P
i
; S
i
)
• asymetryczny algorytm szyfrowania, np: RSA,
– każdy użytkownik zna klucze publiczne pozostałych
użytkowników,
– każdy użytkownik zna klucz K symetrycznego
algorytmu szyfrowania,
• np: AES.
2014-05-20
8
Podpisy pierścieniowe
• Podpis
– użytkownik u oblicza:
• v = h(m)
• losuje wartości y
i
dla 1
i
t i i
u,
– dla wylosowanych y
i
oblicza x
i
= D
Pi
(y
i
),
– oblicza x
u
takie, że
• v
= E(x
1
E(x
2
E(…
x
u
E(…x
t
E(v)))))
– oblicza y
u
= E
Si
(x
u
),
– podpisem pod m jest (v; y
1
; y
2
; ..; y
u
;…; y
t
).
Podpisy pierścieniowe
• Weryfikacja
– weryfikujący (B) oblicza
• x
i
= D
Pi
(y
i
) dla 1
i
t,
– sprawdza czy
• v = E(x
1
E(x
2
E(… x
u
E(…x
t
E(v)))))
Dziękuję za uwagę