ROZTWORY ELEKTROLITÓW

Obecnie przejdziemy do opisu termodynamicznego roztworów elektrolitów i poznania przyczyn, powodujących, że roztwory te nigdy nie można traktować jak roztwory doskonałe (idealne).

Elektrolity to substancje, które w roztworze rozpadają się jony. Należą tu kwasy zasady i sole. Wyróżniamy elektrolity mocne i słabe.

Zauważmy, że w roztworze nieskończenie rozcieńczonym słabe elektrolity są całkowicie zdysocjowane na jony.

Opis termodynamiczny roztworów elektrolitów

Wszystkie roztwory elektrolitów, nawet bardzo rozcieńczone, wykazują odchylenia od doskonałości, są roztworami rzeczywistymi. Przyczyny istnienia tych odchyleń spowodowane są tym, że w roztworze elektrolitu mamy jony - indywidua obdarzone ładunkiem elektrycznym. Istnieją dwie główne przyczyny odchyleń od doskonałości :

• Oddziaływania jonów z cząsteczkami rozpuszczalnika (solwatacja) czyli oddziaływania jon - dipol

• Oddziaływania jonów nawzajem ze sobą (powstawanie atmosfery jonowej) czyli oddziaływania jon - jon

Oba rodzaje oddziaływań mają charakter elektrostatyczny (kulombowski), gdyż są to oddziaływania pomiędzy ładunkami elektrycznymi.

Przypomnijmy sobie jak opisujemy potencjał chemiczny składnika w roztworze rzeczywistym i jak wybieramy stan standardowy. Dla roztworu rzeczywistego potencjał chemiczny składnika rozpuszczonego wyraża się wzorem :

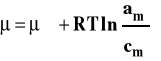
Aktywność można powiązać ze stężeniem przez współczynnik aktywności.

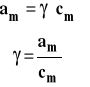
Aktywność i współczynnik aktywności dobieramy tak, aby aktywność dążyła do stężenia, gdy stężenie dąży do zera czyli gdy dążymy do roztworu nieskończenie rozcieńczonego. Współczynnik aktywności dąży wówczas do jedności.

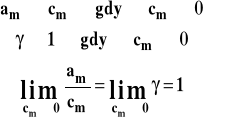
Stanem standardowym jest hipotetyczny stan składnika rozpuszczonego w roztworze o stężeniu 1 mol/kg w dowolnej stałej temperaturze i pod dowolnym stałym ciśnieniem, gdyby zachowywał się on jak w roztworze idealnie rozcieńczonym. Wybór stanu standardowego przedstawiono na rysunku 1. Stanem odniesienia jest stan składnika w roztworze idealnie rozcieńczonym. Kreślimy więc styczną do tej zależności przy stężeniu zerowym i ekstrapolacja jej wyznacza stan standardowy przy stężeniu 1 mol/kg.

Rysunek 1. Dobór stanu standardowego dla substancji rozpuszczonej w roztworze rzeczywistym, gdy skład wyrażony jest przez stężenie molarne (w mol/kg).

W dalszych rozważaniach dla uproszczenia zapisu nie uwzględniamy stężenia standardowego w zapisie wzoru na potencjał chemiczny. Wartość stężenia standardowego wynosi 1 mol/kg, więc nie zmienia to wartości liczbowych, a tylko redukuje jednostkę. Należy pamiętać, że wartość aktywności (stężenia) wprowadzamy teraz jako bezwymiarową. Wobec tego potencjał chemiczny elektrolitu w roztworze wyrażamy jako :

Zakładamy, że mamy mocny elektrolit w roztworze, który dysocjuje następująco :

Roztwór elektrolitu jest zawsze elektroobojętny, co oznacza, że suma ładunków pochodzących od kationów jest równa wartości bezwzględnej sumy ładunków pochodzących od anionów.

Potencjał chemiczny całego elektrolitu wyrażamy jako sumę potencjałów chemicznych poszczególnych jonów, na które rozpada się on w roztworze :

Potencjał chemiczny jony w roztworze wyrażamy wyrażeniem analogicznym jak potencjał całego elektrolitu :

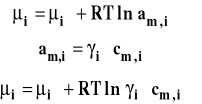
Wobec tego :

Porządkujemy prawą stronę tego wyrażenia, grupując wyrazy pod logarytmem.

Odpowiednie wyrazy po lewej i prawej stronie tego wyrażenia muszą być sobie równe czyli :

Ostatecznie aktywność elektrolitu można wyrazić przez aktywności jonów.

Jak już powiedziano, roztwór elektrolitu jest zawsze elektroobojętny. W roztworze zawsze kationom towarzyszą aniony. Nie można wobec tego zrobić roztworu jednego rodzaju jonów, na przykład roztworu tylko jonów Na⁺. Skoro nie można zrobić roztworu, to nie można zbadać doświadczalnie własności jonu w roztworze i wyznaczyć w sposób doświadczalny jego współczynnika aktywności. Natomiast jak już wiemy, możliwe jest wyznaczenie doświadczalne współczynnika aktywności substancji rozpuszczonej (na przykład w oparciu o pomiar wielkości koligatywnych), w tym wypadku całego elektrolitu. Dlatego też w opisie termodynamicznym roztworów elektrolitów wprowadzamy średnią aktywność jonową definiowana równaniem :

Średnia aktywność jonowa

gdzie :  - suma liczby kationów i anionów, na jakie dysocjuje elektrolit

Średnią aktywność jonową możemy powiązać ze średnim jonowym współczynnikiem aktywności i średnim stężeniem jonowym.

Średni jonowy współczynnik aktywności

Średnie stężenie jonowe

Średnie stężenie molowe można powiązać ze stężeniem całego elektrolitu następująco :

Oddziaływanie jonów z cząsteczkami rozpuszczalnika - solwatacja

Rozpuszczalniki mogą mieć charakter polarny, gdy ich cząsteczki są dipolami elektrycznymi (na przykład woda) lub niepolarny, wówczas ich cząsteczki nie są dipolami (na przykład benzen). Dla przypomnienia, dipol elektryczny to układ dwu ładunków, ujemnego i dodatniego, rozdzielonych na stałe na pewną odległość. Kiedy w rozpuszczalniku niepolarnym znajdzie się ładunek zlokalizowany na jonie, to powoduje on wyindukowanie w cząsteczkach otaczających go chwilowego momentu dipolowego. Dipole elektryczne czy to stałe czy wyindukowane, układają się wokół jonu w taki sposób, aby końce o ładunku przeciwnym do ładunku jonu, były blisko niego na skutek przyciągania elektrostatycznego (rysunek 2). W efekcie jon jest otoczony cząsteczkami rozpuszczalnika. Proces taki nazywamy solwatacją i zachodzi on samorzutnie, po wprowadzeniu jonu do rozpuszczalnika.

Solwatacja

Rysunek 2. Solwatacja jonów.

W przypadku, gdy rozpuszczalnikiem jest woda, solwatację nazywamy hydratacją. Hydratacja jonów ma pewne szczególne cechy. Cząsteczka wody jest obdarzona wyjątkowo dużym momentem dipolowym, toteż oddziaływania jon - dipol będą w tym wypadku bardzo silne. Powoduje to, że zwykle z jonem jest związane na stałe kilka cząsteczek wody. Cząsteczki te są uporządkowane, co zmienia wybitnie własności wody, a w szczególności obniża silnie jej względną stałą dielektryczną. Te cząsteczki wody są na tyle trwale związane z jonem, że gdy zostanie on wprawiony w ruch przez zewnętrzne pole elektryczne, to poruszają się razem z nim. Dlatego promienie hydrodynamiczne jonów są znacznie większe niż promienie „gołych” jonów, uzyskane z danych krystalograficznych. Tą warstwę cząsteczek wody związanych z jonem nazywamy pierwotną warstwą hydratacyjną. Wokół niej mamy znacznie szerszą warstwę częściowo uporządkowanych dipoli wody - wtórną warstwę hydratacyjną, w której własności wody są częściowo zmienione.

Rysunek 3. Hydratacja.

Oddziaływanie jonów nawzajem ze sobą - teoria roztworów mocnych elektrolitów Debye'a-Hückla

Teoria roztworów mocnych elektrolitów, stworzona przez Debye'a i Hückla, pozwala na obliczenie współczynników aktywności jonów w roztworze po uwzględnieniu oddziaływań elektrostatycznych pomiędzy jonami. Celem tej teorii jest obliczenie różnicy pomiędzy potencjałem chemicznym jonu w roztworze idealnym (doskonałym), a potencjałem chemicznym jonu w roztworze rzeczywistym.

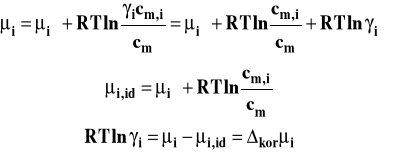
Aby tego dokonać, trzeba zbudować cykl termodynamiczny pokazany na rysunku 4.

Rysunek 4. Schemat cyklu termodynamicznego wykorzystywanego przy obliczaniu współczynników aktywności w teorii Debye'a-Hückla.

Bezpośrednie przeniesienie jonu z roztworu idealnego do rzeczywistego jest procesem nieodwracalnym. Aby obliczyć pracę elektryczną, wykonaną przy takim przeniesieniu, tworzymy alternatywną drogę procesu, która może być wykonana w sposób odwracalny. W pierwszym etapie dokonujemy rozładowania jonu w roztworze idealnym, czemu towarzyszy praca elektryczna w₁, co może być dokonane w sposób odwracalny. Rozładowane indywiduum przenosimy do roztworu rzeczywistego, czemu nie towarzyszy praca elektryczna, a następnie znowu ładujemy w sposób odwracalny wykonując pracę w₂. W warunkach izotermiczno-izobarycznych praca jest równa zmianie entalpii swobodnej. Dla jednego mola jonów praca wykonana w tym cyklu będzie więc równa poszukiwanej różnicy korekcyjnej pomiędzy potencjałem chemicznym jonu w roztworze rzeczywistym a idealnym.

Aby móc obliczyć obie te prace, trzeba przyjąć pewien uproszczony model roztworu elektrolitu.

Założenia teorii Debye'a-Hückla

• Jony traktujemy jako punkty materialne.

• Rozpuszczalnik oddziaływuje na jony tylko poprzez swoją stałą dielektryczną (pomijamy solwatację).

• Jony w polu elektrycznym jonu centralnego podlegają rozkładowi Boltzmanna.

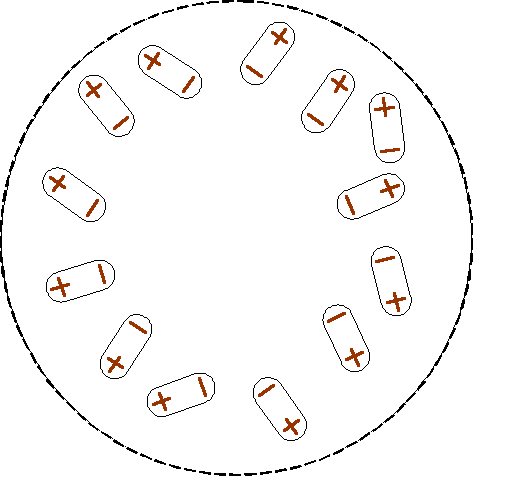
Jak wiadomo, ładunki tego samego znaku odpychają się, a ładunki przeciwnego znaku - przyciągają. Jon, traktowany jako punktowy ładunek, wytwarza wokół siebie pole elektrostatyczne, którego potencjał maleje w funkcji odległości od niego. Wobec tego jeśli weźmiemy pod uwagę pojedynczy jon, na przykład kation, to będzie on odpychał od siebie inne kationy, a przyciągał aniony. Oczywiście wszystkie jony są w stałym ruchu, porozdzielane cząsteczkami rozpuszczalnika i nigdy nie będziemy mieli stałego, nieruchomego układu jonów. Niemniej jednak wokół danego wybranego jonu będziemy mieć statystycznie nieco więcej jonów przeciwnego znaku, a nieco mniej tego samego znaku niż średnio w roztworze. Rozkład jonów wokół jonu centralnego pokazany jest na rysunku 5. Wokół jonu powstaje tak zwana atmosfera jonowa.

Rysunek 5. Rozkład jonów wokół jonu centralnego ; 1 - rozkład jonów przeciwnego znaku do jonu centralnego, 2 - rozkład jonów o tym samym znaku co jon centralny.

Atmosfera jonowa

Rysunek 6. Atmosfera jonowa.

Przyjmuje się, że atmosfera jonowa ma kształt kuli, o promieniu, który pozwala obliczyć teoria Debye'a-Hückla. Gdy odległość od jonu centralnego jest większa niż promień atmosfery jonowej, to praktycznie można zaniedbać pole elektryczne wytwarzane przez ten jon.

Na podstawie tych założeń wyprowadzono graniczne prawo Debye'a-Hückla, pozwalające na obliczenie współczynników aktywności jonów, które ma następującą postać.

Graniczne prawo Debye'a-Hückla

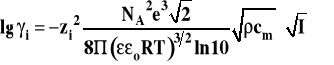
gdzie : N_A - liczba Avogadro e - ładunek elementarny  - względna przenikalność dielektryczna rozpuszczalnika _o - przenikalność dielektryczna próżni ρ - gęstość rozpuszczalnika
- stężenie standardowe 1 mol/kg z_i - wartościowość jonu I - siła jonowa roztworu

Siła jonowa roztworu definiowana jest poniższym wzorem, przy czym sumowanie prowadzimy po wszystkich jonach obecnych w roztworze.

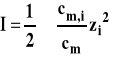
Przy obliczeniach pomijamy stężenie standardowe, ale wówczas podstawiamy wartości stężeń jako wielkości bezwymiarowe. Ponieważ we wzorze opisującym graniczne prawo Debye'a-Hückla mamy kombinację stałych uniwersalnych i parametrów opisujących rozpuszczalnik (stałych w danej temperaturze), to oznaczamy ją razem jako pewną stałą A i prawo zapisujemy w uproszczonej formie :

Prawo to jest słuszne dla sił jonowych nie większych niż 0,01.

I ≤ 0,01

Dla wody w temperaturze 25ºC wartość stałej A wynosi 0,5093.

A = 0,5093

Ponieważ współczynniki aktywności pojedynczych jonów, jak to powiedziano uprzednio, są niemierzalne, to aby porównać wyniki doświadczalne z teorią, używamy średniego jonowego współczynnika aktywności, który można zmierzyć. Graniczne prawo Debye'a-Hückla ma w tym przypadku postać :

Zakres stosowalności granicznego prawa Debye'a-Hückla jest stosunkowo niewielki, obejmuje tylko roztwory bardzo rozcieńczone. Prawo to zostało wyprowadzone przy zastosowaniu wielu uproszczeń matematycznych. Próby rozwiązań dokładnych nie prowadziły do rozszerzenia jego zakresu stosowalności. Znacznie lepsze wyniki daje pominięcie pierwszego z założeń teorii. Jeśli przyjmiemy, ze jony nie są punktami materialnymi, a kulkami o promieniu r_i, to otrzymujemy rozszerzone prawo Debye'a-Hückla.

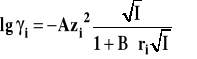
Stała B w tym wzorze wyrażona jest wzorem :

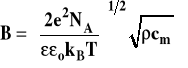
Dla wody w temperaturze 25ºC stała ta wynosi 0,329·10¹⁰ m^-1. Ponieważ promienie typowych jonów nieorganicznych są zwykle rzędu 3·10^-10 m, to można przyjąć, że iloczyn stałej B i promienia jonu jest w przybliżeniu równy jeden i rozszerzone prawo Debye'a-Hückla dla roztworów wodnych zapisać w postaci :

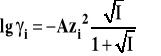
Prawo to można stosować dla sił jonowych nie większych niż 0,1.

I ≤ 0,1

Średni jonowy współczynnik aktywności wyraża się w tym wypadku wzorem :

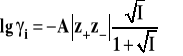
Dalsze rozszerzenie stosowalności prawa Debye'a-Hückla można osiągnąć przez rezygnację z drugiego założenia teorii. Po uwzględnieniu solwatacji prawo przybiera postać :

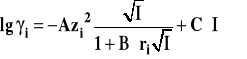
Stała C w tym wzorze zależy nie tylko od rozpuszczalnika, ale i od rodzaju elektrolitu w nim rozpuszczonego. Stała C uwzględnia solwatację jonów. Uwzględnienie solwatacji pozwala na stosowanie prawa zwykle dla sił jonowych nieprzekraczających 0,3, przy czym zakres stosowalności zależy w pewnym stopniu od rozpuszczalnika i elektrolitu. Dla roztworów stężonych, o dużych siłach jonowych współczynniki aktywności (średnie) można wyznaczyć tylko doświadczalnie. Na rysunku 7 pokazano porównanie trzech form prawa Debye'a-Hückla z rzeczywistą zależnością współczynnika aktywności od siły jonowej roztworu.

Rysunek 7. Zależność współczynnika aktywności od siły jonowej ; 1 - graniczne prawo Debye'a-Hückla, 2 - rozszerzone prawo Debye'a-Hückla, 3 - rozszerzone prawo Debye'a-Hückla z uwzględnieniem solwatacji, 4 - zależność rzeczywista

W obszarze bardzo dużych sił jonowych żaden ze wzorów teoretycznych nie opisuje dobrze współczynników aktywności, które mogą nawet stać się większe od jedności. Jest to spowodowane asocjacją jonów.

Elektrolity mocne to takie, które w roztworze są całkowicie zdysocjowane na jony przy dowolnym stężeniu (stopień dysocjacji  = 1 dla dowolnego stężenia).

Elektrolity słabe to takie, które w roztworze są częściowo zdysocjowane na jony ( < 1), a stopień dysocjacji maleje wraz ze wzrostem stężenia. Gdy roztwór jest nieskończenie rozcieńczony (stężenie dąży do 0) stopień dysocjacji dąży do jedności.

c_m

roztwór rzeczywisty

hipotetyczny stan standardowy

roztwór idealnie rozcieńczony

0

1

a

Solwatacja jonu to samorzutne otaczanie jonu przez cząsteczki rozpuszczalnika w wyniku oddziaływań jon - dipol, przy czym dipol elektryczny cząsteczki rozpuszczalnika może być stały lub wyindukowany.

▬

+

niezakłócona struktura wody  = 78

+

wtórna warstwa hydratacyjna - warstwa wody o częściowo uporządkowanej strukturze  = 32

pierwotna warstwa hydratacyjna - ściśle uporządkowana warstwa dipoli wody, trwale związanych z jonem

 = 6

proces odwracalny

proces odwracalny

proces odwracalny

w = 0

w₂

w₁

proces nieodwracalny

roztwór rzeczywisty

roztwór idealnie rozcieńczony

0

0

+ z_ie

- z_ie

z_ie

z_ie

jon w roztworze rzeczywistym

jon w roztworze idealnie rozcieńczonym

Atmosfera jonowa to przestrzenna chmura ładunku o symetrii sferycznej i znaku przeciwnym do znaku jonu centralnego, o wartości bezwzględnej ładunku równej wartości bezwzględnej ładunku jonu centralnego.

+

-

-

+

1

3

2

4

---