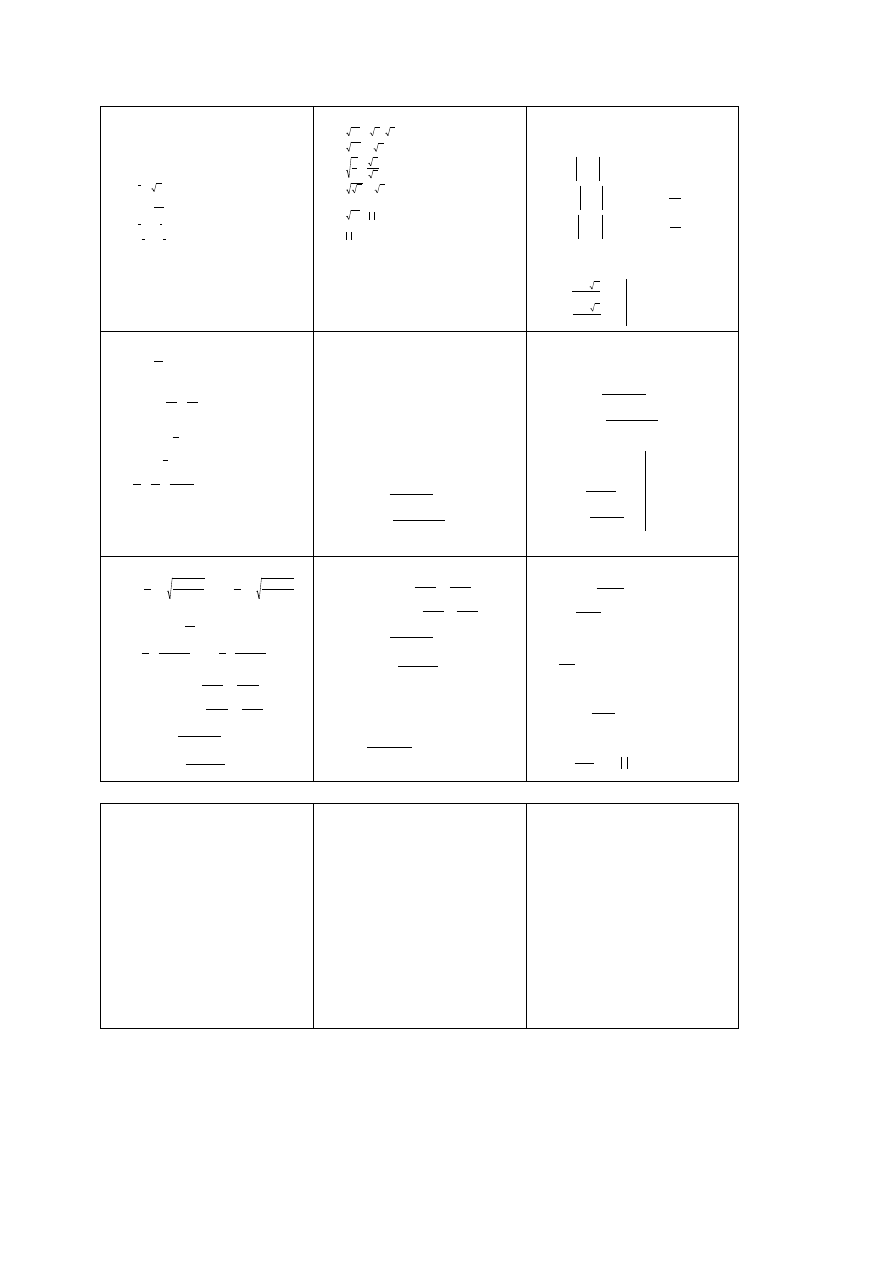
POTĘGOWANIE
a

m

· a

n

= a

m+n

a

m

: a

n

= a

m-n

(dla m>n ^ a



0)

(a

m

)

n

= a

m



n

(a



b)

n

= a

n



b

n

(a/b)

n

= a

n

/b

n

(dla b



0)

a

0

=1

a

a

a

a

a

a

a

a

n

m

n

n

m

n

n

n

n

n

m

m

1

1

1

1















( )

( )

WZORY SKRÓCONEGO MNOŻENIA
(a+b)

2

= a

2

+2ab+b

2

(a-b)

2

= a

2

-2ab+b

2

(a+b)

3

= a

3

+3a

2

b+3ab

2

+b

3

(a-b)

3

= a

3

-3a

2

b+3ab

2

-b

3

a

2

-b

2

= (a-b)(a+b)

a

3

-b

3

= (a-b)(a

2

+ab+b

2

)

a

3

+b

3

= (a+b)(a

2

-ab+b

2

)

PIERWIASTKOWANIE

ab

a

b

a

a

a
b

a
b

a

a

n

n

n

m

n

n

m

n

n

n

m

n

mn











(

)

WARTOŚĆ BEZWZGLĘDNA

x

x

x

x

gdy

x gdy

x
x

2

0
0
















RÓWNANIA I NIERÓWNOŚCI Z WARTOŚCIĄ
BEZWZGLĘDNĄ
Równanie:



x-a



= b, oznacza, że

x-a = b



x-a = -b.

Nierówność:



x-a



<b, jest spełniona



gdy:

x-a>-b



x-a<b

Nierówność:



x-a



>b, jest spełniona



gdy:

x-a<-b



x-a>b

UKŁADY RÓWNAŃ

ax by c

a x b y c

W

a

b

a

b

ab

a b

W

W

c

b

c

b

cb

c b

x

W

W

W

a

c

a

c

ac

a c

y

W

W

X

X

Y

Y







































1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

0

TRÓJMIAN KWADRATOWY
f(x)=ax

2

+bc+c



=b

2

-4ac

Jeżeli



>0, wtedy:

x

b

a

x

b

a

1

2

2

2



 



 





Postać kanoniczna

f x

a x p

q

Postać iloczynowa

f x

a x x x x

( )

(

)

( )

(

)(

)













2

1

2

Jeżeli



=0, wtedy:

x

b

a

0

2

 

Współrzędne wierzchołka paraboli:

W

b

a

a













2

4

,



Wzory Viete’a:

x

x

b
a

x x

c

a

x

x

x

x

x x

1

2

1

2

1

2

1

2

1

2

1

1



 













TRYGONOMETRIA
sin

2



+ cos

2



= 1

tg



ctg



= 1

Wzory redukcyjne:
sin(90



+



) = cos



sin(180



+



) = -sin



cos(90



+



) = -sin



cos(180



+



) = -cos



tg(90



+



) = -ctg



tg(180



+



) = tg



ctg(90



+



) = -tg



ctg(180



+



)= ctg



sin(270



+



) = -cos



sin(360



+



) = sin



cos(270



+



) = sin



cos(360



+



) = cos



tg(270



+



) = -ctg



tg(360



+



) = tg



ctg(270



+



)= -tg



ctg(360



+



) = ctg



Fukncje trygonometryczne sumy kątów:

















sin

sin cos

cos sin

cos

cos cos

sin sin

 









 









 









 









































tg

tg

tg

tg

tg

ctg

ctg

ctg

ctg

ctg

1

1

Funkcje trygonometryczne różnicy kątów:

















sin

sin cos

cos sin

cos

cos cos

sin sin

 









 









 









 









































tg

tg

tg

tg

tg

ctg

ctg

ctg

ctg

ctg

1

1

Funkcje trygonometryczne kąta podwojonego:

sin

sin cos

cos

cos

sin

2

2

2

2

2

1

2

1

2

2

2

2

2







































tg

tg

tg

ctg

ctg

ctg

cos

cos

sin

cos

sin

cos

cos

2
2

1 2

2

2

1

2

2

2

2



















 




Funkcje tygonometryczne połowy kąta:

sin

cos

,

cos

cos









2

1

2

2

1

2

 



 



znak + lub -

bierzemy zależnie od tego, do której

ćwiartki należy



2

tg

ctg













2

1

2

1









cos

sin

,

cos

sin

Sumy funkcji trygonometrycznych:









sin

sin

sin

cos

cos

cos

cos

cos

sin

cos

cos

sin

sin

sin





 

 





 

 





 









 





































2

2

2

2

2

2

tg

tg

ctg

ctg

Różnice funkcji trygonometrycznych:









sin

sin

sin

cos

cos

cos

sin

sin

sin

cos

cos

sin

sin

sin





 

 





 

 





 









 















 





















2

2

2

2

2

2

tg

tg

ctg

ctg

CIĄGI LICZBOWE

CIĄGIEM ARYTMETYCZNYM nazywamy taki ciąg
liczbowy, w którym różnica kolejnych wyrazów jest
stała



r =a

n+1

- a

n

a

a

a

n

n

n









1

1

2

Wyraz ogólny ciągu: a

n

= a

1

+ (n-1)r

Suma częściowa:





S

na

n

n

r

S

a

a

n

n

n

n















1

1

1

2

2

CIĄG GEOMETRYCZNY to taki ciąg liczbowy, w
którym iloraz kolejnych wyrazów jest stały



a

a

q

n

n





1

Wyraz ogólny ciągu: a

n

= a

1



q

n-1

Suma częściowa:

S

a

q

q

gdy q

S

n a gdy q

n

n

n

 







 



1

1

1

1

1

1

,

,

Suma nieskończonego ciągu geometrycznego:

S

a

q

dla

q







1

1

1

,

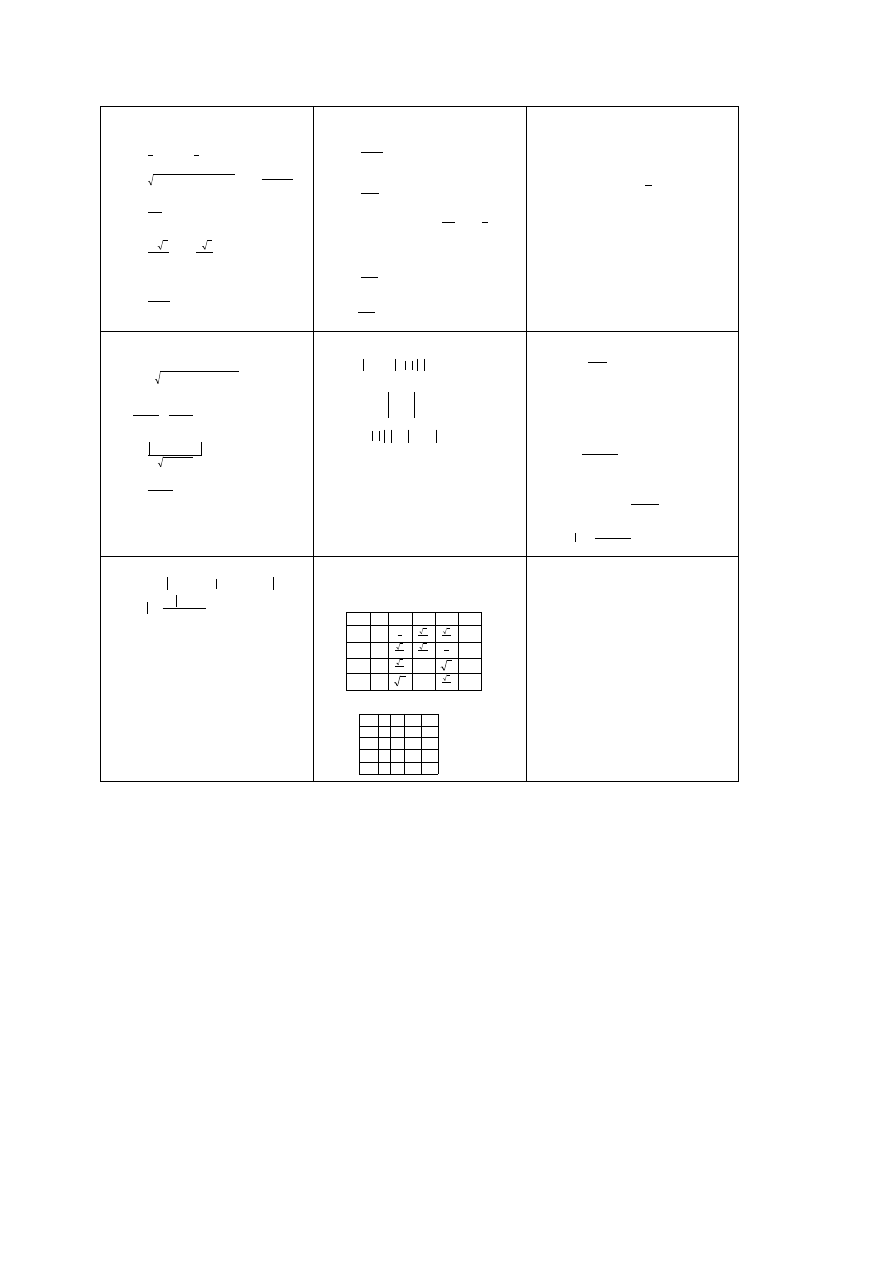
POLA FIGUR PŁASKICH

Trójkąt:

S

ah

S

ab

S

p p a p b p c

p

a b c

 

 













 

1
2

1
2

2

,

sin

(

)(

)(

) ,



S = pr, p - p

ołowa obwodu; r - pr. okręgu wpisanego

S

abc

R



4

, R -

pr. okręgu opisanego

Trójkąt równoboczny:

S

a

h

a





2

3

4

3

2

Równoległobok:

S ah

S ab

S

d d













sin

sin





1

2

2

Romb:

S ah

S a

S

d d









2

1

2

2

sin



Trapez:

S

a b

h







2

Koło i okrąg:
S =



r

2

R

abc

S

r

S

p





4

2p = 2



r

p -

połowa obwodu

Pole wycinka koła:

S

r









360

2



Długość łuku koła:

l

r









180



LOGARYTMY

log
log

log

log

log

log

log

log

log

log

log

log

log

a

b

a

a

a

a

a

a

a

a

a

m

a

a

x

x

x b

a

x

a

x

y

xy

x

y

x
y

x

m

x

a

x

a

x

a

 















 





1 0

1

STEREOMETRIA

Sześcian: V=a

3

Prostopadłościan: V=abh
Walec: V=



r

2

h

Ostrosłup foremny: V=1/3a

2

h

Stożek: V=1/3



r

2

h, S-boczne=



rl

Kula: V=4/3



r

3

, S=4



r

2

GEOMETRIA ANALITYCZNA

AB

x

x y

y

AB

x

x

y

y

















[

,

]

(

)

(

)

2

1

2

1

2

1

2

2

1

2

Równanie prostej przechodzącej przez dwa punkty:

y y

y

y

x x

x

x











1

2

1

1

2

1

Odległość punktu od prostej:

d

Ax

By

C

A

B









0

0

2

2

Współczynnik kierunkowy:

a

y

y

x

x






2

1

2

1

Waru

nek równoległości: A

1

B

2

= A

2

B

1

Warunek prostopadłości: ac = -1

Wyznacznik (Dla trójkąta 1/2 det):

S

a b

a b

a a a

b b b

a b

a

a

b

b

a b

a b

x

y

x

y

x

y

x

y

x y

y x



  







det( , )

sin

[ , ]

[ , ]

det( , )

 

 





 



Iloczyn skalarny:







 



 

a b

a b

a b

  

cos ( , )

 

















a b

a b

a

a a

b

b b

a b

a b

a b

x

y

x

y

x x

y y

 











0

[ , ]

[ , ]

oblicznie długości wektorów z iloczynu skalarnego
OKRĄG
Równanie okręgu:
(x - a)

2

+ (y - b)

2

= r

2

x

2

+y

2

-2ax-2by+c=0

PRAWDOPODOBIEŃSTWO

P A

n A
n

( )

( )
( )





Własności:
P(



)=0

A



B



P(A)



P(B)

P(A)



1

P(A’)=1-P(A)
P(A



B)=P(A) + P(B) - P(A



B)

Symbol Newtona:

n
k

n

k n k









 



!

!(

)!

Wariacje:
z powtórzeniami:

W

n

n

k

k



bez

powtórzeń:

V

n

n k

n

k





!

(

)!

Prawdopodobieństwo warunkowe:

P A B

P A

B

P B

(

)

(

)

( )





Prawdopodobieństwo przyczyny:

P A P A B P B

P A B P B

P A B

P B

P Bi A

P A Bi P Bi

P A

n

n

( )

(

) ( )

(

) ( ) ... (

)

( )

(

)

(

) ( )

( )









 







1

1

2

2

Zdarzenie niezależne:
P(A



B)=P(A)



P(B)

FUNKCJE I WYKRESY FUNKCJI

Funkcja różnowartościowa

x

x

f x

f x

Funkcja rosn ca

x

x

f x

f x

Funkcja malej ca

x

x

f x

f x

Funkcja parzysta

f

x

f x

Funkcja nieparzysta

f

x

f x

x x

x x

x x

x

x

























  

   

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

,

,

,

[(

)

( ( )

( ))]

ą

[

( )

( )]

ą

[

( )

( )]

:

(

)

( )

(

)

( )

sin(

)

sin

cos(

) cos

(

)

(

)



 







 



 

















tg

tg

ctg

ctg



0

30

45

60

90

0

1

1

0

0

1

3

3

1

0

1

2

2

2

3

2

3

2

2

2

1
2

3

3

3

3











sin

cos

tg

ctg





I

II

III

IV

tg

ctg

sin

cos

 





 





 





 



