Matematyka dyskretna

Zagadnienia na egzamin i rozwiązania tych zagadnieo

Semestr zimowy 2012/2013

1. Zasada indukcji matematycznej oraz przykład.
2. Sformułowad zasadę maksimum, zasadę minimum, zasadę Archimedesa dla liczb naturalnych.
3. Definicja o własności działao w pierścieniu Z

p

mod p i umiejętnośd rozwiązania równao modulo p.

4. Definicja i własności funkcji sufitu i podłogi, umiejętnośd rysowania wykresu.
5. Definicja i własności takich funkcji jak o, O, θ,Ω oraz przykład.
6. Sformułowad twierdzenie o rekurencji uniwersalnej, umiejętnośd podawania rzędu wzrostu ciągu

danego rekurencyjnie.

7. Definicja i własności funkcji tworzących (podad kilka własności).
8. Twierdzenie o postaci funkcji tworzących dla ciągu rekurencyjnego oraz przykład zastosowania.
9. Definicja i własności operatora Δ i E, przykład typu: dla ciągu y

1

, y

2

, y

3

wyznaczyd ciąg Δy

1

, Δy

2

, Δy

3

.

10. Sformułowad twierdzenie MontMorta.
11. Rozwiązad proste równanie różnicowe, liniowe stopnia 1 lub 2.
12. Zadania kombinatoryczne np. obliczyd liczbę elementów w zbiorze.
13. Sformułowad zasadę szufladkową Dirichleta.
14. Dla zliczania podad prawo sumy, iloczynu, potęgi i ewentualnie proste zadanie.
15. Znajomośd wzoru dwumianowego Newtona np. policzyd (1+x)

4

i podad współczynnik rozwinięcia.

Ad 1. Zasada indukcji matematycznej oraz przykład.

Jeżeli M N i 1 M i wraz z ) ), to M=N lub inaczej, symbolicznie

)

Ad 2. Sformułowad zasadę maksimum, zasadę minimum, zasadę Archimedesa dla liczb naturalnych.

Zasada maksimum – Każdy ograniczony z góry podzbiór zbioru N ma element największy.
UWAGA! Ta zasada jest spełniona tylko w zbiorze Z ale nie jest spełniona w zbiorze Q oraz R (przykłady B i
C). Przypomnijmy, że podzbiór zbioru np. B (dowolny zbiór) nazywamy ograniczonym z góry, gdy istnieje
liczba c taka, że dla każdego elementu x ze zbioru X. )

Zasada minimum – Każdy podzbiór zbioru liczb naturalnych ma element najmniejszy.
UWAGA! Ta zasada nie jest spełniona w następujących zbiorach:
Z –zbiór liczb całkowitych np. parzystych A={…,-4, -2, 0, 2, 4,…} nie ma elementu najmniejszego
Q – zbiór liczb wymiernych, np. B= to B nie ma elementu najmniejszego
R – zbiór liczb rzeczywistych, np. C= nie ma elementu najmniejszego

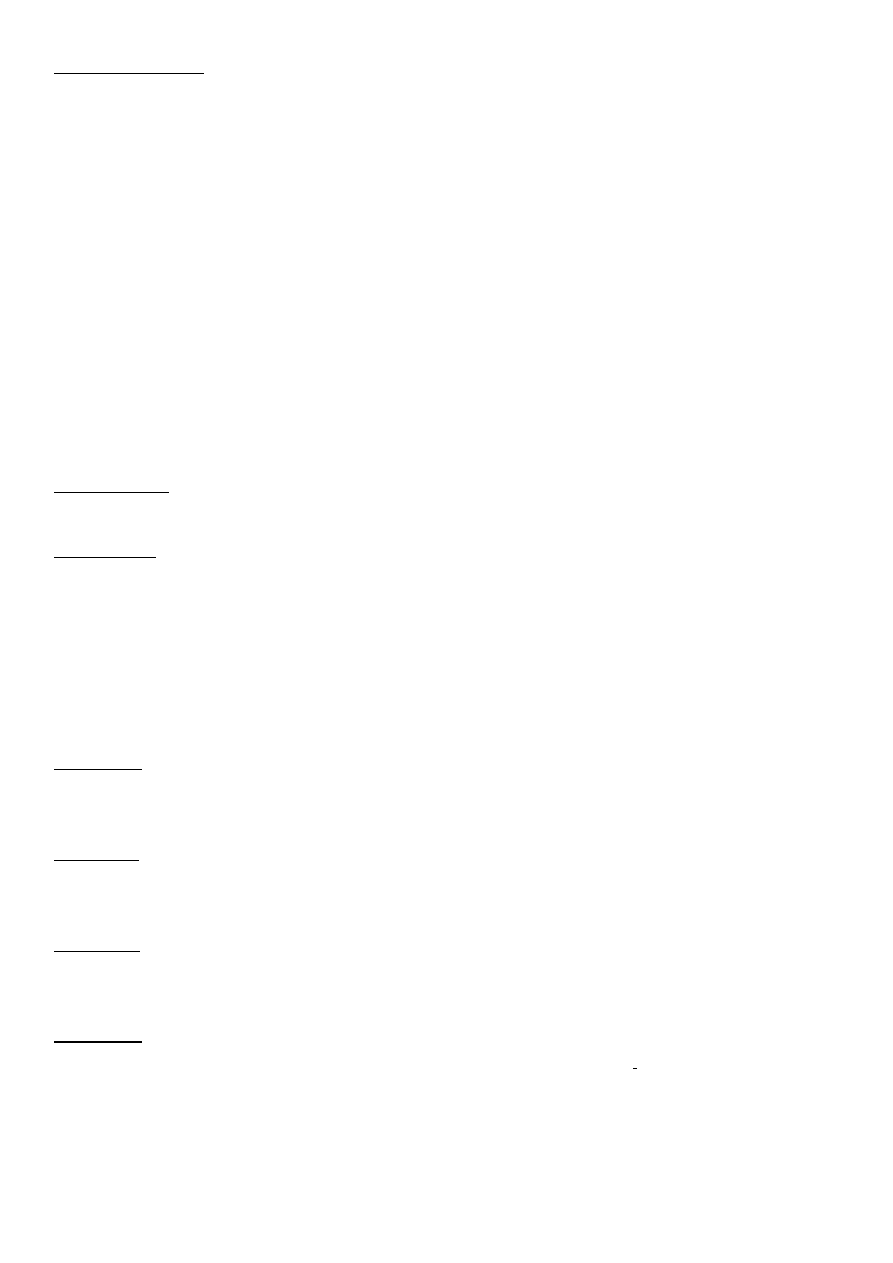
Zasada Archimedesa – dla dowolnych liczb rzeczywistych istnieje liczba naturalna
taka, że .
Wniosek: Biorąc y=1 otrzymujemy następujący wniosek:
Dla każdej liczby rzeczywistej istnieje liczba naturalna taka, że .

Ad 3. Definicja o własności działao w pierścieniu Z

p

mod p i umiejętnośd rozwiązania równao modulo p.

Pierścieo Z

p

liczb całkowitych (mod p) jest to zbiór {0,1,…,p-1} w, którym działania określamy następująco

liczby a + b przez p
liczby a * b przez p
Otrzymujemy wtedy:
Gdy p jest liczbą pierwszą to jest ciałem a każdy element ma element odwrotny.

Ad 4. Definicja i własności funkcji sufitu i podłogi, umiejętnośd rysowania wykresu.

Funkcją podłogi nazywamy funkcję przyporządkowujące liczbie rzeczywistej największą
liczbę całkowitą nie większą niż x.

Funkcją sufitu nazywamy funkcję

przyporządkowujące liczbie rzeczywistej najmniejszą

liczbę całkowitą nie mniejszą niż x.

Ad. 5 Definicja i własności takich funkcji jak o, O, θ, Ω oraz przykład.

Funkcje f nazywamy asymptotycznie dodatnią, gdy istnieje n

0

to

f(n)>0 . Wszystkie podane są

funkcjami asymptotycznymi.

Notacja „O” Piszemy f(n)=O(g(n)), gdy istnieje c>0, n

0

takie, że dla dowolnego n>n

0

0<f(n)<c*g(n)

mówimy wówczas, że f jest co najwyżej rzędu g(n).
Własności: zwrotnośd, przechodniośd, dodawanie, max, mnożenie

Notacja „o” Piszemy f(n)=o(g(n)) gdy dla dowolnej stałej c>0 istnieją n

0

takie, że dla dowolnego n> n

0

zachodzi 0<f(n) c*g(n). Mówimy wówczas, że f jest pomijalna względem g.
Zatem jeżeli f(n)=o(g(n)), to f(n)=O(g(n)).

Notacja „θ” Piszemy f(n)= θ (g(n)), gdy istnieją c

1

, c

2

>0 n

0

takie, że dla dowolnego n>n

0

c

1

*g(n) f(n)

c

2

*g(n). Mówimy wówczas, ze f jest dokładnie rzędu g lub, że g jest asymptotycznie dokładnym

oszacowaniem funkcji f.

Notacja „Ω” Piszemy f(n)= Ω(g(n)) gdy istnieje stała c>0 oraz n

0

takie, że dla n>n0 f(n) c*g(n).

Mówimy, że f jest co najmniej rzędu g. ) ( )) ) )).

Ad 6. Sformułowad twierdzenie o rekurencji uniwersalnej, umiejętnośd podawania rzędu wzrostu ciągu
danego rekurencyjnie.

Niech dana będzie funkcja f:

asymptotycznie dodatnia oraz niech T(n)=a*T(

) gdzie

wówczas:
1) Jeżeli istnieje takie, że )

) to )

)

2) Jeżeli )

) to )

)

3) Jeżeli istnieje takie, że )

) oraz istnieje ) takie, że (

) )

dla dostatecznie dużych n. ) ))

Ad 7. Definicja i własności funkcji tworzących (podad kilka własności).

Załóżmy, że a

0

, a

1

, a

2

,…=

jest ciągiem liczb rzeczywistych w szczególności całkowitych.

Własności:
1) Sumowanie (a

0

+b

0

)

∑

)

) )

2) Przesunięcie w prawo (0, a

0

, a

1

, a

2

)

∑

)

3) Przesunięcie w lewo (a

2

, a

1

, a

0

, 0)

∑

)

4) Mnożenie przez indeks – pochodna (1*a

1

, 2*a

2

, 3*a

3

) ∑

)

)

5) Dzielenie przez indeks – całka (0,

)

∑

∫ )

6) Skalowanie

)

∑

)

7) Różnica (a

0

, a

1

-a

0

, a

2

-a

1

)

∑

) ) )

8) Mnożenie splot (a

0

b

0

, a

0

b

1

+a

1

b

0

)

∑

∑

)

) )

9) Szereg sum częściowych (a

0

, a

0

+a

1

, a

0

+a

1

+a

2

)

∑

∑

)

)

Ad 8. Twierdzenie o postaci funkcji tworzących dla ciągu rekurencyjnego oraz przykład zastosowania.

Jeżeli ciąg (a

k

) spełnia rekurencję liniową

)

∑

. Wówczas funkcja tworząca tego ciągu ma postad )

)
)

, gdzie )

. Funkcja jest wielomianem, który tworzy nowy warunek przez kolejne podstawianie wartości

początkowych.

Ad 9. Definicja i własności operatora Δ i E, przykład typu: dla ciągu y

1

, y

2

, y

3

wyznaczyd ciąg Δy

1

, Δy

2

, Δy

3

.

Operator Δ:
Def. Dla dowolnego ciągu y

n

definiujemy ciąg y

n

jako ciąg różnic Δy

n

=y

n+1

- y

n

Operator E:
Def. Rozważmy ciąg yn, yn+1, yn+2… Przyjmując, że dana funkcja y=y(x) zmiennej rzeczywistej taka, że
yn=y(n). Otrzymujemy, że ciąg wyjściowy możemy zapisad w postaci:
y(n), y(n+1), y(n+2), …, y(n+p)

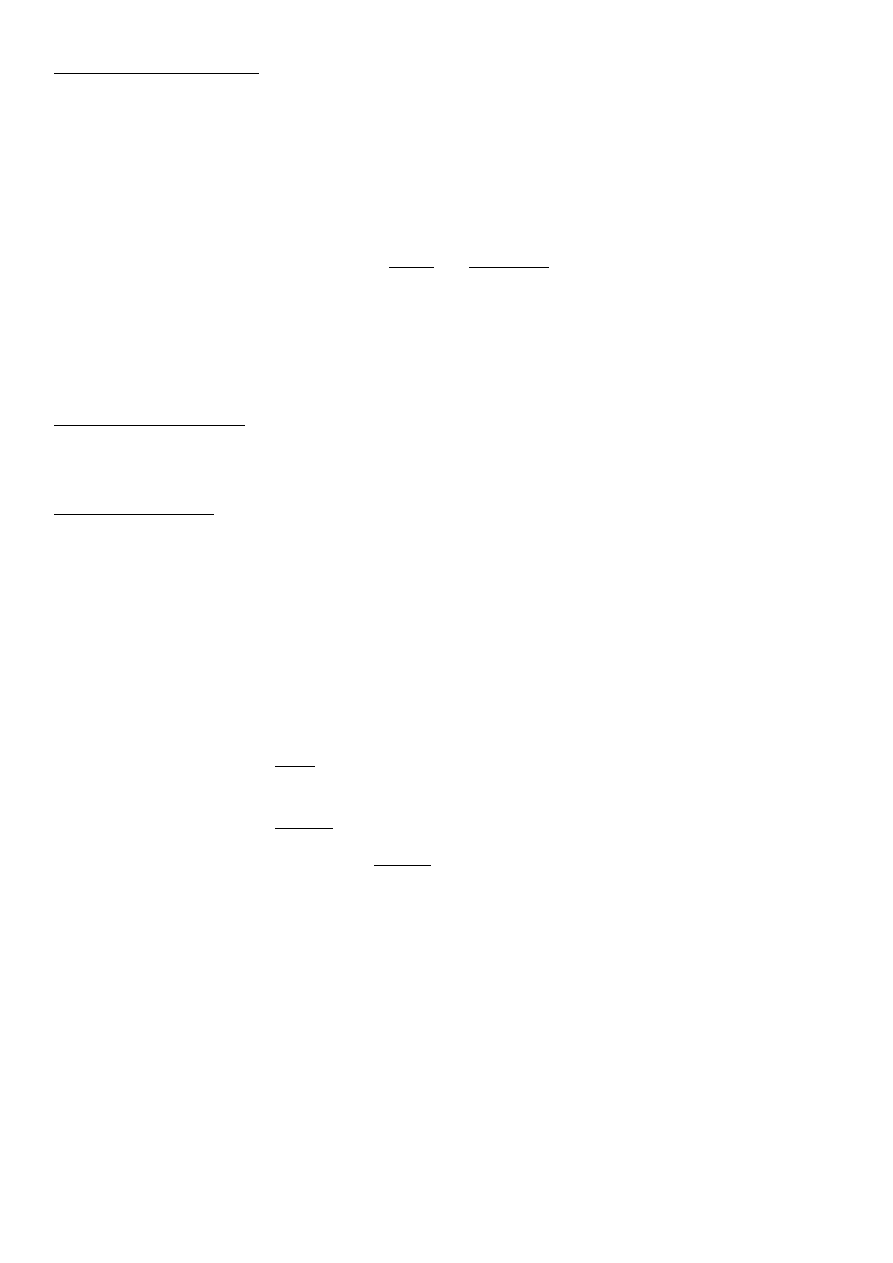
Własności tych operatorów:
-prawo rozdzielności
-prawo przemienności
-prawo wykładnicze

Ad. 10 Sformułowad twierdzenie MontMorta.

Szereg skooczony n składników postaci:

)

) )

gdzie jest operatorem

różnicowym w przód.

Ad 11. Rozwiązad proste równanie różnicowe, liniowe stopnia 1 lub 2

Rozwiązanie równania np. ) ) )

) )

)

)

Rozwiązanie ciągu np.

)

)

)

Ostatecznie:

Ad 12. Zadania kombinatoryczne np. obliczyd liczbę elementów w zbiorze.

Wzory:
1) Wariacja z powtórzeniami:

2) Wariacja bez powtórzeo:

)

3) Permutacje

4) Kombinacje bez powtórzeo

)

(

)

5) Kombinacja z powtórzeniami (

)

)

)

(

)

Ad 13. Sformułowad zasadę szufladkową Dirichleta.

Jeżeli m przedmiotów włożymy do n różnych szufladek, przy czym m>n, to co najmniej w jednej szufladce
znajdą się co najmniej dwa przedmioty.
- Twierdzenie (wersja I). Jeżeli |X|>|Y| to dla dowolnej funkcji f istnieją takie

i

)

) czyli f nie jest różno wartościowa

- Twierdzenie (wersja II) Jeżeli |X|>s*|Y| to dla każdej funkcji f: to istnieje (s+1) różnych postaci

takich, że

)

)

)

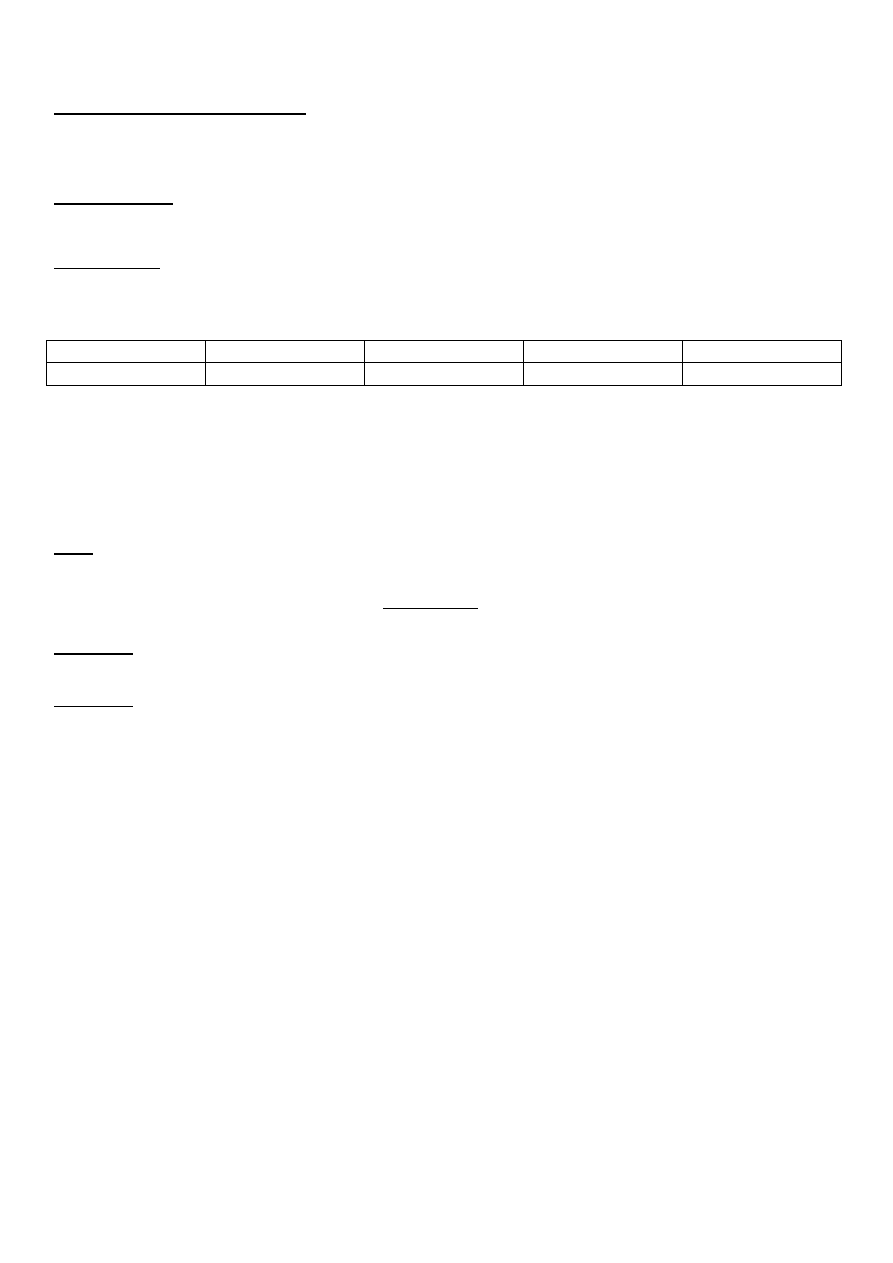
Ad 14. Dla zliczania podad prawo sumy, iloczynu, potęgi i ewentualnie proste zadanie.

Zasada włączeo i wyłączeo (sumy). Załóżmy, że A, B są zbiorami rozłącznymi, |A| - długośd zbioru

| | | | | | | |

Tw. Dla dowolnych zbiorów A

1

, A

2

, …, A

n

mamy liczbę elementów |

|

Zasada iloczynu. Dla dowolnych zbiorów A, B iloczynem kartezjaoskim zbiorów A i B nazywamy zbiór
)

Zasada potęgi. Załóżmy, że mamy dwa zbiory X, Y.
Funkcją określoną w zbiorze X ze zbioru Y mamy reguły zatem ze zbioru X odpowiedni jest element zbioru
Y. Jak są zbiorami skooczonymi nie może powstad tabela funkcji.

X

x

1

x

2

….

x

k

Y

f(x

1

)

f(x

2

)

…

f(x

k

)

Liczba wszystkich funkcji z X do Y jest zbiorem wszystkich liczb ze zbiorów. Na ile sposobów można wpisad
wartości? Na l sposobów i jest k rubryk. Czyli ostatecznie

a to jest równe

| |

| |

Ad 15. Znajomośd wzoru dwumianowego Newtona np. policzyd (1+x)

4

i podad współczynnik rozwinięcia.

Wzór dwumianowy Newtona (bez kreski ułamkowej) (

)

)

(

)

)

(

)

Przykład 1. )

(

) (

) (

)

(

)

(

)

Przykład 2. Obliczyd liczbę wszystkich możliwych podzbiorów n – elementowego wyznaczając zbiór X.
Podzbiory 0, 1, 2, 3, … n elementowe czyli (

) (

) (

)

Liczba zbiorów (

) (

) (

) )