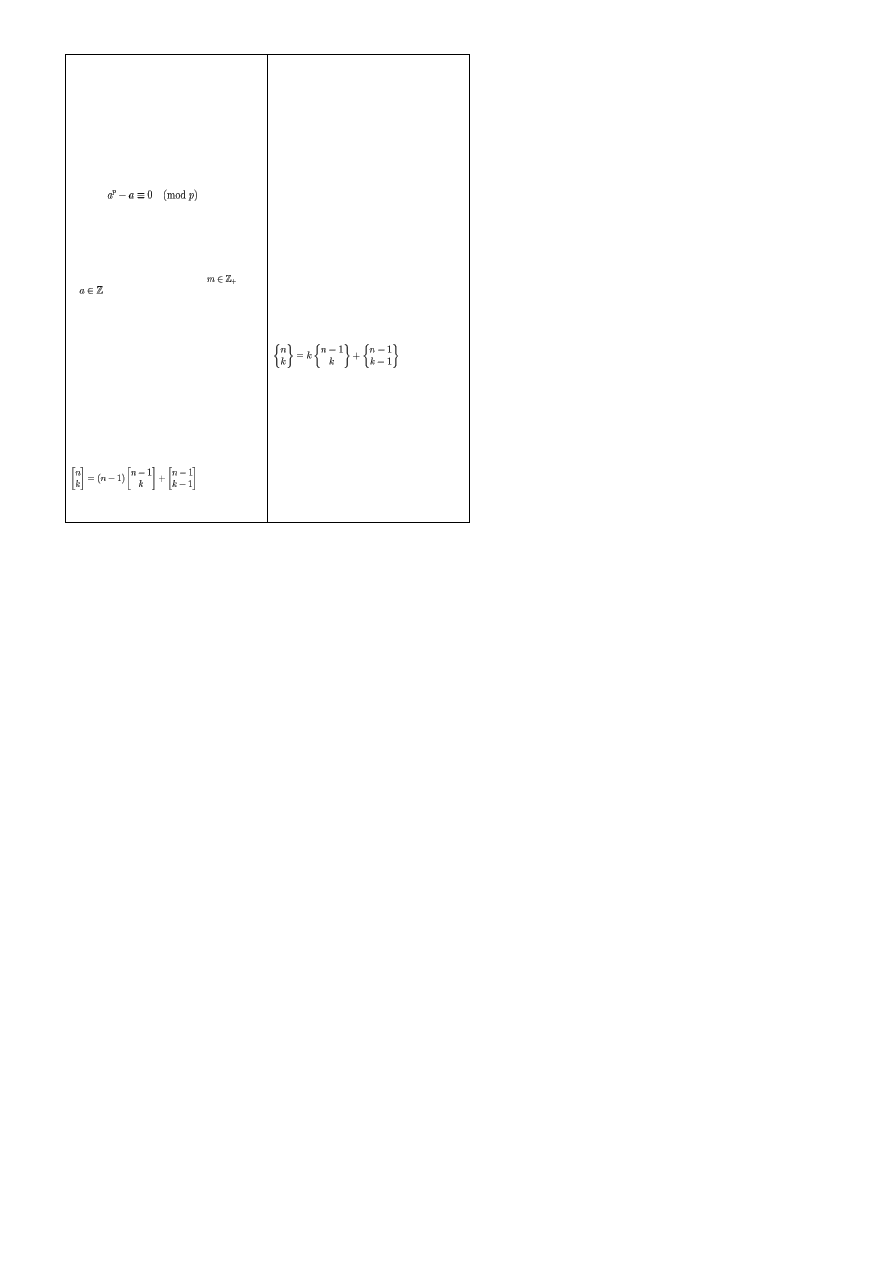
ZASADA MINIMUM -

 

Jeżeli zbiór A jest 

zbiorem 
niepustym, to istnieje w nim element będący 
wartością najmniejszą czyli taką która od 
pozostałych elementów tego zbioru jest 
mniejsza lub równa. 

WIELKIE TWIERDZENIE FERMATA -

 dla 

liczby naturalnej 

n

 

> 2 nie istnieją takie dodatnie 

liczby naturalne 

x

, 

y

, 

z

, które spełniałyby 

równanie 

x

n

 + 

y

n

 = 

z

n

. 

MAŁE TWIERDZENIE FERMATA - 

jeżeli 

p

 jest 

liczbą pierwszą, to dla dowolnej 

liczby całkowitej 

a

, liczba 

a

p

 

− 

a

 jest podzielna 

przez 

p

. 

. 

LEMAT EUKLIDESA -

 

Jeżeli liczba naturalna 

dzieli iloczyn dwóch innych liczb naturalnych i 
jest względnie pierwsza z jedną z nich, to jest 
dzielnikiem drugiej. 

SITO ERASTOTENESA -

  algorytm 

wyznaczania liczb pierwszych z zadanego 
przedziału [2,n]. 

TWIERDZENIE EULERA -

 

Jeżeli 

 i 

 

są liczbami względnie pierwszymi, 

to 

m

 

dzieli liczbę 

a

φ(

m

)

 

− 1, gdzie φ(

m

) oznacza 

wartość funkcji Eulera, czyli liczbę tych liczb 
całkowitych dodatnich mniejszych od 

m

, które 

są z 

m 

względnie pierwsze. 

SZUFLADKOWA ZASADA DIRICHLEA -

 

Niech 

X 

i 

Y 

bedą dowolnymi zbiorami 

skończonymi, przy czym 

|X| > |Y|: 

Wówczas dla 

dowolnej funkcji 

F 

okreslonej na zbiorze 

X 

o 

wartosciach w zbiorze 

Y 

istnieja elementy 

x

1

; x

2

 

€ X; x

1

 

≠ x

2

; 

dla których 

F(x

1

) = F(x

2

). 

DEFINICJA FUNKCJI 

ⱷ  EULERA: 

ⱷ

(

n

) = liczba takich 

k 

€ {

1

, 

2

, . . . , n}

, ze 

NWD(

k, n

) = 1 

LICZBY STIRLINGA I RODZAJU:

 

Opisują liczbę sposobów na rozmieszczenie n 
liczb w k cyklach

, oznaczane są symbolem:

 

 

 

GRAF PROSTY 

– 

graf jest grafem prostym, w 

którym dla każdej pary węzłów istnieje krawędź 
je łącząca. 

GRAF SPÓJNY -

 

dla każdej pary wierzchołków 

istnieje 

ścieżka, która je łączy. 

GRAF DWUDZIELNY -

  

graf, którego zbiór 

wierzchołków można podzielić na dwa 
rozłączne zbiory tak, że krawędzie nie łączą 
wierzchołków tego samego zbioru. 

GRAF REGULARNY -

 graf stopnia n to graf, w 

którym wszystkie wierzchołki są stopnia n, czyli 
z każdego wierzchołka grafu regularnego 
wychodzi n krawędzi. 

GRAF EULEROWSKI -

 

da się w nim 

skonstruować cykl Eulera, czyli cykl, który 
przechodzi przez każdą jego krawędź dokładnie 
raz i wraca do punktu wyjściowego. 

GRAF HAMILTONOWSKI 

–

 graf  

zawierający 

ścieżkę (drogę) przechodzącą przez każdy 
wierzchołek dokładnie jeden raz zwaną ścieżką 
Hamiltona. 

GRAF PLANARNY 

-  

graf, który można 

narysować na płaszczyźnie tak, by krzywe 
obrazujące krawędzie grafu nie przecinały się 
ze sobą. 

LICZBY STIRLINGA II RODZAJU:

 

Opisują liczbę sposobów podziału zbioru n 
elementowego na k niepustych podzbiorów.