Ostatnia aktualizacja: 2010-01-23



M. Tomera

Akademia Morska w Gdyni
Katedra Automatyki Okrętowej

Teoria sterowania

Badanie stabilności

−

kryterium Routha

Mirosław Tomera

1. WPROWADZENIE

Z analizy rozwiązań liniowych równań różniczkowych o stałych współczynnikach dla układów o
jednym wejściu i jednym wyjściu (SISO) wynika, że rozwiązania opisujące odpowiedź przejściową
układu zależą od pierwiastków równania charakterystycznego. Projekt układów sterowania liniowego
może być sprowadzony do rozwiązania problemu polegającego na takim rozmieszczeniu zer i
biegunów transmitancji, że układ będzie spełniał założone wymagania projektowe.

Spośród wielu rodzajów wymagań nakładanych na projekt, najważniejszym jest, aby układ był

stabilny. Układ niestabilny należy traktować jako nieużyteczny. Gdyby rozważać wszystkie typy
układów

−

liniowe, nieliniowe, stacjonarne i niestacjonarne

−

definicja stabilności może być określona

na wiele różnych sposobów. Tutaj rozważania będą dotyczyły tylko układów liniowych, stacjonarnych
o jednym wejściu i jednym wyjściu.

Dla celów analizy i projektowania rozróżnia się dwa pojęcia stabilności: bezwzględną

(absolutną) i względną. Stabilność bezwzględna odnosi się do warunków przy których układ jest
stabilny lub nie. Gdy już zostanie zapewniona stabilność układu to wówczas interesuje nas w jakim
stopniu dany układ jest stabilny i to właśnie określa stabilność względna.

2. STABILNOŚĆ ASYMPTOTYCZNA UKŁADÓW CIĄGŁYCH

Stabilność asymptotyczna określana jest dla układów z zerowym wymuszeniem, w których odpowiedź
y(t) zależy tylko od warunków początkowych. Wówczas odpowiedź y(t), korzystając z całki splotu,
można wyrazić następująco

( )

∫

∞

=

0

)

(

τ

τ

d

g

t

y

(1)

Biorąc wartość bezwzględną z obydwu stron równania (1), odpowiedź wyjściowa y(t) jest ograniczona
z obydwu stron, jeśli istnieje taka liczba dodatnia Q, przy której spełnione jest następujące wyrażenie

( )

∫

∞

∞

<

≤

=

0

)

(

Q

d

g

t

y

τ

τ

(2)

Warunek (2) oznacza, że obszar pod

)

(

τ

g

w funkcji

τ

musi być skończony. Funkcja g(

τ

) jest

odpowiedzią impulsową transmitancji G(s), której charakter zależy od położeń pierwiastków równania
charakterystycznego.

Pierwiastki równania charakterystycznego mogą być wyrażone jako

i

i

i

j

s

ω

σ +

=

, i = 1, 2,..., n.

Jeśli m z n pierwiastków jest jednokrotnych natomiast pozostałe pierwiastki są wielokrotne, to
wówczas odpowiedź układu może być wyrażona w następującej postaci

Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

2

∑

∑

−

−

=

=

+

=

1

0

1

)

(

m

n

i

t

s

i

i

m

i

t

s

i

i

i

e

t

L

e

K

t

y

(3)

gdzie K

i

oraz L

i

są stałymi współczynnikami. Czynniki ekspotencjalne

t

s

i

e

w równaniu (3) decydują

o odpowiedzi y(t) gdy

∞

→

t

. Aby spełniony był warunek (2), części rzeczywiste s

i

muszą być

ujemne. Innymi słowy pierwiastki równania charakterystycznego muszą się znajdować w lewej
półpłaszczyźnie. W ten prosty oto sposób przez znalezienie rozkładu biegunów transmitancji można
określić czy układ jest stabilny czy też nie. Bardzo często spotyka się sytuacje w których pojedyncze
pierwiastki równania charakterystycznego znajdują się na osi liczb urojonych, wówczas mówi się
o takim układzie, że znajduje się na granicy stabilności.

Ponieważ pierwiastki równania charakterystycznego są takie same jak wartości własne

macierzy A uzyskanej z równań stanu, to i w tym przypadku warunki stabilności dla wartości
własnych są takie same. Możliwe warunki stabilności układu zebrane są w tabeli 1 z uwzględnieniem
do równania charakterystycznego.

Przykład 1

Poniższy przykład ilustruje warunki stabilności układu w odniesieniu do biegunów
transmitancji, które są również pierwiastkami równania charakterystycznego.

( )(

)(

)

3

2

1

)

4

(

20

)

(

+

+

+

−

=

s

s

s

s

s

G

Układ stabilny

(

)

( )

(

)

2

2

1

3

20

)

(

2

+

+

−

+

=

s

s

s

s

s

G

Układ niestabilny z powodu bieguna s = 1

(

)

( )

4

2

)

1

(

20

)

(

2

+

+

−

=

s

s

s

s

G

Układ na granicy stabilności z powodu biegunów w

2

j

s

±

=

( )

(

)

10

4

20

)

(

2

2

+

+

=

s

s

s

G

Układ niestabilny z powodu biegunów wielokrotnych w

2

j

s

±

=

(

)

10

2

)

1

(

1

10

)

(

2

+

−

+

+

=

s

s

s

s

s

s

G

Układ niestabilny z powodu biegunów w

3

1

j

s

±

=

Tabela 1. Warunki stabilności układów liniowych ciągłych i stacjonarnych

Warunki stabilności

Wartości pierwiastków

Asymptotycznie stabilny

0

<

i

σ

dla wszystkich i, i = 1, 2,..., n. (Wszystkie pierwiastki znajdują się

w lewej półpłaszczyźnie)

Na granicy stabilności

0

=

i

σ

dla pewnych pojedynczych pierwiastków oraz brak

0

>

i

σ

dla

i = 1, 2,..., n. (Przynajmniej jeden pojedynczy pierwiastek oraz brak
pierwiastków wielokrotnych na osi

ω

j

; brak pierwiastków w prawej

półpłaszczyźnie)

Niestabilny

0

>

i

σ

dla pewnych pierwiastków i, lub

0

=

i

σ

dla pewnych

pierwiastków wielokrotnych. i = 1, 2,..., n. (Przynajmniej jeden
pojedynczy pierwiastek w prawej półpłaszczyźnie lub przynajmniej
jeden pierwiastek wielokrotny na osi

ω

j

.

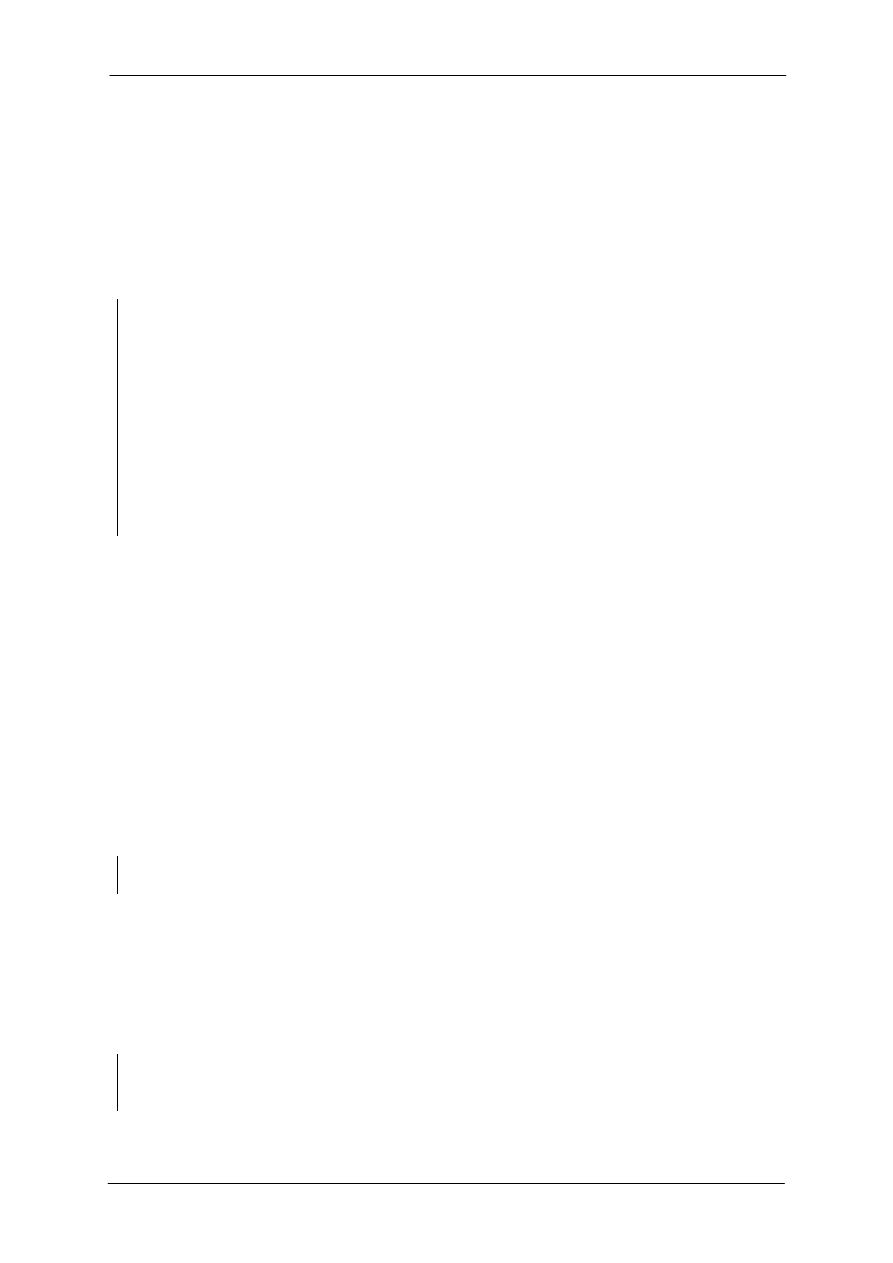
Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

3

3. METODY OKREŚLANIA STABILNOŚCI

Kiedy znane są wszystkie parametry układu to wówczas pierwiastki równania charakterystycznego
mogą zostać znalezione przez użycie odpowiedniego oprogramowania, dla przykładu w MATLABie
pierwiastki wielomianu charakterystycznego M(s) znajduje się przy użyciu funkcji

roots

, natomiast

wartości własne macierzy A przy użyciu funkcji

eig

.

Dla celów projektowania, kiedy nie wszystkie parametry równania charakterystycznego są

znane, nie jest możliwe zastosowanie programów komputerowych znajdujących pierwiastki. Metody
wymienione poniżej są dobrze znane i stosowane do określania stabilności liniowych układów
ciągłych, bez znajdowania pierwiastków.

1. Kryteria Routha i Hurwitza. Kryteria te są metodami algebraicznymi dostarczającymi

informacji o stabilności absolutnej liniowych układów ciągłych, stacjonarnych mających
równania charakterystyczne ze stałymi współczynnikami. Kryteria te sprawdzają czy są
pierwiastki równania charakterystycznego, które znajdują się w prawej półpłaszczyźnie. Przy
użyciu kryterium Routha możliwe jest również określenie liczby pierwiastków znajdujących
się na osi liczb urojonych i w prawej półpłaszczyźnie.

2. Kryterium Nyquista. Kryterium to jest metodą wykreślną dającą informację o różnicy

pomiędzy liczbą biegunów i zer transmitancji układu zamkniętego które są w prawej
półpłaszczyźnie przez obserwację zachowania wykresu Nyquista transmitancji pętli.

3. Charakterystyki logarytmiczne Bodego. Wykresy amplitudy transmitancji pętli

( ) ( )

ω

ω

j

H

j

G

w decybelach i fazy

( ) ( )

ω

ω

j

H

j

G

w stopniach, obie w funkcji pulsacji

ω

. Stabilność układu

zamkniętego może zostać określona przez obserwację zachowania tych wykresów.

Projektant dokonuje właściwego wyboru najlepszego narzędzia analitycznego w danej sytuacji.
Poniżej zamieszczony został szczegółowy opis kryterium stabilności Routha i Hurwitza.

4. KRYTERIUM ROUTHA I HURWITZA

Kryteria Routha i Hurwitza są metodami określania położeń zer wielomianu ze stałymi
współczynnikami rzeczywistymi z uwzględnieniem do prawej lub lewej półpłaszczyzny, bez
dokładnego wyznaczania ich położeń. Programy komputerowe mogą łatwo wyznaczyć zera
wielomianów, kryteria Routha i Hurwitza pozwalają na rozwiązywanie równań z nieznanymi
parametrami.

Równanie charakterystyczne układu liniowego stacjonarnego z pojedynczym wejściem i

pojedynczym wyjściem na następującą postać

0

...

)

(

1

1

2

2

1

1

=

+

+

+

+

+

=

−

−

−

n

n

n

n

n

a

s

a

s

a

s

a

s

s

M

(4)

gdzie wszystkie współczynniki są rzeczywiste. Aby równanie (4) nie miało pierwiastków z częścią
rzeczywistą dodatnią konieczne jest aby spełnione były następujące warunki:

1. Wszystkie współczynniki równania muszą mieć ten sam znak.
2. Żadnego ze współczynników nie może brakować

Te dwa warunki mogą być bardzo łatwo sprawdzone i szybko można udzielić odpowiedzi, czy w
prawej półpłaszczyźnie znajdują się pierwiastki. Są to jednak warunki niewystarczające, możliwe jest
że wszystkie współczynniki występują i są tego samego znaku, a mimo to są pierwiastki w prawej
półpłaszczyźnie.

4.1. KRYTERIUM HURWITZA
Kryterium Routha opiera się na kryterium Hurwitza, które brzmi następująco:

Warunkiem koniecznym i wystarczającym na to, aby wszystkie pierwiastki równania (4)
znajdowały się w lewej półpłaszczyźnie jest, aby wszystkie wyznaczniki Hurwitza
D

k

, > 0, k = 1, 2, ..., n.

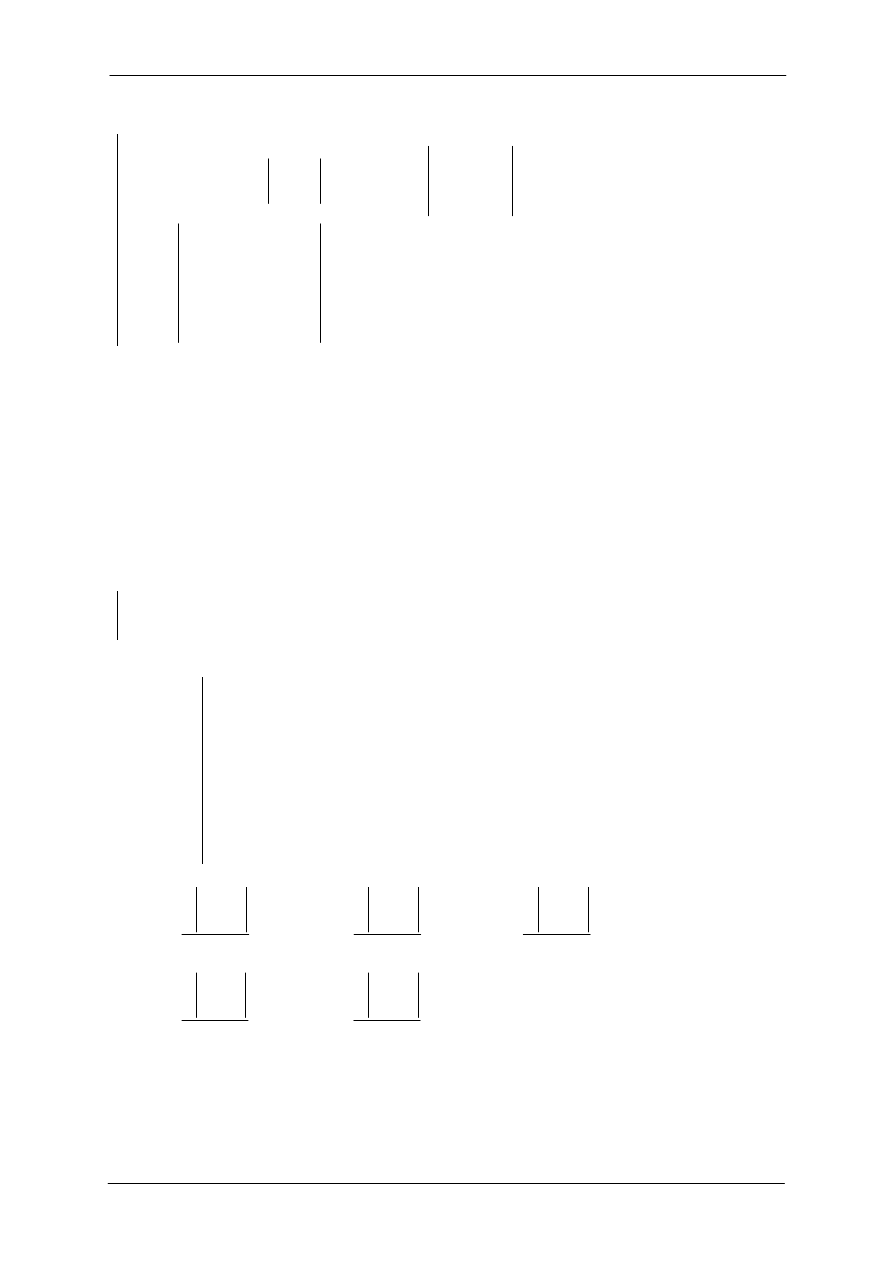
Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

4

Wyznaczniki Hurwitza D

k

są wyznaczane z następujących wzorów:

D

1

=

1

a

,

2

3

1

2

1

a

a

a

D

=

3

1

5

4

2

3

1

2

0

1

a

a

a

a

a

a

a

D

=

n

n

a

a

a

a

a

a

a

a

D

...

0

0

0

...

...

...

...

...

0

...

0

...

0

...

0

1

3

4

5

1

2

3

1

=

(5)

Zastosowanie wyznaczników Hurwitza jest bardzo kłopotliwe dla równań wyższych rzędów, gdyż
wzrasta nakład pracy potrzebny do obliczenia wszystkich wyznaczników w równaniu (5). Na
szczęście Edward John Routh w 1874 roku uprościł ten proces przez wprowadzenie metody tablicowej
w miejsce wyznaczników Hurwitza.

4.2. TABLICA ROUTHA

Pierwszym krokiem w uproszczeniu kryterium Hurwitza, nazywanym kryterium Routha, jest
umieszczenie współczynników równania (4) w dwóch wierszach. Pierwszy wiersz składa się
z nieparzystych współczynników, natomiast drugi wiersz z parzystych współczynników licząc od
najwyższej potęgi wielomianu charakterystycznego. Dla równania (4) pierwsze dwa wiersze tablicy są
następujące:

...

...

1

7

5

3

1

6

4

2

a

a

a

a

a

a

a

Następnym krokiem jest wypełnienie następnych wierszy tablicy Routha w następujący sposób:

n

s

1

2

a

4

a

6

a

1

−

n

s

1

a

3

a

5

a

7

a

2

−

n

s

1

b

2

b

3

b

3

−

n

s

1

c

2

c

3

c

.

.

.

.

.

.

.

.

.

.

.

.

0

s

1

h

gdzie

1

3

1

2

1

1

a

a

a

a

b

−

=

1

5

1

4

2

1

a

a

a

a

b

−

=

1

7

1

6

3

1

a

a

a

a

b

−

=

1

2

1

3

1

1

b

b

b

a

a

c

−

=

1

3

1

5

1

2

b

b

b

a

a

c

−

=

i tak dalej. Kolumna z lewej strony tablicy Routha jest kolumną odniesienia i służy do identyfikacji
obliczeń. Ostatni wiersz tablicy Routha ma zawsze w tej kolumnie element s

0

. Po skompletowaniu

tablicy Routha ostatnim krokiem jest określenie znaków współczynników pierwszej kolumny tablicy,
która zawiera informacje o pierwiastkach równania. Przyjęte zostało następujące założenie:

Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

5

Wszystkie pierwiastki równania charakterystycznego znajdują się w lewej półpłaszczyźnie jeśli
wszystkie elementy pierwszej kolumny tablicy Routha mają ten sam znak. Liczba zmian znaków
w elementach pierwszej kolumny równa jest liczbie pierwiastków w prawej półpłaszczyźnie.

Przykład 2

Rozważmy równanie

M(s) = s

4

+2s

3

+ 3s

2

+ 4s + 5 = 0

(2.1)

w którym nie brakuje elementów i wszystkie współczynniki są tego samego znaku. Spełniony
jest warunek konieczny dotyczący współczynników, jednak warunek dostateczny musi zostać
jeszcze sprawdzony. Pierwszą czynnością jest zainicjowanie tablicy, w kolumnie z lewej strony
znajdują się potęgi s, natomiast współczynniki wielomianu rozdziela się pomiędzy pierwszy
i drugi wiersz w sposób pokazany poniżej. W pierwszym wierszu znajdują się w kolejności
współczynniki nieparzyste, natomiast w drugim parzyste

4

s

1

3

5

4

s

1

3

5

3

s

2

4

0

3

s

2

4

0

Drugi wiersz można podzielić przez 2

1

2

Tablica kompletowana jest poczynając od góry wiersz po wierszu, obliczając elementy
następnego wiersza. Każdy obliczany element wyprowadzany jest na podstawie czterech
elementów znajdujących się w dwóch wyższych wierszach, dwa z nich są w lewej kolumnie
i dwa w kolumnie znajdującej się na prawo od obliczanego elementu. W każdym przypadku,
obliczany element ma ujemny wyznacznik z czterech znajdujących się wyżej elementów,
podzielony jest przez lewy dolny element wyznacznika. Dla przykładu, pierwszy element
wiersza s

2

1

2

4

2

3

1

=

−

drugi element wiersza s

2

5

2

0

2

5

1

=

−

pierwszy element wiersza s

1

6

1

5

1

4

2

−

=

−

i tak dalej.

4

s

1

3

5

4

s

1

3

5

4

s

1

3 5

3

s

2

4

0

3

s

2

4

0

3

s

2

4

2

s

1

2

s

1

5

2

s

1

5

1

s

1

s

1

s

−

6

0

s

0

s

0

s

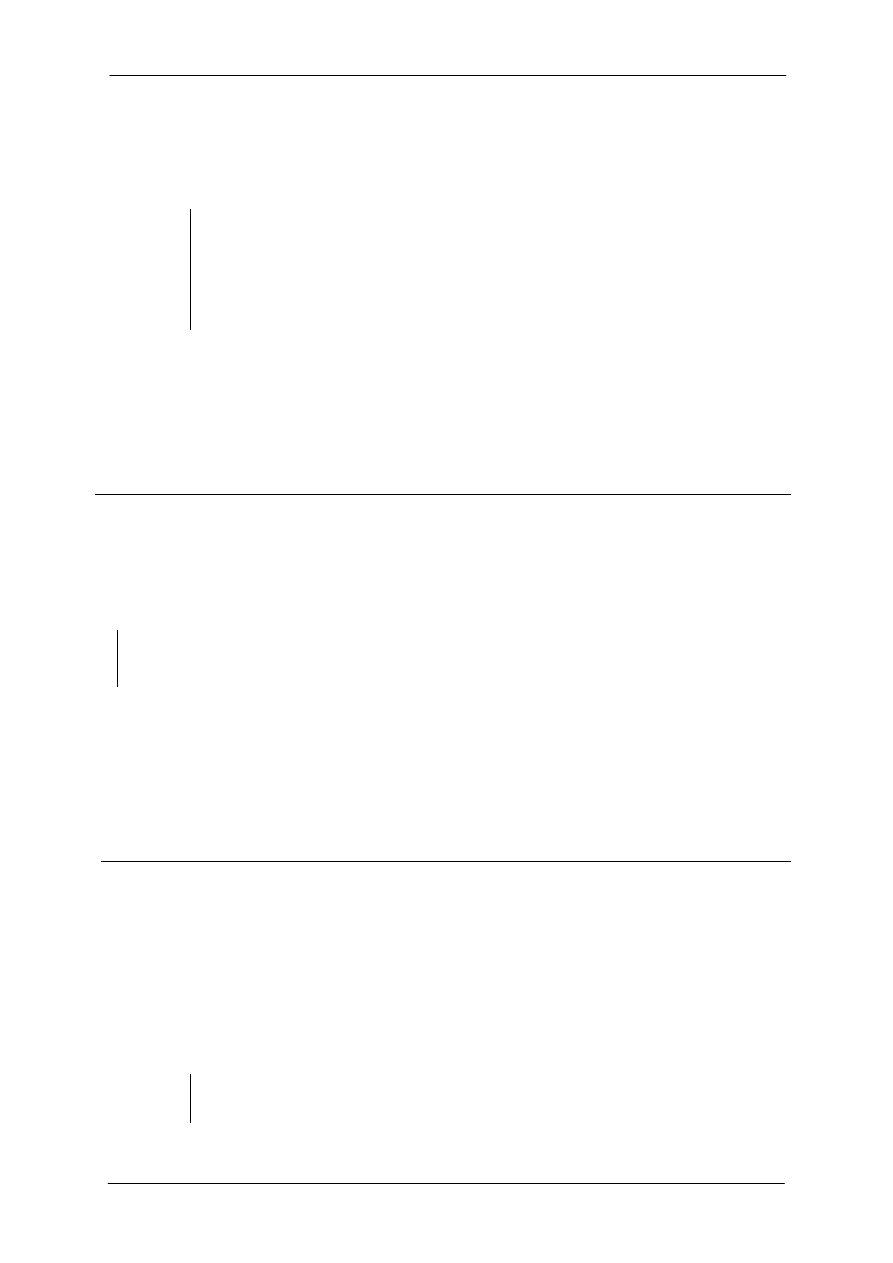
Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

6

Skompletowana tablica Routha pokazana jest poniżej. Liczba pierwiastków wielomianu M(s)
znajdująca się w prawej półpłaszczyźnie jest równa liczbie zmian znaków lewej kolumny
tablicy, przesuwając się z góry na dół.

4

s

1

3

5

3

s

2

4

2

s

1

5

1

s

−

6

0

s

5

W tym przykładzie są dwie zmiany znaków w lewej kolumnie co oznacza, że wielomian M(s)
ma dwa pierwiastki w prawej półpłaszczyźnie. Rozwiązując równanie (2.1) otrzymuje się cztery
pierwiastki 4161

.

1

2878

.

0

2

,

1

j

s

±

=

oraz

8578

.

0

2878

.

1

4

,

3

j

s

±

−

=

. Rzeczywiście dwa ostatnie

pierwiastki znajdują się w prawej półpłaszczyźnie, co powoduje że układ jest niestabilny.
Zauważ, że współczynniki w drugim wierszu można podzielić przez pewną dodatnią liczbę
w celu uproszczenia obliczeń. Sprawdź, czy uzyskasz takie same wartości wyznaczanych
współczynników po podzieleniu współczynników drugiego wiersza przez 2.

4.3. PRZYPADKI SZCZEGÓLNE TABLICY ROUTHA

W przykładzie 2 obliczanie kolejnych współczynników przebiegało bez komplikacji. Zależnie od
rodzajów współczynników wielomianu mogą się pojawić pewne trudności w obliczaniu kolejnych
elementów tablicy Routha.

1. Pierwszy element w pewnym wierszu tablicy Routha jest zerowy, lecz nie wszystkie

współczynniki są równe zero.

2. Wszystkie elementy pewnego wiersza tablicy Routha są zerowe.

4.3.1. Zero w pierwszej kolumnie tablicy Routha

W pierwszym przypadku, jeśli zero pojawia się w pierwszym elemencie wiersza, wówczas wszystkie
elementy w następnym wierszu mają wartości równe nieskończoności i dalsze wypełnianie tablicy nie
jest możliwe. Aby poradzić sobie z tą sytuacją zastępuje się pierwszy element w pierwszej kolumnie
przez bardzo mała liczbę dodatnią

ε

i kontynuuje się obliczanie pozostałych elementów. Przypadek

ten zostanie zilustrowany przez następujący przykład.

Przykład 3

Rozważmy następujące równanie charakterystyczne układu liniowego

0

2

6

2

3

3

)

(

2

3

4

5

6

=

−

−

+

+

−

−

=

s

s

s

s

s

s

s

M

(3.1)

Nie wszystkie współczynniki mają ten sam znak, czyli na pewno występują pierwiastki
w prawej półpłaszczyźnie. Sprawdźmy przy użyciu kryterium Routha ile pierwiastków znajduje
się w prawej półpłaszczyźnie. Przy kompletowaniu tablicy Routha dwa pierwsze wiersze
uzyskuje się bezpośrednio ze współczynników wielomianu. Brakujące współczynniki uzupełnia
się zerami.

6

s

1

−1

2

−

2

5

s

−

3

3

−

6

0

Współczynniki drugiego wiersza można podzielić przez 3, co pozwoli na uproszczenie obliczeń.

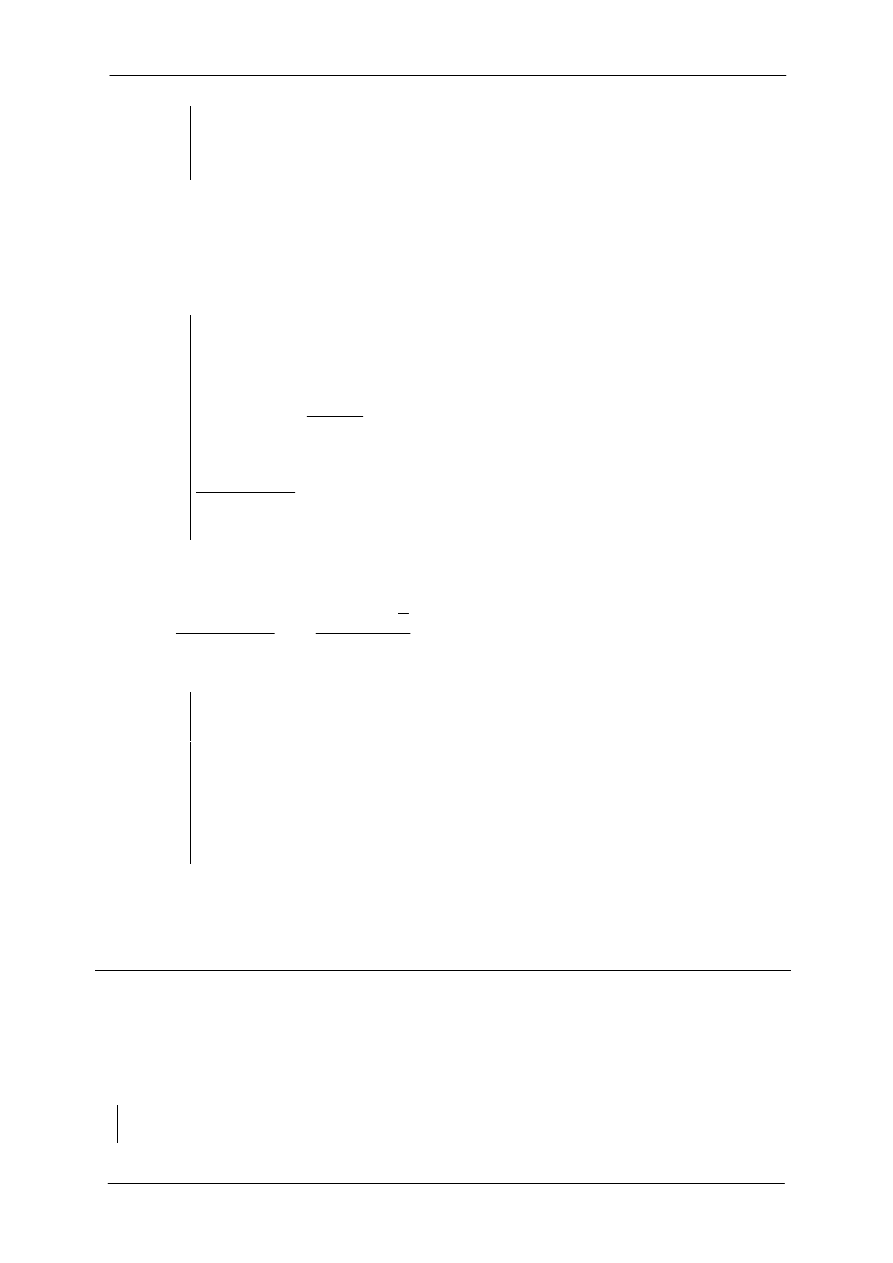
Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

7

6

s

1

−1

2

−

2

5

s

−1

1

−

2

0

4

s

0

0

−

2

0

Tablica ta nie może być dalej kompletowana w zwykły sposób, ponieważ nie można dzielić
przez zero. W pierwszej kolumnie pojawiło się zero, przy czym nie cały wiersz jest zerowy.
Sytuacja z zerem w pierwszej kolumnie rozwiązywana jest w ten sposób, że zamiast zera
wprowadza się bardzo małą liczbę dodatnią

ε

. Dla powyższego wielomianu zastępując zero

w pierwszej kolumnie przez

ε

i po wyznaczeniu kolejnych elementów tablicy w zależności od

ε

otrzymuje się

6

s

1

−1

2

−

2

5

s

−1

1

−

2

0

4

s

ε

0

−

2

3

s

1

ε

ε

2

2

−

−

2

s

2

ε

+2

−

2

1

s

ε

ε

ε

ε

2

2

4

6

4

2

2

+

−

−

−

0

s

−

2

Dla wszystkich wyrażeń w pierwszej kolumnie zawierających

ε

wyznacza się granicę

0

→

ε

,

przy założeniu dodatniej wartości

ε

, na przykład dla

−∞

=

+

−

−

−

=

+

−

−

−

→

→

2

2

1

4

6

4

lim

2

2

4

6

4

lim

0

2

2

0

ε

ε

ε

ε

ε

ε

ε

ε

ε

Uzyskane znaki elementów pierwszej kolumny tablicy Routha

6

s

+

5

s

−

4

s

+

3

s

+

2

s

+

1

s

−

0

s

−

W tym przypadku są trzy zmiany znaku w pierwszej kolumnie, więc badany wielomian ma trzy
pierwiastki w prawej półpłaszczyźnie. Rozwiązując równanie (3.1) otrzymuje się cztery
pierwiastki

3158

.

0

1

−

=

s

, 6693

.

0

9018

.

0

3

,

2

j

s

±

−

=

, 7452

.

0

0553

.

1

5

,

4

j

s

±

=

oraz

0088

.

3

6

=

s

trzy ostatnie pierwiastki znajdują się w prawej półpłaszczyźnie.

4.3.2. Zerowy wiersz w tablicy Routha

W drugim przypadku szczególnym, kiedy wszystkie elementy w pewnym wierszu tablicy Routha są
zerowe dalsze wyznaczanie elementów jest przerywane, oznacza to, że istnieje jeden z następujących
przypadków:

1. Równanie ma przynajmniej jedną parę pierwiastków o przeciwnych znakach (rys. 1a).
2. Równanie ma jedną lub więcej par pierwiastków sprzężonych na osi urojonych (rys. 1b).

Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

8

3. Równanie ma pary pierwiastków tworzących symetrie wokół początku układu (rys 1c).

Powyższe trzy przypadki zostały zilustrowane na rysunku 1. W sytuacji gdy pojawia się cały wiersz
zerowy w tablicy Routha, tworzy się równanie pomocnicze p(s) = 0, które formuje się ze
współczynników wiersza znajdującego się powyżej wiersza zerowego w tablicy Routha.

Im

Re

-a

a

Im

Re

b

-b

Im

Re

-a

a

-b

b

(a)

(b)

(c)

Rys. 1. Możliwe położenia pierwiastków wielomianu w przypadku, gdy w tablicy Routha pojawia się wiersz

zerowy.

Rozwiązując równanie pomocnicze otrzymuje się również pierwiastki równania oryginalnego. Aby
dalej wypełniać tablicę Routha wykonuje się następujące kroki:

1. Tworzy się równanie pomocnicze p(s) = 0 przez użycie współczynników z wiersza znajdującego

się powyżej wiersza zerowego.

2. Wyznacza się pochodną równania pomocniczego względem s; daje to

0

/

)

(

=

ds

s

dp

.

3. Zastępuje się wiersz zerowy współczynnikami wielomianu

0

/

)

(

=

ds

s

dp

.

4. Kontynuuje się wypełnianie tablicy Routha z użyciem nowo utworzonego wiersza

współczynnikami zastępującymi wiersz zerowy.

5. Interpretuje się zmianę znaków współczynników w pierwszej kolumnie tablicy Routha w zwykłay

sposób.

Przykład 4

Rozważmy następujące równanie charakterystyczne układu liniowego

0

8

2

2

5

)

(

2

3

4

5

6

=

−

−

+

+

+

+

=

s

s

s

s

s

s

s

M

(4.1)

z badania współczynników widać, że w wielomianie występują pierwiastki z prawej
półpłaszczyzny.

Tablica Routha zaczyna się następująco:

6

s

1

5

2

−

8

5

s

1

1

−

2

0

4

s

4

4

−

8

współczynniki wiersza s

4

można podzielić przez 4

4

s

1

1

−

2

po podzieleniu przez 4

3

s

0

0

Pojawił się wiersz zerowy. Wprowadzamy równanie pomocnicze ze współczynników
znajdujących się nad wierszem zerowym w wierszu s

4

0

2

)

(

2

4

=

−

+

=

s

s

s

p

(4.2)

Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

9

Różniczkując wielomian p(s) względem s otrzymuje się

(

)

0

2

4

2

)

(

3

2

4

=

+

=

−

+

=

s

s

s

s

ds

d

ds

s

dp

(4.3)

Otrzymanymi współczynnikami 4 oraz 2 zastępujemy wiersz zerowy.

3

s

4

2

Współczynniki równania dp(s)/ds

Współczynniki uzyskanego wiersza można podzielić przez 2. Pozostała część tablicy Routha
jest następująca

3

s

2

1

Uproszczone wartości współczynników równania dp(s)/ds

2

s

2

1

−

2

1

s

9

0

s

−

2

Wielomian pomocniczy jest czwartego rzędu, czyli w równaniu (4.1) występują dwie pary
pierwiastków. Z badania pierwszej kolumny tablicy Routha uzyskanej dla równania (4.1) widać,
że występuje jedna zmiana znaku, czyli jedna para pierwiastków jest o przeciwnych znakach
(rys. 1a), Dwa pozostałe pierwiastki muszą znajdować się na osi urojonej (rys. 1b). Z analizy
tablicy Routha dla tego przykładowego wielomianu wyznaczyliśmy następujące typy
pierwiastków:

Lewa półpłaszczyzna LP = 3
Prawa półpłaszczyzna PP = 1
Oś urojona IA = 2

Przy użyciu kryterium Routha takie informacje mogą być uzyskane dla każdego wielomianu.
Rozwiązując równanie pomocnicze (4.2) znajdujemy cztery następujące pierwiastki

1

1

−

=

s

,

1

2

=

s

, 4142

.

1

4

,

3

j

s

±

=

, które są również pierwiastkami równania (4.1). Pierwiastki połączone

w pary mają w tablicy Routha wiersz zerowy. Ponieważ w tym przypadku równanie
pomocnicze było czwartego rzędu, więc występowały dwie pary pierwiastków połączonych:
jedna o przeciwnych znakach, a druga sprzężona.

5. UKŁADY ZE STROJONYMI PARAMETRAMI

Bardzo często potrzebna jest wiedza o zakresie lub zakresach przestrajalnego parametru K dla których
układ jest stabilny. Poniższe przykłady ilustrują praktyczne wykorzystanie kryterium Routha
w prostych problemach projektowych.

Przykład 5

Rozważony zostanie prosty układ z jednostkowym sprzężeniem zwrotnym. Należy znaleźć
zakres wzmocnienia K przy którym układ ten będzie stabilny oraz jeśli to możliwe, wyznaczyć
wartość wzmocnienia K przy którym układ generuje drgania o stałej amplitudzie (posiada
bieguny sprzężone na osi urojonej) oraz okres tych oscylacji.

R(s)

Y(s)

s+1

s(s+2)(s

2

+2s+9)

K

Dla powyższego układu transmitancja zastępcza układu zamkniętego jest następująca:

Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

10

( )

(

)

K

s

K

s

s

s

s

K

s

R

s

Y

s

G

+

+

+

+

+

+

=

=

18

13

4

1

)

(

)

(

)

(

2

3

4

(5.1)

i równanie charakterystyczne:

(

)

0

18

13

4

)

(

2

3

4

=

+

+

+

+

+

=

K

s

K

s

s

s

s

M

(5.2)

Tablica Routha dla równania (5.2):

4

s

1

13

K

3

s

4

18+K

2

s

4

34 K

−

K

1

s

K

K

−

−

34

612

2

0

s

K

Na podstawie powyższej tablicy uzyskuje się dwa warunki stabilności: z wiersza s

2

,

otrzymanym warunkiem stabilności jest 34

−

K > 0, z wiersza s

1

warunek

(

−

K

2

+ 612)/(34

−

K) > 0, natomiast dla s

0

warunek

K > 0.

2

s

K < 34

1

s

−

24.739 < K < 24.739

0

s

K > 0

Z rozważenia tych dwóch warunków otrzymany zakres stabilności dla parametru K

0 < K < 24.739

(5.3)

Układ znajdzie się na granicy stabilności jeśli w tablicy Routha w wierszu s

1

pojawią się same

zera, natomiast współczynnik w wierszu s

0

będzie większy od zera. Dla układu opisanego

równaniem charakterystycznym (5.2) uzyskuje się wówczas warunek 612

−

K

2

= 0, czyli

K

kr

= 24.739

(5.4)

Częstotliwość oscylacji wyznacza się z wiersza przy s

2

, w tym przypadku wielomian

pomocniczy uzyskany z wiersza przy s

2

0

4

34

2

=

+

−

kr

kr

K

s

K

(5.5)

Podstawiając do równania (5.5) warunek przy którym układ jest na granicy stabilności (5.4)
czyli K

kr

= 24.739 uzyskuje się z rozwiązania dwa pierwiastki sprzężone umiejscowione na osi

urojonej punktach

j

j

s

±

=

±

=

ω

2

,

1

3.269. W układzie pojawią się oscylacje o stałej amplitudzie,

gdy wzmocnienie będzie wynosiło K = 24.739, natomiast okres tych oscylacji

[ ]

s

T

osc

922

.

1

269

.

3

2

2

=

=

=

π

ω

π

Przykład 6

Rozważony zostanie układ opisany przy użyciu równań stanu, należy tak jak w przykładzie 5
znaleźć zakres wzmocnienia K przy którym układ ten będzie stabilny oraz jeśli to możliwe,
wyznaczyć wartość wzmocnienia K przy którym układ generuje drgania o stałej amplitudzie
oraz okres tych oscylacji.

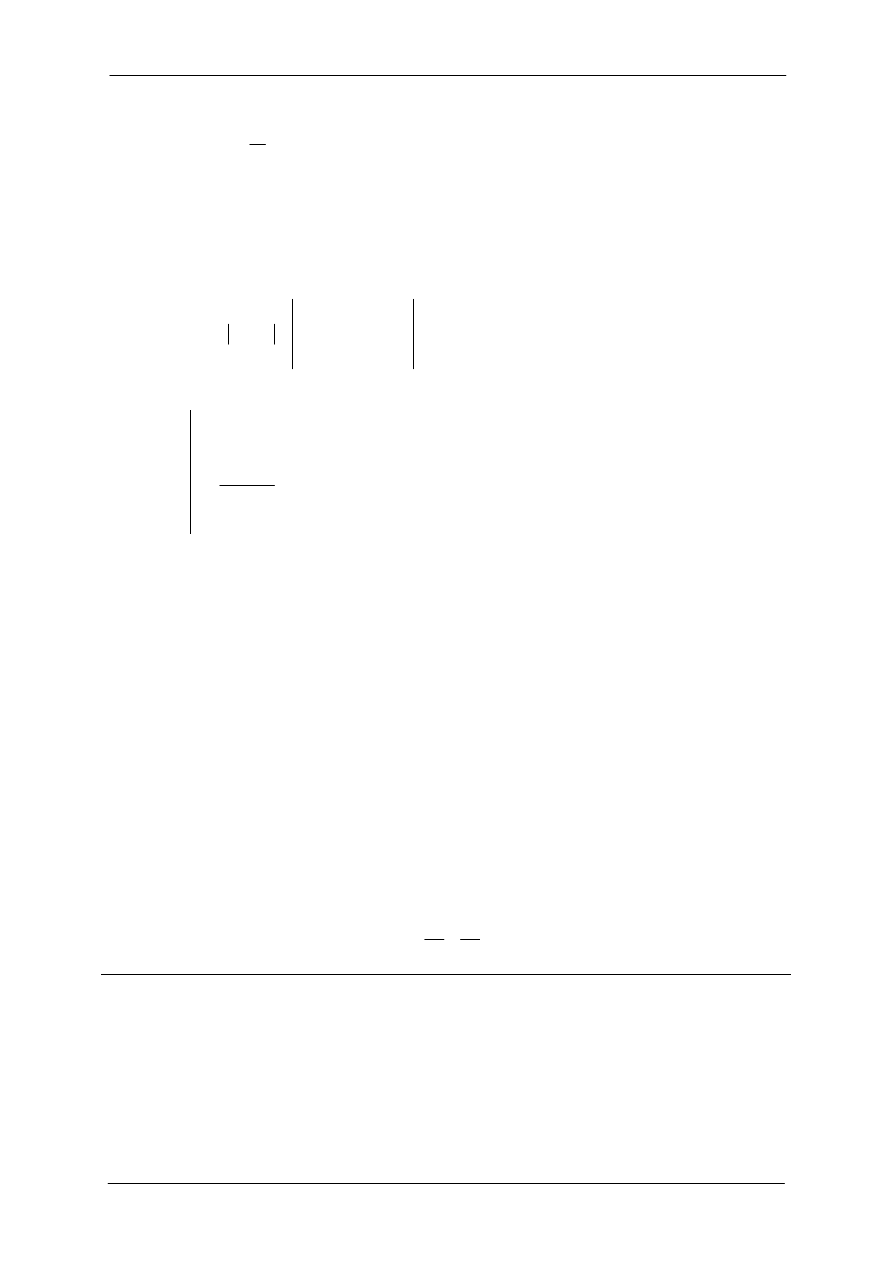
Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

11

)

(

1

0

0

0

0

6

1

4

3

0

1

0

3

2

1

3

2

1

t

u

x

x

x

K

K

x

x

x

dt

d

⋅





















+





















⋅





















−

−

−

−

=





















(6.1)

[

]





















⋅

=

3

2

1

6

0

)

(

x

x

x

K

K

t

y

(6.2)

Dla układu opisanego równaniami (6.1) oraz (6.2), równanie charakterystyczne jest następujące:

(

)

0

6

3

4

0

6

1

4

3

0

1

2

3

=

+

+

+

+

=

−

+

+

−

=

−

K

s

K

s

s

s

K

s

K

s

s

A

I

(6.3)

Tablica Routha dla równania (6.3):

3

s

1

3+K

2

s

4

6K

1

s

4

2

12

K

−

0

s

6K

Na podstawie powyższej tablicy uzyskuje się dwa warunki stabilności: z wiersza s

1

,

otrzymanym warunkiem stabilności jest 12

−

2K > 0, natomiast z wiersza s

0

warunek K > 0. Po

rozważeniu tych dwóch warunków otrzymany zakres dla parametru K przy którym układ
opisany równaniami (6.1) oraz (6.2) będzie stabilny

0 < K < 6

(6.4)

Układ znajdzie się na granicy stabilności jeśli w tablicy Routha w wierszu s

1

pojawią się same

zera, natomiast współczynnik w wierszu s

0

będzie większy od zera. Dla układu opisanego

równaniem charakterystycznym (6.3) uzyskuje się wówczas warunek 12

−

2K = 0, czyli

K = 6

(6.5)

Częstotliwość oscylacji wyznacza się z wiersza przy s

2

, w tym przypadku wielomian

pomocniczy uzyskany z wiersza przy s

2

0

6

4

2

=

+

K

s

(6.6)

Podstawiając do równania (6.6) warunek przy którym układ jest na granicy stabilności (6.5)
czyli K = 6 uzyskuje się z rozwiązania dwa pierwiastki sprzężone umiejscowione na osi
urojonej punktach

3

2

,

1

j

j

s

±

=

±

=

ω

. W układzie pojawią się oscylacje o stałej amplitudzie, gdy

wzmocnienie będzie wynosiło K = 6, natomiast okres tych oscylacji

[ ]

s

T

09

.

2

3

2

2

osc

=

=

=

π

ω

π

Trzeba zaznaczyć, że kryterium Routha daje poprawne wyniki jeśli współczynniki wielomianu
charakterystycznego są liczbami rzeczywistymi. Jeśli wystąpią współczynniki zespolone lub uzyskane
równanie nie jest algebraiczne, gdyż zawiera funkcje ekspotencjalne lub wykładnicze wówczas
kryterium Routha nie może być stosowane. Innym ograniczeniem tego kryterium jest to, że określenie
pierwiastków równania charakterystycznego uzyskujemy z dokładnością do półpłaszczyzny.

Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

12

ZAGADNIENIA KONTROLNE

1. Czy kryterium Routha może być zastosowane do analizy stabilności następujących układów?

a)

0

2

3

2

5

)

(

2

2

3

4

=

+

+

+

+

=

−

s

e

s

s

s

s

s

M

b)

0

3

5

)

(

2

2

3

4

=

+

+

+

−

=

K

Ks

s

s

s

s

M

2. Dwa pierwsze wiersze tablicy Routha układu trzeciego rzędu są następujące:

3

s

2

2

2

s

4

4

Wybierz poprawną odpowiedź z następującej listy
a) Równanie ma jeden pierwiastek w prawej półpłaszczyźnie PP.
b) Równanie ma dwa pierwiastki na osi urojonych IA w punktach s = j oraz s =

−

j. Trzeci

pierwiastek znajduje się w lewej półpłaszczyźnie LP.

c) Równanie ma dwa pierwiastki na osi urojonych IA w punktach s = 2j oraz s =

−

2j. Trzeci

pierwiastek znajduje się w lewej półpłaszczyźnie LP.

d) Równanie ma dwa pierwiastki na osi urojonych IA w punktach s = 2j oraz s =

−

2j. Trzeci

pierwiastek znajduje się w prawej półpłaszczyźnie PP.

3. Jeśli w pierwszej kolumnie tablicy Routha wszystkie znaki są ujemne, wówczas równanie dla

którego utworzona została ta tablica ma przynajmniej jeden pierwiastek znajdujący się w prawej
półpłaszczyźnie PP.

(Tak) (Nie)

4. Pierwiastki równania pomocniczego, p(s) = 0, uzyskane z tablicy Routha muszą być również

pierwiastkami równania charakterystycznego.

(Tak) (Nie)

5. Poniższe równanie charakterystyczne opisuje układ niestabilny, gdyż zawiera współczynniki

ujemne.

(Tak) (Nie)

0

10

5

)

(

2

3

=

+

+

−

=

s

s

s

s

M

6. Poniższe równanie charakterystyczne opisuje układ niestabilny, gdyż posiada współczynnik

zerowy.

(Tak) (Nie)

0

4

5

)

(

2

3

=

+

+

=

s

s

s

M

7. Jeśli w tablicy Routha znajduje się wiersz zerowy, oznacza to, że równanie ma pierwiastki na osi

urojonych IA zmiennej zespolonej s.

(Tak) (Nie)

ĆWICZENIA

C.1.

Bez korzystania z kryterium Routha

zaklasyfikuj układy o poniższych
transmitancjach do jednej z trzech klas:
stabilny, na granicy stabilności, niestabilny.

a)

( ) (

)

3

1

)

3

(

10

)

(

2

+

+

−

=

s

s

s

s

G

b)

(

)

10

2

1

10

)

(

2

+

−

+

=

s

s

s

s

s

G

c)

(

)

(

)

10

9

4

)

(

2

2

+

+

−

=

s

s

s

s

s

G

d)

10

2

10

)

(

2

+

+

=

s

s

s

G

e)

( )(

)(

)

5

3

1

1

)

(

−

+

+

−

=

s

s

s

s

s

G

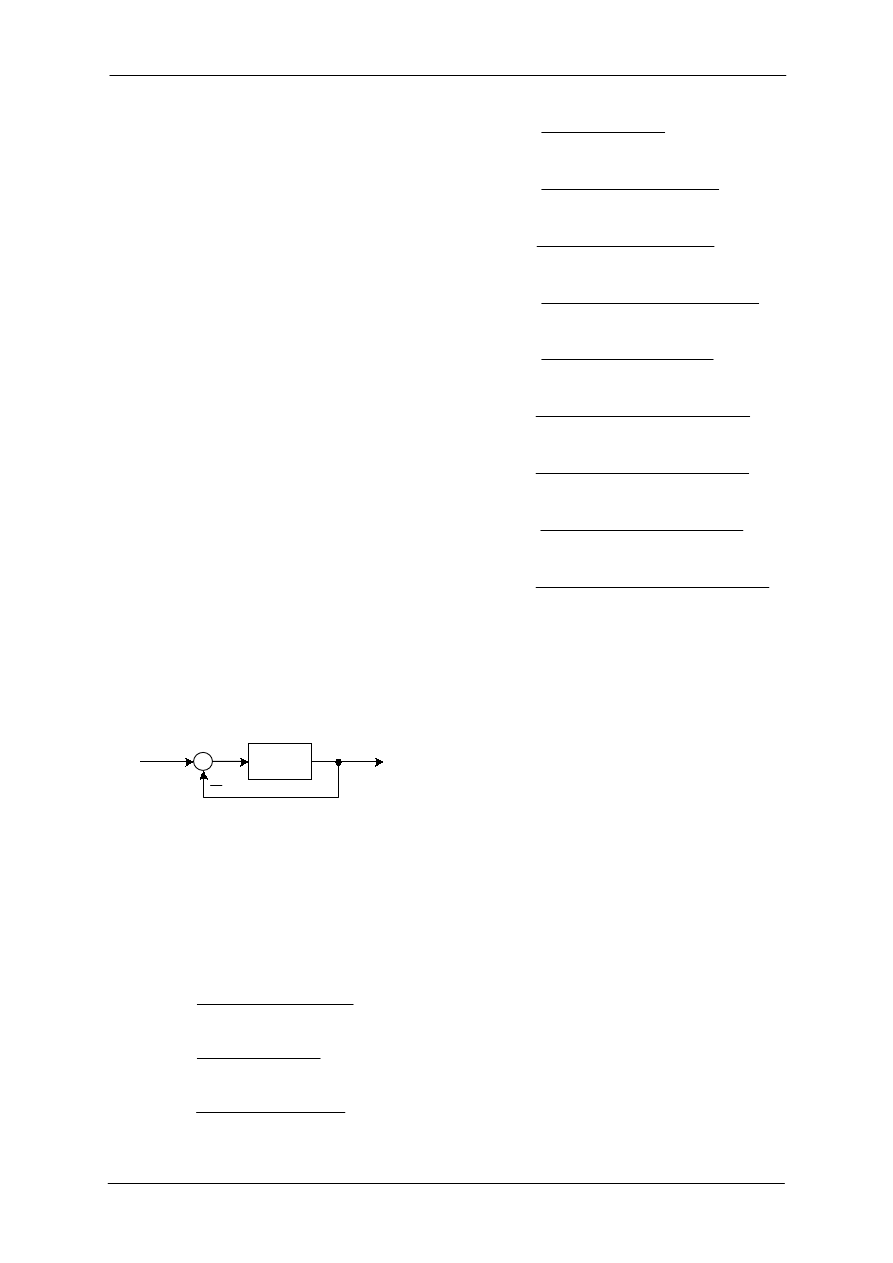
Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

13

C.2.

Korzystając z kryterium Routha, określ ile

pierwiastków poniższego wielomianu znajduje
się:

•

w prawej półpłaszczyźnie PP:

•

na osi urojonej IA:

•

w lewej półpłaszczyźnie LP:

a)

0

4

3

2

4

=

+

+

s

s

b)

0

14

4

5

2

2

3

4

=

−

−

+

+

s

s

s

s

c)

0

4

2

6

3

2

2

3

4

5

=

+

+

+

+

+

s

s

s

s

s

d)

0

2

3

3

5

=

+

+

s

s

s

e)

0

6

3

2

4

2

2

3

4

5

=

+

+

+

+

+

s

s

s

s

s

f)

0

16

16

20

15

8

2

2

3

4

5

6

=

+

+

+

+

+

+

s

s

s

s

s

s

g)

0

4

3

2

2

3

4

5

=

+

+

+

+

+

s

s

s

s

s

h)

0

25

25

6

6

2

3

4

5

=

+

+

+

+

+

s

s

s

s

s

i)

0

12

16

11

8

2

2

3

4

5

=

+

+

+

+

+

s

s

s

s

s

j)

0

2

3

4

4

2

3

4

5

=

−

+

−

+

−

s

s

s

s

s

k)

0

2

2

3

3

2

3

4

5

=

−

+

−

+

−

s

s

s

s

s

l)

0

2

2

4

2

2

2

3

4

5

6

=

−

+

−

−

+

−

s

s

s

s

s

s

C.3.

Dla obiektów opisanych poniższymi

transmitancjami operatorowymi objętymi
jednostkowym ujemnym sprzężeniem
zwrotnym

G(s)

R(s)

R(s)

przy użyciu kryterium Routha, określ ile
pierwiastków równania charakterystycznego
znajduje się:

•

w prawej półpłaszczyźnie PP:

•

na osi urojonej IA:

•

w lewej półpłaszczyźnie LP:

Na podstawie tych rozważań, stwierdź czy
rozważany układ jest stabilny asymptotycznie?

a)

2

7

9

5

1

)

(

2

3

4

+

+

+

+

+

−

=

s

s

s

s

s

s

G

b)

s

s

s

s

s

s

G

2

3

2

)

(

2

3

4

+

+

+

+

=

c)

2

6

7

2

)

(

2

3

4

+

+

+

+

−

=

s

s

s

s

s

s

G

d)

s

s

s

s

s

s

s

G

4

5

3

2

)

(

2

3

4

2

+

+

+

+

+

=

e)

1

2

2

1

3

)

(

2

3

4

5

2

3

4

+

−

−

+

−

−

+

+

−

=

s

s

s

s

s

s

s

s

s

s

G

f)

1

2

2

1

4

4

)

(

2

3

4

5

2

3

−

−

+

+

−

−

+

−

=

s

s

s

s

s

s

s

s

s

G

g)

15

10

10

7

2

3

6

)

(

2

3

4

5

2

3

+

+

+

+

+

−

+

+

=

s

s

s

s

s

s

s

s

s

G

h)

3

2

3

)

(

2

3

4

5

2

3

+

+

+

+

+

−

+

+

=

s

s

s

s

s

s

s

s

s

G

i)

2

2

2

1

)

(

2

3

4

5

6

2

+

+

+

+

+

+

−

−

=

s

s

s

s

s

s

s

s

s

G

j)

3

4

2

1

)

(

2

3

4

5

6

2

3

+

+

+

+

+

+

−

−

+

=

s

s

s

s

s

s

s

s

s

s

G

k)

1

2

5

5

5

3

)

(

2

3

4

5

6

2

3

+

+

+

+

+

+

−

−

−

−

=

s

s

s

s

s

s

s

s

s

s

G

l)

1

10

6

4

3

3

5

2

3

)

(

2

3

4

5

6

2

3

4

+

+

+

+

+

+

+

+

−

+

=

s

s

s

s

s

s

s

s

s

s

s

G

C.4.

Znajdź zakres przestrajalnego parametru K

dla którego układy opisane poniższymi
równaniami charakterystycznymi są stabilne.
Jeśli to możliwe, wyznacz wartość
wzmocnienia K przy którym układ generuje
drgania o stałej amplitudzie oraz okres tych
oscylacji.

a)

(

)

(

)

0

6

8

2

2

3

=

+

+

+

+

+

s

K

s

K

s

b)

(

)

(

)

0

10

3

4

2

6

2

2

3

=

+

+

+

−

+

s

K

s

K

s

c)

0

10

10

5

2

3

4

=

+

+

+

+

K

s

s

Ks

s

d)

0

4

2

2

2

3

4

=

+

+

+

+

+

K

s

s

s

s

e)

(

)

0

10

5

4

2

3

=

+

+

+

+

s

K

Ks

s

f)

(

)

0

1

2

2

3

3

=

+

+

+

s

s

K

s

g)

( )

(

) ( )

0

1

4

1

2

2

=

+

+

+

+

s

K

s

s

s

h)

0

10

20

2

2

3

=

+

+

+

K

s

s

s

i)

(

)

(

)

0

2

3

3

3

=

+

+

+

+

s

K

s

s

s

j)

(

) (

)

0

1

1

2

2

2

3

=

+

+

+

+

+

+

s

s

K

s

s

s

s

k)

(

)(

)(

)

0

10

5

2

=

+

+

+

+

K

s

s

s

s

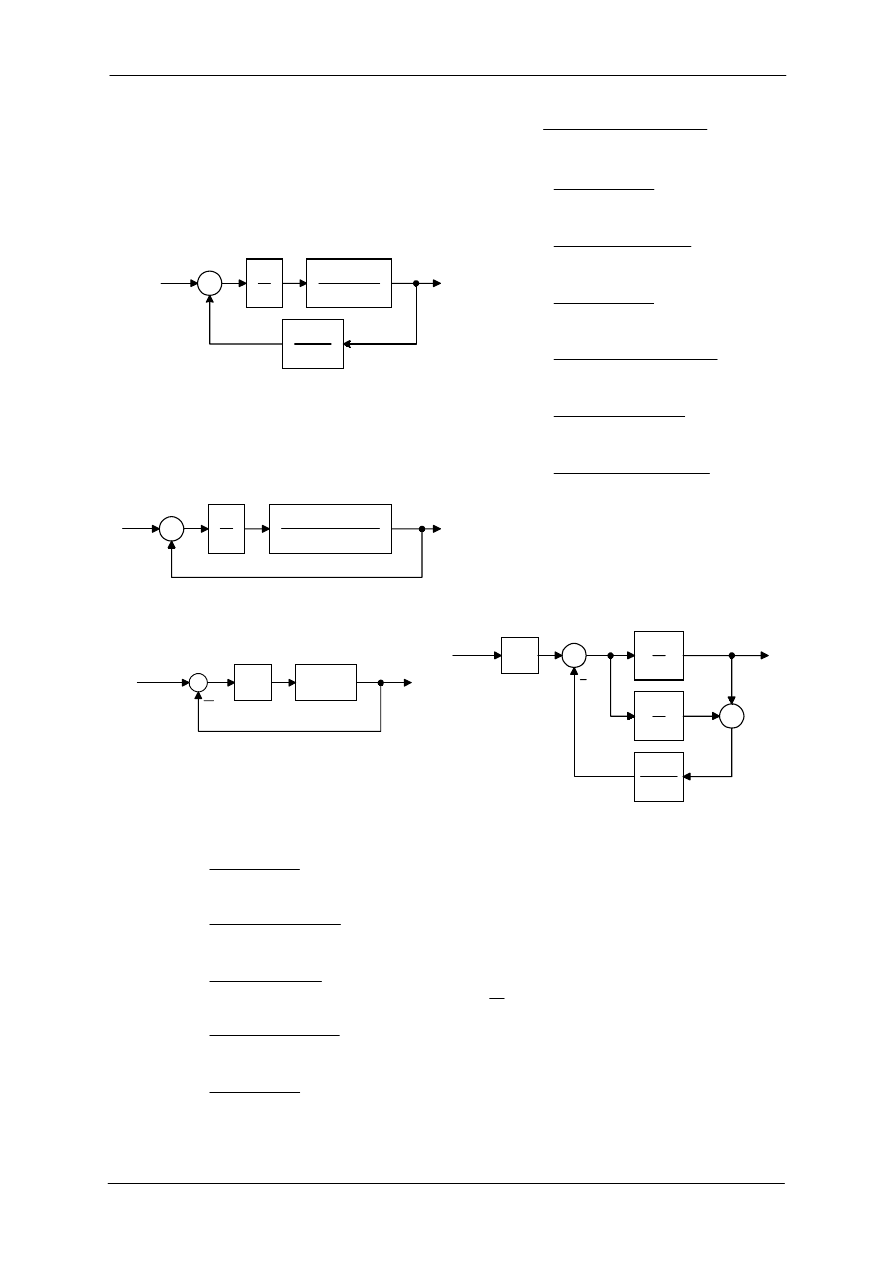
Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

14

l)

(

) (

)(

)

(

)

0

4

6

5

2

2

2

=

+

+

+

+

+

s

K

s

s

s

C.5.

Znajdź zakres stałej K, dla której poniższy

układ jest stabilny. Jeśli to możliwe, wyznacz
wartość wzmocnienia K przy którym układ
generuje drgania o stałej amplitudzie oraz
okres tych oscylacji.

R(s)

Y(s)

K

s

10

s

2

+ s + 10

−

1

s + 2

C.6.

Znajdź zakres stałej K, dla której

poniższy układ jest stabilny. Jeśli to możliwe,
wyznacz wartość wzmocnienia K przy
którym układ generuje drgania o stałej
amplitudzie oraz okres tych oscylacji.

R(s)

Y(s)

K

s

s + 1

(s + 2)(s

2

+ s + 1)

−

C.7.

Dla układów o poniższych

transmitancjach objętych pętlą
jednostkowego sprzężenia zwrotnego,

R(s)

Y(s)

G(s)

K

znajdź zakres stałej K, dla której poniższy
układ jest stabilny. Jeśli to możliwe, wyznacz
wartość wzmocnienia K przy którym układ
generuje drgania o stałej amplitudzie oraz
okres tych oscylacji.

a)

( )(

)

2

1

1

)

(

+

+

=

s

s

s

s

G

b)

(

)

(

)

5

4

10

1

)

(

2

+

+

+

=

s

s

s

s

G

c)

1

3

2

10

)

(

2

3

+

+

+

+

=

s

s

s

s

s

G

d)

( )

(

)

25

6

1

2

)

(

2

+

+

+

−

=

s

s

s

s

s

G

e)

( )(

)

( ) (

)

3

1

2

1

)

(

2

+

−

+

+

=

s

s

s

s

s

G

f)

(

)

(

)( )

1

4

2

2

2

)

(

2

−

+

+

+

+

=

s

s

s

s

s

s

G

g)

2

3

4

2

6

4

10

2

)

(

s

s

s

s

s

s

G

+

+

+

+

=

h)

s

s

s

s

s

s

s

G

12

3

3

2

3

)

(

2

3

4

2

+

+

+

+

−

=

i)

2

3

4

2

5

2

2

3

)

(

s

s

s

s

s

s

G

+

+

+

+

=

j)

4

10

9

4

3

)

(

2

3

4

2

+

+

+

+

+

=

s

s

s

s

s

s

s

G

k)

2

3

4

2

3

6

5

4

7

15

2

)

(

s

s

s

s

s

s

s

G

+

+

+

+

+

=

l)

5

2

4

3

40

38

11

)

(

2

3

4

2

3

+

+

+

+

+

+

+

=

s

s

s

s

s

s

s

s

G

C.8.

Dla poniższego układu znajdź wartość stałej

K przy układ ten jest stabilny. Wyznacz
wartość wzmocnienia K przy którym układ
generuje drgania o stałej amplitudzie oraz
okres tych oscylacji. Jaki wówczas będzie
okres oscylacji o stałej amplitudzie.

R(s)

Y(s)

K
s

2

2

s

1

s + 1

s

2

C.9.

Dla układu opisanego za pomocą równań

stanu, znajdź zakres stałej K, dla której
poniższy układ jest stabilny. Jeśli to możliwe,
wyznacz wartość wzmocnienia K przy
którym układ generuje drgania o stałej
amplitudzie oraz okres tych oscylacji.

)

(

8

0

0

0

10

8

1

0

3

0

1

6

3

2

1

3

2

1

t

u

K

K

x

x

x

K

K

x

x

x

dt

d

⋅





















+





















⋅





















+

−

−

−

−

=





















[

]





















⋅

=

3

2

1

0

0

1

)

(

x

x

x

t

y

Teoria sterowania

Badanie stabilności - kryterium Routha

Ostatnia aktualizacja: 2010-01-23



M. Tomera

15

ODPOWIEDZI DO WYBRANYCH ĆWICZEŃ

C1.

a) stabilny.
b) niestabilny.
c) na granicy stabilności
d) stabilny.
e) niestabilny.

C2.

a) PP = 2; IA = 0, LP = 2,
b) PP = 1; IA = 0, LP = 3,
c) PP = 0; IA = 4, LP = 1,
d) PP = 2; IA = 1, LP = 2,
e) PP = 2; IA = 0, LP = 3,
f) PP = 4; IA = 0, LP = 2,
g) PP = 2; IA = 0, LP = 3,
h) PP = 2; IA = 0, LP = 3,
i) PP = 0; IA = 2, LP = 3,
j) PP = 3; IA = 0, LP = 2,
k) PP = 1; IA = 4, LP = 0,
l) PP = 3; IA = 0, LP = 3,

C3.

a) PP = 0; IA = 0, LP = 4, Tak
b) PP = 2; IA = 0, LP = 2, Nie
c) PP = 0; IA = 3, LP = 1, Nie
d) PP = 2; IA = 0, LP = 2, Nie
e) PP = 2; IA = 1, LP = 2, Nie
f) PP = 1; IA = 4, LP = 0, Nie
g) PP = 0; IA = 2, LP = 3, Nie
h) PP = 2; IA = 1, LP = 2, Nie
i) PP = 2; IA = 0, LP = 4, Nie
j) PP = 2; IA = 0, LP = 4, Nie
k) PP = 1; IA = 2, LP = 3, Nie
l) PP = 0; IA = 4, LP = 2, Nie

C4.

a) K >

−

1.127;

kr

K

=

−

1.127,

osc

T

= 2.4 [s]

b)

2

3

1

<

<

−

K

;

kr

K

=

3

1

−

,

osc

T

= 5.13 [s]

kr

K

= 2,

osc

T

= 2.81 [s]

c) Układ niestabilny dla każdej wartości K
d) Układ niestabilny dla każdej wartości K
e) K > 0.458;

kr

K

= 0.458,

osc

T

= 2.69 [s]

f) układ niestabilny dla każdego K
g) K > 0
h) 0 < K < 4;

kr

K

= 4,

osc

T

= 2.81 [s]

i) Układ niestabilny dla każdej wartości K
j) K > 0
k) 0 < K < 436;

kr

K

= 436,

osc

T

= 2.59 [s]

l) K >

−

30

C5.

0 < K < 3.55;

kr

K

= 3.55,

osc

T

= 2.43 [s]

C6.

0 < K < 2.24;

kr

K

= 2.24,

osc

T

= 5.28 [s]

C7.

a) 0 < K < 6;

kr

K

= 6,

osc

T

= 4.4429 [s]

b)

−

50 < K < 580;

kr

K

= 580,

osc

T

= 0.9366 [s]

c)

−

0.1< K <0.625;

kr

K

=0.625,

osc

T

=3.3001[s]

d)

−

21.3333<K<12.5;

kr

K

=

−

21.3333,

osc

T

= 2.0209

e) K >2.4305;

kr

K

=2.4305,

osc

T

= 4.1507 [s]

f) 4 < K < 5.0278;

kr

K

= 5.0278,

osc

T

= 8.0743 [s]

g) K >28;

kr

K

=28,

osc

T

= 1.6793 [s]

h) 0.7192 < K < 2.7808;

kr

K

= 0.7192,

osc

T

= 3.4689 [s]

kr

K

= 2.7808,

osc

T

= 5.6903 [s]

i) 0< K <7.3333;

kr

K

=7.3333,

osc

T

=1.8945[s]

j)

−

2.4283 < K < 0;

kr

K

=

−

2.4283,

osc

T

= 7.6263 [s]

k) 0 < K <

∞

;

kr

K

=brak,

osc

T

= brak

l) 0.6651 < K <

∞

;

kr

K

=0.6651,

osc

T

= 2.5035 [s]

C8.

0 < K < 2;

kr

K

= 2,

osc

T

= 4.44 [s]

C9.

1.25 < K < 14;

kr

K

= 14,

osc

T

= 1.52 [s]

LITERATURA

1. Hostetter G.H., C.J. Savant, R.T. Stefani, Design of Feedback Control Systems, Saunders College

Publishing, 1989.

2. Kuo B. C. Automatic Control of Dynamic Systems, 7th ed, Addison-Wesley & Sons Inc., 1995.