Katedra Systemów Elektroniki Morskiej WETI PG

Marek S. Makowski: Obwody i Sygnały sem.2 – dwiczenia tablicowe_2011, konsultacje wt. 12-13

Wersja 2010

Bank Zadao Wzorcowych (omówienie rozwiązao, Kompendium Wiedzy Studenta)
URL:

http://www.eti.pg.gda.pl/katedry/ksem/pracownicy/Czeslaw.Stefanski/PomoceDydaktyczne/10

_ObwodyIsygnaly_semII/050_BankZadanWzorcowych_2010/

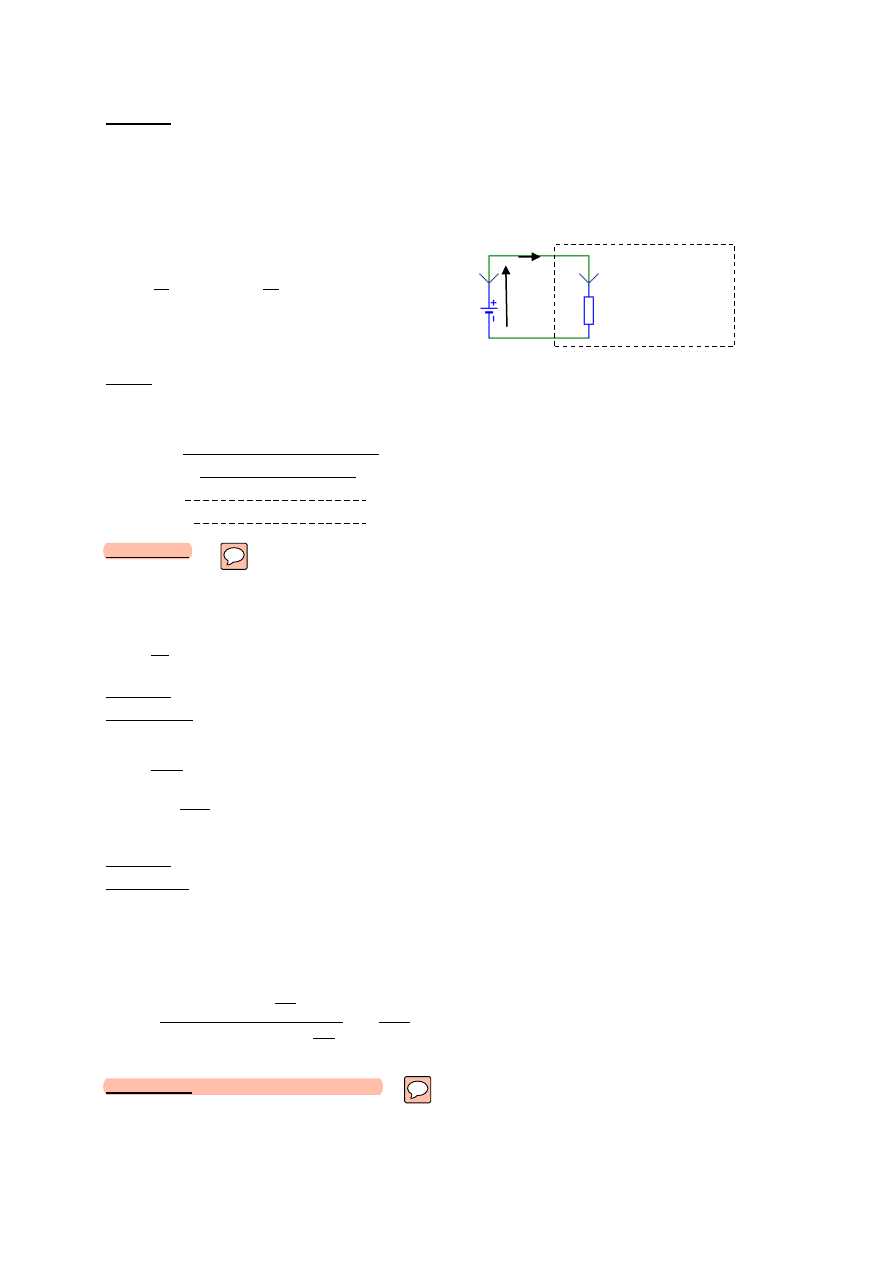
Zadanie 1 (wzmacniacz operacyjny)

a) wzmacniacz nieodwracajacy

Zapisujemy r-nie wg schematu powyżej:

Spostrzeżenie. Rezystor

nie ma wpływu na rozwiązanie (dlaczego ?)

b) wzmacniacz odwracający

Tym razem zapiszemy równanie postaci (korzystamy z zasady superpozycji):

c) w tym punkcie korzystamy z wyprowadzonych wyżej wzorów dla idealnego wzmacniacza

operacyjnego oraz z zasady superpozycji tj. znajdujemy odpowiedź (napięcie wyjściowe) jako
sumę odpowiedzi układu na dwa napięcia wejściowe z osobna:

Katedra Systemów Elektroniki Morskiej WETI PG

Marek S. Makowski: Obwody i Sygnały sem.2 – dwiczenia tablicowe_2011, konsultacje wt. 12-13

Wersja 2010

Zadanie 2 (rezystancja zastępcza)
b) skorzystamy z metody źródła pomiarowego

:

podłączamy źródło napięciowe

do zacisków obwodu (możemy alternatywnie podłączyd źródło

prądowe

) i wyznaczamy prąd

jaki popłynie w obwodzie (gdybyśmy podłączyli źródło prądowe

to wyznaczalibyśmy napięcie

jakie pojawi się na zaciskach obwodu), następnie znajdujemy

wejściową rezystancję jako:

ew.

Uwaga nt. wyłączania źródeł niezależnych (o ile występują w naszej sieci).
Przed „pomiarem” rezystancji

(lub konduktancji

) wejściowej należy wyłączyd

wszystkie niezależne źródła, mianowicie:
- wszystkie niezależne źródła napięciowe

zastępujemy źródłami o wydajności zerowej

(

czyli zastępujemy zwarciami

- wszystkie niezależne źródła prądowe

zastępujemy źródłami o wydajności zerowej

(

czyli zastępujemy rozwarciami

Rozwiązanie
Analizujemy obwód. Nie występują tu źródła niezależne. Po podłączeniu źródła pomiarowego

mamy tu 2 niewiadome napięcia i 2 (lub 3) niewiadome prądy. Zapisujemy kolejno 1 r-nie

napięciowe Kirchhoffa oraz 1 r-nie prądowe a następnie związki gałęziowe. Dostajemy

Zadanie 3 (rezystancja zastępcza)
Rozwiązanie (częściowe)
Jeżeli potencjał węzła 1-go

to zastępcza rezystancja wejściowa wyniesie:

gdzie

Zadanie 4 (bilans mocy)
Rozwiązanie (1-sza metoda)
W obwodzie mamy 4 niewiadome napięcia i 4 niewiadome prądy. Tworzymy układ 8 r-o:
NPK: 2 r-nia, PPK: 2 r-nia oraz 4 r-nia gałęziowe. Po uporządkowaniu dostajemy np. wyrażenie na
napięcie na źródle prądowym (2A) czyli potencjał węzła nr 1:

Rozwiązanie (2-a metoda, wydajniejsza)
Zadanie rozwiązujemy metodą potencjałów węzłowych. Mamy tylko 2 niewiadome i macierz
konduktancji węzłowych 2×2. (dokooczenie rozwiązania na str. 4)

I

p

E

p

R

in

Badana sied liniowa
z wyłączonymi źród-
łami niezależnymi

Katedra Systemów Elektroniki Morskiej WETI PG

Marek S. Makowski: Obwody i Sygnały sem.2 – dwiczenia tablicowe_2011, konsultacje wt. 12-13

Wersja 2010

Ważne

: Jak modyfikuje się metoda potencjałów węzłowych w obecności źródeł sterowanych ?

Załóżmy, że w obwodzie występują tylko źródła prądowe niezależne i sterowane napięciem (ten
przypadek ma miejsce w zadaniu). Postępujemy w 2-ch krokach:
1) traktujemy źródła sterowane jak źródła prądowe niezależne (czyli wpisujemy je w równaniu
macierzowym po prawej stronie w kolumnie wyrazów wolnych),
2) następnie porządkujemy r-nie przenosząc z prawej strony na lewą wyrazy zawierające niewiadome
potencjały węzłowe; w wyniku tego uporządkowania ulega modyfikacji macierz współczynników czyli
macierz konduktancji węzłowych; macierz ta może przestad byd macierzą symetryczną względem
głównej przekątnej.
Następnie wyznaczamy potencjały w znany sposób (np. metodą Cramera).

Analogiczna zasada postępowania obowiązuje w metodzie prądów oczkowych w obecności źródeł
napięciowych sterowanych prądem.

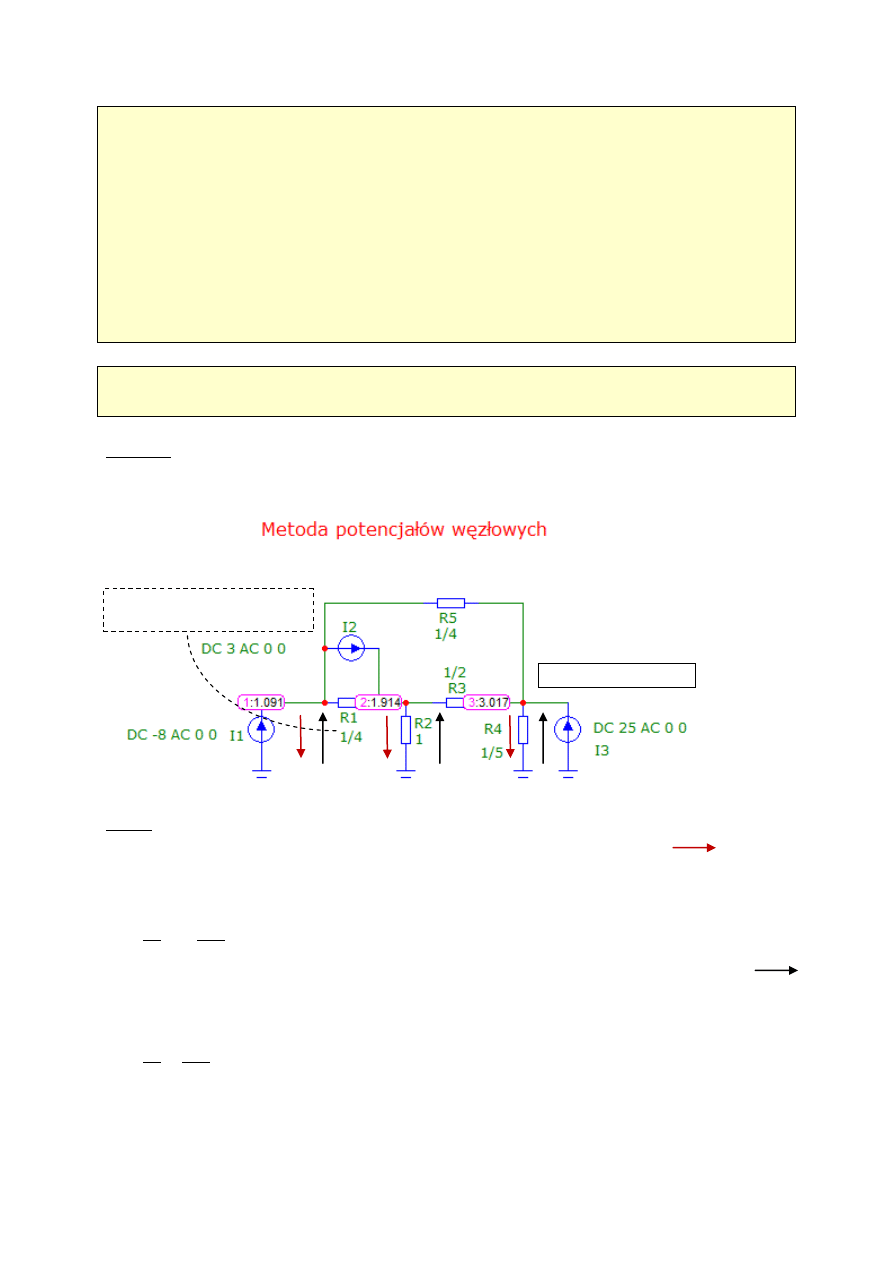
Zadanie 8 (metoda potencjałów węzłowych, rozwiązanie wspomagane komputerowo)

Uwaga nt. znaków źródeł prądowych (wektor wyrazów wolnych = wektor pobudzeo prądowych)
Np. potencjał węzła 1-go, przy przyjętej orientacji (zwrocie) potencjałów węzłowych

Potencjał węzła 1-go, przy orientacji potencjałów węzłowych jak w programie PSpice (MicroCap)

Zwrot źródła zgodny (+) lub przeciwny
(-) względem zwrotu potencjału węzła

I1, I2, I3 – źródła prądowe

Katedra Systemów Elektroniki Morskiej WETI PG

Marek S. Makowski: Obwody i Sygnały sem.2 – dwiczenia tablicowe_2011, konsultacje wt. 12-13

Wersja 2010

Zadania 4 i 5 (ciąg dalszy, szczegóły rozwiązania)
Dane

J[A]

R

1

*Ω+

R

2

*Ω+

E

3

[V]

R

4

*Ω+

g

m

[S]

Zadanie 4

2

1

2

5

3

0.3

Zadanie 5

3

1

2

2

3

0.3

Rozwiązanie
Analizujemy obwód. Metoda potencjałów węzłowych wymaga jako pobudzeo źródeł prądowych.
W przykładzie są 3 źródła: jedno niezależne źródło prądowe J (OK), jedno niezależne nieidealne
źródło napięciowe E

3

(to źródło zamieniamy na ekwiwalentne źródło prądowe o wydajności prądowej

oraz równoległej do źródła konduktancji wewnętrznej

. Trzecie

źródło (sterowane) pozostawiamy (w 1-szym kroku) bez zmian.

Wybieramy i oznaczamy graficznie węzeł zerowy (masa

) np. węzeł „dolny”. Pozostają dwa

niezależne węzły. Zaznaczamy zwroty wszystkich potencjałów węzłowych zgodnie np. „od masy do
węzła”, czyli groty strzałek skierowane do węzłów (1) i (2).
Zapiszmy teraz równanie macierzowe (dla ułatwienia bezpośrednio na liczbach – dane z Zad.4),
pamiętając o przyjętej konwencji znaków:
Ad.1) krok 1-szy:

Ad.2) krok 2-gi:
Napięcie

jest kombinacją liniową potencjałów węzłowych, mianowicie z NPK dostajemy:

Wstawiamy ten związek do równania macierzowego dostając:

Teraz nasze równanie wymaga uporządkowania gdyż wyrazy z niewiadomymi występują po prawej
stronie. Wyrazy te należy przenieśd na lewą stronę równania co spowoduje modyfikację macierzy
konduktancji węzłowych. Zauważmy, że jedynie 2-gi wiersz tej macierzy ulegnie zmianie. Otrzymamy:

Stąd potencjał węzła (1) wynosi:

(przyjęliśmy dla gałęzi źródła J zwroty stowarzyszone – przeciwnie strzałkowane napięcie i prąd)
Moc w źródle J liczymy jako:

jest to więc ze względu na znak moc dostarczana.

KONIEC cz .i