Sztuczne sieci neuronowe
Małgorzata Kr towska
Katedra Oprogramowania
e-mail: mmac@ii.pb.bialystok.pl
Wykład 4: Algorytmy optymalizacji
Sztuczne sieci neuronowe
2
Plan wykładu
• Algorytmy gradientowe optymalizacji
– Algorytm najwi kszego spadku
– Algorytm zmiennej metryki
– Algorytm gradientów sprz onych
• Algorytmy doboru współczynnika uczenia
– adaptacyjny dobór współczynnika uczenia
– dobór współczynnika przez minimalizacj kierunkow
– reguła delta-bar-delta
– metoda gradientów sprz onych z regularyzacj
• Algorytmy heurystyczne
– algorytm Quickprop
– algorytm RPROP
Sztuczne sieci neuronowe
3
Uczenie z nauczycielem
• Minimalizacja funkcji celu E
• Zakładaj c ci gł funkcj aktywacji, minimalizacja odbywa si
metodami gradientowymi
• W ka dym kroku uczenia wyznacza si tzw. kierunek minimalizacji p
(W(k))
• Korekcja wag odbywa si według wzoru:
gdzie
η jest współczynnikiem uczenia z przedziału [0, 1].
))
(
(
)
(
)
1
(
k
W
p
k
W
k
W
η
+
=
+
Sztuczne sieci neuronowe
4
Algorytmy gradientowe optymalizacji
Algorytmy gradientowe bazuj na rozwini ciu w szereg Taylora funkcji
celu E(
W) w najbli szym s siedztwie znanego rozwi zania W=
[w
1
,w
2
, ..., w
n
]
T
(na starcie algorytmu jest to punkt pocz tkowy W
0
):
gdzie:
+
+
+
=
+
p
W
H
p
p
W
g
W
E
p
W
E
T
T
)
(
2
1
)]
(
[
)
(
)
(
T
n
W
E
W
E
W
E
E
W
g
∂
∂
∂
∂
∂
∂
=
∇
=
,
,
,
)
(
2
1
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
n
n
n
n
W
W
E
W
W
E
W
W
E
W
W
E
W
H
1
1
1
1
)
(
Sztuczne sieci neuronowe
5
Algorytmy gradientowe optymalizacji
• Punkt W=W
k
jest punktem optymalnym funkcji E(W), je li
– g(W
k
)=0
– hesjan H(W
k
) jest dodatnio okre lony
• W praktyce ( ze wzgl du na na sko czon dokładno oblicze ) zakłada
si , e punkt W
k
jest punktem optymalnym, je eli:
gdzie
τ przyj ta dokładno oblicze
(
)
(
)
(
)
)
(
1
)
(
1
)
(
1
)
(
)
(
3
1
1
k
k
k
k
k
k
k
k
W
E
W
g
W
W
W
W
E
W
E
W
E
+
≤
+
≤
−
+
≤
−
−
−
τ
τ
τ
Sztuczne sieci neuronowe
6
Ogólny algorytm optymalizacji
Zakładamy W
0
=W
k
• Test: je eli W
k
spełnia warunki testowe jest punktem optymalnym to
ko czymy obliczenia, w przeciwnym przypadku pkt. 2
• Wyznaczanie wektora kierunku poszukiwa p
k
w punkcie W
k
.
• Minimalizacja kierunkowa funkcji E(W) na kierunku p
k
w celu
wyznaczenia takiej warto ci
η
k
, aby E(W
k
+
η
k
p
k
) < E(W
k
)
• Wyznaczenie nowego rozwi zania W
k+1
=W
k
+
η
k
p
k
oraz odpowiadaj cej
mu warto ci E(W
k
), g(W
k
) ( i ew. H(W
k
)) i powrót do pkt 1.
Ró nice: wyznaczanie kierunku poszukiwa p oraz kroku
η.
Sztuczne sieci neuronowe
7
Algorytm najwi kszego spadku
Ograniczenie do liniowego przybli enia funkcji E(W) w najbli szym
s siedztwie znanego rozwi zania W:
aby E(W
k+1
)<E(W
k
) wystarczy aby [g(W
k
)]
T
p < 0
Wektor kierunkowy w metodzie najwi kszego spadku przyjmuje posta :
p
k
=-g(W
k
)
)
(
)]
(
[
)
(
)
(
2
h
O
p
W
g
W
E
p
W
E
T
+
+
=
+
Sztuczne sieci neuronowe
8
Algorytm najwi kszego spadku
• Podej cie klasyczne
• Metoda momentu
Uwagi:
– na płaskich odcinkach
(dla =0.9 oznacza to 10 krotne przyspieszenie procesu uczenia)
– pozwala na wyj cie z minimów lokalnych
– nale y kontrolowa warto E
k
k
k
W
W
W
∆
+
=
+1
k
k
p
W
η
=
∆
)
(
1
−
−
+
=
∆
k
K
k
k
W
W
p
W
α
η
k
k
p
W
α
η
−
=
∆
1
Sztuczne sieci neuronowe
9
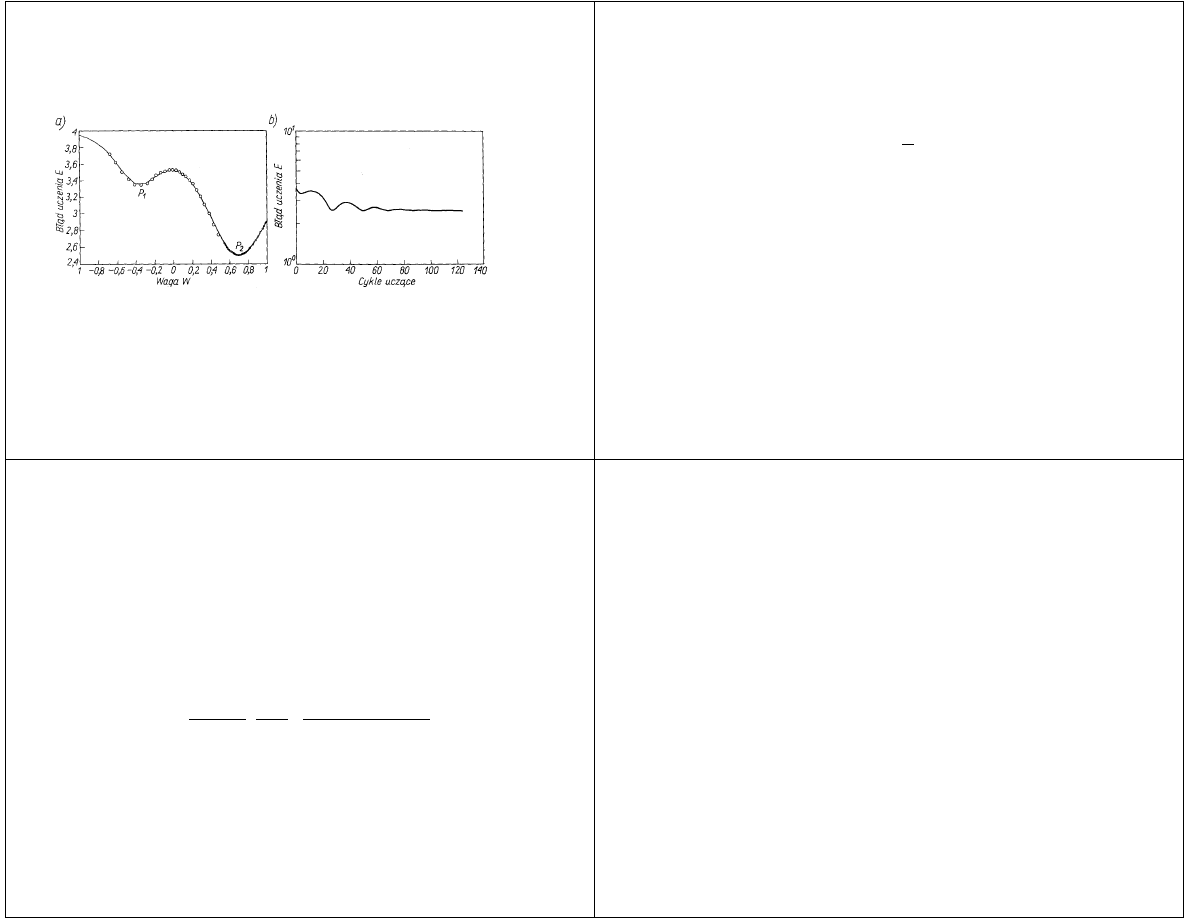
Algorytm najwi kszego spadku
Wykres wpływu działania momentu na proces uczenia
• Metoda „weight decay”
zabezpiecza przez zbytnim wzrostem wag
k
k
k
W
p
W
β
η
−
=
∆
k
k
k
W
p
W
β
η
−
=
∆
Sztuczne sieci neuronowe
10
Algorytm zmiennej metryki (quasi-Newtona)
Kwadratowe przybli enie funkcji E(W) w s siedztwie znanego
rozwi zania W
k
:
kierunek p jest wyznaczony ze wzoru:
Problemy:
– wymóg dodatniej okre lono ci hesjanu w ka dym kroku
Rozwi zanie
– zastosowanie przybli enia hesjanu przy u yciu metody zmiennej metryki
)
(
)
(
2
1
)]
(
[
)
(
)
(
3
h
O
p
W
H
p
p
W
g
W
E
p
W
E
T
T
+
+
+
=
+
)
(
)]
(
[
1
k
k
k
W
g
W
H
p
−
−
=
Sztuczne sieci neuronowe
11
Algorytm zmiennej metryki (quasi-Newtona)
Przybli enie hesjanu polega na modyfikacji hesjanu z kroku poprzedniego
o pewn poprawk , która powoduje, e aktualna warto hesjanu G(W
k
)
przybli a krzywizn funkcji celu E zgodnie z zale no ci :
G(W
k
)(W
k
-W
k-1
)=g(W
k
)-g(W
k-1
)
Na podstawie powy szego zało enia mo na otrzyma wzory okre laj ce
hesjan w kroku k-tym:
gdzie s
k
=W
k
-W
k-1
;
r
k
=g(W
k
)-g(W
k-1
);
V
l
=[G(W
k
)]
-1
.
k
T
k
T
k
k
k
k
T
k
k
k
T
k
T
k
k
k
T
k
k
k
T
k
k
k
r
s
s
r
V
V
r
s
r
s
s
s
r
s
r
V
r
V
V
1
1
1
1
1
−
−
−
−
+
−
+
=
Sztuczne sieci neuronowe
12
Algorytm zmiennej metryki (quasi-Newtona)
• warto startowa V
0
=1
• pierwsza iteracja zgodnie z algorytmem najwi kszego spadku
• odtwarzana macierz hesjanu jest w ka dym kroku dodatnio okre lona
(st d g(W
k
)=0 odpowiada rozwi zaniu problemu optymalizacji)
• metoda uwa ana za jedn z najlepszych metod optymalizacji funkcji
wielu zmiennych
Wady:
• stosunkowo du a zło ono obliczeniowa (n
2
elementów hesjanu)
• du e wymagania co do pami ci przy przechowywaniu macierzy hesjanu
Sztuczne sieci neuronowe
13
Metoda gradientów sprz onych
• rezygnacja z bezpo redniej informacji o hesjanie
• nowy kierunek poszukiwa ma by ortogonalny i sprz ony z poprzednim
kierunkami p
0
, p
1
, ..., p
k-1
, st d:
co mo na upro ci do postaci:
współczynnik sprz enia (g
k
=g(W
k
)):
Zbiór wektorów p
i
jest wzajemnie sprz ony wzgl dem macierzy H, je eli
−
=
+
−
=
1
0
)
(
k
j
j
kj
k
k
p
W
g
p
β
1
1
)
(
−
−
+
−
=
k
k
k
k
p
W
g
p
β
1
1
1
1
)
(
−
−
−
−
−
=
k
T
k
k
k
T
k
k
g
g
g
g
g
β
j
i
Hp
p
j
T
i
≠
= ,
0
Sztuczne sieci neuronowe
14
Metoda gradientów sprz onych
• metoda mniej skuteczna od metody zmiennej metryki, ale bardziej
skuteczna ni metoda najwi kszego spadku
• stosuje si j do optymalizacji przy bardzo du ej liczbie zmiennych
• ze wzgl du na bł dy zaokr gle w trakcie zatraca si własno
ortogonalno ci mi dzy wektorami kierunków minimalizacji. Po
wykonaniu n iteracji przeprowadza si jej ponowny start ( w I kroku
zgodnie z algorytmem najwi kszego spadku)
Sztuczne sieci neuronowe
15
Metody doboru współczynnika uczenia
Po okre leniu wła ciwego kierunku p
k
minimalizacji, nale y dobra
odpowiedni warto współczynnika uczenia, aby nowy punkt W
k+1
le ał mo liwie najbli ej minimum funkcji E(W) na kierunku p
k
k
k
k
k
p
W
W
η
+
=
+1
Sztuczne sieci neuronowe
16
Stały współczynnik uczenia
• Stały współczynnik uczenia
– stosuje si głównie w poł czeniu z metod najwi kszego spadku
– sposób najmniej efektywny, gdy nie uzale nia warto ci współczynnika od
od wektora gradientu oraz kierunku poszukiwa
p w danej iteracji
– algorytm ma skłonno utykania w minimach lokalnych
– cz sto dobór współczynnika odbywa si oddzielnie dla ka dej warstwy,
przyjmuj c
gdzie n
i
liczba wej i-tego neuronu w warstwie
≤
i
n
1
min
η
Sztuczne sieci neuronowe
17
Adaptacyjny dobór współczynnika uczenia
• zmiany współczynnika uczenia dopasowuj si do aktualnych zmian
warto ci funkcji celu w czasie. Warto bł du
ε w i-tej iteracji:
okre la strategi zmian warto ci współczynnika uczenia.
• Przyspieszenie procesu uczenia uzyskuje si poprzez ci głe zwi kszanie
współczynnika
η sprawdzaj c jednocze nie czy nie zacznie wzrasta w
porównaniu z bł dem obliczonym przy poprzedniej warto ci
η
(
)
=
−
=
M
j
j
j
d
y
1
2
ε
Sztuczne sieci neuronowe
18
Adaptacyjny dobór współczynnika uczenia
Adaptacja współczynnika uczenia:
gdzie:
ε
i-1
,
ε
i
- bł d odpowiednio w (i-1)-szej iteracji oraz w i-tej iteracji
η
i-1
;
η
i
- współczynnik uczenia w kolejnych iteracjach
k
w
- dopuszczalny współczynnik wzrostu bł du
ρ
d
- współczynnik zmniejszania warto ci
ρ
i
- współczynnik zwi kszaj cy warto
Przykładowe warto ci współczynników: k
w
= 1,04;
ρ
d
=0.7;
ρ
i
= 1.05
≤
>
=
−
−
+
1
1
1
i
w
i
i
i
i
w
i
d
i
i
k
gdy
k
gdy
ε
ε
ρ
η
ε
ε
ρ
η
η
Sztuczne sieci neuronowe
19
Adaptacyjny dobór współczynnika uczenia
Wpływ adaptacyjnego doboru współczynnika uczenia na proces uczenia
Sztuczne sieci neuronowe
20
Dobór współczynnika uczenia przez
minimalizacj kierunkow
• Polega na minimalizacji kierunkowej funkcji celu na wyznaczonym
wcze niej kierunku p
k
.
• Cel: takie dobranie warto ci η
k
aby nowy punkt W
k+1
=W
k
+
η
k
p
k
odpowiadał minimum funkcji celu na danym kierunku
– Je eli η
k
odpowiada dokładnie minimum funkcji na danym kierunku p
k
to
pochodna kierunkowa w punkcie W
k+1
=W
k
+
η
k
p
k
musi by równa 0
• W praktyce wyznaczony punkt W
k+1
odpowiada tylko w przybli eniu
rzeczywistemu punktowi minimalnemu na danym kierunku.
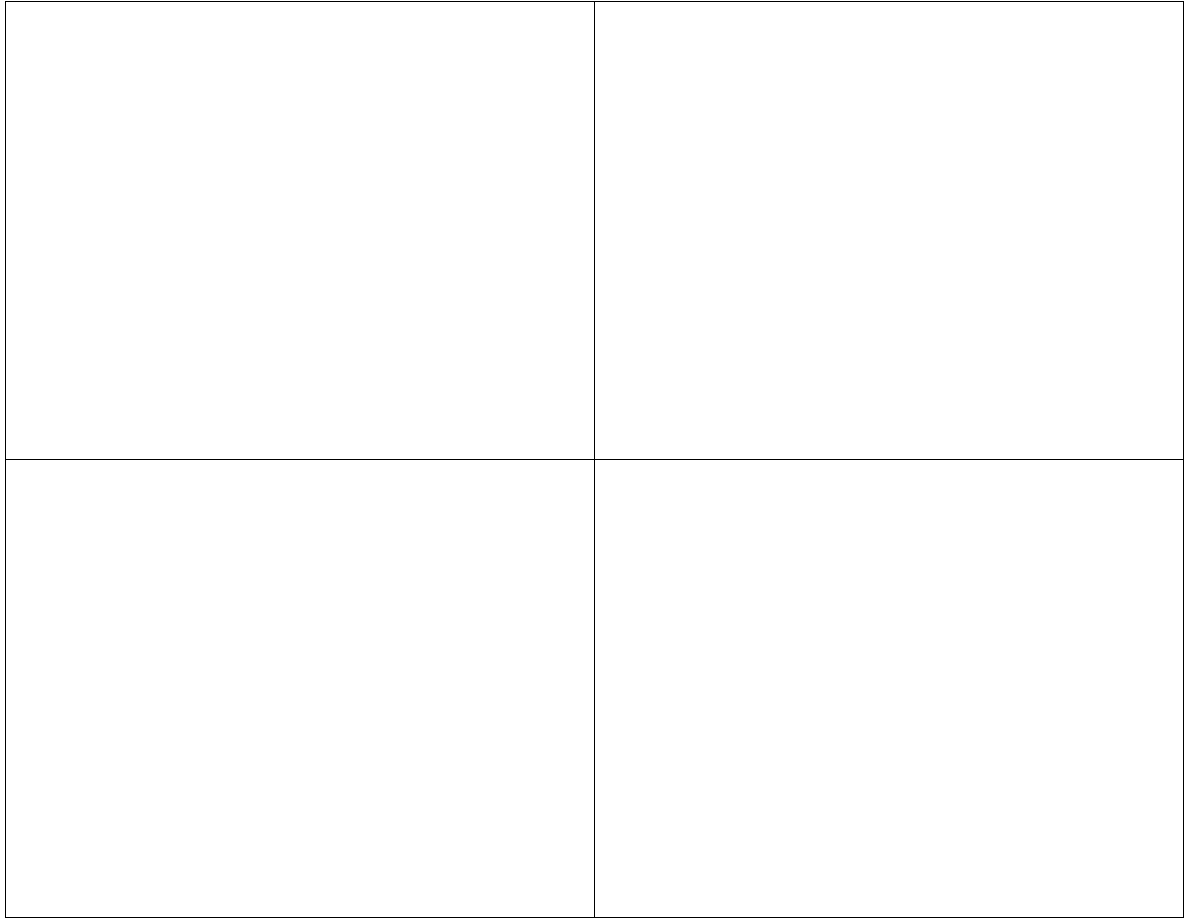
Sztuczne sieci neuronowe
21
Dobór współczynnika uczenia przez
minimalizacj kierunkow
W celu „regulacji” dokładno ci wyznaczenia współczynnika uczenia
wprowadza si współczynnik 0<
γ
2
<1, który stanowi ułamek pochodnej
funkcji celu na kierunku p
k
w punkcie wyj ciowym W
k
.
Algorytm pozwalaj cy na wyznaczenie optymalnej warto ci
η
k
przeprowadza si dopóty, dopóki spełnione s nast puj ce warunki:
oraz
przyj cie 0
≤ γ
1
≤ γ
2
< 1 gwarantuje jednoczesne spełnienie obu tych
warunków.
[
]
[
]
k
T
k
k
T
k
k
k
p
W
g
p
p
W
g
)
(
)
(
2
γ
η
≥
+
[
]
k
T
k
k
k
k
k
k
p
W
g
W
E
p
W
E
)
(
)
(
)
(
1
η
γ
η
≥
−
+
Sztuczne sieci neuronowe
22
Minimalizacja kierunkowa
• Metody bezgradientowe
– informacje o warto ciach funkcji celu
– wyznaczanie minimum poprzez kolejne podziały zało onego na wst pie
zakresu warto ci wektora W
• Metody gradientowe
– wykorzystuj zarówno warto funkcji jak te jej pochodn wzdłu
wektora kierunku p
k
.
– znaczne przyspieszenie wyznaczenia minimum na danym kierunku
informacja o kierunku spadku)
Sztuczne sieci neuronowe
23
Przykład metody bezgradientowej
• Metoda bazuje na aproksymacji funkcji celu na kierunku p
k
, a nast pnie
wyznacza minimum otrzymanej w ten sposób funkcji jednej zmiennej
η
• Wielomian aproksymuj cy:
P(
η)=a
2
η
2
+a
1
η +a
0
gdzie a
2
,a
1
,a
0
- współczynniki wielomianu okre lane w ka dym cyklu
optymalizacyjnym
• Wyznaczanie współczynników wielomianu
– wybór trzech dowolnych punktów W
1
, W
2
, W
3
le cych na kierunku p
k
, tzn.
W
1
=W+
η
1
p
k
;
W
2
=W+
η
2
p
k
;
W
3
=W+
η
3
p
k
;
(W - poprzednie rozwi zanie);
– E
1
=E(W
1
); E
2
=E(W
2
); E
3
=E(W
3
); wówczas
P(
η
1
)= E
1
; P(
η
2
)= E
2
; P(
η
3
)= E
3
;
– Rozwi zuj c układ równa otrzymujemy współczynniki wielomianu
• Porównuj c pochodn wielomianu do zera otrzymujemy
η
mi
n
=(-a
1
/2a
2
)
• Po okre leniu s sprawdzane warunki. Je li algorytm ma by kontynuowany to
wybiera si kolejne punkty le ce na kierunku p
k
w pobli u punktu W+
η
mi
n
p
k
.
Sztuczne sieci neuronowe
24
Inne metody doboru współczynnika uczenia
• Reguła delta-bar-delta
– jest metod adaptacyjn opracowan dla kwadratowej definicji funkcji celu
i metody najwi kszego spadku
– ka dej wadze W
ij
jest przyporz dkowany indywidualnie dobrany
współczynnik uczenia
– Wada: du a zło ono obliczeniowa
– Zaleta: przyspieszenie procesu uczenia i zwi kszenie prawdopodobie stwa
osi gni cia minimum globalnego
• Metoda gradientów sprz onych z regularyzacj
– odmiana zwykłej metody gradientów sprz onych ł cz c jednocze nie
wyznaczanie kierunku p oraz optymalnego kroku
Sztuczne sieci neuronowe
25
Algorytm Quickprop
• odmiana algorytmu gradientowego zawiera elementy metody
newtonowskiej i wiedzy heurystycznej
• zawiera elementy zabezpieczaj ce przez utkni ciem w płytkim
minimum lokalnym (ze wzgl du na nasycenie neuronu)
• Zmiana wagi w k-tym kroku
• Zalety: szybka zbie no dla wi kszo ci trudnych problemów
• kilkusetkrotne przyspieszenie procesu uczenia (w porównaniu z
algorytmem najwi kszego spadku)
• małe prawdopodobie stwo utkni cia w minimum lokalnym
)
1
(
)
(
))
(
(
)
(
−
∆
+
+
∂
∂
−
=
∆
k
W
k
W
W
k
W
E
k
W
ij
k
ij
ij
ij
k
ij
α
γ
η
Sztuczne sieci neuronowe
26
Algorytm RPROP
(ang. Resilent backPROPagation)
gdzie
– a=1.2; b=0.5
η
min
;
η
max
- minimalna i maksymalna warto współczynnika uczenia (10
-6
; 50)
Zalety
– przyspieszenie procesu uczenia w obszarach gdzie nachylenie funkcji celu
jest niewielkie
∂
∂
−
=
∆
ij
k
ij
ij
W
k
W
E
k
W
))
(
(
sgn
)
(
)
(
η
(
)
(
)
<
−
>
−
=
−
−
−
h
przypadkac
h
pozostalyc
w
k
S
k
S
dla
b
k
S
k
S
dla
a
k
ij
ij
ij
k
ij
ij
ij
k
ij
k
ij
)
1
(
min
)
1
(
max
)
1
(
)
(
0
)
1
(
)
(
,
max
0
)
1
(
)
(
,
min
η
η
η
η
η
η
ij
ij
W
k
W
E
k
S
∂
∂
=
))
(
(
)
(