Algorytmy rastrowe:

rysowanie okręgu i

elipsy.

Urządzenia rastrowe:



Monitor



Kartka papieru w drukarce,ploterze

Obraz składa się ze skończonej liczby

elementów nazywanych pikselami.

Piksele tworzą siatkę prostokątną

uporządkowana w l linii i k kolumn.

l x k –rozdzielczość urządzenia graficznego.
Aspekt urządzenia graficznego - odległość

między środkami sąsiednich pikseli w
poziomie do odległości w pionie.

Rasteryzacja

Zamiana ciągłej funkcji 2D na funkcję
dyskretną (rysowanie okręgu na podstawie
równania okręgu).

Problem sprowadza się do wyboru pikseli,
którym trzeba nadać kolor, aby w efekcie
otrzymać wymagany kształt.

Algorytmy generacji
krzywych



Algorytmy numeryczne



Algorytmy inkrementacyjne

Algorytmy numeryczne -
idea

Numeryczna analiza krzywej podanej w
sposób jawny przez funkcję opisującą
krzywą i funkcje będące różniczkami
cząstkowymi.

Algorytmy
inkrementacyjne - idea



Generacja krzywych od punktu
początkowego do punktu końcowego.
Na podstawie punktu bieżącego liczy się
elementarne przesunięcie określające
punkt następny.



Wykorzystują własności geometryczne
krzywych w przestrzeni dyskretnej
(rastrowej) i ich własności strukturalne.

Algorytmy rysowania
okręgu:

Algorytm Bresenhama



dla 1/4 okręgu



dla 1/8 okręgu

Algorytm DDA(Digital Differential Analized)

Algorytm Bresenhama

Założenia:



równanie okręgu x

2

+y

2

=R

2



R - liczba naturalna



Środek okręgu w początku układu współrzędnych



kreślona jest ¼ okręgu



Kierunek kreślenia – ruch wskazówek zegara



Kolejne punkty wybierane są metodą

inkrementacyjną (dla ¼ okręgu wybierany jest

jeden z trzech sąsiednich punktów rastra)

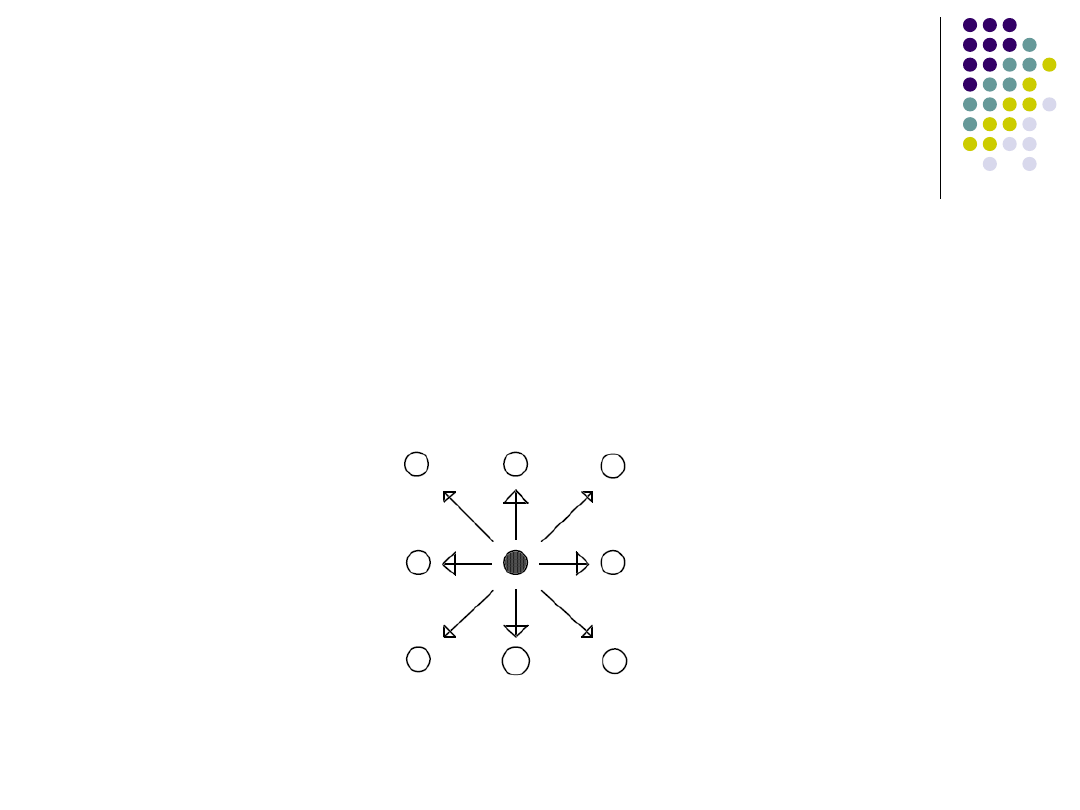
Algorytm Bresenhama

Założenia:



Aspekt ekranu a=p/q ≠1



Ośmiokierunkowy wybór pikseli
przybliżających krzywą F(x,y)=p

2

x

2

+q

2

y

2

-

q

2

R

2

=0

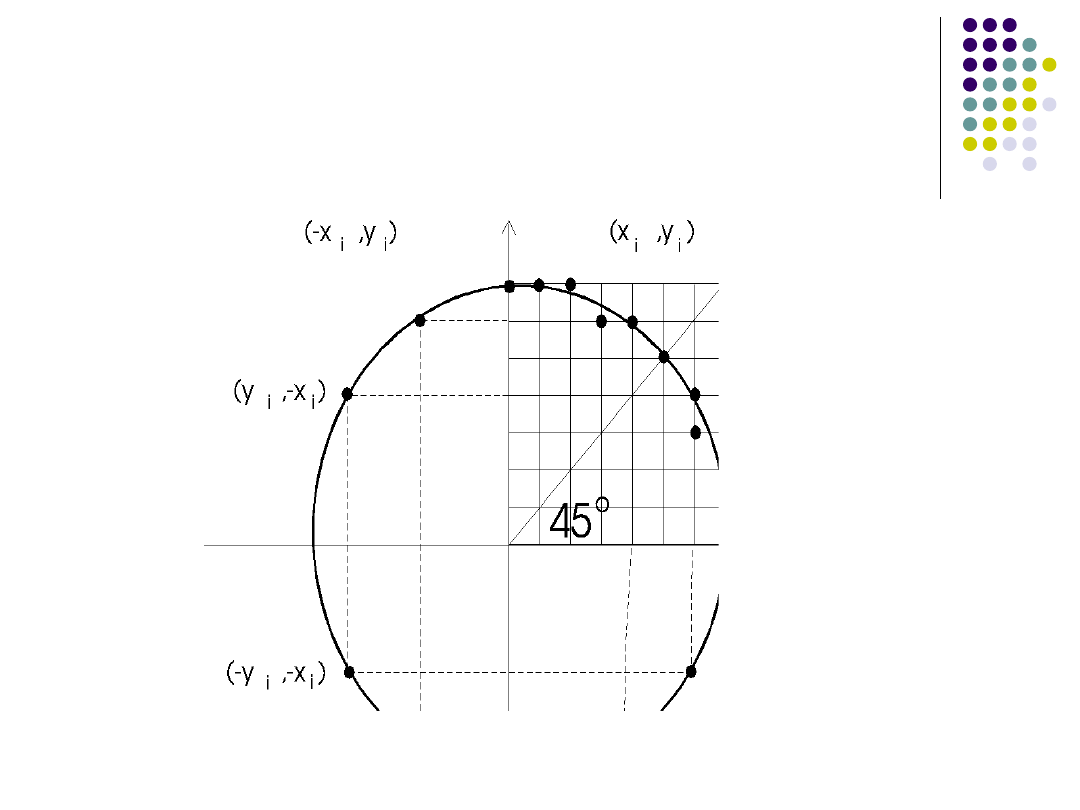
Algorytm Bresenhama

Punkty okręgu generowane przez
algorytm

Algorytm Bresenhama -
idea

Taki wybór punktów aby różnica pomiędzy
promieniem poprowadzonym do
wybranego punktu rastra, a rzeczywistym
promieniem R była jak najmniejsza.

Wybór sprowadza się do analizy trzech
pikseli.

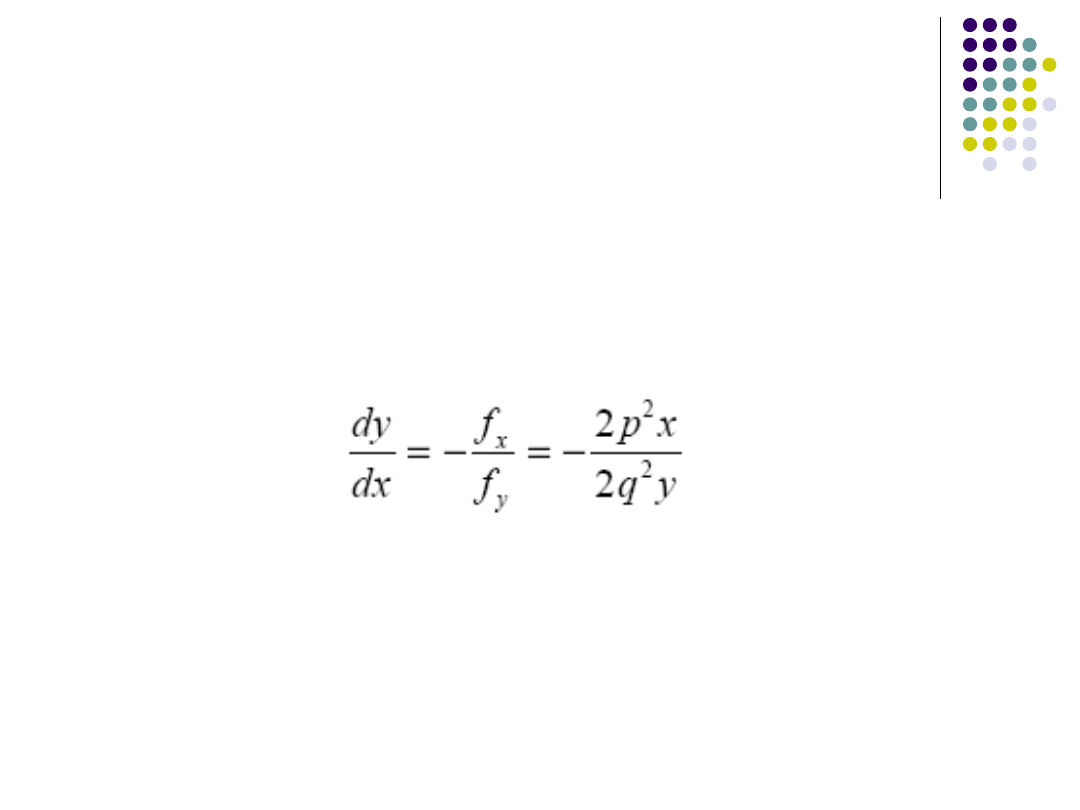
Algorytm Bresenhama



Analizę zaczynamy od punktu P

0

=(0,R)



Istotny jest punkt, którego współczynnik
kierunkowy wynosi -1

Dzieli on ćwiartkę okręgu na dwa fragmenty,

w których wybieramy różne piksele.

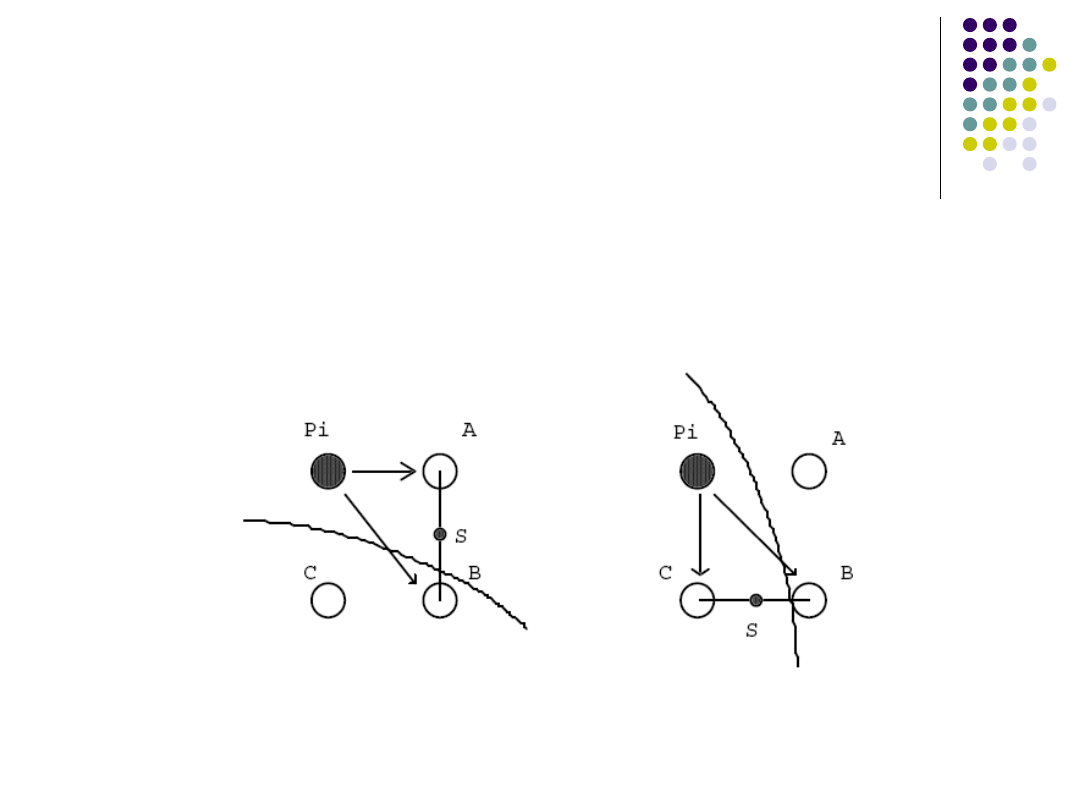
Algorytm Bresenhama

W pierwszym fragmencie wybieramy

pomiędzy pikselami A i B w drugim
pomiędzy B i C

Algorytm Bresenhama
Analiza punktów środkowych

Kryterium Van Akenema – rozstrzygnięcie, środek

którego z pikseli leży bliżej przybliżanego
okręgu.

Wybór zależy od wartości funkcji f w punkcie

środkowym S między alternatywnymi pikselami.

I: II:
fs

i

=f(x

i

+1,y

i

-1/2)

fs

i

=f(x

i

+1/2 ,y

i

-1)

fs

i

> 0 to punk zew. -> wybieramy I:B, II:C

fs

i

< 0 to punk wew. -> wybieramy I:A, II:B

Algorytm Bresenhama
Wartość zmiennej
decyzyjnej

Dla startowego piksela P

0

=(x

0

,y

0

)=(0,R)

wartość zmiennej decyzyjnej:

fs

0

=f(x

0

+1,y

0

-1/2)=p

2

(0+1)

2

+q(R-1/2)

2

-

q

2

R

2

=

=p

2

-q

2

R+q

2

/4

Algorytm Bresenhama
Wartość zmiennej
decyzyjnej

Dla pierwszego fragmentu okręgu p

2

x<q

2

x

zwiększamy wartość x o 1 i wybieramy A lub B
Przejście:

P

i

-> P

i+1

=A

x

i+1

=x

i

+1 y

i+1

=y

i

f(x

i+1

+1, y

i+1

-1/2)=f(x

i

+1, y

i

-1/2 ) +2p

2

x

i+1

+p

2

lub krócej:

fs

i+1

=fs

i

+2p

2

x

i+1

+p

2

Przejście:

P

i

-> P

i+1

=B

x

i+1

=x

i

+1 y

i+1

=y

i

-1

fs

i+1

=fs

i

+2p

2

x

i+1

+p

2

-2q

2

y

i+1

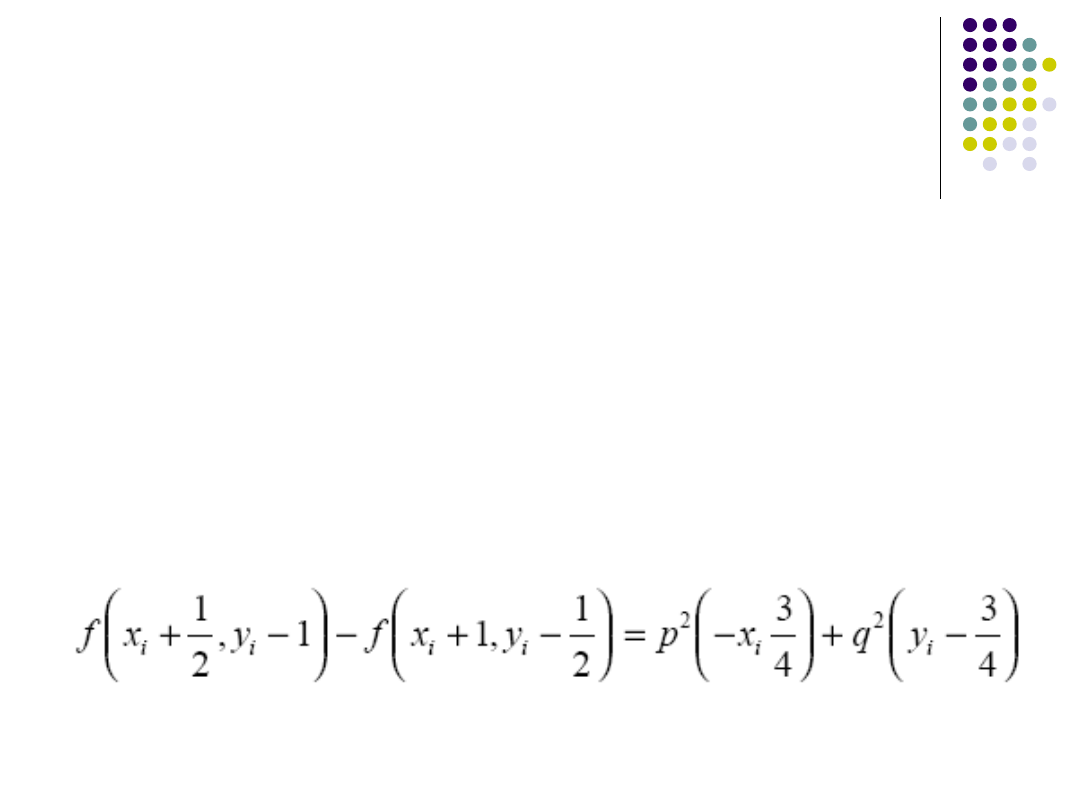
Algorytm Bresenhama
Wartość zmiennej
decyzyjnej

Dla drugiego fragmentu okręgu p

2

x>q

2

x

zwiększamy wartość y o 1 i wybieramy B lub

C.

Wybór B,lub C powinien zależeć od nowej

wartości

f(x

i+1

+1/2, y

i+1

-1), a nie od starej f(x

i+1

+1,

y

i+1

-1/2).

Różnica pomiędzy nimi wynosi:

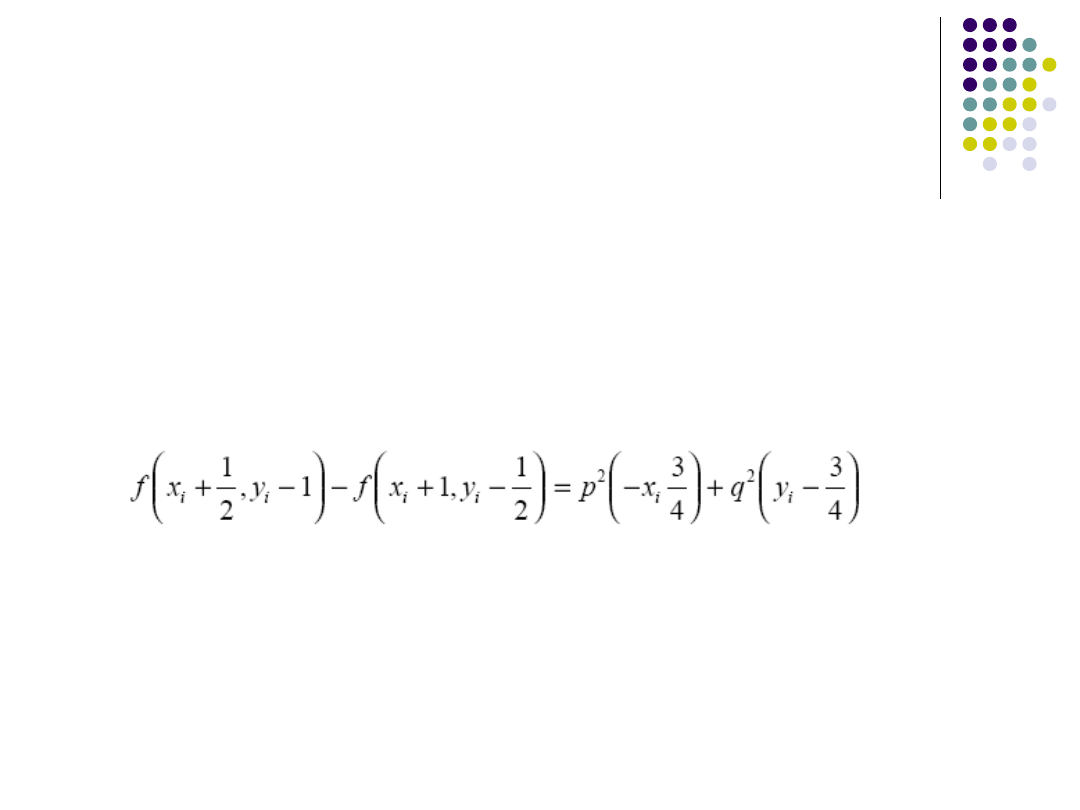
Algorytm Bresenhama

Nowa wartość zmiennej
decyzyjnej

Poprzednio obliczoną zmienną decyzyjną

wystarczy zmodyfikować o tę wartość:

Korzystając z rekurencji przeanalizować

wybór punktu B lub C.

Algorytm Bresenhama
Wartość zmiennej
decyzyjnej

Przejście P

i

-> P

i+1

=B

x

i+1

=x

i

+1 y

i+1

=y

i

-1

fs

i+1

= f(x

i+1

+1/2, y

i+1

-1)=fs

i

+2p

2

x

i+1

-

2q

2

y

i+1

+q

2

Przejście P

i

-> P

i+1

=C

x

i+1

=x

i

y

i+1

=y

i

-1

fs

i+1

=fs

i

-2q

2

y

i+1

+q

2

Algorytm Bresenhama -
przypomnienie



p,q,R – liczby naturalne



Znak zmiennej decyzyjnej fs

i

decyduje o

wyborze piksela.

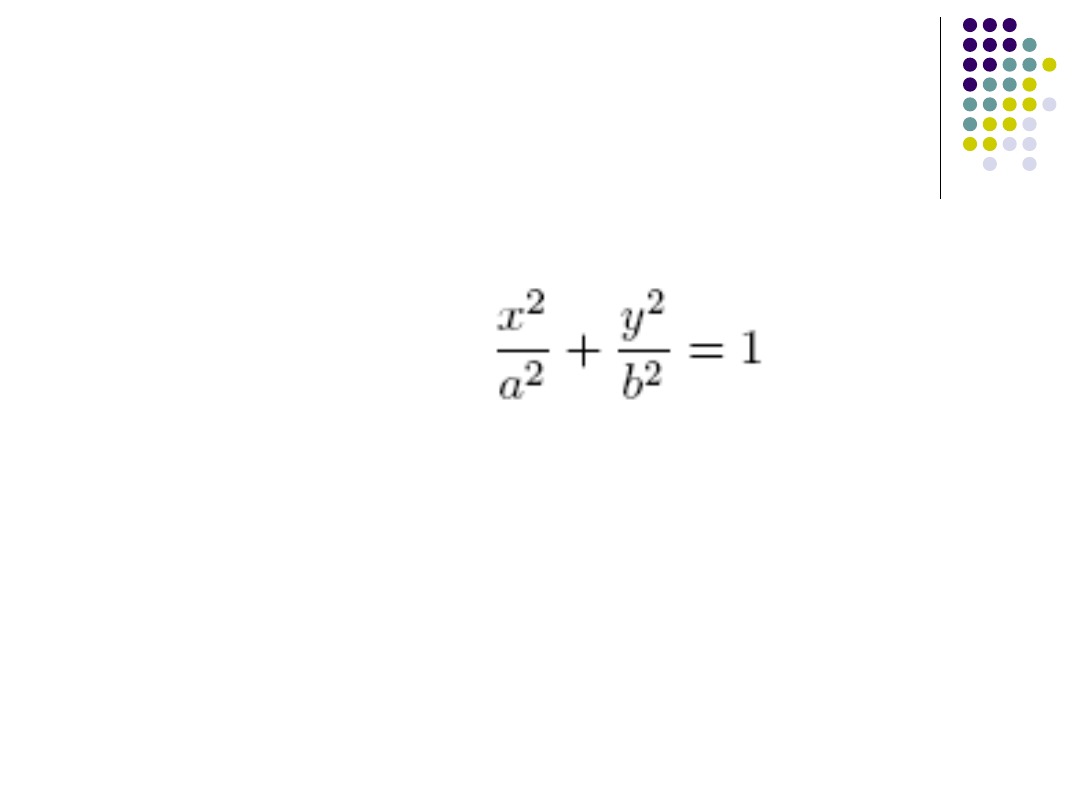
Algorytm Bresenhama dla
elipsy

Ta sama procedura jak przy rysowaniu koła.
Założenia:



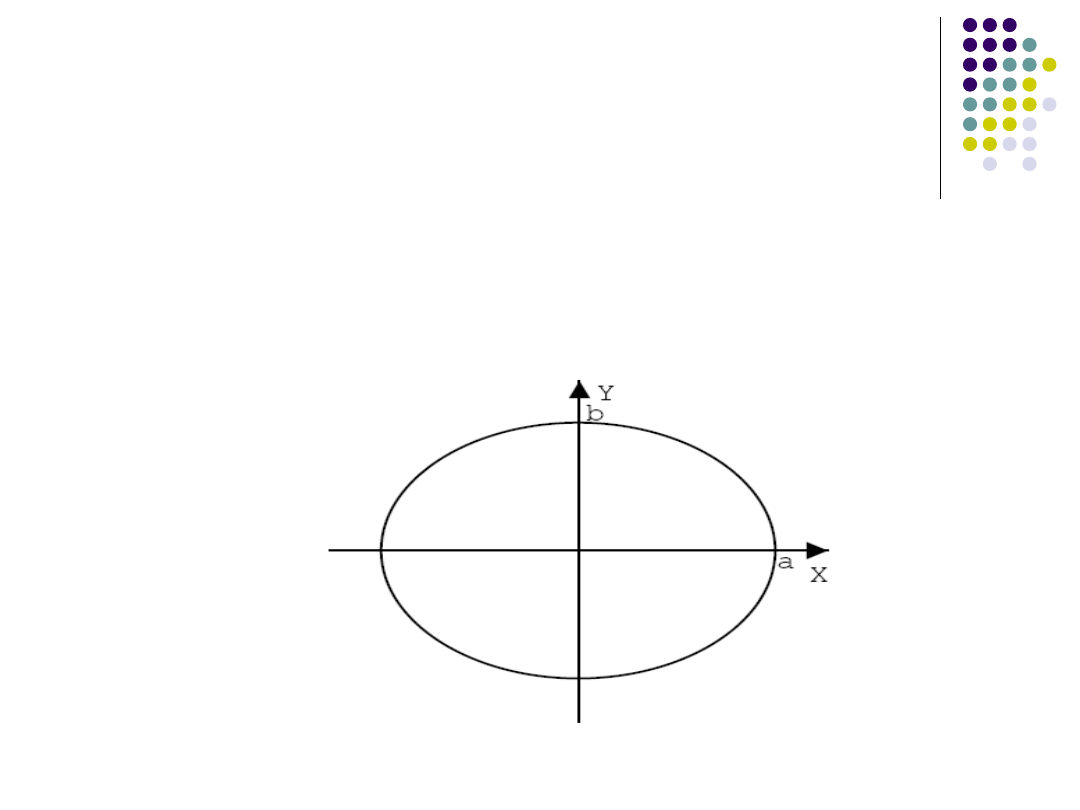
Równanie elipsy:



Rysujemy w I ćwiartce układu współrzędnych



Zaczynamy od pkt (0,b) zgodnie z ruchem
wskazówek zegara.



W każdym kroku stawiamy symetrycznie 4
pkt. elipsy.

Algorytm Bresenhama dla
elipsy

Założenia:



Ośmiokierunkowy wybór pikseli
przybliżających krzywą F(x,y)=b

2

x

2

+a

2

y

2

-

a

2

b

2

=0



Początkową osią wiodącą jest oś OX



W punkcie zmiany osi wiodącej
współczynnik nachylenia stycznej do elipsy
wynosi -1 (tg 135

o

)

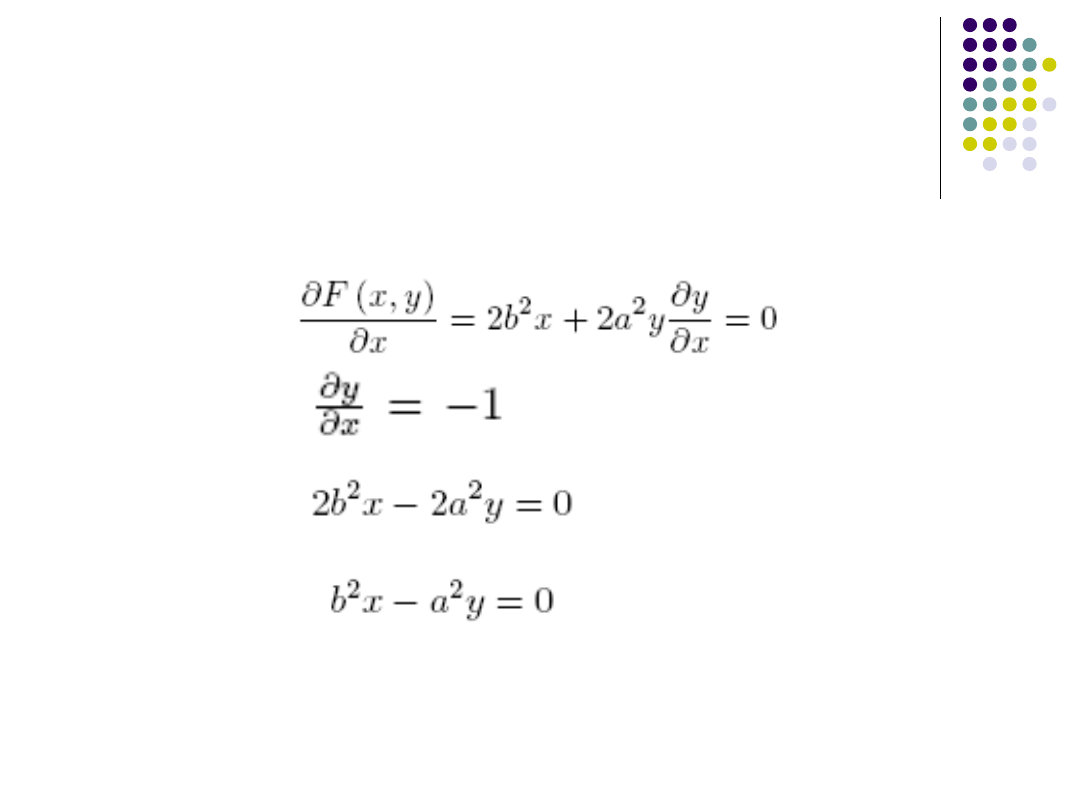
Algorytm Bresenhama dla
elipsy



Kryterium przejścia osi wiodącej z OX na
OY.

Algorytm Bresenhama dla
elipsy



Do określenia, który piksel znajduje się
bliżej kreślonej figury stosujemy jak dla
okręgu kryterium Van Akenema

Algorytm DDA



Podstawą rysowania figury jest postać
opisującego ją równania różniczkowego.



Algorytm korzystający z operacji
mnożenia i funkcji trygonometrycznych,
wolna realizacja.



Zasada działania – równoczesne
zwiększanie x i y o niewielki przyrost ε.



Rysujemy 1/8 okręgu.

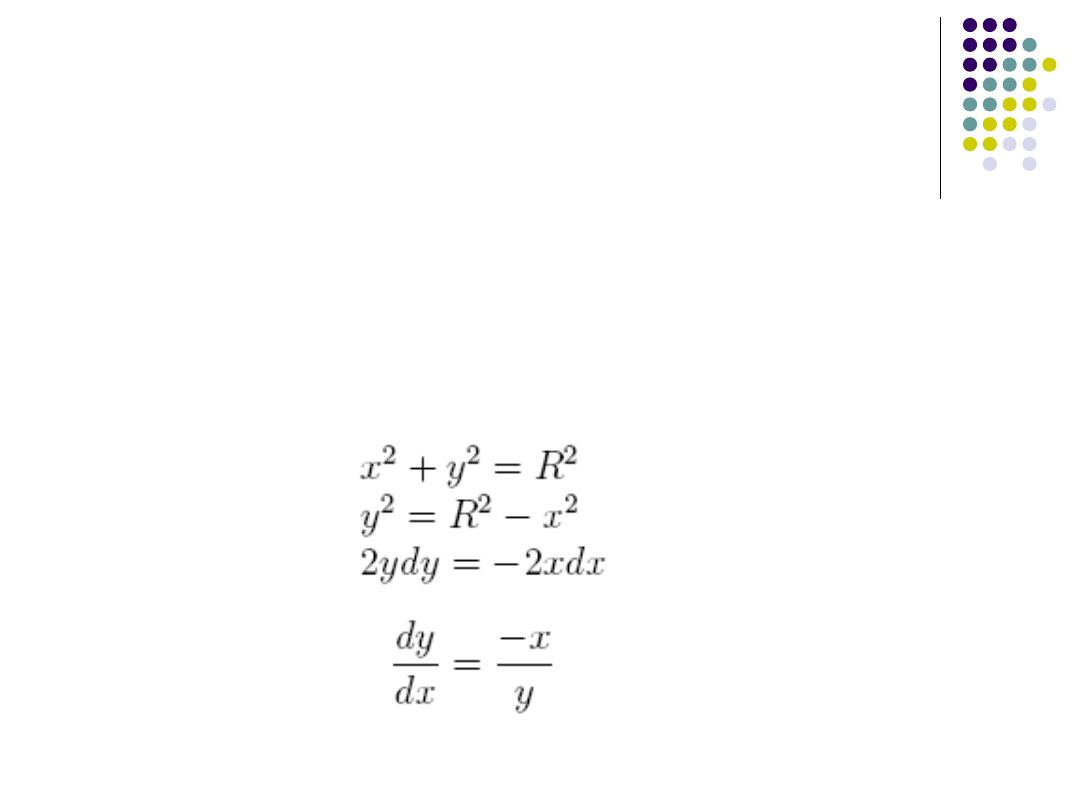
Algorytm DDA



Postać równania różniczkowego przy
założeniach:

środek okręgu=początek układu

współrzędnych

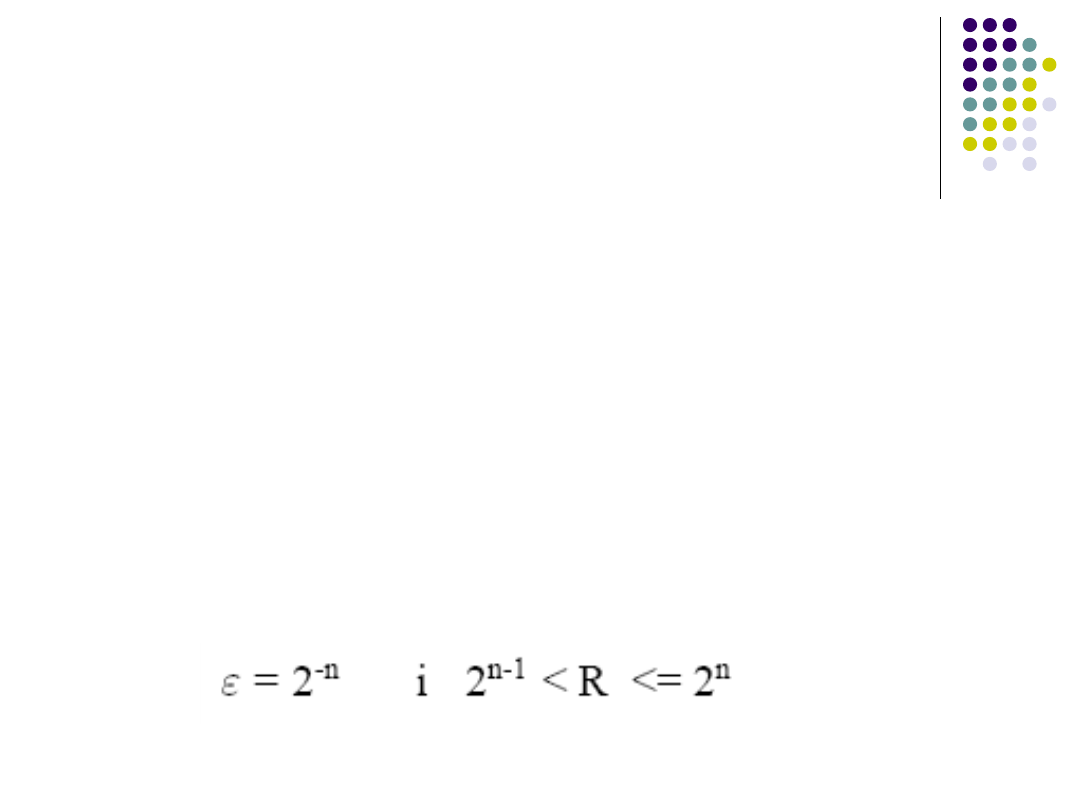
Algorytm DDA



Obliczanie współrzędnych kolejnych punktów:
x

i+1

=x

i

+εy

i

y

i+1

=y

i

-ε

2

y

i

- ε x

i

Wartości przyrostów nie są stałe i muszą być

obliczane dla każdego x,y przy użyciu
operacji mnożenia.



Mnożenie można zastąpić przesunięciami
przy

założeniu:

Algorytm DDA



Algorytm ten nie rysuje okręgu lecz
elipsę ale dla małych ε, błąd ten można
uważać za pomijalnie mały.

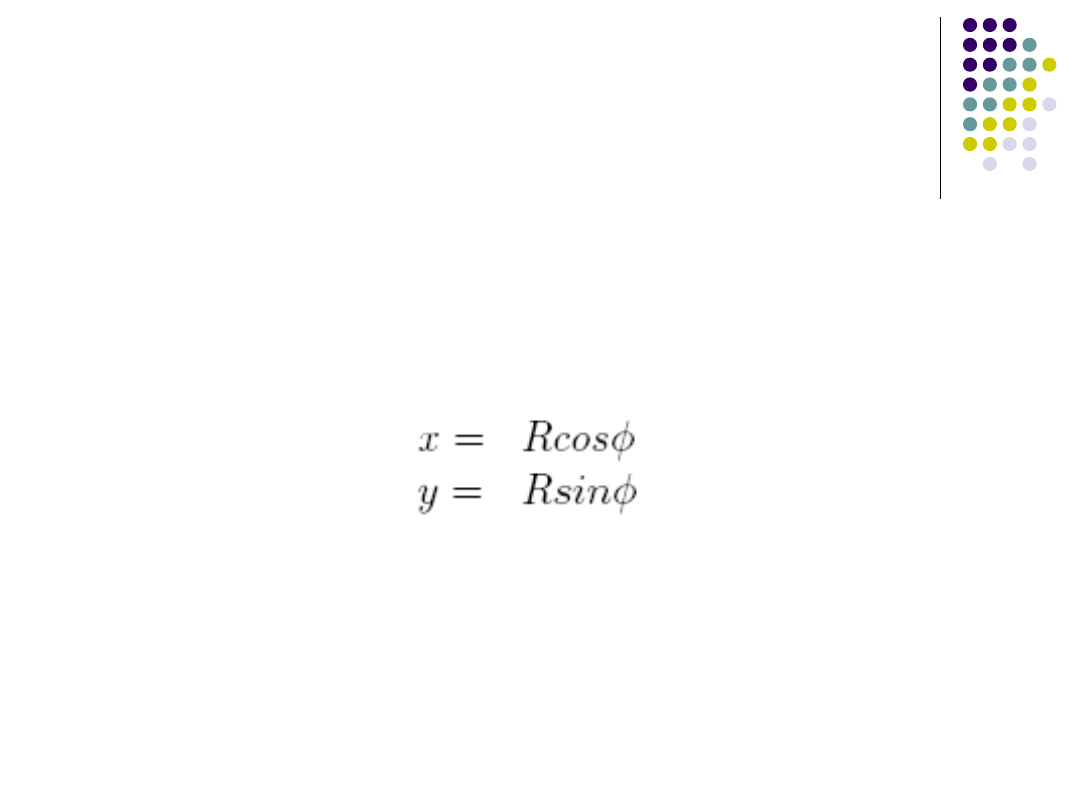
Dokładny algorytm DDA -
okrąg



Punktem wyjścia dla tej metody jest
równanie parametryczne okręgu o
promieniu R i środku w początku układu
współrzędnych.

Dokładny algorytm DDA -
okrąg

Zależności trygonometryczne dla sąsiednich

punktów okręgu:

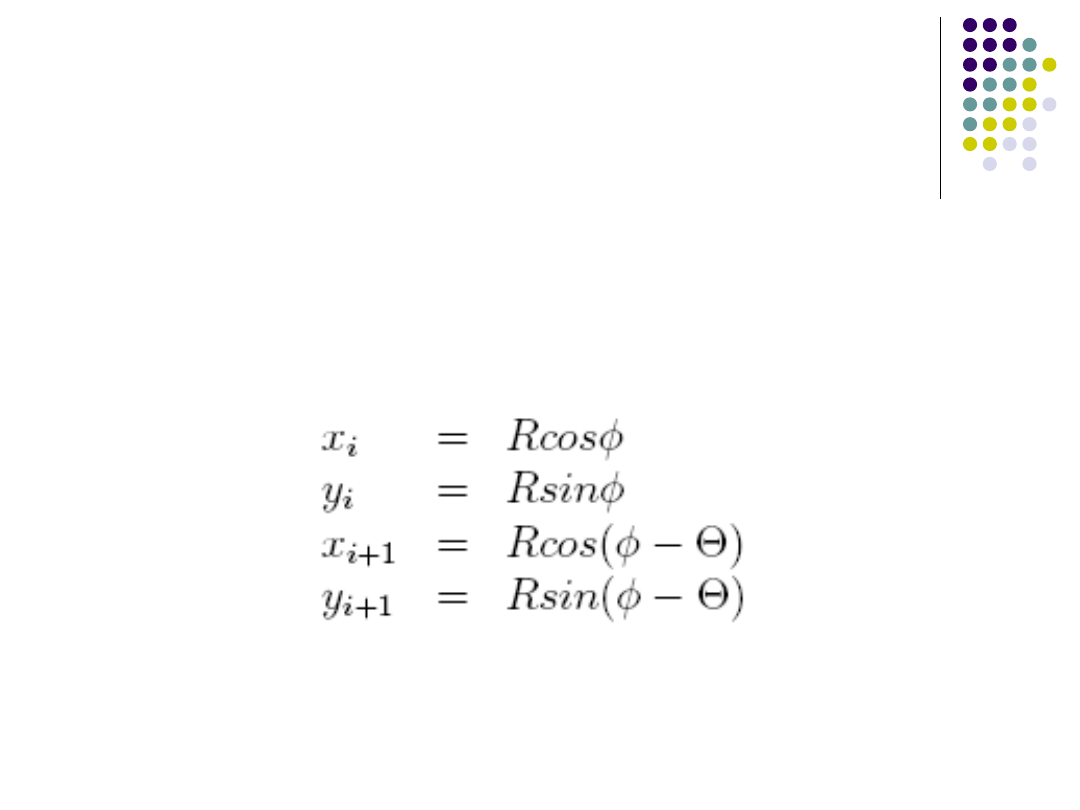
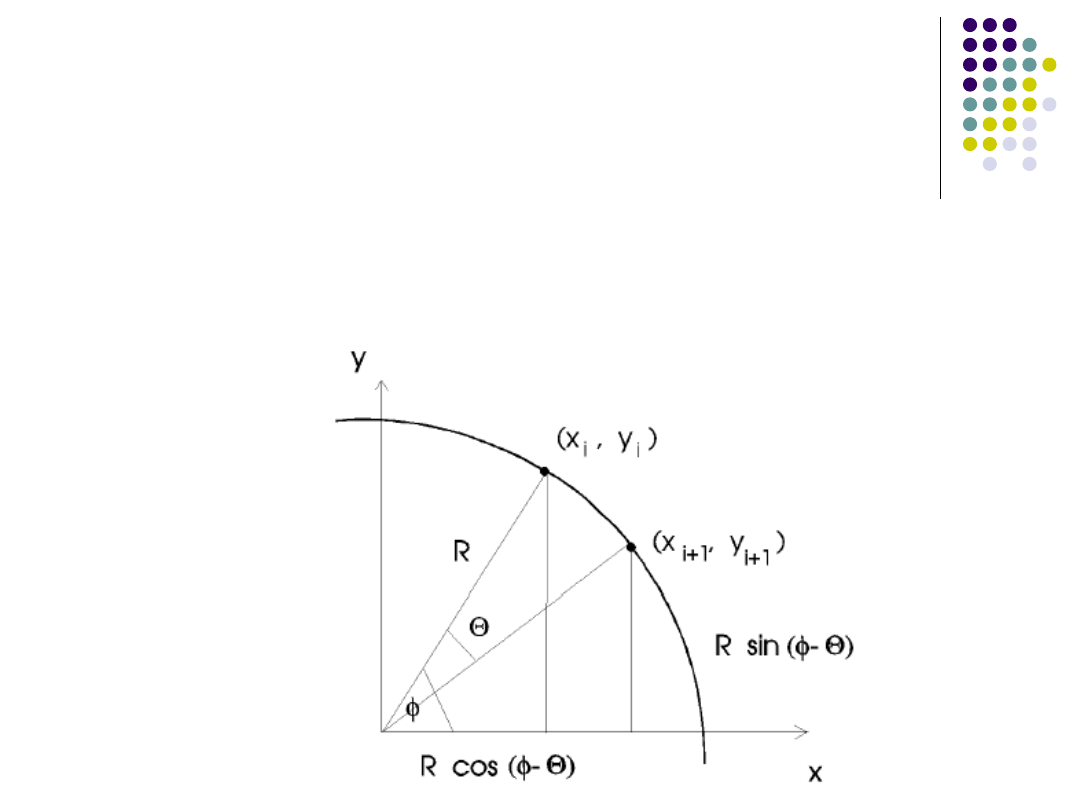
Dokładny algorytm DDA -
okrąg

Definiujemy Θ jako kąt pomiędzy
promieniami poprowadzonymi do dwóch
sąsiednich punktów okręgu.

Dokładny algorytm DDA -
okrąg

Po przekształceniach

trygonometrycznych:

postać macierzowa:

Dokładny algorytm DDA -
okrąg



Z rekurencyjnego charakteru zależności
wynika, że wielkość kąta Θ jest stała dla
każdej iteracji.



Wielkość kąta Θ zależy od liczby punktów
tworzących okrąg, a ta zwiększa się wraz z
promieniem.



Dla małych Θ algorytm generuje ciągłe i
dokładne łuki ale dla małych promieni bardzo
wydłuża się czas kreślenia jeżeli zakres
rozdzielczości zostanie przekroczony.