Wykład

Algorytmy rastrowe

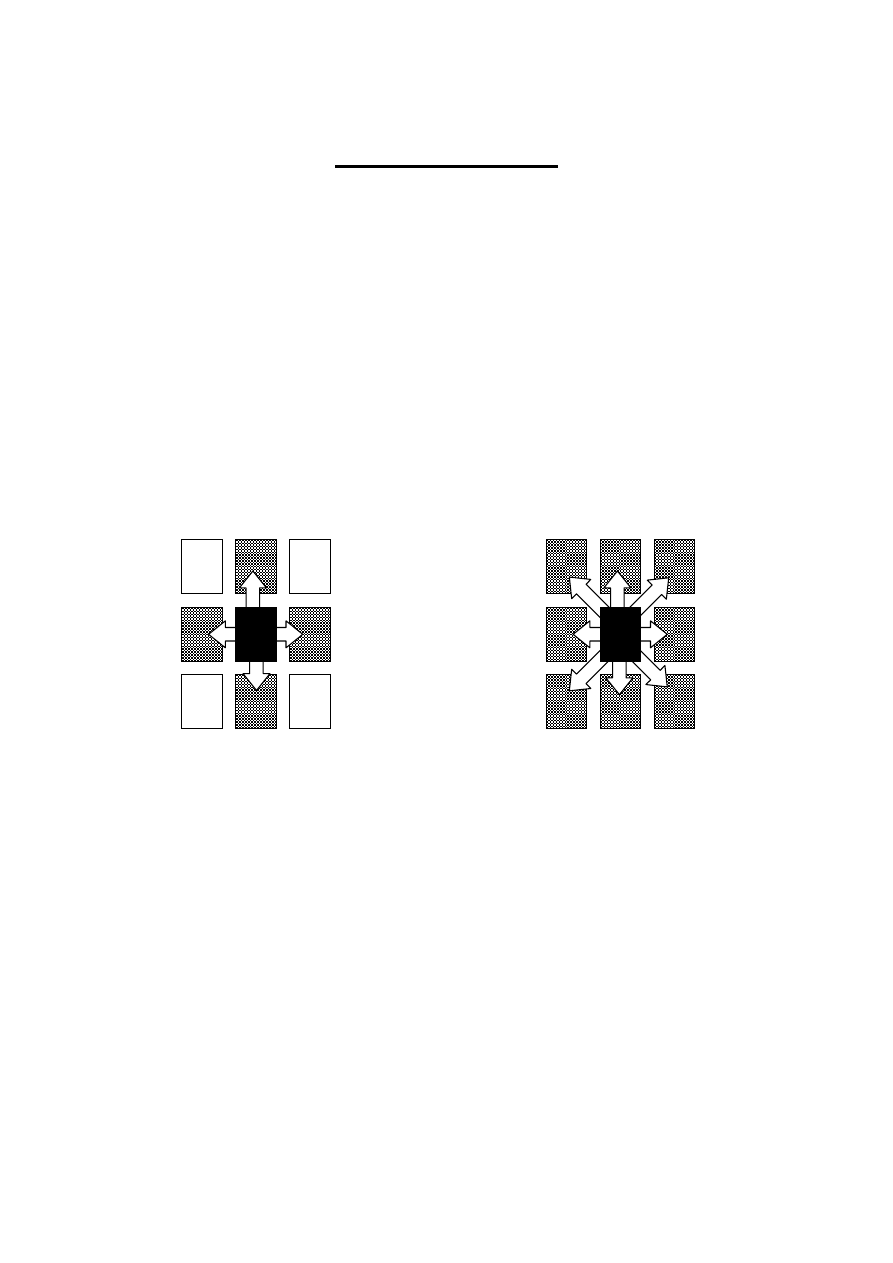
Rysowanie odcinka

Rodzaje odcinków:

- pionowe;
- poziome;
- ukośne.

W układzie współrzędnych pikselowych problemem jest wybór pikseli
przybliżających kształt odcinka, który nie jest równoległy do układu
pikseli. Wyboru pikseli można dokonywać w dwóch trybach:

- tryb czterokierunkowy;
- tryb ośmiokierunkowy.

czterokierunkowy

ośmiokierunkowy

Rys. Tryby wyboru pikseli.

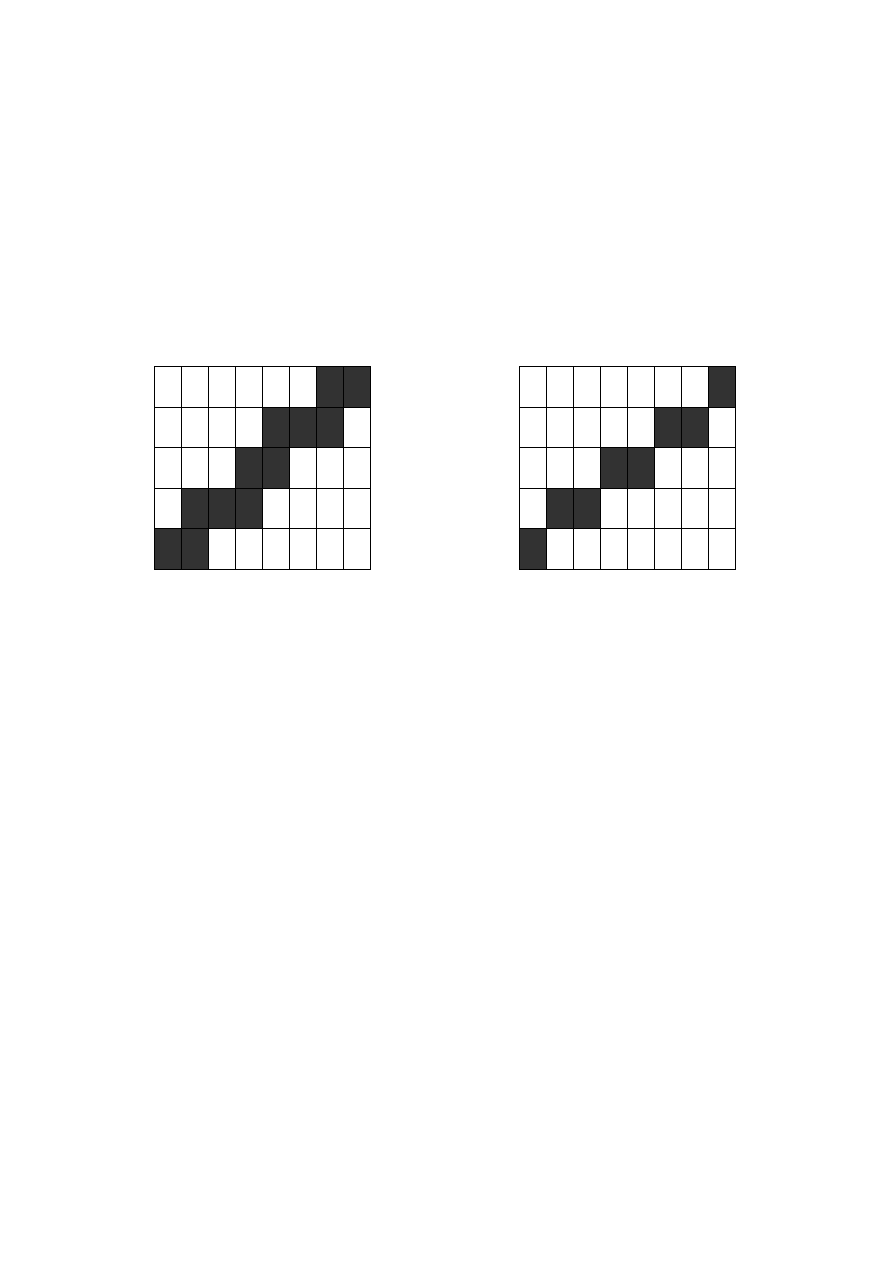
Odcinek definiowany jest przez współrzędne punktu początkowego
(x1, y1) i końcowego (x2, y2). Są to zwykle wartości rzeczywiste.
Rysując odcinek na urządzeniu rastrowym należy przejść od układu
współrzędnych rzeczywistych do układu współrzędnych całkowitych -
układu współrzędnych pikselowych. Jako pierwszy piksel przybliżający
rysowany odcinek przyjmujemy jeden z pikseli krańcowych. Następne
piksele wybieramy w trybie czterokierunkowym lub ośmiokierunkowym.
Wybieramy te piksele, których środek leży najbliżej odcinka.

czterokierunkowy

ośmiokierunkowy

Rys. Piksele przybliżające ten sam odcinek z wyborem cztero-

i ośmiokierunkowym.

Rysunki sprawiają wrażenie "schodkowych". W monitorach kolorowych
efekt ten można osłabić, stosując wybór czterokierunkowy i wyświetlając
piksele z różnymi odpowiednio dobranymi jasnościami. Na ekranie
monitora monochromatycznego (o jednym kolorze, jasności) linie
poziome wydają się grubsze (jaśniejsze) niż ukośne, gdyż ta sama ilość
ś

wiatła pada na mniejszy obszar. W takich urządzeniach wizualnie lepszy

efekt uzyskuje się poprzez wybór ośmiokierunkowy. Jest on realizowany
w najbardziej popularnym algorytmie rastrowego rysowania odcinków,
zaproponowanym przez Bresenhama.

Aliasing

– występowanie niepożądanych efektów schodkowych przy

rysowaniu odcinków ukośnych na urządzeniu rastrowym (tzw. artyfakt).

Antyliasing

– proces usuwania efektów schodkowych (wyrównywania

schodków, wygładzania krawędzi) realizowany poprzez wyświetlanie
pikseli w kolorach pośrednich, pomiędzy tłem a kolorem odcinka.

Algorytm DDA (ang. Digital Differential Analyzis)

- wykorzystuje równanie prostej: y = ax+ b lub x = (y-b)/a

- bazuje na obliczeniu stałego kroku przyrostu dla współrzędnych x i y

oraz funkcji zaokrąglającej wartości rzeczywiste do całkowitych;

- wadą

algorytmu

jest

konieczność

stosowania

arytmetyki

zmiennoprzecinkowej oraz to, że daje różne wyniki dla różnych
funkcji zaokrąglających.

/* rysuj odcinek od (x1, y1) do (x2, y2) */

Function: Int(x); Sign(x); Putpixel(x,y, color);
Integer:

i, x1, x2, y1, y2, length, color;

Real: x, y, Dx, Dy;

Begin

(* wyznaczenie długości odcinka w pikselach *)

if (ABS(x2-x1)>= ABS(y2-y1)) then length:= ABS(x2-x1)

else length:= ABS(y2-y1);

(* wyznaczenie kroku w kierunku x i y *)

Dx:=(x2-x1)/length;

Dy:=(y2-y1)/length;

(* wyznaczenie wartości początkowych x i y *)

x:=x1+0.5

*

Sign(Dx);

y:=y1+0.5

*

Sign(Dy);

(* pętla rysująca odcinek *)

for i:=0 to (i<length) do

begin

Putpixel(Int(x), Int(y), color);

x:=x+Dx;

y:=y+Dy;

end;

End.

Przykład: odcinek (0,0) -> (5,3)

Putpixel(0, 0, color); Putpixel(1, 1, color); Putpixel(2, 1, color);
Putpixel(3, 2, color); Putpixel(4, 2, color); Putpixel(5, 3, color);

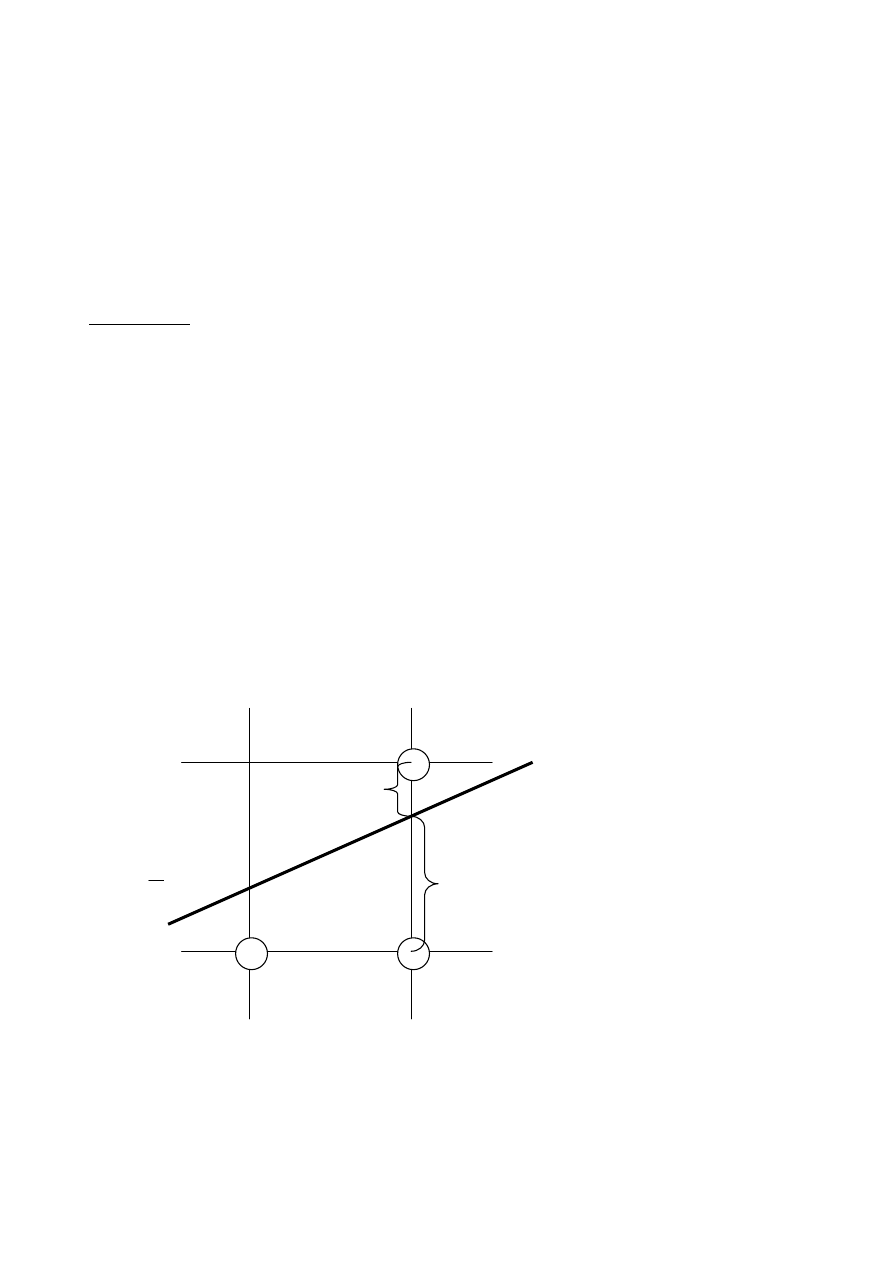
Algorytm Bresenhama

Rysowanie odcinka metodą Bresenhama opiera się na zmiennej
decyzyjnej, której znak decyduje o kolejnym kroku algorytmu. Zmienna
określa kierunek poziomy, pionowy lub idealnie skośny rysowania
kolejnego piksela odcinka. Algorytm działa na liczbach całkowitych.

Założenia:
- odcinek określony przez współrzędne początku i końca (x

0

,y

0

) i (x

k

,y

k

)

;

- x

0

< x

k

;

- współczynnik kierunkowy odcinka spełnia nierówność: 0<dy/dx

≤

1

gdzie: dy = y

k

- y

0

dx = x

k

- x

0

Rysowanie zaczynamy od piksela P

0

=

(x

0

,y

0

). Ponieważ kąt nachylenia

odcinka jest ograniczony do przedziału [0, 45°], więc po znalezieniu
kolejnego P

i

=

(x

i

,y

i

) następny piksel wybieramy z pośród tylko dwóch:

S

i+1

=

(x

i

+1, y

i

) i T

i+1

=

(x

i

+1, y

i

+1)

Rys. Wybór między pikselami S

i+1

i T

i+1

w algorytmie Bresenhama

rysowania odcinka.

0

0

y

x

x

dx

dy

y

+

+

+

+

−

−

−

−

=

=

=

=

)

(

S

i+1

= (x

i

+1, y

i

)

s

t

T

i+1

= (x

i

+1, y

i

+1)

P

i

= (x

i

, y

i

)

Wielkości s i t są określone równaniami:

)

(

)

(

0

i

0

i

y

y

x

1

x

dx

dy

s

−

−

−

−

−

−

−

−

−

−

−

−

+

+

+

+

=

=

=

=

)

(

)

(

0

i

0

i

x

1

x

dx

dy

y

1

y

t

−

−

−

−

+

+

+

+

−

−

−

−

−

−

−

−

+

+

+

+

=

=

=

=

Odejmując te równania stronami i mnożąc przez dx otrzymujemy:

dx

dy

2

y

y

dx

2

x

x

dy

2

t

s

dx

d

0

i

0

i

i

−

−

−

−

+

+

+

+

−

−

−

−

−

−

−

−

−

−

−

−

=

=

=

=

−

−

−

−

=

=

=

=

)

(

)

(

)

(

(1)

Ponieważ dx

>

0

, więc znak d

i

określa, która z wielkości s i t jest większa.

Jeśli d

i

>

0

, to i za P

i+1

przyjmujemy piksel T

i+1

, w przeciwnym razie,

jeżeli d

i

<

0

, wybierzemy piksel S

i+1

. Równość d

i

= 0

oznacza, że oba

piksele S

i+1

i T

i+1

leżą w tej samej odległości od odcinka i wtedy możemy

arbitralnie decydować, np., że P

i+1

= T

i+1

.

Dla i+1 wzór (1) ma postać:

dx

dy

2

y

y

dx

2

x

x

dy

2

d

0

1

i

0

1

i

1

i

−

−

−

−

+

+

+

+

−

−

−

−

−

−

−

−

−

−

−

−

=

=

=

=

+

+

+

+

+

+

+

+

+

+

+

+

)

(

)

(

(2)

Odejmując od niego stronami równanie (1) uzyskujemy zależność:

)

(

)

(

i

1

i

i

1

i

i

1

i

y

y

dx

2

x

x

dy

2

d

d

−

−

−

−

−

−

−

−

−

−

−

−

=

=

=

=

−

−

−

−

+

+

+

+

+

+

+

+

+

+

+

+

stąd:

)

(

i

1

i

i

1

i

y

y

dx

2

dy

2

d

d

−

−

−

−

−

−

−

−

+

+

+

+

=

=

=

=

+

+

+

+

+

+

+

+

gdyż: x

i+1

- x

i

= 1.

Jeśli d

i

≥

0

(wybieramy wtedy P

i+1

= T

i+1

) to y

i

= y

i

+ 1

i zależność

rekurencyjna (2) upraszcza się do postaci:

dx

2

dy

2

d

d

i

1

i

−

−

−

−

+

+

+

+

=

=

=

=

+

+

+

+

a jeżeli d

i

<

0

(wybieramy wtedy P

i+1

= S

i+1

) to y

i

= y

i

i mamy:

dy

2

d

d

i

1

i

+

+

+

+

=

=

=

=

+

+

+

+

Dla i = 0, ze wzoru (1) dostajemy wartość początkową zmiennej
decyzyjnej

dx

dy

2

d

0

−

−

−

−

=

=

=

=

Zgodnie z przyjętymi założeniami możemy napisać algorytm Bresenhama
wyboru zbioru pikseli obrazujących odcinek (x

0

, x

0

) → (x

k

, y

k

).

Begin

dx:= x

k

- x

0

;

dy:= y

k

- y

0

;

d

0

:= 2*dy – dx;

(* wartość początkowa zmiennej decyzyjnej *)

Putpixel(x

0

, y

0

, kolor);

for i:= 0 to k-1 do

Begin

x

i+1

:= x

i

+ 1;

if d

i

≥

0

then

(* ruch diagonalny – wybór T *)

begin

d

i+1

:= d

i

+ 2*dy – 2*dx;

y

i+1

:= y

i

+ 1;

end

else

(* ruch poziomy – wybór S *)

begin

d

i+1

:= d

i

+ 2*dy;

y

i+1

:= y

i

;

end;

Putpixel(x

i+1

, y

i+1

, kolor);

end;

End.

Dla odcinków o założonym współczynniku kierunkowym dx/dy∈(0,1],
wybieramy kolejne piksele wykonując na siatce rastrowej ruchy poziome
(wybór S

i

) i diagonalne (wybór T

i

). Niech S oznacza ruch poziomy, T

diagonalny a (S

2

T)

3

niech będzie skróconym zapisem ciągu SST SST

SST. Rysując odcinek (0,0) → (131,16) wykonamy następujące ruchy:

S

4

T(S

7

T)

4

S

8

T(S

7

T)

5

S

8

T(S

7

T)

4

S

4

Uogólniony algorytm Bresenhama rysowania odcinka

od punktu (x1, y1) do (x2, y2), dla dowolnego współczynnika

kierunkowego nachylenia odcinka

Założenie: (x1, y1, x2, y2) – wartości całkowite

Function: Sign(x); Putpixel(x,y, color);
Integer:

Inter, temp, x1, x2, y1, y2, Dx, Dy, p, color;

Begin

x:=x1;

(* parametry początkowe *)

y:=y1;

Dx:= (ABS(x2-x1);

Dy:= (ABS(y2-y1);

s1:=Sign(x2-x1);

s2:=Sign(y2-y1);

if Dx>Dy then

(* zmiana Dx z Dy w zależności od nachylenia odcinka *)

begin

temp:=Dx;

Dx:=Dy;

Dy:=temp;

Inter:=1;

end

else Inter:=0;

p:=2*Dy-Dx;

(* początkowa wartość zmiennej decyzyjnej *)

for i:=1 to Dx do

(* pętla rysująca odcinek *)

begin

Putpixel(x, y, color);

if p>0 then

begin

if Inter=1 then x:=x+s1 else y:=y+s2;

p:=p-2*Dx;

end;

if Inter=1 then y:=y+s2 else x:=x+s1;

p:=p+2*Dy;

end;

End.

Rysowanie okręgu

Aspekt urządzenia graficznego (a): stosunek odległości środków pikseli
sąsiednich w pionie (p) do odległości środków pikseli sąsiednich w
poziomie (q). Typowe wartości: 4/3, 5/4, 16/9.

q

p

a =

=

=

=

gdzie: p i q liczby naturalne

Rysując okrąg należy uwzględnić wpływ aspektu. Inaczej, dla a ≠ 1
zamiast okręgu otrzymamy elipsę. Aspekt nie jest istotny w przypadku
rysowania odcinka.

W ogólnym przypadku piksele urządzenia rastrowego tworzą siatkę
prostokątną, którą można opisać dwoma układami:
- układem współrzędnych pikselowych 0xy;
- układem współrzędnych rzeczywistych 0XY, gdzie: X = xa, Y = y.

Rysowanie okręgu polega na wybraniu pikseli przybliżających kształt
krzywej opisanej równaniem:

0

R

Y

X

2

2

2

=

=

=

=

−

−

−

−

+

+

+

+

lub inaczej:

0

R

Y

xa

2

2

2

=

=

=

=

−

−

−

−

+

+

+

+

)

(

po przekształceniu otrzymamy:

0

R

q

y

q

x

p

y

x

f

2

2

2

2

2

2

=

=

=

=

−

−

−

−

+

+

+

+

=

=

=

=

)

,

(

Algorytm Bresenhama:
Założenia:
- promień okręgu R jest liczbą naturalną, a jego środek leży w początku

układu współrzędnych;

- ośmiokierunkowy wybór piksela;
- ze względu na symetrię okręgu ograniczymy wyznaczanie piksela

tylko do 1/4 okręgu (dla a = 1 wystarczy rozważenie 1/8 okręgu).

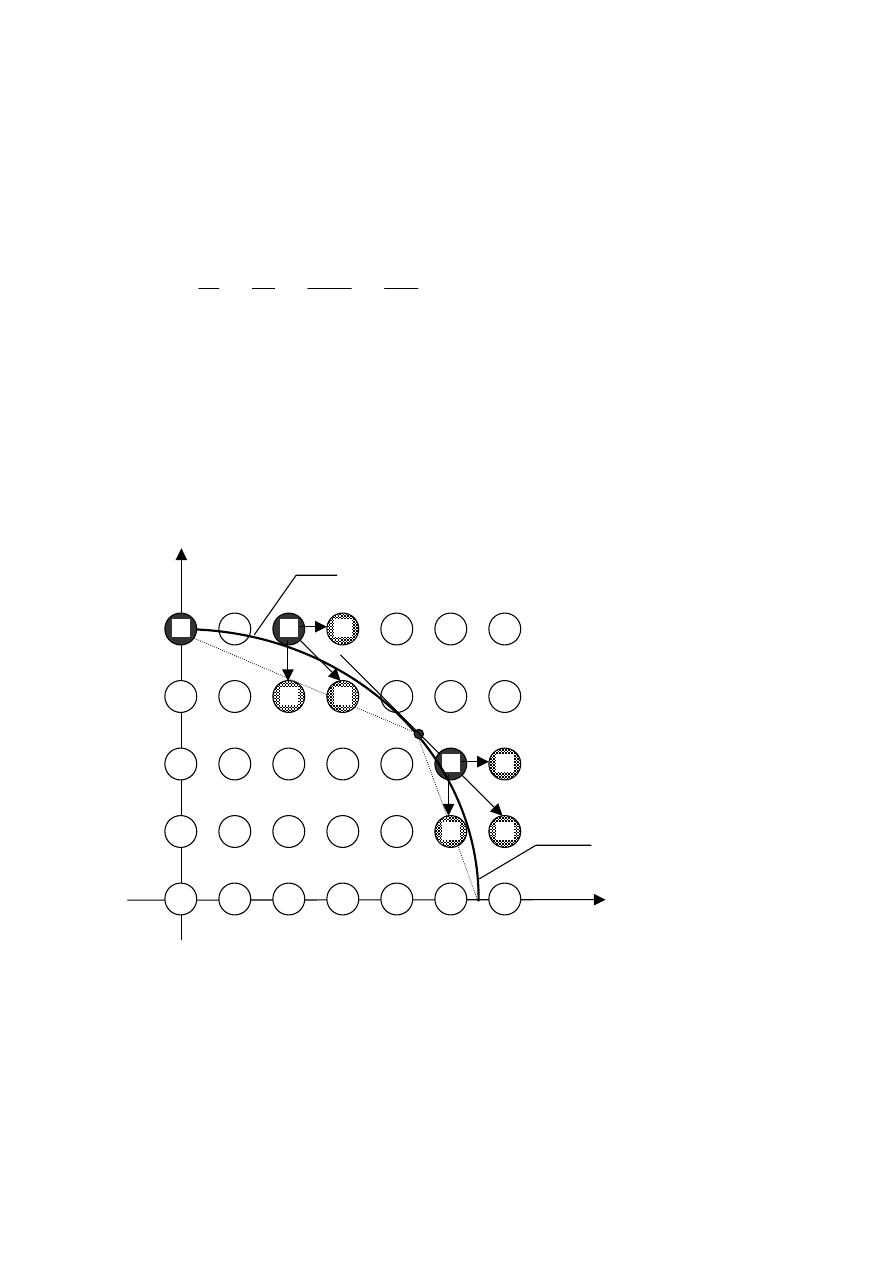
Rysowanie zaczynamy od piksela P

0

=(0,R), następne wyznaczamy

zgodnie z kierunkiem obrotu wskazówek zegara. Po znalezieniu piksela
P

i

, wybór następnego P

i+1

ogranicza się do jednego z trzech pikseli

oznaczonych na rysunku literami A, B lub C. Punkt Z, w którym
współczynnik kierunkowy wektora stycznego:

y

q

x

p

y

q

2

x

p

2

f

f

dx

dy

2

2

2

2

y

x

−

−

−

−

=

=

=

=

−

−

−

−

=

=

=

=

−

−

−

−

=

=

=

=

jest równy –1, dzieli ćwiartkę okręgu na dwa wycinki:

- w wycinku 1:

y

q

x

p

2

2

<

<

<

<

- wybieramy piksel P

i+1

spośród pikseli A i B

zwiększając kolejno wartość x;

- w wycinku 2:

y

q

x

p

2

2

≥

≥

≥

≥

- wybieramy piksel P

i+1

spośród pikseli B i C

zmniejszając kolejno wartość y.

Rys. Podział ćwiartki okręgu na wycinki

Wybór piksela leżącego bliżej okręgu (A czy B lub B czy C) dokonujemy
wyznaczając wartości f(x,y) dla odpowiednich współrzędnych x i y.
Sposób nie efektywny – działa na liczbach rzeczywistych. W przypadku
krzywych opisanych równaniem wyższego stopnia złożony obliczeniowo.
Wygodniej zastosować inne kryterium wyboru - von Akenema.

A

B

C

P

i

P

i

C

B

A

P

0

Z

Z

x

y

wycinek 1

wycinek 2

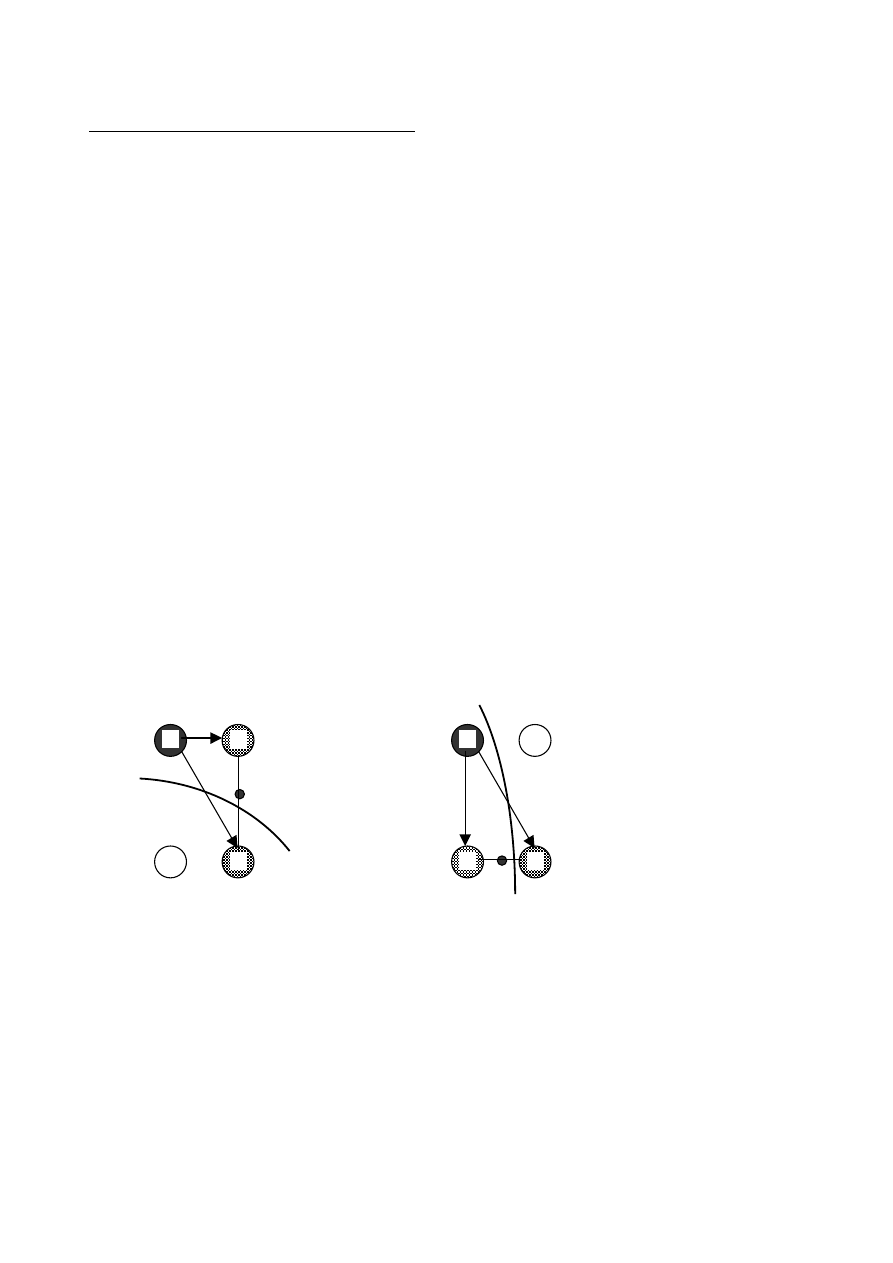
Kryterium wyboru von Akenema:

o wyborze piksela decyduje wartość funkcji f(x,y) w punkcie środkowym
S

pomiędzy alternatywnymi pikselami

Dla wycinka 1: obliczamy

)

.

,

(

5

0

y

1

x

f

fs

i

i

i

−

−

−

−

+

+

+

+

=

=

=

=

- jeżeli

0

fs

i

>

>

>

>

to punkt S leży na zewnątrz okręgu: wybieramy piksel

P

i+1

= B;

- jeżeli

0

fs

i

<

<

<

<

to punkt S leży wewnątrz okręgu: wybieramy piksel

P

i+1

= A;

Dla wycinka 2: obliczamy

)

,

.

(

1

y

5

0

x

f

fs

i

i

i

−

−

−

−

+

+

+

+

=

=

=

=

- jeżeli

0

fs

i

>

>

>

>

to punkt S leży wewnątrz okręgu: wybieramy piksel

P

i+1

= C;

- jeżeli

0

fs

i

<

<

<

<

to punkt S leży na zewnątrz okręgu: wybieramy piksel

P

i+1

= B;

Dla obu wycinków:
- jeżeli

0

fs

i

=

=

=

=

to punkt S leży na okręgu: piksel wybieramy arbitralnie

spośród pikseli A i B dla wycinka 1 lub pikseli C i B dla wycinka 2.

wycinek 1

wycinek 2

Rys. Wybór pikseli w algorytmie Bresenhama rysowania okręgu.

C

P

i

B

A

S

S

A

P

i

B

C

Algorytm:

1. Piksel początkowy P

0

=(x

0

,y

0

)=(0,R)

- wartość zmiennej decyzyjnej:

2

2

2

2

2

2

2

2

2

0

0

0

q

25

0

R

q

p

R

q

5

0

R

q

1

0

p

5

0

y

1

x

f

fs

.

)

.

(

)

(

)

.

,

(

+

+

+

+

−

−

−

−

=

=

=

=

−

−

−

−

−

−

−

−

+

+

+

+

+

+

+

+

=

=

=

=

−

−

−

−

+

+

+

+

=

=

=

=

2. Piksel kolejny: przejście z P

i

=(x

i

,y

i

) do P

i+1

=(x

i+1

,y

i+1

)

dla wycinka 1:

- przy wyborze piksela A mamy x

i+1

=x

i

+1, y

i+1

= y

i

- wartość zmiennej decyzyjnej:

2

1

i

2

i

2

1

i

2

i

i

2

2

2

i

2

2

i

2

2

2

2

1

i

2

2

1

i

2

1

i

1

i

1

i

p

x

p

2

fs

p

x

p

2

5

0

y

1

x

f

R

q

5

0

y

q

1

1

x

p

R

q

5

0

y

q

1

x

p

5

0

y

1

x

f

fs

+

+

+

+

+

+

+

+

=

=

=

=

=

=

=

=

+

+

+

+

+

+

+

+

−

−

−

−

+

+

+

+

=

=

=

=

=

=

=

=

−

−

−

−

−

−

−

−

+

+

+

+

+

+

+

+

+

+

+

+

=

=

=

=

=

=

=

=

−

−

−

−

−

−

−

−

+

+

+

+

+

+

+

+

=

=

=

=

−

−

−

−

+

+

+

+

=

=

=

=

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

)

.

,

(

)

.

(

)

(

)

.

(

)

(

)

.

,

(

- przy wyborze piksela B mamy x

i+1

=x

i

+1, y

i+1

= y

i

-1

- wartość zmiennej decyzyjnej:

1

i

2

2

1

i

2

i

1

i

2

2

1

i

2

i

i

2

2

2

i

2

2

i

2

2

2

2

1

i

2

2

1

i

2

1

i

1

i

1

i

y

q

2

p

x

p

2

fs

y

q

2

p

x

p

2

5

0

y

1

x

f

R

q

1

5

0

y

q

1

1

x

p

R

q

5

0

y

q

1

x

p

5

0

y

1

x

f

fs

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

−

−

−

−

+

+

+

+

+

+

+

+

=

=

=

=

=

=

=

=

−

−

−

−

+

+

+

+

+

+

+

+

−

−

−

−

+

+

+

+

=

=

=

=

=

=

=

=

−

−

−

−

−

−

−

−

−

−

−

−

+

+

+

+

+

+

+

+

+

+

+

+

=

=

=

=

=

=

=

=

−

−

−

−

−

−

−

−

+

+

+

+

+

+

+

+

=

=

=

=

−

−

−

−

+

+

+

+

=

=

=

=

)

.

,

(

)

.

(

)

(

)

.

(

)

(

)

.

,

(

dla wycinka 2:
Przy wyznaczeniu pierwszego piksela o wyborze decyduje nowa wartość

zmiennej decyzyjnej

)

,

.

(

1

y

5

0

x

f

i

i

−

−

−

−

+

+

+

+

a nie ostatnia

)

.

,

(

5

0

y

1

x

f

i

i

−

−

−

−

+

+

+

+

.

Różnica między nimi wynosi:

)

.

(

)

.

(

)

.

,

(

)

,

.

(

75

0

y

q

75

0

x

p

5

0

y

1

x

f

1

y

5

0

x

f

i

2

i

2

i

i

i

i

−

−

−

−

−

−

−

−

+

+

+

+

+

+

+

+

−

−

−

−

=

=

=

=

−

−

−

−

+

+

+

+

−

−

−

−

−

−

−

−

+

+

+

+

O tą różnicę należy zmodyfikować wartość poprzednio obliczonej
zmiennej decyzyjnej. Następnie korzystamy z zależności rekurencyjnych:

- przy wyborze piksela B mamy x

i+1

=x

i

+1, y

i+1

= y

i

-1

- wartość zmiennej decyzyjnej:

2

1

i

2

1

i

2

i

1

i

1

i

1

i

q

y

q

2

x

p

2

fs

1

y

5

0

x

f

fs

+

+

+

+

−

−

−

−

+

+

+

+

=

=

=

=

−

−

−

−

+

+

+

+

=

=

=

=

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

)

,

.

(

- przy wyborze piksela C mamy x

i+1

=x

i

, y

i+1

=y

i

-1

- wartość zmiennej decyzyjnej:

2

1

i

2

i

1

i

1

i

1

i

q

y

q

2

fs

1

y

5

0

x

f

fs

+

+

+

+

−

−

−

−

=

=

=

=

−

−

−

−

+

+

+

+

=

=

=

=

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

)

,

.

(

Zgodnie z przyjętymi założeniami możemy napisać algorytm Bresenhama
wyboru zbioru pikseli obrazujących 1/4 okręgu o promieniu R i środku
w początku układu współrzędnych na urządzeniu rastrowym o aspekcie
a=p/q

, gdzie: R, p, q – liczby naturalne.

Begin

x :=0;

(* wartości początkowe*)

y:=R;

fx:= p*p*x;
fy:= q*q*y;
fs:=p*p-q*q*R+0.25*q*q;

(* wartość początkowa zmiennej decyzyjnej *)

while fx < fy do

(* wycinek 1 -

y

q

x

p

2

2

<

<

<

<

*)

begin

Putpixel(x, y, kolor);
x:=x+1;
fx:=fx+2*p*p;

if fs

≤

0 then fs:=fs+fx+2*p*p else

(* wybór punktu A *)

begin
y:=y-1;

(* wybór punktu B *)

fy:=fy-2*q*q;
fs:=fs+fx+p*p-fy;
end;

end;

fs:=fs-(fx-fy)/2+3*(pp-qq);

(* wartość fs dla pierwszego punktu wycinka 2 *)

while y

≥

0 do

(* wycinek 2 -

y

q

x

p

2

2

≥

≥

≥

≥

*)

begin

Putpixel(x, y, kolor);
y:=y-1;
fy:=fy-2*q*q;

if fs

≤

0 then

begin
x:=x+1;

(* wybór punktu B *)

fx:=fx-2*p*p;
fs:=fs+fx-fy+2*q*q;
end
else fs:=fs-fx+q*q;

(* wybór punktu C *)

end;

End.

Wypełnianie obszaru

Def.

Zbiór pikseli nazywamy spójnym, gdy do dowolnego piksela z tego
zbioru można przejść do każdego innego przez piksele sąsiednie.

Relacje sąsiedztwa:

zbiór czterospójny

zbiór ośmiospójny

Algorytm wypełniania przez sianie (ang. seed fill algorithm)

Założenia:
- wnętrze obszaru jest zbiorem czterospójnym, a ograniczający je brzeg

zbiorem ośmiospójnym;

- brzeg obszaru jest narysowany kolorem cb;
- wnętrze obszaru wypełniamy kolorem cn
- możliwe występowanie dziur wewnątrz obszaru: będą nimi obszary

ograniczone ośmiospójnymi brzegami pikseli w kolorze cb, w
szczególnym przypadku mogą to być pojedyncze piksele w tym
kolorze;

- znamy położenie ziarna (ang. seed), czyli piksela leżącego wewnątrz

obszaru. Od tego piksela rozpoczynamy działanie algorytmu
wypełniania. Piksel wypełniamy nowym kolorem i następnie
sprawdzamy w czterech kierunkach czy piksele należą do wnętrza
obszaru i czy nie zostały jeszcze wypełnione nowym kolorem.

Algorytm wypełniania przez sianie

- x,y – współrzędne piksela;

- color – kolor sprawdzanego piksela;

- cb – kolor brzegu obszaru;

- cn – kolor wypełniania obszaru.

procedure fill4(integer: x, y, cb, cn)

begin

getpixel(x, y, color);

if (color

≠

cb

) and (color

≠

cn

) then

begin

putpixel(x, y, cn);

fill4(x, y-1, cb, cn);

fill4(x, y+1, cb, cn);

fill4(x-1, y, cb, cn);

fill4(x+1, y, cb, cn);

end;

end.

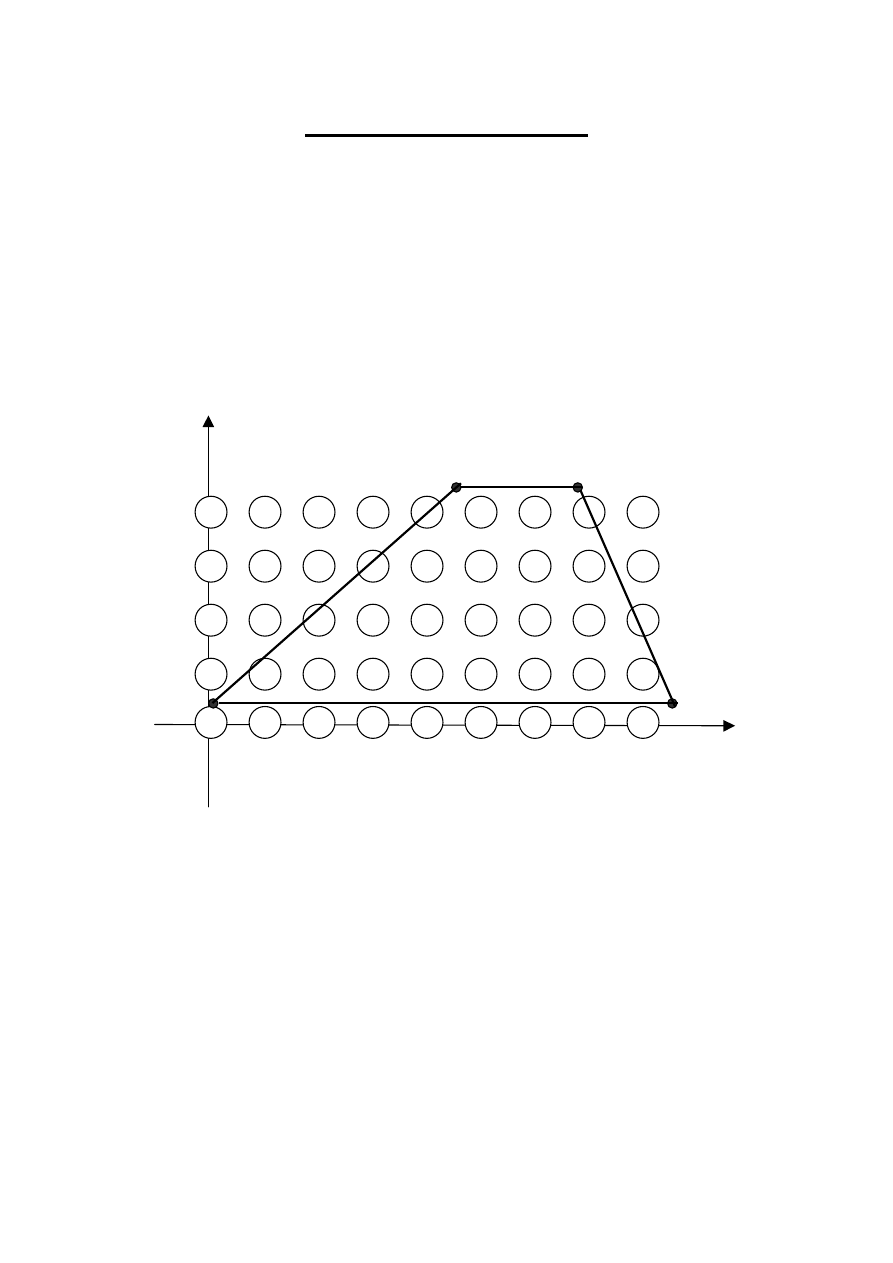
Wypełnianie wielokątów

Założenie:

- obszar jest określony analitycznie jako trapez, o podstawach

równoległych do osi x;

- płaszczyzna rysunku opisana będzie współrzędnymi pikselowymi;

- wierzchołki trapezu mają współrzędne rzeczywiste, nie pokrywające się

ze środkami pikseli, tak jak na rysunku;

Rys. Wypełnianie trapezu

x

y

)

,

(

2

2

y

x

)

,

(

3

3

y

x

)

,

(

1

1

y

x

)

,

(

4

4

y

x

Niech:

y

min

= Int(y

1

); y

max

= Int(y

3

);

gdzie:

Int(r) -

zaokrąglenie liczby rzeczywistej r do najbliższej liczby

całkowitej.

Wyznaczamy współczynniki kierunkowe nachylenia boków trapezu:

c

l

= (x

4

-x

1

)/(y

4

-y

1

); c

p

= (x

3

-x

2

)/(y

3

-y

2

)

;

Przy tych założeniach algorytm wypełniania trapezu jest następujący:

start:

dla y = y

min

, y

min

+1, ..., y

max

wykonaj:

1). wyznacz przecięcia x

l

i x

p

linii poziomej y z prostymi:

x = x

1

+ (y-y

1

)c

l

i x = x

2

+ (y-y

2

)c

p

;

2). wypełnij nowym kolorem (wzorcem) piksele leżące na tej linii

od Int(x

l

)

do Int(x

p

)

;

end.

Można zauważyć, że:
- dla y = y

1

= y

2

jest x

l

= x

1

, x

p

= x

2

;

- między punktami przecięć x

l

i x

p

z linią poziomą y i punktami przecięć

x

l

'

i x

p

'

z kolejną linią poziomą y + 1 zachodzą zależności:

x

l

'

= x

l

+ c

l

i x

p

'

= x

p

+

c

p

Jeśli wykorzystamy te zależności to algorytm uprości się do postaci:

start:

x

l

:= x

1

; x

p

:= x

2

;

dla y = y

min

, y

min

+1, ..., y

max

wykonaj:

1). wypełnij nowym kolorem (wzorcem) piksele leżące na linii y

od Int(x

l

)

do Int(x

p

)

;

2). x

l

:= x

l

+ c

l

; x

p

:= x

p

+ c

p

;

end.

Uwaga:
zadanie wypełniania dowolnego wielokąta można sprowadzić do
omówionego powyżej przypadku szczególnego.

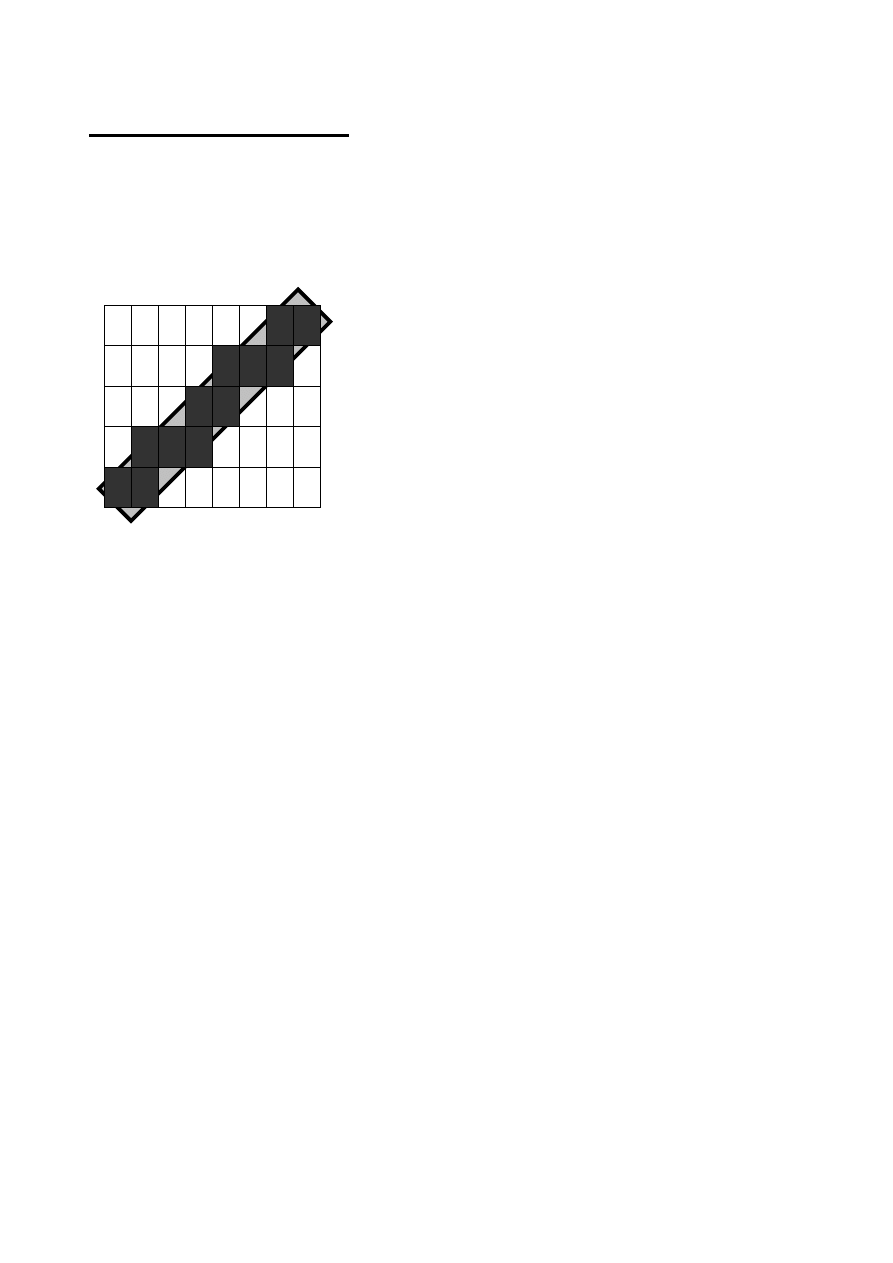
Problem antyaliasingu

W trakcie rysowania na urządzeniach grafiki rastrowej dochodzi do
zjawiska powstawania schodków na krawędziach linii ukośnych.
Zjawisko to nosi nazwę aliasingu.

Pochylony prostokąt reprezentuje idealną linię,
zaczernione punkty pokazują reprezentację tej linii
na rastrze o określonej rozdzielczości

Aliasing

- niedokładne wyświetlanie obrazu wynikające z ograniczonej

rozdzielczości urządzenia rastrowego. Zjawisko to, jest widoczne w
postaci postrzępionych brzegów wokół linii ukośnych, krzywych i
obiektów o nieregularnych kształtach.

Antyaliasing

- wygładzanie krawędzi rysunku (łuków, okręgów,

krzywych) poprzez nałożenie na brzegach dodatkowych pikseli o
mniejszym nasyceniu i jasności niż piksele obiektu, przez co brzegi są
bardziej wyraziste. Inną metodą wygładzania brzegów jest zastosowanie
urządzeń wyjściowych o wyższej rozdzielczości.

Antyaliasing pozwala zredukować efekt "schodków" w rysunkach, lecz w
pewnym stopniu przyczynia się do pogorszenia ostrości obrazu.
Stosowany w odniesieniu do fontów czcionek poprawia wygląd i
czytelność tekstów wyświetlanych na ekranie monitora.

Przykład tekstu, w którym zastosowano
antyaliasing







Tekst bez aliasingu

Metody antyaliasingu

Metody (techniki) antyaliasingu dotyczą sposobu rozmywania krawędzi
w celu uzyskania gładkości krzywych.

Przykład:

W przypadku czarnego prostokąta na białym tle, przejście z czerni do
bieli może być wygładzone poprzez zastosowanie szarych pikseli na
krawędzi prostokąta. Takie reprezentowanie krawędzi jest obserwowane
przez ludzkie jako płynne przejście pomiędzy kolorem prostokąta i tła.
Krawędź zostaje wygładzona.

Istnieją trzy główne metody antyaliasingu:

1. Prefiltering

2. Supersampling

3. Postfiltering

Prefiltering

Metoda prefilteringu oblicza poziom intensywności (nasycenia koloru)
piksela na podstawie wielkości powierzchni piksela zajętej przez dany
obiekt.

Przykład:

Intensywność koloru określona jest w przedziale od 0 dla czerni (kolor
tła) do 15 dla bieli (kolor obiektu). Wielokąt położony jest na siatce
kwadratów reprezentujących piksele, gdzie środek kwadratu oznacza
ś

rodek piksela. Jeżeli piksel pokryty jest w 1/n części przez wielokąt to

powinien przyjąć odcień o wartości 1/n*15. Na rysunku pokazano
wartości odcieni poszczególnych pikseli reprezentujących wielokąt na
siatce rastrowej.

Wadą metody jest duża złożoność obliczeniowa związana z obliczeniem
powierzchni piksela zajmowanej przez obiekt.

0

0

0

0

1

6

0

0

0

0

0

6

13

15

8

0

0

3

11

15

15

9

7

3

3

11

14

15

12

2

0

0

0

0

1

6

5

0

0

0

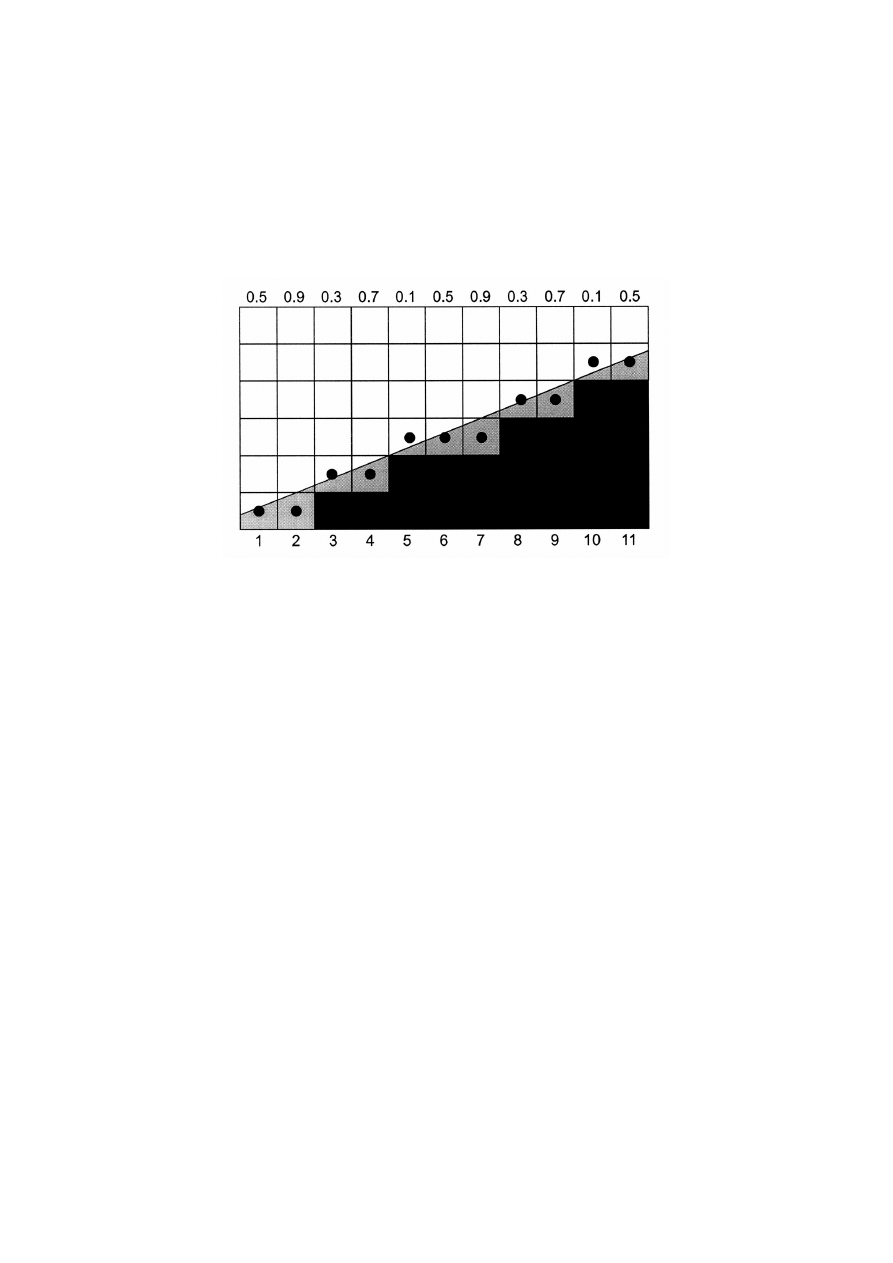
Prefiltering – metoda Pitteway’a-Watkinsona

Metoda wykorzystuje algorytm kreślenia odcinka Bresenhamma. Dla
każdej krawędzi wielokąta, podczas wyznaczania położenia piksela,
obliczany jest również stopień jego pokrycia przez wielokąt. Zasadę
działania tego algorytmu pokazuje rysunek.

Piksele wyznaczone za pomocą klasycznego algorytmu Bresenhamma
oznaczono kropkami. Szare ich części to powierzchnie pikseli należące
do wielokąta. Wartości numeryczne na górze rysunku reprezentują te
powierzchnie. Piksele zaznaczone kropkami rysowane są kolorem o
nasyceniu określonym wyznaczoną wartością. Nasycenie koloru
dobierane jest z przedziału od 0 do 1.

Supersampling (oversampling, nadsampling)

Problem rasteryzacji obiektów można sprowadzić do problemu
dyskretyzacji funkcji opisujących kształt obiektu, z krokiem równym
wielkości rastra (piksela). Jeżeli krawędź obiektu opisana jest funkcją to
rasteryzacja polega na dyskretnym próbkowaniu, czyli obliczeniu
wartości tej funkcji z częstotliwością odpowiadającą gęstości rastra.

Metoda supersamplingu polega na zwiększeniu liczby próbek podczas
dopasowywania rzeczywistego kształtu obiektu do siatki rastrowej a
następnie

uśrednienie

próbek

do

wartości

odpowiadającym

poszczególnym pikselom.

Przykład:

Aby wyznaczyć barwę piksela znajdującego się na krawędzi obiektu
należy zdyskretyzować funkcję opisującą tę krawędź z częstotliwością
większą od rzeczywistej gęstości rastra, a następnie dla każdego piksela
obliczyć uśrednioną wartość barwy na podstawie wyznaczonych wartości
barw poszczególnych próbek należących do danego piksela.

Rys. Przykład realizacji nadsamplingu

Jeżeli liczba próbek dla pojedynczego piksela będzie rosnąć to metoda ta
sprowadzać się będzie do obliczenia rzeczywistej powierzchni piksela
jaka należy do obiektu. Najczęściej stosuje się nadsampling z liczbą
próbek na piksel 2, 4 i 8.

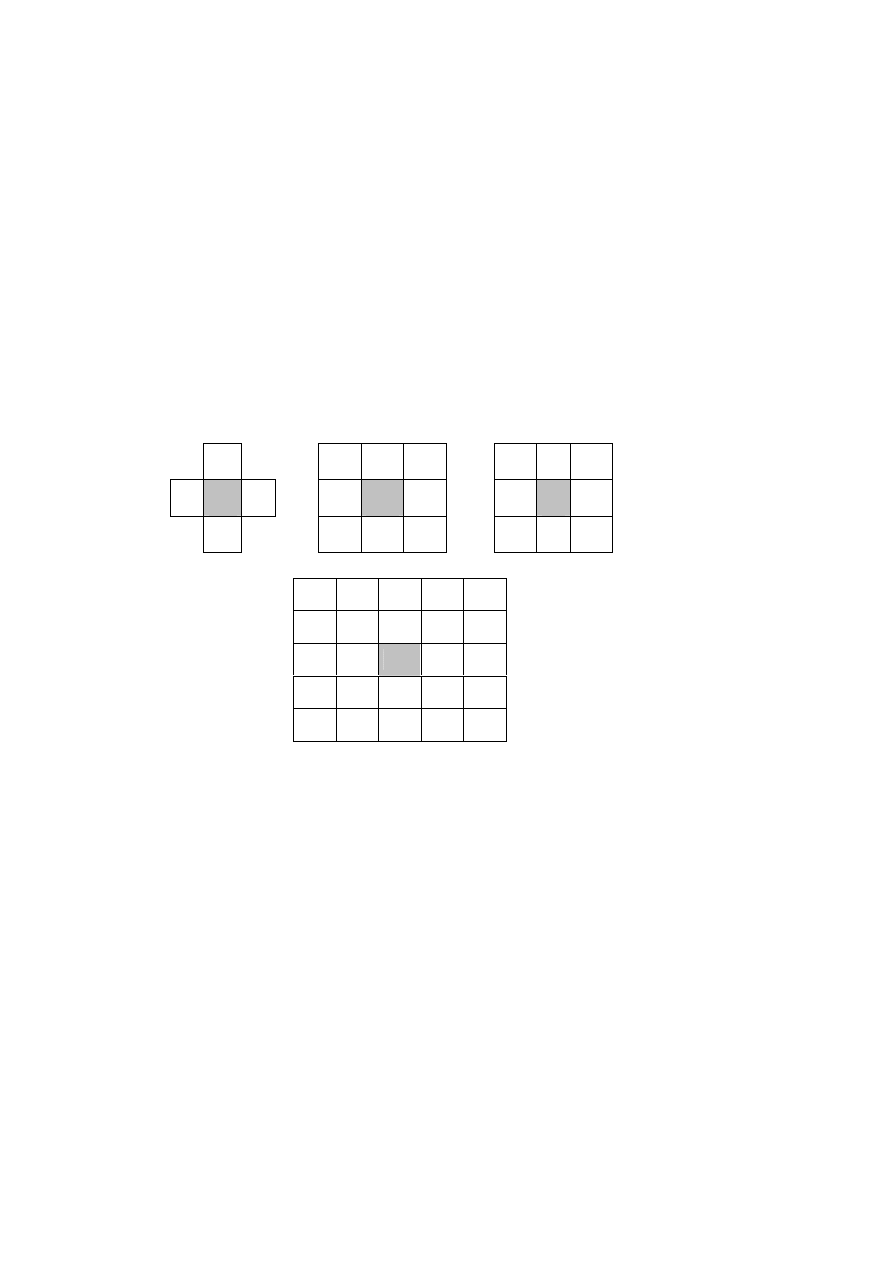
Postfiltering

Metoda polega na uśrednieniu wartości barwy każdego piksela w oparciu
o barwę tego piksela i barwy pikseli sąsiadujących z nim. Najczęściej
stosowana jest średnia ważona, gdzie waga piksela, którego barwa jest
wyznaczana, jest największa.

W algorytmie definiuje się sąsiedztwo piksela i nadaje wagi każdemu
pikselowi tego otoczenia. Następnie dla każdego piksela w obrazie
oblicza się jego nową wartość. W metodzie istotny jest dobór sąsiedztwa
piksela oraz wagi nadane poszczególnym pikselom.

Rys. Przykłady sąsiedztwa w metodzie postfilteringu.

Metoda postfilteringu wymaga znajomości barw wszystkich pikseli.
Realizowana jest po narysowaniu wszystkich obiektów na mapie bitowej.

1/8

1/8 ½ 1/8

1/ 8

1/16 1/16 1/16

1/16 ½ 1/16

1/16 1/16 1/16

1/81 2/81 3/81 2/81 1/81

2/81 4/81 6/81 4/81 2/81

3/81 6/81 9/81 6/81 3/81

2/81 4/81 6/81 4/81 2/81

1/81

2/81

3/81

2/81

1/81

1/16 1/8 1/16

1/8 1/4 1/8

1/16 1/8 1/16