6. STATECZNOŚĆ SKARP, ZBOCZY I USKOKÓW NAZIOMU

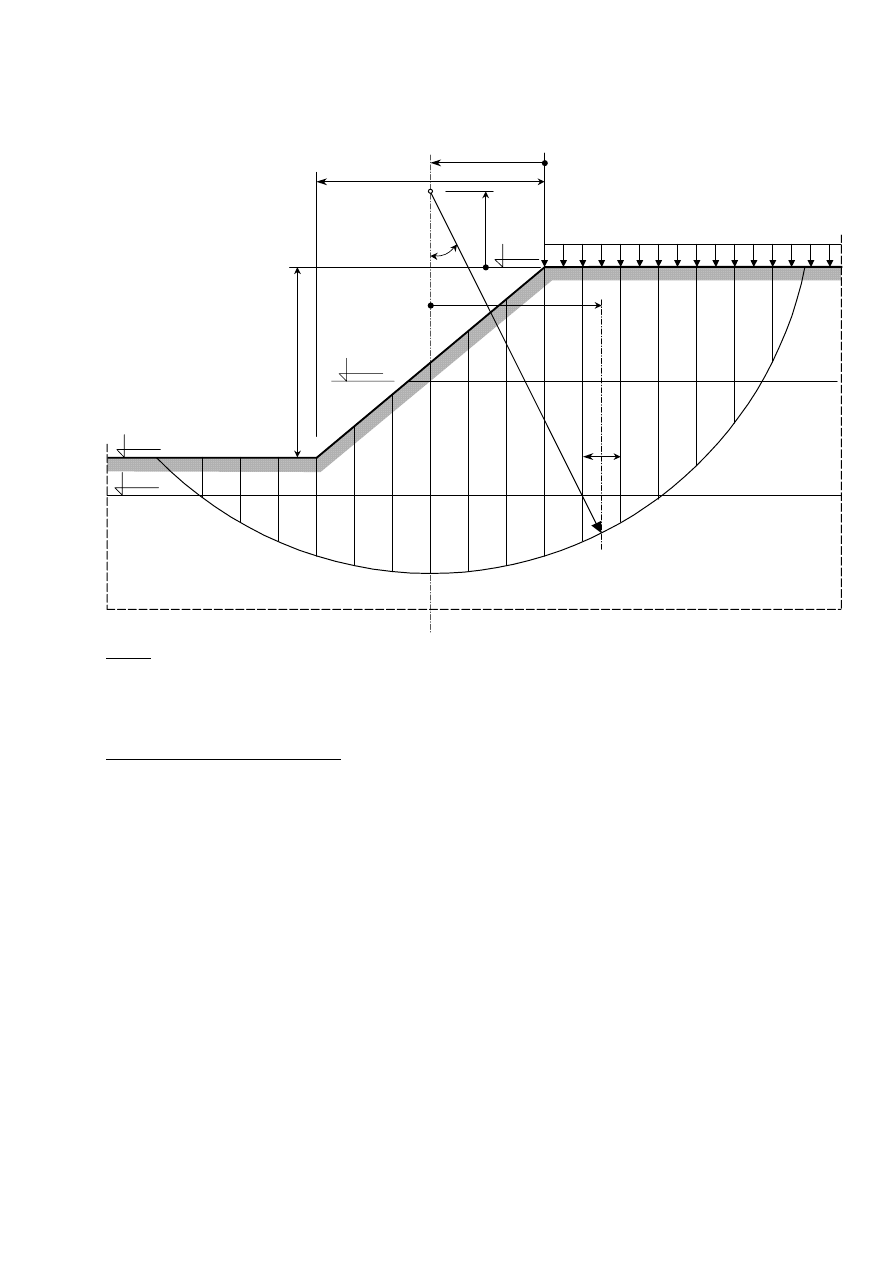
Zad. 6.1. Sprawdzić metodą Felleniusa stateczność skarpy przedstawionej na rysunku poniżej.

Dane:
Nasyp budowlany: Ps, I

D

= 0.6,

φ

= 32

°,

γ

= 18 kN/m

3

Piasek gliniasty: Pg, I

L

= 0.2,

φ

= 20

°, c = 15 kPa,

γ

= 19 kN/m

3

Glina pylasta: G

π, I

L

= 0.40,

φ

= 15

°, c = 10 kPa,

γ

= 19.5 kN/m

3

Ciężary poszczególnych bloków:
W

1

= 1.25

⋅1.0⋅18.0 + 1.0⋅20 = 42.5 kN/mb

W

2

= (2.5

⋅1.0 + 0.5⋅0.87)⋅18.0 + 0.5⋅1.1⋅0.75⋅19.0 + 1.0⋅20 = 80.67 kN/mb

W

3

= 3.0

⋅1.0⋅18.0 + 1.7⋅1.0⋅19.0 + 1.0⋅20 = 106.3 kN/mb

W

4

= 3.0

⋅1.0⋅18.0 + 2.7⋅1.0⋅19.0 + 1.0⋅20 = 125.3 kN/mb

W

5

= 3.0

⋅1.0⋅18.0 + 3.0⋅1.0⋅19.0 + 0.4⋅1.0⋅19.5 + 1.0⋅20 = 138.8 kN/mb

W

6

= 3.0

⋅1.0⋅18.0 + 3.0⋅1.0⋅19.0 + 1.0⋅1.0⋅19.5 + 1.0⋅20 = 150.5 kN/mb

W

7

= 3.0

⋅1.0⋅18.0 + 3.0⋅1.0⋅19.0 + 1.4⋅1.0⋅19.5 + 1.0⋅20 = 158.3 kN/mb

W

8

= 2.6

⋅1.0⋅18.0 + 3.0⋅1.0⋅19.0 + 1.75⋅1.0⋅19.5 = 137.93 kN/mb

W

9

= 1.75

⋅1.0⋅18.0 + 3.0⋅1.0⋅19.0 + 1.95⋅1.0⋅19.5 = 126.53 kN/mb

W

10

= 0.9

⋅1.0⋅18.0 + 3.0⋅1.0⋅19.0 + 2.0⋅1.0⋅19.5 = 112.2 kN/mb

W

11

= 0.5

⋅0.5⋅0.6⋅18.0 + 0.4⋅0.8⋅19.0 + 2.6⋅1.0⋅19.0 + 2.0⋅1.0⋅19.5 = 97.18 kN/mb

W

12

= 2.25

⋅1.0⋅19.0 + 1.95⋅1.0⋅19.5 = 80.78 kN/mb

W

13

= 1.4

⋅1.0⋅19.0 + 1.75⋅1.0⋅19.5 = 60.73 kN/mb

W

14

= 1.0

⋅1.0⋅19.0 + 1.4⋅1.0⋅19.5 = 46.3 kN/mb

W

15

= 1.0

⋅1.0⋅19.0 + 1.0⋅1.0⋅19.5 = 38.5 kN/mb

W

16

= 1.0

⋅1.0⋅19.0 + 0.45⋅1.0⋅19.5 = 27.78 kN/mb

W

17

= 0.55

⋅1.15⋅19.0 = 12.02 kN/mb

x

0

= 3.0 m

y

0

=

2.

0 m

α

i

x

i

b

i

=R/10

p = 20 kN/m

2

R = 10 m

0.00

- 3.00

- 5.00

- 6.00

H =

5

.0

m

B = 6.0 m

Nasyp budowlany

Piasek gliniasty

Glina pylasta

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

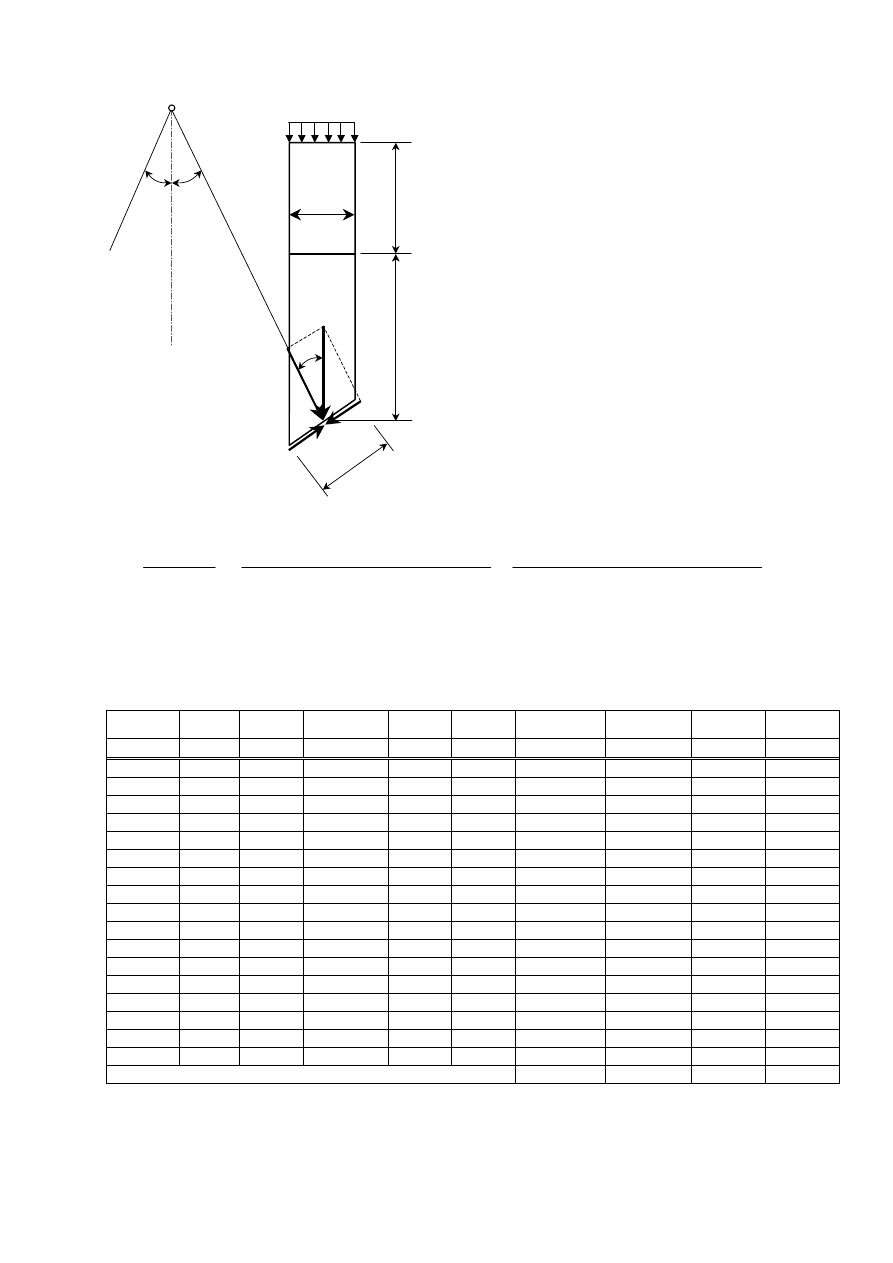
Układ sił działających na pojedynczy blok

Położenie punktu „0” oraz wartość promienia R ustala się metodą kolejnych prób tak, aby otrzymać
najmniejszą wartość współczynnika F. W zadaniu wielkości te przyjęto arbitralnie (w celach
akademickich).
Tablica: Obliczenia stateczności skarpy

Nr bloku

W

i

x

i

sin

α

i

= x

i

/R

cos

α

i

φ

i

W

i

⋅cos

α

i

⋅tg

φ

i

c

i

c

i

⋅b

i

/cos

α

i

W

i

⋅sin

α

i

[kN/m]

[m]

[

°]

[kN/mb] [kPa] [kN/mb]

[kN/mb]

1 42.50

9.4 0.94

0.3412

32

9.06

0

0.00

39.95

2 80.67

8.5 0.85

0.5268 23

(śr.) 18.04

11.25

(śr.) 21.36

68.57

3 106.30 7.5 0.75

0.6614

20

25.59

15

22.68

79.73

4 125.30 6.5 0.65

0.7599

20

34.66

15

19.74

81.45

5 138.80 5.5 0.55

0.8352

15

31.06

10

11.97

76.34

6 150.50 4.5 0.45

0.8930

15

36.01

10

11.20

67.73

7 158.30 3.5 0.35

0.9367

15

39.73

10

10.68

55.41

8 137.93 2.5 0.25

0.9682

15

35.78

10

10.33

34.48

9 126.53 1.5 0.15

0.9887

15

33.52

10

10.11

18.98

10 112.20 0.5 0.05

0.9987

15

30.03

10

10.01

5.61

11 97.18

-0.5 -0.05

0.9987

15

26.01

10

10.01

-4.86

12 80.78

-1.5 -0.15

0.9887

15

21.40

10

10.11

-12.12

13 60.73

-2.5 -0.25

0.9682

15

15.76

10

10.33

-15.18

14 46.30

-3.5 -0.35

0.9367

15

11.62

10

10.68

-16.21

15 38.50

-4.5 -0.45

0.8930

15

9.21

10

11.20

-17.33

16 27.78

-5.5 -0.55

0.8352

15

6.22

10

11.97

-15.28

17 12.02

-6.6 -0.65

0.7513

20

3.29

15

19.97

-7.93

SUMA

386.98

212.34

439.33

Współczynnik stateczności:

F = (386.98 + 212.34)/439.33 = 1.36 > F

min

= 1.3

Skarpa jest stateczna

O

W

i

N

i

B

i

T

i

+C

i

p

α

i

b

i

γ

1

,

φ

1

, c

1

γ

2

,

φ

2

, c

2

α

i

α

i

(-) (+)

h

1

h

2

l

i

R

Szerokość bloku przyjmuje się zwykle:

b

i

= R/10

Ciężar bloku:
W

i

= (p + h

1

⋅γ

1

+ h

2

⋅γ

2

)

⋅b

i

Składowe normalna i styczna do powierzchni
ścinania:

N

i

= W

i

⋅cos

α

i

, B

i

= W

i

⋅sin

α

i

- siła ścinająca

Siła przeciwdziałająca ścinaniu:
T

i

+ C

i

= N

i

⋅tgφ

2

+ c

2

⋅l

i

= W

i

⋅cosα

i

⋅tgφ

2

+ c

2

⋅b

i

/cos

α

i

Moment wywracający:
M

wi

= B

i

⋅R = W

i

⋅sin

α

i

⋅

R

Moment utrzymujący:
M

ui

= (T

i

+C

i

)

⋅R = (W

i

⋅cosα

i

⋅tgφ

2

+ c

2

⋅b

i

/cos

α

i

)

⋅

R

Współczynnik stateczności:

F =

Σ

M

ui

Σ

M

wi

=

Σ

(W

i

⋅cosα

i

⋅tgφ

2

+ c

2

⋅b

i

/cos

α

i

)

⋅

R

Σ

W

i

⋅sin

α

i

⋅

R

=

Σ

(W

i

⋅cosα

i

⋅tgφ

2

+ c

2

⋅b

i

/cos

α

i

)

Σ

W

i

⋅sin

α

i

≥ 1.3