1

Fundamenty Specjalne - projekt fundamentu płytowo-palowego - część 2

Nośność pali – metoda

α

α

α

α

i

β

β

β

β

, z dostosowaniem do EC7

(dr hab. inż. Adam Krasiński)

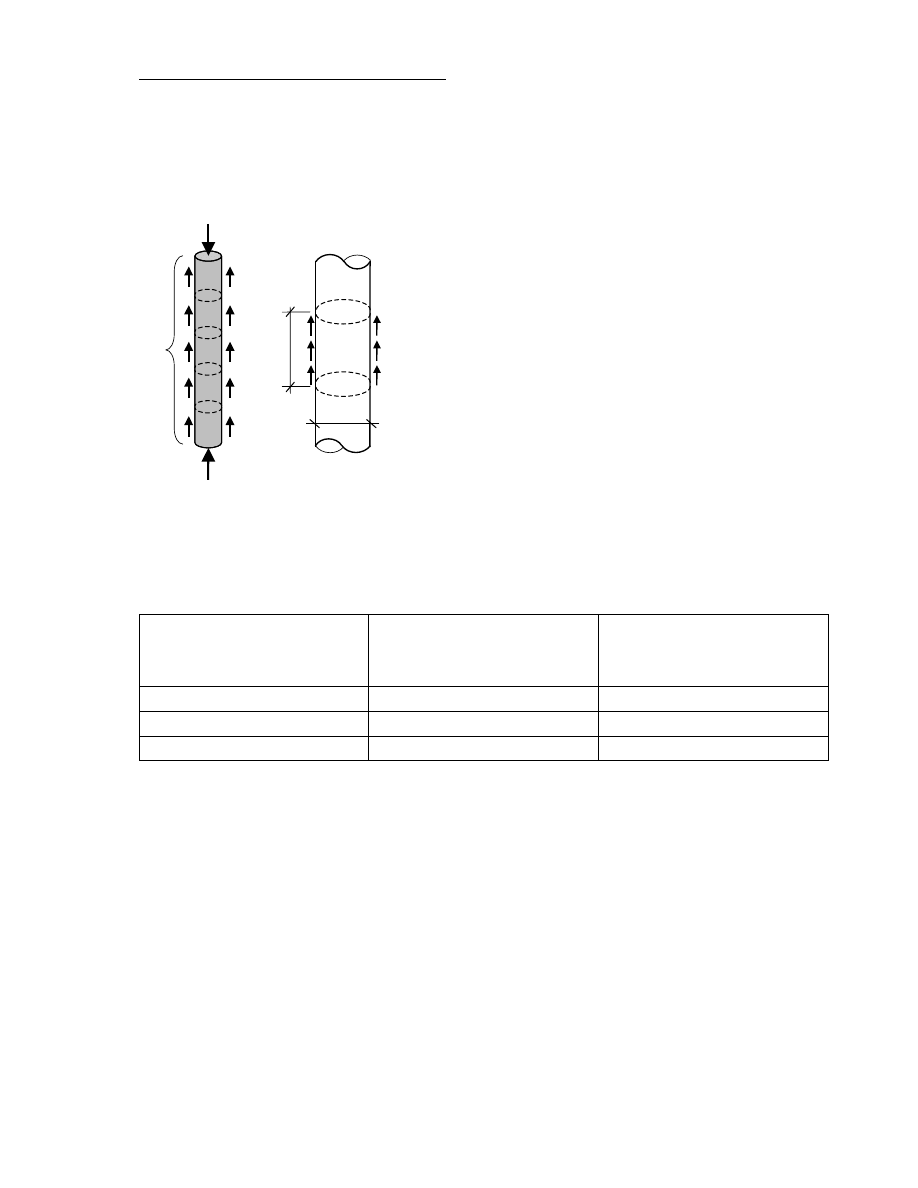
Nośność pala jest sumą nośności pobocznicy i podstawy pala:

b

i

si

b

s

c

R

R

R

R

R

+

=

+

=

∑

gdzie: R

s

– nośność pobocznicy pala, która jest sumą nośności wszystkich odcinków obliczenio-

wych wzdłuż pobocznicy pala

si

R

,

R

b

– nośność podstawy pala.

Zgodnie z EC7 wyróżnia się:

- nośność obliczoną pala

cal

b

cal

s

cal

c

R

R

R

,

;

;

+

=

- jest to nośność otrzymana z obliczeń daną metodą i dla danego profilu

geotechnicznego

- nośność charakterystyczną pala

k

b

k

s

k

c

R

R

R

,

;

;

+

=

- jest to nośność skorygowana przez współczynniki

ξ

3

i

ξ

4

zależne od liczby

przebadanych i przeliczonych profili geotechnicznych. Dodatkowo można jeszcze uwzględnić

współczynnik modelu

γ

Rd

.













⋅

=

4

min

,

3

,

;

)

(

;

)

(

min

1

ξ

ξ

γ

cal

s

mean

cal

s

Rd

k

s

R

R

R

;













⋅

=

4

min

,

3

,

;

)

(

;

)

(

min

1

ξ

ξ

γ

cal

b

mean

cal

b

Rd

k

b

R

R

R

(R

s;cal

)

mean

, (R

s;cal

)

min

- odpowiednio średnia i minimalna nośność pobocznicy pala z wartości

obliczonych dla n profili geotechnicznych,

(R

b;cal

)

mean

, (R

b;cal

)

min

- odpowiednio średnia i minimalna nośność podstawy pala z wartości

obliczonych dla n profili geotechnicznych,

W przypadku gdy pale zwieńczone są sztywnym oczepem, współczynniki

ξ

3

i

ξ

4

można

zmniejszyć, dzieląc przez 1,1, przy czym

ξ

4

nie może być mniejsze niż 1,0.

- nośność projektową pala

b

k

b

s

k

s

d

c

R

R

R

γ

γ

;

;

;

+

=

- jest to nośność przyjmowana w projekcie przy sprawdzaniu warunku stanu

granicznego nośności.

Zgodnie z aktualnym zaleceniem PKN należy stosować podejście obliczeniowe 2 (lub 2*),

w którym współczynniki częściowe przyjmują wartości

γ

s

=

γ

b

= 1,1.

Warunek nośności:

Q

v;d

≤ R

c;d

2

Metoda

α

α

α

α - nośność krótkoterminowa pala

Korzystając z tej metody można oszacować nośność pojedynczego pala pracującego w warunkach

bez odpływu. Oznacza to, że metoda może być zastosowana tylko w przypadku zagłębienia pala

w gruntach spoistych. Opór gruntu zależy głównie od wytrzymałości gruntu na ścinanie

w warunkach bez odpływu C

u

.

Nośność pobocznicy pala dla i-tego odcinka obliczenio-

wego:

i

si

si

si

si

si

si

h

D

f

S

A

f

S

R

⋅

⋅

⋅

⋅

=

⋅

⋅

=

π

gdzie: f

si

– opór gruntu na pobocznicy i-tego odcinka

obliczeniowego pala.

Dla warunków bez odpływu f

si

=

α

i

· C

ui

w którym

α

i

wyznaczamy wg tablicy 1,

A

si

– pole powierzchni bocznej i-tego odcinka

obliczeniowego pala,

S

si

– współczynnik technologiczny.

Dla pali:

- wierconych w rurach - S

s

= 1,0;

- pali CFA - S

s

= 1,2;

- Vibro i wkręcanych - S

s

= 1,4;

- pali prefabrykowanych - S

s

= 1,0.

Tablica 1. Współczynnik

α

α

α

α

Wytrzymałość gruntu na

ś

cinanie bez odpływu

C

u

[kPa]

Pale przemieszczeniowe,

wbijane i wkręcane

Pale wiercone i CFA

≤

25

α

=

1,0

α

=

0,7

25÷70

α

=

1,0 – 0,011· (C

u

– 25)

α

=

0,7 – 0,008· (C

u

– 25)

>70

α

=

0,5

α

=

0,35

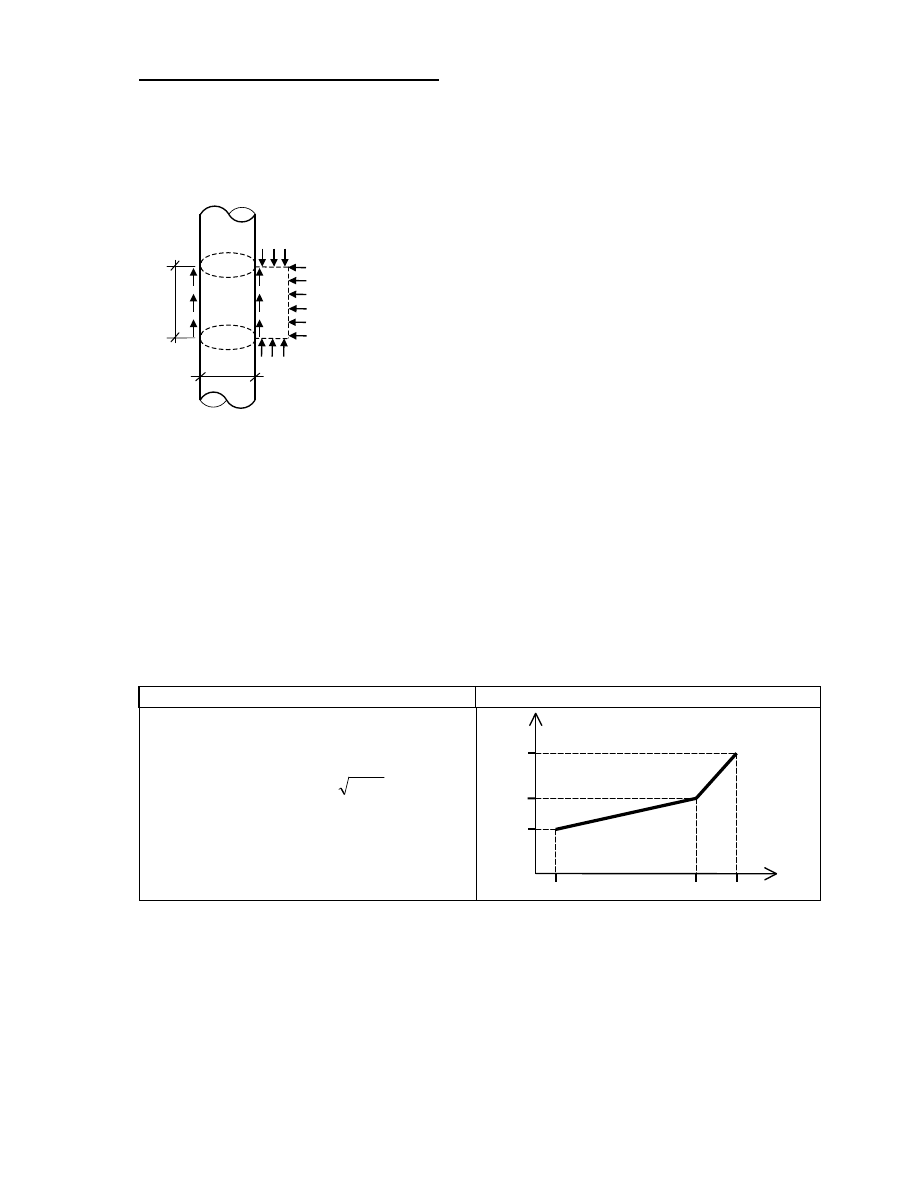
Nośność podstawy pala:

2

25

,

0

D

q

S

A

q

S

R

b

b

b

b

b

b

⋅

⋅

⋅

⋅

=

⋅

⋅

=

π

gdzie: q

b

= 9·C

ub

– opór gruntu pod podstawą pala,

A

b

– powierzchnia podstawy pala ( dla pali Vibro D jest średnicą „buta” stalowego),

S

b

– współczynnik technologiczny.

Dla pali:

- wierconych i CFA - S

b

= 1,0;

- wkręcanych - S

b

= 1,1;

- prefabrykowanych - S

b

= 1,2;

- Vibro - S

b

= 1,3.

h

i

D

f

si

Q

c

R

b

Σ

R

S

i

=

R

s

R

si

3

Metoda

β

β

β

β

– nośność długoterminowa pala

Korzystając z tej metody można oszacować nośność pojedynczego pala pracującego w warunkach
z odpływem w gruntach spoistych i niespoistych. Opór gruntu zależy od stanu naprężenia
efektywnego w gruncie. Metodę

β

stosuje się do wszystkich rodzajów gruntów.

Nośność pobocznicy pala dla i-tego odcinka obliczeniowego:

i

si

si

si

si

si

si

h

D

f

S

A

f

S

R

⋅

⋅

⋅

⋅

=

⋅

⋅

=

π

gdzie: f

si

– opór gruntu na pobocznicy i-tego odcinka pala.

Dla warunków z odpływem f

si

=

β

i

·

σ

’

vi

,

A

si

– pole powierzchni bocznej i-tego odcinka

obliczeniowego pala,

S

si

– współczynnik technologiczny.

Dla pali:
- wierconych w rurach - S

s

= 0,9;

- CFA - S

s

= 1,0;

- Vibro - S

s

= 1,4;

- wkręcanych - S

s

= 1,3;

- prefabrykowanych - S

s

= 1,1.

Wyznaczanie oporu gruntu f

si

na pobocznicy pala:

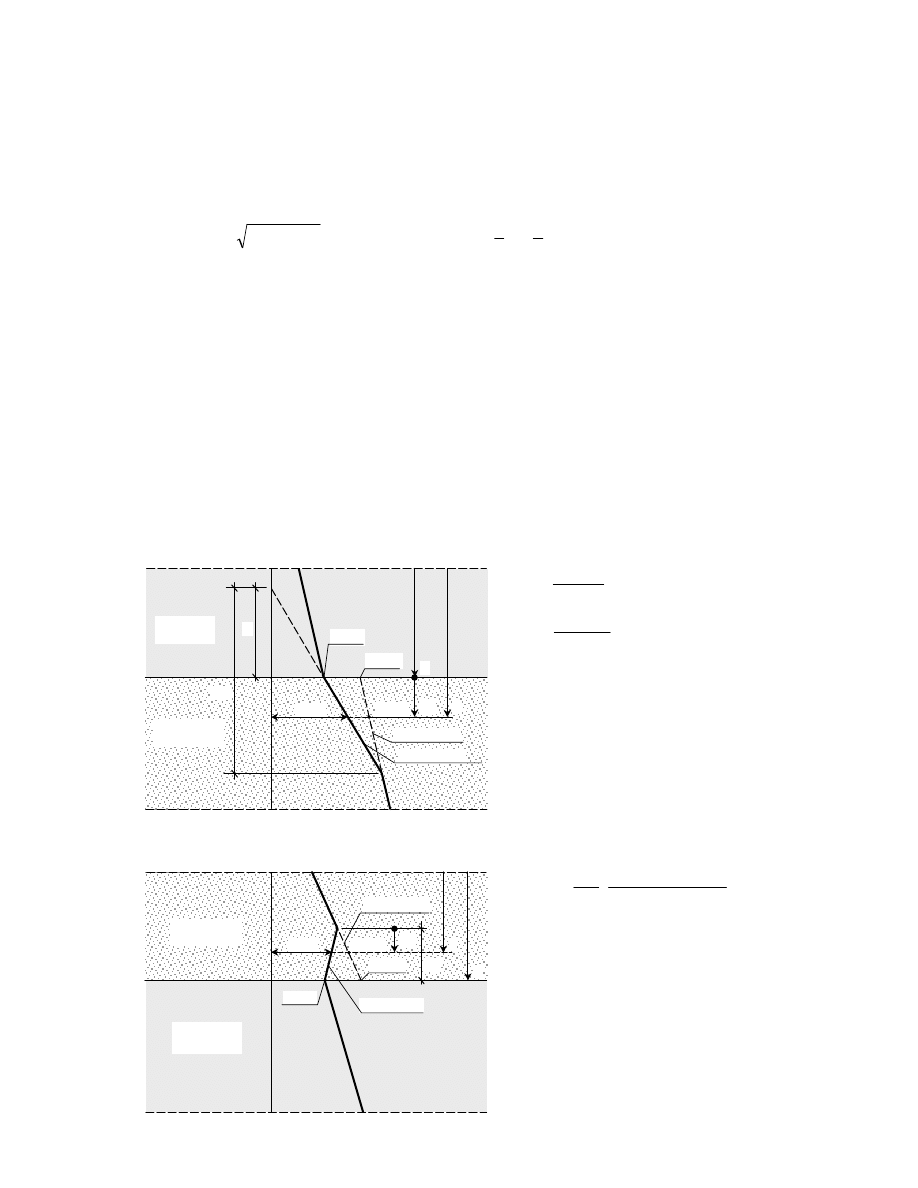
Opór gruntu na pobocznicy pala wyraża się wzorem:

vi

i

i

vi

i

i

vi

i

si

K

K

f

'

tan

'

'

0

0

σ

δ

σ

µ

σ

β

⋅

⋅

=

⋅

⋅

=

⋅

=

;

200

'

≤

vi

σ

kPa

gdzie:

σ

’

vi

– jest średnim, efektywnym naprężeniem pionowym, działąjącym w i-tej obliczeniowej

warstwie gruntu. Ze względu jednak na zjawisko głębokości krytycznej, w obliczeniach
przyjmujemy maksymalnie

σ

’

vi

= 200 kPa.

β

i

– jest współczynnikiem zależnym od efektywnego naprężenia poziomego, działąjącego w i-tej

obliczeniowej warstwie gruntu (

vi

i

hi

K

'

'

0

σ

σ

⋅

=

)

oraz szorstkości powierzchni pobocznicy pala

(

i

i

δ

µ

tan

=

). Współczynnik należy przyjmować wg tablicy 2.

Tablica 2. Współczynnik

β

β

β

β

.

Grunty spoiste

Grunty niespoiste

φ

β

′

⋅

=

tan

0

K

(

)

OCR

K

⋅

−

=

'

sin

1

0

φ

OCR

– współczynnik prekonsolidacji

(wyznaczony na podstawie badań

laboratoryjnych bądź in situ)

Nośność podstawy pala:

2

25

,

0

D

q

S

A

q

S

R

b

b

b

b

b

b

⋅

⋅

⋅

⋅

=

⋅

⋅

=

π

gdzie: q

b

– opór gruntu pod podstawą pala,

A

b

– powierzchnia podstawy pala ( dla pali Vibro D jest średnicą „buta” stalowego),

S

b

– współczynnik technologiczny

Dla pali:
- wierconych i CFA - S

b

= 1,0;

- wkręcanych - S

b

= 1,1;

- prefabrykowanych - S

b

= 1,3;

- Vibro - S

b

= 1,4.

β

β

β

β

1,20

0,75

0,44

28°

35°

37°

φ

φφ

φ

’

h

i

D

σ

σ

σ

σ

vi

’

σ

σ

σ

σ

hi

’

f

si

4

Wyznaczanie oporu gruntu q

b

pod podstawą pala:

Opór gruntu pod podstawą pala przyjmujemy wg rozwiązania Terzaghi’ego:

c

b

q

vb

b

N

c

N

q

⋅

+

⋅

=

'

'

σ

gdzie:

σ′

vb

– naprężenie efektywne w poziomie podstawy pala, przy czym ze względu na zjawisko

głębokości krytycznej w obliczeniach przyjmujemy maksymalnie

σ′

vi

= 200 kPa,

c’

b

– spójność efektywna gruntu w poziomie posadowienia,

N

c

, N

q

– współczynniki nośności:

(

)

(

)

b

e

N

b

b

q

'

tan

2

2

2

'

tan

1

'

tan

φ

η

φ

φ

⋅

⋅

⋅

+

+

=

gdzie:













÷

=

π

π

η

5

3

3

1

Kąt wypierania gruntu

η

spod podstawy pala. Przyjmujemy w przedziale od 1/3

π

dla plastycznych

gruntów spoistych do 2/3

π

dla zagęszczonych piasków.

b

q

c

N

N

'

cot

)

1

(

φ

⋅

−

=

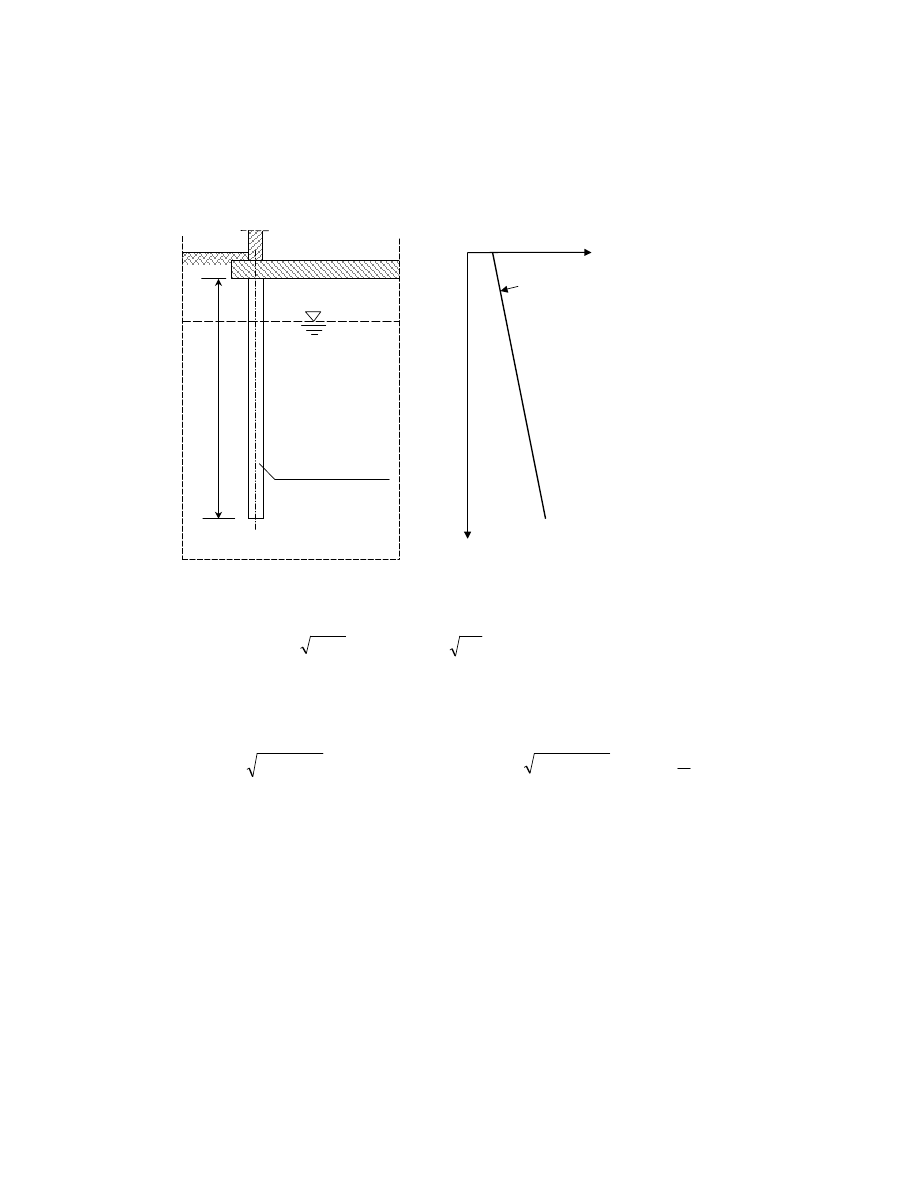
Wpływ zmiany warstwy gruntowej na nośność podstawy pala

Wyżej podane wzory w metodach

α

i

β

, dotyczące nośności podstaw pali, są ważne dla przypadku

podłoża jednorodnego. W przypadku podłoża uwarstwionego, w sytuacji gdy występuje zmiana
warstwy o różnych parametrach wytrzymałościowych, na granicy obu warstw może pojawić się
przeskok w nośności podstawy. Taki przeskok jest nierzeczywisty. Zmiany nośności podstaw
przebiegają w rzeczywistości stopniowo. Można zastosować zmodyfikowaną propozycję
Meyerhofa (1983), przedstawioną na rysunkach poniżej.

Przypadek 1 – warstwa górna (1) o mniejszej nośności niż warstwa dolna (2)

D

z

R

z

R

h

b

b

z

10

)

(

)

(

1

2

1

1

⋅

′

=

; D – średnica pala

0

,

1

10

2

2

≤

∆

+

=

D

z

h

z

η

Skorygowana

nośność

podstawy

pala

w warstwie 2:

)

(

)

(

2

2

2

z

R

z

R

b

b

′

⋅

=

η

Wartość R

′

b

2

(z) oblicza się według wzorów

na str. 1 i 2.

Przypadek 2 – warstwa górna (1) o większej nośności niż warstwa dolna (2)

0

,

1

)

(

)

(

)

(

3

1

1

1

1

2

1

1

1

1

≤

′

−

′

⋅

∆

−

=

z

R

z

R

z

R

D

z

b

b

b

η

;

D – średnica pala;

∆

z

1

= 0

÷ 3D

Skorygowana

nośność

podstawy

pala

w warstwie 1:

)

(

)

(

1

1

1

z

R

z

R

b

b

′

⋅

=

η

Wartość R

′

b

1

(z) oblicza się według wzorów

na str. 1 i 2.

R

b2

(z

1

)

R

′

b1

(z

1

)

R

b1

(z)

warstwa 1

(mocniejsza)

warstwa 2

(słabsza)

3D

∆z

1

R

′

b1

(z)

wykres R

′

b1

(z)

wykres

R

b1

(z)

z

1

z

h

z

10D

R

b1

(z

1

)

R

′

b2

(z

1

)

R

b2

(z)

R

′

b2

(z) ∆z

2

wykres R

′

b2

(z)

warstwa 1

(słabsza)

warstwa 2

(mocniejsza)

wykres

R

b2

(z)

z

z

1

5

Przykład obliczeniowy

Dobrać długość L pala wierconego φ800 mm, aby w zadanych warunkach gruntowych uzyskał

nośność wystarczającą do przeniesienia obciążenia projektowego Q

d

= 1500 kN. Obliczenia

wykonać metodą

α

α

α

α

i

β

β

β

β

z uwzględnieniem zaleceń Eurokodu 7 (EC7).

Obliczenia wielkości pomocniczych

Współczynnik parcia spoczynkowego:

977

,

0

0

,

2

)

18

sin

1

(

)

sin

1

(

0

=

⋅

°

−

=

⋅

′

−

=

OCR

K

φ

32

,

0

18

tan

977

,

0

tan

0

=

°

⋅

=

′

⋅

=

φ

β

K

Współczynniki nośności gruntu pod podstawą pala:

przyjęto

η

=

π

/2

(

)

(

)

255

,

5

)

18

tan

2

2

exp(

18

tan

1

18

tan

)

tan

2

exp(

tan

1

tan

2

2

2

2

=

°

⋅

⋅

⋅

°

+

+

°

=

′

⋅

⋅

′

+

+

′

=

π

φ

η

φ

φ

q

N

(

)

(

)

1

,

13

18

cot

1

255

,

5

cot

1

=

°

⋅

−

=

′

⋅

−

=

φ

q

c

N

N

Współczynniki technologiczne:

do metody

α

: S

s

= 1,0; S

b

= 1,0

do metody

β

: S

s

= 0,9; S

b

= 1,0

Współczynniki korekcyjne do nośności (wg EC7): przyjęto

ξ

3

= 1,25/1,1 = 1,14

Współczynniki częściowe do nośności (podejście obliczeniowe 2 wg EC7):

γ

s

= 1,1;

γ

b

= 1,1

zwg

0,0

-1,0

-3,0

ił pylasto-piaszczysty

I

L

=0,30

γ = 20 kN/m

3

γ′ = 10 kN/m

3

φ′ = 18°, c′=45 kPa
OCR = 2,0

Profil geotechniczny

L

=

?

pal wiercony

φ800 mm

C

u

[kPa]

z [m ppt]

25

0

C

u

(z) = 25 + 5,0

⋅z [kPa]

6

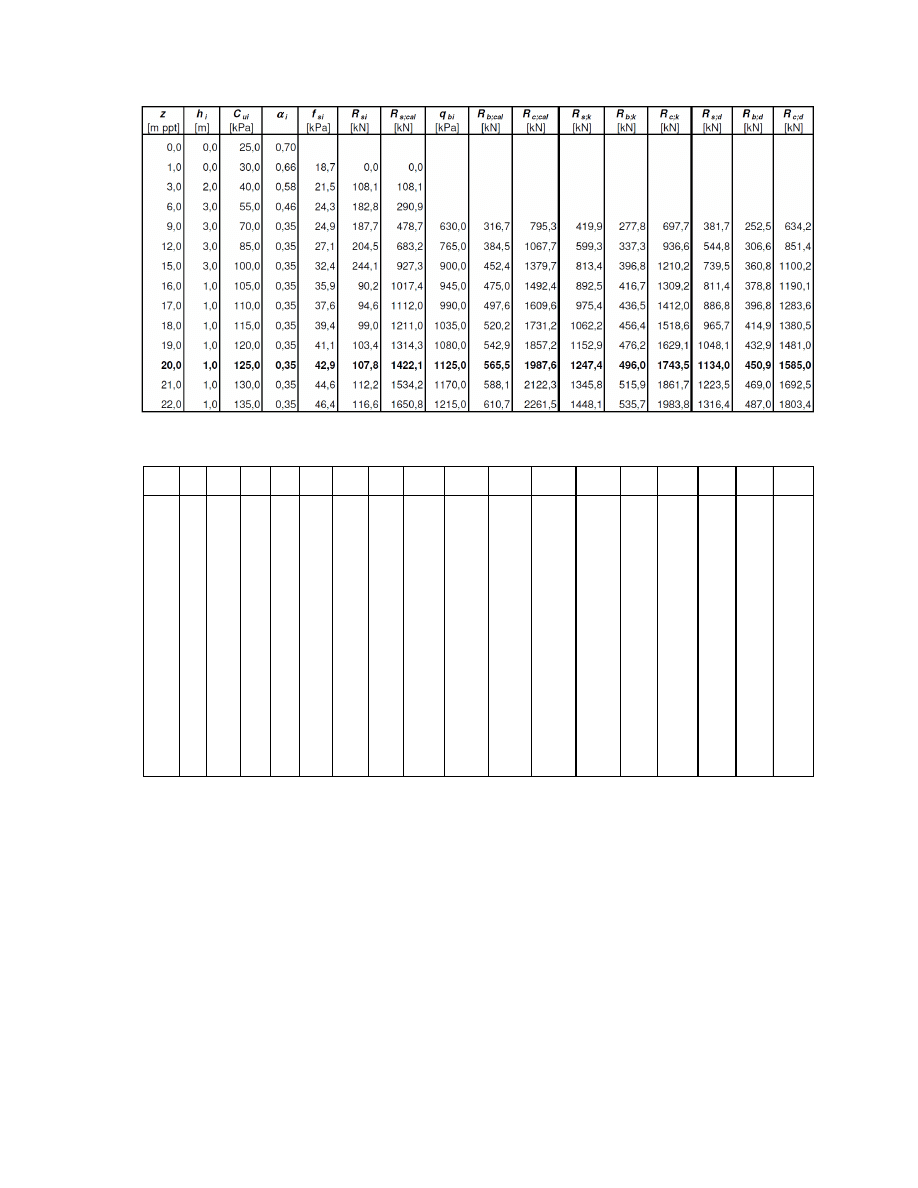
Obliczenie nośności pala metodą

α

α

α

α

Obliczenie nośności pala metodą

β

β

β

β

z

h

i

σ

σ

σ

σ

'

vi

φ

φφ

φ

'

i

c'

i

β

ββ

β

i

f

si

R

si

R

s;cal

q

bi

R

b;cal

R

c;cal

R

s;k

R

b;k

R

c;k

R

s;d

R

b;d

R

c;d

[m ppt] [m]

[kPa]

[

o

]

[kPa]

[kPa]

[kN]

[kN]

[kPa]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

0,0

0,0

0,0

1,0

0,0

20,0 18,0 45,0

0,32

6,35

0,0

0,0

3,0

2,0

60,0 18,0 45,0

0,32

12,70

57,4

57,4

6,0

3,0

90,0 18,0 45,0

0,32

23,81 161,6

219,0

9,0

3,0 120,0 18,0 45,0

0,32

33,33 226,2

445,2

1220,0

613,2

1058,4

390,5

537,9

928,4

355,0

489,0

844,0

12,0

3,0 150,0 18,0 45,0

0,32

42,86 290,8

736,0

1377,6

692,5

1428,5

645,6

607,4 1253,0

586,9

552,2 1139,1

13,0

1,0 160,0 18,0 45,0

0,32

49,20 111,3

847,3

1430,2

718,9

1566,2

743,2

630,6 1373,8

675,7

573,3 1249,0

14,0

1,0 170,0 18,0 45,0

0,32

52,38 118,5

965,8

1482,7

745,3

1711,1

847,2

653,8 1500,9

770,2

594,3 1364,5

15,0

1,0 180,0 18,0 45,0

0,32

55,55 125,7 1091,4

1535,3

771,7

1863,1

957,4

676,9 1634,3

870,4

615,4 1485,8

16,0

1,0 190,0 18,0 45,0

0,32

58,73 132,8 1224,3

1587,8

798,1

2022,4

1073,9

700,1 1774,0

976,3

636,5 1612,8

17,0

1,0 200,0 18,0 45,0

0,32

61,90 140,0 1364,3

1640,4

824,5

2188,8

1196,7

723,3 1920,0 1088,0

657,5 1745,5

18,0

1,0 210,0 18,0 45,0

0,32

63,49 143,6 1507,9

1640,4

824,5

2332,4

1322,7

723,3 2046,0 1202,5

657,5 1860,0

19,0

1,0 220,0 18,0 45,0

0,32

63,49 143,6 1651,5

1640,4

824,5

2476,1

1448,7

723,3 2172,0 1317,0

657,5 1974,5

20,0

1,0 230,0 18,0 45,0

0,32

63,49 143,6 1795,1

1640,4

824,5

2619,7

1574,7

723,3 2298,0 1431,5

657,5 2089,0

Wniosek z obliczeń:

Wartości nośności pala otrzymane z obu metod obliczeniowych są dość rozbieżne.

Zadecydował wynik obliczeń metodą

α

Potrzebna długość pala: L = 20,0 - 1,0 = 19,0 m

Warunek nośności: Q

d

= 1500 kN < R

c;d

= 1585 kN

Uwaga:

W przypadku obiektu budowanego w sposób powolny i przy niewielkiej zmienności obciążeń

podczas eksploatacji obiektu, można zrezygnować z metody

α

obliczania nośności pali.