1

Fundamenty Specjalne - projekt

Część 2 – Nośność pali – metoda

α

i

β

(dr inż. Adam Krasiński, mgr inż. Tomasz Kusio)

Nośność pala jest sumą nośności pobocznicy i podstawy pala:

b

i

si

b

s

c

R

R

R

R

R

+

=

+

=

∑

gdzie: R

s

– nośność charakterystyczna pobocznicy pala, która jest sumą nośności wszystkich

odcinków obliczeniowych wzdłuż pobocznicy pala

si

R ,

R

b

– nośność charakterystyczna podstawy pala.

Metoda

α - nośność krótkoterminowa

Korzystając z tej metody można oszacować nośność pojedynczego pala pracującego w warunkach
bez odpływu. Oznacza to, że metoda może być zastosowana tylko w przypadku zagłębienia pala w
gruntach spoistych. Opór gruntu zależy głównie od wytrzymałości gruntu na ścinanie w warunkach
bez odpływu C

u

.

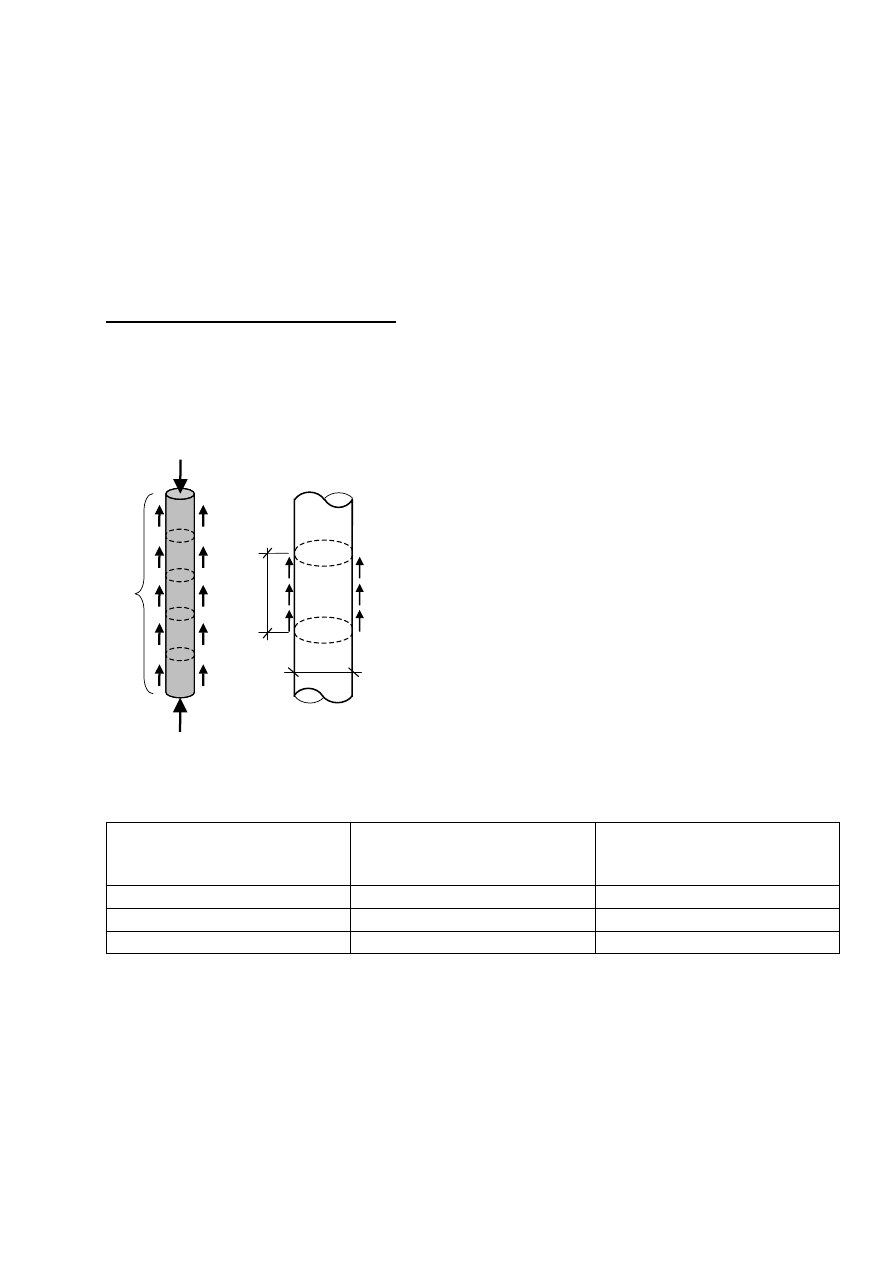
Nośność pobocznicy pala dla i-tego odcinka obliczenio-
wego:

i

si

si

si

si

si

si

h

D

f

S

A

f

S

R

⋅

⋅

⋅

⋅

=

⋅

⋅

=

π

gdzie: f

si

– opór gruntu na pobocznicy i-tego odcinka

obliczeniowego pala.

Dla warunków bez drenażu f

si

=

α

i

· C

ui

w którym

α

i

wyznaczany wg tablicy 1,

A

si

– pole powierzchni bocznej i-tego odcinka

obliczeniowego pala,

S

si

– współczynnik technologiczny.

Dla pali:
- wierconych w rurach S

s

= 1,0;

- pali CFA S

s

= 1,2;

- Vibro i wkręcanych S

s

= 1,4;

- pali prefabrykowanych S

s

= 1,0.

Tablica 1. Współczynnik

α

wg Viggiani’ego (1993).

Wytrzymałość gruntu na

ścinanie bez odpływu

C

u

[kPa]

Pale przemieszczeniowe,

wbijane i wkręcane

Pale wiercone i CFA

≤25

α

= 1,0

α

= 0,7

25÷70

α

= 1,0 – 0,011· (C

u

– 25)

α

= 0,7 – 0,008· (C

u

– 25)

>70

α

= 0,5

α

= 0,35

Nośność podstawy pala:

2

25

,

0

D

q

S

A

q

S

R

b

b

b

b

b

b

⋅

⋅

⋅

⋅

=

⋅

⋅

=

π

gdzie: q

b

= 9 · C

ub

– opór gruntu pod podstawą pala wg Skempton’a (1959) ,

A

b

– powierzchnia podstawy pala ( dla pali Vibro D jest średnicą „buta” stalowego),

S

b

– współczynnik technologiczny.

Dla pali:
- wierconych i CFA S

b

= 1,0;

- wkręcanych S

b

= 1,1;

- prefabrykowanych S

b

= 1,2;

- Vibro S

b

= 1,3.

h

i

D

f

si

Q

c

R

b

Σ

R

Si

=

R

s

R

si

2

Metoda

β

– nośność długoterminowa

Korzystając z tej metody można oszacować nośność pojedynczego pala pracującego w warunkach z
odpływem w gruntach spoistych i niespoistych. Opór gruntu zależy od stanu naprężenia
efektywnego w gruncie. Metodę

β

stosuje się do wszystkich rodzajów gruntów.

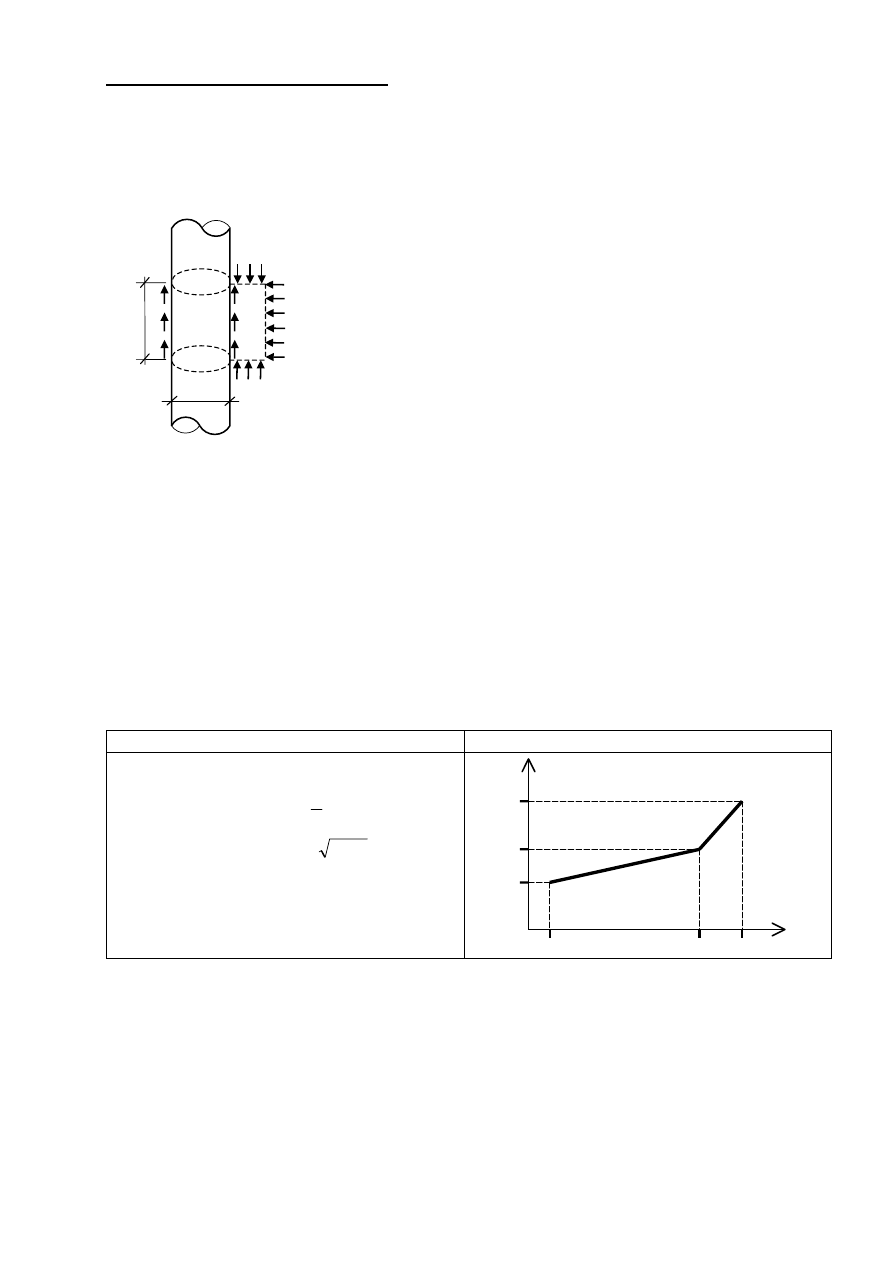
Nośność pobocznicy pala dla i-tego odcinka obliczeniowego:

i

si

si

si

si

si

si

h

D

f

S

A

f

S

R

⋅

⋅

⋅

⋅

=

⋅

⋅

=

π

gdzie: f

si

– opór gruntu na pobocznicy i-tego odcinka pala.

Dla warunków z odpływem f

si

=

β

i

·

σ

’

vi

,

A

si

– pole powierzchni bocznej i-tego odcinka

obliczeniowego pala,

S

si

– współczynnik technologiczny.

Dla pali:
- wierconych w rurach S

s

= 0,9;

- CFA S

s

= 1,0;

- Vibro S

s

= 1,4;

- wkręcanych S

s

= 1,3;

- prefabrykowanych S

s

= 1,1.

Wyznaczanie oporu gruntu f

si

na pobocznicy pala:

Opór gruntu na pobocznicy pala wyraża się wzorem:

vi

i

i

vi

i

i

vi

i

si

K

K

f

'

tan

'

'

0

0

σ

δ

σ

µ

σ

β

⋅

⋅

=

⋅

⋅

=

⋅

=

; 200

'

≤

vi

σ

kPa

gdzie:

σ

’

vi

– jest średnim, efektywnym naprężeniem pionowym, działąjącym w i-tej obliczeniowej

warstwie gruntu. Jednak ze względu na zjawisko głębokości krytycznej, w obliczeniach
przyjmujemy maksymalnie

σ

’

vi

= 200 kPa.

β

i

– jest współczynnikiem zależnym od efektywnego naprężenia poziomego, działąjącego w i-tej

obliczeniowej warstwie gruntu (

vi

i

hi

K

'

'

0

σ

σ

⋅

=

)

oraz szorstkości powierzchni pobocznicy pala

(

i

i

δ

µ

tan

=

). Współczynnik należy przyjmować wg tablicy 2.

Tablica 2. Współczynnik

β

.

Grunty spoiste; wg Burlanda (1973)

Grunty niespoiste; wg Meyerhofa (1976)











 ⋅

⋅

=

'

3

2

tan

0

φ

β

K

(

)

OCR

K

⋅

−

=

'

sin

1

0

φ

OCR – współczynnik prekonsolidacji

(wyznaczony na podstawie badań

laboratoryjnych bądź in situ)

Nośność podstawy pala:

2

25

,

0

D

q

S

A

q

S

R

b

b

b

b

b

b

⋅

⋅

⋅

⋅

=

⋅

⋅

=

π

gdzie: q

b

– opór gruntu pod podstawą pala,

A

b

– powierzchnia podstawy pala ( dla pali Vibro D jest średnicą „buta” stalowego),

S

b

– współczynnik technologiczny

Dla pali:
- wierconych i CFA S

b

= 1,0;

- wkręcanych S

b

= 1,2;

- prefabrykowanych S

b

= 1,3;

- Vibro S

b

= 1,4.

β

1,20

0,75

0,44

28°

35°

37°

φ

’

h

i

D

σ

vi

’

σ

hi

’

f

si

3

Wyznaczanie oporu gruntu q

b

pod podstawą pala:

Opór gruntu pod podstawą pala przyjmujemy wg rozwiązania Terzaghi’ego:

c

b

q

vb

b

N

c

N

q

⋅

+

⋅

=

'

'

σ

gdzie:

σ′

vb

– naprężenie efektywne w poziomie podstawy pala, przy czym ze względu na zjawisko

głębokości krytycznej w obliczeniach przyjmujemy maksymalnie

σ′

vi

= 200 kPa,

c’

b

– spójność efektywna gruntu w poziomie posadowienia,

N

c

, N

q

– współczynniki nośności:

(

)

(

)

b

e

N

b

b

q

'

tan

2

2

2

'

tan

1

'

tan

φ

η

φ

φ

⋅

⋅

⋅

+

+

=

gdzie:













÷

=

π

π

η

5

3

3

1

Kąt wypierania gruntu

η

spod podstawy pala. Przyjmujemy w przedziale od

π

3

1

dla plastycznych

gruntów spoistych do

π

5

3

dla zagęszczonych piasków.

b

q

c

N

N

'

cot

)

1

(

φ

⋅

−

=

Nośność projektowa pala

Nośność projektową pala wyznaczamy w następujący sposób:

b

b

s

s

d

b

d

s

d

c

R

R

R

R

R

γ

γ

+

=

+

=

;

;

;

Współczynniki częściowe do nośności (podejście obliczeniowe 2, kombinacja 1, zalecane przez
PKN):

γ

s

=

γ

b

= 1,1 (podejście obliczeniowe 2, kombinacja 1, zalecane przez PKN)

Warunek nośności:
Q

v;d

≤ R

c;d

Wpływ zmiany warstwy gruntowej na nośność podstawy pala

Wyżej podane wzory w metodach

α

i

β

, dotyczące nośności podstaw pali, są ważne dla przypadku

podłoża jednorodnego. W przypadku podłoża uwarstwionego, w sytuacji gdy występuje zmiana
warstwy o różnych parametrach wytrzymałościowych, na granicy obu warstw może pojawić się
przeskok w nośności podstawy. Taki przeskok jest nierzeczywisty. Zmiany nośności podstaw
przebiegają w rzeczywistości stopniowo. Można zastosować zmodyfikowaną propozycję
Meyerhofa (1983), przedstawioną na rysunkach poniżej.

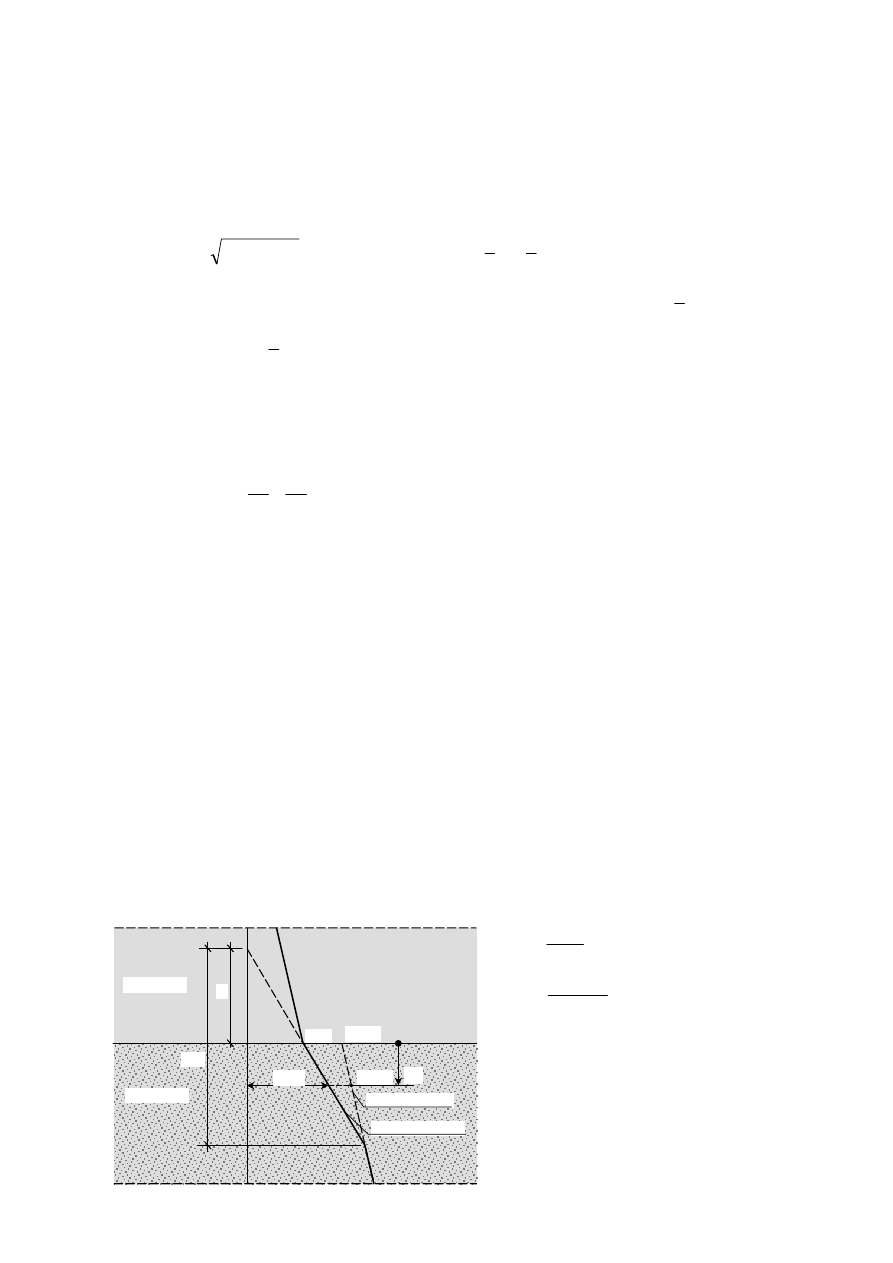
Przypadek 1

– warstwa górna (1) o mniejszej nośności niż warstwa dolna (2)

D

R

R

h

b

b

z

10

1

2

2

1

⋅

′

=

−

−

; D – średnica pala

0

,

1

10

2

2

≤

∆

+

=

D

z

h

z

η

Skorygowana nośność podstawy pala
w warstwie 2:

2

2

2

)

(

b

b

R

z

R

′

⋅

=

η

Wartość R

′

b2

(z) oblicza się według wzorów

na str. 1 i 2.

h

z

10D

R

b1-2

R

′

b2-1

R

b2

(z)

R

′

b2

(z)

∆

z

2

wykres teoretyczny

wykres skorygowany

warstwa 1

warstwa 2

4

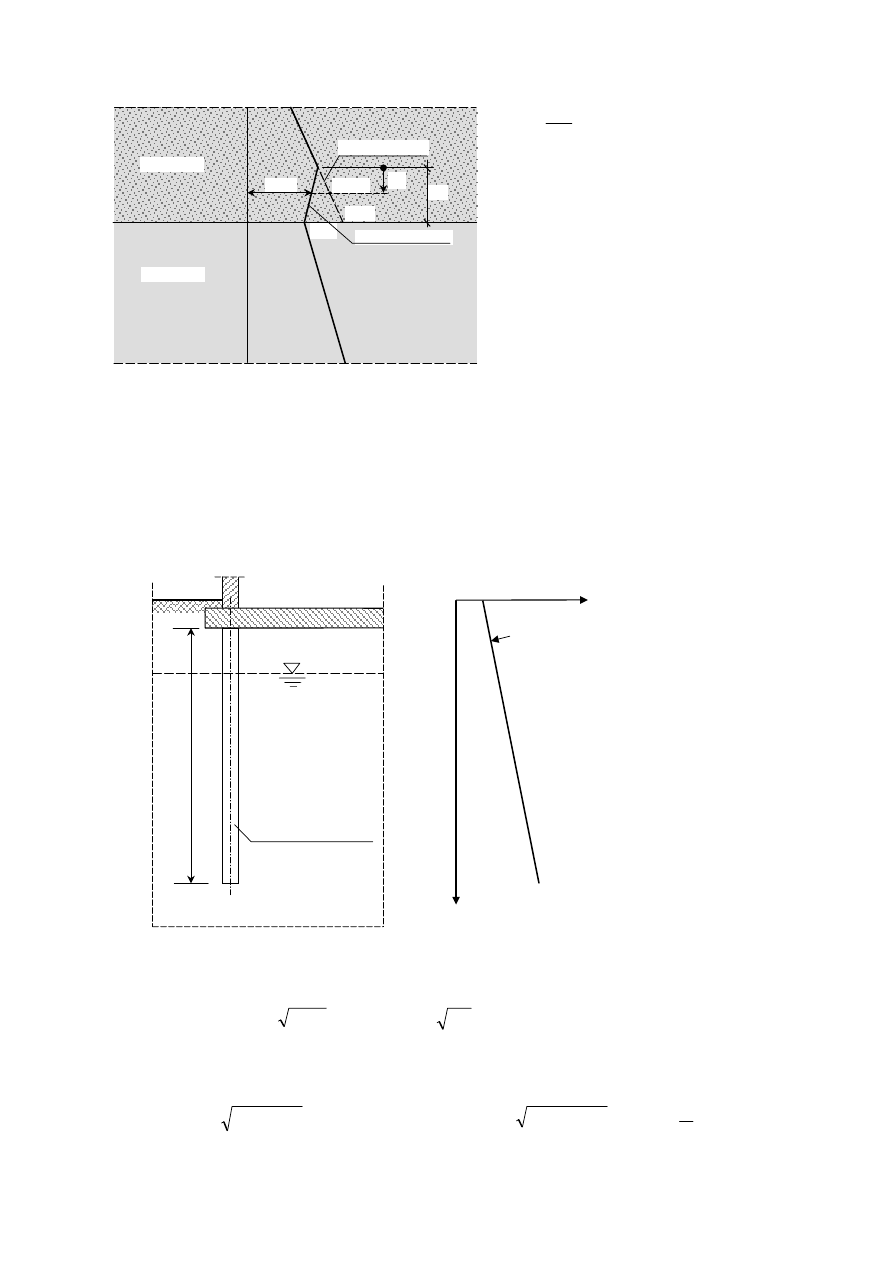
Przypadek 2

– warstwa górna (1) o większej nośności niż warstwa dolna (2)

0

,

1

3

1

1

≤

∆

=

D

z

η

; D – średnica pala

Skorygowana nośność podstawy pala
w warstwie 1:

)

(

)

(

)

(

1

2

2

1

1

1

2

−

−

−

′

⋅

−

′

=

b

b

b

b

R

R

z

R

z

R

η

Wartość R

′

b1

(z) oblicza się według wzorów

na str. 1 i 2.

Zadanie przykładowe 5.1.

Dobrać długość L pala wierconego

φ800 mm, aby w zadanych warunkach gruntowych uzyskał

nośność wystarczającą do przeniesienia obciążenia projektowego Q

d

= 1500 kN. Obliczenia

wykonać metodą

α

i

β

z uwzględnieniem zaleceń Eurokodu 7 (EC7).

Obliczenia wielkości pomocniczych

Współczynnik parcia spoczynkowego:

977

,

0

0

,

2

)

18

sin

1

(

)

sin

1

(

0

=

⋅

°

−

=

⋅

′

−

=

OCR

K

φ

Współczynniki nośności gruntu pod podstawą pala:
przyjęto

η

=

π

/2

(

)

(

)

255

,

5

)

18

tan

2

2

exp(

18

tan

1

18

tan

)

tan

2

exp(

tan

1

tan

2

2

2

2

=

°

⋅

⋅

⋅

°

+

+

°

=

′

⋅

⋅

′

+

+

′

=

π

φ

η

φ

φ

q

N

(

)

(

)

1

,

13

18

cot

1

255

,

5

cot

1

=

°

⋅

−

=

′

⋅

−

=

φ

q

c

N

N

zwg

0,0

-1,0

-3,0

ił pylasto-piaszczysty

I

L

=0,30

γ

= 20 kN/m

3

γ

′ = 10 kN/m

3

φ

′ = 18°, c′=45 kPa

OCR = 2,0

Profil geotechniczny

L

= ?

pal wiercony

φ

800 mm

C

u

[kPa]

z [m ppt]

25

0

C

u

(z) = 25 + 5,0

⋅z [kPa]

R

b2-1

R

′

b1-2

R

b1

(z)

wykres teoretyczny

wykres skorygowany

warstwa 1

warstwa 2

3D

∆

z

1

R

′

b1

(z)

5

Współczynniki technologiczne:
do metody

α

: S

s

= 1,0; S

b

= 1,0

do metody

β

: S

s

= 0,9; S

b

= 1,0

Współczynniki korekcyjne do nośności (wg EC7): przyjęto

ξ

3

= 1,25/1,1 = 1,14

Współczynniki częściowe do nośności (podejście obliczeniowe 2 wg EC7):

γ

s

= 1,1;

γ

b

= 1,1

Obliczenie nośności pala metodą

α

z

h

i

C

ui

α

i

f

si

R

si

R

s

q

bi

R

b

R

c

R

s;k

R

b;k

R

c;k

R

s;d

R

b;d

R

c;d

[m ppt]

[m]

[kPa]

[kPa]

[kN]

[kN]

[kPa]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

0,0

0,0

25,0

0,70

1,0

0,0

30,0

0,66

18,7

0,0

0,0

3,0

2,0

40,0

0,58

21,5

108,1

108,1

6,0

3,0

55,0

0,46

24,3

182,8

290,9

9,0

3,0

70,0

0,35

24,9

187,7

478,7

630,0

316,7

795,3

419,9

277,8

697,7

381,7

252,5

634,2

12,0

3,0

85,0

0,35

27,1

204,5

683,2

765,0

384,5

1067,7

599,3

337,3

936,6

544,8

306,6

851,4

15,0

3,0

100,0

0,35

32,4

244,1

927,3

900,0

452,4

1379,7

813,4

396,8 1210,2

739,5

360,8 1100,2

16,0

1,0

105,0

0,35

35,9

90,2

1017,4

945,0

475,0

1492,4

892,5

416,7 1309,2

811,4

378,8 1190,1

17,0

1,0

110,0

0,35

37,6

94,6

1112,0

990,0

497,6

1609,6

975,4

436,5 1412,0

886,8

396,8 1283,6

18,0

1,0

115,0

0,35

39,4

99,0

1211,0 1035,0

520,2

1731,2

1062,2

456,4 1518,6

965,7

414,9 1380,5

19,0

1,0

120,0

0,35

41,1

103,4

1314,3 1080,0

542,9

1857,2

1152,9

476,2 1629,1 1048,1

432,9 1481,0

20,0

1,0

125,0

0,35

42,9

107,8

1422,1 1125,0

565,5

1987,6

1247,4

496,0 1743,5 1134,0

450,9 1585,0

21,0

1,0

130,0

0,35

44,6

112,2

1534,2 1170,0

588,1

2122,3

1345,8

515,9 1861,7 1223,5

469,0 1692,5

22,0

1,0

135,0

0,35

46,4

116,6

1650,8 1215,0

610,7

2261,5

1448,1

535,7 1983,8 1316,4

487,0 1803,4

Obliczenie nośności pala metodą

β

z

h

i

σ

vi

φ

'

i

c'

i

β

i

f

si

R

si

R

s

q

bi

R

b

R

c

R

s;k

R

b;k

R

c;k

R

s;d

R

b;d

R

c;d

[m ppt] [m] [kPa]

[

o

]

[kPa]

[kPa]

[kN]

[kN]

[kPa]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

0,0

0,0

0,0

1,0

0,0

20,0 18,0 45,0

0,21

4,15

0,0

0,0

3,0

2,0

60,0 18,0 45,0

0,21

8,31

37,6

37,6

6,0

3,0

90,0 18,0 45,0

0,21

15,58

105,7

143,3

9,0

3,0 120,0 18,0 45,0

0,21

21,81

148,0

291,2

1220,0

613,2

904,5

255,5

537,9

793,4

232,2

489,0

721,3

12,0

3,0 150,0 18,0 45,0

0,21

28,04

190,2

481,5

1377,6

692,5

1174,0

422,3

607,4

1029,8

384,0

552,2

936,2

13,0

1,0 160,0 18,0 45,0

0,21

32,19

72,8

554,3

1430,2

718,9

1273,2

486,2

630,6

1116,8

442,0

573,3

1015,3

14,0

1,0 170,0 18,0 45,0

0,21

34,27

77,5

631,8

1482,7

745,3

1377,1

554,2

653,8

1208,0

503,8

594,3

1098,2

15,0

1,0 180,0 18,0 45,0

0,21

36,34

82,2

714,0

1535,3

771,7

1485,7

626,3

676,9

1303,3

569,4

615,4

1184,8

16,0

1,0 190,0 18,0 45,0

0,21

38,42

86,9

800,9

1587,8

798,1

1599,0

702,5

700,1

1402,7

638,7

636,5

1275,1

17,0

1,0 200,0 18,0 45,0

0,21

40,50

91,6

892,5

1640,4

824,5

1717,0

782,9

723,3

1506,2

711,7

657,5

1369,2

18,0

1,0 210,0 18,0 45,0

0,21

41,53

93,9

986,4

1640,4

824,5

1811,0

865,3

723,3

1588,6

786,6

657,5

1444,2

19,0

1,0 220,0 18,0 45,0

0,21

41,53

93,9

1080,4

1640,4

824,5

1904,9

947,7

723,3

1671,0

861,6

657,5

1519,1

20,0

1,0 230,0 18,0 45,0

0,21

41,53

93,9

1174,3

1640,4

824,5

1998,9

1030,1

723,3

1753,4

936,5

657,5

1594,0

21,0

1,0 240,0 18,0 45,0

0,21

41,53

93,9

1268,3

1640,4

824,5

2092,8

1112,5

723,3

1835,8

1011,4

657,5

1668,9

22,0

1,0 250,0 18,0 45,0

0,21

41,53

93,9

1362,2

1640,4

824,5

2186,8

1194,9

723,3

1918,2

1086,3

657,5

1743,8

Wniosek z obliczeń:

Wartości nośności pala otrzymane z obu metod obliczeniowych są zbliżone do siebie.

Zadecydował wynik obliczeń metodą

α

Potrzebna długość pala: L = 20,0 - 1,0 = 19,0 m

Warunek nośności: Q

d

= 1500 kN < R

c;d

= 1585 kN

6

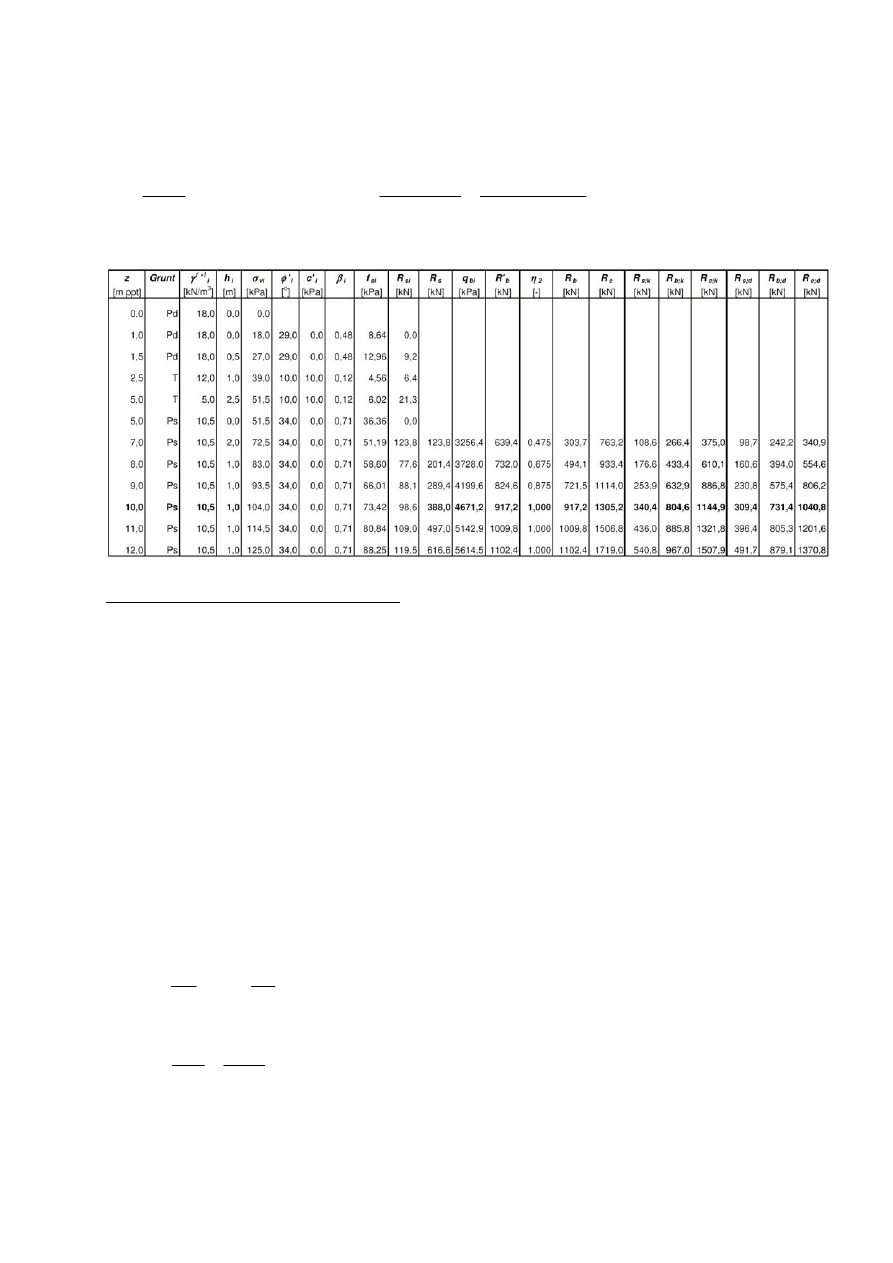
Zadanie przykładowe 5.2.

Policzyć nośność na wciskanie i wyciąganie pala wierconego

φ500 mm, przedstawionego na

rysunku poniżej. Obliczenia wykonać metodą

β

z uwzględnieniem zaleceń Eurokodu 7 (EC7).

Założyć działanie tarcia negatywnego.

Obliczenia wielkości pomocniczych

Współczynnik

β

(według Meyerhofa):

Pd,

φ

' = 29

° →

48

,

0

)

28

29

(

28

35

44

,

0

75

,

0

44

,

0

=

−

⋅

−

−

−

=

β

T,

φ

' = 10

° , K

0

= 1,0

→

117

,

0

10

3

2

tan

0

,

1

=













°

⋅

⋅

=

β

Ps,

φ

' = 34

° →

706

,

0

)

34

35

(

28

35

44

,

0

75

,

0

75

,

0

=

−

⋅

−

−

−

=

β

Współczynnik nośności gruntu pod podstawą pala:

1) Warstwa T - przyjęto

η

= 1/3

π

(

)

05

,

2

369

,

0

exp

42

,

1

)

10

tan

3

2

exp(

10

tan

1

10

tan

2

2

=

⋅

=

°

⋅

⋅

⋅

°

+

+

°

=

π

q

N

95

.

5

10

cot

)

1

05

,

2

(

=

°

⋅

−

=

c

N

2) Warstwa Pd - przyjęto

η

= 3/5

π

(

)

0

,

45

543

,

2

exp

537

,

3

)

34

tan

5

3

2

exp(

34

tan

1

34

tan

2

2

≅

⋅

=

°

⋅

⋅

⋅

°

+

+

°

=

π

q

N

Powierzchnia 1mb pobocznicy pala: A

s

(1mb) =

π⋅0,5 = 1,571 m

2

Powierzchnia podstawy pala: A

b

= 0,25

⋅π⋅0,5

2

= 0,196 m

2

zwg

0,0

-1,0

-2,5

Torf

γ

′ = 10,5 kN/m

3

φ

′ = 34°

η

= 3/5

π

Profil geotechniczny

pal wiercony

φ500 mm

L = 9,0 m

-10,0

-1,5

-2,5

-5,0

Pd,

φ

'= 29

°,

γ

= 18 kN/m

3

γ

= 12 kN/m

3

γ

′ = 5 kN/m

3

φ

′ = 10°, c′=10 kPa

K

0

= 1,0 kPa

Ps

Przyjęto współczynniki:

S

s

= 0,9; S

b

= 1,0, S

s;t

= 0,7

γ

s

= 1,1;

γ

b

= 1,1;

γ

s;t

= 1,15

ξ

3

= 1,25/1,1 = 1,14

Współczynnik obciążenia do tarcia
negatywnego:

γ

Tn

= 1,2

7

Granica warstw na głębokości z = 5,0 m ppt.

1

,

165

95

,

5

0

,

10

05

,

2

5

,

51

2

1

=

⋅

+

⋅

=

−

b

q

kPa

→

4

,

32

1

,

165

196

,

0

2

1

=

⋅

=

−

b

R

kN

5

,

2317

0

,

45

5

,

51

2

1

=

⋅

=

−

b

q

kPa

→

2

,

454

5

,

2317

196

,

0

1

2

=

⋅

=

′

−

b

R

kN

Wysokość zastępcza h

z

:

357

,

0

0

,

5

2

,

454

4

,

32

=

⋅

=

z

h

m

→

0

,

5

357

,

0

0

,

5

10

0

,

5

2

+

−

=

+

−

=

z

D

h

z

z

η

Obliczenie nośności pala na wciskanie metodą

β

Obliczenie wartości tarcia negatywnego:

Tarcie negatywne równa się sumie sił R

si

w warstwach Pd i T

T

n,k

= 9,2 + 6,4 + 21,3 = 36,9 kN

Wartość projektowa tarcia negatywnego:
T

n,d

= 36,9

⋅1,2 = 44,3 kN

Warunek nośności pala na wciskanie:
Q

d

+ T

n,d

≤ R

c;d

= 1040,8 kN

Dopuszczalna wartość projektowej siły wciskającej pal:
Q

d

≤ R

c;d

– T

n,d

= 1040,8 - 44,3 = 996,5 kN

Nośność pala na wyciąganie:
Wartość charakterystyczna:

0

,

265

4

,

340

9

,

0

7

,

0

;

;

;

=

⋅

=

⋅

=

k

s

s

t

s

k

ct

R

S

S

R

kN

Wartość projektowa:

=

=

=

15

,

1

0

,

265

;

;

;

t

s

k

ct

d

ct

R

R

γ

230,0 kN

Do powyższej wartości nośności na wyciąganie można dodać ciężar pala:

4

,

29

)

0

,

10

0

,

25

(

196

,

0

5

,

7

0

,

25

196

,

0

5

,

1

=

−

⋅

⋅

+

⋅

⋅

=

p

G

kN