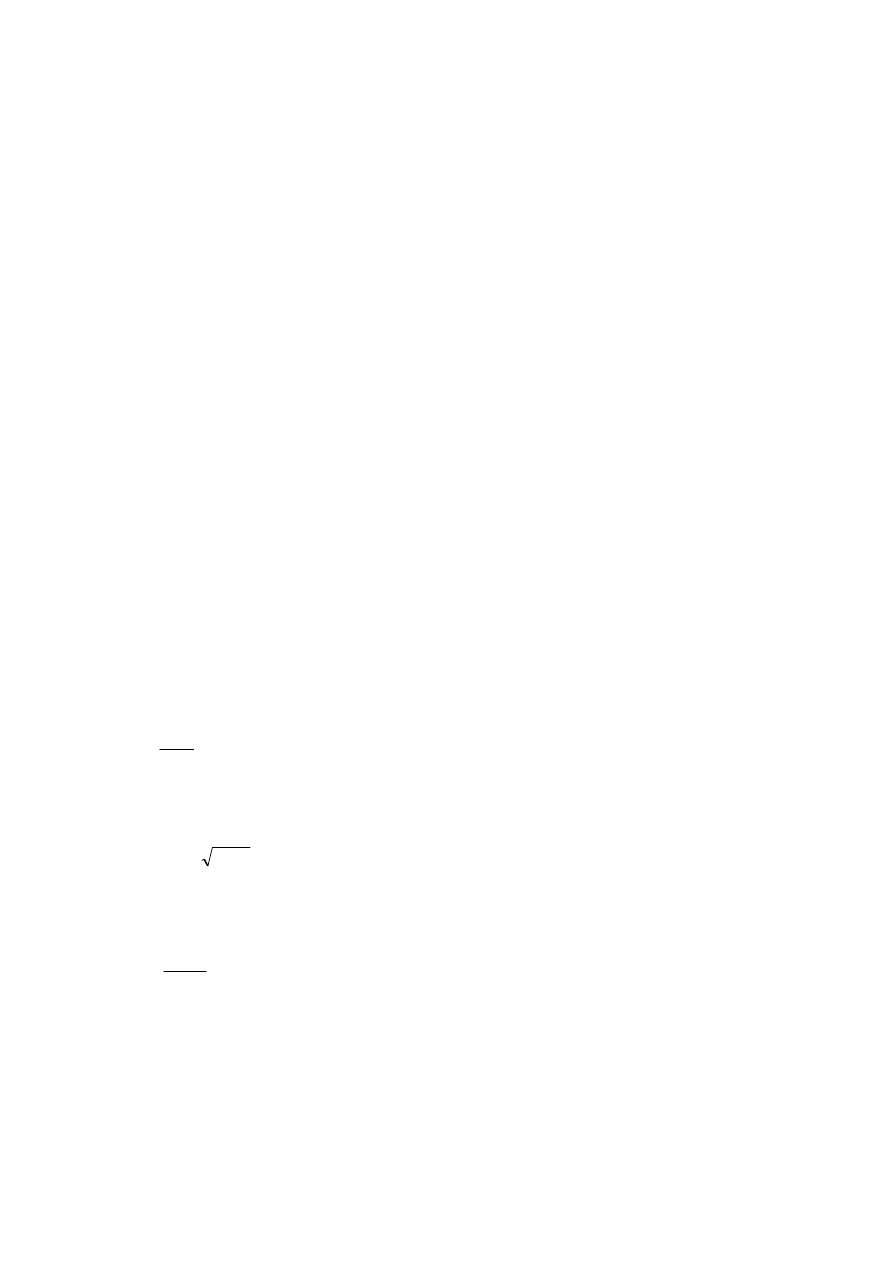
Fundamenty Specjalne – projekt fundamentu płytowo-palowego - część 1
(dr inż. Adam Krasiński)
1.0. Stan naprężenia w podłożu gruntowym
1.1. Stan początkowy (geostatyczny)
Ogólnie przyjmuje się, że pierwotny stan naprężenia w górotworze jest anizotropowy. Składowa
pionowa naprężenia
σ
z;0
jest wynikiem działania sił grawitacji i równa jest sumie ciężarów
wszystkich warstw gruntowych, liczonych od powierzchni terenu:
∑
⋅
=
i
i
z
h
γ
σ
0
;
Wartość efektywna naprężenia jest pomniejszona o ciśnienie u
0
wody, występujące na danej
głębokości (ciśnienie to może być hydrostatyczne lub napięte):
0
0
;
0
;
u
z
z
−
=
′
σ
σ
Składowe poziome
σ′
x;0
i
σ′
y;0
naprężenia efektywnego przyjmuje się, że są sobie równe i wynoszą:
0
0
;
0
;
0
;
K
z
y
x
⋅
′
=
′
=
′
σ
σ
σ
gdzie:
K
0
jest współczynnikiem parcia geostatycznego (parcia spoczynkowego, bądź
współczynnikiem rozporu bocznego).
Dla gruntów normalnie skonsolidowanych (płytkie warstwy holoceńskie)
K
0
=
K
0
NC
. Wartość
współczynnika
K
0
NC
można określić z wzorów:
φ
′
−
=
sin
1
0
NC
K
- dla gruntów niespoistych
ν
ν
−
=
1
0
NC
K
- dla gruntów spoistych
Dla gruntów prekonsolidowanych (głębsze warstwy plejstoceńskie i starsze) K
0
= K
0
OC
. Wartość
współczynnika K
0
NC
można określić z wzoru empirycznego:
OCR
K
K
NC
OC
⋅
=
0
0
gdzie: OCR jest współczynnikiem prekonsolidacji gruntu (OverConsoildation Ratio), który
najprościej definiuje się następująco:
0
;
max
;
z
z
OCR
σ
σ
′
′
=
gdzie:
σ′
z;max
– składowa pionowa maksymalnego naprężenia efektywnego, jakie kiedykolwiek
w historii panowało na danej głębokości,
σ′
z;0
– składowa pionowa aktualnego naprężenia efektywnego na tej samej głębokości.
2
Współczynnik OCR można określić z badania edometrycznego, według schematu przedstawionego
poniżej.
Najczęściej jednak OCR określa się na podstawie badań „in situ” (badania presjometryczne PMT,
dylatometryczne DMT lub sondowania statyczne CPT(U)). Generalnie OCR jest wielkością trudną
do zmierzenia. Często w badaniach nie określa się współczynnika OCR, a bezpośrednio wartość
współczynnika K
0
.
W gruntach silnie prekonsolidowanych współczynnik K
0
OC
może znacznie przekraczać wartość 1,0
co oznacza, że składowe poziome naprężenia mogą być większe niż składowa pionowa. Składowa
pozioma nie może jednak przekroczyć wartości odporu granicznego, więc musi być spełniony
warunek:
p
p
z
y
x
K
c
K
⋅′
+
⋅
′
≤
′
=
′
2
0
;
0
;
0
;
σ
σ
σ
, gdzie
)
2
45
(
tan
2
φ
′
+
°
=
p
K
Istnieje również pogląd, że
ur
ur
OC
K
ν
ν
−
≤
1
0
, gdzie
ν
ur
≈ 0,2 (wsp. Poissona dla obc. wtórnych)
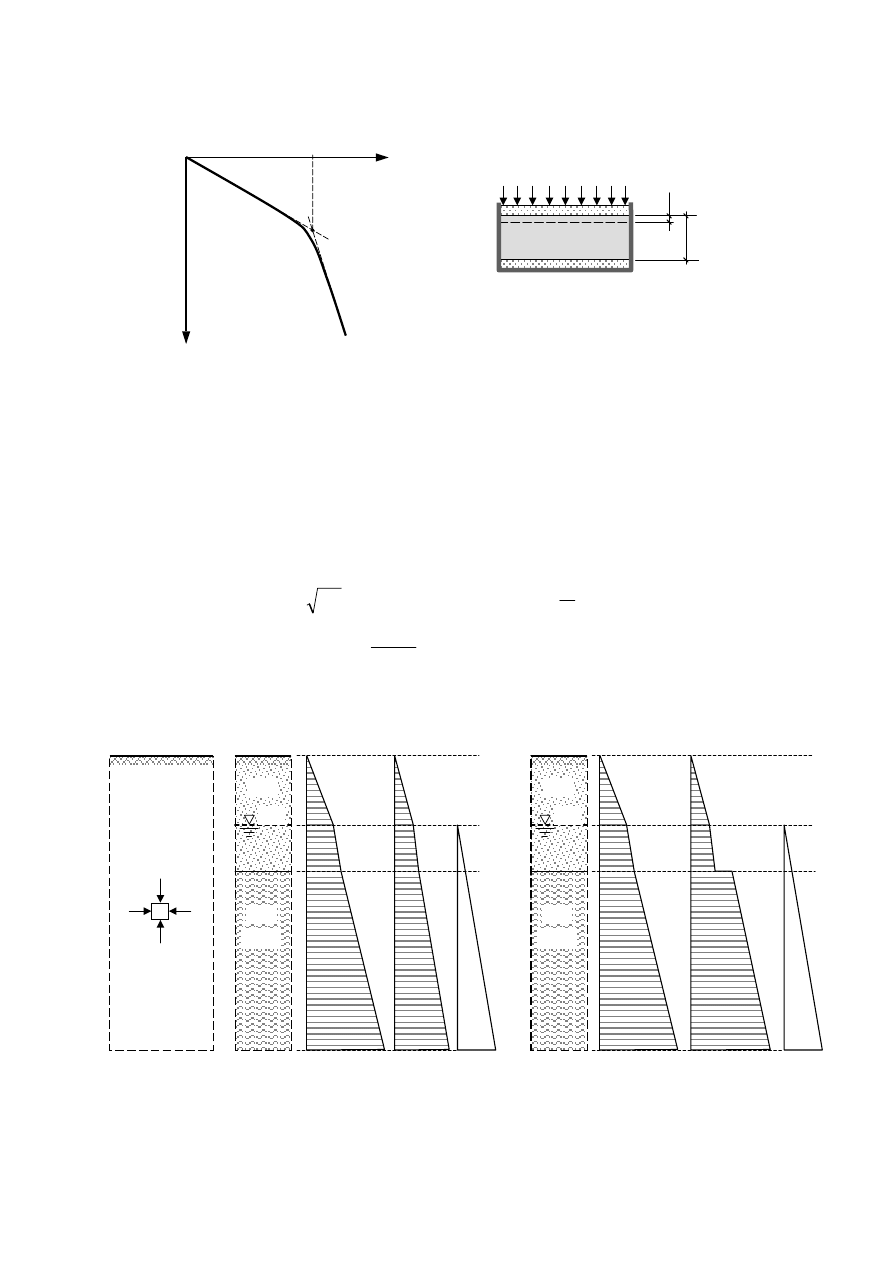
Przykładowe rozkłady składowych efektywnych naprężenia w podłożu normalnie skonsolidowa-
nym i prekonsolidowanym przedstawiono na rysunku poniżej
Prekonsolidacja podłoża gruntowego na terenie Polski jest głównie efektem epok lodowcowych,
podczas których podłoże to było obciążone ciężarem lodowca. Szacuje się, że podczas ostatniego
zlodowacenia, które zakończyło się kilkanaście tysięcy lat temu, grubość pokrywy lodowej
σ′
z;0
σ′
z;0
σ′
x;0
σ′
x;0
σ′
z;0
σ′
x;0
σ′
z;0
σ′
x;0
zwg
(NC)
(NC)
(K
0
NC
)
u
0
zwg
(NC)
(OC)
(K
0
OC
)
u
0
ln
σ'
z
ε
1
ln
σ'
z;max
σ'
z
grunt
∆h
h
ε
1
=
∆h/h
3
wynosiła od 1000 m do 2000 m. Należy jednocześnie zwrócić uwagę, że ze względu na inne
procesy geologiczne (trzęsienia ziemi, ruchy tektoniczne, cementyzacja, erozje, procesy
reologiczne) stan naprężenia w gruncie, w okresie po ustąpieniu lodowca, ulegał różnym zmianom
(najczęściej współczynnik prekonsolidacji ulegał zmniejszeniu).
1.2. Zależność parametrów mechanicznych gruntu od głębokości i poziomu naprężenia
1.2.1. Edometryczny moduł ściśliwości M
0
Edometryczny moduł ściśliwości M
0
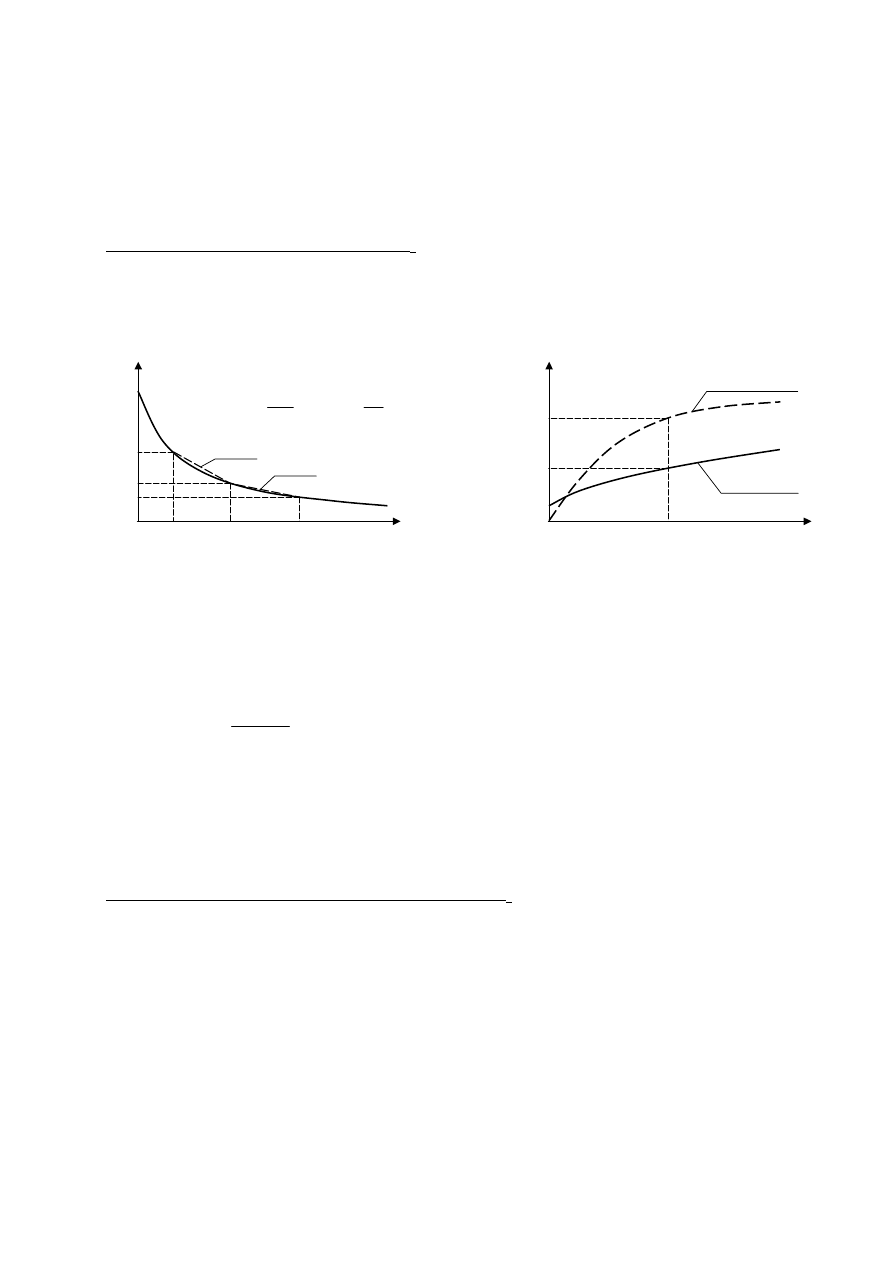
nie parametrem stałym dla danego gruntu, tylko zależy od
poziomu naprężenia w gruncie. Wartość modułu wzrasta z poziomem naprężenia, przy czym wzrost
ten jest przeważnie nieliniowy (patrz rys. poniżej).
Podawana w dokumentacjach geotechnicznych wartość modułu M
0
powinna się odnosić do jakieś
wartości naprężenia. Najczęściej wartość tę przyjmuje się równą 100 kPa i określa się je mianem
naprężenia referencyjnego p
ref
. Moduł M
0
o wartości odpowiadającej naprężeniu referencyjnemu
p
ref
nazywa się modułem referencyjnym
ref
M
;
0
.
Zmienność modułu z naprężeniem określa potęgowe prawo ściśliwości:
m
ref
ref
a
p
a
M
M
+
+
′
=
′
min
;
0
0
)
(
σ
σ
; gdzie
φ
′
⋅
′
=
cot
c
a
Wykładnik m przyjmuje się z przedziału 0,3
÷ 0,5 dla gruntów niespoistych lub z przedziału 0,6 ÷
0,9 dla gruntów spoistych.
Naprężenie
σ
'
min
przyjmuje jako najmniejsze spośród składowych
σ
'
x;0
,
σ
'
y;0
i
σ
'
z;0
naprężenia
geostatycznego w gruncie.
1.2.2. Wytrzymałość gruntu na ścinanie bez odpływu C
u
Wytrzymałość każdego gruntu na ścinanie, w każdych warunkach zależy od naprężeń efektywnych
σ
' i od efektywnych parametrów wytrzymałościowych
φ
' i c'. W warunkach bez odpływu wody
z porów gruntu, podczas obciążania gruntu wzrasta ciśnienie wody u w porach gruntu, w wyniku
czego naprężenia efektywne w gruncie bądź nie wzrastają w ogóle, bądź wzrastają niewiele, co
w rezultacie sprawia, że wytrzymałość gruntu na ścinanie nie wzrasta lub słabo wzrasta ze
wzrostem obciążeń zewnętrznych. Wytrzymałość ta wzrasta z głębokością, wraz ze wzrostem
wartości naprężeń geostatycznych.
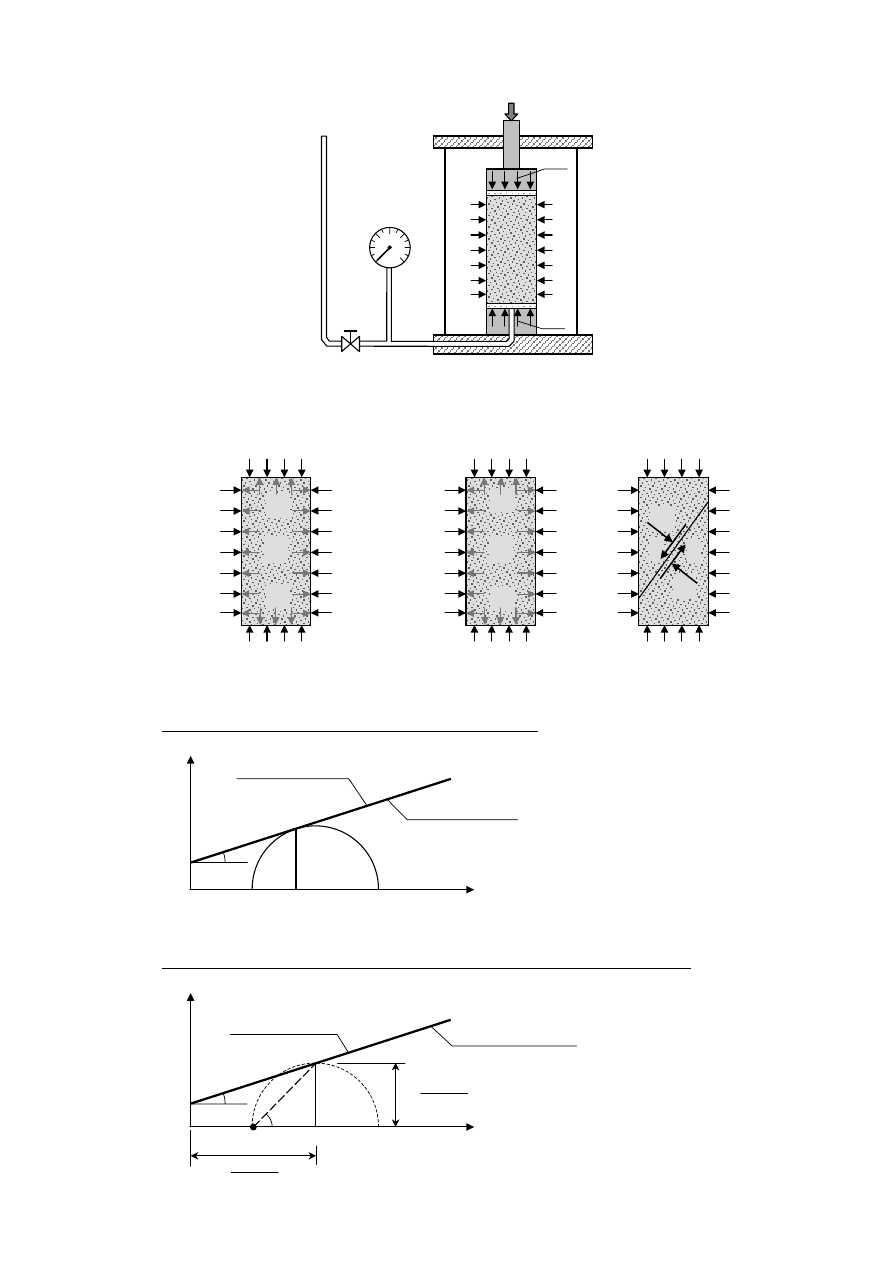
Zagadnienie powyższe zostanie zobrazowane na przykładzie badania gruntu w aparacie
trójosiowego ściskania.
h
σ′
σ′
a
σ′
c
Badanie w edometrze
0
σ′
b
h
0
h
a
h
b
h
c
M
0;a-b
M
0;b-c
ε
σ
′
∆
=
0
M
;
h
h
∆
=
ε
M
0;b-c
> M
0;a-b
σ′
grunt niespoisty
M
0
σ′
i
(1)
(2)
grunt spoisty
M
0;2
(
σ′
i
)
M
0;1
(
σ′
i
)
4
1) Badanie z drenażem (z odpływem)
manometr
u = 0
zawór
"O"
σ
3
σ
3
σ
1
σ
1
Q
1) Prezentacja wyniku badania w układzie klasycznym
σ - τ
σ
3
σ
3
σ
1
=
σ
3
σ′
3
σ′
3
σ′
3
σ
1
=
σ
3
Stan początkowy
(ściskanie izotropowe)
σ
3
σ
3
σ
1;ult
=
σ
3
+
∆σ
1
σ′
3
σ′
1
Stan końcowy
(graniczny)
σ′
1
σ
1;ult
=
σ
3
+
∆σ
1
u = 0
→
σ′
3
=
σ
3
;
σ′
1
=
σ
1
σ
3
σ
3
σ
1;ult
σ
1;ult
σ′
n
σ′
n
τ
f
τ
f
τ
σ
σ′
3
σ′
1
c
′
φ′
τ
f
prosta graniczna
(prosta Coulomba)
τ
f
=
σ′
n
⋅tg
φ′ + c'
σ′
n
2) Prezentacja wyniku badania w układzie płaskim s - t (płaski stan odkształcenia)
s
′
0
= σ′
3
σ′
1
c
′
t
α′
prosta graniczna
t
f
= s
′⋅tanα′ + c′
t
s
′
t
45
°
tan
α′ = sinφ′
c
′
t
= c
′⋅cosφ′
σ′
1
–
σ′
3
2
t =
σ′
1
+
σ′
3
2
s
′ =
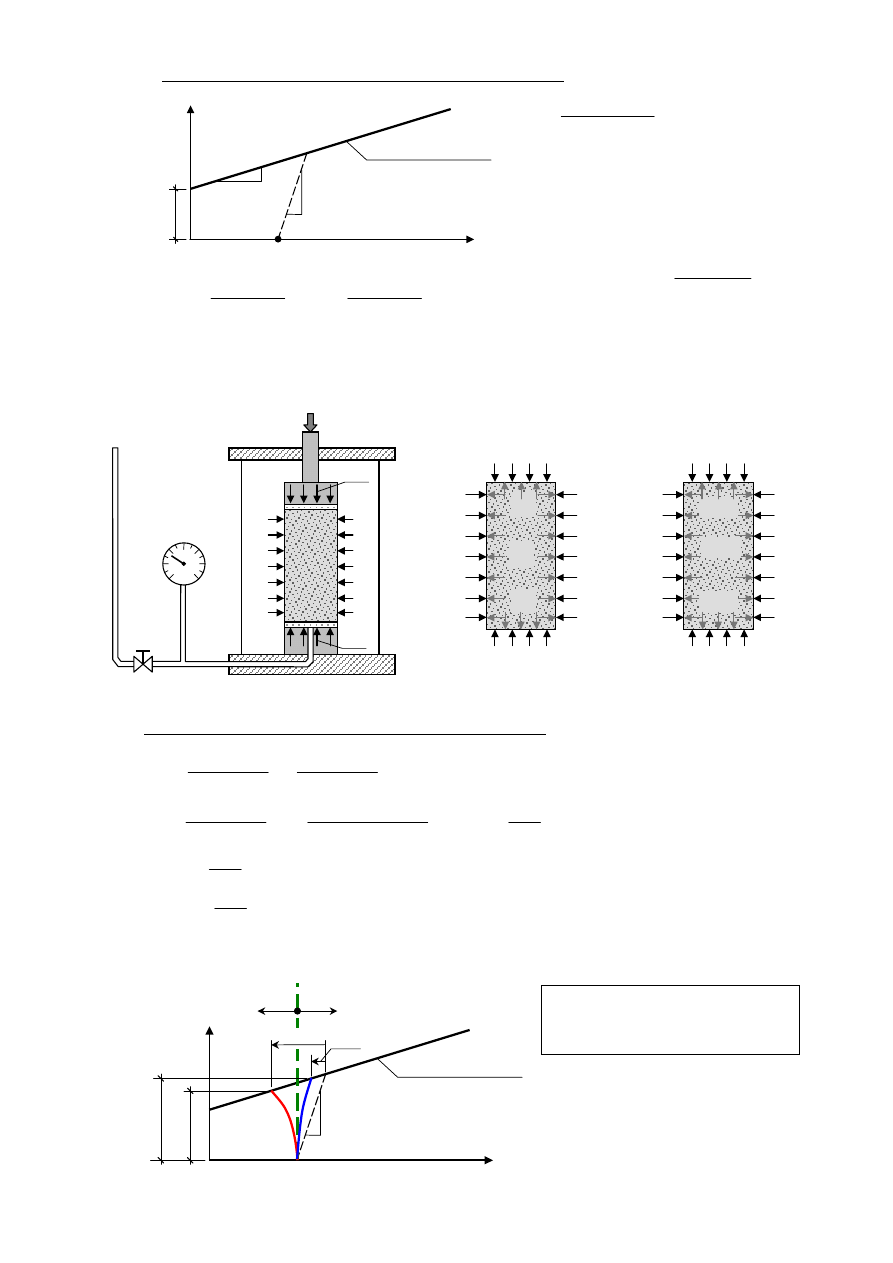
5
2) Badanie bez drenażu (bez odpływu)
manometr
u
≠ 0
zawór
"Z"
σ
3
σ
3
σ
1
σ
1
Q
σ
3
σ
3
σ
1
=
σ
3
σ′
3
σ′
3
σ′
3
σ
1
=
σ
3
Stan początkowy
(ściskanie izotropowe
z drenażem, u = 0)
σ
3
σ
3
σ
1;ult
=
σ
3
+
∆σ
1
σ′
1
+u
Stan końcowy (graniczny)
(bez drenażu)
σ
1;ult
=
σ
3
+
∆σ
1
σ′
3
=
σ
3
- u ;
σ′
1
=
σ
1
- u
σ′
3
+u
σ′
1
+u
Prezentacja wyniku badania w układzie przestrzennym p - q
p
′ =
σ′
1
+ 2
σ′
3
3
=
σ
1
+ 2
σ
3
3
- u = p - u
q =
σ′
1
-
σ′
3
=
σ
1
-
σ
3
=
σ
3
+
∆σ
1
-
σ
3
=
∆σ
1
p
′ =
σ
1
+ 2
σ
3
3
- u =
σ
3
+
∆σ
1
+ 2
σ
3
3
- u =
σ
3
+
∆σ
1
3
- u
gdy u >
∆σ
1
3
→ p
′ maleje → grunt normalnie skonsolidowany lub nieskonsolidowany
gdy u <
∆σ
1
3
→ p
′ rośnie → grunt prekonsolidowany
→ q rośnie
3) Prezentacja wyniku badania w układzie przestrzennym p - q
p
′
0
=
σ
3,0
q
f
= p
′⋅M + c′
q
p
′
q
3
1
OC
NC
q
f
NC
q
f
OC
u
NC
u
OC
C
u
NC
= 0,5
⋅q
f
NC
Grunt normalnie skonsolidowany:
C
u
= 0,5
⋅q
f
OC
Grunt prekonsolidowany:
C
u
= 0,5
⋅q
f
Wytrzymałość gruntu na ścinanie
w warunkach bez odpływu:
p
′
0
=
σ′
3
c
′
q
(prosta graniczna)
q
f
= p
′⋅M + c′
q
p
′
q
p
′ =
σ′
1
+
σ′
2
+
σ′
3
3
q =
σ′
1
-
σ′
3
3
1
M =
6sin
φ′
3 - sin
φ′
; c
′
q
=
6c
′⋅cosφ′
3 - sin
φ′
- naprężenie średnie
- dewiator naprężenia
σ′
1
>
σ′
2
>
σ′
3
σ′
2
=
σ′
3
W układzie osiowo-symetrycznym:
p
′ =
σ′
1
+2
σ′
3
3
→
1
M
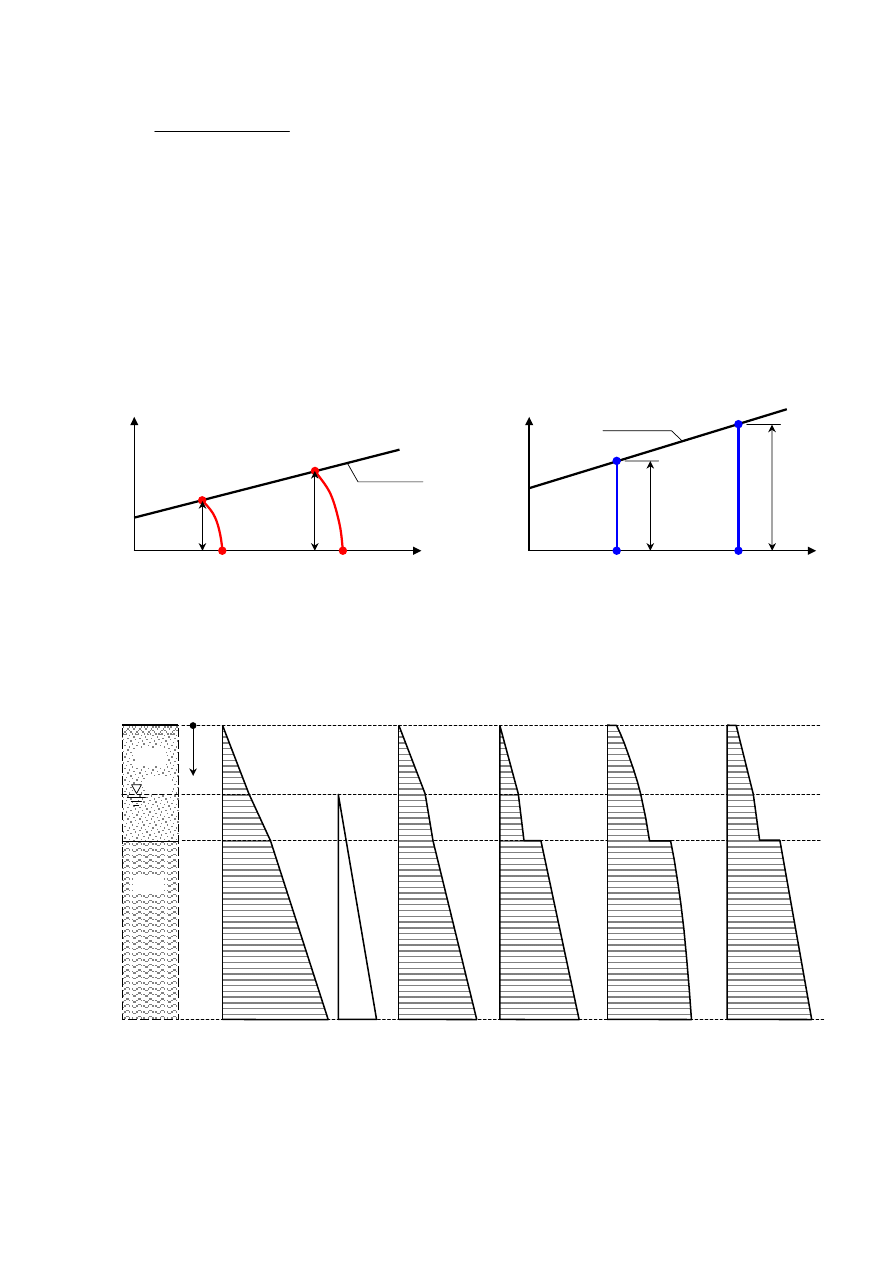
6
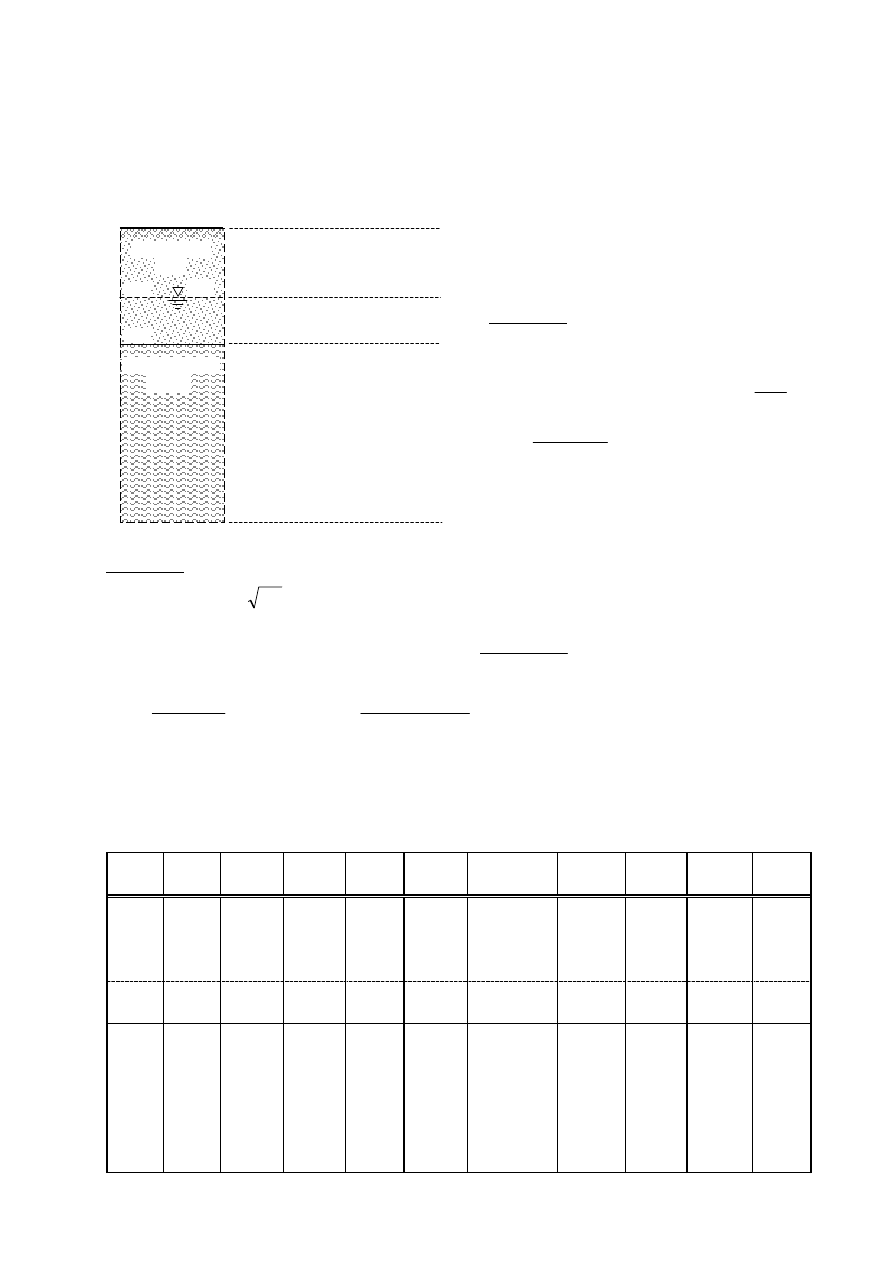
Przeniesienie do warunków terenowych
Można w przybliżeniu przyjąć, że:
- dla gruntów normalnie skonsolidowanych:
- dla gruntów prekonsolidowanych:
Wraz ze wzrostem głębokości z wzrastają naprężenia geostatyczne
σ′
z;0
,
σ′
x;0
i
σ′
y;0
. Wzrastają
również wielkości p
′
0
i q
f;0
, a zatem i wytrzymałość gruntu na ścinanie bez odpływu C
u
. Obrazuje
to poniższy rysunek.
Należy dodać, że w gruntach prekonsolidowanych wartości parametrów
φ′
i c
′
są odpowiednio
większe niż w gruntach normalnie skonsolidowanych co sprawia, że wytrzymałość C
u
tych gruntów
jeszcze bardziej wzrasta w stosunku do gruntów normalnie skonsolidowanych.
p
′
0
=
σ′
z;0
+
σ′
x;0
+
σ′
y;0
3
q
f;0
= p
′
0
⋅ M + c
′
q
;
C
u
NC
= 0,8
⋅0,5⋅q
f,0
= 0,4
⋅q
f,0
C
u
OC
= 1,0
⋅0,5⋅q
f,0
= 0,5
⋅q
f,0
p
′
0
(z
1
)
q
f;0
(z)
p
′
q
p
′
0
(z
2
)
2C
u
(z
2
)
2C
u
(z
1
)
Grunt normalnie skonsolidowany
p
′
0
(z
1
)
q
f;0
(z)
p
′
q
p
′
0
(z
2
)
2C
u
(Z
2
)
2C
u
(Z
1
)
Grunt prekonsolidowany
σ
z;0
σ′
x;0
=
σ′
y;0
zwg
(NC)
(OC)
u
0
σ′
z;0
z
M
0
C
u
7
Przykład obliczeniowy
Wyznaczyć rozkłady składowych naprężenia geostatycznego w podłożu gruntowym przedstawio-
nym na rysunku poniżej oraz rozkłady wartości modułu edometrycznego M
0
i wytrzymałości gruntu
na ścinanie w warunkach bez odpływu C
u
.
Obliczenia przygotowawcze:
Warstwa 1
531
,
0
28
sin
1
1
;
0
=
°
−
=
K
a
1
= 0 bo c
′
= 0
→
5
,
0
min
1
;
0
100
0
,
70
′
⋅
=
σ
M
11
,
1
28
sin
3
28
sin
6
1
=
°
−
°
⋅
=
M
;
0
1
;
=
′
q
c
, bo c
′
= 0
1
;
0
1
;
11
,
1
p
q
f
′
⋅
=
;
1
;
0
1
;
1
;
444
,
0
4
,
0
p
q
C
f
u
′
⋅
=
⋅
=
Warstwa 2
12
,
1
5
,
2
)
17
sin
1
(
2
;
0
=
⋅
°
−
=
K
2
,
147
17
cot
45
2
=
°
⋅
=
a
kPa ;
→
7
,
0
min
2
;
0
2
,
147
100
2
,
147
0
,
55
+
+
′
⋅
=
σ
M
648
,
0
17
sin
3
17
sin
6
2
=
°
−
°
⋅
=
M
;
4
,
95
17
sin
3
17
cos
0
,
45
6
2
=
°
−
°
⋅
⋅
=
′
q
c
kPa
4
,
95
648
,
0
2
;
0
2
;
+
′
⋅
=
p
q
f
;
7
,
47
324
,
0
)
4
,
95
648
,
0
(
5
,
0
2
;
0
2
;
0
2
;
+
′
⋅
=
+
′
⋅
⋅
=
p
p
C
u
Obliczenia zasadnicze:
Tabela obliczeń
z
γ
σ
z ;0
u
0
σ
'
z ;0
K
0
σ
'
x ;0
=
σ
'
y ;0
σ
'
min
M
0
p'
0
C
u
[m]
[kPa]
[kPa]
[kPa]
[kPa]
[kPa]
[MPa]
[kPa]
[kPa]
0,0
18,0
0,0
0,0
0,0
0,531
0,0
0,0
0,0
0,0
0,0
1,0
18,0
18,0
0,0
18,0
0,531
9,6
9,6
21,6
12,4
5,5
2,0
18,0
36,0
0,0
36,0
0,531
19,1
19,1
30,6
24,7
11,0
3,0
18,0
54,0
0,0
54,0
0,531
28,7
28,7
37,5
37,1
16,5
4,0
19,7
73,7
10,0
63,7
0,531
33,8
33,8
40,7
43,8
19,4
5,0
19,7
93,4
20,0
73,4
0,531
39,0
39,0
43,7
50,5
22,4
5,0
20,5
93,4
20,0
73,4
1,120
82,2
73,4
50,8
79,3
73,4
7,0
20,5
134,4
40,0
94,4
1,120
105,7
94,4
54,1
102,0
80,7
10,0
20,5
195,9
70,0
125,9
1,120
141,0
125,9
59,0
136,0
91,8
15,0
20,5
298,4
120,0
178,4
1,120
199,8
178,4
66,7
192,7
110,1
20,0
20,5
400,9
170,0
230,9
1,120
258,6
230,9
74,1
249,4
128,5
25,0
20,5
503,4
220,0
283,4
1,120
317,4
283,4
81,1
306,1
146,9
30,0
20,5
605,9
270,0
335,9
1,120
376,2
335,9
87,9
362,8
165,2
zwg
Piasek pylasty
saclSi
0,0
siSa
Pył piaszcz-ilasty
-3,0
-5,0
γ
= 18 kN/m
3
,
γ
sr
= 19,7 kN/m
3
φ′
= 28
°, c
′
= 0, M
0;ref
= 70 MPa
OCR = 1,0 ,
ν
= 0,25 , m = 0,5
γ′
=
γ
sr
-
γ
w
= 19,7 - 10,0 = 9,7 kN/m
3
γ
sr
= 20,5 kN/m
3
,
γ′
= 10,5 kN/m
3
φ′
= 17
°, c
′
= 45 kPa, M
0;ref
= 55 MPa
OCR = 2,5 ,
ν
= 0,30 , m = 0,7
8
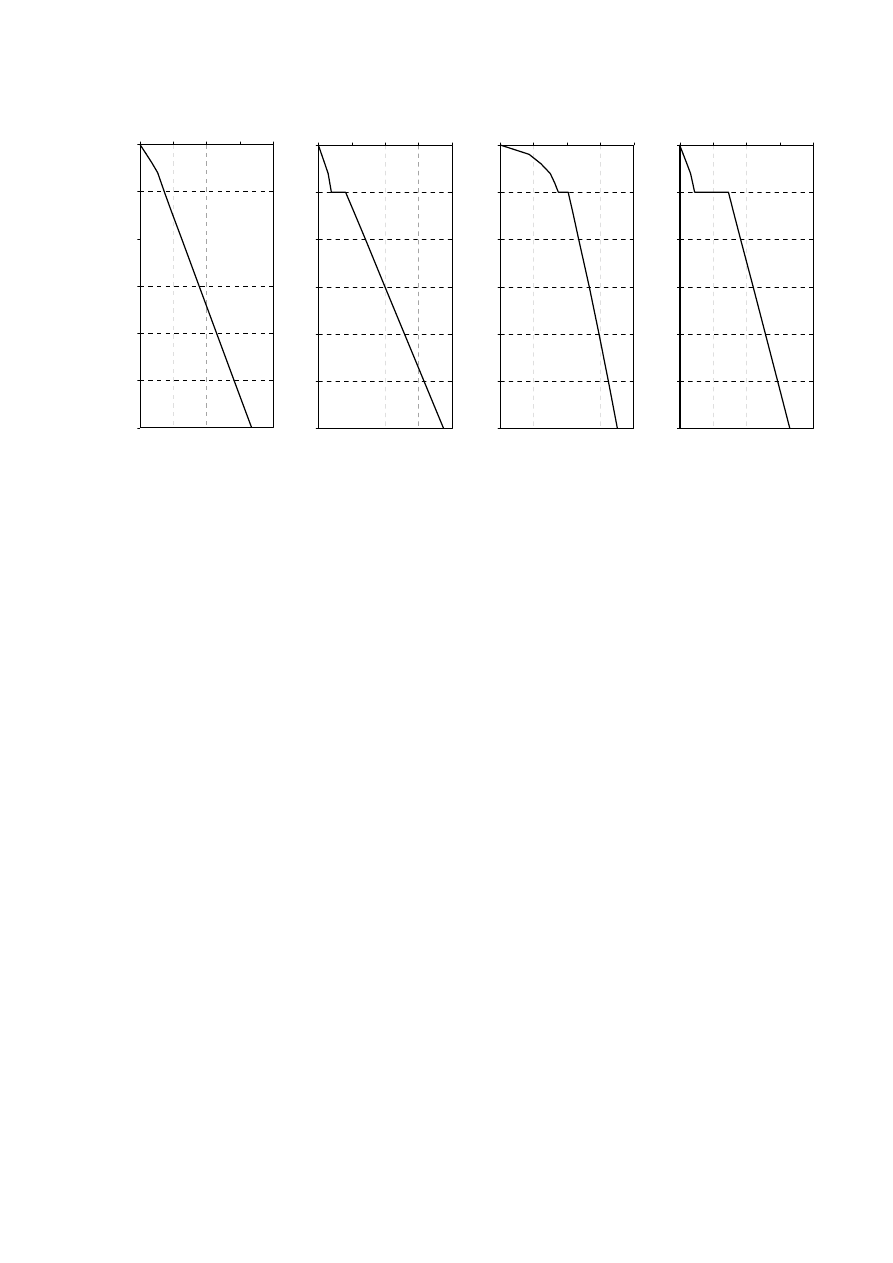
Wykresy obliczanych wielkości fizycznych
0
5
10
15
20
25
30
0
100
200
300
400
σ '
z ;0
[kPa]
z
[m
]
0
5
10
15
20
25
30
0
100
200
300
400
σ '
x ;0
[kPa]
z
[m
]
0
5
10
15
20
25
30
0
25
50
75
100
M
0
[MPa]
z
[m
]
0
5
10
15
20
25
30
0
50
100
150
200
C
u
[kPa]
z
[m
]
9