1

PROJEKTOWANIE WYROBU. WYBRANE ELEMENTY.

JOANNA CZERSKA, 1999

Ponieważ każde nowe przedsięwzięcie pociąga za sobą podjęcie określonych inwestycji
przedsiębiorstwo zmuszone jest do maksymalnego zwiększenia szans powodzenia nowego
produktu na rynku.
Ważną rolę w tym zakresie odgrywają prace związane z przygotowaniem i projektowaniem
produkcji oraz rozwojem produktu i jego wprowadzaniem na rynek.

Proces nowego produktu można przedstawić w ujęciu kilku faz. W układzie liczba idei i czas,
fazy te można zobrazować za pomocą krzywej rozwoju nowego produktu.




















Rys. Krzywa nowego produktu

Czas [%]

Liczba

idei

Poszukiwanie
pomysłów

Selekcja
pomysłów

Analiza
ekonomiczna

Rozwój
produktu

Testowanie
produktu

Koncepcja
produktu

Wprowadzenie
produktu

100

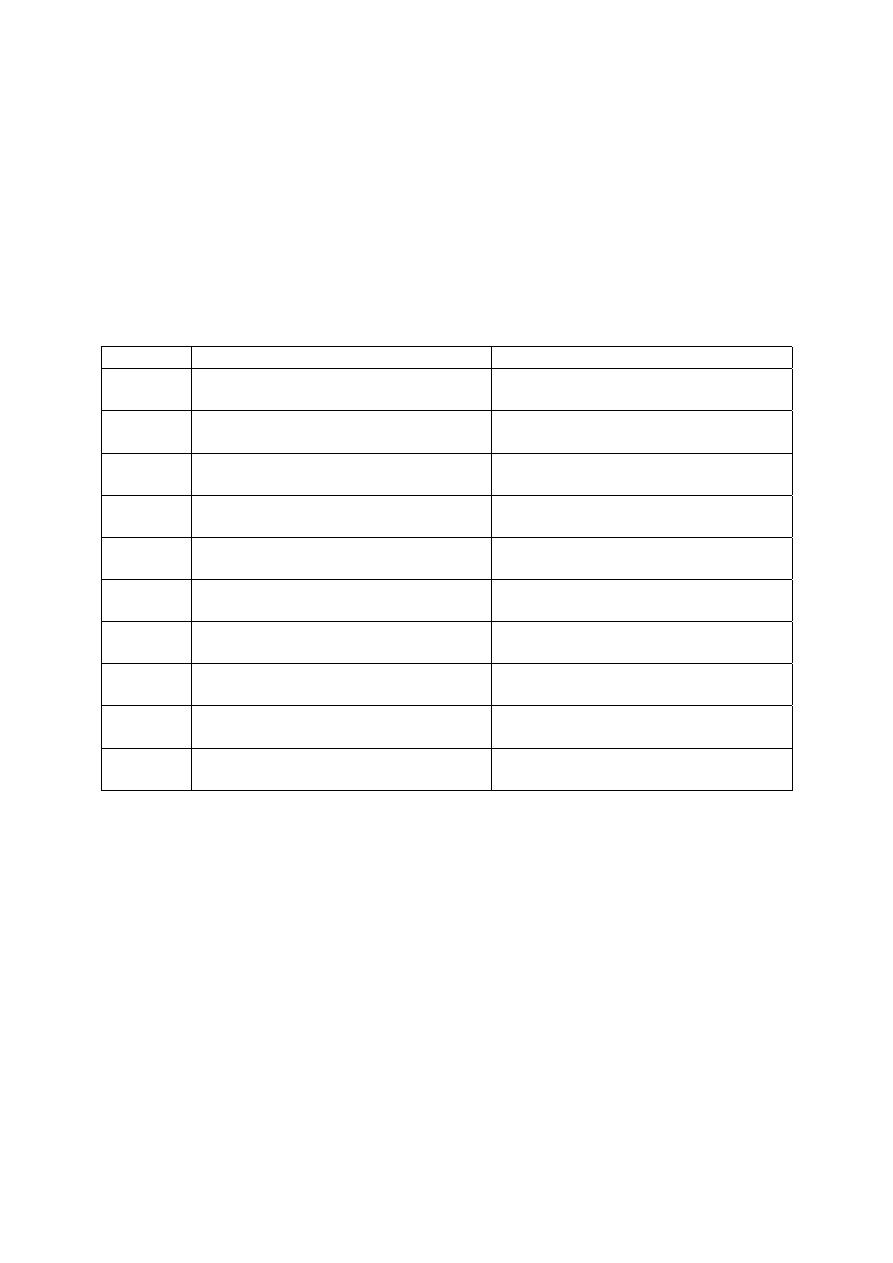
2

1. Poszukiwanie pomysłów

Proces rozwoju nowego produktu zaczyna się tworzeniem i poszukiwaniem pomysłów. Jest to
najbardziej twórcza faza.

Załóżmy, że firma poszukuje nowego rozwiązania na realizację potrzeby pt.
WBICIE GWOŹDZIA.

Dokonujemy zestawienia produktów, które spełnią potrzebę pt. WBICIE
GWOŹDZIA

Nazwa

Szkic

Produkt 1 młotek standardowy

Produkt 2 Pistolet do wstrzeliwania gwoździ

Produkt 3 Kamień

Produkt 4 Kafar spalinowy

Produkt 5 Kafar elektryczny

Produkt 6 Kafar parowy (urz. do wbijania pali)

Produkt 7 Dźwignia (przekładnia)

Produkt 8 Ścisk śrubowy (imadło)

Produkt 9

Produkt 10

2. Selekcja pomysłów

Zgromadzone w poprzednim etapie pomysły poddawane są wstępnej selekcji, celem wyboru
pomysłów, które będą przedmiotem dalszych badań.
W tej fazie eliminujemy pomysły niemożliwe do realizacji ze względu na możliwości
techniczno-produkcyjne oraz finansowe przedsiębiorstwa.

Najczęściej wstępna selekcja pomysłów odbywa się wg kryteriów uwzględniających:
- cele

przedsiębiorstwa

- potencjał produkcyjny przedsiębiorstwa
- możliwości finansowe przedsiębiorstwa
- rynek

docelowy

3

Dokonamy teraz selekcji pomysłów w aspekcie celów i zasobów firmy przy następujących
założeniach:
1. Firma NNN od 20 lat zajmuje się produkcją elektronarzędzi i narzędzi ręcznych.

Narzędzia ręczne wykonywane są z materiałów drewnianych i metalowych oraz tworzyw
sztucznych. Do wyrobu elektronarzędzi wykorzystuje się gotowe podzespoły związane z
napędem elektrycznym.

2. Firma posiada dział konstrukcyjny i wykwalifikowaną kadrę pracowników bezpośrednio

produkcyjnych.

3. Przedsiębiorstwo ma dobrą sytuację finansową pozwalającą rozwinąć w zasadzie każdy

nowy produkt związany z grupą produktów dotychczas oferowanych.

4. Firma posiada sieć dystrybucji wyrobów prowadzącą do hurtowych odbiorców

elektronarzędzi i narzędzi ręcznych na terenie Polski północnej.

5. Działalność marketingowa firmy jest we wstępnej fazie rozwoju.
6. Prestiż przedsiębiorstwa jest niski.


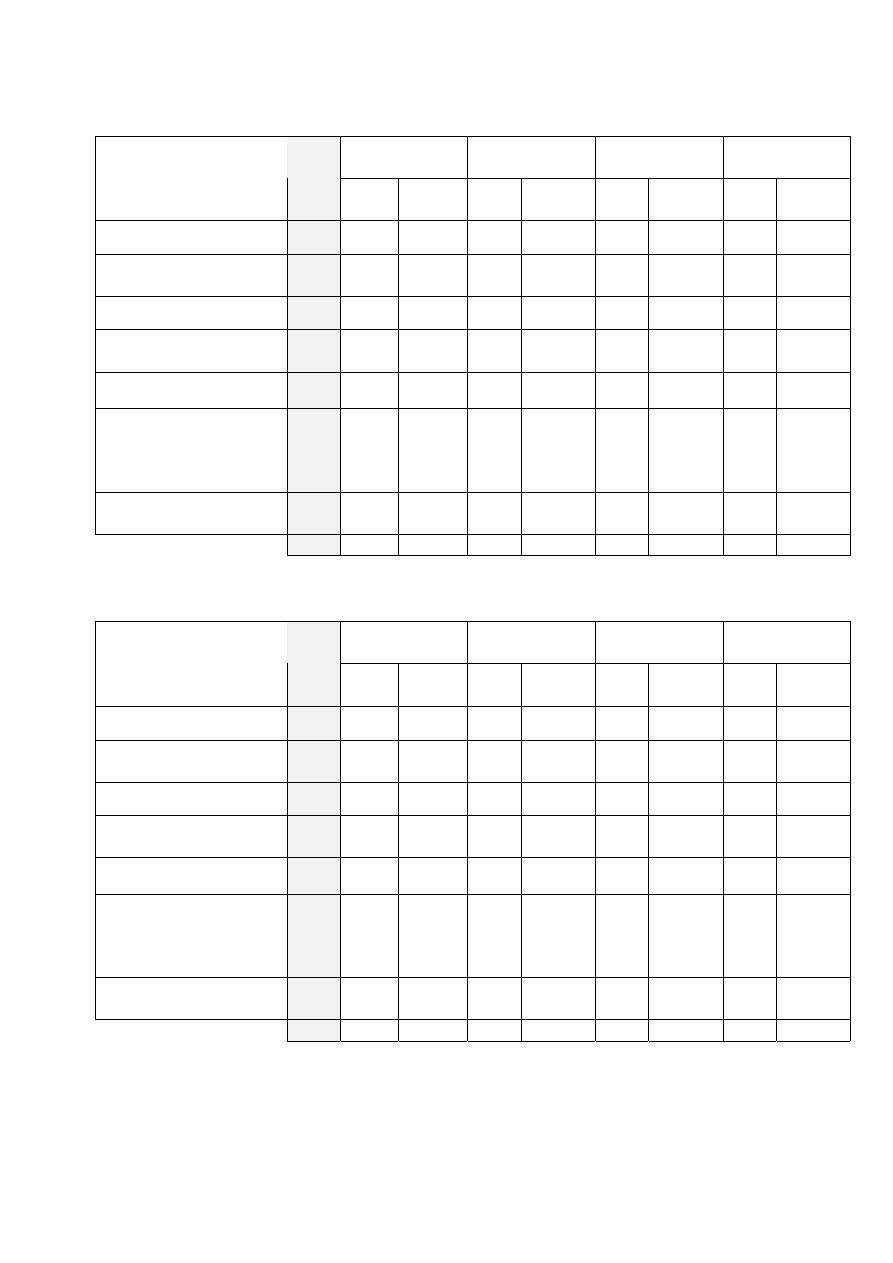
Dokonujemy selekcji pomysłów w aspekcie celów przedsiębiorstwa

Ocena pomysłu z
punktu widzenia
celów firmy

Osiągnięcie

zysku

Wzrost

sprzedazy

Niezbędny

kapitał

Wymagane „know-

how”można pozyskać tanio

Ocena pomysłu

z punktu

widzenia

zasobów firmy

Niezbędne

„know-how”

niezb. formy

dystrybucji

niezb. działania

marketingowe

Przejście do

następnego etapu

Rezygnacja z

pomysłu

Wymagany kapitał można

pozyskać tanio

Wymagane formy dystryb.

można pozyskać tanio

NIE

NIE

NIE

NIE

NIE

NIE

NIE

NIE

NIE

NIE

NIE

TAK

TAK

TAK

TAK

TAK

TAK

TAK TAK

TAK

TAK

Utrzymywanie i poprawa

wizerunku

Wymagane działania marketing.

można pozyskać tanio

4

Pomysły które przeszły przez wstępną selekcję zgodnie z powyższym rysunkiem ocenimy
stosując punktową ocenę pomysłów z punktu widzenia możliwości i zasobów naszej firmy.

kryteria oceny

waga

ocena ocena

ważona

ocena ocena

ważona

ocena ocena

ważona

ocena ocena

ważona

Możliwości finansowe

0,25

Potencjał techniczno-
produkcyjny

0,2

Prestiż przedsiębiorstwa

0,1

Działalność
marketingowa

0,1

Lokalizacja firmy

0,1

Doświadczenie i
predyspozycje
menedżerskie
kierownictwa

0,1

Kwalifikacje
pracowników

0,15

1,0

kryteria oceny

waga

ocena ocena

ważona

ocena ocena

ważona

ocena ocena

ważona

ocena ocena

ważona

Możliwości finansowe

0,25

Potencjał techniczno-
produkcyjny

0,2

Prestiż przedsiębiorstwa

0,1

Działalność
marketingowa

0,1

Lokalizacja firmy

0,1

Doświadczenie i
predyspozycje
menedżerskie
kierownictwa

0,1

Kwalifikacje
pracowników

0,15

1,0

Odrzucamy 3 pomysły o najmniejszej wartości oceny ważonej

5

3. Koncepcja produktu

Zakwalifikowane do dalszej realizacji pomysły zostają w tym etapie przekształcone w
koncepcje produktu.
Nabywcy nie kupują bowiem pomysłów, ale określone produkty zaspokajające ich potrzeby.
Każda koncepcja produktu może być przedstawiona w kilku wariantach uwzględniających
upodobania odbiorców.
W tym celu należy określić potencjalnych nabywców, ich wymagania i preferencje.

Załóżmy, że dla zapewnienia odpowiedniego rynku zbytu (który został określony przez nasz
dział marketingu) odbiorcami produktu mają być następujące grupy klientów:
1. domowy majsterkowicz
2. pani domu
3. budowniczy domów z drewna

Dokonajmy charakterystyki potrzeb poszczególnych grup klientów

klient Charakterystyka

potrzeb

1. domowy majsterkowicz

Urządzenie stosunkowo niedrogie,
zajmujące niewiele miejsca,
może być nieco skomplikowane w obsłudze,
do gwoździ do średniej wielkości
trwałe

2. pani domu

Urządzenie tanie,
Proste w obsłudze, zajmujące niewiele miejsca
do gwoździ do średniej wielkości
trwałe

3. budowniczy domów z drewna

Urządzenie profesjonalne,
Może być drogie
Poręczne,
do wszystkich wymiarów i rodzajów gwoździ
Duża wydajność
Bardzo trwałe

6

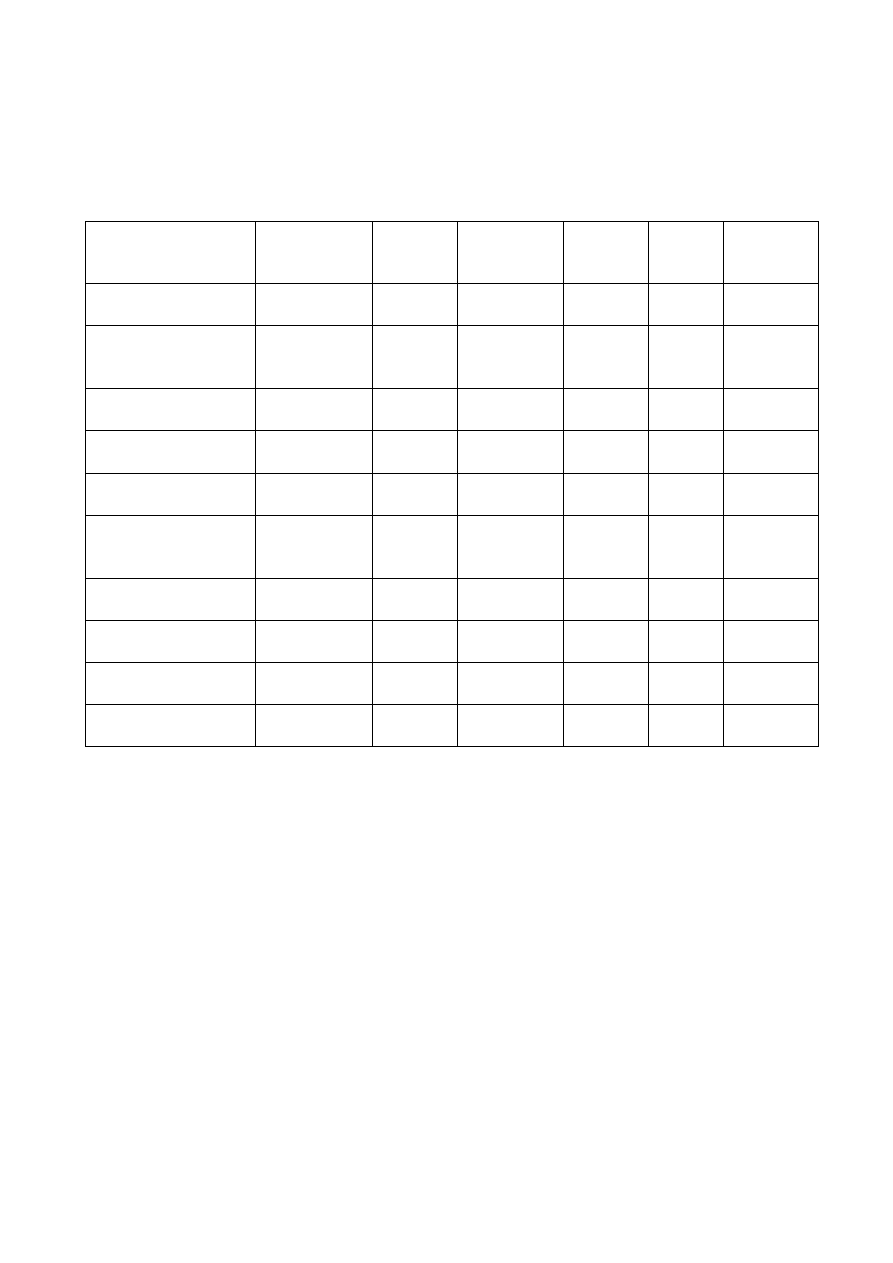
W tym miejscu dokonujemy charakterystyki produktu:

1) rysunek
2) przeznaczenie
3) spełniane funkcje
4) charakterystyka techniczna

a) wymiary
b) ciężar
c) rodzaj materiałów potrzebnych do jego produkcji

5) stopień nowości

grupa 1 – wyroby będące odwzorowaniem istniejących bez istotnych zmian

konstrukcyjnych

grupa 2 – wyroby pochodne modeli bazowych z wykorzystaniem części

zunifikowanych – modernizacja wyrobu

grupa 3 – wyroby, które odznaczają się nowymi parametrami
grupa 4 - nowy wyrób pod względem konstrukcyjnym (lecz nie pod względem zasad

funkcjonowania), mogą wystąpić potrzeby modelowania

grupa 5 – zupełnie nowe wyroby, nowe konstrukcje, nowe funkcje

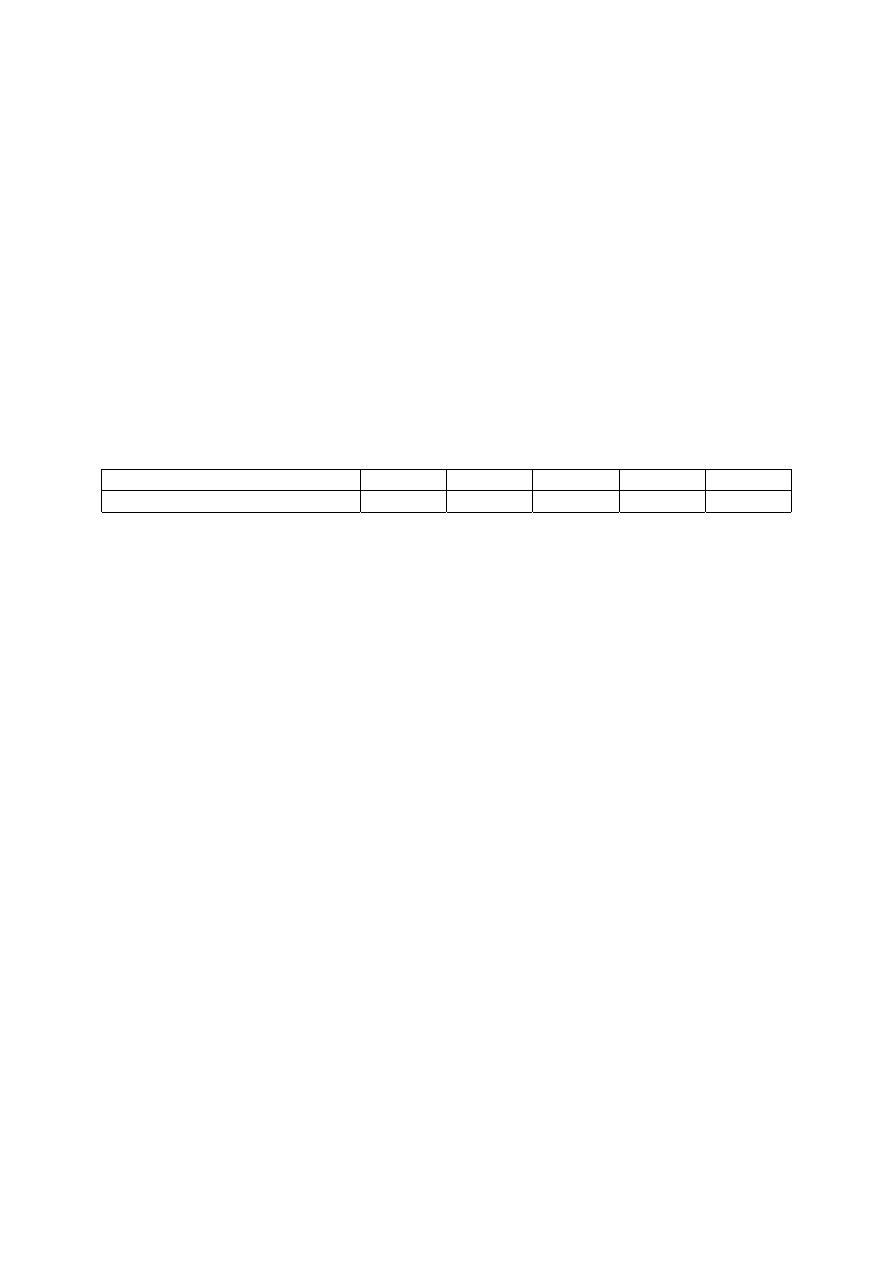
Grupa nowości

1 2 3 4 5

Współczynnik utrudnienia k

u

1 1,2 1,3 1,5 1,7

6) grupa złożoności wyrobu (skomplikowania wyrobu)

grupa A – maszyny z prostą kinematyką, ruchy nie zautomatyzowane
grupa B – maszyny z prostą kinematyką, stopniowa zmiana prędkości, sterowanie

zdecentralizowane

grupa C - maszyny ze zmianą prędkości z napędem scentralizowanym lecz nie

automatycznym, ograniczone urządzenia elektryczne i hydrauliczne

grupa D – maszyny automatyczne i półautomatyczne z centralnym sterowaniem,

sterowane elektronicznie bez mikroprocesorów

– automaty i półautomaty z wykorzystaniem elektroniki i hydrauliki, automatyczna regulacja
parametrów, sterowanie mikroprocesorowe

7

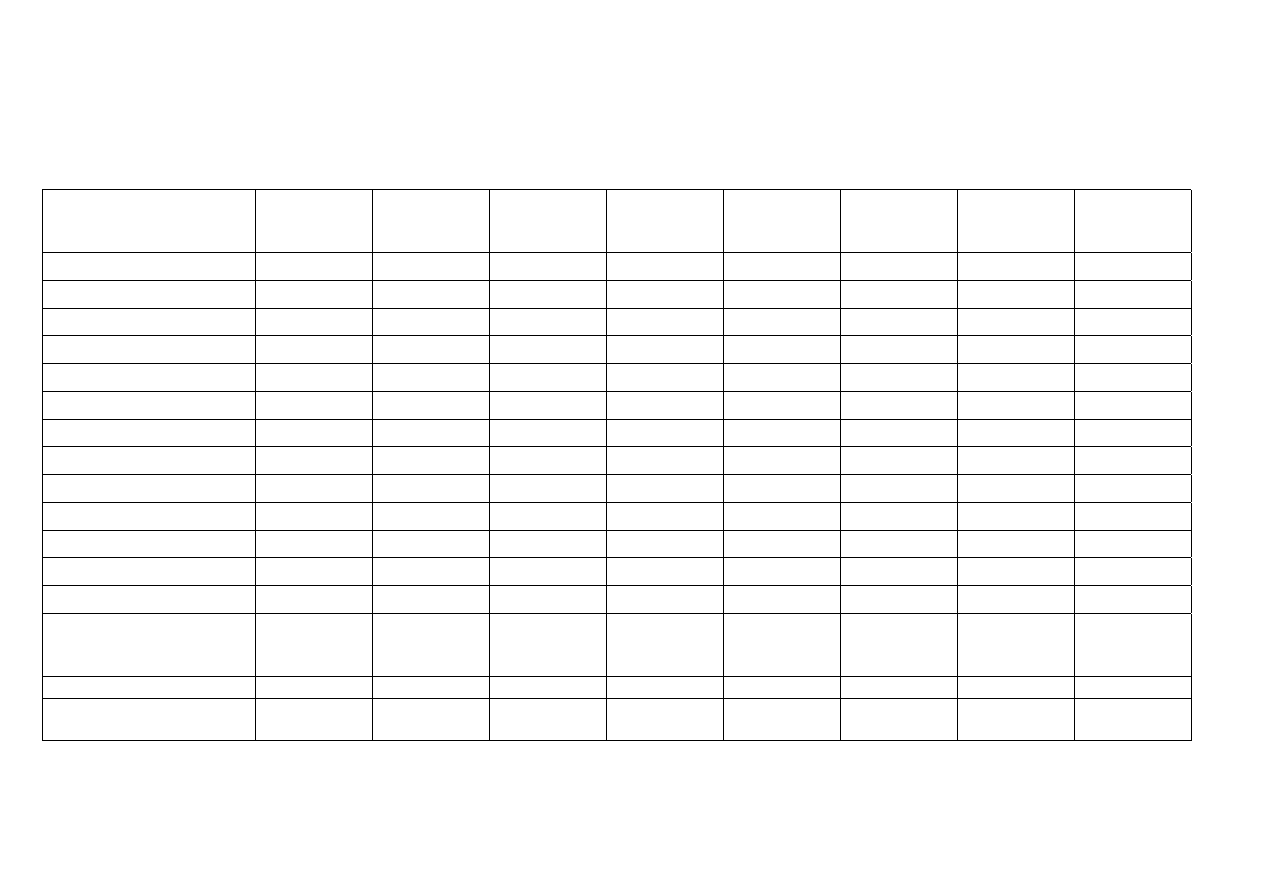
Na podstawie określonych wymagań rynku i charakterystyk produktów dokonujemy

w etapie I

eliminacji koncepcji starając się znaleźć taki wyrób który w miarę możliwości spełniałby
potrzeby wszystkich odbiorców jednocześnie.

a) przez porównanie charakterystyki potrzeb odbiorców i produktów

Nazwa produktu

domowy

majsterkowicz

pani

domu

budowniczy

domów z

drewna

SUMA
+
-

Suma Wniosek

1) młotek

standardowy

+ + - +2

-1

1

do dalszej

analizy

2) Pistolet do

wstrzeliwania
gwoździ

- - +

+1

-2

-1 odrzucam

3) Kamień +-

+-

-

+2

-3

-1 odrzucam

4) Kafar spalinowy

-

-

+

+1

-2

-1 odrzucam

5) Kafar elektryczny

+

+-

+

+3

-1

2

do dalszej

analizy

6) Kafar parowy

(urz. do wbijania
pali)

- - - -3 -3

odrzucam

7) Dźwignia

(przekładnia)

+ +- - +2

-2

0

do dalszej

analizy

8) Ścisk śrubowy

(imadło)

+- + +- +3

-2

1

do dalszej

analizy

9)

10)

+ spełnia potrzebę

- nie spełnia potrzeby

8

Kolejnym krokiem jest eliminacja koncepcji

b) przez porównanie właściwości funkcjonalnych

Kryteria

młotek

standardowy

Pistolet do

wstrzeliwania

gwoździ

Kamień

Kafar

spalinowy

Kafar

elektryczny

Kafar parowy

(urz. do

wbijania pali)

Dźwignia

(przekładnia)

Ścisk śrubowy

(imadło)

Trwałość

Łatwość obsługi

Przenośność

Wielkość

Ciężar

Potrzeba mediów – en.el

para

benzyna

dokładność

wydajność

uniwersalność

Koszt wytworzenia/cena

Łatwość wytworzenia*

SUMA
+
-

Suma

Wniosek

odrzucam do

dalszej

analizy

Punktacja od 1 (słaba) do 10 (najlepsza)

*punkty od 1-5 za grupę nowości i złożoności

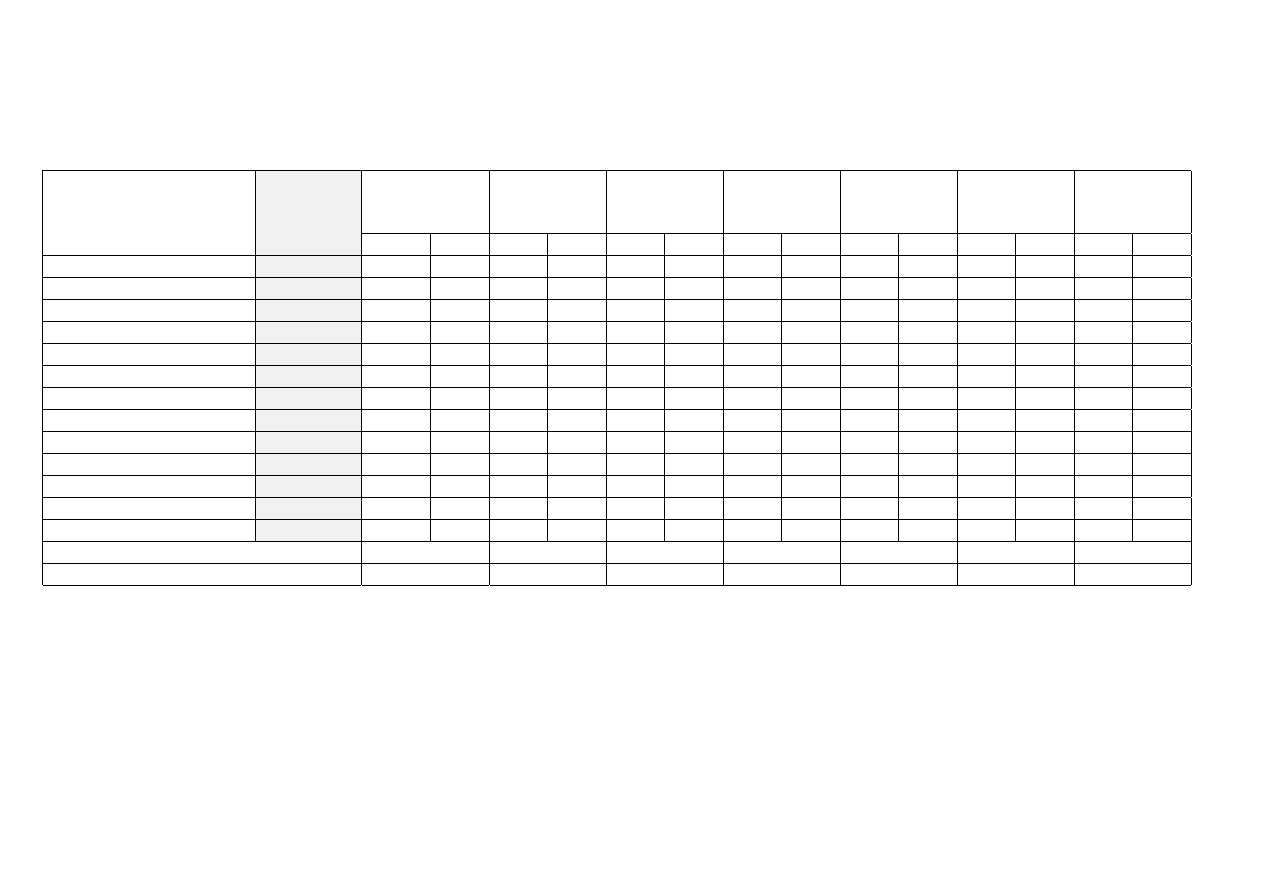
9

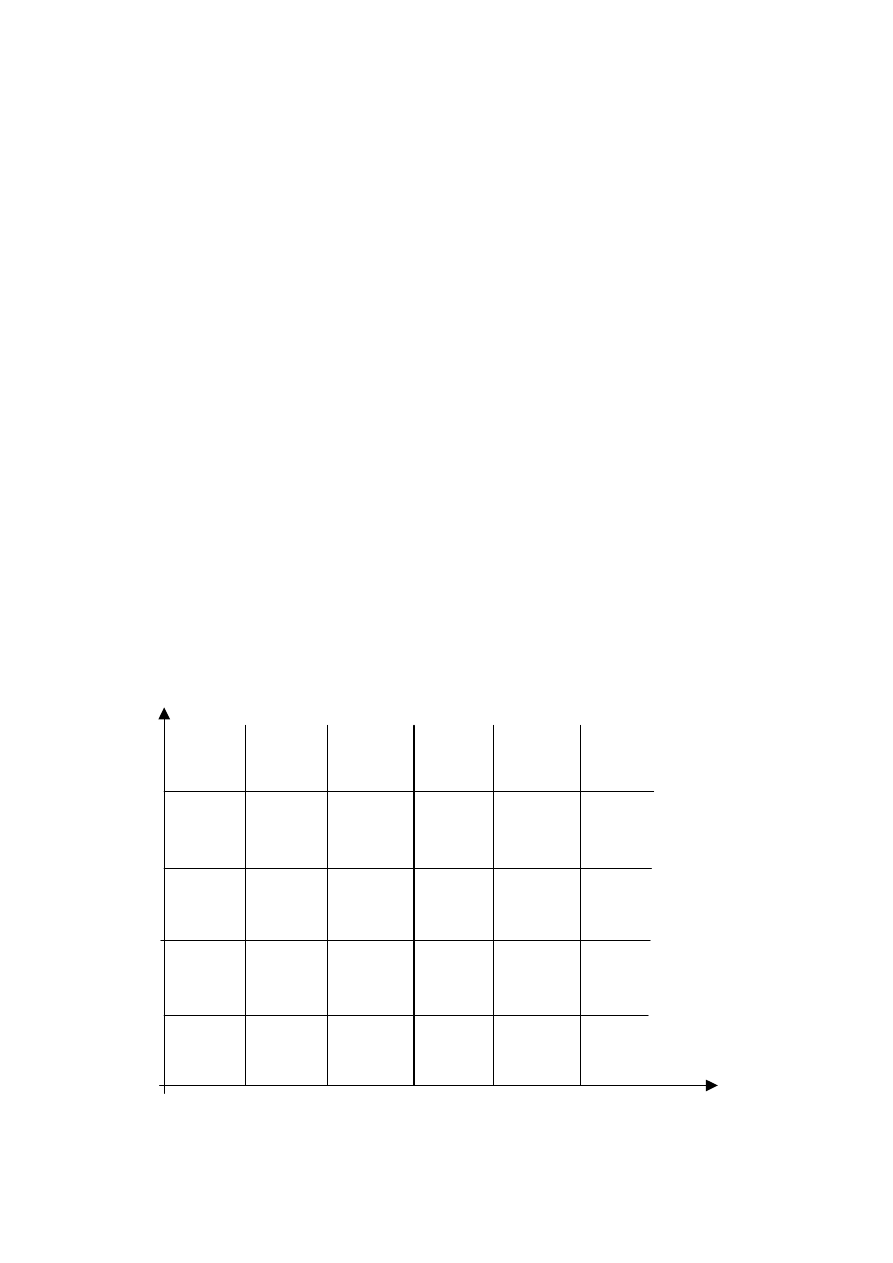
Etap II. Ocena koncepcji

Uwzględniamy tu tylko te pomysły, które pomyślnie przeszły etap I

młotek

standardowy

Pistolet do

wstrzeliwania

gwoździ

Kafar

spalinowy

Kafar

elektryczny

Kafar parowy

(urz. do

wbijania pali)

Dźwignia

(przekładnia)

Ścisk śrubowy

(imadło)

Kryteria

Waga

ocena wynik ocena wynik ocena wynik ocena wynik ocena wynik ocena wynik ocena wynik

Trwałość

Łatwość obsługi

Przenośność

Wielkość

Ciężar

Potrzeba mediów – en.el

para

benzyna

dokładność

wydajność

uniwersalność

Koszt wytworzenia/cena

Łatwość wytworzenia

Suma

Wniosek

Skala ocen
1 – najgorsza

4 – lepsza

2 – gorsza

5 - najlepsza

3 – taka sama

10

Badanie konsumentów

Po opracowaniu, analizie i wyborze koncepcji produktu należy zaprezentować je potencjalnym
klientom, którzy ocenią wybrane koncepcje pod kątem cech oraz korzyści w porównaniu z
wyrobami konkurencyjnymi.

Studenci dzielą się na trzy grupy: panie domu, domowych majsterkowiczów, budowniczych domów
z drewna.
3 osoby przeprowadzają badania ankietowe poszczególnych grup klientów



Studenci – 2 osoby – charakteryzują wielkość potencjalnego rynku docelowego

Prezentacja wniosków z ankiety:

1. wielkość rynku docelowego – procent nabywców określonych przez

potencjalny rynek docelowy

2. wielkość sprzedaży i cykl życia produktu– odpowiedź na pytanie : jak

często będą kupować, jak długo będą kupować

3. cena produktu – akceptowalna przez klienta
4. strategia dystrybucji i promocji – w jaki sposób produkt ma trafić do

klienta i jak klient go zauważy

5. jakie produkty konkurencyjne i substytucyjne dostrzega klient
6. najważniejsze cechy produktu z punktu widzenia konsumenta

Na podstawie określonych przez konsumentów/studentów najważniejszych cech produktu
zbudować mapę produktów do wbijania gwoździ























Nanieść koncepcje produktów oferowanych przez firmę NNN oraz produktów konkurencyjnych.

11

Wybrać koncepcję bez bezpośredniej konkurencji na rynku - Zostają dwie koncepcje!!!!!!

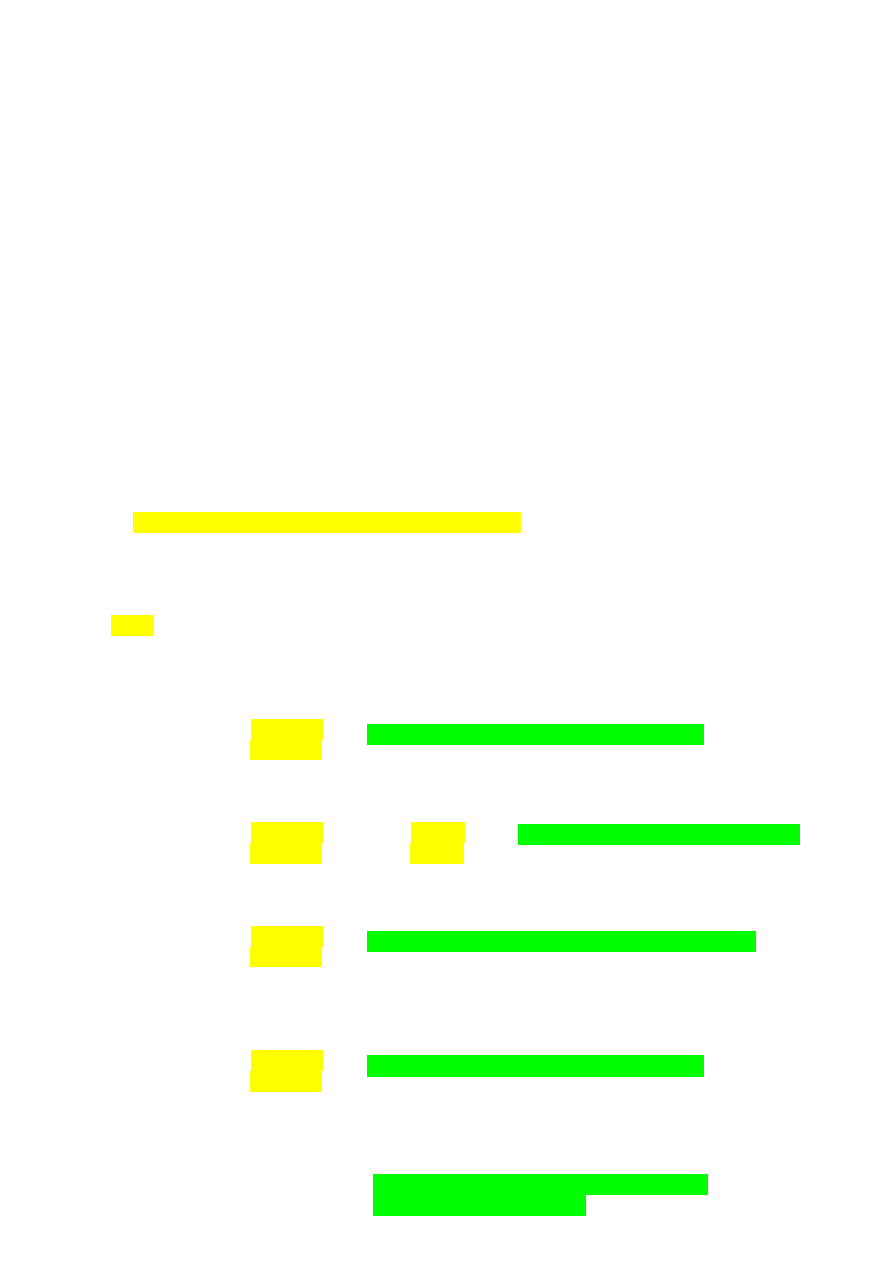
12

4. Analiza ekonomiczna

W tej fazie następuje dalsza selekcja koncepcji na podstawie kryteriów ekonomicznych.
Faza ta koncentruje się na badaniu kosztów wytwarzania nowego produktu oraz na prognozowaniu
jego sprzedaży.
Analiza ta ma charakter wstępny gdyż nie można wyznaczyć wielu czynników określających
wysokość kosztów oraz wielkość sprzedaży. Do tych czynników zaliczamy m.in.: zachowanie
konkurencji, przepisy prawa gospodarczego, przepisy podatkowe i celne.
Wraz ze zmianami zachodzącymi w przedsiębiorstwie i jego otoczeniu oraz w miarę pozyskiwania
nowych informacji analiza ekonomiczna musi być uzupełniana i powtarzana wielokrotnie.

Celem analizy ekonomicznej jest określenie przyszłych przychodów firmy, co pozwala zmniejszyć
ryzyko powstania strat z tytułu wprowadzenia na rynek „nieudanego” wyrobu.
W tym celu konieczna jest prognoza przyszłej sprzedaży produktu i rentowności tej sprzedaży.

Pierwszym krokiem przy prognozowaniu sprzedaży są badania marketingowe, które pozwalają
odpowiedzieć na pytanie – jaki jest popyt na rynku przy uwzględnieniu konkurencji i produktów
substytucyjnych

Zakładamy, że takie informacje posiadamy –

- PREZENTACJA

CYKLU

ŻYCIA PRODUKTU 1 i 2

Zadanie
Firma NNN zastanawia się nad produkcja jednego z dwóch urządzeń do wbijania gwoździ
A i B.

Jak wskazują badania rynkowe prawdopodobieństwo odniesienia sukcesu rynkowego wynosi (skala
1-10):

- dla produktu A ................
- dla produktu B ................

Średnia roczna wielkośćsprzedaży wynosi:

- dla produktu A ................ w okresie ............ lat
- dla produktu B ................ w okresie ............ lat

Prawdopodobieństwo pomyślnego wdrożenia produktu wynosi (skala 1-10):

- dla produktu A ................
- dla produktu B ................


Koszt wytworzenia

- dla produktu A ................
- dla produktu B ................


Cena sprzedaży wynosi

Na podstawie wielkości rynku docelowego !!!!

Na podstawie cyklu życia produktu !!!!

Na podstawie wielkości rynku docelowego !!!!

Marża zakładana ok. 30% w zależności od cen
określonych przez klienta !!!!

Na podstawie punktacji z oceny możliwości firmy !!!!

13

- dla produktu A ................
- dla produktu B ................

Koszt projektowania

- dla produktu A ................
- dla produktu B ................

Koszt nowego wyposażenia

- dla produktu A ................
- dla produktu B ................

Koszt obsługi maszyn

- dla produktu A ................ osoby z wynagrodzeniem ................
- dla produktu B ................ osoby z wynagrodzeniem ................



Używając Indeksu Wartości Projektu (PVI) podjąć decyzję który z produktów powinien być dalej
rozwijany.

TPC

L

P

AV

CCS

CTS

PVI

*

*

*

*

=

gdzie:

CTS - prawdopodobieństwo odniesienia sukcesu rynkowego [pkt]
CCS - prawdopodobieństwo pomyślnego wdrożenia produktu [pkt]
AV - roczna sprzedaż w fazie dojrzałości [szt.]
P - zysk [zł] = cena - koszt
L - długość cyklu życia produktu [lata]
TPC - całkowity koszt przedsięwzięcia [zł]

- Koszt

obsługi maszyn (długość cyklu życia produktu * 2 000h/rok*

*wysokość wynagrodzenia za rbh)

- Koszt nowego wyposażenia
- Koszt

projektowania

- Koszt

wytworzenia

Im wyższy Indeks tym lepiej !!!

W zależności od stopnia złożoności od. 100 000zł – 1 000 000 zł

W zależności od stopnia złożoności od. 250 000zł – 800 000 zł

W zależności od stopnia złożoności od. 4-6 osób, 10-20 zł/rbh

14

Kolejnym elementem analizy ekonomicznej jest

analiza progu rentowności.

Podstawowym warunkiem przeprowadzenia analizy progu rentowności w standardowej postaci

jest podział kosztów całkowitych na dwie części:

KOSZTY STAŁE I KOSZTY ZMIENNE

Koszty stałe – te składniki kosztów produkcji, których poziom nie zależy od wielkości

produkcji

Koszty zmienne – zależne od wielkości produkcji; są to przede wszystkim podstawowe pozycje

kosztów bezpośrednich, a więc koszty zużycia materiałów bezpośrednich, koszty robocizny
bezpośredniej oraz koszty zużycia paliwa technologicznego

Przyjmuje się przy tym, ze koszty stałe mają charakter bezwzględnie stały, a koszty zmienne są

kosztami proporcjonalnie zmiennymi w stosunku do wajhań wielkosci produkcji. Konsekwencja
tych założeń jest liniowy przebieg kosztów całkowitych w zależności od zmian wielkosci produkcji.

Zakłada się również, że przychód ze sprzedaży zmienia się proporcjonalnie do zmian wielkości

produkcji (sprzedaży).

Przy tych założeniach suma kosztów całkowitych może być zapisana następująco:

K = K

s

+ K

z

(1)

gdzie:

K – koszty całkowite
K

s

– koszty stałe

Jednocześnie koszty zmienne K

z

mogą być zapisane jako iloczyn:

K

z

= k

z

* Q

(2)

gdzie:

K

z

- koszty zmienne

k

z

- jednostkowe koszty zmienne

Q – wielkość produkcji

Jednocześnie założyliśmy, że przychód całkowity uzyskany ze sprzedaży wyrobu jest
proporcjonalny do wielkości sprzedaży, co możemy zapisać jako iloczyn:

S = p * Q

(3)

gdzie:

S – przychód całkowity
Q – wielkość produkcji
p – cena sprzedaży wyrobu

Próg rentowności produkcji jest taką wielkością produkcji, przy której przychód ze sprzedaży
równa się kosztom całkowitym, czyli:

S = K

(4)

Uwzględniając równania 1-3 równość ta przyjmuje następującą postać: P * Q = K

s

+ k

z

*Q (5)

15

Przekształcając to równanie otrzymujemy:

K

s

= Q (p-k

z

)

(6)

Skąd szukana wielkość produkcji (czyli próg rentowności) w ujęciu ilościowym wynosi:

z

s

o

k

p

K

Q

−

=

(7)

Interpretacja tego wzoru:

Produkcja wyrobu na poziomie Q

o

jednostek zapewnia pokrycie kosztów poniesionych na jego

wytworzenie przychodami uzyskanymi ze sprzedaży.

Przy produkcji z przedziału 0 < Q< Q

o

przedsiębiorstwo ponosi stratę na sprzedaży danego wyrobu

Przy produkcji Q> Q

o

produkcja wyrobu przynosi zysk.

Próg rentowności w ujęciu wartościowym określamy jako:

S

o

= p * Q

o

=

p

k

K

z

s

−

1

Mianownik ułamka (7) oznaczymy jako z = p – k

z

marżę pokrycia przypadającą na jednostkę

wyrobu (inaczej zyskowność brutto)

Oznacza to , że różnica pomiędzy ceną sprzedaży wyrobu i jednostkowymi kosztami zmiennymi nie
może być niższa niż wartość z złotych

Stopę marzy pokrycia (czyli ile procent ceny wyrobu wynosi marża pokrycia) obliczamy
następująco:

p

z

p

k

m

z

=

−

=

1

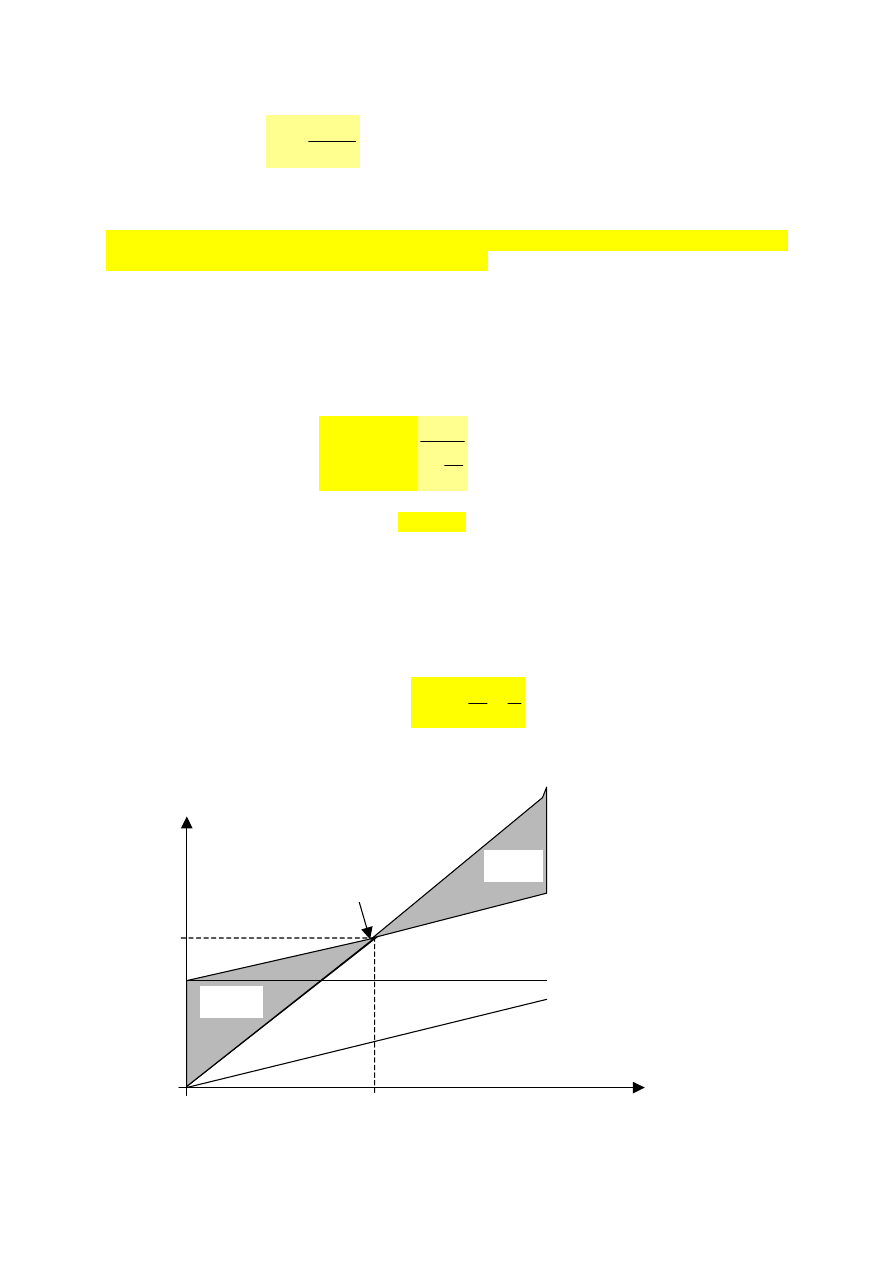
Graficzną interpretację wyznaczania progu rentowności można przedstawić następująco:


















Q

o

– próg rentowności ilościowy

S

o

– próg rentowności wartościowy

K
S

Q

S

K

Q

o

S

o

strata

zysk

K

s

K

z

Próg

rentowności

16

Analiza progu rentowności, oprócz ustalenia krytycznej wielkości produkcji i sprzedaży, pozwala
także na ocenę ekonomicznych konsekwencji decyzji dotyczących wielkości produkcji i sprzedaży,
poziomu cen, wysokości kosztów oraz kwoty zysku.
Spróbujemy teraz określić próg rentowności dla naszego wyrobu

ZADANIE
Załóżmy, że dla naszego produktu mamy następujące parametry:

Koszty stałe

K

s

= 25 000 zł

Jednostkowy koszt zmienny

k

z

= 30 zł

Cena sprzedaży

p = 50 zł

Obliczyć próg rentowności ilościowy i wartościowy.
Ile wynosi minimalna marża pokrycia przypadająca na jednostkę wyrobu?
Rozwiązanie przedstawić również w formie graficznej

Wyznaczamy ilościowy próg rentowności

sztuk

Q

o

1250

30

50

25000

=

−

=

Wyznaczamy wartościowy próg rentowności

S

o

= 50 * 1250 = 62 500 zł

lub

zl

S

o

62500

4

,

0

25000

6

,

0

1

25000

50

30

1

25000

=

=

−

=

−

=

Marża

pokrycia:

Stopa

marży pokrycia:

z = 50-30 = 20 zł

6

,

0

50

30

=

=

m

czyli marża pokrycia wynosi 60% ceny wyrobu

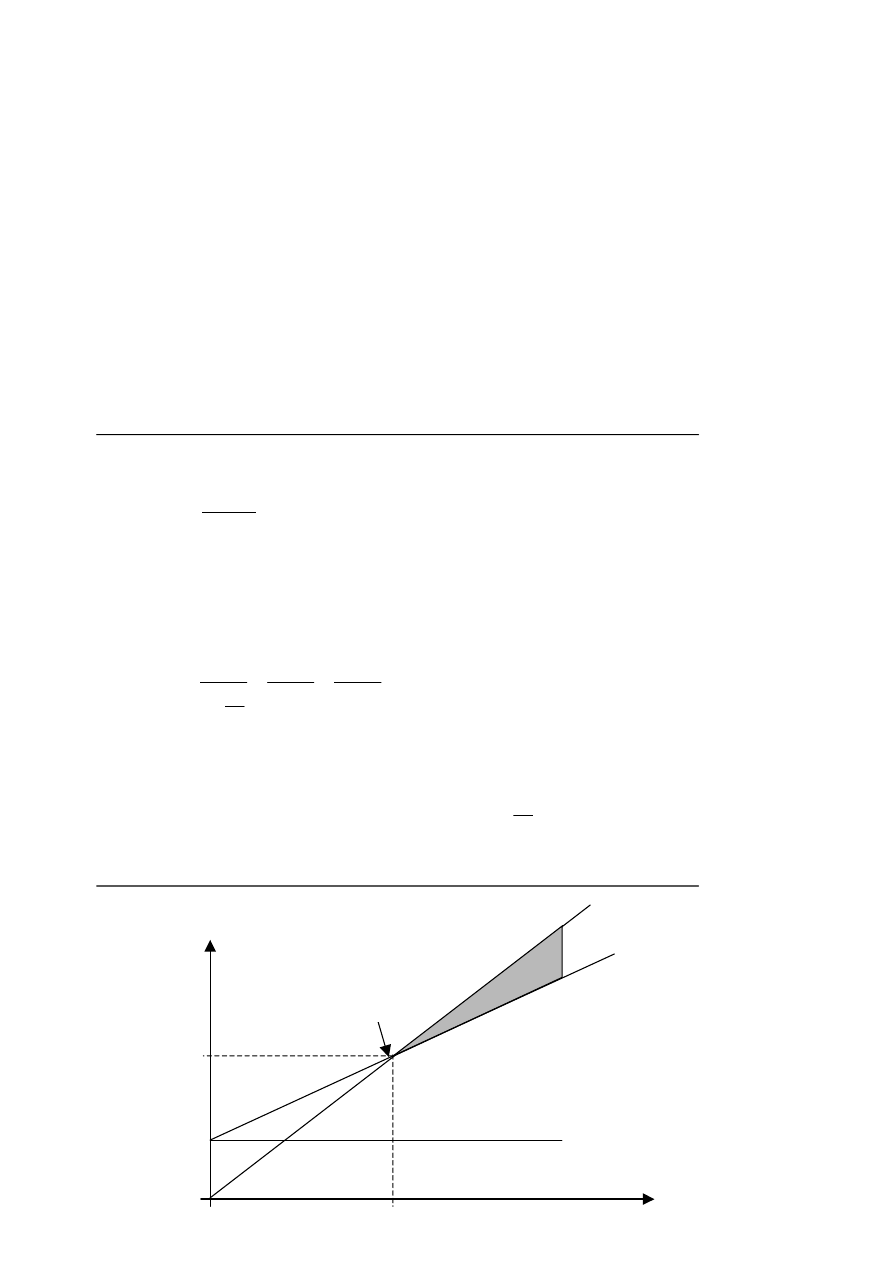
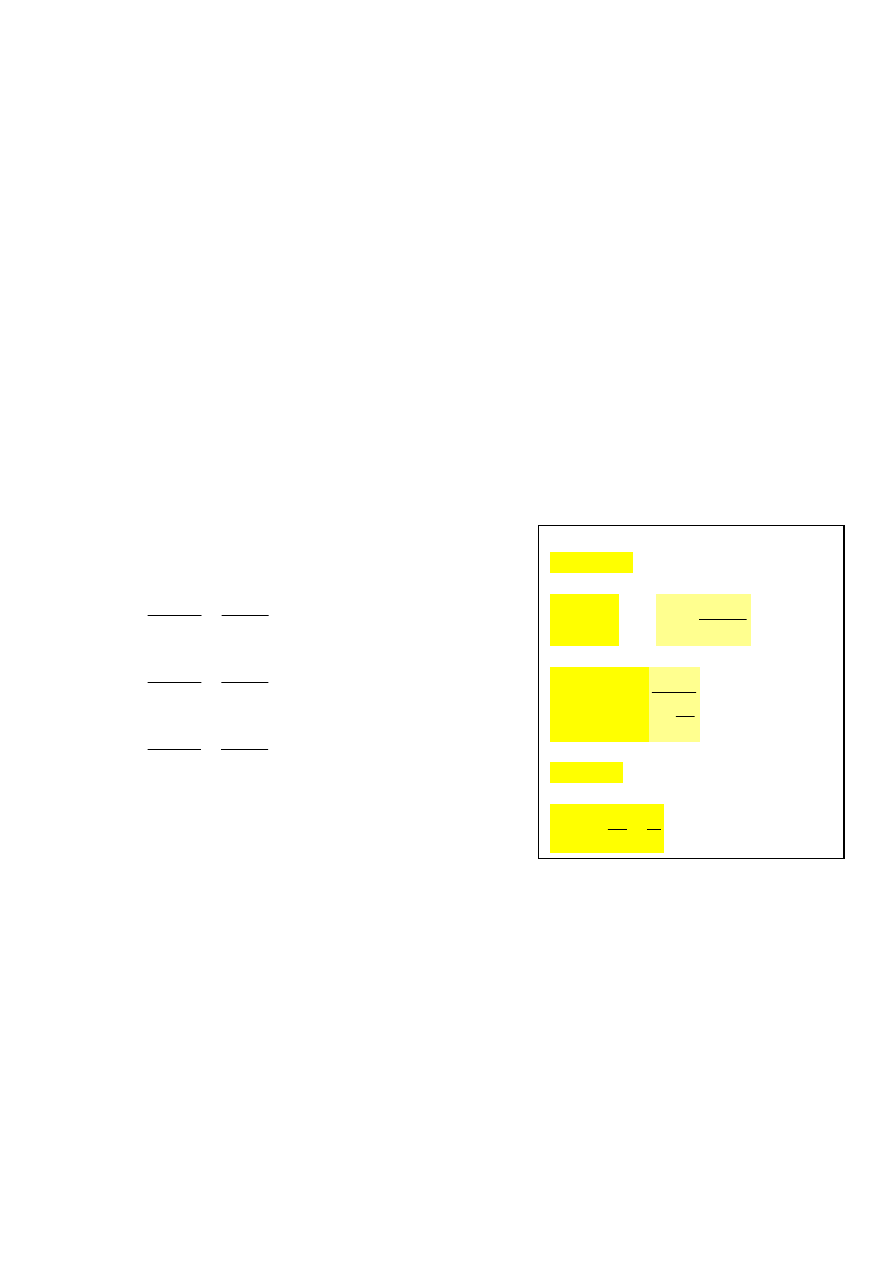
Interpretacja graficzna

K
S

Q

S

K

1 250

Q

o

62 500

strata

zysk

K

s

Próg

rentowności

500 1

500

25 000

17

Odpowiedź:
Produkcja wyrobu w ilości Q

o

= 1 250 szt. Zapewni zrównoważenie kosztów poniesionych na jego

wytworzenie przychodami uzyskanymi ze sprzedaży. Odpowiada temu wartość krytyczna
sprzedaży S

o

= 62 500 zł. Przedsięwzięcie przyniesie zysk przy produkcji wyrobu powyżej 1250

szt. Zyskowność brutto produkowanego wyrobu wynosi 20 zł, czyli 60% ceny wyrobu.


Na podstawie analizy rynku, możliwości produkcyjnych firmy i obliczonego progu
rentowności dla wyrobu sprawdzamy czy opłacalna jest jego produkcja.

Jeżeli zdolność produkcyjna firmy nie pozwala na wyprodukowanie zakładanej wielkości
produkcji lub rynek jest zdolny wchłonąć tę ilość produktów po niższej cenie wówczas produkt
przyniesie stratę. W takiej sytuacji należy rozważyć następujące możliwości:

A. Zmiana ceny jednostkowej p
B. Zmniejszenie jednostkowych kosztów zmiennych k

z

C. Zmniejszenie kosztów stałych Ks wskutek np. redukcji zatrudnienia administracji, zmiany

technologii, sprzedaży majątku nieprodukcyjnego.

A. Zmiana ceny wyrobu, a próg rentowności

Załóżmy, że przedsiębiorstwo zamierza zmienić cenę wyrobu z poziomu p do p’(wyższa cena) lub
p” (niższa cena).
Ilościowy i wartościowy próg rentowności wyniesie obecnie:

z

s

o

k

p

K

Q

−

=

'

'

o

o

Q

Q

>

'

z

s

o

k

p

K

Q

−

=

"

"

o

o

Q

Q

<

"

Dla nowej
niższej ceny p’

Dla nowej
wyższej ceny p”

'

'

1

p

k

K

S

z

s

o

−

=

o

o

S

S

>

'

"

"

1

p

k

K

S

z

s

o

−

=

o

o

S

S

<

"

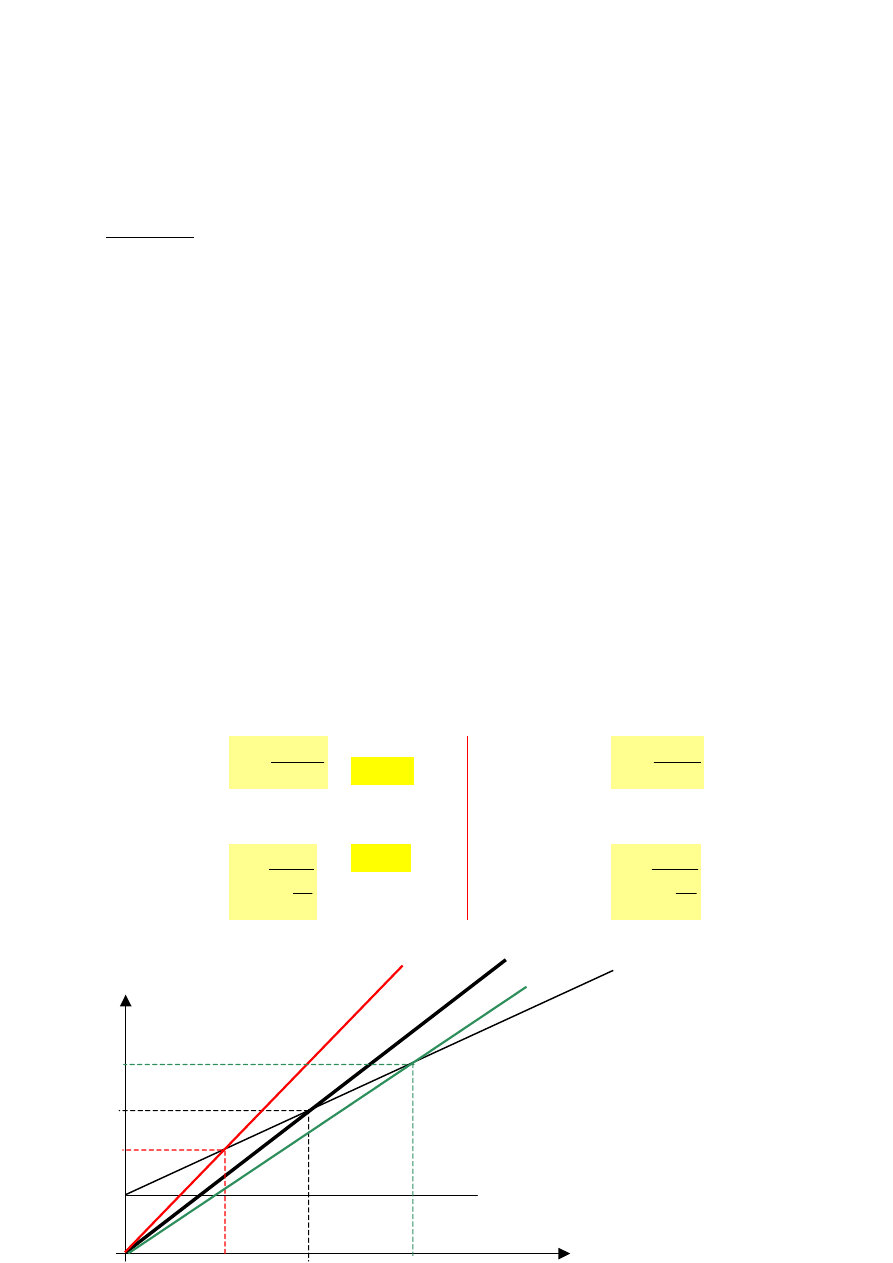
Graficzną ilustrację wpływu obniżki i podwyżki ceny na wysokość progu rentowności przedstawia
poniższa ilustracja:

K
S

Q

S

K

S

o

K

s

25 000

S”

S

o

S

o

”

S

o

’

S’

Należy jednak
stwierdzić czy zmiana
ceny nie poziągnie za
sobą zbyt dużego
spadku planowanej
liczby odbiorców. –
badania
marketingowe !!

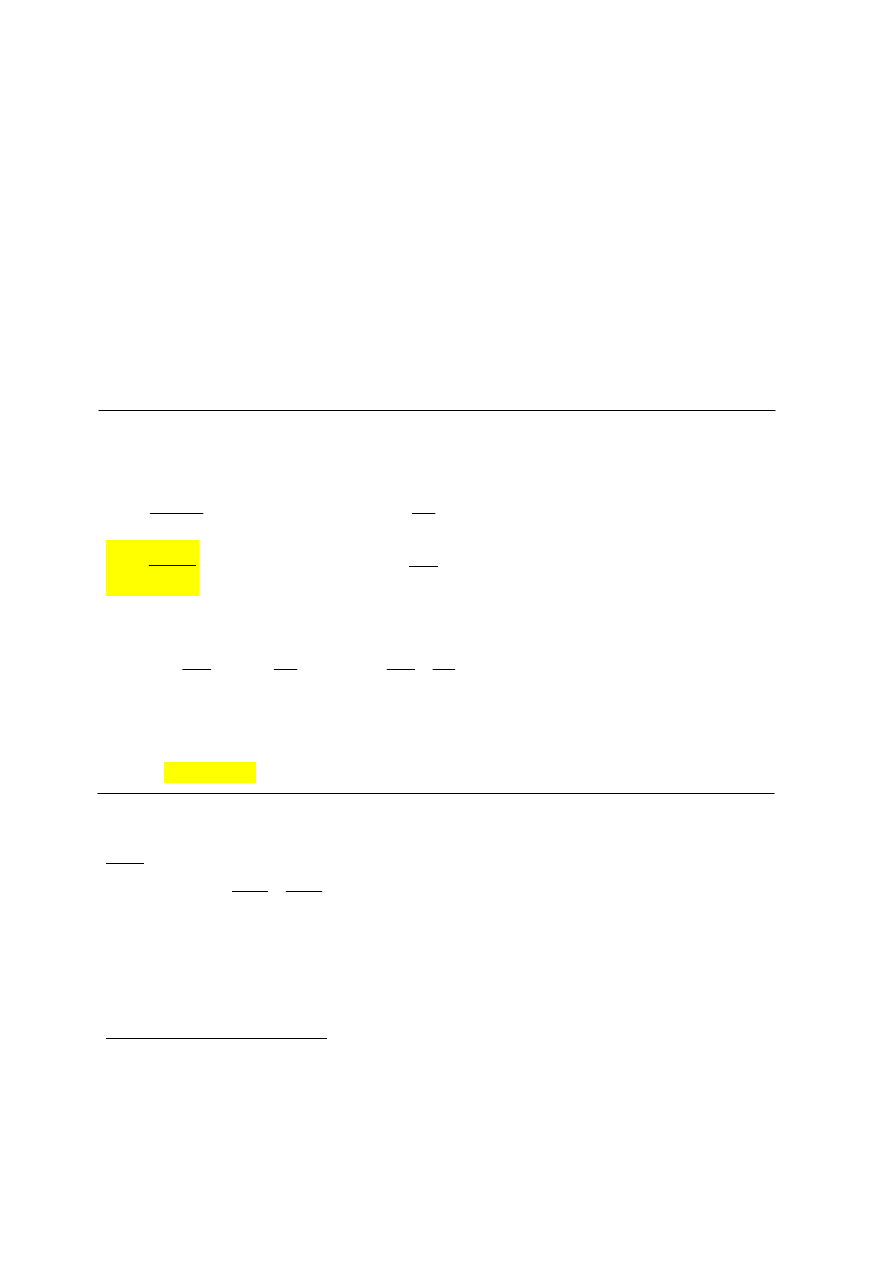
18

ZADANIE
O ile należy zwiększyć cenę wyrobu z poprzedniego zadania jeśli rynek jest w stanie wchłonąć
tylko 1000 szt wyrobu? Jak zmieni się graniczna wartość sprzedaży?

Dane
Koszty stałe

K

s

= 25 000 zł

Jednostkowy

koszt

zmienny

k

z

= 30 zł

Cena sprzedaży

p

1

= 50 zł

Graniczna wielkość sprzedaży przy cenie p

Q

o

= 1250 szt

Zakładana wielkość sprzedaży Q

o

”=1000 szt

Graniczna wartość sprzedaży przy cenie p

S

o

= 62 500 szt

Działania na wzorach
Z wzorów na Q

o i

Q

o

” wyznaczamy cenę p

1

i p”

stąd p”

z

s

o

k

p

K

Q

−

=

1

stąd

z

o

s

k

Q

K

p

+

=

1

z

s

o

k

p

K

Q

−

=

"

"

stąd

z

o

s

k

Q

K

p

+

=

"

"

wyznaczamy różnicę w cenie (p”- p)

p” – p

1

=















+

z

o

s

k

Q

K

"

-









+

z

o

s

k

Q

K

=









−

o

o

s

Q

Q

K

1

"

1

Graniczną wartość sprzedaży wyznaczymy ze wzoru

S

o

= p” * Q

o

gdzie : Q

o

– zakładana wielkość sprzedaży

Obliczenia

Ceny:

p” – p

1

=













−

1250

1

1000

1

25000

=25000 (0,001-0,00125) = 25000 *0,00025 =6,25 zł

stąd

p” = 50 + 6,25 = 56,25 zł


granicznej wartości sprzedaży:

S

o

” = 1000 * 56,25 = 56 250 zł

S

o

- S

o

” = 62 500 – 56 250 = 6 250 zł

Odpowiedź:

19

Dla planowanego poziomu sprzedaży w wysokości 1000 szt wyrobu, należy zwiększyć cenę min o
6, 25 zł. Graniczna wartość sprzedaży zmaleje wówczas o 6 250 zł do poziomu 56 250 zł.


ZADANIE
Firma rozważa następujące trzy poziomy cen dla wyrobu:
p

1

= 45 zł

p

2

= 50 zł

p

3

= 55 zł

Koszty stałe wynoszą 25 000 zl miesięcznie. Jednostkowy koszt zmienny wynosi 30zł.
Powszechnie stosowane marże wynoszą 50% ceny detalicznej tzn. p

d

= 2p

Podjąć decyzję co do wyboru ceny dla nowo wprowadzanego produktu, przy założeniu, że
konkurencja oferuje podobny wyrób w cenie 125 zł, a my chcemy sprzedawać nasz wyrób o co
najmniej 10 % taniej. Przy firma nie jest w stanie wyprodukować więcej niż 1500 szt wyrobu /
miesiąc.


p

d1

= 90 zł

p

d2

= 100 zł

p

d3

= 110 zł

+ 10%

p

d1

= 99 zł

p

d2

= 110 zł

p

d3

= 121zł

Obliczamy próg rentowności

Ilościowy

Q

1

=

szt

67

,

1666

15

25000

30

45

25000

=

=

−

-

odrzucamy

Q

2

=

szt

1250

20

25000

30

50

25000

=

=

−

Q

3

=

szt

1000

25

25000

30

55

25000

=

=

−

Wartościowy

S

2

= 50 * 1250 = 62 500 zł

S

3

= 55 * 1000 = 55 000 zł

Jak widać przy cenie p

3

szybciej osiągniemy zysk, a cena i tak będzie niższa niż cena konkurencji.

Przy niższym poziomie produkcji istnieje większe prawdopodobieństwo sprzedaży produktu.
Jeśli badania marketingowe wykażą, że rynek jest w stanie wchłonąć większą ilość produktu można
rozważyć obniżenie ceny.

Możemy takie wnioski przyjąć ponieważ nie mamy danych dot. wielkości potencjalnego rynku. W
przeciwnym wypadku może się okazać, że większy zysk wygenerujemy przy niższej cenie, lecz
wyższej podaży.

Odpowiedź:
Należy więc wybrać cenę

nr

3.

Wzory
K

z

= k

z

* Q

S = p * Q

z

s

o

k

p

K

Q

−

=

S

o

= p * Q

o

=

p

k

K

z

s

−

1

z = p – k

z

p

z

p

k

m

z

=

−

=

1

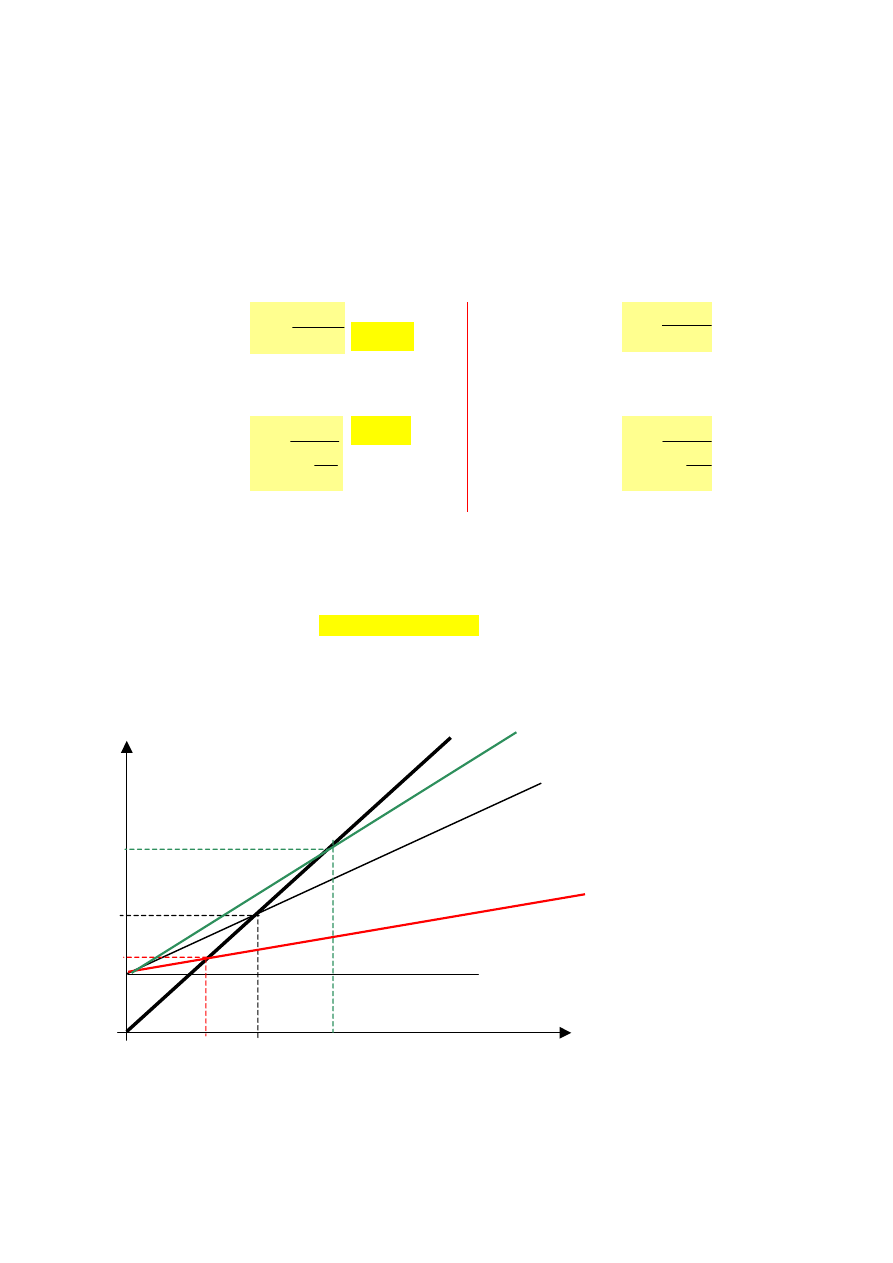
20

B. Zmiana poziomu kosztów a próg rentowności

Załóżmy, że następuje zmiana jednostkowego kosztu zmiennego z poziomu k

z

do k

z

’ oraz zmiana

wysokości kosztów stałych z poziomu K

s

do K

s

’.

Ilościowy i wartościowy próg rentowności wyniesie obecnie:

z

s

o

k

p

K

Q

'

'

'

−

=

o

o

Q

Q

>

'

z

s

o

k

p

K

Q

"

"

"

−

=

o

o

Q

Q

<

"

Dla wzrostu
poziomu K

s

lub k

z

Dla obniżenia
poziomu K

s

lub k

z

p

k

K

S

z

s

o

'

1

'

'

−

=

o

o

S

S

>

'

p

k

K

S

z

s

o

"

1

"

"

−

=

o

o

S

S

<

"

Przy wytworzeniu zaplanowanej wielkości produkcji Q

1

, której odpowiada sprzedaż wyrobu o

wartości S

1

zostanie zrealizowany zysk w kwocie:

Z

1

= (p – k’

z

) Q

1

– K’

s

Graficzną ilustrację wpływu obniżki i podwyżki kosztów zmiennych na wysokość progu
rentowności przedstawia poniższa ilustracja:

Q

Q

o

Q

o

”

Q

o

’

K
S

S

K

S

o

K

s

K”

S

o

”

S

o

’

K’

21

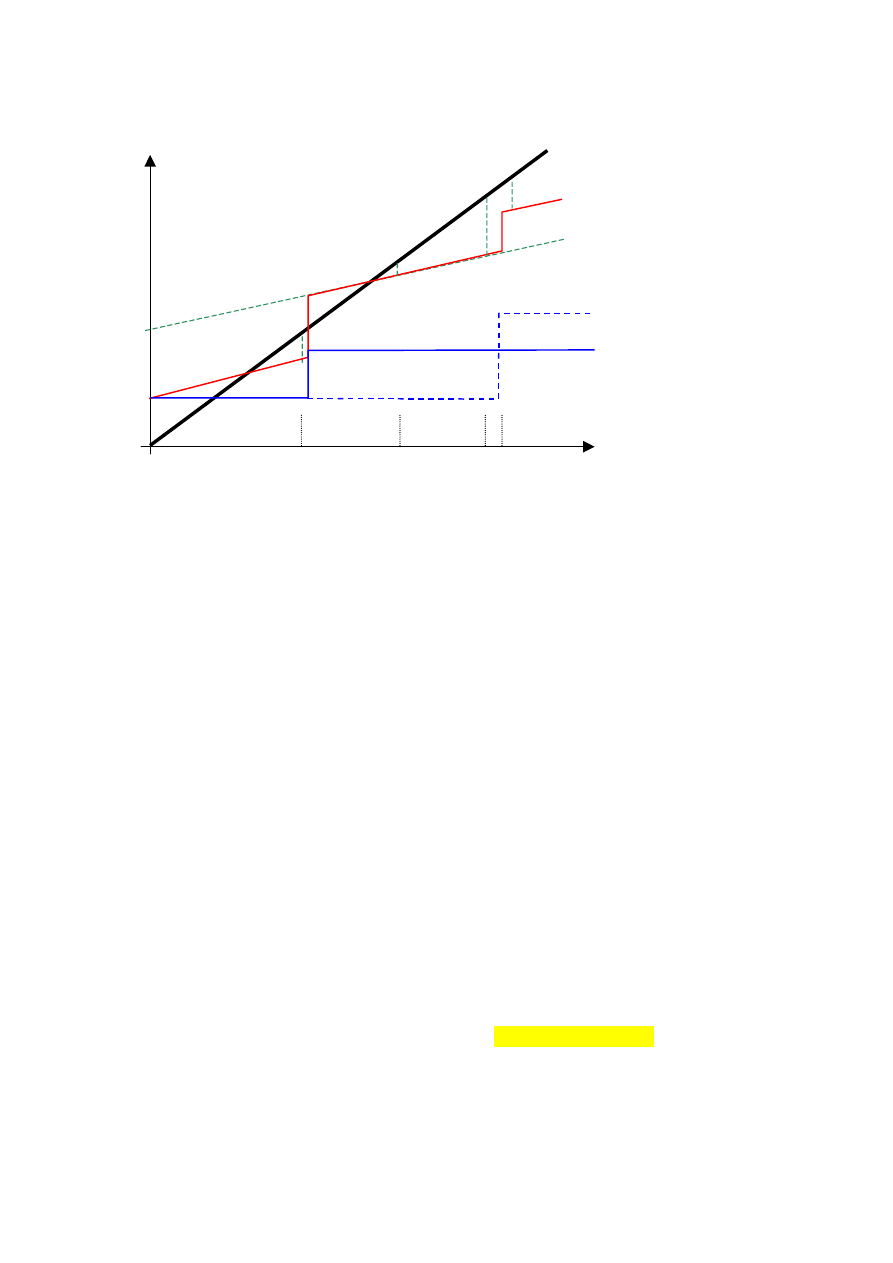
Graficzną ilustrację wpływu obniżki i podwyżki kosztów stałych na wysokość progu rentowności
oraz kwotę realizowanego zysku przedstawia poniższa ilustracja:



















Aktualny poziom produkcji wynosi Q

1

jednostek. Osiągany zysk wynosi Z

1

.

Dodatkowe wyposażenie przedsiębiorstwa (czyli wzrost K

s

do wartości K’

s

) wymaga, aby

produkcja kształtowała się na poziomie nie niższym niż Q

2

jednostek.

Z rysunku wynika jednak, że zysk Z

2

realizowany przy produkcji Q

2

jednostek jest niższy od zysku

Z

1

osiąganego przy wielkości produkcji Q

1

.

Należałoby zatem znaleźć zbyt dla produkcji Q

3

gdyż w tym przypadku zysk Z

3

będzie wyższy od

realizowanego przed zakupem dodatkowego wyposażenia.
Zastanówmy się nad sytuacja w której dodatkowe wyposażenie przedsiębiorstwa wymagałoby
wzrostu K

s

do poziomu K”

s

.

Jeżeli firma spodziewa się, że będą trudności ze zbytem produkcji na poziomie Q

4

to wówczas

należy podjąć decyzję o dodatkowym wyposażeniu przedsiębiorstwa umożliwiającym osiągnięcie
produkcji tylko do poziomu Q

3

.

Zadanie
Określić wielkość zysku jaki zostanie zrealizowany za sprawą nowej inwestycji przy której nastąpi
redukcja jednostkowego kosztu zmiennego z wartości 30 zł do 25 zł i jednoczesny wzrost kosztów
stałych z poziomu 25 000 zł do 40 000 zł. Cena sprzedaży zostaje utrzymana na pierwotnym
poziomie 50 zł. Dotychczasowa produkcja wyrobu to 1500 szt. Dział marketingu określa zbyt na
2000 szt. Czy inwestycja będzie opłacalna ?

Koszty stałe

K

s

= 25 000 zł

K

s

= 40 000 zł

Jednostkowy koszt zmienny

k

z

= 30 zł

k

z

= 25 zł

Cena sprzedaży

p = 50 zł

Wielkość

produkcji

Q

o

= 1500 szt

Q

o

’ = 2000 szt

Z

1

= (p – k’

z

) Q

1

– K’

s

Z = (50-30) 1500 – 25 000 = 30 000 – 25 000 = 5 000 [zł]
Z

1

= (50-25) 2000 – 40 000 = 50 000 – 40 000 = 10 000 [zł]

Odpowiedź:
Inwestycja będzie opłacalna. Dzięki nowej inwestycji zwiększymy zysk do poziomu 10 000 zł.

K
S

S

F

A

K’

s

B

C

E

Q

1

Q

2

Q

3

Q

4

Q

Z

1

Z

2

Z

3

Z

4

K”

s

22

PRÓG RENTOWNOŚCI PRODUKCJI WIELOASORTYMENTOWEJ (99s, [3])


Zadanie 6
Firma produkuje meble: krzesła i biurka. Produkcja może być jednoasortymentowa (albo krzesła
albo biurka) lub dwuasortymentowa (równocześnie krzesła i biurka). Wilekość produkcji jest
określona przez zdolność produkcyjną firmy q

max

= 600 szt.

Wiadomo również, że :
- krzeseł można wyprodukować 4 razy więcej niż biurek
- jednostkowy koszt produkcji biurka k

B

= 730 zł/szt.

- jednostkowy koszt produkcji krzesła k

K

= 95 zł

- koszt stałe produkcji wynoszą K

S

= 76 500 zł

- cena biurka wynosi c

B

= 900 zł/szt.

- cena krzesła wynosi c

K

= 145 zł/szt.

Na podstawie powyższych danych przeprowadzić analizę opłacalności produkcji mebli.


Podstawowe wzory i zależności:

Koszt całkowity produkcji:

K = K

S

+ k

B

q

B

+

k

K

q

K

K = 76 500 + 730q

B

+

95q

K

gdzie q - liczba wyprodukowanych krzeseł/biurek [szt.]

Zdolność produkcyjna:

q

B

+

q

K

/4 = q

max

= 600 szt

Przychód:

S = c

B

q

B

+

c

K

q

K

S = 900 q

B

+

145 q

K

Zysk:

Z = S-K = 900 q

B

+

145 q

K

-(76 500 + 730q

B

+

95q

K

) = 170 q

B

+

50q

K

-76 500

Próg rentowności:

Jeśli Z= 0 to
170 q

B

+

50q

K

=76 500

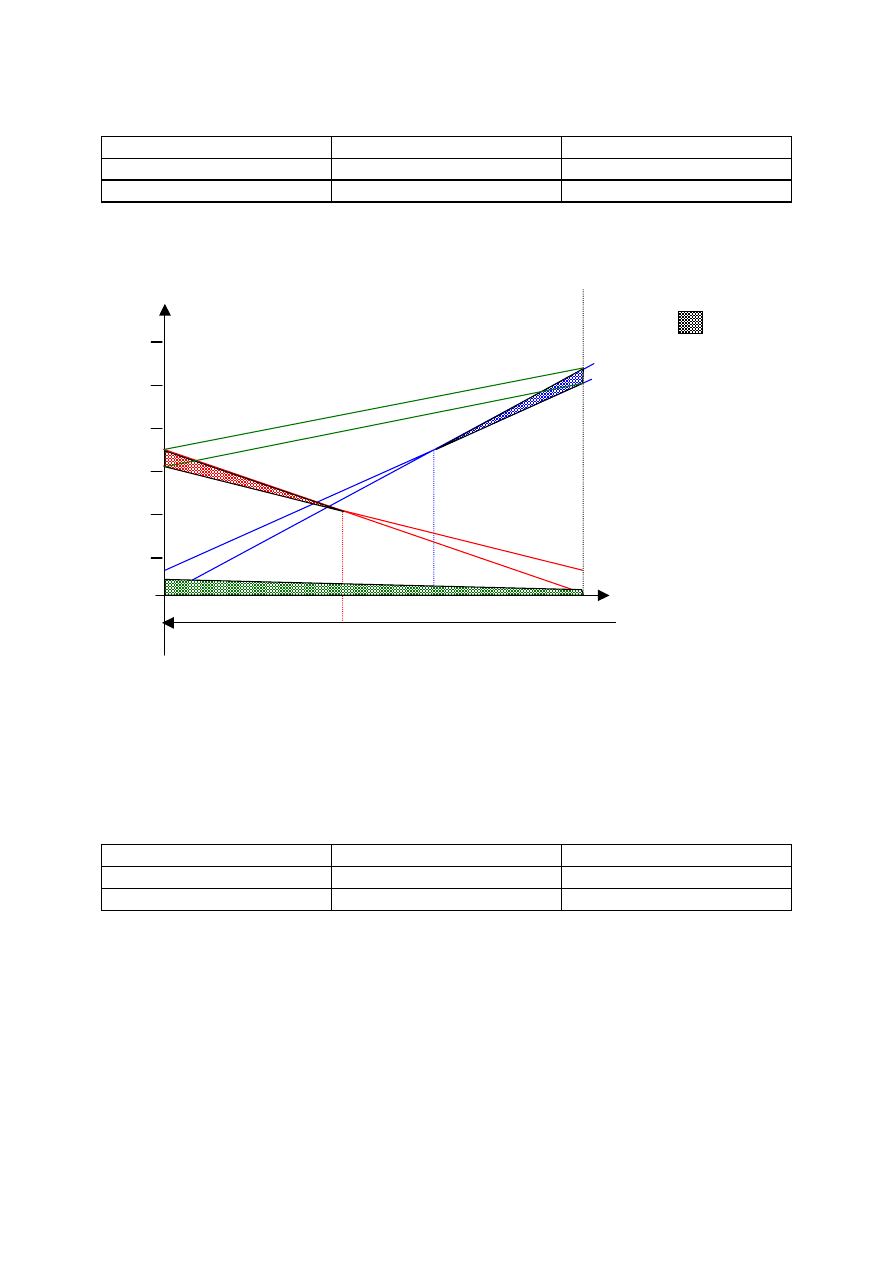
SYTUACJA 1

Firma produkuje tylko biurka w ilości w ilości 0< q

B

< 600 (q

K

= 0)

liczba 600 wynika z max zdolności produkcyjnych

23

W celu wyznaczenia prostych obrazujących koszty produkcji biurek K

B

oraz przychód ze sprzedaży

biurek S

B

przyjęto graniczne ilości biurek (q

B

= 0, q

B

= 600)

q

B

= 0

q

B

= 600

K

B

76 500

514 500 = 76 500 +600*730

S

B

0

540 000 = 900*600

próg rentowności q

oB

= 450 szt = 76 500/170

Zysk przedstawia zakreskowane pole na rysunku

SYTUACJA 2

Firma produkuje tylko krzesła w ilości w ilości 0< q

B

< 2400 (q

K

= 0)

liczba 2400 wynika z max zdolności produkcyjnych (4 x więcej niż biurek = 4*600 = 2400)

W celu wyznaczenia prostych obrazujących koszty produkcji krzeseł K

K

oraz przychód ze

sprzedaży krzeseł S

K

przyjęto graniczne ilości krzeseł (q

K

= 0, q

K

= 2400)

q

K

= 0

q

K

= 2400

K

K

76 500

304 500 = 76 500 +2400*95

S

K

0

348 000 = 145*2400

próg rentowności q

oK

= 1530 szt = 76 500/50

Zysk przedstawia zakreskowane pole na rysunku

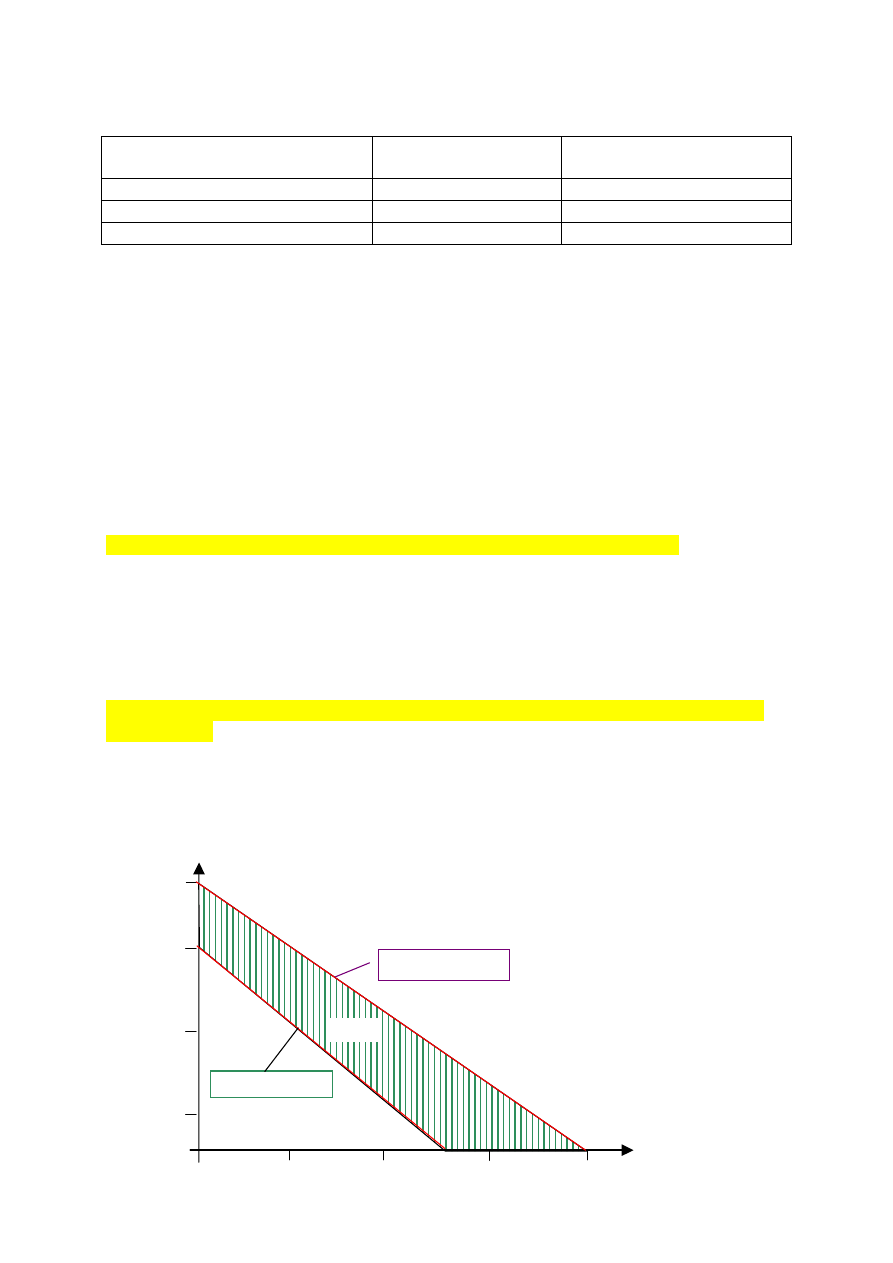
SYTUACJA 3

Firma produkuje krzesła i biurka wykorzystując maksymalnie swoje zdolności produkcyjne

q

K

= 2400 - 4 q

B

q

B

= 600- q

K

/4

W celu wyznaczenia prostych obrazujących koszty produkcji oraz przychód ze sprzedaży przyjęto
graniczne ilości mebli

K, S [zł]

S

B

100.000

q

oB.

= 450

2400

Q

biurka

[zł]

zysk

K

B

Q

krzesła

[zł]

200.000

300.000

400.000

500.000

600

600.000

S

K

K

K

q

ok.=

1530

P

K

24

q

Kmax

= 600 dla q

B min

= 0

q

Bmax

= 2400 dla q

k min

= 0

q

Kmax

= 600

q

B min

= 0

q

Bmax

= 2400

q

k min

= 0

K = K

S

+ k

B

q

B

+

k

K

q

K

304 500

514 500

S = c

B

q

B

+

c

K

q

K

348 000

540 000

Z = S-K = 170 q

B

+

50q

K

-76 500

43 500

25 500

Wniosek: każde zlecenie w rozważanej sytuacji przynosi zysk, przy czym produkcja krzeseł jest
zdecydowanie bardziej opłacalna.
Zysk przedstawia zakreskowane pole na dole rysunku

SYTUACJA 4

Firma produkuje krzesła i biurka nie wykorzystując swych zdolności produkcyjnych

q

B

+ q

K

/4 < 600

W celu wyznaczenia obszaru opłacalnej produkcji tj. takiej która przyniesie zysk wyznaczymy
proste:

minimalnej wielkości produkcji krzeseł i biurek – opartej na progu rentowności

170 q

B

+

50q

K

=76 500

q

B

=76 500/170 – 50/170q

K

q

B

=450 – 5/17q

K

maksymalnej wielkości produkcji krzeseł i biurek – opartej na maksymalnych zdolnościach
produkcyjnych

q

B

+

q

K

/4 = 600 szt

q

B

=

600 - q

K

/4

q

B

150

q

K

Z > 0

300

450

2400

600

q

B

=450 –

1800

1200

600

1530

q

B

=

600 - q

K

/4

Z < 0

q > q

max

25

Wniosek: jeżeli ilości poszczególnych asortymentów wyznaczają punkt który leży w obszarze
pomiędzy ww. prostymi, to ich produkcja przynosi zysk.

26

UOGÓLNIENIE ANALIZY PROGU RENTOWNOŚCI

Zaproponuję teraz pewne uogólnienie przedstawionej klasycznej wersji analizy progu

rentowności produkcji. Istota tego uogólnienia sprowadza się do odejścia od założenia o liniowej
formie zależności kosztów całkowitych od wielkości produkcji.

Przypuśćmy, że funkcją całkowitego kosztu produkcji jest funkcja K(Q), a funkcją przychodu

uzyskanego ze sprzedaży tej produkcji jest funkcja D (Q). Zakładamy, że obie funkcje są
różniczkowalne.

Zysk zrealizowany na sprzedaży wytworzonej produkcji jest także funkcją wielkości produkcji

Z(Q), przy czym wyraża się on ogólnym wzorem:

Z(Q) = D(Q) - K(Q) (1)

Wiadomo, że optymalnym programem produkcji jest taki program, który zapewnia maksymalny

zysk. Dlatego zadanie sprowadza się do wyznaczenia maksimum funkcji Z(Q).

Funkcja zysku Z ( Q ) ma maksimum dla tych wielkości produkcji Q, dla których pierwsza

pochodna:

a jednocześnie druga pochodna:

Koniecznym warunkiem istnienia maksimum funkcji zysku jest spełnienie równości:

czyli aby krańcowy koszt produkcji był równy krańcowemu przychodowi z produkcji.
Natomiast maksimum funkcji zysku odpowiada takiej wielkości produkcji Q, dla której zachodzi

nierówność:

a więc prędkość wzrostu krańcowego przychodu jest mniejsza od prędkości wzrostu kosztu
krańcowego.

Znając funkcję całkowitych kosztów produkcji K(Q) oraz funkcję przychodu ze sprzedaży D

(Q) można, zgodnie z przedstawionymi wyżej zasadami, wyznaczyć taką wielkość produkcji,
która zapewnia maksymalny zysk. Z kolei analizując miejsca zerowe funkcji zysku można
wyznaczyć takie wielkości produkcji, przy których koszty całkowite równają się przychodom ze
sprzedaży produkcji. Są to punkty, w których wartość funkcji zysku:

Z (Q) = 0

Tak wyznaczone miejsca zerowe są progami rentowności produkcji.

W zależności od kształtu funkcji Z (Q) punktów tych może być więcej niż jeden. W takich
wypadkach możliwe jest wyznaczenie przedziału wielkości produkcji zapewniającej przewagę
przychodów ze sprzedaży nad kosztami produkcji.

0

)

(

)

(

)

(

=

−

=

dQ

Q

dK

dQ

Q

dD

dQ

Q

dZ

0

)

(

)

(

)

(

2

2

2

2

2

2

<

−

=

dQ

Q

dK

dQ

Q

dD

dQ

Q

Z

d

dQ

Q

dK

dQ

Q

dD

)

(

)

(

=

2

2

2

2

)

(

)

(

dQ

Q

dK

dQ

Q

dD

<

27

Zadanie
Przeprowadzone rozważania teoretyczne zilustrujemy przykładem empirycznym dotyczącym

pewnego przedsiębiorstwa produkującego jeden wyrób.

Na podstawie danych statystycznych pochodzących z 15 kolejnych miesięcy oszacowano

funkcję regresji opisującą zależność między całkowitymi kosztami produkcji K a wielkością
produkcji Q. Funkcja ta przyjęła następującą postać:

K(Q) = 1,2 Q

2

+ 20 Q + 200,

gdzie: Q - wielkość produkcji w tys. szt.; K - koszty całkowite w mln zł.

Cena, po której przedsiębiorstwo sprzedaje swój wyrób, wynosi 68 tys. zł/szt.
Przyjmujemy, że cała zaplanowana wielkość produkcji jest sprzedawana. Równanie przychodu

osiąganego ze sprzedaży produkcji wynosi:

D (Q) = 68 Q.

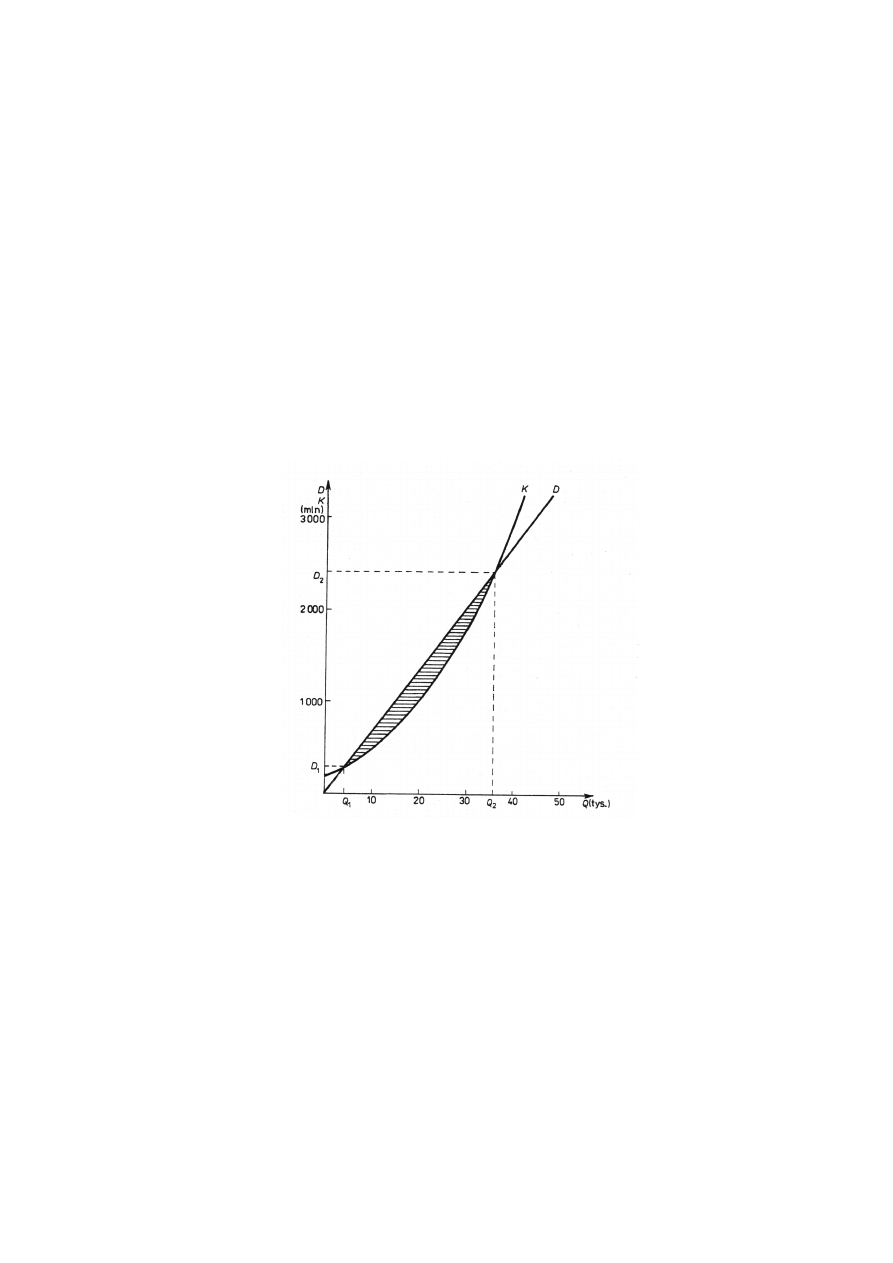
Punkty przecięcia uzyskanych funkcji K(Q) i D (Q) na rys. 24 są progowymi wielkościami

rentowności produkcji.

Rys. Zależność kosztów i dochodów od wielkości produkcji w przykładowym zadaniu

Funkcja zysku przedsiębiorstwa zrealizowanego na sprzedaży produkcji wynosi:

Z(Q) = D (Q) - K(Q) =
=68 Q - (1,2 Q2 + 20 Q + 200)
= -1,2 Q2 + 48 Q – 200

28

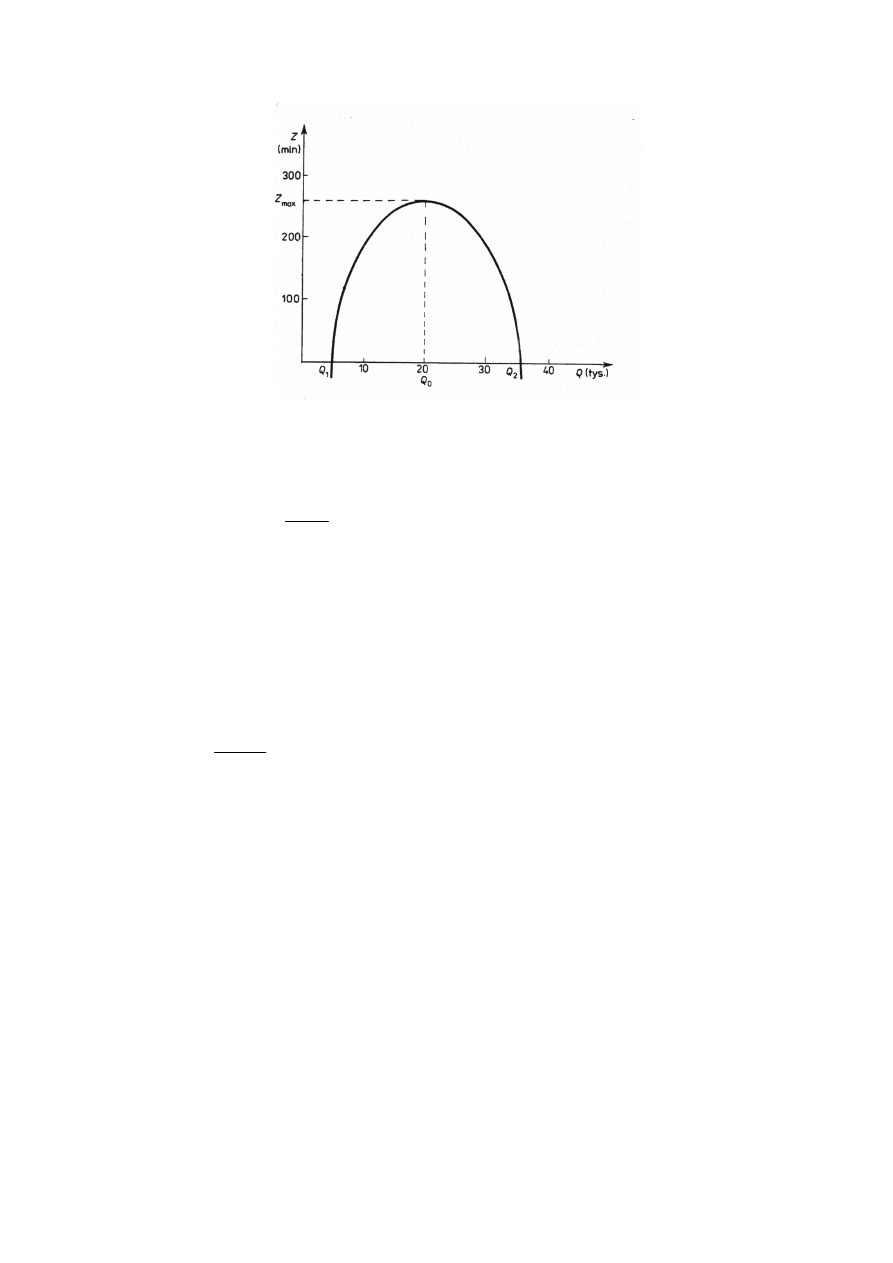
Wykresem powyższej funkcji zysku jest parabola przedstawiona na rys. 25.

Rys. Zależność zysku od wielkości produkcji w przykładowym zadaniu

Obliczamy pierwszą pochodną funkcji zysku:

Przyrównujemy tę pochodną do zera:

-2,4Q+48=0

i otrzymujemy:

Qo = 20 tys. szt.

Sprawdzamy drugą pochodną:

Ponieważ pochodna ta jest ujemna dla wszystkich wielkości produkcji Q, zatem decyzja o

produkcji wynoszącej 20 tys. szt. wyrobu jest optymalną decyzją dotyczącą wielkości produkcji.

Przy powyższej optymalnej wielkości produkcji uzyskujemy maksymalny zysk z jej sprzedaży

równy:

Z (20) = -1,2 * 20

2

+ 48 * 20 - 200 = 280.

Otrzymany wynik wskazuje, że produkcja na poziomie 20 tys. szt. zapewni największy zysk
równy 280 mln zł.

Wyznaczamy miejsca zerowe funkcji zysku i otrzymujemy:

Q1 = 4 725 szt.,
Q2 = 35 275 szt.

Z wyliczeń tych oraz z powyższych rysunków wynika, że przy wielkości produkcji

4 725 < Q < 35 275

48

4

,

2

)

(

+

−

=

Q

dQ

Q

dZ

0

4

,

2

)

(

2

2

<

−

=

dQ

Q

Z

d

29

przedsiębiorstwo osiąga zyski, przy czym zysk jest maksymalny przy produkcji Qo = 20 000 sztuk.

Jeśli produkcja Q

1

= 4 725 lub Q

2

= 35275, to przychody ze sprzedaży równają się całkowitym

kosztom produkcji.
Natomiast jeśli wielkość produkcji jest mniejsza od 4 725 szt. lub większa od 35 275 szt.,
przedsiębiorstwo ponosi straty. Powyższe punkty są jednocześnie progami rentowności produkcji
wyrobu.

30

KOSZTY A WYBÓR TECHNOLOGII

Specyfika różnych gałęzi przemysłu polega m. in. na tym, że wiele wyrobów może być
wytwarzanych przy zastosowaniu równych sposobów produkcji (różnych procesów
technologicznych i różnych sposobów organizacji produkcji). Podobnie w wielu przypadkach
niektóre identyczne operacje technologiczne mogą być wykonywane na różnych obrabiarkach.

Różne technologiczne warianty produkcji danego wyrobu charakteryzują się zazwyczaj
odmiennymi parametrami ekonomicznymi i technologicznymi.
Odmienności te mogą wynikać z różnic w poziomie technologicznych współczynników zużycia
poszczególnych czynników produkcji czy też w poziomie jednostkowej wydajności rozważanych
sposobów produkcji.
W tych warunkach istotnym zagadnieniem staje się poszukiwanie optymalnych, w konkretnych
warunkach przedsiębiorstwa, procesów technologicznych.

Do podjęcia decyzji w tym zakresie możemy wykorzystać metody poznane na przedmiocie Badania
Operacyjne tj. maksymalizacja korzyści płynących z zastosowania odmiennych technologii, czy
minimalizacji kosztów eksploatacji.
Inną metodą wyboru technologii jest wykorzystanie funkcji całkowitych kosztów produkcji.


Przykład
Załóżmy, że istnieje możliwość wyboru jednej z dwóch technologii wytwarzania pewnego wyrobu.
Przy zastosowaniu technologii I koszt stały wynosi K

s1

, a jednostkowy koszt zmienny k

1

;

przy zastosowaniu technologii II koszt stały wynosi K

s2

, a jednostkowy koszt zmienny k

2.

Zachodzą przy tym nierówności:

K

s1

<K

s2

k

1

>k

2

Należy podjąć decyzję dotyczącą wyboru technologii.

Oznaczmy przez Q wielkość produkcji, która może być wytworzona w określonym czasie.

Dla technologii I całkowity koszt produkcji wyniesie:

K

1

= K

s1

+k

1

Q

Dla technologii II

K

2

= K

s2

+k

2

Q

Powyższą sytuację przedstawia rysunek:
Funkcje całkowitych kosztów produkcji wyrobu dla dwóch różnych technologii.

K

Q

K

0

K

s2

K

s1

K

K

1

K

2

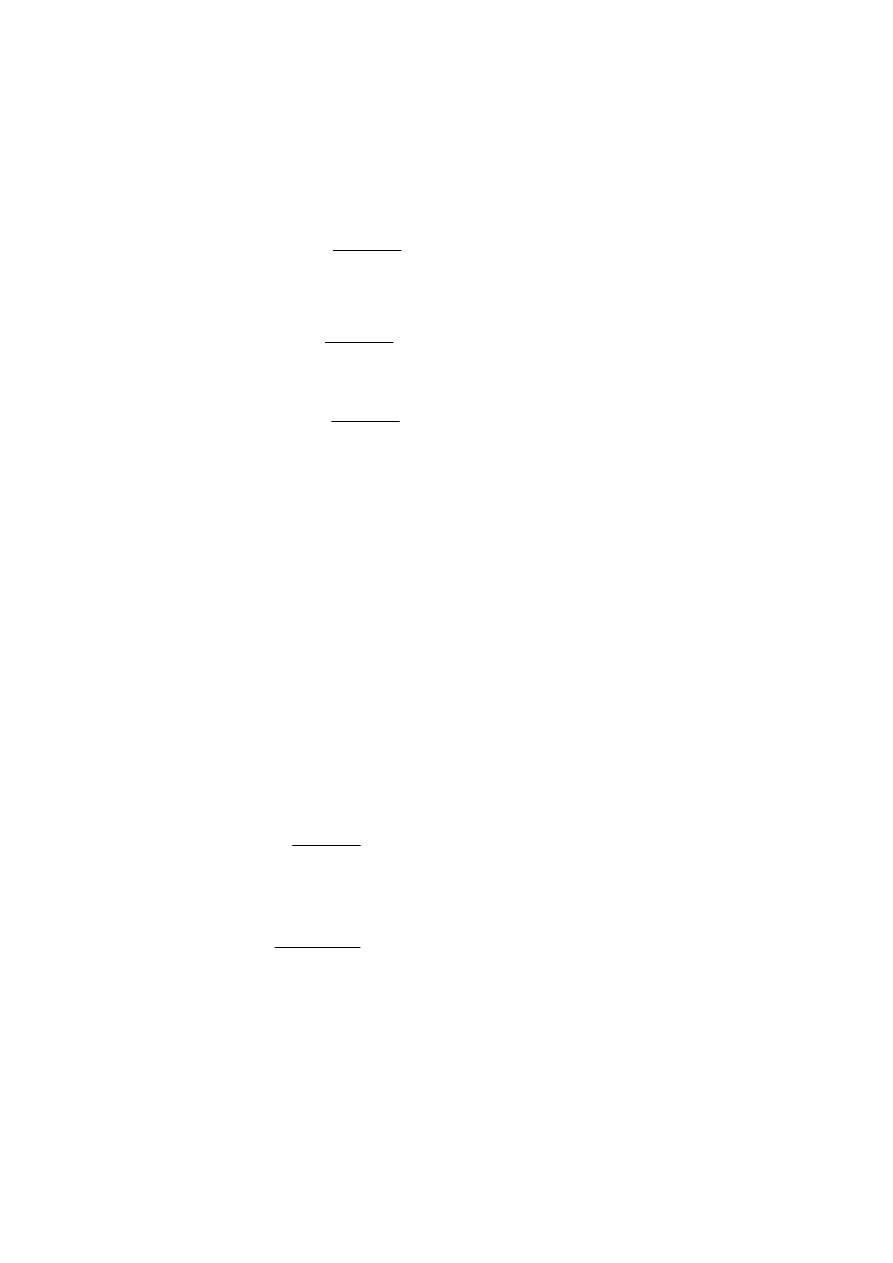
31

Z rysunku tego wynika, że przy produkcji mniejszej niż Q

0

korzystniejsza jest technologia I, a przy

produkcji większej niż Q

0

mniej kosztowna w eksploatacji jest technologia II.

Punkt Q

0

jest punktem w którym w którym koszt produkcji w obu wariantach jest taki sam.

Oznacza to , że:

K

s1

+k

1

Q = K

s2

+k

2

Q

Z równości tej otrzymujemy:

Zatem przy produkcji

należy zastosować technologię I, natomiast przy wielkości produkcji

należy zastosować technologię II.


Zadanie
Rozważmy produkcję wyrobu za pomocą dwóch technologii charakteryzujących się następującymi
kosztami:

- technologia

I

K

s1

= 1000

k

1

= 20

- technologia

II

K

s2

= 1200

k

2

= 15

Podstawiając dane do wzoru

otrzymujemy

Tak więc, jeśli wielkość produkcji ma być mniejsza niż 40 jednostek wyrobu, to należy stosować
technologię I, natomiast jeśli wielkość produkcji ma przekroczyć 40 jednostek, należy zastosować
technologię II.


Jeśli zostanie czas studenci za dodatkowe punkty rozwiążą zadania 2 i 3 s 141, 143 [3]

2

1

1

2

0

k

k

K

K

Q

s

s

−

−

=

2

1

1

2

k

k

K

K

Q

s

s

−

−

<

2

1

1

2

k

k

K

K

Q

s

s

−

−

>

2

1

1

2

0

k

k

K

K

Q

s

s

−

−

=

40

15

20

1000

1200

0

=

−

−

=

Q

32

Zadanie 2
Zakład ma możliwość stosowania trzech różnych procesów technologicznych przy produkcji
pewnych wyrobów. Przy produkcji tych wyrobów zużywane są cztery rodzaje surowców zasoby są
ograniczone. Jednostkowe normy zużycia tych surowców dla produkcji poszczególnych wyrobów,
jednostkowe koszty produkcji, ceny sprzedaży oraz zyski osiągnięte ze sprzedaży poszczególnych
wyrobów uzyskanych przy zastosowaniu rozważanych procesów technologicznych są podane w
poniższej tabeli.

Wyrób

Surowiec

W1 W2 W3

Zasoby

S1 2 5 6

6

000

S2 4 9 3

2

000

S3 7 3 8

5

000

S4 6 4 5

5

000

koszt jednostkowy

72

150

130

cena sprzedaży 88

180

150

zysk jednostkowy

16

30

20

Określić intensywność zastosowania każdego z procesów technologicznych, zapewniającej
maksymalny zysk ze sprzedaży wyrobów.

Oznaczamy przez x

1

, x

2

, x

3

wielkość produkcji wyrobów przy zastosowaniu poszczególnych

procesów technologicznych. Przy tych oznaczeniach program liniowy rozważanej sytuacji
decyzyjnej przyjmie przedstawioną niżej postać:

Z

max

= 16x

1

+ 30x

2

+ 20x

3

przy ograniczeniach:
2x

1

+ 5x

2

+ 6x

3

≤

6 000

4x

1

+ 9x

2

+ 3x

3

≤

2 000

7x

1

+ 3x

2

+ 8x

3

≤

5 000

6x

1

+ 4x

2

+ 5x

3

≤

5 000

x

1,

x

2

, x

3

≥

0

rozwiązanie metodą simplex jest następujące
x

1

=0

x

2

=16

x

3

=520

przy czym funkcja celu przyjęła wartość Z

max

= 10 400

Uzyskany wynik wskazuje, że pierwszy sposób produkcji nie powinien być stosowany. Przy
wykorzystaniu sposobu drugiego należy wytworzyć 16 sztuk wyrobu, a przy zastosowaniu sposobu
trzeciego 520 sztuk wyrobu. Taki plan produkcji zapewni firmie maksymalny zysk w kwocie 1 400
jedn. pieniężnych.

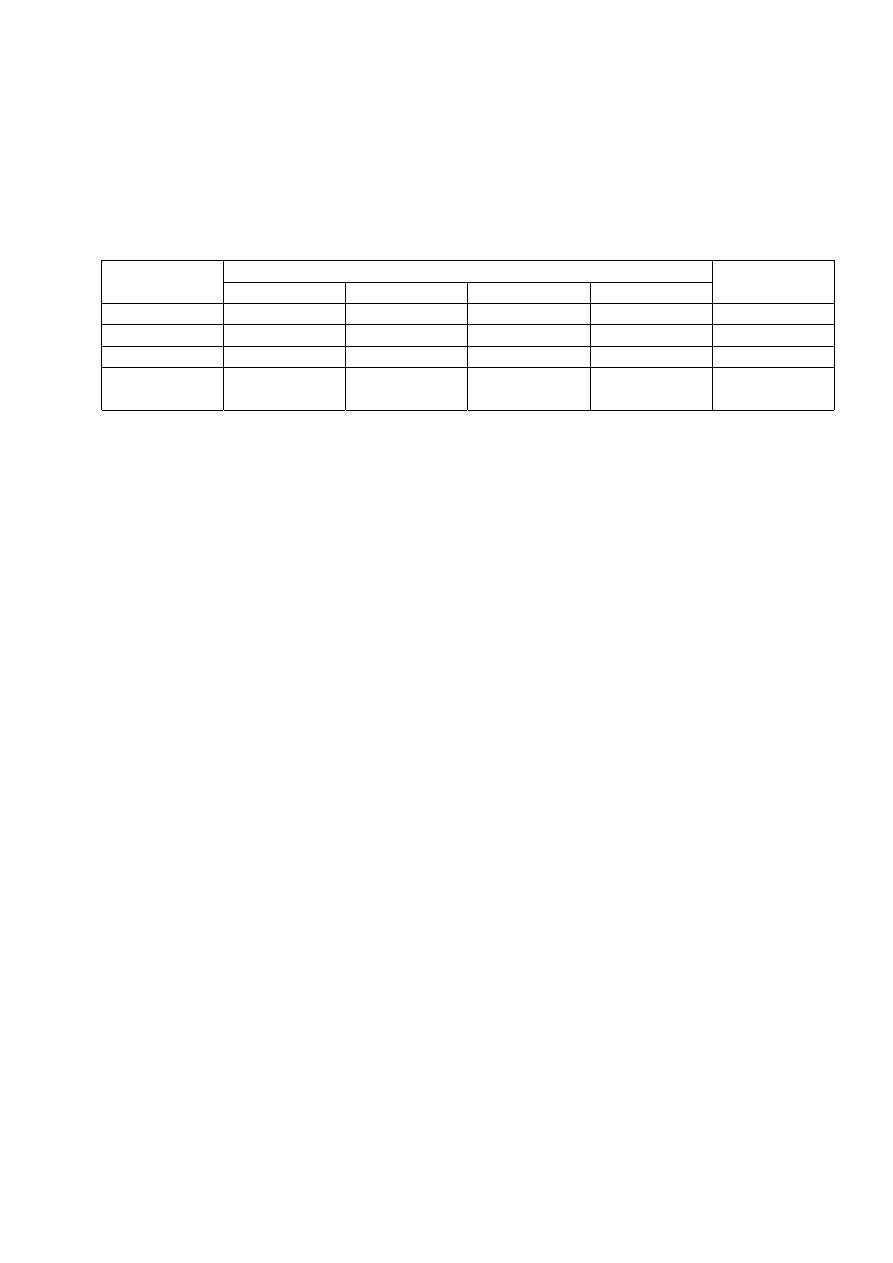
33

Zadanie 3
Przedsiębiorstwo ma dostarczyć 3 różne detale w ilościach
b

1

= 2 000

b

2

= 1 000

b

3

= 4 000

Przedsiębiorstwo ma możliwość zastosowania czterech różnych procesów technologicznych.
Liczba detali uzyskanych w wyniku zastosowania poszczególnych sposobów obróbki w jednostce
czasu oraz jednostkowe koszty obróbki są podane w poniższej tabeli

procesy technologiczne

detale

1 2 3 4

plan produkcji

I 25 40 40 10

2

000

II 15 8 20 5

1

000

III 40 32 25 30

4

000

jednostkowy

koszt obróbki

420 380 450 200

Określić intensywność zastosowania każdego z procesów technologicznych, zapewniającej
maksymalny zysk ze sprzedaży wyrobów.

Oznaczamy przez x

1

, x

2

, x

3,

x

4

skalę produkcji w jakiej należy zastosować poszczególne procesy

technologiczne.
Otrzymujemy następujący program liniowy:

Z

max

= 420x

1

+ 380x

2

+ 450x

3

+200 x

4

przy ograniczeniach:
25x

1

+ 40x

2

+ 40x

3

+10 x

4

= 2 000

15x

1

+ 8x

2

+ 20x

3

+5 x

4

= 1 000

40x

1

+ 32x

2

+ 25x

3

+30 x

4

= 4 000

x

1,

x

2

, x

3,

x

4

≥

0

brak rozwiązania przy modelu całkowitoliczbowym wg QSB
x

1

=37,5

x

2

=7,813

x

3

=0

x

4

=75

Z

max

= 33 718,75

jeśli przyjąć ograniczenia jako mniejsze równe wówczas uzyskujemy rozwiązanie
całkowitoliczbowe:
x

1

=38

x

2

=8

x

3

=0

x

4

=73

Z

max

= 33 600

jednak ilość detali nie będzie odpowiadała żądanej, a:
b

1

= 2 000

b

2

= 999

b

3

= 3966

34

Źródła:
1. B. Siuta, „Strategia zarządzania produktem”, TNOiK, Bydgoszcz 1996
2. R.B. Chase, N.J.Aquilano, „Production and operatins management”, IRWIN 1989
3. E. Nowak, „Teoria kosztów w zarządzaniu przedsiębiorstwem”, PWN, Warszawa 1996
4. W. Stachowski, „Materiały do projektowania z PPP”, rękopis 1996