Fundamenty Specjalne - projekt

Część 5 – Wymiarowanie zbrojenia w palach – metoda uproszczona

(dr hab. inż. Adam Krasiński)

W poniższej metodzie przyjęto kilka założeń upraszczających, które ogólnie dają wyniki obliczeń po
bezpiecznej stronie. Proces obliczeniowy przebiega metodą prób. Zbrojenie pala wymiarowane jest tylko ze
względu na nośność. W celu sprawdzenia np. warunków zarysowania należy wykonać dodatkowe obliczenia
specjalistyczne (patrz kurs żelbetu). Generalnie wymiarowanie zbrojenia w palach powinno przebiegać
w podobny sposób jak w słupach ściskanych ze zginaniem lub rozciąganych ze zginaniem. Zagadnienie
komplikuje się ze względu na kołowy przekrój pala. W palach wciskanych całkowicie zagłębionych
w gruncie z reguły pomija się zjawisko wyboczenia.

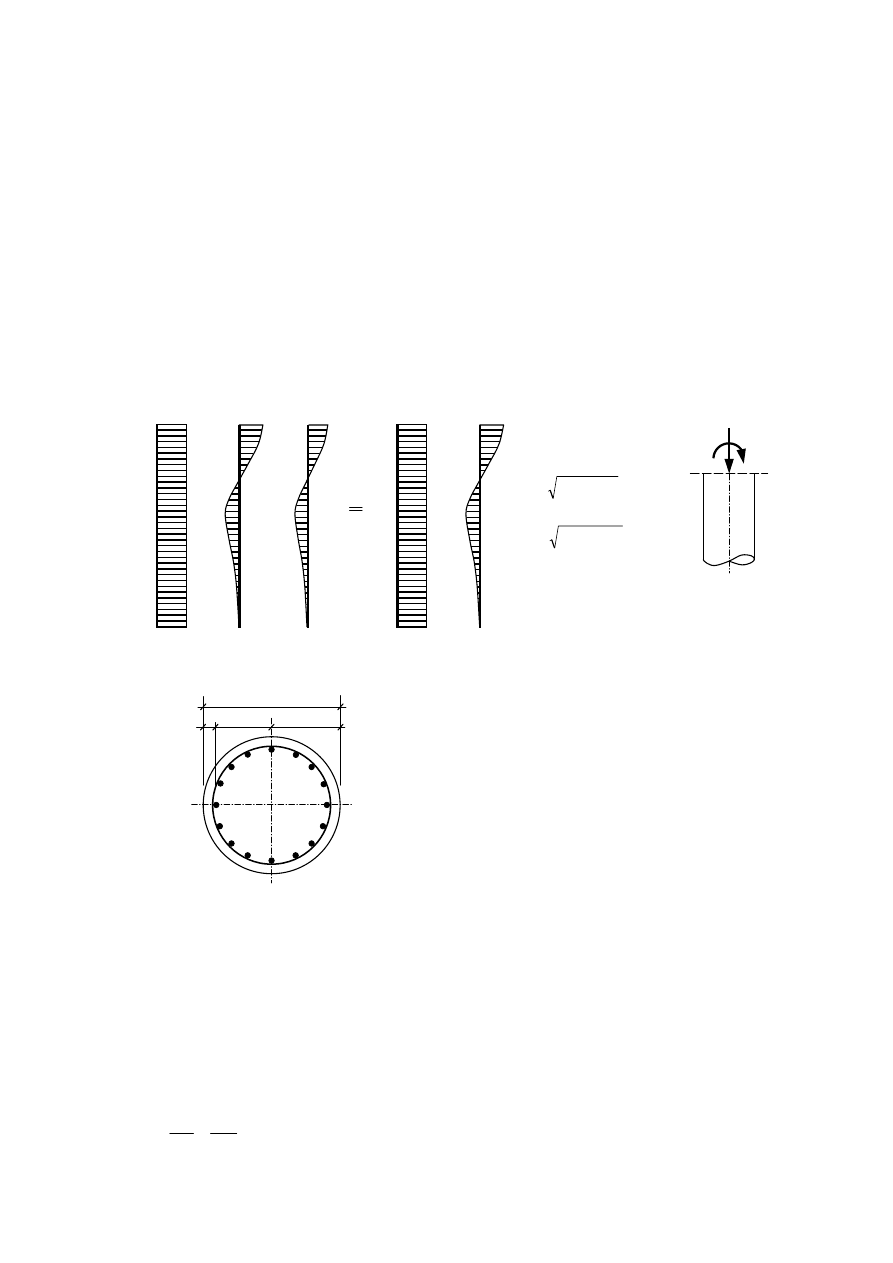
1. Pal obciążony siłą ściskającą i momentem zginającym

Procedura obliczeniowa
1.1. Wynik z obliczeń statycznych fundamentu palowego (np. z programu „ROBOT”)












1.2. Przyjmujemy wstępny przekrój pala: liczbę prętów zbrojenia podłużnego, otulenie zbrojenia,

klasę betonu i klasę stali, a następnie obliczamy parametry przekroju.

1.3. Obliczamy mimośród siły normalnej:

e

N

= M/N

c

jeżeli e

N

≤ 0,25r , to mamy przypadek małego mimośrodu – cały przekrój ściskany

jeżeli e

N

> 0,25r , to mamy przypadek dużego mimośrodu – przekrój ściskany i rozciągany

1.4. Przypadek małego mimośrodu
1.4a Obliczamy parametry przekroju zastępczego:
F

bz

= F

b

+ (n-1)

⋅F

a

; J

b

=

π⋅

D

4

/64 ; J

a

≈

0,01

⋅π⋅

F

a

⋅

r

a

2

; J

bz

= J

b

+ (n-1)

⋅

J

a

, W

bz

= J

bz

/r

1.4b Obliczamy i sprawdzamy naprężenia ściskające w betonie:

bc

bz

bz

c

bc

f

W

M

F

N

≤

+

=

σ

;

f

bc

– wytrzymałość obliczeniowa betonu na ściskanie

Jeżeli warunek nie jest spełniony należy zwiększyć zbrojenie pala lub zwiększyć klasę betonu.

N

c

M

y1

M

y2

M

z1

M

z2

N

M

1

M

2

N

c

M

2

1

2

1

1

z

y

M

M

M

+

=

2

2

2

2

2

z

y

M

M

M

+

=

M = max {M

1

, M

2

}

D

r

a

całkowity przekrój betonu: F

b

całkowity przekrój zbrojenia: F

a

stopień zbrojenia:

µ

a

= F

a

/F

b

stopień zbrojenia powinien spełniać warunki:
µ

a

≥ µ

amin

= 0,005 i

µ

a

≤ µ

amax

= 0,04

stosunek modułów betonu i stali: n = E

a

/E

b

≈ 7

r

a

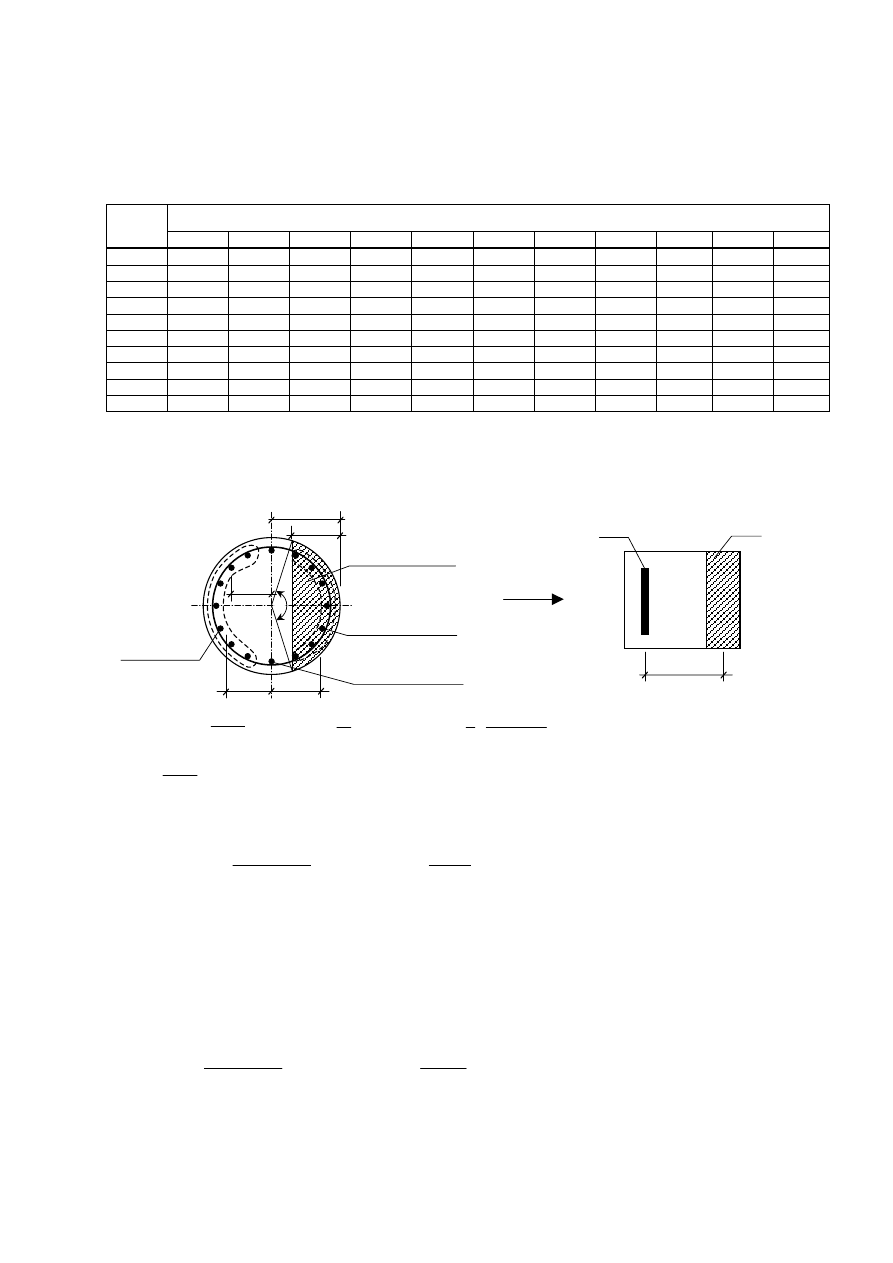
1.5. Przypadek dużego mimośrodu
1.5a Określamy wysokość

x

c

strefy ściskanej w przekroju według wzoru:

x

c

=

ξ

1

⋅r

w którym współczynnik

ξ

1

odczytujemy z tabl. 1 zależnie od stosunku

e

N

/

r i stopnia zbrojenia

µ

a

Tablica 1. Wartości współczynnika

ξ

1

dla przekroju pala ściskanego i zginanego

e

N

/r

µ

a

0,3 0,4 0,5 0,6 0,8 1,0 1,5 2,0 3,0 4,0 5,0

0,005 0,680 0,605 0,570 0,540 0,505 0,485 0,455 0,440 0,420 0,415 0,410

0,0075 0,760 0,680 0,635 0,605 0,570 0,545 0,510 0,495 0,480 0,470 0,465

0,010 0,820 0,735 0,685 0,655 0,615 0,590 0,555 0,540 0,520 0,510 0,505

0,0125 0,865 0,775 0,725 0,690 0,650 0,625 0,590 0,570 0,550 0,545 0,540

0,015 0,900 0,805 0,755 0,720 0,680 0,655 0,620 0,600 0,580 0,570 0,565
0,020 0,955 0,855 0,805 0,770 0,725 0,700 0,660 0,645 0,625 0,615 0,610
0,025 0,985 0,895 0,840 0,805 0,760 0,735 0,695 0,675 0,660 0,650 0,645
0,030 1,0 0,920 0,865 0,830 0,785 0,760 0,725 0,705 0,685 0,675 0,670
0,035 1,0 0,945 0,890 0,855 0,810 0,780 0,745 0,725 0,710 0,700 0,690
0,040 1,0 0,960 0,905 0,870 0,830 0,800 0,765 0,745 0,725 0,720 0,710

1.5b Przyjmujemy przekrój obliczeniowy pala i przekrój zastępczy oraz obliczamy parametry

geometryczne przekroju

1.5c Obliczamy i sprawdzamy naprężenia w zbrojeniu rozciąganym

bc

a

c

at

F

F

n

N

n

N

+

⋅

⋅

−

=

)

(

σ

;

at

at

F

z

M

M

⋅

=

)

(

σ

;

→

)

(

)

(

M

N

at

at

at

σ

σ

σ

+

=

≤ f

d

f

d

– wytrzymałość obliczeniowa stali na rozciąganie

Jeżeli warunek nośności nie jest spełniony należy zwiększyć liczbę lub średnicę prętów,
ewentualnie zastosować wyższą klasę stali zbrojeniowej. W przypadku dużego przekroczenia
nośności i przy

µ

a

bliskim

µ

amax

należy zwiększyć średnicę pala.

1.5d Obliczamy i sprawdzamy naprężenia ściskające w betonie

bc

a

c

bc

F

F

n

N

N

+

⋅

=

)

(

σ

;

bcz

bc

F

z

M

M

⋅

=

)

(

σ

;

→

)

(

)

(

M

N

bc

bc

bc

σ

σ

σ

+

=

≤ f

bc

f

bc

– wytrzymałość obliczeniowa betonu na ściskanie

Jeżeli warunek nośności nie jest spełniony należy zwiększyć klasę betonu, bądź zwiększyć
zbrojenie lub średnicę pala.

x

c

x

ai

e

bc

e

at

strefa ściskana

zbrojenie ściskane

n

c

, F

ac

zbrojenie

rozciągane

n

t

, F

at

zbrojenie obojętne

F

bcz

F

at

z =e

at

+e

bc

Przekrój zastępczy

t

ai

at

n

x

e

∑

=

F

bcz

= F

bc

+ (n-1)

⋅F

ac

n

t

– liczba prętów rozciąganych

F

bc

r











 −

=

r

x

r

c

arccos

2

ϕ

[rad];

(

)

ϕ

ϕ

sin

2

2

−

=

r

F

bc

;

(

)

ϕ

ϕ

ϕ

sin

)

2

/

(

sin

3

4

3

−

= r

e

bc

Przekrój obliczeniowy

z – ramię sił wewnętrznych

ϕ

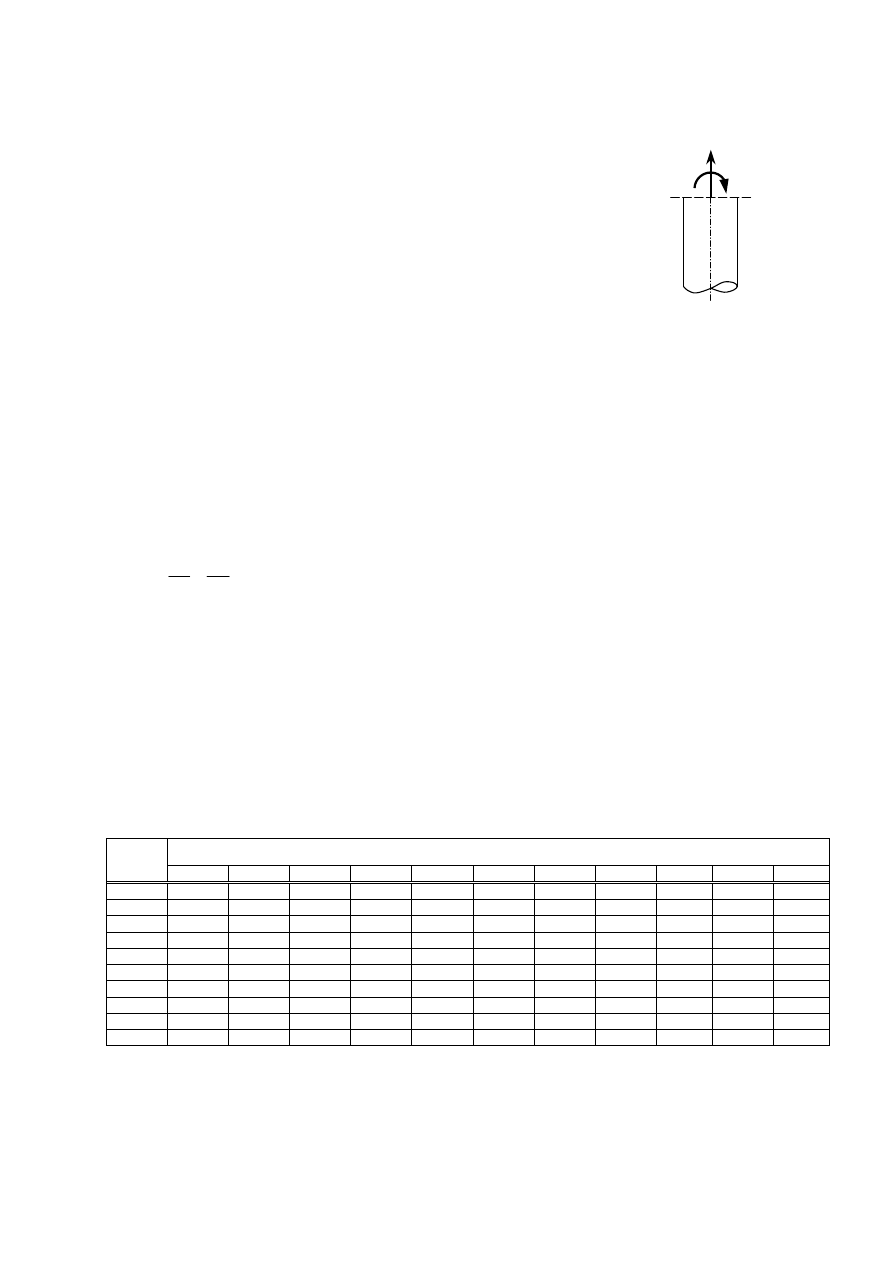
2. Pal obciążony siłą rozciągającą i momentem zginającym

Procedura obliczeniowa

2.1. Z obliczeń statycznych fundamentu palowego określamy

wartości sił przekrojowych N

t

i M (podobnie jak w pkt. 1.1)

2.2. Przyjmujemy wstępny przekrój pala i obliczamy parametry

przekroju (jak w pkt. 1.2).

2.3. Obliczamy mimośród siły normalnej:

e

N

= M/N

t

jeżeli e

N

≤ 0,25r , to mamy przypadek małego mimośrodu – cały przekrój rozciągany

jeżeli e

N

> 0,25r , to mamy przypadek dużego mimośrodu – przekrój rozciągany i ściskany

2.4. Przypadek małego mimośrodu – w przekroju pracuje tylko zbrojenie
2.4a Obliczamy parametry przekroju zbrojenia:

J

a

≈

0,01

⋅π⋅

F

a

⋅

r

a

2

; W

a

= J

a

/r

a

2.4b Obliczamy i sprawdzamy naprężenia rozciągające w zbrojeniu:

a

a

a

t

at

f

W

M

F

N

⋅

≤

+

=

2

,

1

σ

; f

a

– wytrzymałość obliczeniowa stali zbrojeniowej na rozciąganie

Jeżeli warunek nośności nie jest spełniony należy zwiększyć liczbę lub średnicę prętów, albo
zastosować wyższą klasę stali zbrojeniowej. W przypadku dużego przekroczenia nośności i przy

µ

a

bliskim

µ

amax

należy zwiększyć średnicę pala.

2.5. Przypadek dużego mimośrodu
2.5a Określamy wysokość x

c

strefy ściskanej w przekroju według wzoru:

x

c

=

ξ

2

⋅r

w którym współczynnik

ξ

2

odczytujemy z tabl. 2 zależnie od stosunku e

N

/r i stopnia zbrojenia

µ

a

Tablica 2. Wartości współczynnika

ξ

2

dla przekroju pala rozciąganego i zginanego

e

N

/r

µ

a

0,3 0,4 0,5 0,6 0,8 1,0 1,5 2,0 3,0 4,0 5,0

0,005 0,080 0,105 0,135 0,165 0,215 0,255 0,305 0,325 0,350 0,360 0,365

0,0075 0,105 0,135 0,175 0,210 0,265 0,305 0,355 0,375 0,400 0,410 0,415

0,010 0,125 0,165 0,205 0,245 0,305 0,340 0,390 0,415 0,440 0,450 0,455

0,0125 0,145 0,190 0,235 0,275 0,335 0,375 0,425 0,445 0,470 0,480 0,490

0,015 0,165 0,215 0,260 0,305 0,365 0,400 0,450 0,475 0,495 0,510 0,515
0,020 0,195 0,255 0,305 0,350 0,410 0,445 0,495 0,520 0,540 0,550 0,560
0,025 0,225 0,290 0,345 0,390 0,445 0,485 0,530 0,555 0,575 0,585 0,590
0,030 0,255 0,320 0,380 0,420 0,480 0,515 0,560 0,580 0,605 0,615 0,620
0,035 0,275 0,350 0,405 0,450 0,505 0,540 0,585 0,605 0,630 0,640 0,645
0,040 0,300 0,375 0,430 0,475 0,530 0,565 0,605 0,630 0,650 0,660 0,665

N

t

M

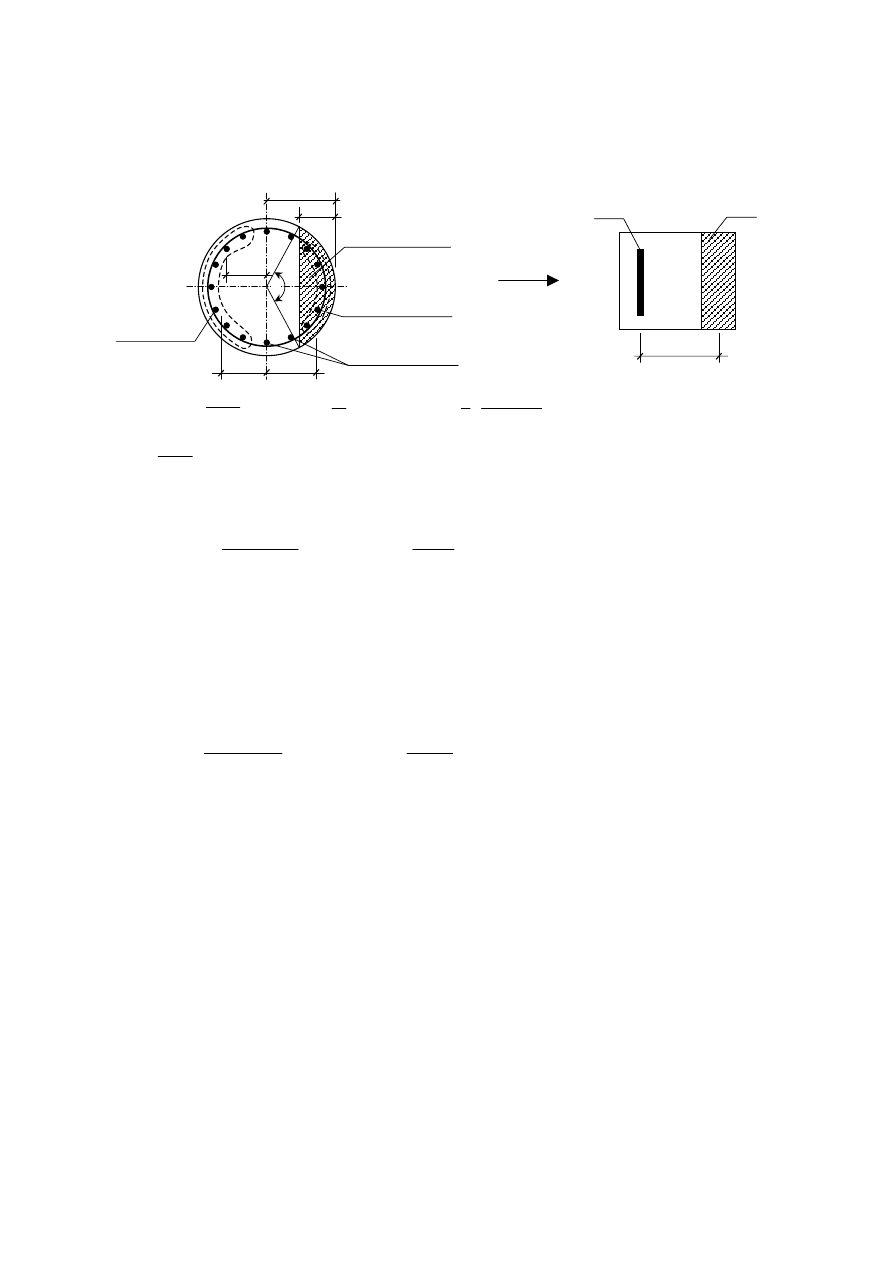
2.5b Przyjmujemy przekrój obliczeniowy pala i przekrój zastępczy oraz obliczamy parametry

geometryczne przekroju (tak samo jak w pkt. 1.5b)

2.5c Obliczamy i sprawdzamy naprężenia w zbrojeniu rozciąganym

bc

a

t

at

F

F

n

N

n

N

+

⋅

⋅

=

)

(

σ

;

at

at

F

z

M

M

⋅

=

)

(

σ

;

→

)

(

)

(

M

N

at

at

at

σ

σ

σ

+

=

≤ f

d

f

d

– wytrzymałość obliczeniowa stali na rozciąganie

Jeżeli warunek nośności nie jest spełniony należy zwiększyć liczbę lub średnicę prętów,
ewentualnie zastosować wyższą klasę stali zbrojeniowej. W przypadku dużego przekroczenia
nośności i przy

µ

a

bliskim

µ

amax

należy zwiększyć średnicę pala.

2.5d Obliczamy i sprawdzamy naprężenia ściskające w betonie

bc

a

t

bc

F

F

n

N

N

+

⋅

−

=

)

(

σ

;

bcz

bc

F

z

M

M

⋅

=

)

(

σ

;

→

)

(

)

(

M

N

bc

bc

bc

σ

σ

σ

+

=

≤ f

bc

f

bc

– wytrzymałość obliczeniowa betonu na ściskanie

Jeżeli warunek nośności nie jest spełniony należy zwiększyć klasę betonu, bądź zwiększyć
zbrojenie lub średnicę pala.

Uwagi na temat zbrojenia pali:
Minimalna średnica prętów podłużnych –

φ

16 mm, a w palach wielkośrednicowych –

φ

25 mm.

Zbrojenie spiralne – średnica prętów min.

φ

/3 zbrojenia podłużnego, skok spirali -

∼ D/(3÷4).

Stal zbrojenia podłużnego – żebrowana min. A-II, zbrojenia spiralnego – gładka lub żebrowana.
Otulenie zbrojenia w palach – min. 7 cm, a w palach wielkośrednicowych – min. 10 cm.

x

c

x

ai

e

bc

e

at

strefa ściskana

zbrojenie ściskane

n

c

, F

ac

zbrojenie

rozciągane

n

t

, F

at

zbrojenie obojętne

F

bcz

F

at

z =e

at

+e

bc

Przekrój zastępczy

t

ai

at

n

x

e

∑

=

F

bcz

= F

bc

+ (n-1)

⋅F

ac

n

t

– liczba prętów rozciąganych

F

bc

r











 −

=

r

x

r

c

arccos

2

ϕ

[rad];

(

)

ϕ

ϕ

sin

2

2

−

=

r

F

bc

;

(

)

ϕ

ϕ

ϕ

sin

)

2

/

(

sin

3

4

3

−

= r

e

bc

Przekrój obliczeniowy

z – ramię sił wewnętrznych

ϕ

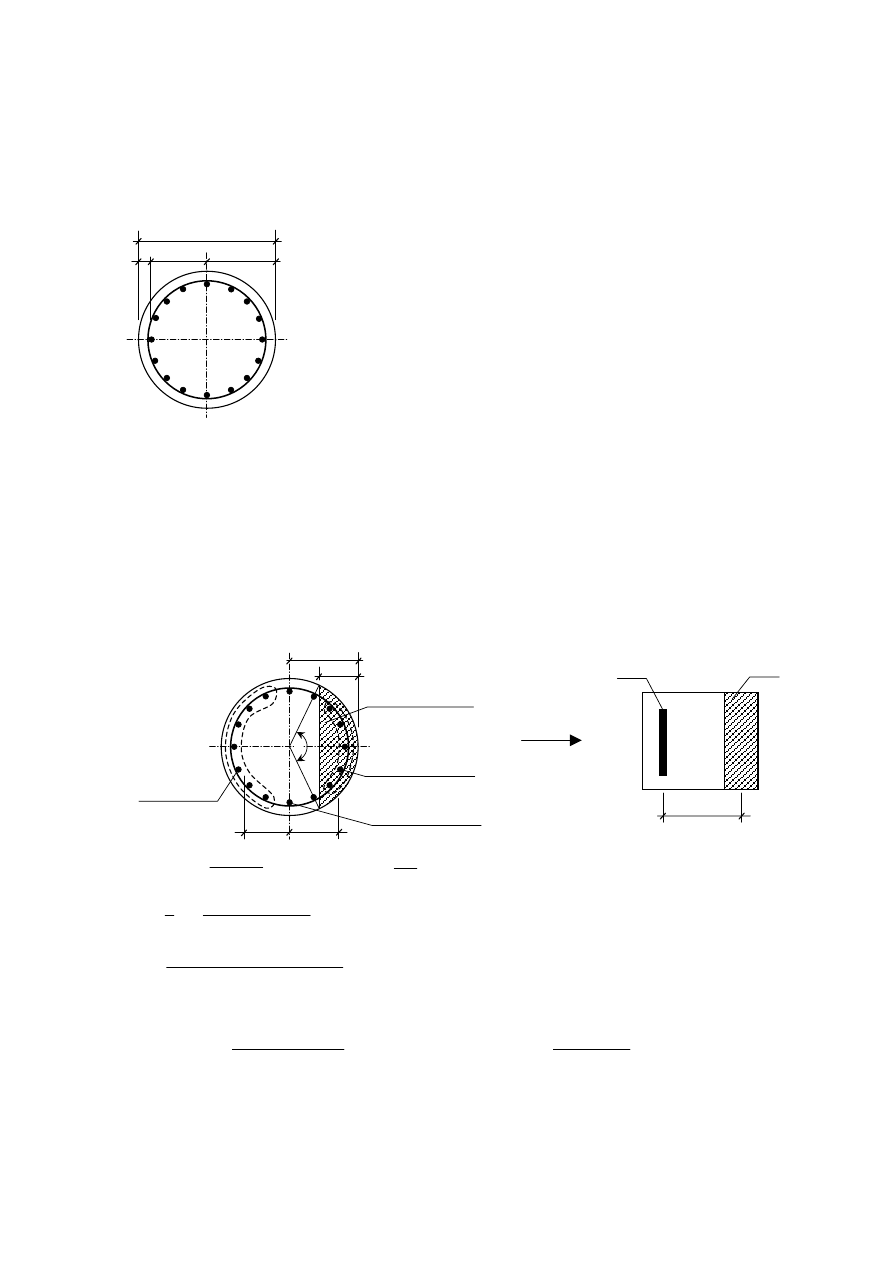
Przykład obliczeniowy 1 - pal obciążony siłą ściskającą i momentem zginającym

1. Wynik obliczeń statycznych fundamentu palowego:
N

c

= 3000 kN, M = 2000 kNm

1.2. Przyjęty wstępny przekrój pala i parametry przekroju.

1.3. Mimośród siły normalnej:

e

N

= 2000/3000 = 0,67 m = 67 cm > 0,25r = 0,25

⋅60 = 15 cm

- przypadek dużego mimośrodu

1.5a Wysokość x

c

strefy ściskanej w przekroju:

dla

µ

a

= 0,0087 i e

N

/r = 67/60 = 1,12

→

ξ

1

⋅≈ 0,56 (Tabl. 1)

x

c

= 0,56

⋅60 = 33,6 cm

1.5b Parametry przekroju obliczeniowego i zastępczego













1.5c Naprężenia w zbrojeniu rozciąganym:

4

,

6

2591

56

,

98

7

3000

7

)

(

−

=

+

⋅

⋅

−

=

N

at

σ

kN/cm

2

;

95

.

60

12

,

43

1

,

76

200000

)

(

=

⋅

=

M

at

σ

kN/cm

2

;

55

,

54

95

,

60

4

,

6

=

+

−

=

at

σ

kN/cm

2

= 545,5 MPa > f

d

= 400 MPa

D = 120 cm

r

a

przekrój betonu: F

b

= 0,25

⋅

π⋅120

2

= 11310 cm

2

stopień zbrojenia:

µ

a

= 98,56/11310 = 0,0087

≥

µ

amin

= 0,005

klasa betonu: B30 – f

bc

= 17,1 MPa

stosunek modułów betonu i stali: n = E

a

/E

b

≈ 7

r

a

r = 60 cm; a = 10 cm; r

a

= 50 cm

zbrojenie – 16 prętów

φ28: F

a

= 16

⋅6,16 = 98,56 cm

2

klasa stali: A-IIIN – f

d

= 400 MPa

x

c

e

bc

e

at

strefa ściskana

zbrojenie ściskane

n

c

, F

ac

zbrojenie

rozciągane

n

t

, F

at

zbrojenie obojętne

F

bcz

F

at

z

Przekrój zastępczy

9

,

35

7

1

,

19

2

4

,

35

2

2

,

46

2

50

=

⋅

+

⋅

+

⋅

+

=

at

e

cm;

F

bc

r = 60

230

,

2

60

6

,

33

60

arccos

2

=













−

=

ϕ

rad;

(

)

2591

230

,

2

sin

230

,

2

2

60

2

=

−

=

bc

F

cm

2

;

(

)

2

,

40

230

,

2

sin

230

,

2

)

2

/

230

,

2

(

sin

60

3

4

3

=

−

⋅

⋅

=

bc

e

cm;

Przekrój obliczeniowy

ϕ

64

,

24

16

,

6

4

=

⋅

=

ac

F

cm

2

;

1

,

76

2

,

40

9

,

35

=

+

=

z

cm

2739

64

,

24

)

1

7

(

2591

=

⋅

−

+

=

bcz

F

cm

2

;

12

,

43

16

,

6

7

=

⋅

=

at

F

cm

2

;

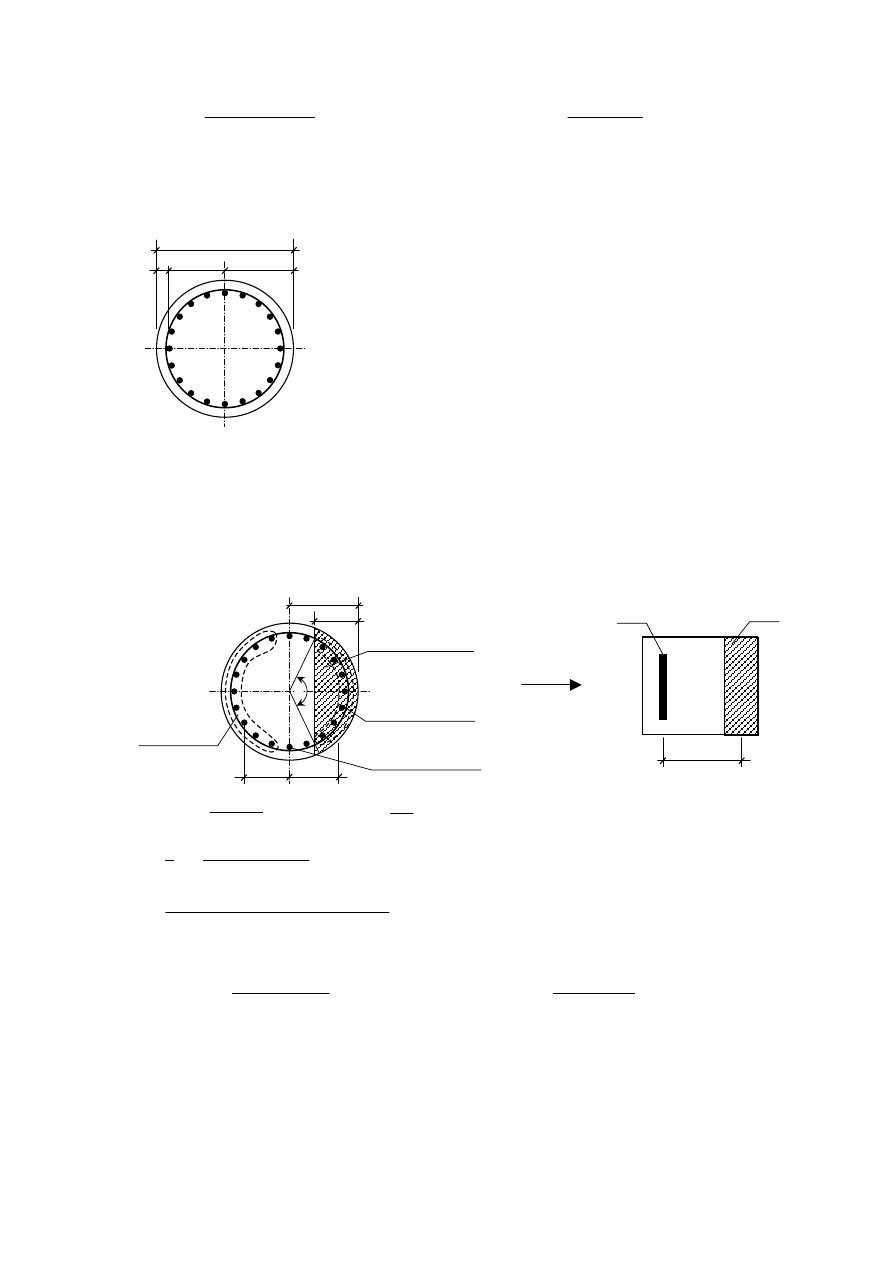
1.5d Naprężenia ściskające w betonie

91

,

0

2591

56

,

98

7

3000

)

(

=

+

⋅

=

N

bc

σ

kN/cm

2

;

96

,

0

2739

1

,

76

200000

)

(

=

⋅

=

M

bc

σ

kN/cm

2

;

87

,

1

96

,

0

91

,

0

=

+

=

bc

σ

kN/cm

2

= 18,7 MPa > f

bc

= 17,1 MPa

Warunki nośności są przekroczone

→ zwiększono zbrojenie pala do 20 φ 32.

1.5a Wysokość x

c

strefy ściskanej w przekroju:

dla

µ

a

= 0,0142 i e

N

/r = 67/60 = 1,12

→

ξ

1

⋅≈ 0,63 (Tabl. 1)

x

c

= 0,63

⋅60 = 37,8 cm

1.5b Parametry przekroju obliczeniowego i zastępczego













1.5c Naprężenia w zbrojeniu rozciąganym:

02

,

5

3054

161

7

3000

7

)

(

−

=

+

⋅

⋅

−

=

N

at

σ

kN/cm

2

;

87

,

38

45

,

72

9

,

72

200000

)

(

=

⋅

=

M

at

σ

kN/cm

2

;

85

,

33

87

,

38

02

,

5

=

+

−

=

at

σ

kN/cm

2

= 338,5 MPa < f

d

= 400 MPa

Warunek spełniony.

D = 120 cm

r

a

przekrój betonu: F

b

= 0,25

⋅

π⋅120

2

= 11310 cm

2

stopień zbrojenia:

µ

a

= 161/11310 = 0,0142

≥

µ

amin

= 0,005

stosunek modułów betonu i stali: n = E

a

/E

b

≈ 7

r

a

zbrojenie – 20 prętów

φ32: F

a

= 20

⋅8,05 = 161 cm

2

x

c

e

bc

e

at

strefa ściskana

zbrojenie ściskane

n

c

, F

ac

zbrojenie

rozciągane

n

t

, F

at

zbrojenie obojętne

F

bcz

F

at

z

Przekrój zastępczy

1

,

35

9

5

,

15

2

4

,

29

2

5

,

40

2

6

,

47

2

50

=

⋅

+

⋅

+

⋅

+

⋅

+

=

at

e

cm;

F

bc

r = 60

384

,

2

60

8

,

37

60

arccos

2

=













−

=

ϕ

rad;

(

)

3054

384

,

2

sin

384

,

2

2

60

2

=

−

=

bc

F

cm

2

;

(

)

8

,

37

384

,

2

sin

384

,

2

)

2

/

384

,

2

(

sin

60

3

4

3

=

−

⋅

⋅

=

bc

e

cm

;

Przekrój obliczeniowy

ϕ

35

,

56

05

,

8

7

=

⋅

=

ac

F

cm

2

;

9

,

72

1

,

35

8

,

37

=

+

=

z

cm

3392

35

,

56

)

1

7

(

3054

=

⋅

−

+

=

bcz

F

cm

2

;

45

,

72

05

,

8

9

=

⋅

=

at

F

cm

2

;

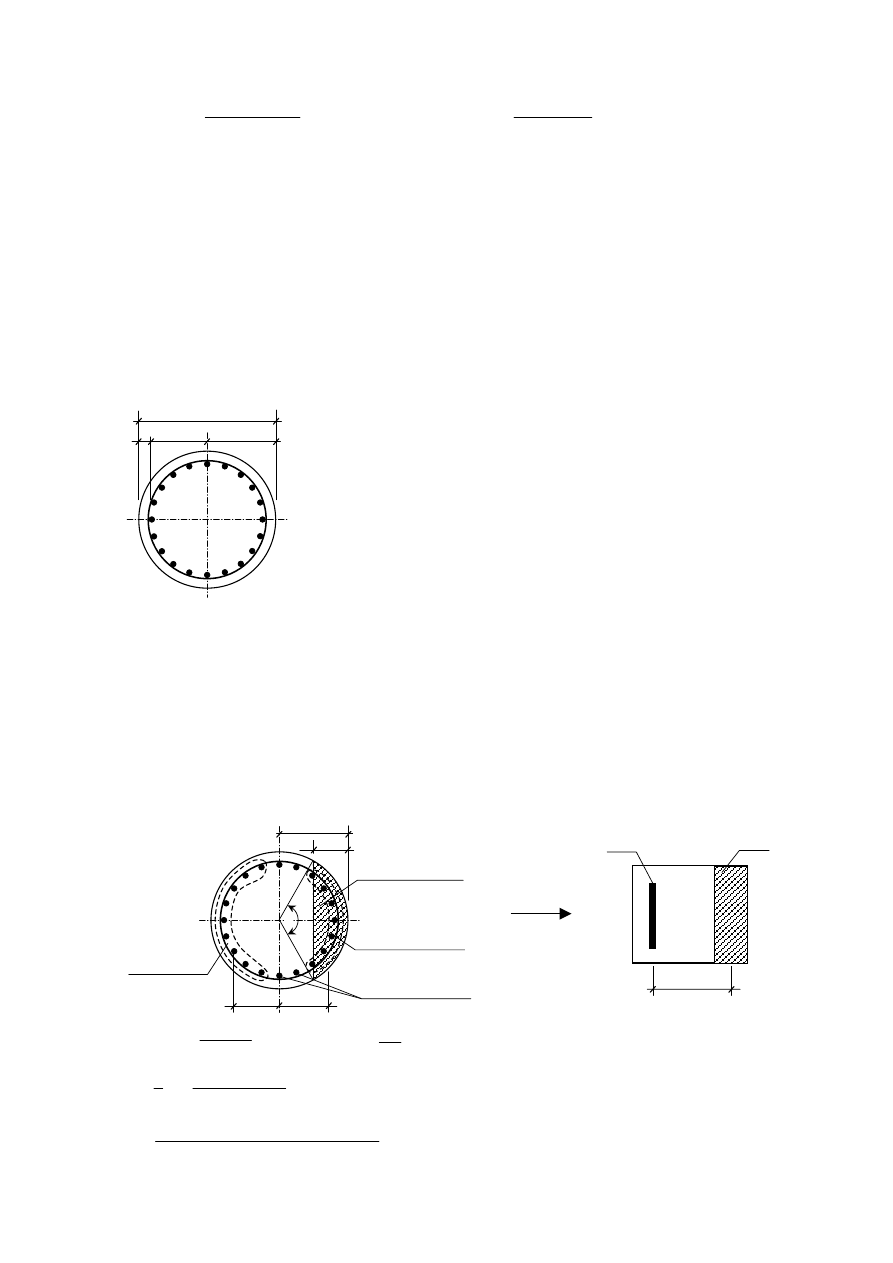
1.5d Naprężenia ściskające w betonie

72

,

0

3054

161

7

3000

)

(

=

+

⋅

=

N

bc

σ

kN/cm

2

;

81

,

0

3392

9

,

72

200000

)

(

=

⋅

=

M

bc

σ

kN/cm

2

;

53

,

1

81

,

0

72

,

0

=

+

=

bc

σ

kN/cm

2

= 15,3 MPa > f

bc

= 17,1 MPa

Warunki nośności pala na zginanie ze ściskaniem są spełnione.


Przykład obliczeniowy 2 - pal obciążony siłą rozciągającą i momentem zginającym

2. Wynik obliczeń statycznych fundamentu palowego:
N

t

= 800 kN, M = 1600 kNm

2.2. Przyjęty wstępny przekrój pala i parametry przekroju.

2.3. Mimośród siły normalnej:

e

N

= 1600/800 = 2,0 m = 200 cm > 0,25r = 0,25

⋅60 = 15 cm

- przypadek dużego mimośrodu

2.5a Wysokość x

c

strefy ściskanej w przekroju:

dla

µ

a

= 0,0142 i e

N

/r = 200/60 = 3,33

→

ξ

2

⋅≈ 0,485 (Tabl. 2)

x

c

= 0,485

⋅60 = 29,1 cm

2.5b Parametry przekroju obliczeniowego i zastępczego

przekrój betonu: F

b

= 0,25

⋅

π⋅120

2

= 11310 cm

2

klasa betonu: B30 – f

bc

= 17,1 MPa

stosunek modułów betonu i stali: n = E

a

/E

b

≈ 7

r = 60 cm; a = 10 cm; r

a

= 50 cm

klasa stali: A-IIIN – f

d

= 400 MPa

D = 120 cm

r

a r

a

stopień zbrojenia:

µ

a

= 161/11310 = 0,0142

≥

µ

amin

= 0,005

zbrojenie – 20 prętów

φ32: F

a

= 20

⋅8,05 = 161 cm

2

x

c

e

bc

e

at

strefa ściskana

zbrojenie ściskane

n

c

, F

ac

zbrojenie

rozciągane

n

t

, F

at

zbrojenie obojętne

F

bcz

F

at

z

Przekrój zastępczy

1

,

35

9

5

,

15

2

4

,

29

2

5

,

40

2

6

,

47

2

50

=

⋅

+

⋅

+

⋅

+

⋅

+

=

at

e

cm;

F

bc

r = 60

06

,

2

60

1

,

29

60

arccos

2

=













−

=

ϕ

rad;

(

)

2119

06

,

2

sin

06

,

2

2

60

2

=

−

=

bc

F

cm

2

;

(

)

8

,

42

06

,

2

sin

06

,

2

)

2

/

06

,

2

(

sin

60

3

4

3

=

−

⋅

⋅

=

bc

e

cm

;

Przekrój obliczeniowy

ϕ

3

,

48

05

,

8

6

=

⋅

=

ac

F

cm

2

;

9

,

77

1

,

35

8

,

42

=

+

=

z

cm

2409

3

,

48

)

1

7

(

2119

=

⋅

−

+

=

bcz

F

cm

2

;

45

,

72

05

,

8

9

=

⋅

=

at

F

cm

2

;

2.5c Naprężenia w zbrojeniu rozciąganym:

73

,

1

2119

161

7

800

7

)

(

=

+

⋅

⋅

=

N

at

σ

kN/cm

2

;

35

,

28

45

,

72

9

,

77

160000

)

(

=

⋅

=

M

at

σ

kN/cm

2

;

08

,

30

35

,

28

73

,

1

=

+

=

at

σ

kN/cm

2

= 300,8 MPa < f

d

= 400 MPa

2.5d Naprężenia ściskające w betonie

25

,

0

2119

161

7

800

)

(

−

=

+

⋅

−

=

N

bc

σ

kN/cm

2

;

853

,

0

2409

9

,

77

160000

)

(

=

⋅

=

M

bc

σ

kN/cm

2

;

60

,

0

85

,

0

25

,

0

=

+

−

=

bc

σ

kN/cm

2

= 6,0 MPa < f

bc

= 17,1 MPa

Warunki nośności na zginanie z rozciąganiem są spełnione.

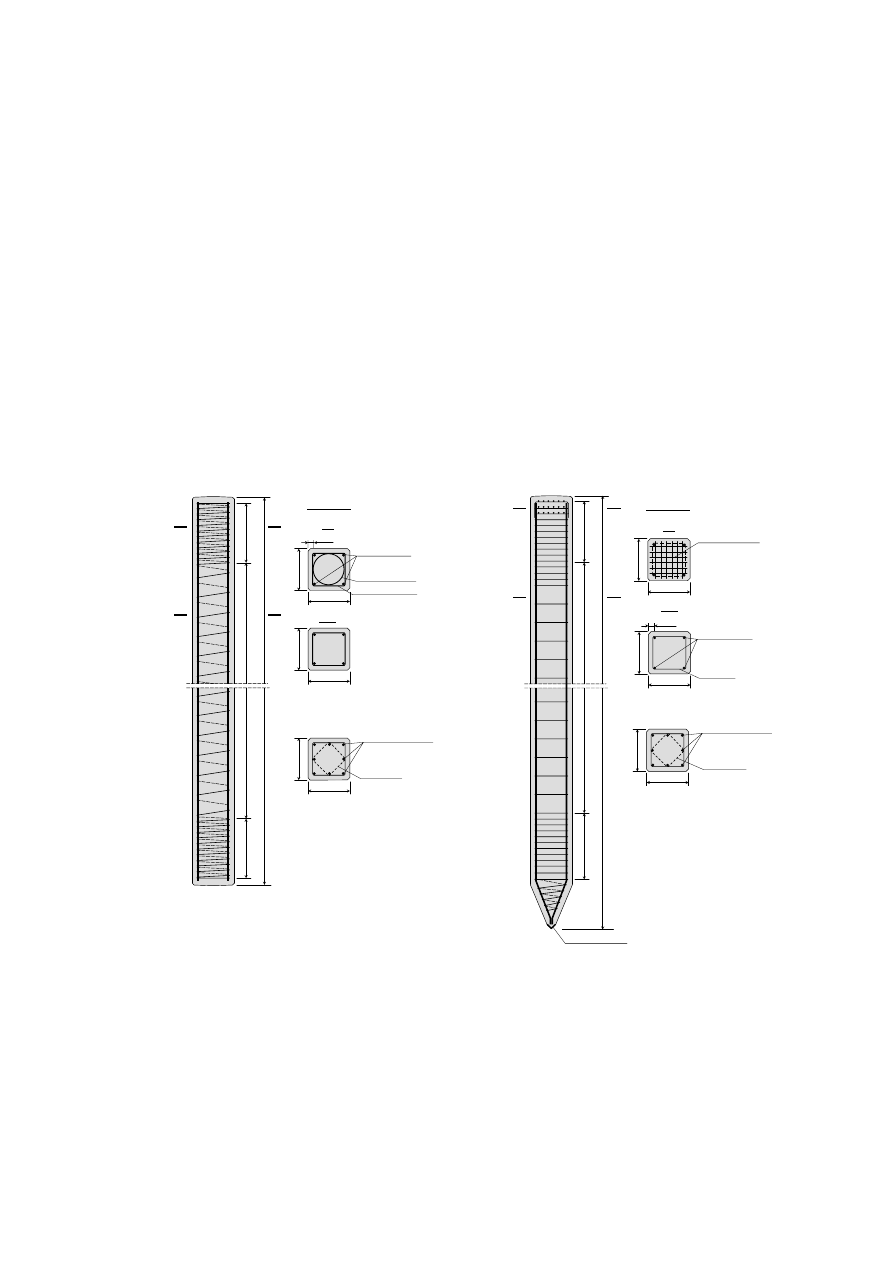
Załącznik

Zbrojenie pali

Pale zbroi się prętami podłużnymi oraz zbrojeniem poprzecznym w postaci spirali lub strzemion.
Pręty podłużne wykonuje się najczęściej ze stali żebrowanej (A-II, A-III), natomiast zbrojenie
poprzeczne ze stali gładkiej (A-I). Minimalny stopień zbrojenia podłużnego w palach wynosi

µ

amin

= 0.5%.

W palach prefabrykowanych pręty podłużne stosuje się o średnicy od

φ14 do φ25 mm,

a strzemiona o średnicy

φ6 do φ8 mm. W górnej i dolnej części pala stosuje się wzmocnione

zbrojenie poprzeczne przez zagęszczenie strzemion i/lub dodatkowe siatki, co ma zabezpieczyć te
miejsca pala na obciążenia udarowe od wbijania. Głowica pala powinna być lekko wypukła, co
sprawia, że siła udarowa jest skoncentrowana w osi pala i przez to zmniejsza się niebezpieczeństwo
rozkruszenia głowicy. Przed rozkruszeniem chroni głowicę również stosowanie drewnianych
przekładek pod podbabnikiem młota oraz sfazowania krawędzi. Również ze względu na obciążenia
udarowe, pale prefabrykowane wykonuje się z betonu wysokiej klasy (B35 do B50). Zbrojenie pali
prefabrykowanych należy liczyć również na zginanie w fazie wyciągania pala z formy oraz
podnoszenia w celu przystawienia do kafara. Dół pala może być zaostrzony lub tępy.

Rys. Konstrukcje pali prefabrykowanych: a) według rozwiązania „Aarsleff”, b) według „Projmorsu”

ostrze z kątownika

walcowanego

a

a

4 pręty podłużne

φ14 ÷ φ25

strzemiona

φ5 ÷ φ8

∼5cm

st

rz

em

iona c

o

5c

m

st

rz

em

iona c

o

∼

15c

m

st

rz

em

iona c

o

5c

m

L =

6.

0

÷ 16.0 m

a

a

przekrój

wzmocniony

50

÷ 100

cm

50

÷ 100

cm

strzemiona

pomocnicze

co

∼100cm

Przekroje

a

× a = 25 × 25 cm

30

× 30 cm

35

× 35 cm

40

× 40 cm

45

× 45 cm

II - II

8 prętów podłużnych

φ14 ÷ φ25

a

a

I - I

siatki zbrojeniowe

φ6 co 5 cm

I

I

II

II

a

a

4 pręty podłużne

φ14 ÷ φ25

spirala kwadratowa

φ5 ÷ φ8

∼5cm

sp

ir

al

a

co

∼

5c

m

sp

ir

al

a co

∼

15

cm

sp

ir

al

a

c

o

∼

5c

m

L = 6.

0

÷ 1

6

.0

m

a

a

przekrój

wzmocniony

50

÷ 100 c

m

50

÷

10

0 c

m

strzemiona

pomocnicze

co

∼100cm

Przekroje

a

× a = 25 × 25 cm

30

× 30 cm

35

× 35 cm

40

× 40 cm

spirala kołowa

φ6

45

× 45 cm

a

a

II - II

I - I

8 prętów podłużnych

φ14 ÷ φ25

lub

I I

II II

a) b)

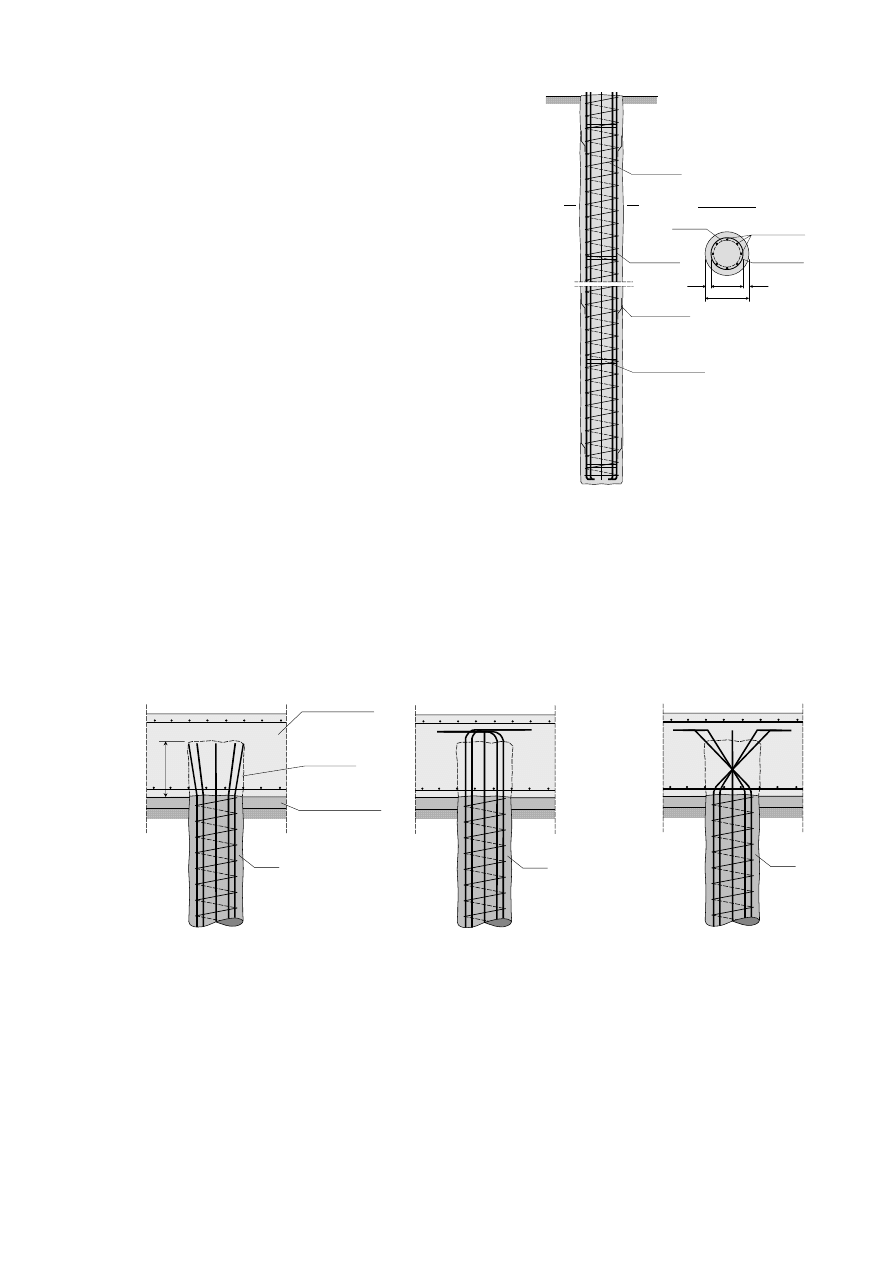
W palach monolitycznych – betonowanych
w

gruncie, o przekroju kołowym, zbrojenie

wykonuje się z co najmniej 6 prętów podłużnych
żebrowanych o średnicy minimum

φ16 mm i spirali

z pręta gładkiego o średnicy minimum

φ6 mm.

W palach wielkośrednicowych średnice prętów
głównych dochodzą do

φ32 mm, a ich liczba do 32

sztuk, natomiast spiralę wykonuje się z pręta

φ12

÷14 mm i skoku 25 ÷ 30 cm.
W konstrukcji zbrojenia powinno stosować się
ponadto elementy dystansowe, które zapewniają
centryczne umiejscowienie zbrojenia w palu oraz
wymaganą otulinę zbrojenia, która w palach
monolitycznych powinna wynosić minimum 7 cm.
W celu zapewnienia sztywności i nadania odpowied-
niego kształtu zbrojenia stosuje się obręcze
profilowe z grubego płaskownika lub pręta. Co
trzeci styk spirali z prętami podłużnymi łączy się
przez spawanie, co również zwiększa sztywność
kosza zbrojeniowego. Sztywność kosza ułatwia
podnoszenie go i wprowadzanie do rury obsadowej.

Zbrojenie pala należy w odpowiedni sposób zagłębić w konstrukcji oczepu fundamentowego,
w zależności od tego czy pal jest wciskany czy wyciągany oraz czy połączenie ma być sztywne, czy
przegubowe (rysunek poniżej).

Rys. Połączenie pali z oczepem fundamentowym: a) sztywne połączenie pala wciskanego, b) sztywne

połączenie pala wyciąganego, c) przegubowe połączenie pala wyciąganego lub wciskanego.

pręty podłużne

np. 8

φ20

Przekrój I - I

pręty podłużne

np. 8

φ20

spirala

np.

φ8 co 15cm

pręty dystansowe

φ8 ÷ 10

spirala

np.

φ8 co 15cm

φ500 mm

φ360

70

70

I

I

pierścienie profilujące

np. z płaskownika

pierścień

profilujący

podkład z chudego

betonu 10 cm

pal

skuta

głowica pala

∼0.5

÷0.6

m

żelbetowy oczep

fundamentowy

pal

pal

a) b)

c)

Rys. Zbrojenie pala

betonowanego w gruncie.