1
Obliczenia sił w palach metodą sztywnego oczepu - zadanie przykładowe
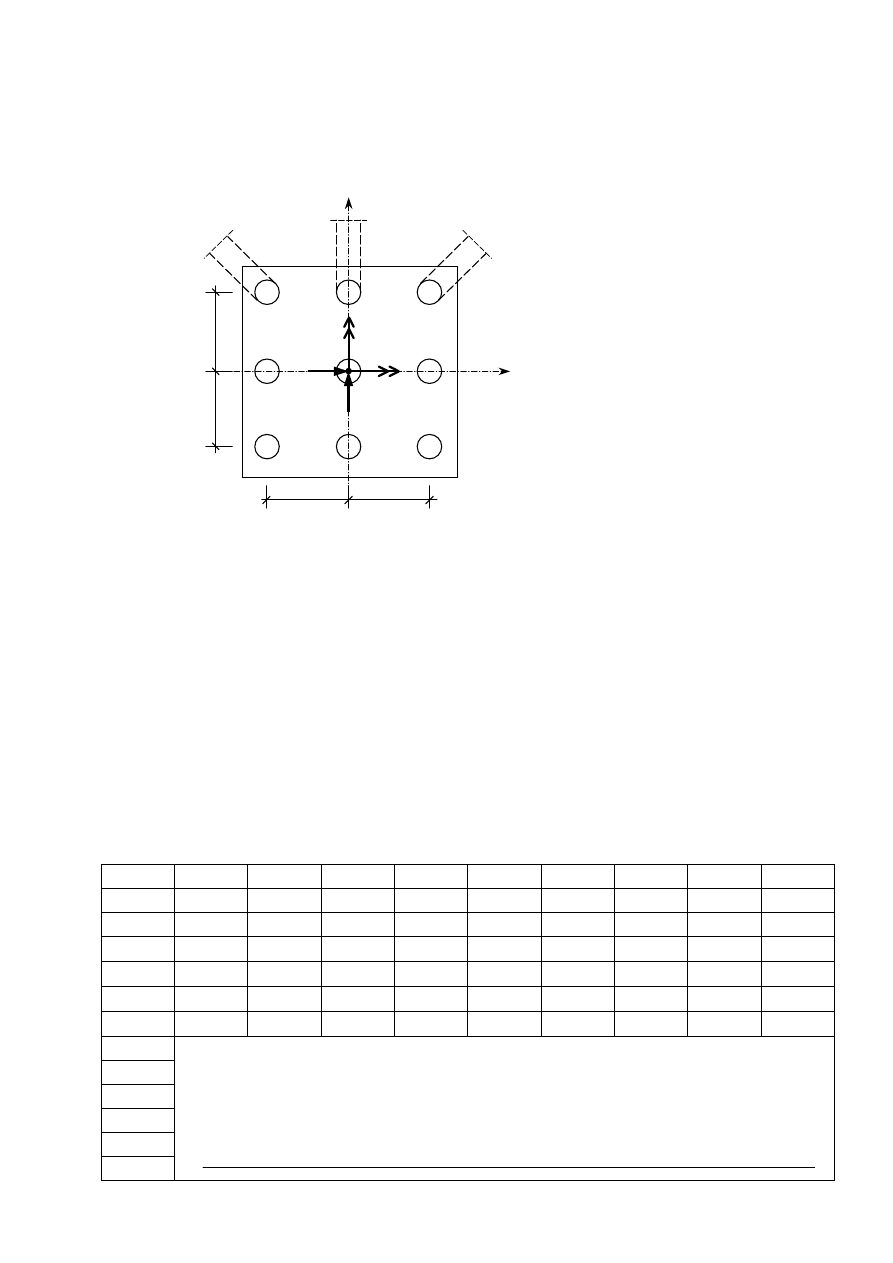
Policzyć siły w palach w fundamencie przedstawionym na rysunku.
Przyjąć schemat fundamentu ze sztywnym oczepem i z palami w postaci prętów obustronnie
przegubowych.
Obliczenia wykonać metodą macierzową i za pomocą programu ROBOT.
Obliczenia metodą macierzową
Pale 1, 2, 3 – ukośne o pochyleniu 10:1
tg
α
1,2,3
= 0,10
→
α
1,2,3
= 5,72
° → sin
α
1,2,3
= 0,10; cos
α
1,2,3
= 0,995
ω
1
= -45
° → sin
ω
1
= –0,707; cos
ω
1
= 0,707;
ω
2
= 0
° → sin
ω
2
= 0,0; cos
ω
2
= 0,707;
ω
3
= 45
° → sin
ω
3
= 0,707; cos
ω
3
= 0,707
Pozostałe pale - pionowe
α
i
= 0
→ sin
α
i
= 0 , cos
α
i
= 1,0 ;
ω
i
= 0
→ sin
ω
i
= 0, cos
ω
i
= 1,0
Wektor transformacji:
{p
i
}
T
=
{p
xi
, p
yi
, p
zi
, p
ai
, p
bi
, p
ci
,
}
p
xi
= sin
α
i
⋅sin
ω
i
; p
yi
= sin
α
i
⋅cos
ω
i
; p
zi
= cos
α
i
; p
ai
= –p
zi
⋅y
i
; p
bi
= p
zi
⋅x
i
; p
ci
= p
xi
⋅y
i
- p
yi
⋅x
i
Globalna macierz transformacji [P]:
Pal 1 2 3 4 5 6 7 8 9
x
i
-2 0 2 -2 0 2 -2 0 2
y
i
2 2 2 0 0 0 -2 -2 -2
sin
α
i
0,10
0,10
0,10
0 0 0 0 0 0
cos
α
i
0,995
0,995
0,995 1,0 1,0 1,0 1,0 1,0 1,0
sin
ω
i
–0,707
0
0,707
0 0 0 0 0 0
cos
ω
i
0,707 1,0 0,707 1,0 1,0 1,0 1,0 1,0 1,0
p
xi
-0,0707
0
0,0707
0 0 0 0 0 0
p
yi
0,0707
0,0995
0,0707
0 0 0 0 0 0
p
zi
0,995
0,995
0,995 1,0 1,0 1,0 1,0 1,0 1
p
ai
-1,99
-1,99
-1,99
0 0 0 2,0
2,0 2
p
bi
-1,99 0 1,99
-2,0 0 2,0 -2,0 0 2
p
ci
0 0 0 0 0 0 0 0 0
1 2
3
4
5
6
7 8 9
10:1
10:1
10:1
Y
0
X
0
M
y
M
x
H
x
H
y
V
z
2,0 2,0
2,0
2,0
Obciążenia:
V
z
= 10000 kN
H
x
= 500 kN
H
y
= 1200 kN
M
x
= 8000 kNm
M
y
= 7000 kNm
M
z
= 0

2
[ ]
−
−
−
−
−
−
−
=
0
,
2
0
0
,
2
0
,
2
0
0
,
2
99
,
1
0
99
,
1
0
,
2
0
,
2
0
,
2
0
0
0
99
,
1
99
,
1
99
,
1
0
,
1
0
,
1
0
,
1
0
,
1
0
,
1
0
,
1
995
,
0
995
,
0
995
,
0
0
0
0
0
0
0
0707
,
0
0995
,
0
0707
,
0
0
0
0
0
0
0
0707
,
0
0
0707
,
0
P
Macierz sztywności [D]:
Wszystkie pale o takiej samej sztywności
→ przyjęto s
i
= 1,0
[ ]
=
0
,
1
0
0
0
0
0
0
0
0
0
0
,
1
0
0
0
0
0
0
0
0
0
0
,
1
0
0
0
0
0
0
0
0
0
0
,
1
0
0
0
0
0
0
0
0
0
0
,
1
0
0
0
0
0
0
0
0
0
0
,
1
0
0
0
0
0
0
0
0
0
0
,
1
0
0
0
0
0
0
0
0
0
0
,
1
0
0
0
0
0
0
0
0
0
0
,
1
D
Globalna macierz sztywności:
−
−
=
=
92
,
23
0
0
0
2798
,
0
0
88
,
23
0
,
4
4478
,
0
0
0
0599
,
0
97
,
8
2389
,
0
0
0
4478
,
0
2389
,
0
0198
,
0
0
2798
,
0
0
0
0
00998
,
0
]
][
][
[
]
[
T
P
D
P
S
Globalna macierz sztywności po odwróceniu (macierz podatności):
−
−
−
−
−
−
=
−
0625
,
0
0
0
0
7692
,
1
0
1480
,
0
1418
,
0
286
,
5
0
0
1418
,
0
300
,
0
048
,
7
0
0
286
,
5
048
,
7
3
,
263
0
7692
,
1
0
0
0
25
,
151
]
[
1
S
Wektor obciążeń:
{R}
T
= {500; 1200; 10000; 8000; 7000}
Wektor przemieszczeń oczepu:
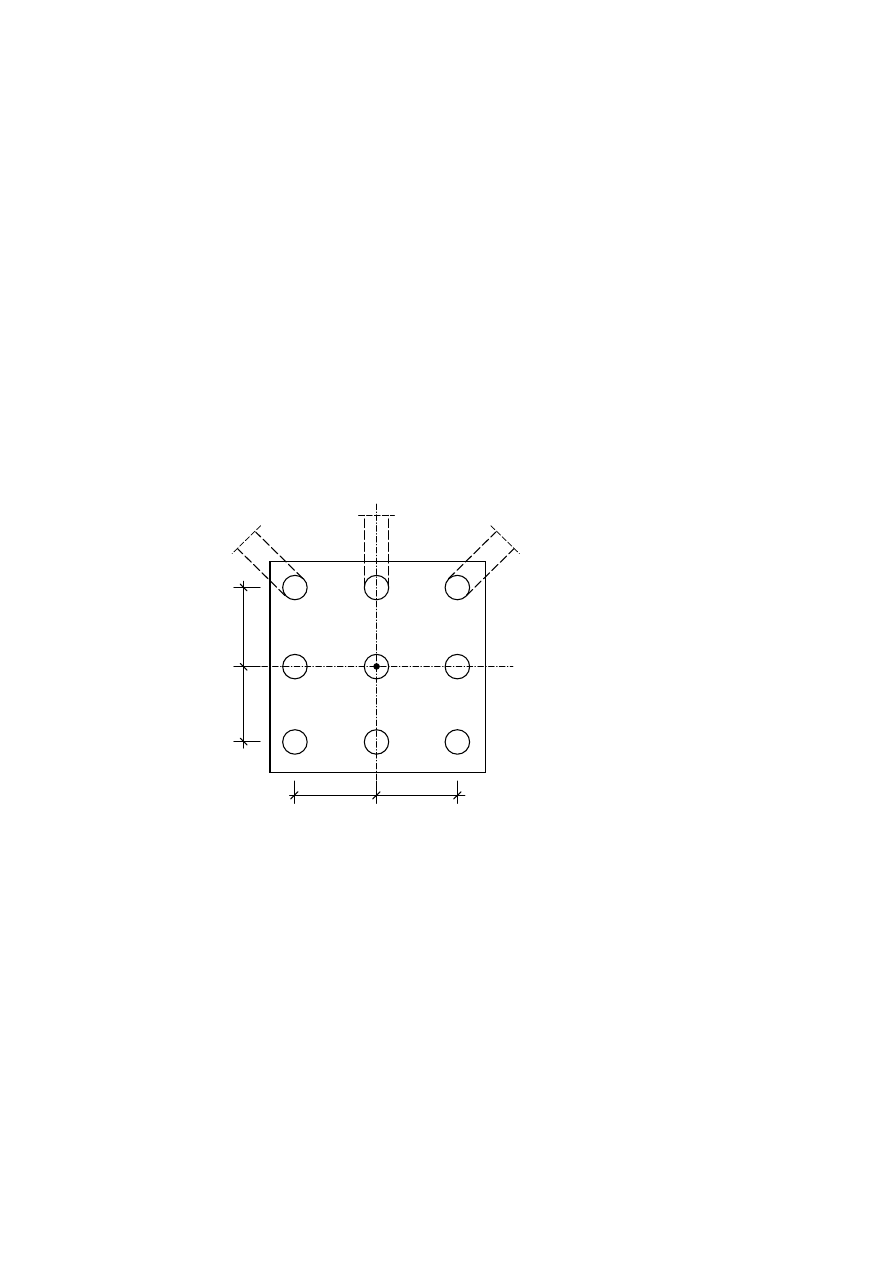
3
{v} = [S]
-1
{R} = {63242; 287770; -2278; 1462; -447}
T
Wektor przemieszczeń pali:
{v
p
} = [P]
T
{v} = {-2041; 9919; 5072; -5696; -6590; -7484; 6523; 5628; 4734}
T
Wektor sił w palach:
N
1
N
2
N
3
N
4
N
5
N
6
N
7
N
8
N
9
{N} = [D]{v
p
} = {-2041; 9919; 5072; -5696; -6590; -7484; 6523; 5628; 4734}
T
Sprawdzenie:
ΣV = ΣN
i
⋅cos
α
i
= 10000 kN
→ O.K.
ΣH
y
=
ΣN
i
⋅sin
α
i
⋅ cos
ω
i
= 1200 kN
→ O.K.
1 2
3
4
5
6
7 8 9
2,0 2,0
2,0
2,0
-2041
9919
5072
-5696 -6590
-7484
6523
5628
4734
SIŁY W PALACH [kN]
(wartość ujemna – pal wyciągany)
4
Obliczenia za pomocą programu ROBOT
Do obliczeń przyjęto pale o średnicy D = 0,80 m, długości L = 10,0 m i wykonane z betonu B30.
Oczep fundamentowy przyjęto o dużej grubości (h = 5,0 m) i z betonu B30 tak, aby miał bardzo
dużą sztywność.
Pale wymodelowano w postaci prętów przegubowo połączonych z płytą. W programie Robot do
modelowania połączeń przegubowych służy komenda „Zwolnienia” w zakładce „Geometria”.
W dolnych węzłach prętów palowych (w podstawach) zadano podpory przegubowe (zwolnione
obroty rx, ry i rz, zablokowane przemieszczenia liniowe ux, uy i uz).
Obciążenia zadano w postaci sił i momentów węzłowych zadanych w środku geometrycznym płyty
fundamentowej. W „tabeli obciążeń” usunięto ciężary własne płyty i pali.
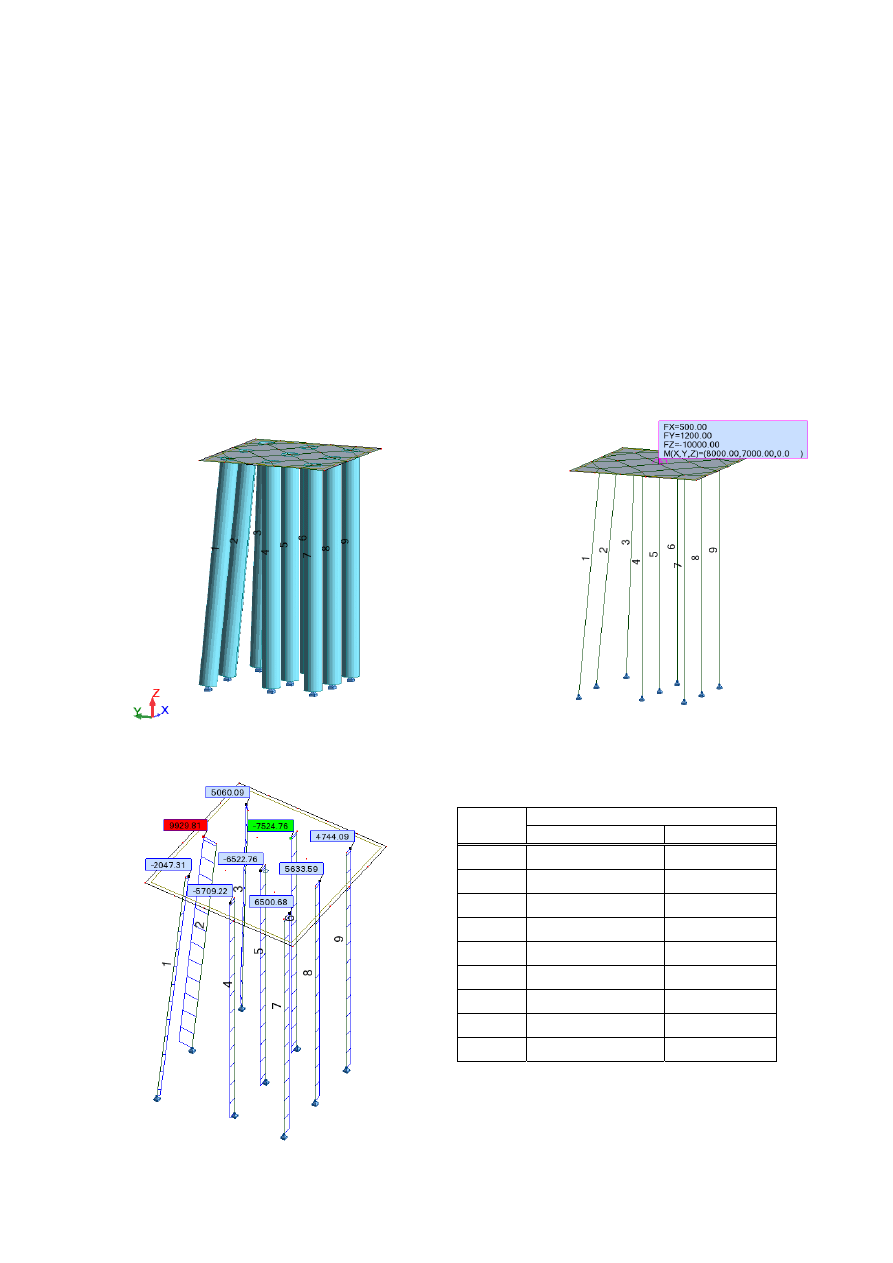
Model geometryczny
Model obliczeniowy z obciążeniami
(nie pokazano grubości płyty)
Wyniki obliczeń – siły osiowe w palach
Opracował:
Dr inż. Adam Krasiński
Katedra
Geotechniki,
Geologii
i
Bud.
Morskiego
Zestawienie porównawcze wyników obliczeń
Siła osiowa Q w palu [kN]
Nr pala
Met. macierzowa
ROBOT
1 -2041 -2047
2 9919 9930
3 5072 5060
4 -5696 -5709
5 -6590 -6523
6 -7484 -7525
7 6523 6501
8 5628 5634
9 4734 4744
Nieznaczne różnice mogą wynikać z zadania w programie
Robot płyty o skończonej sztywności oraz z zaokrągleń
Wyszukiwarka
Podobne podstrony:
Fund Spec proj cz1 id 181424 Nieznany
Fund Spec proj cz5 id 181426 Nieznany
Fund Spec proj cz2 id 181425 Nieznany
Projekt fund płyt pal cz3 A Kra
War zal proj fund
Forma proj fund
proj fund
proj fund
proj fund
mapy do celow proj
Cukrzyca ciężarnych 2012 spec anestetyczki
download Finanse międzynarodowe FINANSE MIĘDZYNARODOWE WSZiM ROK III SPEC ZF
olejki eteryczne cz3
Proj syst log wykl 6
więcej podobnych podstron