1

Fundamenty Specjalne – projekt fundamentu płytowo-palowego - część 4

(dr hab. inż. Adam Krasiński)

4. Procedura przygotowania schematu obliczeniowego fundamentu płytowo-palowego

Procedura przygotowania schematu jest połączeniem dwóch metod: metody zmodyfikowanego
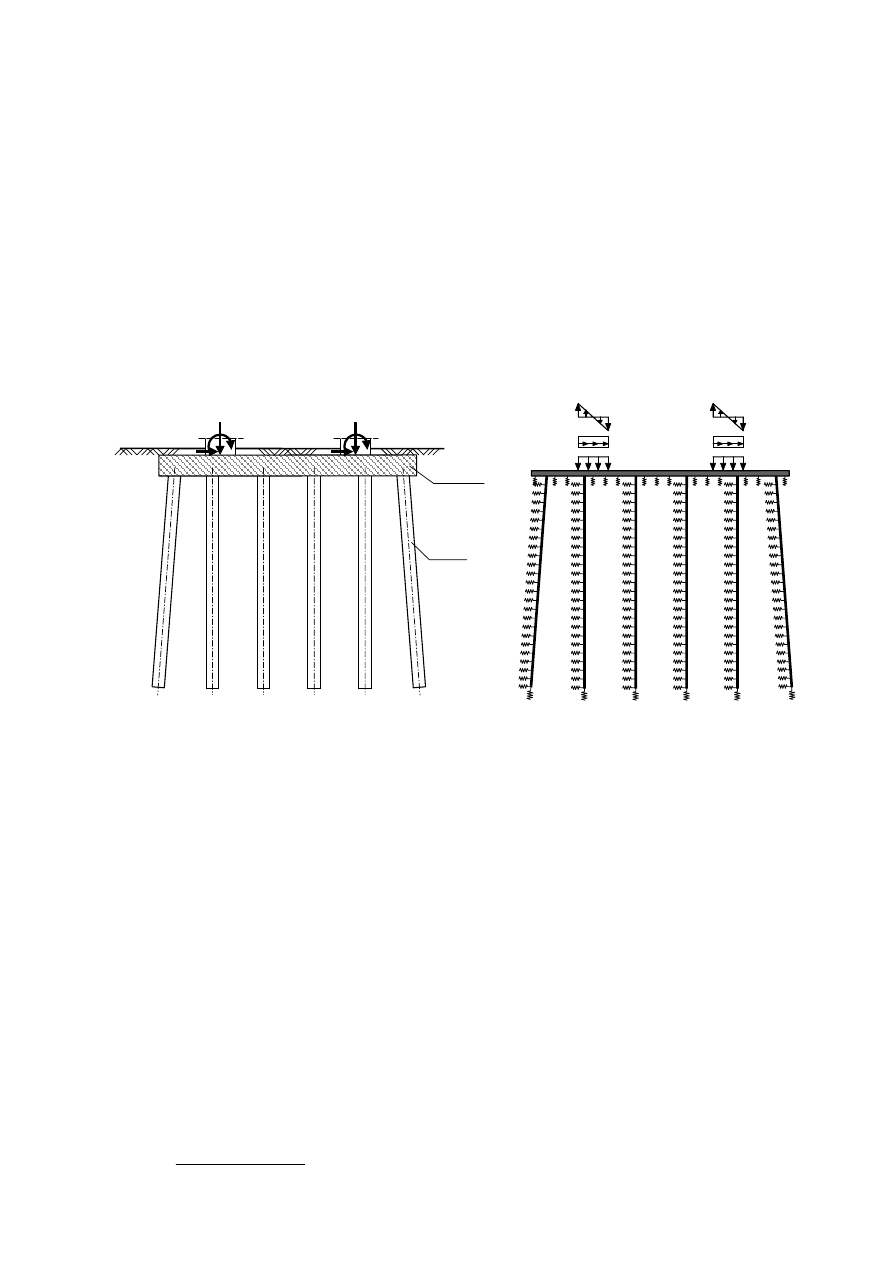
podłoża winklerowskiego i metody uogólnionej. Fundament płytowo-palowy modeluje się
w postaci płyty o rzeczywistej sztywności, spoczywającej na sprężystym podłożu gruntowym
o nierównomiernej sztywności k

zgj

i na palach, wyrażonych w postaci prętów współpracujących

z ośrodkiem gruntowym (rys. 4.1). Pręty palowe są sztywno połączone z płytą fundamentową. Ich
współpraca z ośrodkiem gruntowym wyrażona jest za pomocą szeregu poziomych podpór
sprężystych o sztywnościach k

xi

i k

yi

rozmieszczonych wzdłuż trzonów pali oraz pojedynczych

podpór sprężystych o sztywnościach K

zgj

, umieszczonych pod podstawami i ukierunkowanych

zgodnie z osiami pali. Opisany schemat fundamentu przedstawiono na rysunku poniżej.

Rys. 4.1

4.1. Wyznaczenie sztywności k

zgj

podłoża gruntowego pod płytą fundamentową

Sztywność podłoża gruntowego pod płytą fundamentową określa się na podstawie obliczeń osiadań
tego podłoża. Na osiadania te składają się trzy elementy:
1) osiadanie od nacisków przekazywanych bezpośrednio przez płytę fundamentową,
2) osiadanie od obciążeń przekazywanych przez tarcie na pobocznicach pali,
3) osiadanie gruntu zalegającego pod podstawami pali.
Osiadania całkowite, które są sumą wymienionych trzech składników, są nierównomiernie
rozłożone w planie fundamentu, co jest szczególnie widoczne, gdy obciążony obszar jest znacznych
rozmiarów. Osiadania pod środkiem obszaru są największe, a pod narożnikami najmniejsze.

4.1.1. Osiadania od nacisków przekazywanych bezpośrednio przez płytę fundamentową

Osiadania oblicza się dla obciążenia powierzchniowego q, które powinno w przybliżeniu
odpowiadać spodziewanym naciskom od płyty fundamentowej. Wstępnie można przyjąć wartość q
równą 25% sumy wszystkich obciążeń pionowych (wraz z ciężarem fundamentu):

F

F

F

z

z

L

B

G

V

V

q

⋅

⋅

+

+

⋅

≈

3

,

1

25

,

0

2

1

k

xi

K

zgj

(k

yi

)

k

zgj

q

zMx1

q

zV1

q

x1

q

zMx2

q

zV2

q

x2

V

z1

V

z2

M

y1

M

y2

H

x1

H

x2

płyta fund.

B

F

× L

F

pale

∅, L

p

2

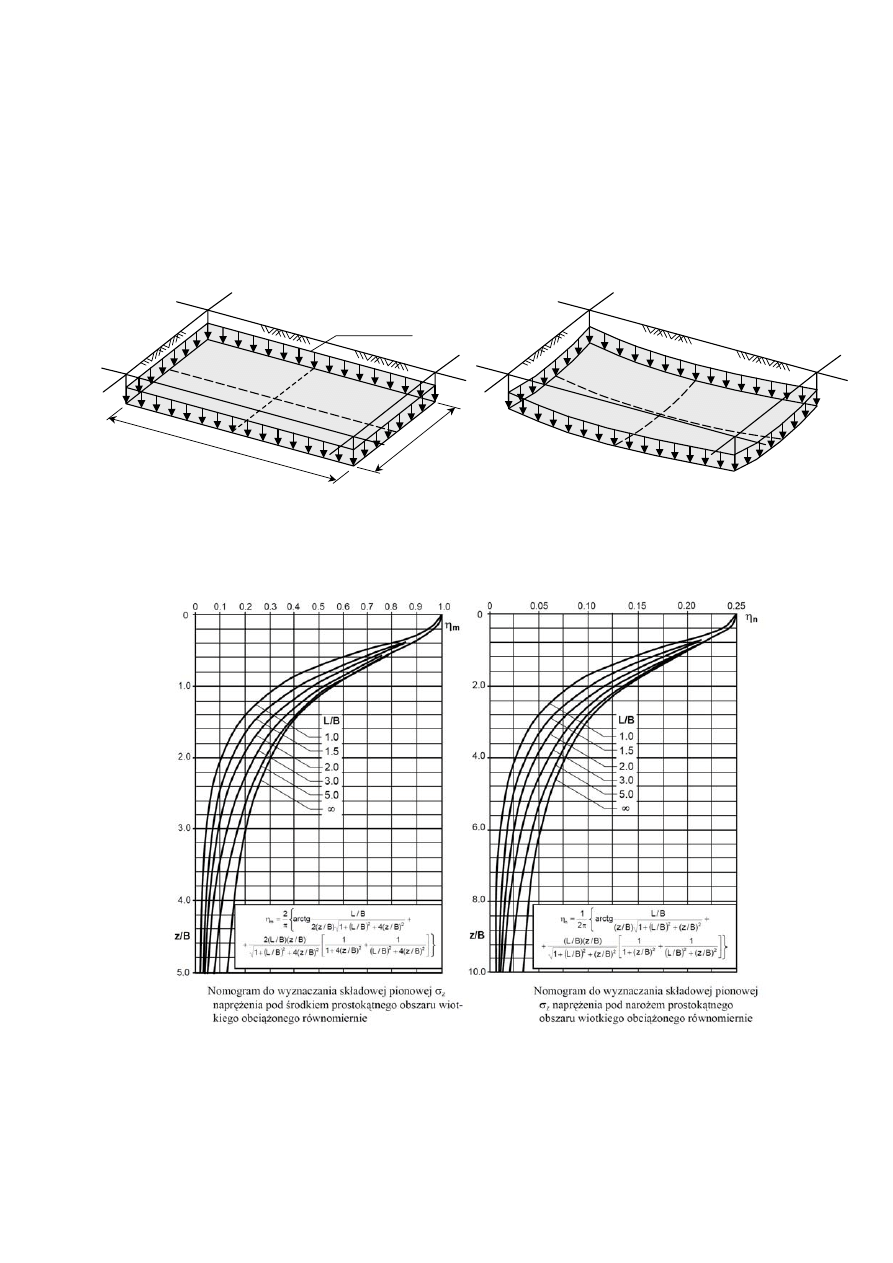
Obliczenia osiadań można wykonać np. metodą odkształceń jednoosiowych, z wykorzystaniem
metod punktu środkowego i narożnego obliczania naprężeń dodatkowych w podłożu gruntowym.
Można przyjąć taki sposób postępowania, że osiadania oblicza się w kilku charakterystycznych
punktach obszaru obciążonego: w środku (punkt 0), w połowach boków (punkty A i B) oraz
w narożnikach (punkt N). Następnie, rozkład osiadań w planie można opisać krzywoliniową
funkcją powierzchniową. Przy jednorodnej budowie podłoża gruntowego pod obszarem, cały układ
można potraktować jako symetryczny względem obu osi X i Y (rys. 4.2 i 4.4).

Rys. 4.2

Do obliczania naprężeń można wykorzystać poniższe nomogramy (rys. 4.3).

Rys. 4.3

B

F

L

F

obciążenie q

Obszar obciążony Osiadania

podłoża

0

N

B

A

N

B A

s

0

s

B

s

N

s

A

s

A

s

N

s

N

s

N

s

B

N

N

3

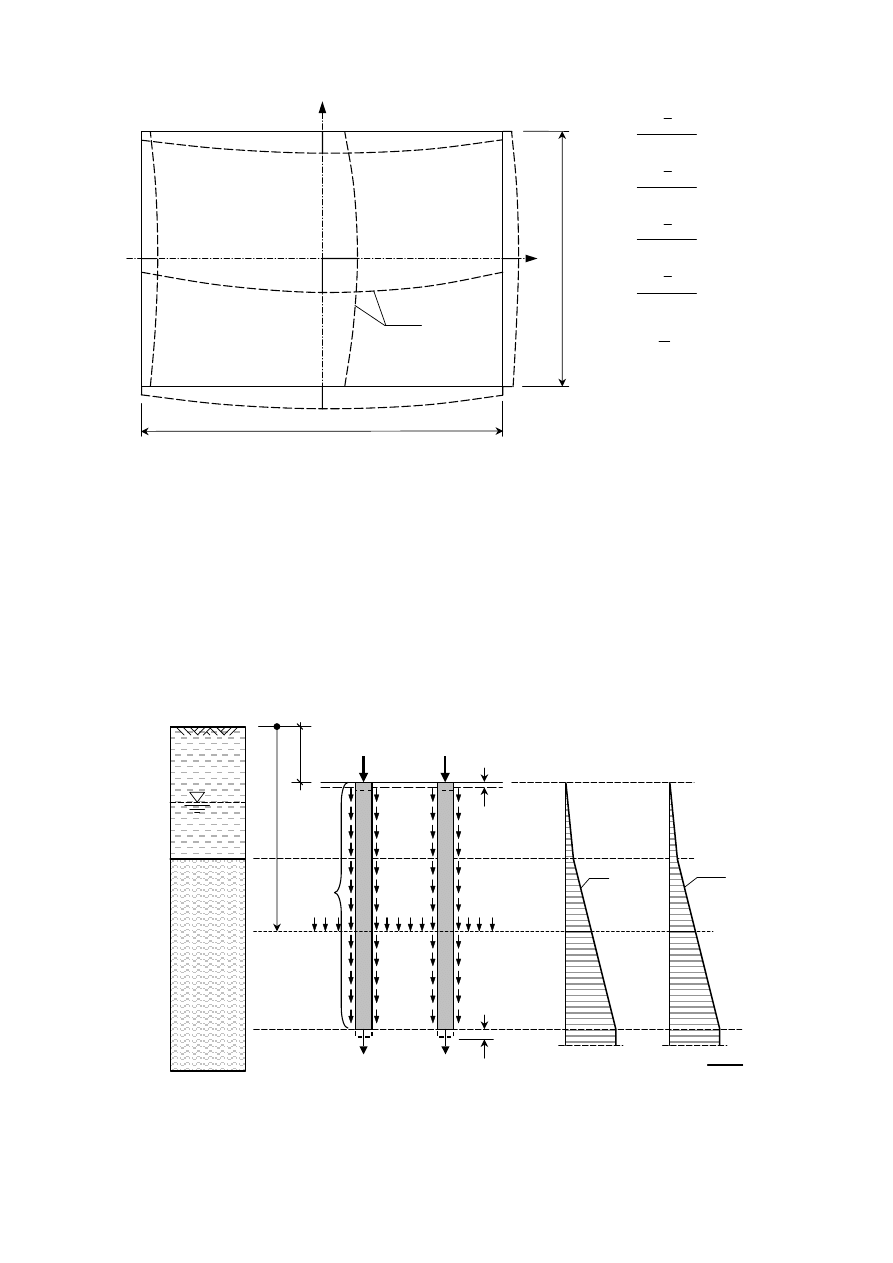
Rys. 4.4

Parametry funkcji powierzchni osiadań można wyznaczyć z zależności:
punkt "0": x = 0, y = 0

→ s(x,y) = s

0

→

wyznaczenie wartości d

punkt A : x = 0, y = B

F

/2

→ s(x,y) = s

A

→

wyznaczenie wartości b

punkt B : x = L

F

/2, y = 0

→ s(x,y) = s

B

→

wyznaczenie wartości a

punkt N : x = L

F

/2, y = B

F

/2

→ s(x,y) = s

N

→

wyznaczenie wartości c

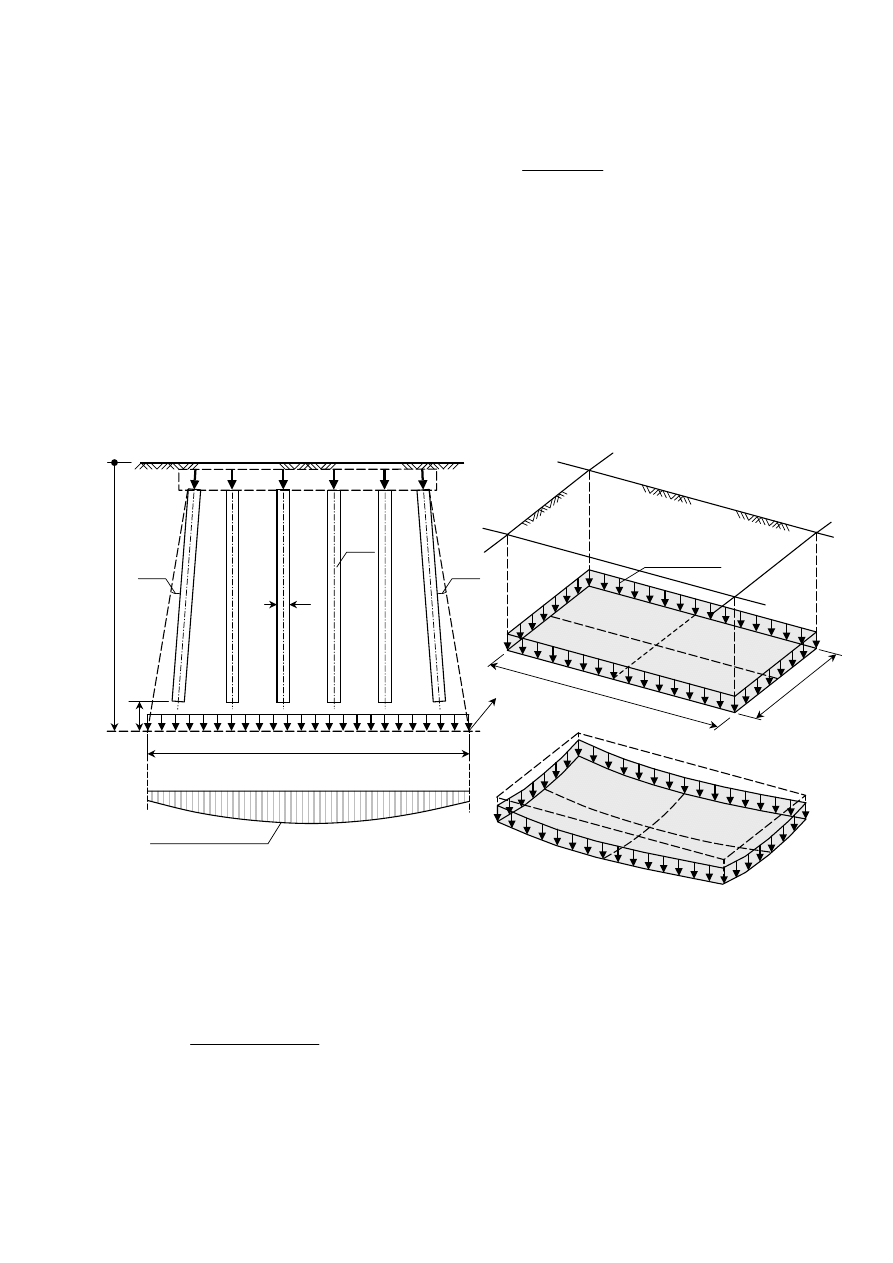
4.1.2. Osiadania od obciążeń przekazywanych przez tarcie na pobocznicach pali

Schemat ideowy powstawania omawianych osiadań s

fs

przedstawiono na rys. 4.5.

Rys. 4.5

Obciążenia Q

p

przykładane do głowic pali przekazywane są na grunt przez tarcie na pobocznicach

(Q

s

) i przez siły pod podstawami pali (Q

b

). Tarcie na pobocznicy f

s

, powodowane przez siłę Q

s

,

Osiadania poszczególnych punktów:

s

0

=

Σ ;

η

0

=

η

m

s

N

=

Σ ;

η

N

=

η

n

s

B

=

Σ ;

η

B

= 2

η

nB

s

C

=

Σ ;

η

C

= 2

η

nC

Funkcja powierzchni osiadań:

s(x,y) = ax

2

+ by

2

+ cx

2

y

2

+ d

L

F

B

F

O

N

A

B

Y

X

N

N

N

B

A

s

0

s

A

s

N

s

B

s

A

s

N

s

N

s

N

s

B

s(x,y)

Osiadania sumujemy do

poziomu podstaw pali.

zwg

Warstwa 2

Warstwa 1

Q

b

f

s

Q

p

Q

p

σ

v

(f

s

)

Q

s

Q

p

= Q

s

+ Q

b

Q

s

z

i

D

F

σ

v;i

(f

s

)

σ

v

(f

s

)

Q

s;i

Q

s;i

=

ψ

s

⋅

ΣR

s;cal;i

σ

v;i

(f

s

) =

Q

s;i

A

g

s

fs

s

p1

Q

b

η

0i

⋅q⋅h

i

M

0i

η

ni

⋅q⋅h

i

M

0i

η

Bi

⋅q⋅h

i

M

0i

η

Ci

⋅q⋅h

i

M

0i

Naciski dodatkowe:

q = q -

γ⋅D

F

4

sukcesywnie wprowadza w gruncie dodatkowe naprężenia pionowe

σ

v

(f

s

), które w konsekwencji

wywołują osiadania s

fs

tego gruntu.

Wartość obciążenia Q

p

pojedynczego pala można wstępnie przyjąć z wyrażenia:

p

F

z

z

p

n

G

V

V

Q

3

,

1

75

,

0

2

1

⋅

+

+

⋅

≈

gdzie: n

p

- liczba pali w fundamencie.

Rozdziału obciążenia Q

p

na składowe Q

s

i Q

b

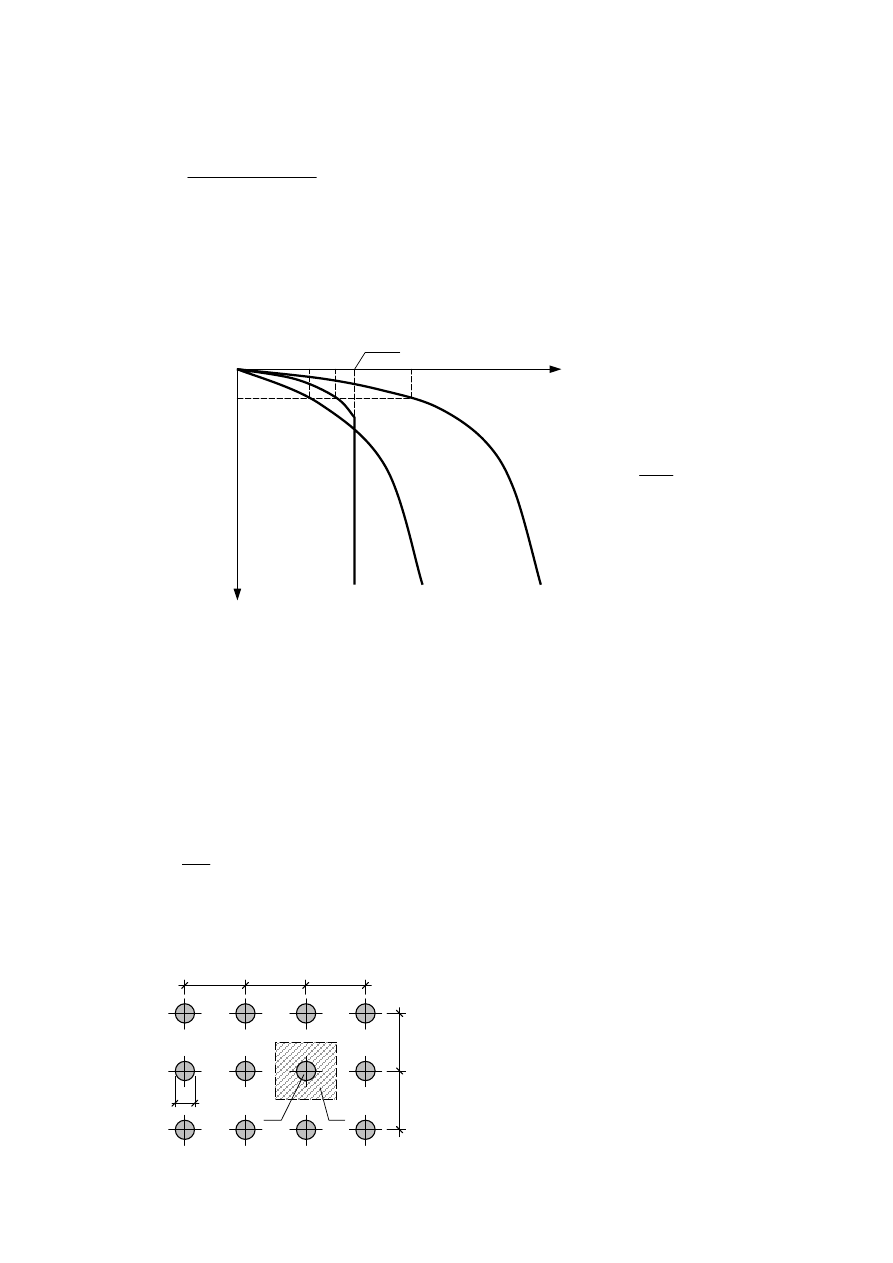
można dokonać wykorzystując charakterystykę Q-s

pala, wyznaczoną wcześniej metodą funkcji transformacyjnych (zobacz cz. 3) i odczytując wartości
Q

s

i Q

b

z wykresów, jak to pokazano na rys. 4.6.

Rys. 4.6

Z wykresu można jednocześnie odczytać wartość osiadania pala pojedynczego s

p1

od obciążenia Q

p

.

Następnie należy obliczyć wartość współczynnika

ψ

s

, który określa stopień zmobilizowania oporu

granicznego pobocznicy pala (wzór na rys. 4.6). Rozkład siły Q

s

na długości pala przyjmuje się

według rys. 4.5. Wartość siły Q

s;i

na głębokości z

i

oblicza się z wzoru:

∑

⋅

=

i

cal

s

s

i

s

R

Q

;

;

;

ψ

w którym:

ΣR

s;cal;i

- nośność graniczna pobocznicy pala zliczona od góry do głębokości z

i

.

Wartość naprężeń pionowych

σ

v;i

(f

s

) na głębokości z

i

obliczymy z wzoru:

g

i

s

s

i

v

A

Q

f

;

;

)

(

=

σ

gdzie: A

g

- powierzchnia przekroju poziomego bryły gruntu otaczającego pojedynczy pal,

określana zgodnie z rys. 4.7.

Rys. 4.7

R

s

R

c

R

R

b

Q

p

s

p1

s

Q

s

Q

b

R

s;cal

ψ

s

=

Q

s

R

s;cal

r

x

r

x

r

x

r

y

r

y

A

g

= r

x

⋅

r

y

- A

p

A

p

A

g

A

p

= 0,25

⋅π⋅

D

2

D

5

Przy obliczaniu naprężenia

σ

v

(f

s

) zakłada się, że jest ono równomierne na powierzchni A

g

. Rozkład

tego naprężenia z głębokością jest podobny do rozkładu siły Q

s

(rys. 4.5).

Osiadania podłoża gruntowego od naprężeń

σ

v

(f

s

) oblicza się według wzorów:

- pod elementami wewnętrznymi fundamentu:

∑

⋅

=

i

i

s

i

v

fs

M

h

f

s

;

0

;

0

;

)

(

σ

- pod elementami krawędziowymi fundamentu:

0

;

,

;

8

,

0

fs

B

A

fs

s

s

⋅

=

- pod elementami narożnymi fundamentu:

0

;

;

6

,

0

fs

N

fs

s

s

⋅

=

Sumowania osiadań dokonuje się do głębokości na poziomie podstaw pali.

4.1.3. Osiadania gruntu zalegającego pod podstawami pali

Podobnie jak osiadania gruntu pod płytą fundamentową, tak i osiadania gruntu zalegającego pod
podstawami pali są niejednorodne w planie, co jest wynikiem mniej więcej z takich samych
zjawisk.
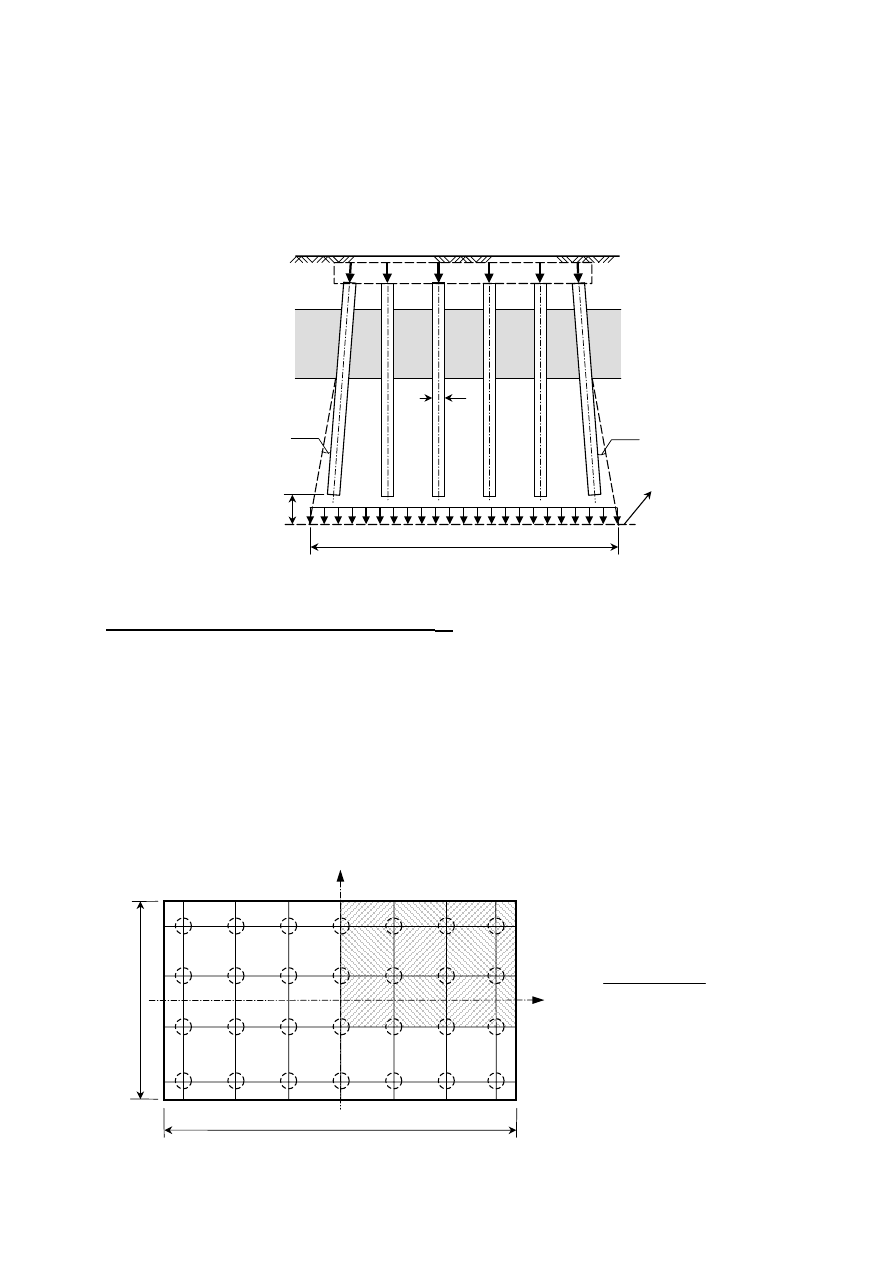
Osiadania s

pg

gruntu określa się według schematu przedstawionego na rys. 4.8.

Rys. 4.8

Na głębokości z

pg

(2D poniżej podstaw pali) wyznacza się obszar prostokątny o wymiarach L

z

× B

z

.

Wartość obciążenia równomiernie rozłożonego q

pg

działającego na wyznaczonym obszarze oblicza

się według wzoru:

z

z

F

z

z

pg

B

L

G

V

V

q

⋅

⋅

+

+

⋅

≈

3

,

1

75

,

0

2

1

Obliczenia rozkładu osiadań s

pg

przeprowadza się na podobnej zasadzie jak opisane w pkt. 4.1.1

obliczenia osiadań podłoża gruntowego pod płytą fundamentową. Można również zastosować
metodę odkształceń jednoosiowych oraz nomogramy do wyznaczania współczynników zaniku
naprężeń

η

m

i

η

n

, przy czym osiadania sumuje się do głębokości, do której naprężenia dodatkowe

B

z

L

z

obciążenie q

p

rozkład osiadania

0'

N'

B'

A'

N'

B'

A'

s

pg;0

s

pg;B

s

pg;N

s

pg;A

s

pg;A

N'

N'

s

pg;N

s

pg;N

s

pg;B

s

pg;N

D

2D

L

z

B

z

q

pg

α

=5

°

α

=5

°

" j "

rozkład osiadania s

pg

Q

pj

z

pg

6

σ

zd;i

od obciążenia q

pg

będą większe niż 20% naprężeń geostatycznych efektywnych (0,2

σ′

z

γ

;i

).

Podobnie jak poprzednio, rozkład osiadań można opisać funkcją powierzchniową s

pg

(x, y):

s

pg

(x, y) = a'x

2

+ b'y

2

+ c'x

2

y

2

+ d'

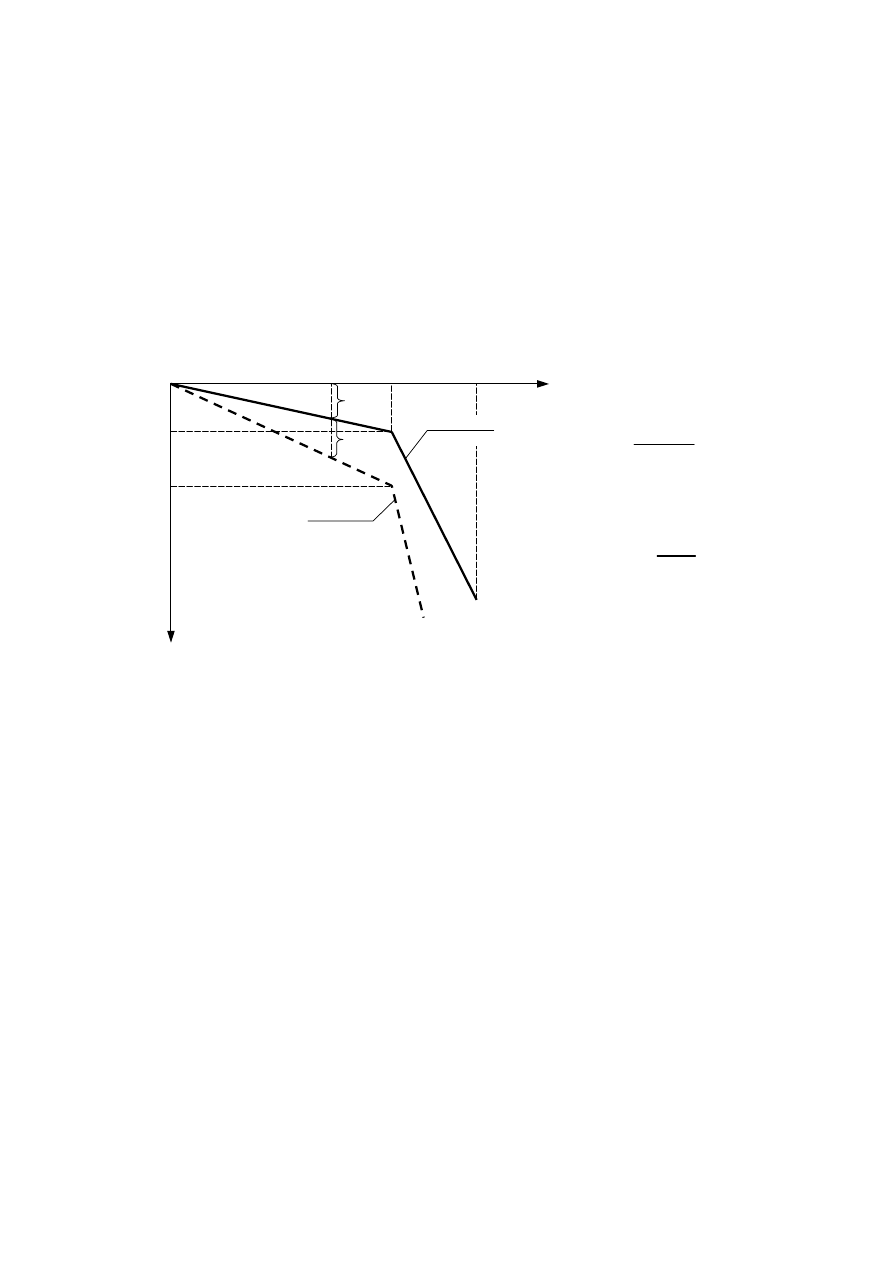
W przypadku, gdy w podłożu gruntowym występują warstwy gruntów słabych (organicznych)
zasięg oddziaływania pali na podłoże gruntowe (powierzchnie boczne odchylone względem pali
pod kątem

α

) określamy rozpoczynając do stropu warstw nośnych (jak na rys. 4.9).

Rys. 4.9

4.1.4. Rozkład sztywności gruntu pod płytą k

zg;j

W programie ROBOT nie ma jak dotąd możliwości definiowania niejednorodnej sprężystości
podłoża pod całą płytą fundamentową (np. za pomocą opisu jakąś funkcją powierzchniową).
Dlatego płytę fundamentową należy podzielić na określoną liczbę prostokątnych elementów (pod-
paneli) o różnych sztywnościach k

zgj

podłoża gruntowego pod każdym z nich, przy czym pod

danym elementem wartość sztywności k

zgj

będzie stała. Przy układzie symetrycznym, sztywności

gruntu wyznacza się pod elementami jednej z ćwiartek płyty fundamentowej (rys. 4.10).
W odpowiadających elementach pozostałych trzech ćwiartek wartości sztywności k

zgj

będą takie

same. Wskazane jest dostosowanie podziału fundamentu na elementy do układu pali.

Rys. 4.10

Sztywność podłoża gruntowego pod
elementem "j" oblicza się z wzoru:

k

zg;j

= [kPa/m]

s

j

; s

fs;j

; s

pg;j

- wartości składowych

osiadań pod środkiem geome-
trycznym elementu "j"

(s

j

+ s

fs;j

+ s

pg;j

)

q

L

F

B

F

Y

X

1 2 3

4

5 6 7

8

9 10

11

12

D

2D

L

z

B

z

q

pg

α

=5

°

α

=5

°

Q

pj

warstwa gruntu
słabego

7

W przyjętym rozwiązaniu sztywność podłoża pod płytą będzie zmieniała się skokowo. Zatem, im
gęstszy podział płyty na elementy składowe, tym dokładniejsze będą wyniki obliczeń. Przyjęty na
rys. 4.10 podział należy traktować jako poglądowy.

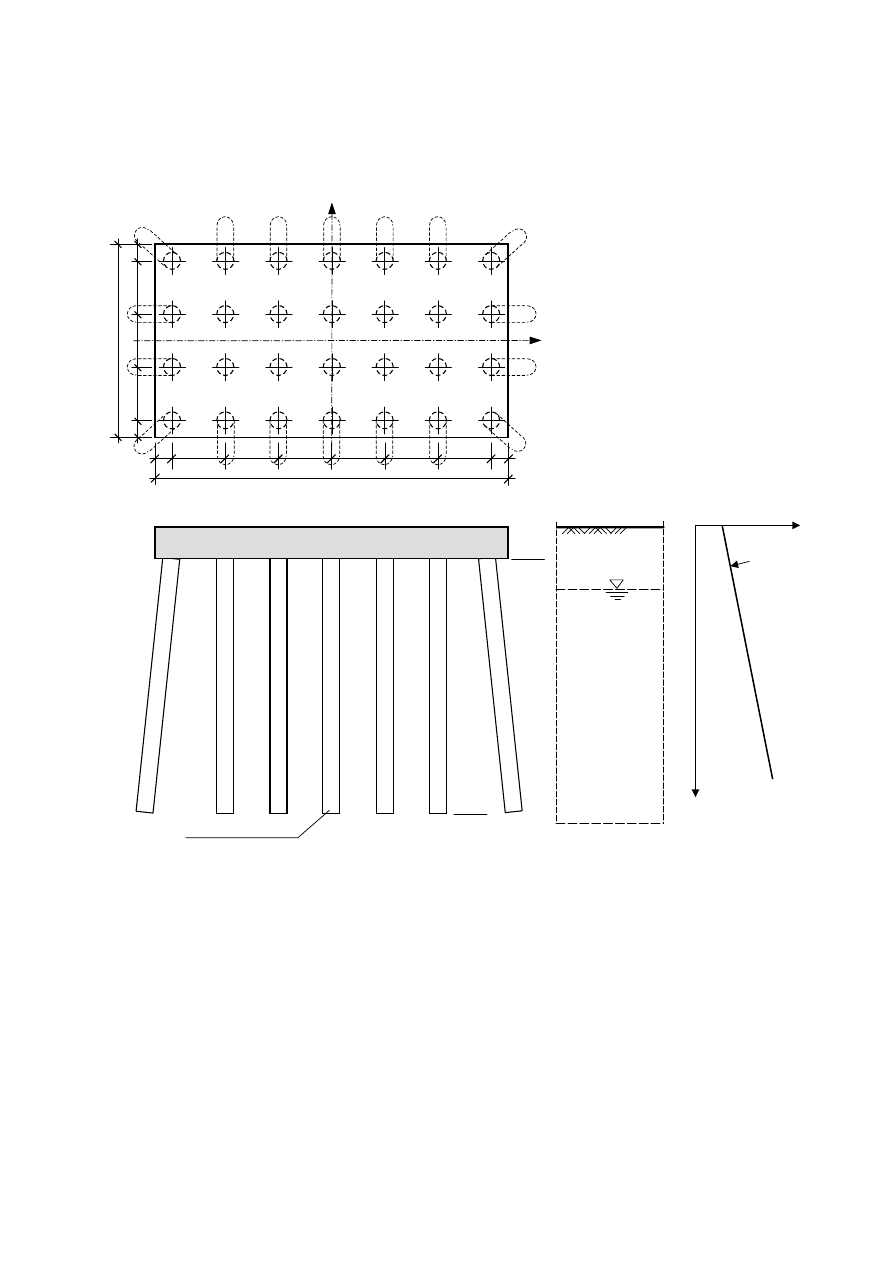
4.2. Określenie parametrów sztywności K

zg;j

pod podstawami pali

Sztywności K

zg;j

pod podstawami pali pracującymi w grupie są niejednakowe ze względu na

nierównomierne osiadania pali w planie fundamentu. Jednocześnie sztywności te są mniejsze od
sztywności pala pracującego pojedynczo. Sztywności K

z1g;j

i K

z2g;j

oblicza się na bazie sztywności

K

z1

i K

z2

pala pojedynczego i współczynnika korekcyjnego m

g;j

, zgodnie ze schematem

przedstawionym na rys. 4.11.

Rys. 4.11

Wartość składnika osiadania s

pg;j

pala "j" określa się z funkcji powierzchni osiadania s

pg

(x, y),

wyznaczonej w pkt. 4.1.3., w zależności od współrzędnych x

j

i y

j

lokalizacji podstawy pala "j".

R

R

c1;k

D

1

s

R

c2;k

K

z1

K

z2

Q

p

D

1g;j

K

z1g

K

z2g;j

s

p1

s

pg;j

pal

pojedynczy

pal

w grupie

s

p1

+ s

pg;j

m

g;j

=

s

p1

Współczynnik korekcyjny:

Parametry wykresu pala w grupie:

K

z1g;j

= m

g;j

⋅ K

z1

D

1g;j

=

D

1

m

g;j

K

z2g;j

= m

g;j

⋅ K

z2

8

4.3. Przykład obliczeniowy

Określić rozkład sztywności k

zg

podłoża gruntowego pod płytą oraz parametrów sztywności K

zg

pod

podstawami pali dla fundamentu płytowo-palowego przedstawionego na rys. 4.12.

Rys. 4.12

Do obliczeń przyjęto: q = 75 kPa, Q

p

= 1000 kN.

zwg

0,0

-1,5

-3,0

ił pylasto-

piaszczysty

I

L

=0,30

γ

= 20 kN/m

3

γ

' = 10 kN/m

3

φ

' = 18

°

c' = 45 kPa

M

0

[MPa]

z [m ppt]

10

0

M

0

(z) =

= 15+3,0

⋅z

[MPa]

PLAN

Profil geotechniczny

L

F

= 16,60

B

F

= 9,10

Y

X

2,50

0,8

2,50

2,50

2,50

2,50

2,50

0,8

0,

8

2,50

2,50

2,50

0,

8

-13,5

10:1

10:1

pale wiercone

D = 0,8 m, L = 12 m

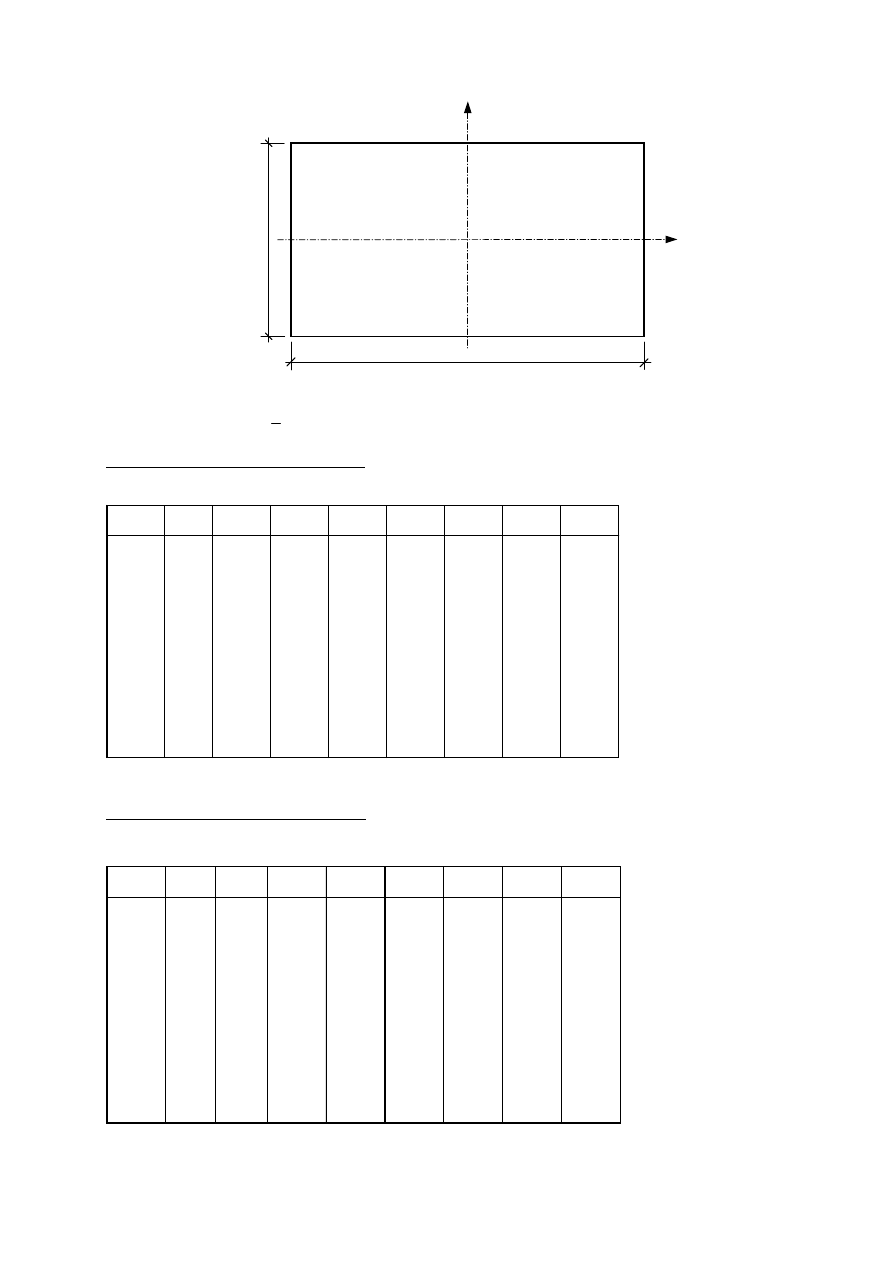
9

4.3.1. Obliczenia osiadań od nacisków q

Rys. 4.13

Naciski dodatkowe:

45

5

,

1

20

75

=

⋅

−

=

⋅

−

=

F

D

q

q

γ

kPa

Obliczenie osiadania w punkcie "0"
L

0

= 16,60 m; B

0

= 9,10 m; L

0

/B

0

= 1,82;

η

0

=

η

m

Rz

i

h

i

z'

i

z'

i

/B

0

η

0i

σ

d0zi

M

0i

s

0i

Σ

s

0i

[m ppt]

[m]

[m]

[-]

[-]

[kPa]

[MPa]

[mm]

[mm]

0,0

0,0

15,0

1,5

1,5

0,00

0

19,5

0,00

0,00

2,0

0,5

0,25

0,055

0,9999

45,00

20,3

1,11

1,11

3,0

1,0

1,00

0,220

0,9954

44,79

22,5

1,99

3,10

4,0

1,0

2,00

0,440

0,9680

43,56

25,5

1,71

4,81

5,0

1,0

3,00

0,659

0,9126

41,07

28,5

1,44

6,25

6,0

1,0

4,00

0,879

0,8383

37,72

31,5

1,20

7,45

7,0

1,0

5,00

1,099

0,7565

34,04

34,5

0,99

8,44

8,0

1,0

6,00

1,319

0,6755

30,40

37,5

0,81

9,25

9,0

1,0

7,00

1,538

0,5999

27,00

40,5

0,67

9,91

10,0

1,0

8,00

1,758

0,5317

23,93

43,5

0,55

10,46

11,0

1,0

9,00

1,978

0,4713

21,21

46,5

0,46

10,92

12,0

1,0

10,00

2,198

0,4185

18,83

49,5

0,38

11,30

13,0

1,0

11,00

2,418

0,3725

16,76

52,5

0,32

11,62

13,5

0,5

11,50

2,527

0,3518

15,83

54,0

0,15

11,76

Obliczenie osiadania w punkcie "A"

L

A

= 9,10 m; B

A

= 8,3 m; L

A

/B

A

= 1,1;

η

A

= 2

η

n

Rz

i

h

i

z'

i

z'

i

/B

A

η

Ai

σ

dAzi

M

0i

s

Ai

Σ s

Ai

[m ppt]

[m]

[m]

[-]

[-]

[kPa]

[MPa]

[mm]

[mm]

0,0

0,0

15,0

1,5

1,5

0,00

0

19,5

0,00

0,00

2,0

0,5

0,25

0,030

0,5000

22,50

20,3

0,56

0,56

3,0

1,0

1,00

0,120

0,4994

22,47

22,5

1,00

1,55

4,0

1,0

2,00

0,241

0,4957

22,31

25,5

0,87

2,43

5,0

1,0

3,00

0,361

0,4865

21,89

28,5

0,77

3,20

6,0

1,0

4,00

0,482

0,4713

21,21

31,5

0,67

3,87

7,0

1,0

5,00

0,602

0,4505

20,27

34,5

0,59

4,46

8,0

1,0

6,00

0,723

0,4255

19,15

37,5

0,51

4,97

9,0

1,0

7,00

0,843

0,3981

17,91

40,5

0,44

5,41

10,0

1,0

8,00

0,964

0,3696

16,63

43,5

0,38

5,79

11,0

1,0

9,00

1,084

0,3413

15,36

46,5

0,33

6,12

12,0

1,0

10,00

1,205

0,3141

14,13

49,5

0,29

6,41

13,0

1,0

11,00

1,325

0,2883

12,98

52,5

0,25

6,66

13,5

0,5

11,50

1,386

0,2762

12,43

54,0

0,12

6,77

L

F

= 16,60

B

F

= 9,10

Y

X

O

A

A

B

B

N

N

N

N

q = 75 kPa

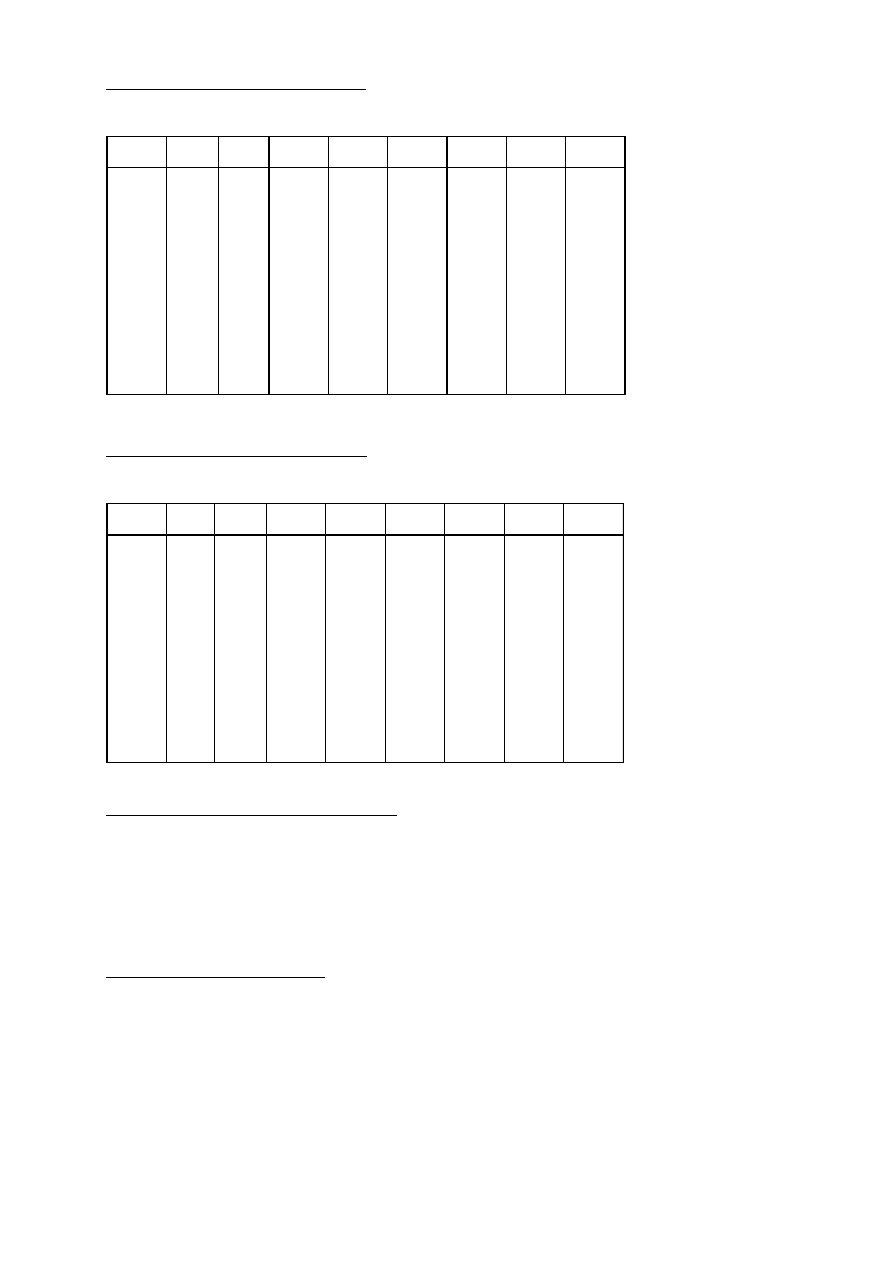
10

Obliczenie osiadania w punkcie "B"

L

B

= 16,60 m; B

B

= 4,55 m; L

B

/B

B

= 3,65;

η

B

= 2

η

n

Rz

i

h

i

z'

i

z'

i

/B

B

η

Bi

σ

dBzi

M

0i

s

Bi

Σ s

Bi

[m ppt]

[m]

[m]

[-]

[-]

[kPa]

[MPa]

[mm]

[mm]

0,0

0,0

10,0

1,5

1,5

0,00

0

12,0

0,00

0,00

2,0

0,5

0,25

0,055

0,5000

22,50

20,3

0,56

0,56

3,0

1,0

1,00

0,220

0,4979

22,40

22,5

1,00

1,55

4,0

1,0

2,00

0,440

0,4853

21,84

25,5

0,86

2,41

5,0

1,0

3,00

0,659

0,4604

20,72

28,5

0,73

3,13

6,0

1,0

4,00

0,879

0,4275

19,24

31,5

0,61

3,75

7,0

1,0

5,00

1,099

0,3920

17,64

34,5

0,51

4,26

8,0

1,0

6,00

1,319

0,3573

16,08

37,5

0,43

4,69

9,0

1,0

7,00

1,538

0,3253

14,64

40,5

0,36

5,05

10,0

1,0

8,00

1,758

0,2964

13,34

43,5

0,31

5,35

11,0

1,0

9,00

1,978

0,2706

12,18

46,5

0,26

5,62

12,0

1,0

10,00

2,198

0,2477

11,14

49,5

0,23

5,84

13,0

1,0

11,00

2,418

0,2272

10,23

52,5

0,19

6,04

13,5

0,5

11,50

2,527

0,2179

9,80

54,0

0,09

6,13

Obliczenie osiadania w punkcie "N"

L

N

= 16,60 m; B

N

= 9,10 m; L

N

/B

N

= 1,82;

η

N

=

η

n

Rz

i

h

i

z'

i

z'

i

/B

N

η

Ni

σ

dNzi

M

0i

s

Ni

Σ s

Ni

[m ppt]

[m]

[m]

[-]

[-]

[kPa]

[MPa]

[mm]

[mm]

0,0

0,0

15,0

1,5

1,5

0,00

0

19,5

0,00

0,00

2,0

0,5

0,25

0,027

0,2500

11,25

20,3

0,28

0,28

3,0

1,0

1,00

0,110

0,2498

11,24

22,5

0,50

0,78

4,0

1,0

2,00

0,220

0,2488

11,20

25,5

0,44

1,22

5,0

1,0

3,00

0,330

0,2463

11,08

28,5

0,39

1,61

6,0

1,0

4,00

0,440

0,2420

10,89

31,5

0,35

1,95

7,0

1,0

5,00

0,549

0,2359

10,61

34,5

0,31

2,26

8,0

1,0

6,00

0,659

0,2282

10,27

37,5

0,27

2,53

9,0

1,0

7,00

0,769

0,2193

9,87

40,5

0,24

2,78

10,0

1,0

8,00

0,879

0,2096

9,43

43,5

0,22

2,99

11,0

1,0

9,00

0,989

0,1994

8,97

46,5

0,19

3,19

12,0

1,0

10,00

1,099

0,1891

8,51

49,5

0,17

3,36

13,0

1,0

11,00

1,209

0,1789

8,05

52,5

0,15

3,51

13,5

0,5

11,50

1,264

0,1738

7,82

54,0

0,07

3,58

Parametry funkcji powierzchni osiadań:
punkt "0" : x = 0, y = 0

→ s(x,y) = s

0

= 11,76 mm

→

d = 11,76

punkt A: x = 0, y = 4,55 m

→ s(x,y) = s

A

= 6,77 mm

→

b = - 0,241

punkt B: x = 8,3 m, y = 0

→ s(x,y) = s

B

= 6,13 mm

→

a = - 0,0817

punkt N: x = 8,3 m, y = 4,55 m

→ s(x,y) = s

N

= 3,58 mm

→

c = 0,00171

Funkcja powierzchni osiadań:

s(x,y) = -0,0817x

2

-0,241y

2

+ 0,00171x

2

y

2

+ 11,76 [mm]; x, y [m]

11

4.3.2. Obliczenia osiadań od obciążeń przekazywanych przez tarcie na pobocznicach pali

Do obliczeń rozpatrywanych osiadań potrzebne są wyniki obliczeń nośności pala i charakterystyki
obciążenie-osiadanie (Q-s).

Wyniki obliczeń nośności pala metodą

β

L

z

h

i

σ

'

vi

φ

'

i

c'

i

β

i

f

si

R

si

R

s;cal

q

bi

R

b;cal

R

c;cal

R

s;k

R

b;k

R

c;k

R

s;d

R

b;d

R

c;d

[m]

[m ppt] [m] [kPa]

[

o

]

[kPa]

[kPa]

[kN]

[kN]

[kPa]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

[kN]

0,0

0,0

0,0

0,0

1,5

0,0

30,0 18,0 45,0

0,32

9,52

0,0

0,0

1,0

2,5

1,0

50,0 18,0 45,0

0,32 12,70

28,7

28,7

2,0

3,5

1,0

65,0 18,0 45,0

0,32 18,25

41,3

70,0

3,0

4,5

1,0

75,0 18,0 45,0

0,32 22,22

50,3

120,3

4,0

5,5

1,0

85,0 18,0 45,0

0,32 25,40

57,4

177,7

5,0

6,5

1,0

95,0 18,0 45,0

0,32 28,57

64,6

242,3

6,0

7,5

1,0 105,0 18,0 45,0

0,32 31,74

71,8

314,1

1141,2

573,6

887,8

275,6 503,2

778,7 250,5 457,4

707,9

7,0

8,5

1,0 115,0 18,0 45,0

0,32 34,92

79,0

393,1

1193,7

600,0

993,2

344,9 526,3

871,2 313,5 478,5

792,0

8,0

9,5

1,0 125,0 18,0 45,0

0,32 38,09

86,2

479,3

1246,3

626,4

1105,7

420,4 549,5

969,9 382,2 499,6

881,8

9,0

10,5

1,0 135,0 18,0 45,0

0,32 41,27

93,3

572,6

1298,8

652,9

1225,5

502,3 572,7 1075,0 456,7 520,6

977,3

10,0

11,5

1,0 145,0 18,0 45,0

0,32 44,44 100,5

673,2

1351,4

679,3

1352,4

590,5 595,8 1186,3 536,8 541,7 1078,5

11,0

12,5

1,0 155,0 18,0 45,0

0,32 47,62 107,7

780,9

1403,9

705,7

1486,6

685,0 619,0 1304,0 622,7 562,7 1185,5

12,0

13,5

1,0 165,0 18,0 45,0

0,32 50,79 114,9

895,8

1456,5

732,1

1627,9

785,8 642,2 1427,9 714,3 583,8 1298,1

13,0

14,5

1,0 175,0 18,0 45,0

0,32 53,97 122,1 1017,8

1509,0

758,5

1776,3

892,8 665,4 1558,2 811,7 604,9 1416,5

14,0

15,5

1,0 185,0 18,0 45,0

0,32 57,14 129,2 1147,1

1561,6

784,9

1932,0

1006,2 688,5 1694,7 914,7 625,9 1540,7

15,0

16,5

1,0 195,0 18,0 45,0

0,32 60,31 136,4 1283,5

1614,1

811,3

2094,8

1125,9 711,7 1837,6 1023,5 647,0 1670,5

16,0

17,5

1,0 205,0 18,0 45,0

0,32 63,49 143,6 1427,1

1640,4

824,5

2251,7

1251,9 723,3 1975,1 1138,1 657,5 1795,6

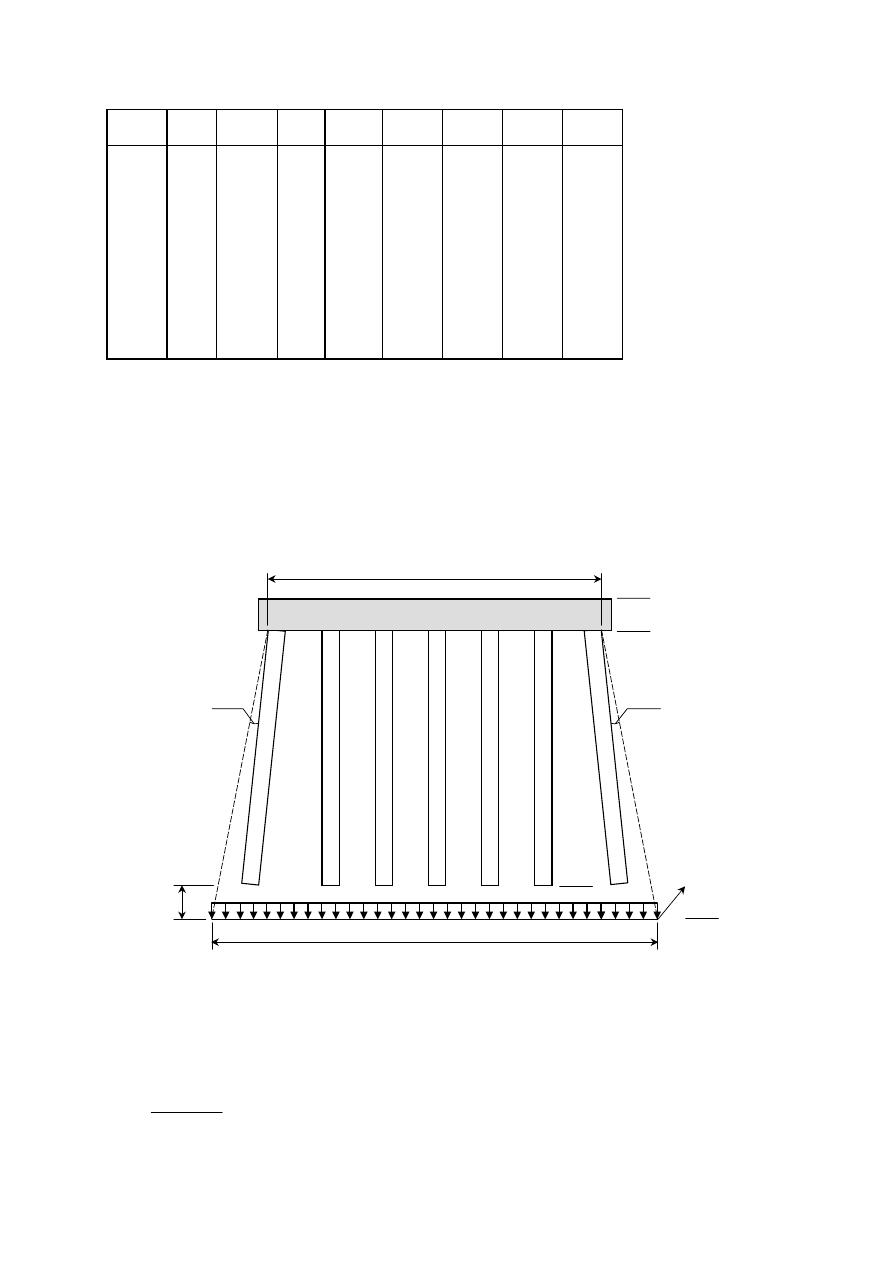
Wyniki obliczeń charakterystyki Q-s pala pojedynczego

s [mm]

Q

s ;k

[kN]

Q

b ;k

[kN]

Q

c ;k

[kN]

0,0

0,0

0,0

0,0

1,0

467,4

101,5

568,9

2,0

555,8

143,6

699,3

3,0

615,1

175,8

790,9

4,0

660,9

203,0

864,0

6,0

731,5

248,6

980,1

8,0

786,0

287,1

1073,1

10,0

786,0

321,0

1107,0

15,0

786,0

393,1

1179,1

20,0

786,0

454,0

1240,0

25,0

786,0

507,5

1293,5

30,0

786,0

556,0

1342,0

35,0

786,0

600,5

1386,5

40,0

786,0

642,0

1428,0

0

5

10

15

20

25

30

35

40

0

300

600

900

1200

1500

Q [kN]

s

[mm]

Z wykresów Q-s odczytano:
dla Q

p

= 1000 kN

→ Q

s

= 735 kN, Q

b

= 265 kN, s

p1

≈ 6,0 mm

Współczynnik zmobilizowania oporu granicznego pobocznicy pala:

82

,

0

8

,

895

0

,

735

;

=

=

=

cal

s

s

s

R

Q

ψ

Pole przekroju poziomego bryły gruntu otaczającego pojedynczy pal:

75

,

5

8

,

0

25

,

0

50

,

2

50

,

2

2

=

⋅

−

⋅

=

−

⋅

=

π

p

y

x

g

A

r

r

A

m

2

Q

p

= 1000 kN

Q

c

Q

s

Q

b

s

p1

≈ 6 mm

12

Wyniki obliczeń osiadań s

fs

Rz

i

h

i

Σ

R

s ;cal ;i

ψ

s

Q

s ;i

σ

v;i

(fs)

M

0i

s

fs; 0 ;i

s

fs; 0

[m ppt]

[m]

[kN]

[-]

[kN]

[kPa]

[MPa]

[mm]

[mm]

0,0
1,5

0,0

0,0

0,82

0,0

0,00

19,5

0,00

0,00

2,5

1,0

28,7

0,82

23,6

4,10

21,0

0,20

0,20

3,5

1,0

70,0

0,82

57,4

9,98

24,0

0,42

0,61

4,5

1,0

120,3

0,82

98,6

17,15

27,0

0,64

1,25

5,5

1,0

177,7

0,82

145,7

25,34

30,0

0,84

2,09

6,5

1,0

242,3

0,82

198,7

34,56

33,0

1,05

3,14

7,5

1,0

314,1

0,82

257,6

44,80

36,0

1,24

4,38

8,5

1,0

393,1

0,82

322,4

56,06

39,0

1,44

5,82

9,5

1,0

479,3

0,82

393,0

68,35

42,0

1,63

7,45

10,5

1,0

572,6

0,82

469,6

81,66

45,0

1,81

9,26

11,5

1,0

673,2

0,82

552,0

96,00

48,0

2,00

11,26

12,5

1,0

780,9

0,82

640,3

111,36

51,0

2,18

13,45

13,5

1,0

895,8

0,82

734,5

127,74

54,0

2,37

15,81

Elementy wewnętrzne: s

fs;0

= 15,81 mm

Elementy krawędziowe: s

fs;A,B

= 0,8

⋅15,81 = 12,65 mm

Elementy narożne: s

fs;N

= 0,6

⋅15,81 = 9,49 mm

4.3.3. Obliczenia osiadań gruntu zalegającego pod podstawami pali

Wyznaczenie obszaru L

z

× B

z

:

Rys. 4.14

90

,

20

)

5

tan

6

,

13

6

,

13

1

,

0

(

2

80

,

15

=

°

⋅

+

⋅

⋅

+

=

z

L

m

40

,

13

)

5

tan

6

,

13

6

,

13

1

,

0

(

2

80

,

0

10

,

9

=

°

⋅

+

⋅

⋅

+

−

=

z

B

m

Naciski q

pg

:

0

,

100

4

,

13

9

,

20

1000

28

=

⋅

⋅

=

pg

q

kPa

-1,5

-13,5

10:1

10:1

-15,1

0,0

α

= 5

°

α

= 5

°

2D = 1,60

L

z

B

z

q

pg

15,80

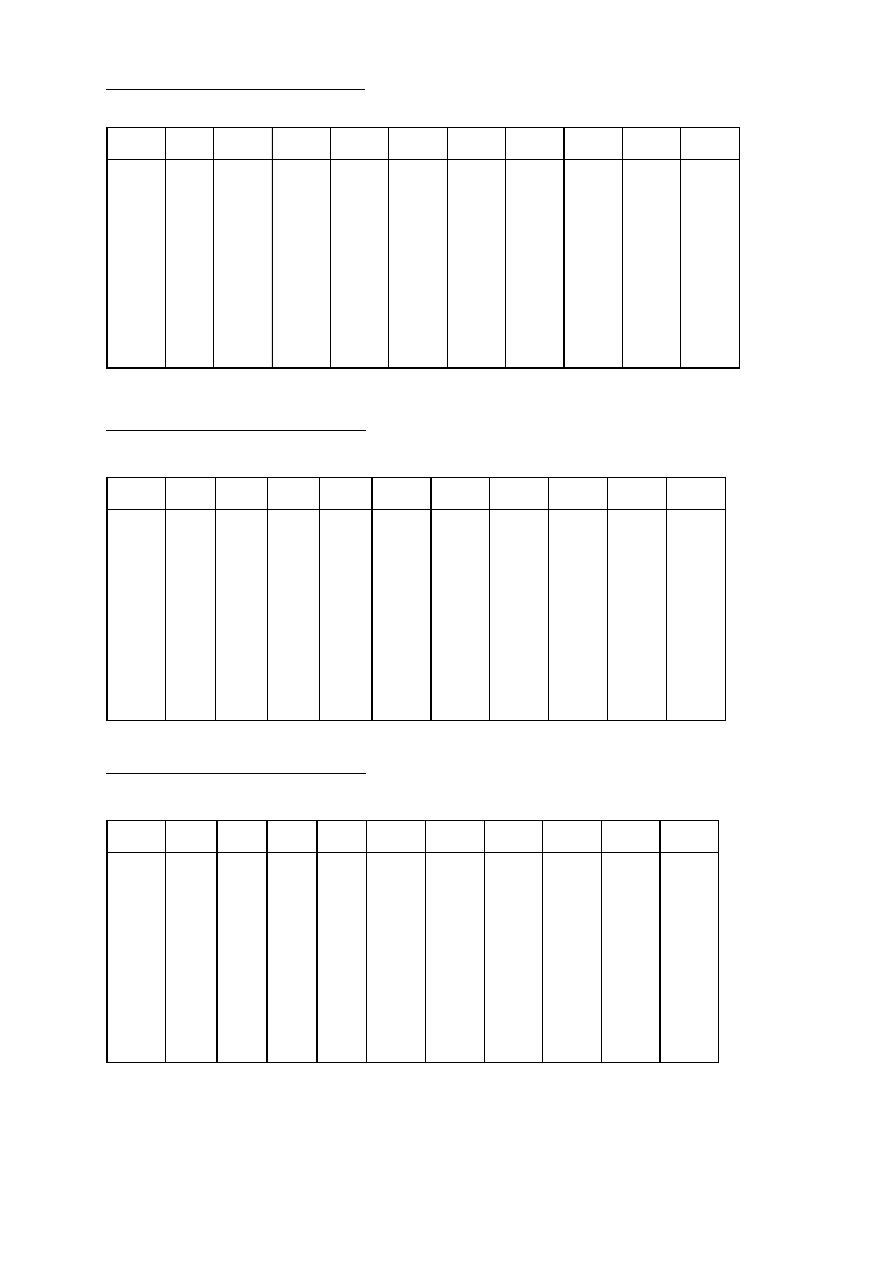
13

Obliczenie osiadania w punkcie "0"
L

0

= 20,90 m; B

0

= 13,40 m; L

0

/B

0

= 1,56;

η

0

=

η

m

Rz

i

h

i

z'

i

σ

γ z ;i

0,2

σ

γ z ;i

z'

i

/B

0

η

0i

σ

d0z ;i

M

0 ;i

s

pg; 0 ;i

Σ s

pg; 0 ;i

[m ppt]

[m]

[m]

[kPa]

[kPa]

[-]

[-]

[kPa]

[MPa]

[mm]

[mm]

15,1

0,0

0,00

181,0

36,2

0

100,00

60,3

0,00

0,00

16,1

1,0

0,50

186,0

37,2

0,075

0,9998

99,98

61,8

1,62

1,62

17,1

1,0

1,50

196,0

39,2

0,224

0,9948

99,48

64,8

1,54

3,15

18,1

1,0

2,50

206,0

41,2

0,373

0,9780

97,80

67,8

1,44

4,60

19,1

1,0

3,50

216,0

43,2

0,522

0,9467

94,67

70,8

1,34

5,93

20,1

1,0

4,50

226,0

45,2

0,672

0,9026

90,26

73,8

1,22

7,16

21,1

1,0

5,50

236,0

47,2

0,821

0,8493

84,93

76,8

1,11

8,26

22,1

1,0

6,50

246,0

49,2

0,970

0,7910

79,10

79,8

0,99

9,25

23,1

1,0

7,50

256,0

51,2

1,119

0,7313

73,13

82,8

0,88

10,14

24,1

1,0

8,50

266,0

53,2

1,269

0,6727

67,27

85,8

0,78

10,92

25,1

1,0

9,50

276,0

55,2

1,418

0,6167

61,67

88,8

0,69

11,61

26,1

1,0

10,50

286,0

57,2

1,567

0,5645

56,45

91,8

0,61

12,23

27,1

1,0

11,50

296,0

59,2

1,716

0,5163

51,63

94,8

0,54

12,77

28,1

1,0

12,50

306,0

61,2

1,866

0,4724

47,24

97,8

0,48

13,26

Obliczenie osiadania w punkcie "A"

L

A

= 13,40 m; B

A

= 10,45 m; L

A

/B

A

= 1,28;

η

A

= 2

η

n

Rz

i

h

i

z'

i

σ

γ z ;i

0,2

σ

γ z ;i

z'

i

/B

A

η

Ai

σ

dAz ;i

M

0 ;i

s

pg;A ;i

Σ s

pg ;A ;i

[m ppt]

[m]

[m]

[kPa]

[kPa]

[-]

[-]

[kPa]

[MPa]

[mm]

[mm]

15,1

0,0

0,00

181,0

36,2

0

50,00

60,3

0,00

0,00

16,1

1,0

0,50

186,0

37,2

0,048

0,5000

50,00

61,8

0,81

0,81

17,1

1,0

1,50

196,0

39,2

0,144

0,4992

49,92

64,8

0,77

1,58

18,1

1,0

2,50

206,0

41,2

0,239

0,4964

49,64

67,8

0,73

2,31

19,1

1,0

3,50

216,0

43,2

0,335

0,4907

49,07

70,8

0,69

3,00

20,1

1,0

4,50

226,0

45,2

0,431

0,4816

48,16

73,8

0,65

3,66

21,1

1,0

5,50

236,0

47,2

0,526

0,4691

46,91

76,8

0,61

4,27

22,1

1,0

6,50

246,0

49,2

0,622

0,4537

45,37

79,8

0,57

4,84

23,1

1,0

7,50

256,0

51,2

0,718

0,4359

43,59

82,8

0,53

5,36

24,1

1,0

8,50

266,0

53,2

0,813

0,4165

41,65

85,8

0,49

5,85

25,1

1,0

9,50

276,0

55,2

0,909

0,3959

39,59

88,8

0,45

6,29

26,1

1,0

10,50

286,0

57,2

1,005

0,3750

37,50

91,8

0,41

6,70

27,1

1,0

11,50

296,0

59,2

1,100

0,3541

35,41

94,8

0,37

7,08

28,1

1,0

12,50

306,0

61,2

1,196

0,3335

33,35

97,8

0,34

7,42

Obliczenie osiadania w punkcie "B"

L

B

= 20,90 m; B

B

= 6,70 m; L

B

/B

B

= 3,12;

η

B

= 2

η

n

Rz

i

h

i

z'

i

σ

γ z ;i

0,2

σ

γ z ;i

z'

i

/B

B

η

Bi

σ

dBzi

M

0 ;i

s

pg;B ;i

Σ s

pg ;B ;i

[m ppt]

[m]

[m]

[kPa]

[kPa]

[-]

[-]

[kPa]

[MPa]

[mm]

[mm]

1,5

0,0

0,00

181,0

36,2

0

50,00

12,0

0,00

0,00

2,0

1,0

0,50

186,0

37,2

0,075

0,4999

49,99

61,8

0,81

0,81

3,0

1,0

1,50

196,0

39,2

0,224

0,4977

49,77

64,8

0,77

1,58

4,0

1,0

2,50

206,0

41,2

0,373

0,4905

49,05

67,8

0,72

2,30

5,0

1,0

3,50

216,0

43,2

0,522

0,4771

47,71

70,8

0,67

2,97

6,0

1,0

4,50

226,0

45,2

0,672

0,4584

45,84

73,8

0,62

3,60

7,0

1,0

5,50

236,0

47,2

0,821

0,4361

43,61

76,8

0,57

4,16

8,0

1,0

6,50

246,0

49,2

0,970

0,4120

41,20

79,8

0,52

4,68

9,0

1,0

7,50

256,0

51,2

1,119

0,3875

38,75

82,8

0,47

5,15

10,0

1,0

8,50

266,0

53,2

1,269

0,3634

36,34

85,8

0,42

5,57

11,0

1,0

9,50

276,0

55,2

1,418

0,3404

34,04

88,8

0,38

5,95

12,0

1,0

10,50

286,0

57,2

1,567

0,3188

31,88

91,8

0,35

6,30

13,0

1,0

11,50

296,0

59,2

1,716

0,2985

29,85

94,8

0,31

6,62

13,5

1,0

12,50

306,0

61,2

1,866

0,2797

27,97

97,8

0,29

6,90

14

Obliczenie osiadania w punkcie "N"

L

N

= 20,90 m; B

N

= 13,40 m; L

N

/B

N

= 1,56;

η

N

=

η

n

Rz

i

h

i

z'

i

σ

γ z ;i

0,2

σ

γ z ;i

z'

i

/B

N

η

Ni

σ

dNz ;i

M

0 ;i

s

pg;N ;i

Σ s

pg ;N ;i

[m ppt]

[m]

[m]

[kPa]

[kPa]

[-]

[-]

[kPa]

[MPa]

[mm]

[mm]

15,1

0,0

0,00

181,0

36,2

0

25,00

60,3

0,00

0,00

16,1

1,0

0,50

186,0

37,2

0,037

0,2500

25,00

61,8

0,40

0,40

17,1

1,0

1,50

196,0

39,2

0,112

0,2498

24,98

64,8

0,39

0,79

18,1

1,0

2,50

206,0

41,2

0,187

0,2492

24,92

67,8

0,37

1,16

19,1

1,0

3,50

216,0

43,2

0,261

0,2480

24,80

70,8

0,35

1,51

20,1

1,0

4,50

226,0

45,2

0,336

0,2459

24,59

73,8

0,33

1,84

21,1

1,0

5,50

236,0

47,2

0,410

0,2429

24,29

76,8

0,32

2,16

22,1

1,0

6,50

246,0

49,2

0,485

0,2390

23,90

79,8

0,30

2,46

23,1

1,0

7,50

256,0

51,2

0,560

0,2342

23,42

82,8

0,28

2,74

24,1

1,0

8,50

266,0

53,2

0,634

0,2287

22,87

85,8

0,27

3,01

25,1

1,0

9,50

276,0

55,2

0,709

0,2225

22,25

88,8

0,25

3,26

26,1

1,0

10,50

286,0

57,2

0,784

0,2158

21,58

91,8

0,24

3,49

27,1

1,0

11,50

296,0

59,2

0,858

0,2088

20,88

94,8

0,22

3,71

28,1

1,0

12,50

306,0

61,2

0,933

0,2015

20,15

97,8

0,21

3,92

Parametry funkcji powierzchni osiadań:
punkt "0" : x = 0, y = 0

→ s

pg

(x,y) = s

pg;0

= 12,23 mm

→

d = 12,23

punkt A: x = 0, y = 6,70 m

→ s

pg

(x,y) = s

pg;A

= 4,27 mm

→

b = - 0,177

punkt B: x = 10,45 m, y = 0

→ s

pg

(x,y) = s

pg;B

= 4,16 mm

→

a = - 0,074

punkt N: x = 10,45 m, y = 6,70 m

→ s

pg

(x,y) = s

pg;N

= 1,84 mm

→

c = 0,00115

Funkcja powierzchni osiadań:

s

pg

(x,y) = -0,074x

2

-0,177y

2

+ 0,00115x

2

y

2

+ 12,23 [mm]; x, y [m]

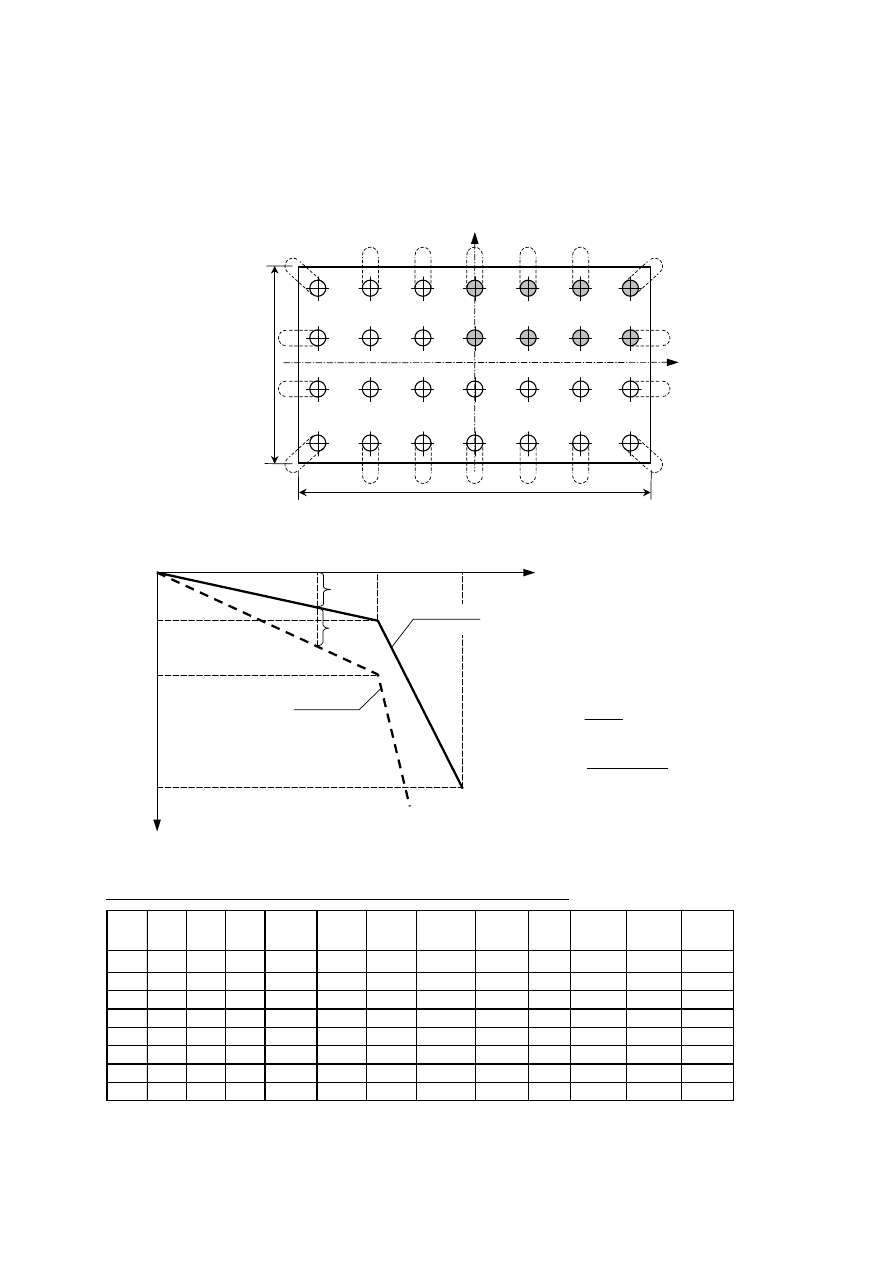
4.3.3. Rozkład sztywności gruntu pod płytą

Obszar pod płytą fundamentową podzielono na 40 prostokątnych elementów. Ze względu na
symetrię układu, sztywności gruntu wyznaczono pod 12 elementami w pierwszej ćwiartce.
W odpowiadających elementach pozostałych trzech ćwiartek wartości sztywności k

zg;j

są takie same

jak w elementach pierwszej ćwiartki.

Rys. 4.15

16,60

9,10

Y

X

1 2 3

4

5

6 7

8

9

10

11

12

Nr

x

j

y

j

s

j

s

j

(fs)

s

pg;j

Σ s

j

q

k

zg;j

elem.

[m]

[m]

[mm]

[mm]

[mm]

[mm]

[kPa] [kPa/m]

1

1,25

0,00 11,63

15,81

12,11

39,56 75,0

1896

2

3,75

0,00 10,61

15,81

11,19

37,61 75,0

1994

3

6,25

0,00

8,57

15,81

9,34

33,72 75,0

2224

4

7,90

0,00

6,66

12,65

7,61

26,92 75,0

2786

5

1,25

2,50 10,14

15,81

11,02

36,97 75,0

2029

6

3,75

2,50

9,26

15,81

10,18

35,25 75,0

2128

7

6,25

2,50

7,48

15,81

8,51

31,80 75,0

2358

8

7,90

2,50

5,82

12,65

6,95

25,43 75,0

2950

9

1,25

4,15

7,53

12,65

9,10

29,27 75,0

2562

10

3,75

4,15

6,87

12,65

8,42

27,94 75,0

2684

11

6,25

4,15

5,57

12,65

7,06

25,28 75,0

2966

12

7,90

4,15

4,35

9,49

5,80

19,64 75,0

3819

15

4.3.4. Sztywności podpór sprężystych pod podstawami pali

Podobnie jak w przypadku sztywności podłoża gruntowego pod płytą fundamentową, również
w odniesieniu do pali wyznaczono sztywności dla 8 pali zlokalizowanych w pierwszej ćwiartce
(rys. 4.16). Dla odpowiadających pali pozostałych trzech ćwiartek wartości sztywności są takie
same jak dla pali w pierwszej ćwiartce.

Rys. 4.16

Obliczenia parametrów wykresów poszczególnych pali w grupie

Nr

x

j

y

j

s

p1

s

pg;j

Σ s

j

m

g ;j

K

z 1

K

z 2

D

1

K

z 1g ;j

K

z 2g ;j

D

1g ;j

pala

[m]

[m]

[mm]

[mm]

[mm]

[-]

[kN/m]

[kN/m]

[mm]

[kN/m]

[kN/m]

[mm]

1

0,00

1,25

6,00

11,95

17,95

0,33

134100

11090

8,0

44816

3706

23,9

2

2,50

1,25

6,00

11,50

17,50

0,34

134100

11090

8,0

45971

3802

23,3

3

5,00

1,25

6,00

10,15

16,15

0,37

134100

11090

8,0

49825

4121

21,5

4

8,70

1,25

6,00

6,49

12,49

0,48

134100

11090

8,0

64428

5328

16,7

5

0,00

4,33

6,00

8,91

14,91

0,40

134100

11090

8,0

53959

4462

19,9

6

2,50

4,33

6,00

8,58

14,58

0,41

134100

11090

8,0

55171

4563

19,4

7

5,00

4,33

6,00

7,60

13,60

0,44

134100

11090

8,0

59160

4892

18,1

8

8,35

4,33

6,00

5,26

11,26

0,53

134100

11090

8,0

71486

5912

15,0

16,60

9,10

Y

X

1 2 3

4

5 6 7

8

R

R

c1;k

D

1

s

R

c2;k

K

z1

K

z2

Q

p

D

1g;j

K

z1g

K

z2g;j

s

p1

s

pg;j

pal

pojedynczy

pal

w grupie

Parametry wykresu pala pojedynczego:

1073

;

1

=

k

c

R

kN ;

1428

;

1

=

k

c

R

kN

0

,

8

1

=

D

mm ;

134100

008

,

0

1073

1

=

=

z

K

kN/m

11090

008

,

0

04

,

0

1073

1428

1

=

−

−

=

z

K

kN/m

0

,

40

2

=

D

mm

D

2

16

4.4. Określenie sztywności k

xi

i k

yi

podpór sprężystych wzdłuż pobocznic pali

Parametry podpór sprężystych modelujących poziomą współpracę pali z ośrodkiem gruntowym
można określać według propozycji Koseckiego (1988, 2006) na podstawie modułu reakcji poziomej
gruntu K

x

, określanego według wzoru:

0

2

1

E

S

n

n

K

n

x

⋅

⋅

⋅

⋅

⋅

=

ϕ

κ

[kPa]

w którym:

n

1

, n

2

– współczynniki zależne od średnicy i rozstawu pali (n

1

, n

2

≤ 1.0)

S

n

– współczynnik zależny od technologii pala

κ

– współczynnik zależny od kształtu przekroju poprzecznego pala

ϕ

– współczynnik zależny od długotrwałości i powtarzalności obciążeń (

ϕ

≤ 1.0)

E

0

– moduł pierwotny odkształcenia gruntu [kPa]

Współczynniki n

1

i n

2

wyznacza się z zależności:

0

,

1

4

,

0

2

,

0

1

1

≤

+

=

D

R

n

;

0

,

1

8

,

1

)

(

)

1

(

0

2

2

≤

⋅

−

⋅

−

+

=

D

D

R

n

β

β

w których:
R

1

– rozstaw osiowy pali w płaszczyźnie prostopadłej do kierunku ustawienia podpór sprężystych,

R

2

– rozstaw osiowy pali w płaszczyźnie równoległej do kierunku ustawienia podpór sprężystych,

D – średnica pala,
D

0

– zastępcza średnica pala, równa: D

0

= D+1,0 [m] dla D

≥ 1,0 m oraz D

0

= 1,5D+0,5 [m] dla

D < 1,0 m,

β

– współczynnik zależny od liczby rzędów pali prostopadłych do kierunku ustawienia podpór

sprężystych, równy:

β

= 1 dla pojedynczego rzędu;

β

= 0,6 dla dwóch rzędów;

β

= 0,5 dla

trzech rzędów;

β

= 0,45 dla więcej niż trzech rzędów pali.

Współczynnik technologiczny S

n

przyjmuje się o wartości: 0,80 dla pali wierconych w zawiesinie,

0,9 dla pali wierconych w rurach, 1,0 dla CFA, 1,1 dla pali wbijanych prefabrykowanych oraz 1,20
dla pali Vibro i SDP.

Współczynnik

κ

zależy od kształtu przekroju poprzecznego pala:

κ

= 1,4 dla przekroju

prostokątnego;

κ

= 1,2 dla przekroju kołowego;

κ

= 1,0 dla ścian ciągłych (palowych,

szczelinowych, szczelnych).

Współczynnik

ϕ

zależy od rodzaju i stanu gruntu:

–

ϕ

= 0,65 – dla gruntów niespoistych o I

D

> 0,67 oraz spoistych o I

L

≤ 0;

–

ϕ

= 0,45 – dla gruntów niespoistych o I

D

= 0,33

÷ 0,67 oraz spoistych o I

L

= 0

÷ 0,25;

–

ϕ

= 0,35 – dla gruntów niespoistych o I

D

= 0,2

÷ 0,33 oraz spoistych o I

L

= 0,25

÷ 0,50;

–

ϕ

= 0,30 – dla gruntów niespoistych o I

D

< 0,2, spoistych o I

L

= > 0,50 i organicznych;

Moduł odkształcenia gruntu E

0

odczytuje się z dokumentacji z badań podłoża gruntowego lub

można go obliczyć na podstawie M

0

i

ν

z zależności:

0

0

)

1

(

)

2

1

)(

1

(

M

E

⋅

−

−

+

=

ν

ν

ν

17

Wartość modułu E

0

zmienia się z głębokością (z poziomem naprężenia) podobnie jak wartość

modułu M

0

. Zgodnie ze zmiennością modułu E

0

zmienia się również wartość modułu reakcji

poziomej K

x

z głębokością.

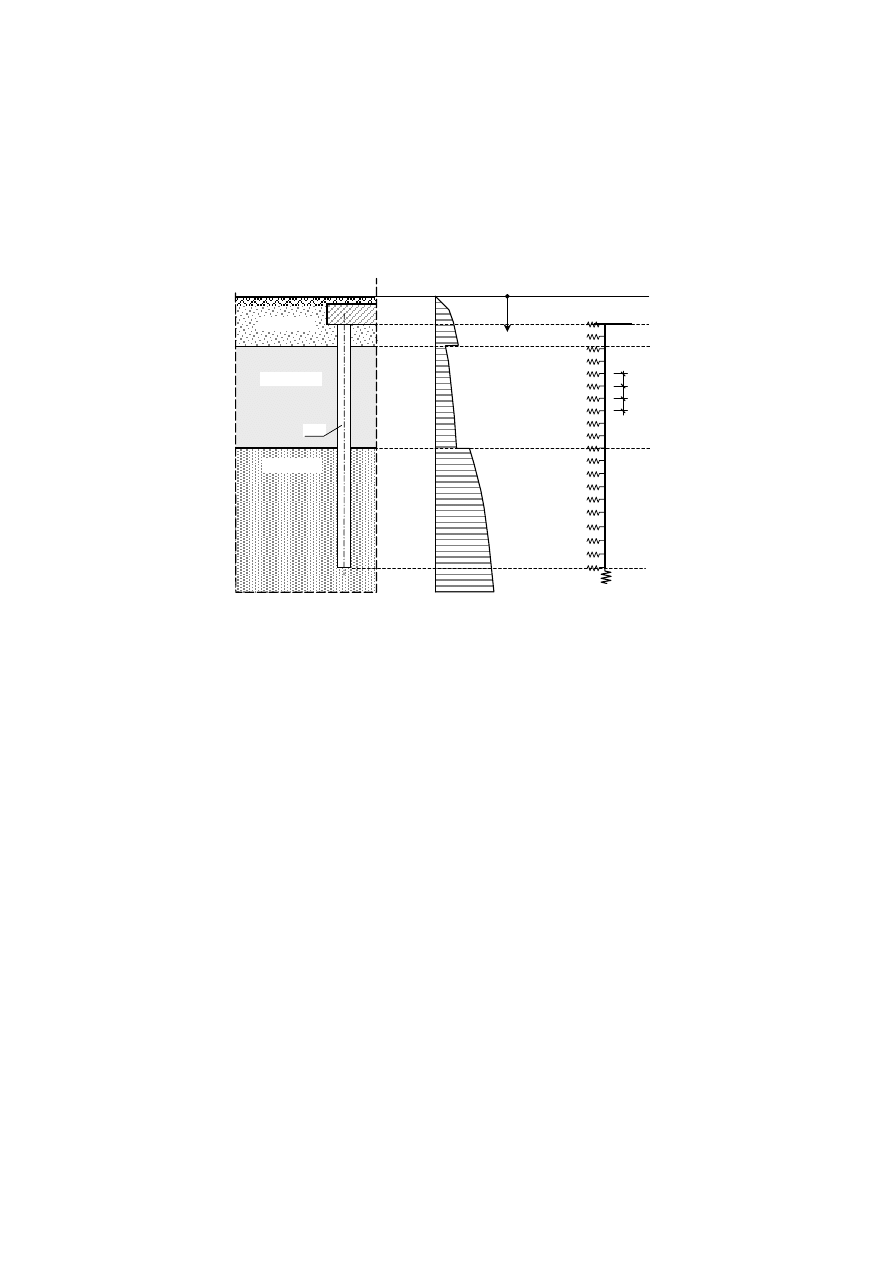
Na podstawie rozkładu modułu K

x

oblicza się sztywności k

xi

poszczególnych podpór sprężystych

według poniższego wzoru i rys. 4.17.

i

i

x

i

x

a

K

k

⋅

=

;

;

[kN/m]

Rys. 4.17

Przy rozwiązywaniu układów przestrzennych, obciążonych wielokierunkowo, podpory sprężyste
należy umieścić na kierunkach x i y. Jeżeli wartości modułów K

x

i K

y

różnią się między sobą

o mniej niż 10%, można przyjąć taką samą, uśrednioną, wartość modułu dla obu kierunków.

Warstwa 2

Warstwa 1

Moduł reakcji

poziomej gruntu

K

x

[kPa]

a

i

a

i

a

i

Warstwa 3

Profil

geotechniczny

Pal

K

x1

(

z

)

k

xi

z

K

x2

(

z

)

K

x3

(

z

)

Pal

z podporami

sprężystymi

k

xi

[kN/m]

K

zj

Zwykle przyjmuje się:
a

i

= 0,5 m