1 

1.  PODSTAWY PROJEKTOWANIA 

UKŁADÓW CYFROWYCH 

 
1.1. Wprowadzenie 
 
Układy  przełączające  (logiczne)  klasyfikuje  się  do  układów  sterowania  cyfrowego.  Układy  te 
przetwarzają  sygnały  dwuwartościowe  w  odróżnieniu  od  sygnałów  ciągłych.  Takie 
dwuwartościowe  sygnały  nazywane  są  także  sygnałami  binarnymi  lub  zerojedynkowymi. 
Działanie  układów  logicznych  zwanych  także  automatami  cyfrowymi,  opisywane  jest  za 
pomocą algebry Boole’a. 
Układy  logiczne  dzielą  się  na  kombinacyjne  i  sekwencyjne.  W  układach  kombinacyjnych 
wyjścia  są  określone  jednoznacznie  przez  aktualne  wejścia.  W  układach  sekwencyjnych  takie 
same  sygnały  wejściowe  mogą  wywoływać  inne  stany  wyjściowe.  Tym  samym  aktualne 
wyjścia,  oprócz  kombinacji  wejść,  są  zależne  także  od  poprzednich  stanów  wyjść.  Ponieważ 
poprzednie  wyjścia  są  określone  przez  stany  poprzednich  wejść  więc  można  powiedzieć,  że 
układy sekwencyjne są to układy zależne od aktualnych i poprzednich sygnałów wejściowych. 
W  układach  sekwencyjnych  występuje  zatem,  sekwencja  zdarzeń  (historia  zdarzeń). 
Uwzględnienie tej historii jest możliwe dzięki zastosowaniu w układzie elementów pamięci.  
Realizacja  układów  sterowania logicznego wymaga zastosowania różnego rodzaju elementów 
logicznych.  Do  grupy  elementów  logicznych,  ze  względu  na  kolejność  ich  zastosowania 
(powstania), można zaliczyć: 
Układy SSI (Small Scale Integration) 
-

 

elementy stykowe - przekaźnikowe, 

-

 

bramki logiczne, 

Układy MSI (Medium Scale Integration) 
-

 

multipleksery, demultipleksery i kodery, 

Układy LSI  (Large Scale Integration) 
-

 

programowalne matryce logiczne PAL/GAL (Programmable Array Logic/ Generic Array 
Logic), 

-

 

programowalne sterowniki logiczne PLC (Programmable Logic Controller). 

 
1.2. Analityczny zapis schematu układu przekaźnikowego 
 
Wielkości  wyjściowe  (obwody  wyjściowe)  uzależnione  są  zwykle  od  kilku  wielkości 
wejściowych.  Interesują  nas  dwa  stany  elementów  wejściowych:  załączania  i  wyłączania. 
Tworzenie  odpowiedniej  funkcji  celu  sterowania  zależy  od  zestyków,  które  w  zależności  od 
swego stanu i sposobu połączeń tworzą bądź zwarcie, bądź przerwę. 
 
Tablica 1.1. Przedstawienie graficzne elementów stykowych (przekaźnikowych)  

stan styków normalnie otwarty  (zwierne) 

stan styków normalnie zamknięty (rozwierne) 

 

 

a  

  a  

 
Dla  analitycznego  zapisu  schematu  układu  przełączającego  przyjmuje  się  zasadę,  że  styki  
połączone  szeregowo  przedstawione  są  w  postaci  iloczynu  literowych  styków,  zaś  styki 
połączone równolegle tworzą sumę tych oznaczeń. 
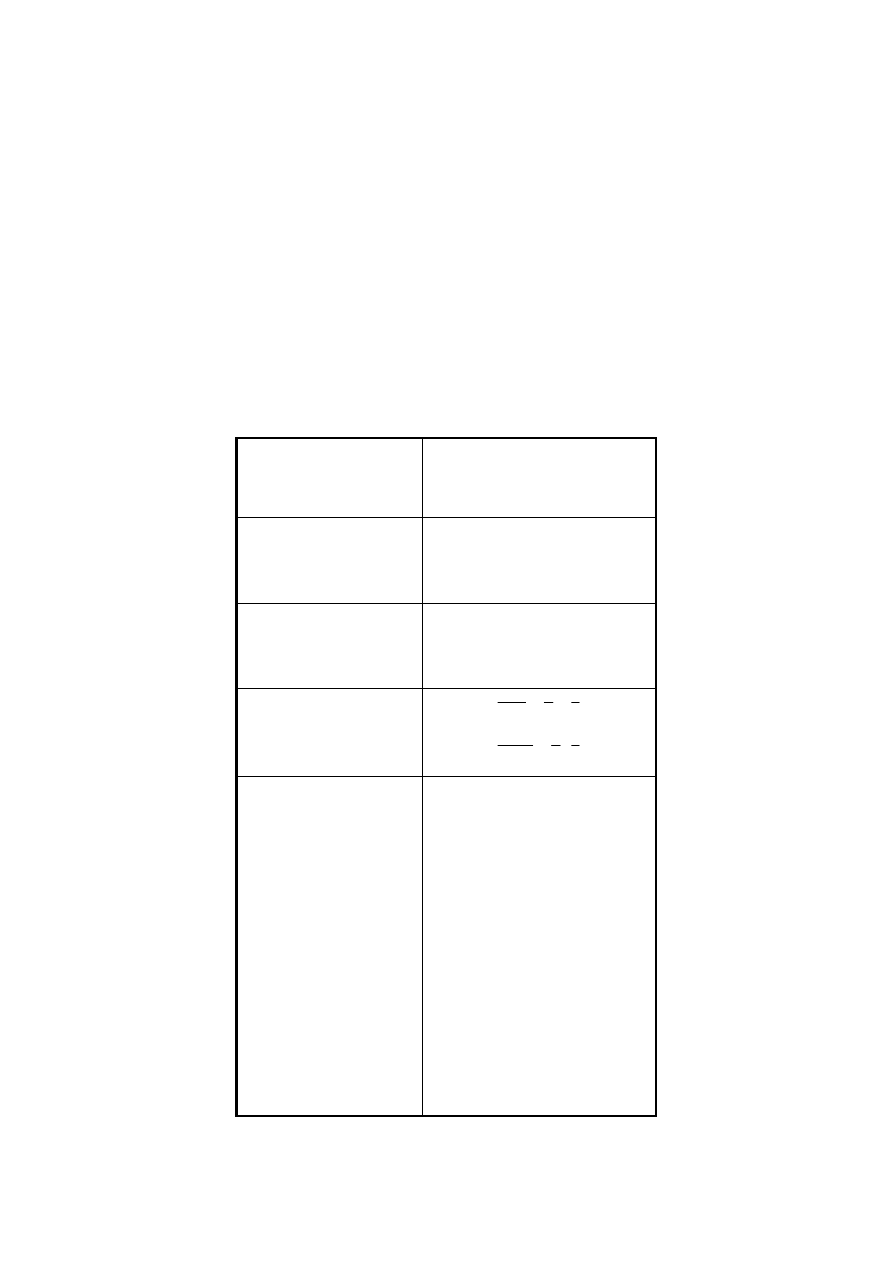
Tak  więc  układ  załączający  cewkę  przekaźnika  F  i  złożony  np.  z  szeregowo  połączonych 

zestyków zwiernego a i rozwiernego 

b

−

 można zapisać: 

 

2 

−

=

b

a

F

 

 

 

 

 

 

(1.1) 

Takie potraktowanie zagadnienia i symbolika pozwalająca na uproszczony zapis, zapożyczone 
są  z  logiki  matematycznej.  Prawa  charakterystyczne  dla  algebry  logiki  nazywane  są  algebrą 
Boole’a.  
 
1.3. Podstawowe prawa algebry Boole’a 
 
George  Boole  (1815-1864)  matematyk  angielski  sprecyzował  matematyczne  reguły  analizy 
zdań logicznych. Podstawą w tym zakresie stanowi tzw. rachunek zdań oparty na koncepcji, że 
zdania  logiczne  muszą  być  określone  wyłącznie  jako  prawdziwe  lub  fałszywe.  Określenie 
prawda  i  fałsz  stanowią,  historycznie  biorąc,  pierwszy  rodzaj  klasyfikacji  binarnej  używany  w 
opisie elementów dwustanowych. Aparat matematyczny (algebra Boole’a) wykorzystuje logikę 
dwustanową zerowo-jedynkową. 
 
Tablica 1.2. Podstawowe prawa algebry Boole’a. 

Prawa przemienności 

a

b

b

a

⋅

=

⋅

 

a

b

b

a

+

=

+

 

Prawa łączności 

c

b

a

c

b

a

⋅

⋅

=

⋅

⋅

)

(

)

(

 

c

b

a

c

b

a

+

+

=

+

+

)

(

)

(

 

Prawa rozdzielności 

)

(

)

(

)

(

c

a

b

a

c

b

a

⋅

+

⋅

=

+

⋅

 

)

(

)

(

)

(

c

a

b

a

c

b

a

+

⋅

+

=

⋅

+

 

Prawa de Morgana 

b

a

b

a

+

=

⋅

 

b

a

b

a

⋅

=

+

 

Prawa tożsamościowe 

a

a

a

=

⋅

 

a

a

a

=

+

 

0

=

⋅

−

a

a

 

1

=

+

−

a

a

 

a

a

=

⋅

1

 

1

1

=

+

a

 

0

0

=

⋅

a

 

a

a

=

+

0

 

 

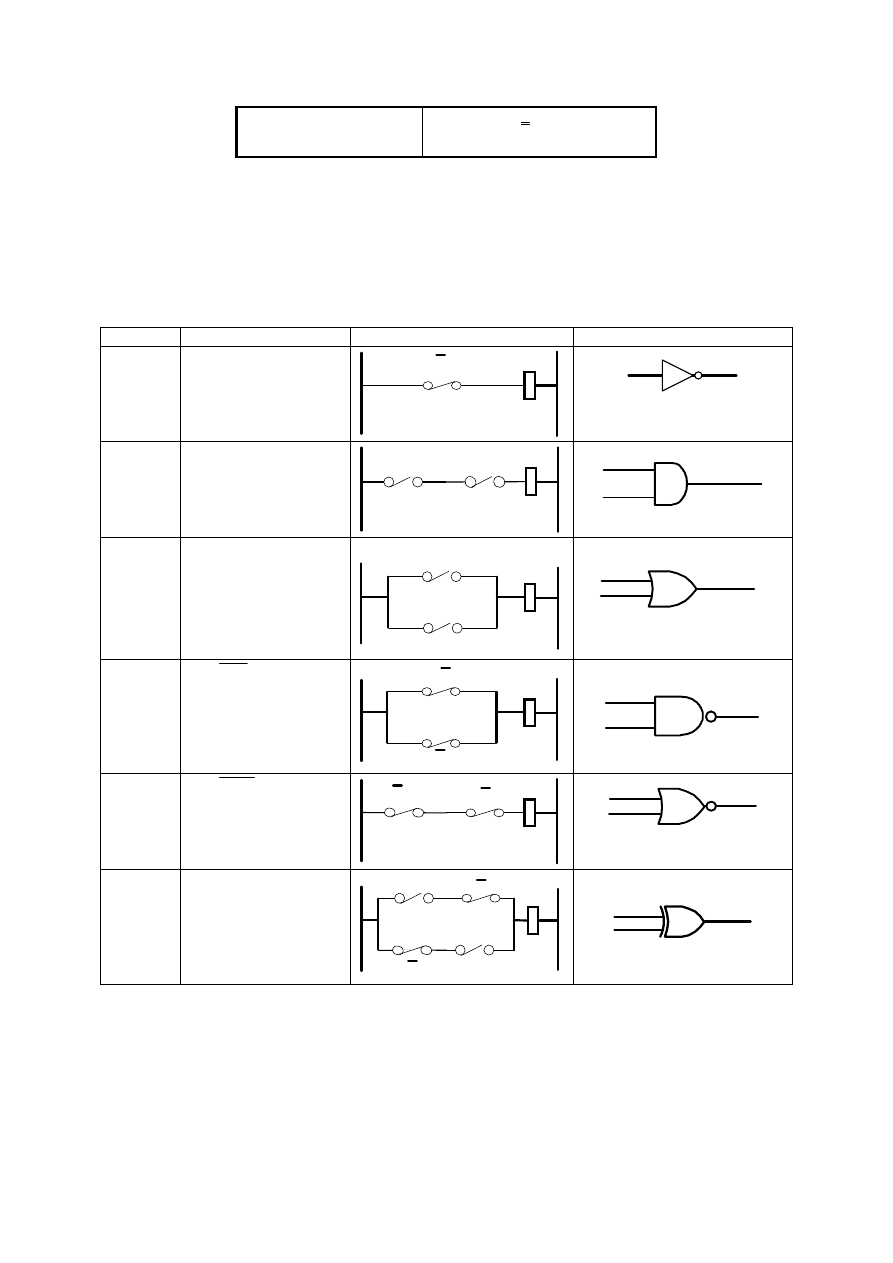
3 

a

a =  

 

1.4. Podstawowe funkcje logiczne  

 
Podstawowe  funkcje  logiczne,  z  których  tworzy  si

ę

  układy  kombinacyjne,  przedstawiono  w 

tablicy  1.3.  W  tablicy  tej  podano  równowa

ż

ne  schematy  układów  bramkowych  i 

przeka

ź

nikowych  

 

Tablica 1.3. Podstawowe schematy przekaźnikowe i ich odpowiedniki bramkowe 

Opis 

Wzór Boole’a 

Schemat przekaźnikowy 

Schemat bramkowy 

NOT 

−

=

a

F

 

F

a

 

a

F

 

 

AND 

b

a

F

⋅

=

 

F

b

a

 

a

b

     F

 

OR 

b

a

F

+

=

 

F

b

a

 

 

a

b

   F

 

NAND 

b

a

F

⋅

=

 

F

a

b

 

 

a

b

F

 

NOR 

b

a

F

+

=

 

F

a

b

 

a

b

F

 

EXOR 

b

a

F

⊕

=

=

−

−

+

b

a

b

a

 

F

b

a

a

b

 

 

a

b

F