LABORATORIUM

Temat 11: Dokładność ustalania przesuwnych zespołów maszyn

1. Wprowadzenie

Szybki wzrost liczby maszyn sterowanych numerycznie oraz robotów przemysłowych

zmusił producentów i użytkowników do stosowania jednoznacznych kryteriów oceny ich ja-

kości. Z uwagi na stosunkowo niewielką pracochłonność, niski koszt badań oraz znaczną

przydatność uzyskanych wyników do oceny jakości i stanu technicznego, jednym z najbar-

dziej rozpowszechnionych testów jest sprawdzanie dokładności ustalania położenia jej ze-

społów. Uzyskane w wyniku takich badań odchyłki ustalania położenia oraz rozrzut poło-

żeń zespołów stanowią ważne kryterium oceny stanu maszyny i jej zespołów. Aby umożliwić

porównywanie wyników uzyskiwanych przez różnych producentów i użytkowników maszyn

sterowanych numerycznie, w szeregu krajach opracowano zalecenia precyzujące tok postę-

powania przy prowadzeniu takich badań. Na świecie stosuje się kilka różnych norm związa-

nych z kontrolą parametrów maszyn: NMTBA – USA, VDI – Niemcy, JIS – Japonia, BSI –

Wielka Brytania, ISO – Unia Europejska. W Unii Europejskiej, dla maszyn z grupy „obra-

biarki skrawające”, podstawę stanowi norma ISO 230 część 1 oraz część 2. Część pierwsza

obowiązuje w kraju jako PN-93/M-55580/01 „Dokładność geometryczna obrabiarek pracują-

cych bez obciążenia lub w warunkach obróbki wykańczającej”

Przyczyną występowania odchyłek położenia zespołów przesuwnych są głównie błędy

geometryczne wykonania maszyny, jej odkształcenia cieplne i odkształcenia pod wpływem

sił: głównie tarcia, ciężkości i związanych z samym procesem. Kompleksowa kontrola błę-

dów geometrycznych maszyny obejmuje cechy: kształtu, położenia oraz przemieszczenia linii

lub powierzchni maszyny. Mogą to być takie cechy jak: prostoliniowość, płaskość, równo-

odległość, prostopadłość i obrót.

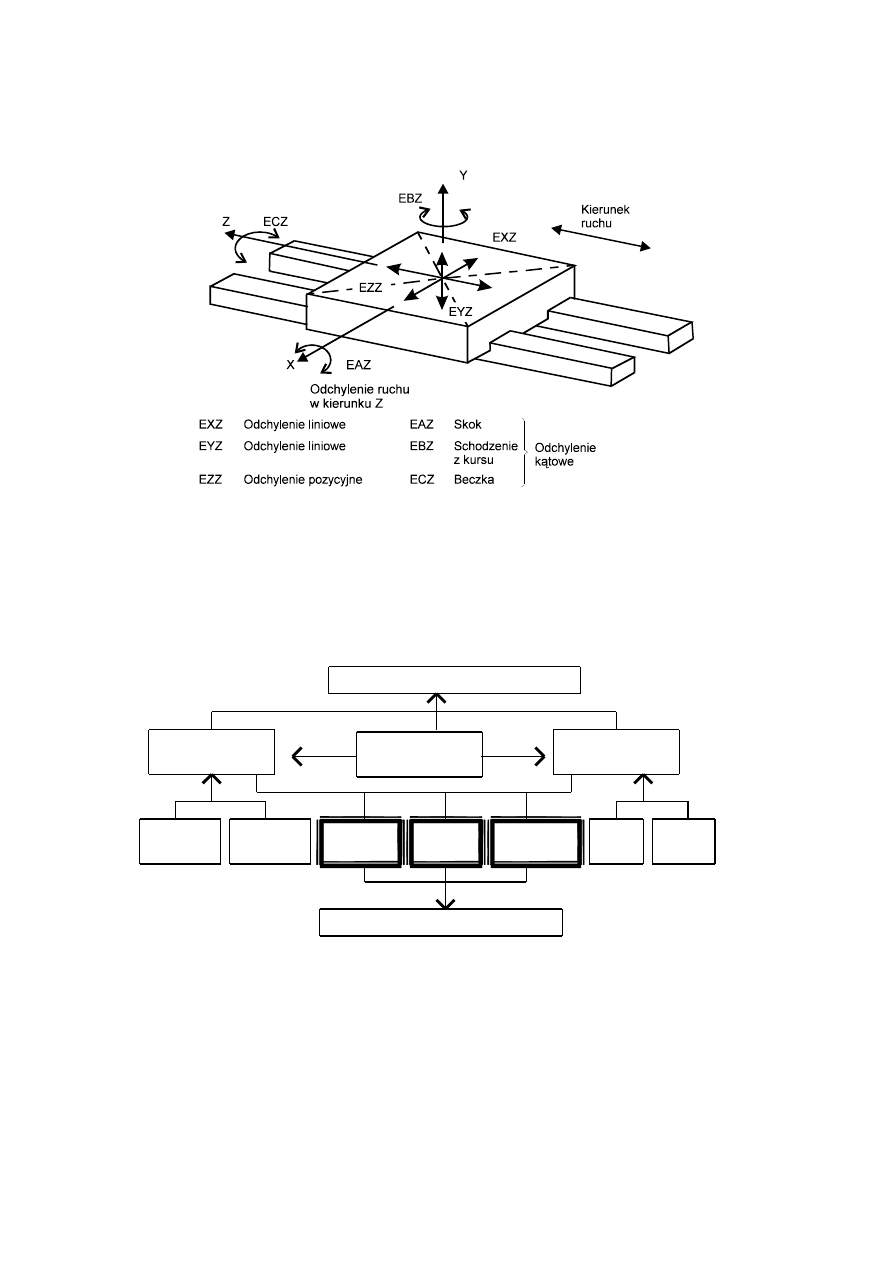
Szczególnie istotnym zagadnieniem przy kontroli maszyny jest badanie przemieszczenia

prostoliniowego zespołu maszyny wzdłuż osi ruchu. Przemieszczenie prostoliniowe zespołu

ruchomego maszyny powoduje sześć elementów odchylenia (rys.1.), decydującego o położe-

niu punktu materialnego w przestrzeni: jedno odchylenie pozycyjne w kierunku ruchu, dwa

odchylenia liniowe trajektorii punktu ruchomego zespołu, trzy odchylenia kątowe zespołu ru-

chomego.

Odchylenia we wszystkich sześciu stopniach swobody wpływają na błędy pozycjono-

wania, ponieważ wynikają one zarówno z niepożądanych ruchów kątowych jak i ruchów po-

2

stępowych i mogą być nawet większe od błędów pozycjonowania linowego w kierunku osi

sterowalnych.

Rys.1. Odchylenia przy przemieszczaniu liniowym

2. Odchyłki ustalania położenia

Odchyłki ustalania położenia, można podzielić na systematyczne i przypadkowe (rys.2).

Odchyłki systematyczne, są spowodowane ograniczoną sztywnością elementów maszyny oraz

błędami jej geometrii.

Odchyłki

systematyczne

sztywność geometria

odchyłka
położenia

luz

zwrotny

rozrzut

położenia

obcią-

żenie

drgania

Odchyłka ustalania położenia

Dokładność obróbki

Temperatura

Odchyłki

przypadkowe

Rys.2. Czynniki wpływające na dokładność obróbki i na odchyłkę ustalania położenia

Błędy przypadkowe są natomiast wynikiem zmiennego, co do wartości, obciążenia oraz

drganiami. Zarówno na odchyłki systematyczne jak i na przypadkowe ma wpływ nagrzewanie

się zespołów maszyny. Odchyłki te określają z kolei odchyłkę położenia, odchyłkę występu-

jącą przy zmianie kierunku obciążenia lub kierunku ruchu, zwaną luzem zwrotnym oraz roz-

rzut położeń przemieszczanego zespołu. Te trzy czynniki wyznaczają całkowitą odchyłkę

3

ustalania położenia zespołu. Jak pokazano na rys.3 o wartości odchyłki ustalania położenia

decydują zarówno odchyłki systematyczne jak i przypadkowe. Ogólnie można stwierdzić, że

odchyłki systematyczne są wyznaczone przez warunki brzegowe pracy danej maszyny i dla

każdego punktu pomiarowego na długości drogi przesuwu zespołu mają określoną wartość i

określony znak. Są one spowodowane głównie, błędami geometrycznymi prowadnic, błędami

wykonania śruby tocznej, obciążeniami, a także błędami układu do pomiaru drogi zastosowa-

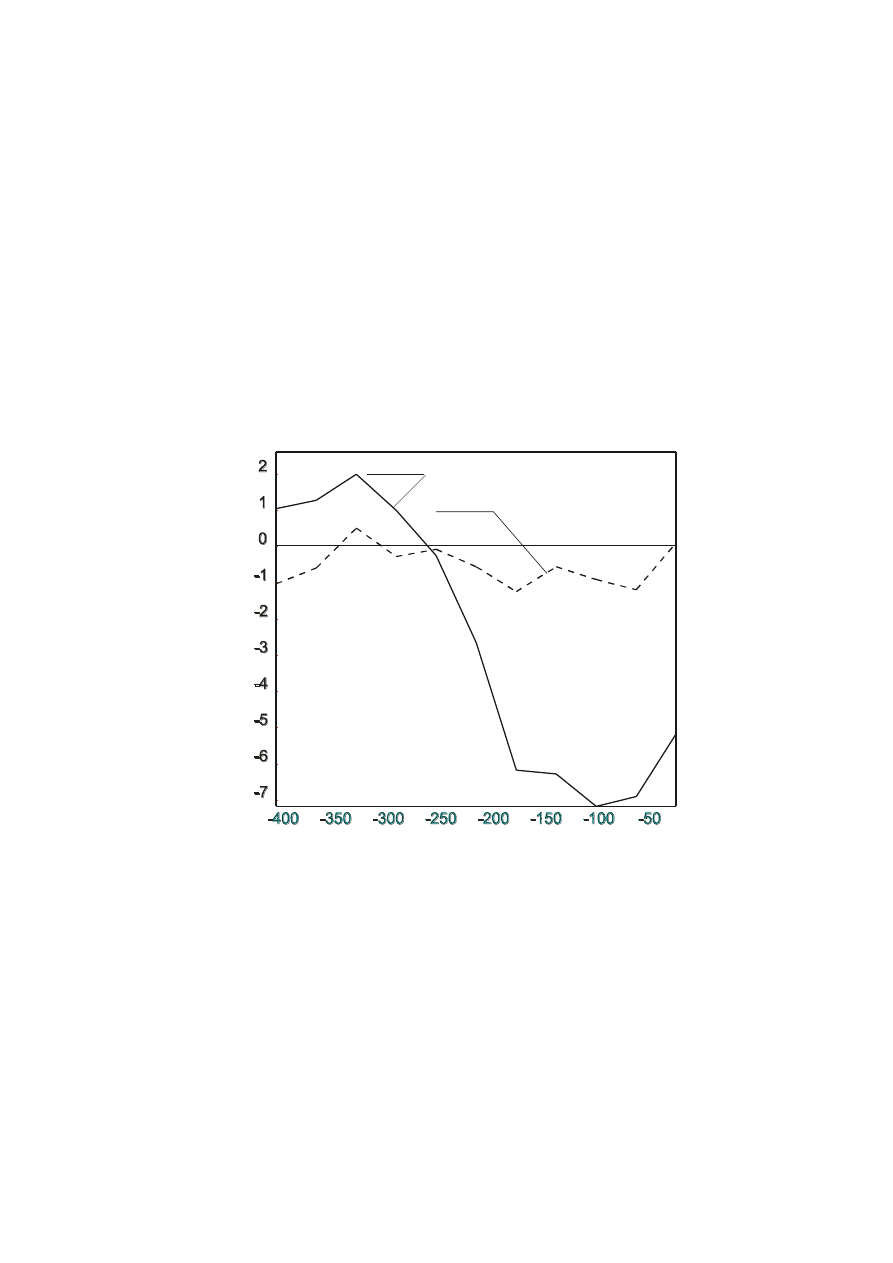
nego w maszynie NC. Z uwagi na stałą ich wartość można je łatwo skorygować Na rys. 3 po-

kazano przykładowy efekt uzyskany dla frezarki pionowej w wyniku wprowadzenia do ukła-

du sterowania odpowiednich poprawek, uzyskanych z pomiarów odchyłek ustalania położe-

nia.

współrzędna w osi Y [mm]

Frezarka pionowa

AVIA

1

2

Analiza trendu - liniowa

o

dc

h

ył

ka

p

o

ło

że

ni

a

[u

m

]

Rys.3. Zmniejszenie odchyłek pozycjonowania w wyniku korekcji.

(linia 1 przed korekcją, linia 2 po korekcji)

Odchyłki przypadkowe mogą mieć wiele przyczyn. Główne przyczyny to: zmienne wa-

runki tarcia w parach kinematycznych, rozrzut czasów przełączania napędu, zmienna tempe-

ratura pracy obrabiarki, zmienne warunki zewnętrzne, zmienne obciążenia, drgania itp. Przy-

padkowe odchyłki położenia zmieniają swą wartość, pomimo zachowania stałych sterowal-

nych warunków pracy i eksploatacji. Są one powodem występowania rozrzutu położeń.

4

3. Opracowanie wyników pomiarów

Występowanie nieuniknionego rozrzutu w pomiarach odchyłek ustalania położenia wy-

musza posłużenie się metodami statystycznymi przy opracowywaniu wyników pomiarów.

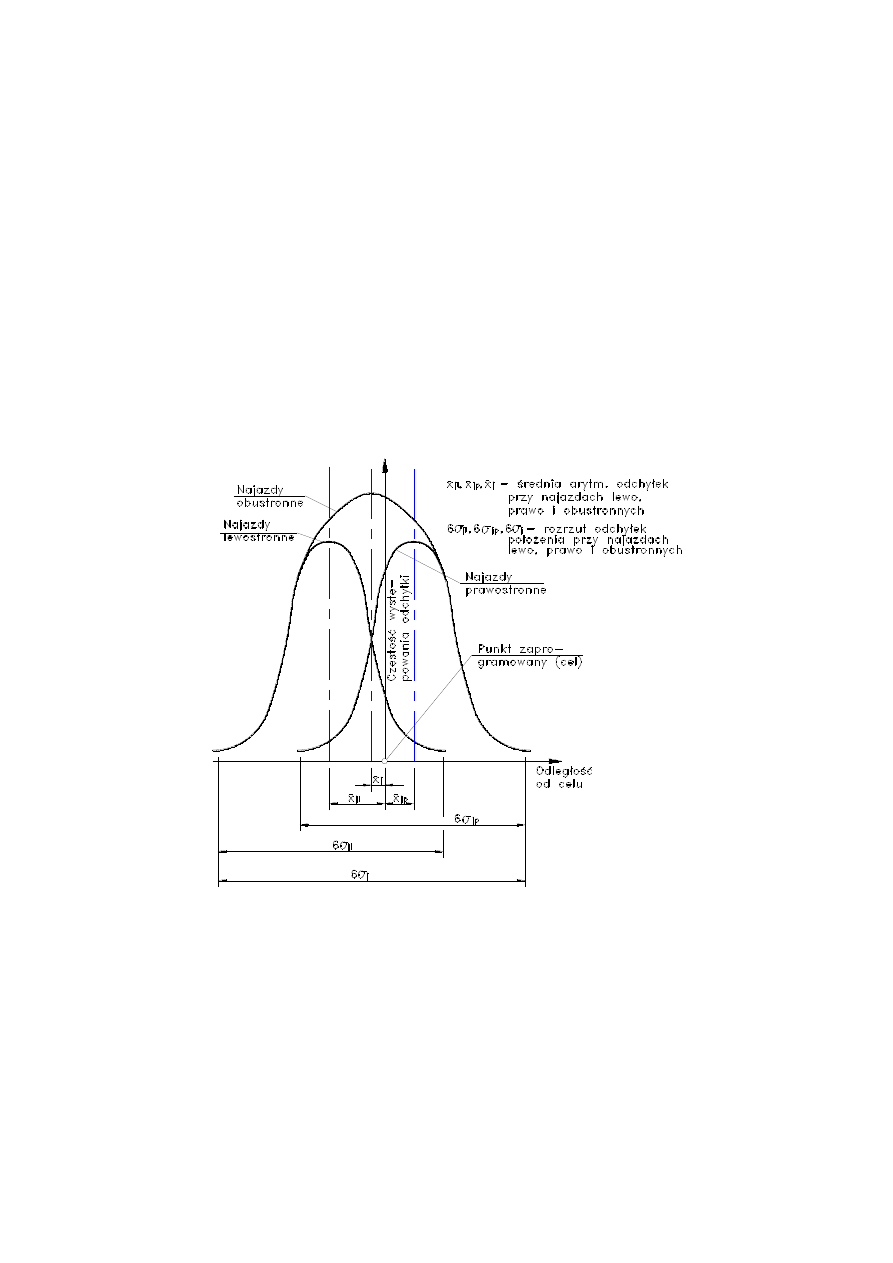
Zakłada się przy tym, że odchyłki położenia od zadanego punktu są rozłożone zgodnie

z rozkładem normalnym. Analizując rozkłady odchyłek przy najazdach lewo i prawostron-

nych dla każdego położenia kontrolnego można przy założonym poziomie ufności wyzna-

czyć:

 Odchyłkę położenia,

 Rozrzut położenia,

 Luz zwrotny

Analizę taką dla jednego położenia pokazano na rys.4.

Rys.4. Krzywe normalnego rozkładu odchyłek położenia

Odchyłkę położenia reprezentują średnie arytmetyczne odchyłek przy odpowiednich na-

jazdach zaś luz zwrotny jest różnicą odchyłki lewo i prawostronnej. Jako rozrzut odchyłek po-

łożenia podaje się najczęściej przedział 6



, w którym mieści się 99,73% wszystkich pomia-

rów. Odchylenie standardowe



dla „n” najazdów, oblicza się z zależności:

5



j







(x

x

n - 1

ji

j

i=1

n

)

2

,

gdzie: x

ji

- „i”-ta odchyłka od punktu „j”,

x

1

n

x

j

ji

i=1

n





- średnia arytmetyczna odchyłek od celu w punkcie j,

n - liczna najazdów na punkt „j”.

4. Pomiary odchyłek ustalania położenia

Rosnąca ciągle dokładność maszyn wymaga, aby narzędzia pomiarowe cechowały się

dokładnością przynajmniej o rząd wyższą. Dla większości obecnie wytwarzanych maszyn

wymaganiom tym są w stanie sprostać tylko interferometry laserowe. Interferometry laserowy

z różnego typu oprzyrządowaniem optycznym są najwyższej klasy przyrządami pomiarowym

wykorzystywanym do kontroli geometrycznej maszyn. Ich zastosowania obejmują pomiary

odchyłek pozycjonowania liniowego i kątowego, prostoliniowości, prostokątności, równole-

głości i płaskości. Możliwa jest też automatyczna transmisja współczynników korekcji linio-

wej do popularnych sterowników CNC.

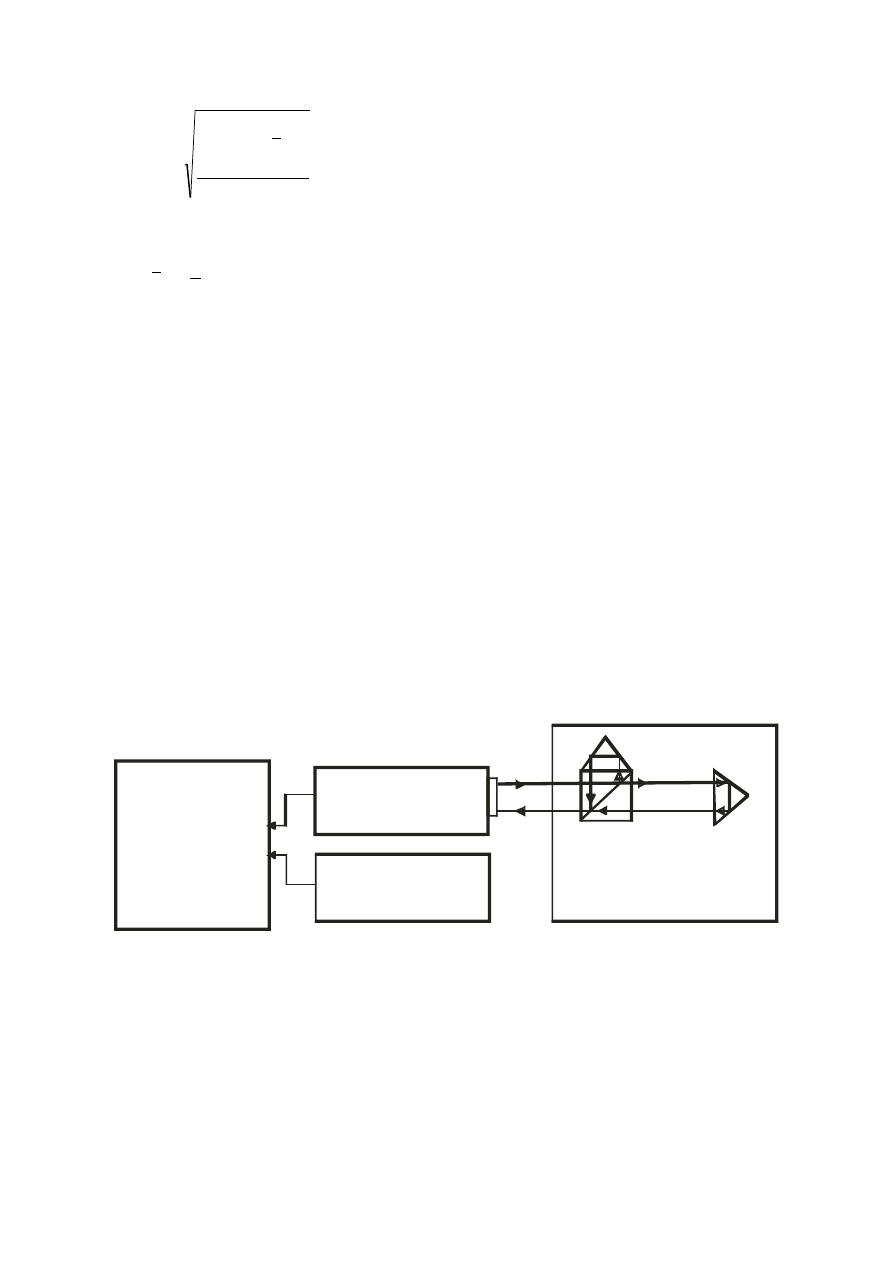
Do pomiaru wykorzystuje się system laserowy w konfiguracji: głowica laserowa, układ

kompensacji, optyka do pomiarów liniowych i komputer z. oprogramowaniem (rys.5).

Rys.5. Schemat blokowy laserowego systemu pomiarowego

4.1.Zasada działania

Interferometria to technika pomiaru, która wykorzystuje długość fali świetlnej jako

jednostkę pomiarową. Laser znajduje w niej zastosowanie, ponieważ stanowi źródło promie-

niowania spójnego, co oznacza, że wszystkie wysyłane przez źródło fale mają taką samą dłu-

gość oraz są dokładnie w fazie. Długość fali lasera HeNe (światło czerwone) wynosi

Głowica

laserowa

Układ

kompensacji

Komputer

PC

Oprzyrządowanie

optyczne

6

0.633



m, a w drodze kolejnych podziałów tej długości osiąga się rozdzielczość pomiarową

nawet 0.001



m czyli 1 nm.

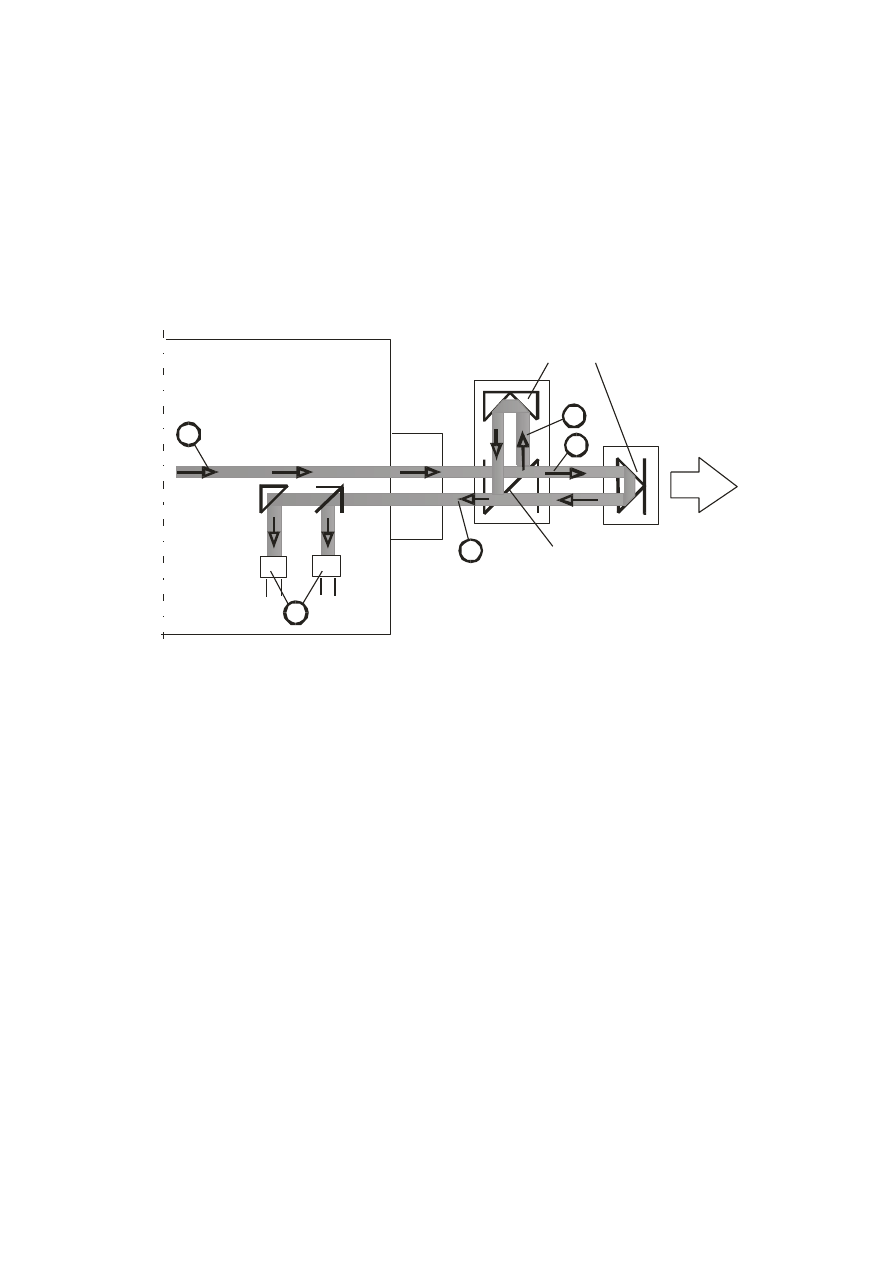
Zasadę działania systemu laserowego ilustruje rysunek 6. Światło lasera (1) spolary-

zowane w dwóch prostopadłych płaszczyznach dochodzi do zwierciadła płaskiego rozdziela-

jącego wiązkę na dwie składowe spolaryzowane liniowo. Światło odbite (2) jest spolaryzo-

wane prostopadle do przechodzącego (3). Obie wiązki są odbijane od odpowiednich pryzma-

tów i powracają do głowicy laserowej.

Rys.6. Zasada działania interferometru laserowego

Nieruchomy układ optyczny znajduje się w stałej odległości od głowicy tworząc w ten

sposób stałe ramie odniesienia interferometru. Drugie układ optyczny może przemieszczać się

względem głowicy tworząc razem z nią układ tak zwanego ramienia pomiarowego interfero-

metru. System laserowy pozwala na dokładne wykrywanie różnic pomiędzy długością ramie-

nia odniesienia i ramienia pomiarowego. Po odbiciu od pryzmatów wiązki (2) i (3) spotykają

się i razem docierają do głowicy. Utworzona w taki sposób wiązka (4) składa się z dwóch

składowych, które posiadają prostopadłe do siebie polaryzacje. Wiązka światła dochodzi na-

stępnie do detektorów (5) czułych na kierunek polaryzacji światła, które dają na wyjściu elek-

tryczny sygnał o przebiegu zmiennym, sinusoidalnym, pozwalający na określenie kierunku

przemieszczania się pryzmatu „pomiarowego” oraz określenie wielkości przesunięcia.

Przy wykorzystaniu interferometru laserowego LSP-30 do pozycjonowania maszyny

można uzyskać następujące parametry pomiaru:

- zakres pomiaru 0 do 30 m

- rozdzielczość pomiaru 0,1 lub 0,01



m

2

3

4

5

Zwierciadło płaskie

Pryzmat

Przesuw

Głowica laserowa

System laserowy LSP-30

1

7

- dokładność pomiaru 1,5



m/m

Proces pomiaru pozycjonowania dla maszyn sterowanych numerycznie wymaga:

- zaprogramowania układu sterowania maszyny; (wpisanie położenia punków pomiarowych

wzdłuż drogi przemieszczania; maszyna powinna zatrzymać się w punkcie pomiaru na ok.

1 sek),

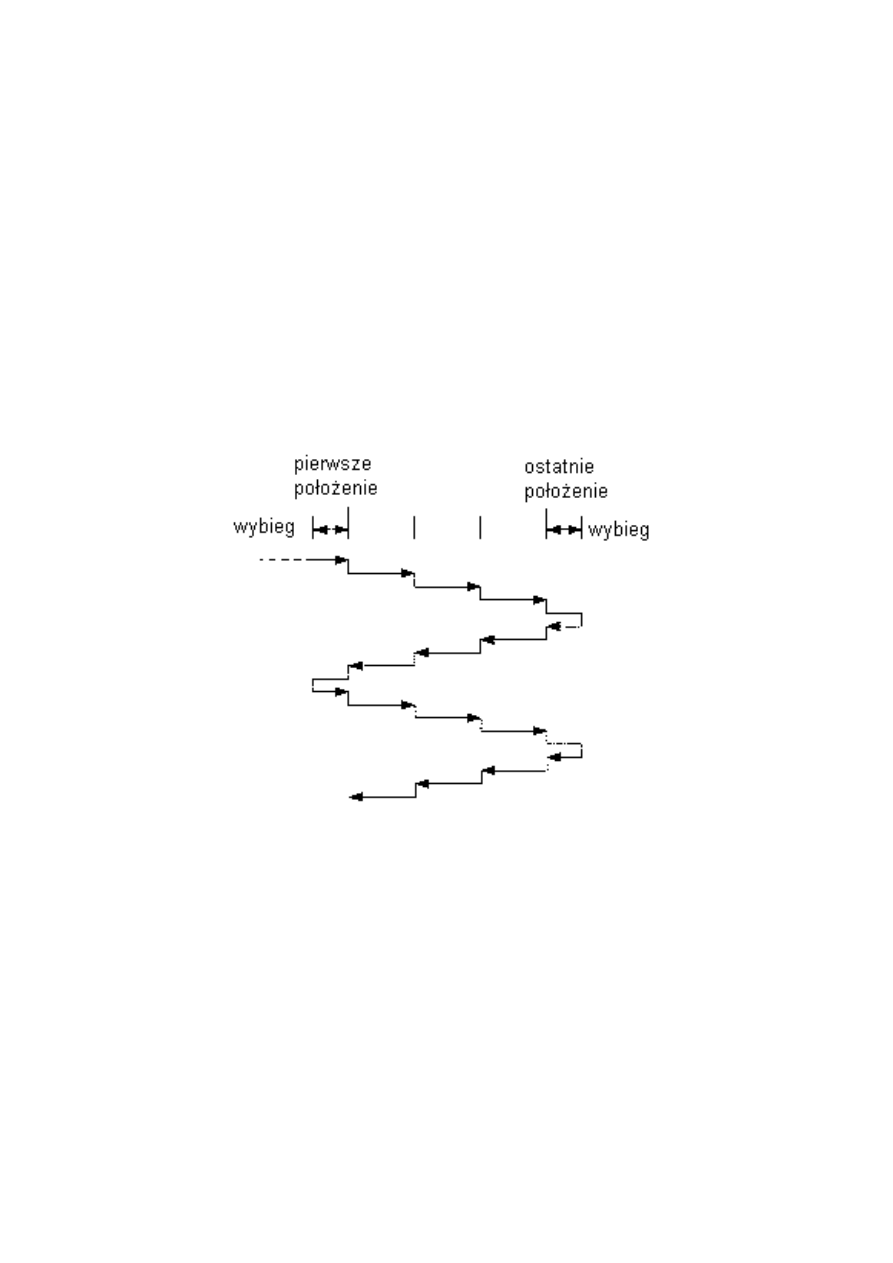
- wykonania co najmniej pięciu cykli pomiarów wg. schematu pokazanego na rys. 7, (reali-

zowany jest pomiar różnicy pomiędzy wpisanym do układu sterowania położeniem punk-

tu pomiarowego a położeniem zmierzonym za pomocą systemu laserowego),

- obróbki statystycznej wyników pomiarowych w komputerze PC dla wyznaczenia wartości

rozrzutu, luzu zwrotnego i odchyłki położenia.

Rys.7. Cykle pomiarowe

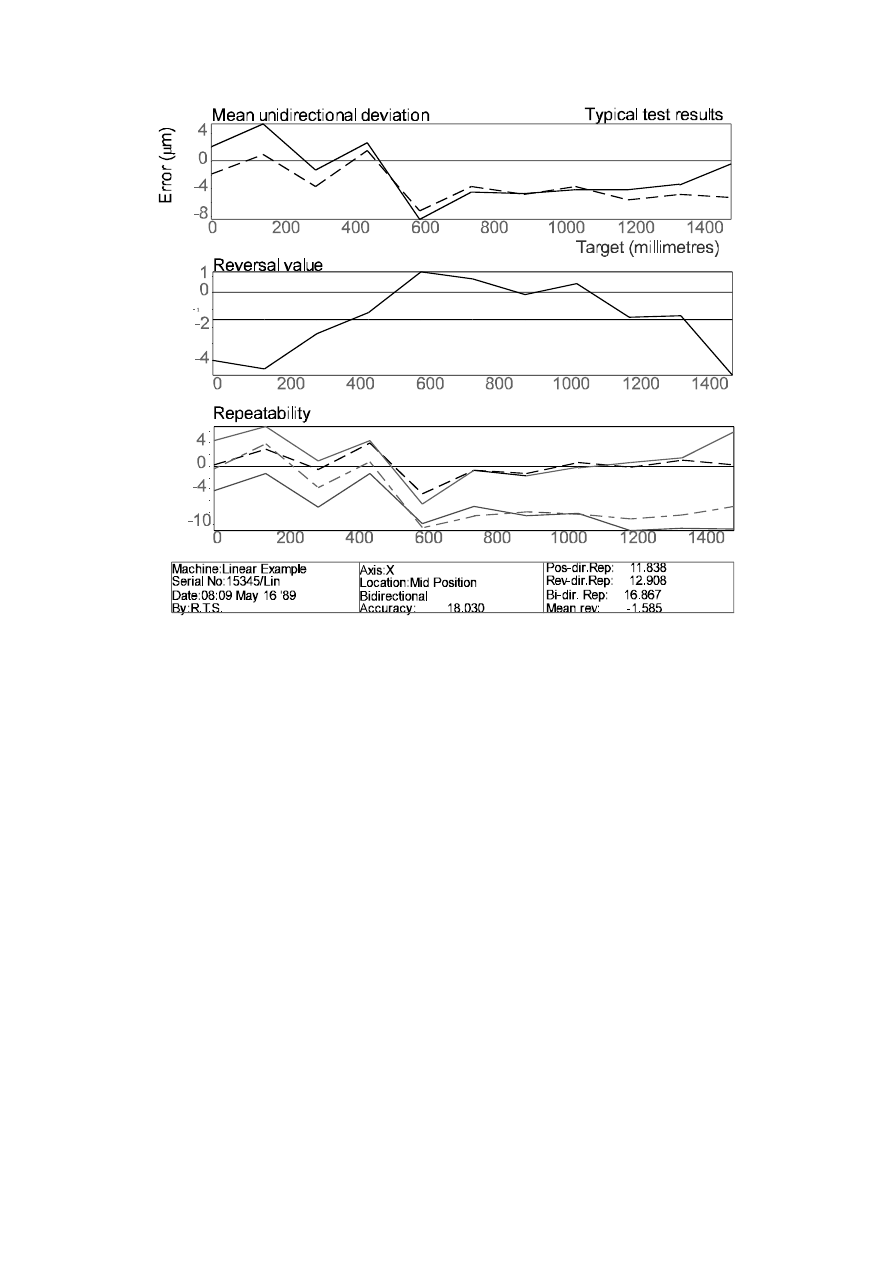
Przykład, opracowanych przez program komputerowy, rezultatów pomiarów dokład-

ności ustalania położenia pokazano na rys. 8.

8

Rys.8 Przykład rezultatów pomiarów dokładności ustalania położenia. (wykres górny : średnie odchylenie dla

położenia, środkowy: luz zwrotny, dolny: rozrzut położeń

5. Stanowisko dydaktyczne

Pomiary rozrzutu położeń, luzu zwrotnego oraz odchyłki położenia wykonywane będą

dla wybranych położeń stołu tokarki numerycznej .

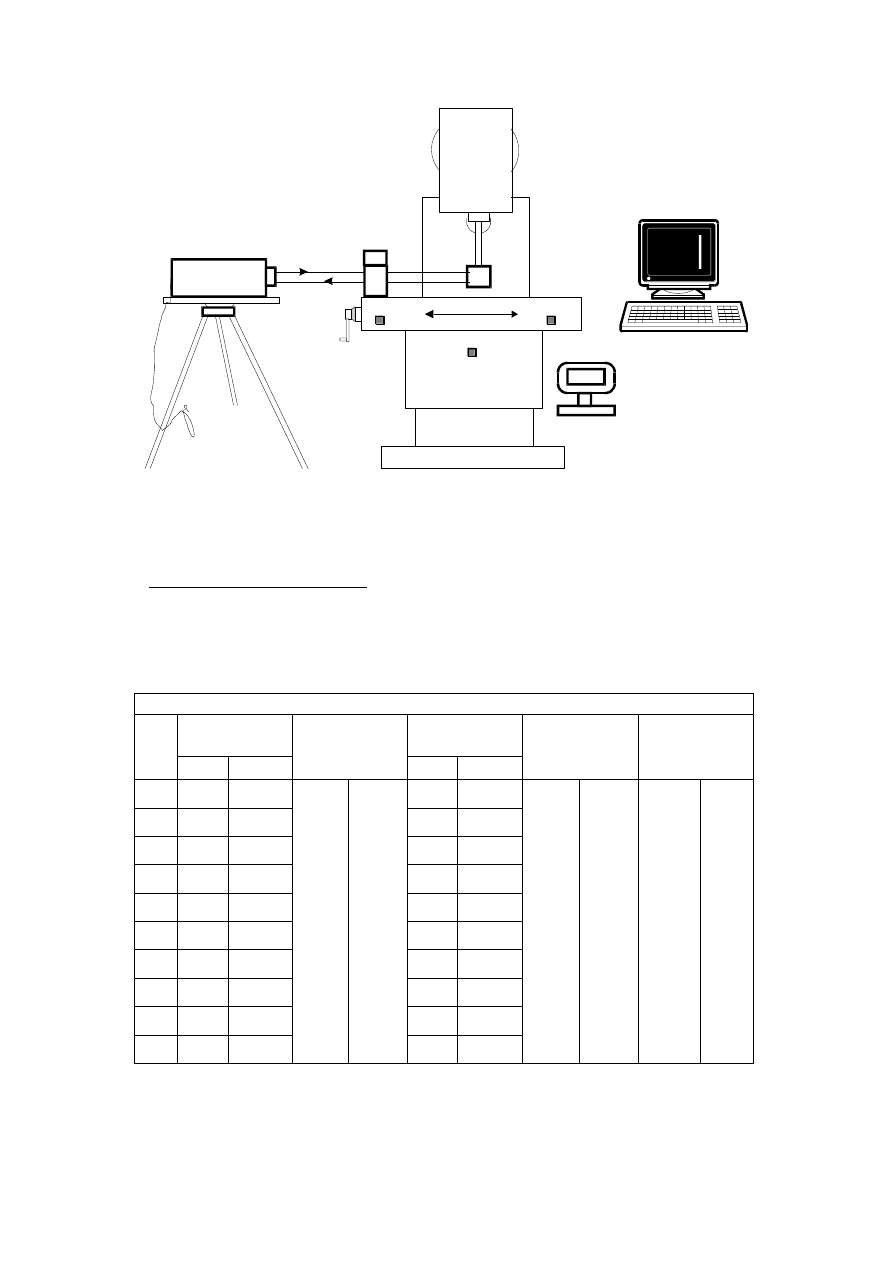
Pomiary przemieszczeń liniowych stołu frezarki wykonuje się zgodnie ze schematem

pokazanym na rys.9. Do pomiaru wykorzystuje się system laserowy w konfiguracji: głowica

laserowa, układ kompensacji, komputer z oprogramowaniem, optyka do pomiarów liniowych.

5.1. Czynności przygotowawcze



zestawienie układu pomiarowego;



ustawienie i uruchomienie głowicy laserowej,



zamocowanie interferometru liniowego na ruchomym stole maszyny, a retroreflektora

(pryzmatu) do nieruchomego zespoły maszyny np. głowicy wrzecionowej,



justowanie układów optyki liniowej na całej drodze przemieszczenia interferometru.

9

FWD

32J

Laser

Interferometr

liniowy

Pryzmat

Meteo

T1

T2

T3

Rys.9. Układ do pomiaru przemieszczeń liniowych w osi maszyny

5.2. Pomiary:

A.

Rozrzut położeń i luz zwrotny

Dla pierwszego wybranego położenia stołu wykonać 10 dojazdów lewostronnych i 10 do-

jazdów prawostronnych – zapisując wskazania systemu laserowego. Na podstawie zbioru

wyników wyznaczyć rozrzut położeń i wartość luzu zwrotnego

Położenie 1/ Położenie 2

Lp

Dojazd lewo-

stronny

Średnia

arytmetyczna

XLsr

Dojazd pra-

wostronny

Średnia

arytmetyczna

XPsr

Luz zwrotny

XLsr-XPsr

1

2

3

4

5

6

7

8

9

10

Rozrzut położeń R wyznaczyć jako R = 6*



lub w przybliżeniu jako

R = Xmax – Xmin (po odrzuceniu błędów grubych).

10

B.

Odchyłka położenia

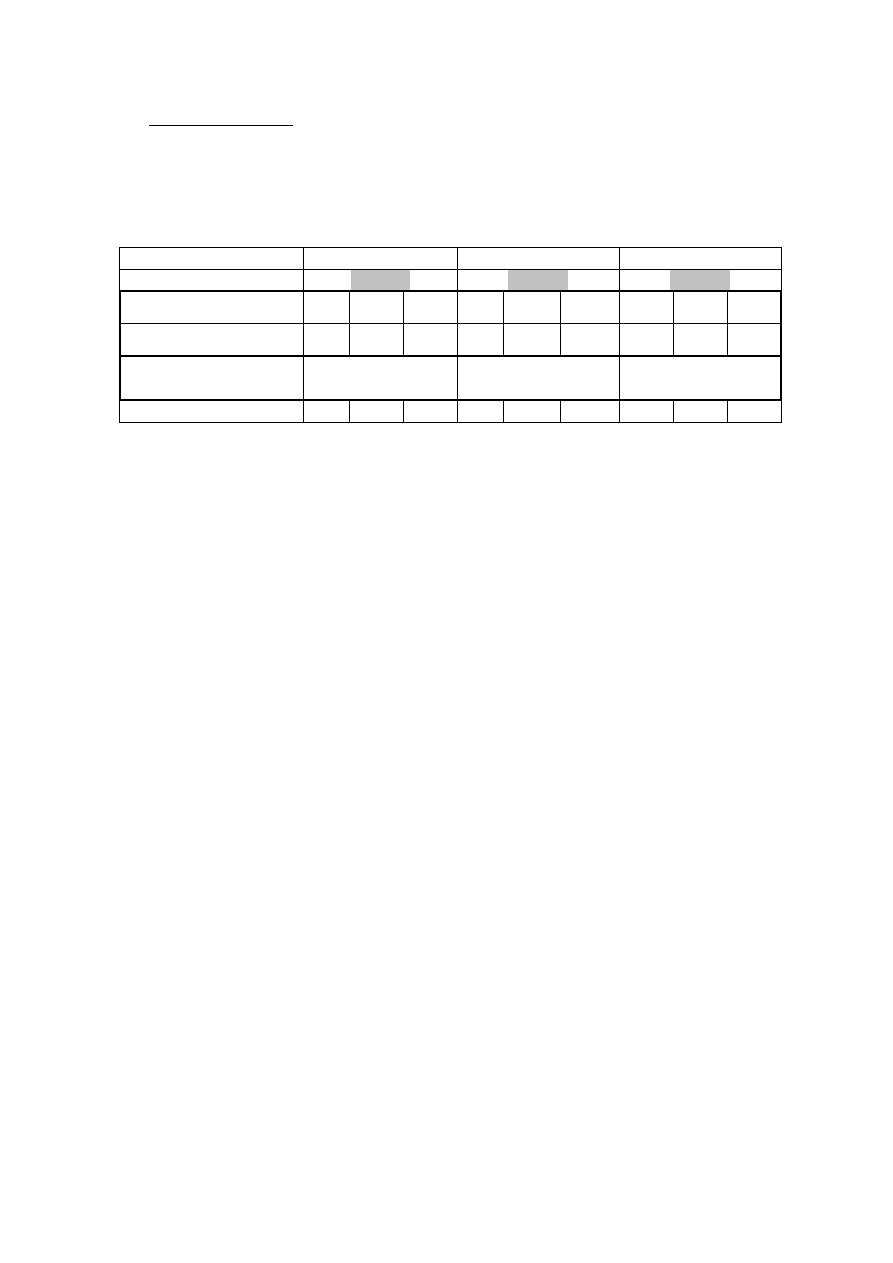
Odchyłkę położenia wyznaczyć dla trzech położeń stołu, odpowiadających 200, 300 i 400

mm. Dla każdego z położeń stołu pomiary powtórzyć trzy razy.

,

,

,

Wartość zadana Z

200 mm

300 mm

400 mm

Wartość zmierzona M

Odchyłka Z - M

Średnia odchyłka po-
łożenia

Pomiar Nr

1

2

3

1

2

3

1

2

3

Opracował:
Wojciech Kwaśny
Zbigniew Wasiak