POLITECHNIKA WROCŁAWSKA

INSTYTUT TECHNIKI CIEPLNEJ I MECHANIKI PŁYNÓW

ZAKŁAD TERMODYNAMIKI

Materiały pomocnicze do ćwiczeń rachunkowych z przedmiotu

Termodynamika stosowana

CZĘŚĆ 1: GAZY WILGOTNE

mgr inż. Piotr Kolasiński

Opracowano na podstawie podręcznika S. Wiśniewskiego – Termodynamika

techniczna

Wrocław, 2007

I. PODSTAWOWE WŁAŚCIWOŚCI GAZÓW WILGOTNYCH

Gazem wilgotnym nienasyconym nazywamy roztwór pary przegrzanej i gazu
suchego.

Gazem wilgotnym nasyconym nazywamy roztwór pary nasyconej suchej i gazu

suchego

Gazem wilgotnym przesyconym nazywamy roztwór pary wilgotnej, mgły ciekłej lub

lodowej i gazu suchego.

Wielkości dotyczące pary będziemy oznaczać dolnym indeksem p, zaś gazu indeksem

g.

1. Ci

ś

nienie gazu wilgotnego:

g

p

p

p

p

=

+

p

g

– ciśnienie gazu

p

p

– ciśnienie pary

2. Temperatura rosy

( )

r

s

p

T

T

p

=

Temperaturą rosy nazywamy temperaturę nasycenia pary przy jej ciśnieniu

składnikowym p

p

.

3. Wilgotno

ść

bezwzgl

ę

dna – wilgo

ć

Wilgotnością bezwzględną pary nazywamy jej gęstość przy ciśnieniu składnikowym p

p

i temperaturze gazu wilgotnego.

p

p

p

p

m

p

V

R T

ρ

=

=

⋅

;

''

0

p

p

ρ

ρ

≤

≤

''

max

s

p

p

p

p

R T

ρ

ρ

=

=

⋅

Wilgotność bezwzględna jest maksymalna i równa gęstości pary nasyconej suchej
gdy ciśnienie składnikowe pary jest równe ciśnieniu nasycenia p

p

=p

s

, tj. gdy

temperatura gazu staje się równa temperaturze rosy.

4. Wilgotno

ść

wzgl

ę

dna gazu

ϕ

Wilgotnością względną gazu nazywamy stosunek wilgotności bezwzględnej

ρ

p do

maksymalnej wilgotności bezwzględnej

ρ

p

’’ dla tej samej temperatury. Może być

również określona jako stosunek ciśnienia składnikowego pary p

p

do jej ciśnienia

maksymalnego p

max

przy tej samej temperaturze.

''

max

p

p

p

p

T

T

p

p

ρ

ϕ

ρ









=

=

























; 0

1

ϕ

≤ ≤

5. Stopie

ń

wilgoci (zawil

ż

enie) gazu X

Jest stosunkiem ilości pary lotnej m

p

i ewentualnie skondensowanej m

s

(w postaci

mgły ciekłej lub lodowej) do ilości gazu suchego m

g

, którego ilość się nie zmienia w

trakcie rozważania wielu zjawisk

p

s

g

m

m

X

m

+

=

; 0 X

≤

≤ ∞

Stopień wilgoci wilgotnego gazu nienasyconego przy

p

s

p

p

ϕ

=

wynosi:

(

)

p

p

g

p

p

p

p

p

p

s

g

g

p

g

g

g

g

s

g

p

m

R p

M p

M p

M

p

X

m

R p

M p

M

p

p

M

p

p

ρ

ϕ

ρ

ϕ

=

=

=

=

=

=

⋅

−

−

;

''

0

X

X

≤ ≤

Dla powietrza i pary wodnej:

18, 015

p

M

kg kmol

=

;

28,967

g

M

kg kmol

=

0, 6219

s

s

p

X

p

p

ϕ

ϕ

=

⋅

−

Stopień wilgoci wilgotnego gazu nasyconego (

ϕ

=1) wynosi:

''

p

s

g

s

M

p

X

M

p

p

=

⋅

−

a dla powietrza i pary wodnej

''

0, 6219

s

s

p

X

p

p

=

⋅

−

Molowy stopień wilgoci:

p

s

s

z

g

s

n

n

p

X

n

p

p

ϕ

ϕ

+

=

=

−

6. Sta

ł

a gazowa gazu wilgotnego

1

1

1

g

p

g

g

s

p

R

XR

R

R

X

R

p

R

p

ϕ

+

=

=

+





− −













dla powietrza i pary wodnej

461, 52

p

R

J kgK

=

;

287, 03

g

R

J kgK

=

0, 6219

287

461, 52

1

1 0, 3781

s

X

R

p

X

p

ϕ

+

=

=

+

−

7. G

ę

sto

ść

wilgotnego gazu

(

)

1

1

g

p

g

g

p

g

p

g

p

p

p

X

R

R

T

R T

ρ ρ

ρ





=

+

=

+

=

+













8. Obj

ę

to

ść

(w

ł

a

ś

ciwa) (1+X) kg wilgotnego gazu, czyli 1 kg suchego gazu wynosi

1

g

X

g

p

p

p

R

T

T

v

R

XR

R

X

p

R

p

+





=

+

=

+













dla powietrza i pary wodnej

(

) ( )

3

1

461, 52 0, 6219

1

X

T

m

v

X

p

X kg

+

=

+

+

9. Entalpia

Entalpia (1+X) kg wilgotnego gazu nienasyconego lub nasyconego (X≤X

’’

) parą o

entalpii parowania r

0

, w stanie odniesienia o temperaturze T

0

wynosi:

(

)

(

)

1

0

0

0

X

g

p

pg

pp

i

i

Xi

c

T

T

X r

c

T

T

+





= +

=

−

+

+

−





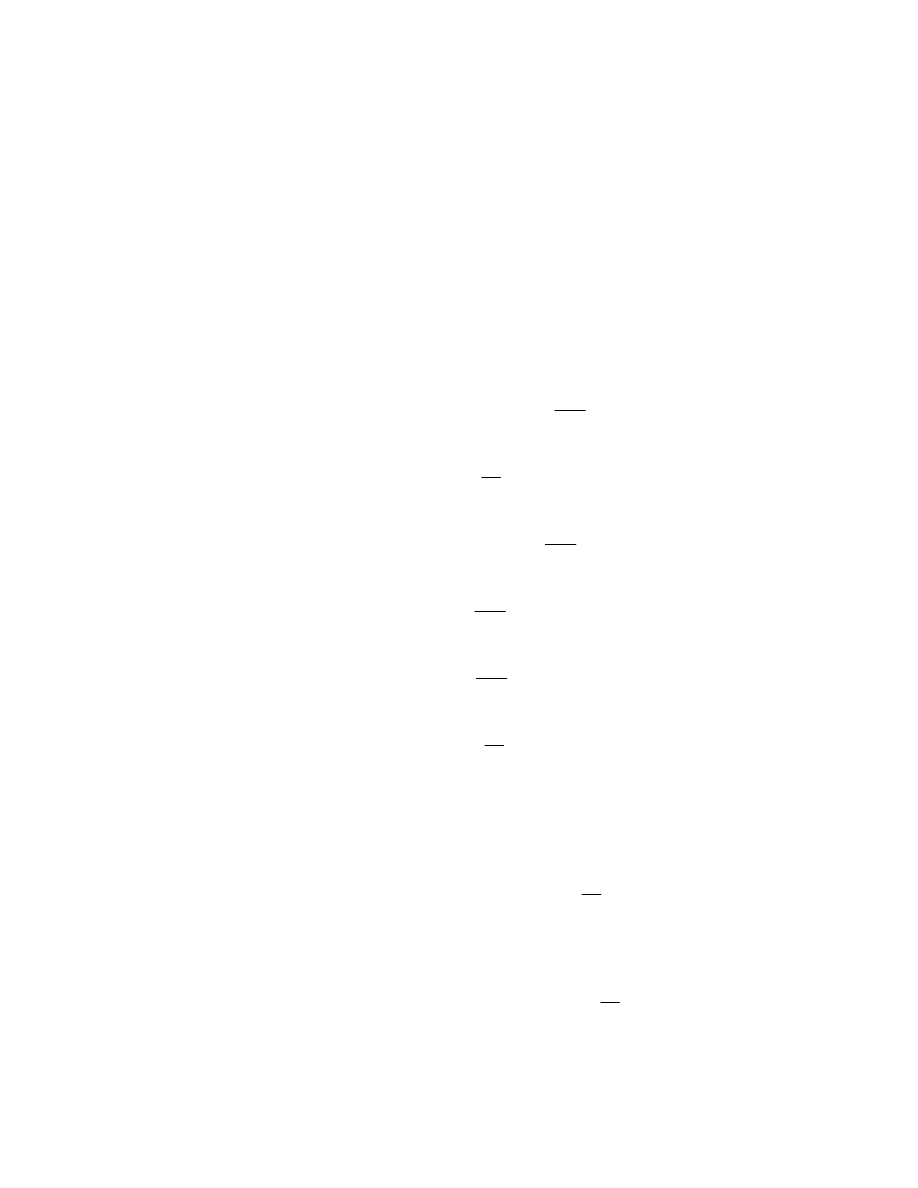
Entalpia (1+X) kg wilgotnego gazu przesyconego (X>X

’’

) z mgłą ciekłą o cieple

właściwym c

1

jest równa:

(

)

(

)

(

)

(

)

''

''

1

0

0

0

1

0

X

pg

pp

i

c

T

T

X

c

T

T

r

X

X

c T

T

+





=

−

+

−

+

+

−

−





Entalpia (1+X) kg wilgotnego gazu przesyconego (X>X

’’

) z mgłą lodową o cieple

właściwym c

s

i entalpii topnienia q

t

wynosi:

(

)

(

)

(

)

(

)

''

''

1

0

0

0

0

X

pg

pp

t

s

i

c

T

T

X

c

T

T

r

X

X

q

c T

T

+





=

−

+

−

+

+

−

−

−













Dla powietrza zawierającego parę wodną, mgłę ciekłą lub lodową za stan odniesienia

przyjmuje się punkt potrójny wody T

Tr

=237,16K oraz właściwości fizyczne wody:

6

1, 0057 13 10

1, 006

pg

C

kJ

c

T

kgK

−

=

+ ⋅

≈

0

2501

kJ

r

kg

=

1,864 0, 0002

1,87

pp

C

kJ

c

T

kgK

=

+

≈

1

4,19

kJ

c

kgK

=

2, 09

s

kJ

c

kgK

=

334,1

t

kJ

q

kg

=

po podstawieniu tych wartości do powyższych równań otrzymujemy:

entalpia właściwa powietrza suchego

(

)

1, 006

273,16

1, 006

275

g

kJ

i

T

T

kg

=

−

=

−

entalpia właściwa pary wodnej

(

)

2501 1,87

273,16

1990 1,87

p

kJ

i

T

T

kg

=

+

−

=

+

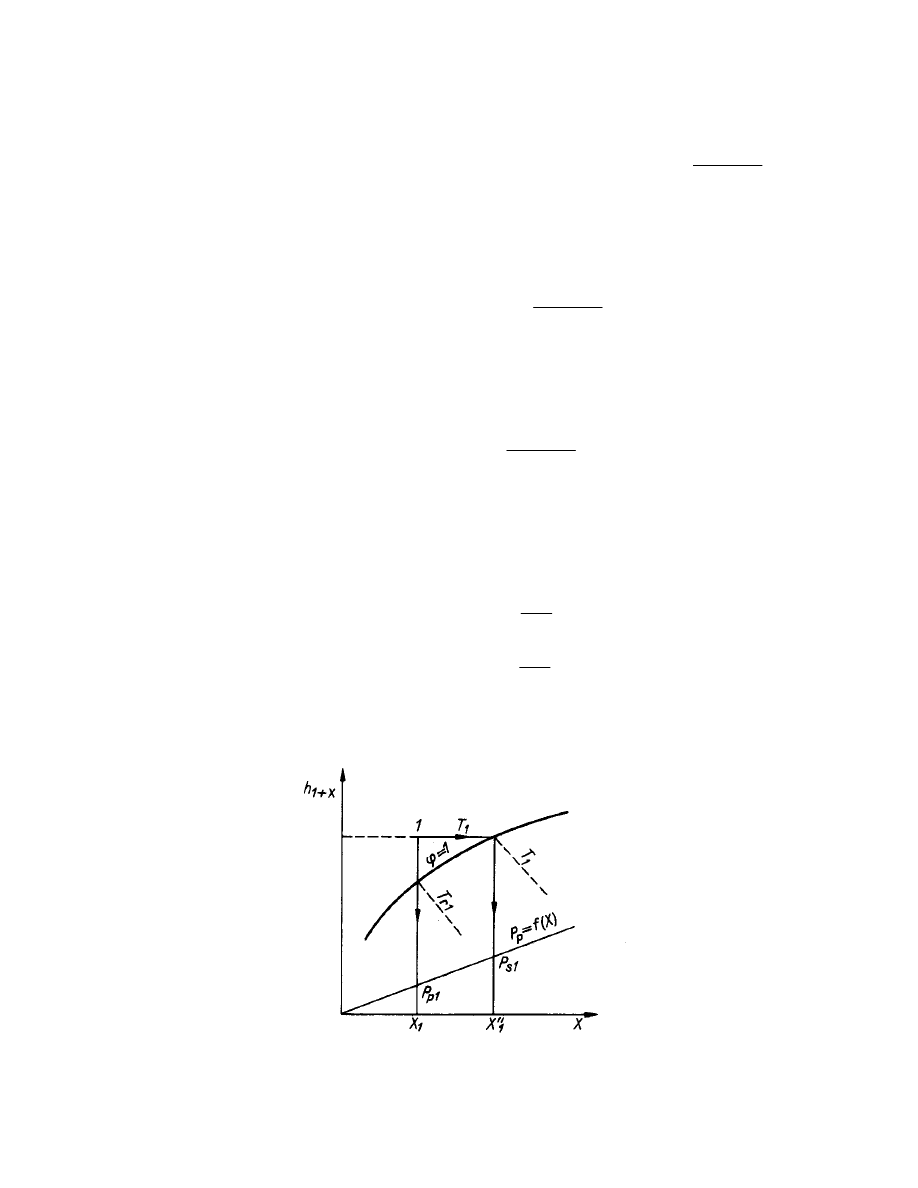
entalpia właściwa powietrza wilgotnego nienasyconego

(

)

(

)

(

)

(

)

1

1, 006

273,16

1990 1,87

1, 006

1990 1,87

1

X

kJ

i

T

X

T

T

X

T

X kg

+

=

−

+

+

=

+

+

− 275

+

entalpia właściwa powietrza wilgotnego przesyconego mgłą ciekłą

(

)

(

)

(

)(

)

(

)

(

)

(

)

1

1, 006

273,16

'' 1,87

273,16

2501

''

'' 3135 2, 32

1145 4,19

1

X

i

T

X

T

X

X

kJ

X

T

X

T

X kg

+

=

−

+

−

+

+ 4,19

−

Τ − 273,16 =









1,006Τ +

−

−

−

− 275

+

entalpia właściwa powietrza wilgotnego przesyconego mgłą lodową

(

)

(

)

(

)

(

)

(

)

(

)

(

)

1

1, 006

273,16

'' 1,87

273,16

2501

''

'' 2895 0, 22

905 2, 09

1

X

i

T

X

T

X

X

kJ

X

T

X

T

X kg

+

=

−

+

−

+

−

−

334,1− 2,09 Τ − 273,16 =

















1,006Τ +

−

−

−

− 275

+

II. RÓWNANIA STANU GAZU WILGOTNEGO

(

)

1

g

pV

X m RT

= +

p

p

p

p

p

p

g

g

g

g

g

g

p V

p V

m R T

m

R T

p V

p V

m R T

m

R T

=

⇒

=

=

⇒

=

III. PRZEMIANY WILGOTNEGO POWIETRZA

Rys.1. Odczytywanie ciśnienia nasycenia i temperatury rosy z wykresu i

1+X

– X.

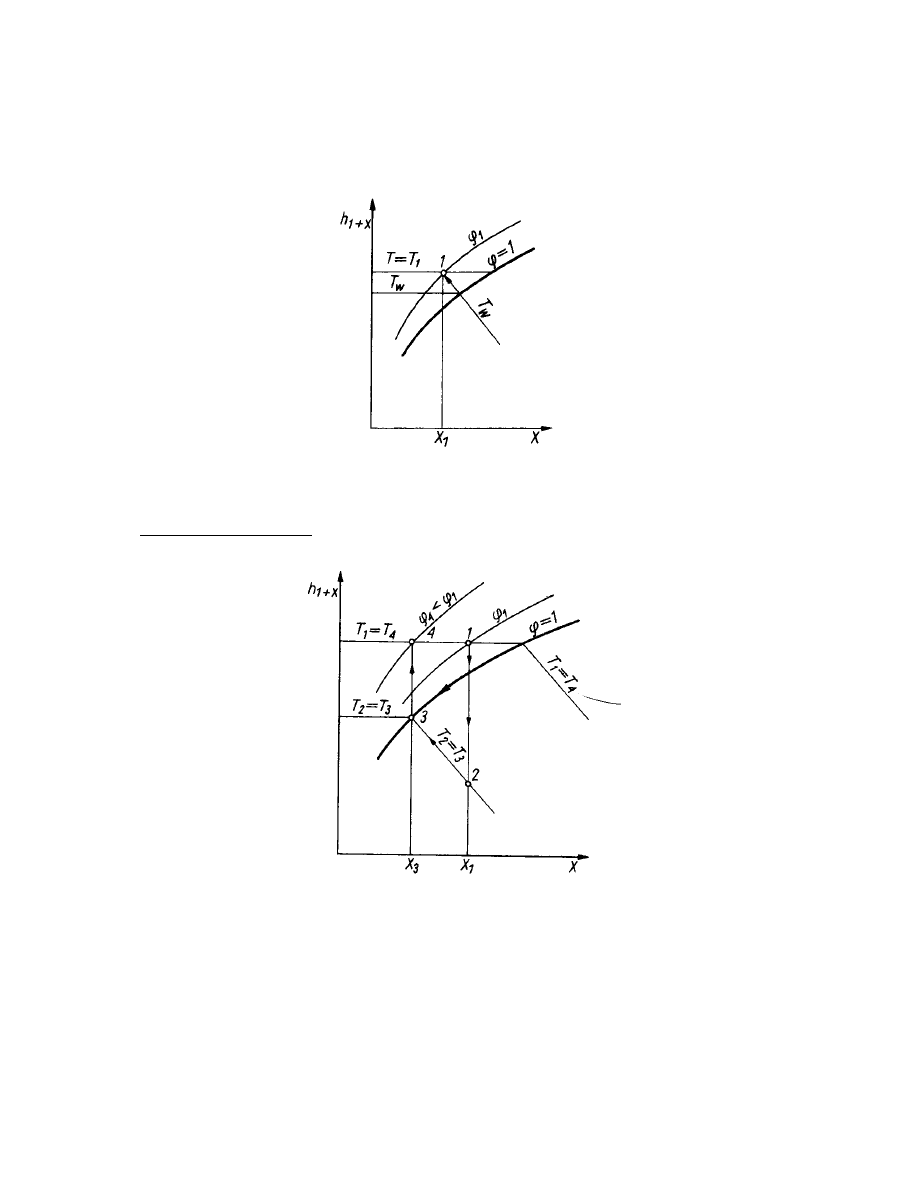
Rys.2. Odczytywanie wilgotności względnej z wykresu i

1+X

– X.

1. Osuszanie powietrza

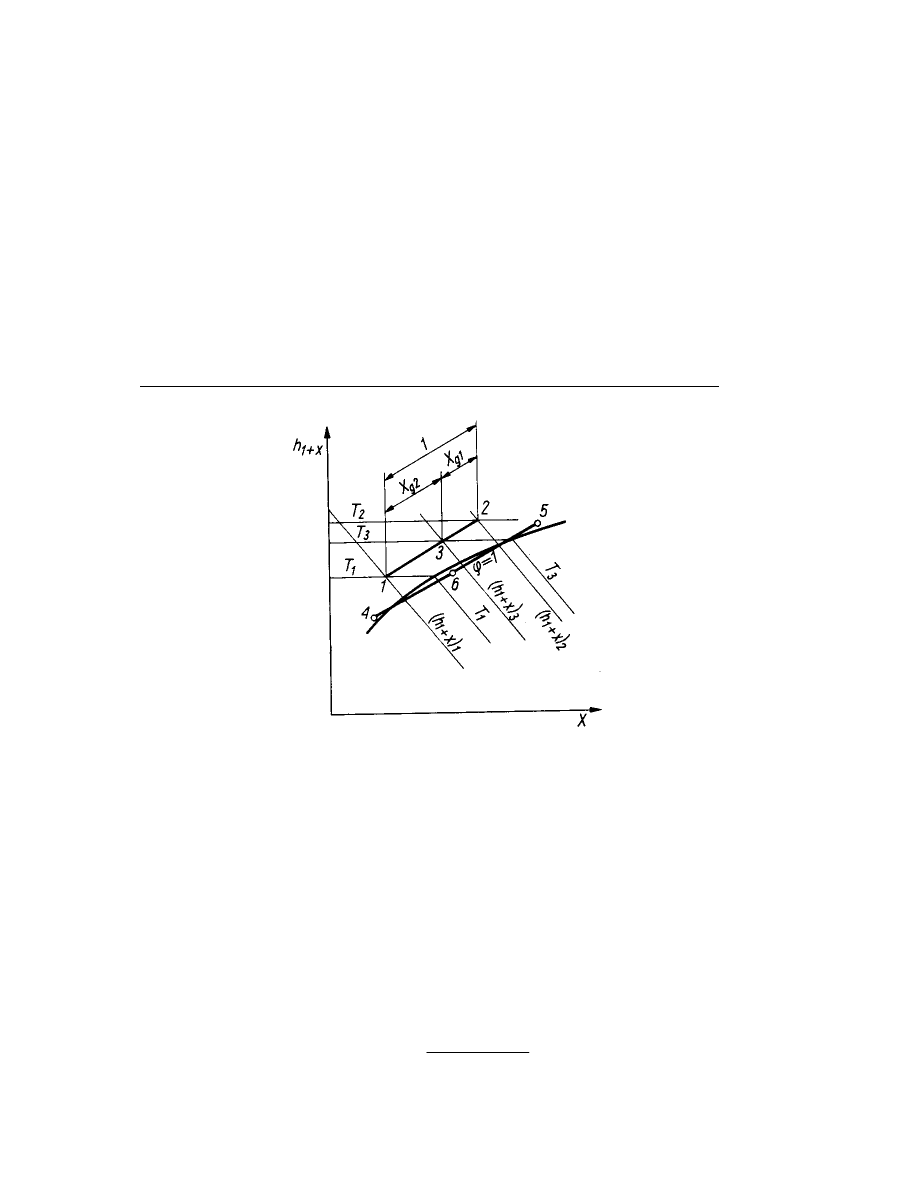
Rys.3. Osuszanie wilgotnego powietrza na wykresie i

1+X

– X.

Osuszanie powietrza (ze stanu 1 na rys.3) wymaga najpierw izobarycznego

ochłodzenia powietrza nienasyconego, podczas którego stopień wilgoci nie zmienia
się. Początkowo wzrasta wilgotność względna do

ϕ

=1, po czym powstaje powietrze

przesycone, które stanowi roztwór powietrza nasyconego i mgły (stan 2).

Doprowadzenie lub odprowadzenie ciepła bez zmiany stopnia wilgoci (X=idem) wiąże

się ze zmianą entalpii

( ) ( )

(

)

(

) (

)(

)

1

1

2

1

2

1

2

1

1, 006 1,87

X

X

pg

pp

i

i

c

Xc

T

T

X

T

T

+

+

−

=

+

−

=

+

−

Stan powietrza nasyconego zmienia się następnie wzdłuż linii nasycenia (stopień

wilgoci i entalpia maleją) aż do stanu 3, wyznaczonego przez punkt przecięcia linii
nasycenia z izotermą odpowiadającą stanowi końcowemu 2 powietrza przesyconego.
Ilość skroplonej wody wynosi

(

)

''

1

3

w

g

m

m

X

X

=

−

2. Mieszanie izobaryczno-adiabatyczne dwóch strumieni powietrza wilgotnego

Rys.4. Mieszanie izobaryczno-adiabatyczne dwóch strumieni wilgotnego powietrza na

wykresie i

1+X

– X.

Rozważmy dwa strumienie masy suchego powietrza

1

g

m

 oraz

2

g

m

 i stanach

określonych przez wartości X

1

, T

1

oraz X

2

, T

2

. Zmieszanie tych strumieni spowoduje

utworzenie strumienia powietrza wilgotnego o stanie X

3

, T

3

i strumieniu masy

powietrza suchego

3

1

2

g

g

g

m

m

m

=

+







Z równania bilansu ilości wody otrzymuje się stopień wilgoci:

1

1

2

2

3

1

2

g

g

g

g

m X

m X

X

m

m

+

=

+









Z równania bilansu entalpii wynika

( )

( )

( )

1

1

2

1

1

2

1

3

1

2

g

X

g

X

X

g

g

m

i

m

i

i

m

m

+

+

+

+

=

+









Po wyeliminowaniu strumieni masy suchego powietrza z równań bilansów otrzymuje
się

( ) ( )

( ) ( )

1

1

1

3

1

3

1

1

3

2

3

2

X

X

X

X

i

i

X

X

i

i

X

X

+

+

+

+

−

−

=

−

−

Stan strumienia otrzymanego po zmieszaniu leży na wykresie o współrzędnych i

1+X

–

X (rys.4) na prostej łączącej stany 1 i 2 mieszanych strumieni wilgotnego powietrza.

Punkt 3 dzieli odcinek 1-2 w stosunku strumieni masy lub udziałów masowych
powietrza suchego mieszanych strumieni.

2

2

1

3

1

1

3

2

g

g

g

g

m

x

X

X

m

x

X

X

−

=

=

−





Należy zauważyć, że mieszanie dwóch strumieni wilgotnego powietrza nienasyconego

o stanach 4 i 5 może doprowadzić do powstania strumienia powietrza przesyconego
(stan 6 z mgłą), gdy prosta 4-5 przecina linię nasycenia (rys.4)

W szczególnym przypadku, kiedy drugi strumień jest strumieniem pary wodnej lub

ciekłej wody o strumieniu masy

w

m

 , wtedy jego stan o X

2

=

∞

nie może być

przedstawiony na wykresie. Z równania ilości substancji wynika

3

1

1

w

g

m

X

X

m

−

=





natomiast z równania bilansu entalpii jest

( ) ( )

1

1

3

1

1

w

X

X

w

g

m

i

i

i

m

+

+

−

=





gdzie i

w

oznacza entalpię właściwą pary wodnej lub ciekłej wody.

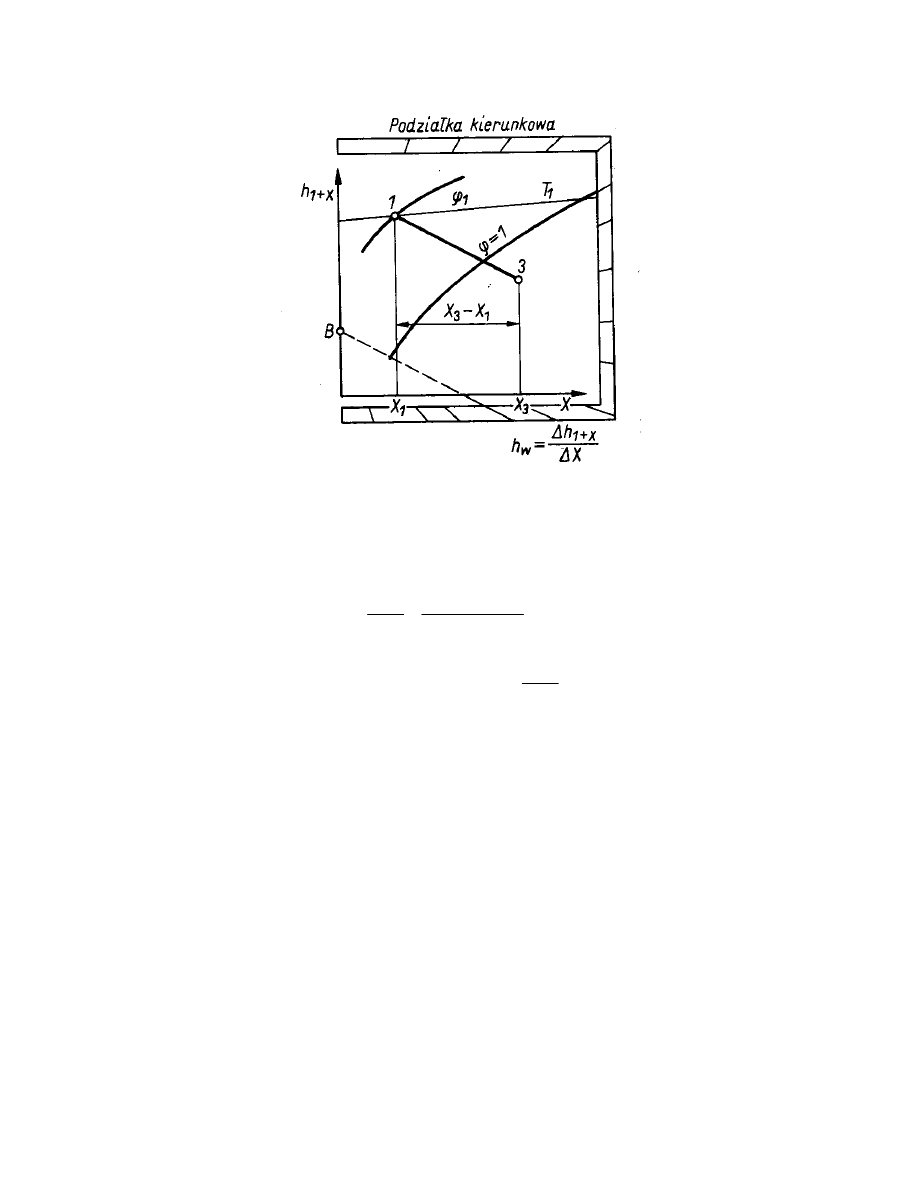
Rys.5. Mieszanie strumienia wilgotnego powietrza z parą wodną na wykresie i

1+X

– X.

Stan 3 powstały po zmieszaniu strumieni znajduje się na prostej wychodzącej z
punktu 1 (rys.5) w kierunku

( ) ( )

1

1

3

1

1

3

1

X

X

X

w

i

i

i

i

X

X

X

+

+

+

−

∆

=

=

∆

−

równoległym do linii łączącej biegun B z wartością

1 X

i

X

+

∆

∆

na dodatkowej podziałce

umieszczonej wokół wykresu. Położenie punktu 3 na tej linii wyznacza wartość X

3

.