UWZGLĘDNIENIE RYZYKA W PLANIE FINANSOWYM

SUŻĄCYCM OCENIE PROJEKTÓW INWESTYCYJNYCH

Podejmując decyzje o wdrożeniu projektów, z natury jesteśmy narażeni

na ryzyko związane z niepewnością oszacowania przepływów pieniężnych z

nimi związanych. Sposobem na zmniejszenie ryzyka wystąpienia znacznej

różnicy pomiędzy prognozą a rzeczywistymi wartościami projektu jest

zastosowanie następujących metod:



analizy jednej różnicy,



analizy scenariuszy



analiza Monte Carlo



analizy drzew decyzyjnych

ANALIZA jednej różnicy polega ona na wyszukiwaniu istotnych

czynników determinujących wartość projektu i szacowaniu, jak się ona

zmieni w zależności od wartości przypisywanych poszczególnym zmiennym.

Sprawdzane są konsekwencje płynące z niewłaściwego ich oszacowania.

Propozycje w tym zakresie powinny być składane z różnych działów

przedsiębiorstwa (m.in.: marketing, produkcja, finanse, logistyka).

ZALETY ANALIZY WRAŻLIWOŚCI







WADA ANALIZY WRAŻLIWOŚCI



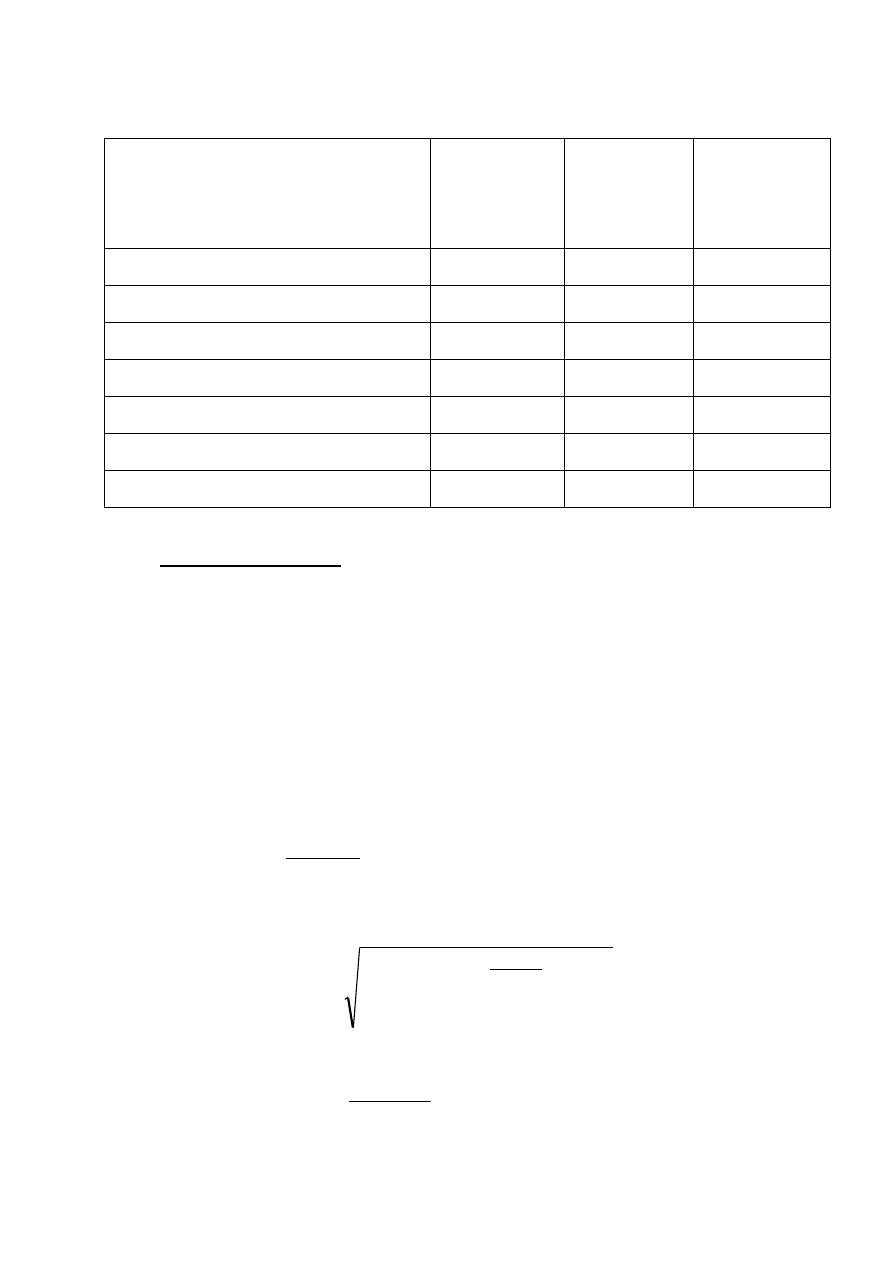
Tabela nr 1. Analiza wrażliwości – wyszukiwanie istotnych zmiennych projektu

zmienna

wartość

wartość

krytyczna

zmiana

prognozowana

(NPV = 0)

(%)

Wydatek inwestycyjny

1 400 000,00 2 373 996,29

69,57%

Cena jednostkowa

850,00

764,92

-10,01%

Ilość sprzedaży (szt.)

6 000,00

3 998,00

-33,37%

Jednostkowy koszt mat. i energii

580,00

663,57

14,41%

Koszty ogólnozakładowe

300 000,00

804 490,59

168,16%

Okres spływu należności

30

385

1183,33%

Stopa dyskontowa (koszt kapitału)

14,00%

42,38%

202,71%

Analiza scenariuszy zakłada jednoczesne – powiązane ze sobą zmiany

większej liczby zmiennych (zbioru parametrów).

Dla każdego scenariusza powinno się oszacować prawdopodobieństwo

jego realizacji. Znając opłacalność projektu (NPV) przy danym

prawdopodobieństwie jej wystąpienia, można wyliczyć oczekiwaną wartość

NPV, odchylenie standardowe NPV, czy też współczynnik zmienności, by

określić stopień ryzyka, jaki wiąże się z uzyskaniem wartości NPV danego

projektu.

)

*

(

1

i

n

i

i

NPV

p

NPV







)

*

)

((

2

1

p

i

n

i

i

NPV

NPV

NPV

S









S

NPV

CV

NPV

=

NPV

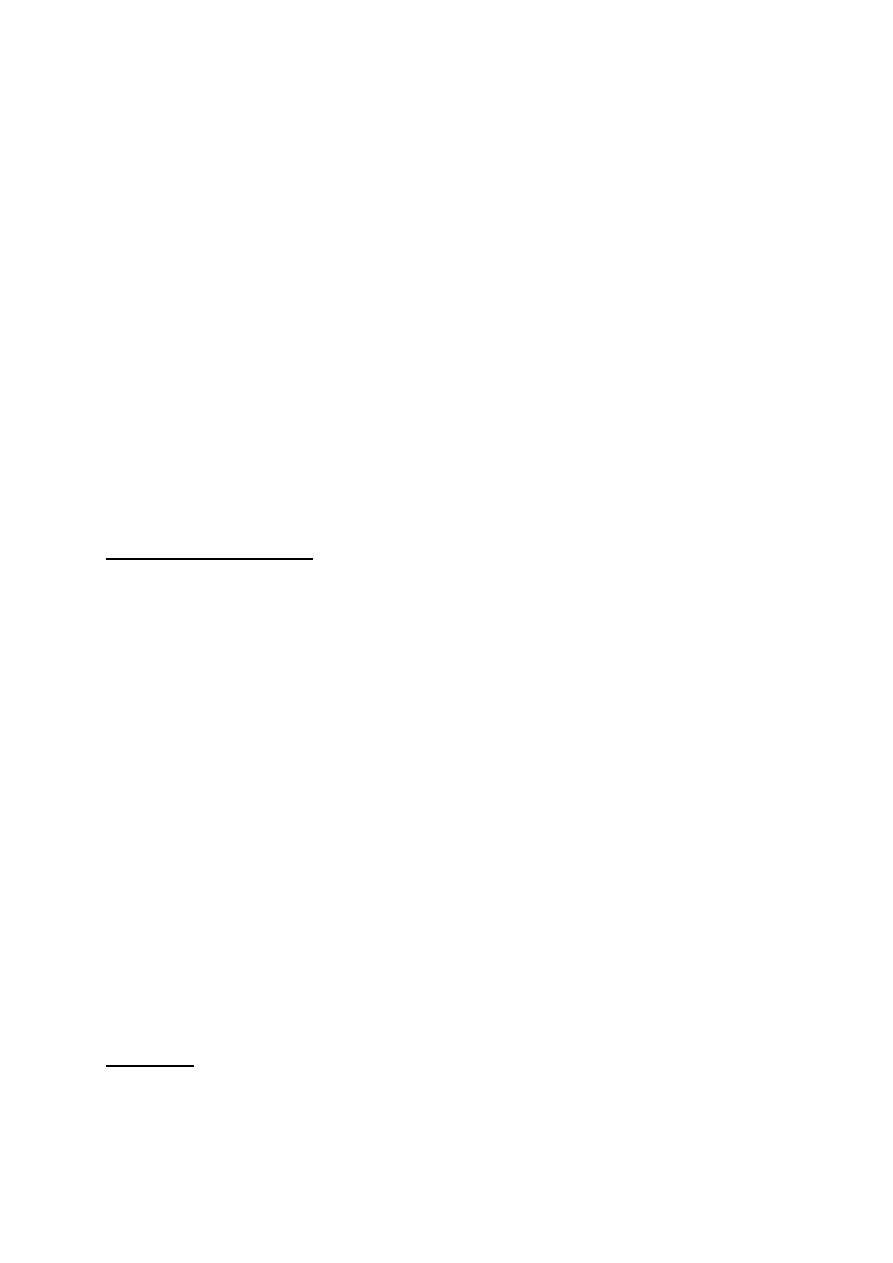
Wady (ograniczenia analizy scenariuszy)

1.

2.

Symulacja Monte Carlo

Analiza scenariuszy ogranicza się do badania wpływu tylko kilku rozwiązań i

ich wpływu na wartość oczekiwaną i ryzyko inwestycji. Znacznie więcej

możliwych kombinacji zmiennych można uwzględnić stosując metodę zwaną

SYMULACJĄ MONTE CARLO.

Polega ona na losowym stworzeniu bardzo dużej liczby scenariuszy w oparciu o

losowe, niezależne podstawienia każdej wartości danego parametru. Wartości te

losowane są z założonego wcześniej rozkładu prawdopodobieństwa o danej

charakterystyce. Scenariusze te podstawiane na wejściu modelu generują

rozkład prawdopodobieństwa danego miernika opłacalności inwestycji (NPV) z

określoną jego charakterystyką (wartość oczekiwana, odchylenie standardowe).

Zastosowanie symulacji wymaga komputera i odpowiedniego specjalistycznego

oprogramowania.

Etapy postępowania w symulacji Monte Carlo

KROK 1. Modelowanie przedsięwzięcia: „Podanie komputerowi” dokładnego

modelu inwestycji. – zaprojektowanie modelu przepływów pieniężnych.

KROK

2.

Określenie prawdopodobieństwa każdego z czynników

determinujących wielkość przepływów pieniężnych (każdej zmiennej).

Zazwyczaj stosuje się tu ciągłe rozkłady normalne. Należy także określić

korelację pomiędzy poszczególnymi rozkładami prawdopodobieństwa (co

zazwyczaj stanowi największy problem dla planistów).

KROK 3. Symulacja przepływów pieniężnych. Po wielu symulacjach

wykonanych przez program, otrzymujemy szacunkowy obraz rozkładów

prawdopodobieństwa przepływów pieniężnych – na tyle dokładny, na ile

dokładny jest skonstruowany model i rozkłady prawdopodobieństwa błędów

prognozy.

Modelowanie i symulacja Monte Carlo ma służyć nie tylko do generowania

rozkładu wartości zaktualizowanej netto, ale także (a może przede wszystkim)

do poznania mechanizmu przedsięwzięcia, prognozowania oczekiwanych

przepływów pieniężnych i do oceny ryzyka – a zatem może służyć LEPSZEMU

ZROZUMIENIU CHARAKTERU INWESTYCJI. Nie ma szans na zbudowanie

modelu umożliwiającego poznania przyszłości i rozważenia wszystkich

możliwych sytuacji.

Drzewa decyzyjne

Analiza drzew decyzyjnych polega na różnicowaniu wybranych

parametrów inwestycyjnych danego okresu w zależności od wyników zdarzeń

jakie miały miejsce w okresie wcześniejszym, a mających wpływ na wartość

tych parametrów. Analizując wydarzenia „w tył” – od przyszłości do

teraźniejszości – można obliczyć, jakie działania należy podjąć w przypadku

zaistnienia każdej z opisanych możliwości.

Dla każdego wariantu należy określić prawdopodobieństwo jego zajścia oraz

opłacalność (NPV). Uzyskujemy zatem zbiór wariantów przebiegu danej

inwestycji. Drzewa przedstawiają więc sumaryczną prezentację przepływów

pieniężnych będącą konsekwencją podjętych decyzji.

Analiza drzew decyzyjnych może być szczególnie przydatna przy analizie

wieloetapowych (sekwencyjnych) projektów. Każdy etap przedzielony jest

węzłem decyzyjnym. Szczególnie istotne jest uwzględnienie w analizie

poszczególnych węzłów możliwości opcji rezygnacji z inwestycji.

Przykład. Rozważane jest podjęcie inwestycji o następującej charakterystyce:

Nakład 10.000 (dane w tys. zł), horyzont inwestycji: 4 lata.

Inne parametry przedstawiono w poniższej tabeli.

Okres:

1

2

3

4

sprzedaż w szt.

15000

15500

16000

16600

cena jednostkowa

1,98

2,02

2,05

2,08

koszt jednostkowy

1,2

1,22

1,24

1,27

koszty stałe

8000

8200

8400

8700

- w tym amortyzacja

2000

2000

2000

2000

Stawka podatku

20%

20%

20%

20%

stopa dyskonta

10%

10%

10%

10%

OSN

27

30

30

30

OUZ

18

18

18

18

ORZ

42

42

42

42

NPV przy tak przyjętych założeniach wynosi 5 854 tys. zł

Zakładamy, że:

 zdarzeniem wpływającym na wartość projektu będzie rozmiar popytu na

produkt w kolejnych okresach inwestycji

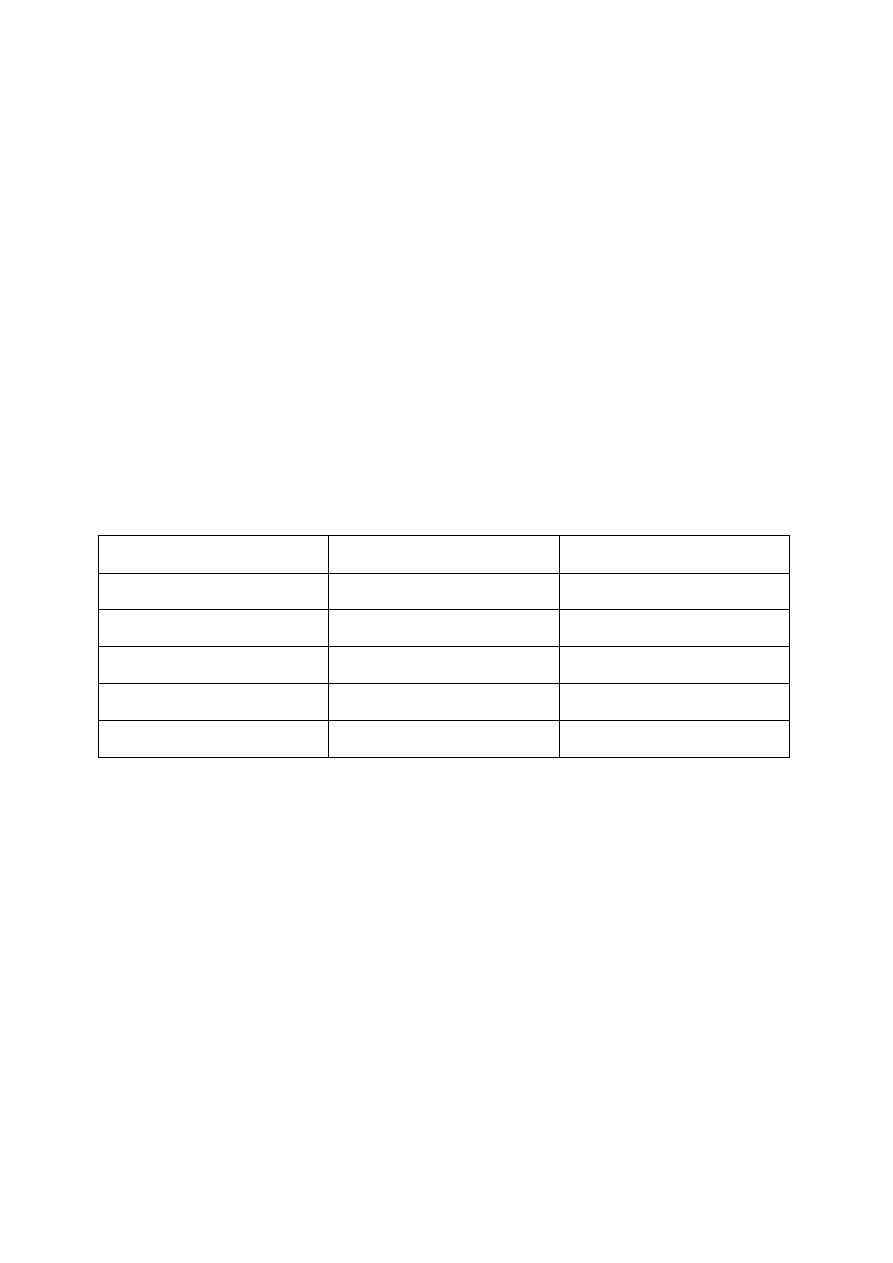
 możliwe są dwa warianty wielkości popytu w każdym z 4 okresów: albo

popyt będzie na zakładanym pierwotnie poziomie (patrz tabela z
parametrami) albo obniży się 45%.

 prawdopodobieństwo

spadku

popytu

o

45%

wynosi

30%,

prawdopodobieństwo utrzymania się popytu na zakładanym poziomie
70%

 W przypadku spadku popytu o 45%, w następnym roku rezygnujemy z

kontynuacji projektu (opcja rezygnacji)

Przy powyższych założeniach można obliczyć 5 wariantów ukształtowania się

wartości projektu (NPV) i oszacować prawdopodobieństwo ich zajścia.

Drzewo decyzyjne wygląda następująco:

Warianty inwestycji przedstawia poniższa tabela (do wypełnienia na wykładzie):

Warianty

p

NPV

I

II

III

IV

V

Wartość oczekiwana NPV wynosi : . zł

ZALETY drzew decyzyjnych:



możliwość opcji rezygnacji z inwestycji



prowadzą do określenia strategii firmy

WADA drzew decyzyjnych



stają się skomplikowane w krótkim czasie