1
Definicja
P
ę
d ciała definiujemy jako iloczyn jego masy i pr
ę
dko
ś
ci (wektorowej)
v
m
p
r
r =
t
r
m
v
m
p
d
d
r
v
r
=
=
k
p
j
p
i
p
p
z
y
x
r
r
r
r
+
+
=
t
x
m
p
x
d
d
=
t
y
m
p
y
d
d
=
t
z
m
p
z
d
d
=
P
ę
d jest wektorem, o kierunku zgodnym z kierunkiem pr
ę
dko
ś
ci.

2
Definicja
Je
ż
eli na ciało o masie m działa siła F, to definiujemy j
ą
jako
zmian
ę
w czasie p
ę
du ciała
t
p
F
d
dr
r
=
t
v
m
v
t
m
t
v
m
F
d
d
d
d
d
)
(
d
r
r
r
r
+
=
=
a
m
t
v
m
F
r
v
r
=
=
d
d
Gdy masa jest stała:
I zasada Newtona
Ciało, na które nie działa
ż
adna siła (lub gdy siła wypadkowa jest równa zeru)
pozostaje w spoczynku lub porusza si
ę
ze stał
ą
pr
ę
dko
ś
ci
ą
po linii prostej.
II zasada Newtona
Tempo zmian p
ę
du ciała jest równe sile wypadkowej działaj
ą
cej na to ciało.
Dla ciała o stałej masie sprowadza si
ę
to do iloczynu masy i przyspieszenia ciała.
III zasada Newtona
Gdy dwa ciała oddziałuj
ą
wzajemnie, to siła wywierana przez ciało drugie na ciało
pierwsze jest równa i przeciwnie skierowana do siły, jak
ą
ciało pierwsze działa na drugie.
t
p
F
d
d
wyp
r
r
=
lub
,
wyp
a
m
F
r
r
=
m = const
1
2
2
1
→
→
−
= F
F
r
r

3
Definicja
Pierwsza zasada dynamiki stwierdza,
ż
e je
ż
eli na ciało nie działa
ż
adna siła
(lub gdy siła wypadkowa jest równa zeru) to istnieje taki układ odniesienia,
w którym to ciało spoczywa lub porusza si
ę
ruchem jednostajnym
prostoliniowym. Taki układ nazywamy układem inercjalnym.
Pierwsza zasada dynamiki wydaje si
ę
by
ć
szczególnym przypadkiem drugiej bo gdy
a = 0 to i F
wyp
= 0 . Przypisujemy jej jednak wielk
ą
wag
ę
dlatego,
ż
e zawiera wa
ż
ne
poj
ę
cie fizyczne: definicj
ę
inercjalnego układu odniesienia.
'
'
'
'
t
t
z
z
y
y
X
x
x
=
=
=
+
=
'
'
'
z
z
y
y
x
x
v
v
v
v
V
v
v
=
=
+
=
'
'
'
z
z
y
y
x
x
a
a
a
a
a
a
=
=
=
Transformacja Galileusza
Nast
ę
pstwem istnienia układu inercjalnego jest zasada wzgl
ę
dno
ś
ci
Galileusza, głosz
ą
ca,
ż
e ruch jednostajny i prostoliniowy układu odniesienia
nie wpływa na przebieg zachodz
ą
cych w nim procesów mechanicznych.
Do porównania wielko
ś
ci fizyczne mi
ę
dzy układami inercjalnymi
stosuje si
ę
transformacja Galileusza.
Z równo
ś
ci przyspiesze
ń
wynika,
ż
e II prawo Newtona w układach poruszaj
ą
cych si
ę
wzgl
ę
dem siebie ze stał
ą
pr
ę
dko
ś
ci
ą
b
ę
dzie miało tak
ą
sam
ą
posta
ć
, a tym samym
obaj obserwatorzy stwierdz
ą
działanie takiej samej siły (przyczyny ruchu).
a
m
F
r
r =
'
'
a
m
F
r
r =
'
a
a
r
r =
const
m
=
'
F
F
r
r =
⇒

4
a
m
F
r
r
=
wyp
)
,
,
(
t
v
r
F
F
r
r
r
r =
K
r
r
r
r
+
+
+
=
3
2
1
wyp
F
F
F
F
)
,
d
d
,
(
d
d
2
2
t
t
r
r
F
t
r
m
r
r
r
r
=
)
,
d
d
,
d
d
,
d
d
,
,
,
(
d
d
2
2
t
t
z
t
y
t
x
z
y
x
F
t
x
m
x
=
)
,
d
d
,
d
d
,
d
d
,
,
,
(
d
d
2
2
t
t
z
t
y
t
x
z
y
x
F
t
y
m
y
=
)
,
d
d
,
d
d
,
d
d
,
,
,
(
d
d
2
2
t
t
z
t
y
t
x
z
y
x
F
t
z
m
z
=
k
F
j
F
i
F
F
z
y
x
r
r
r
r
+
+
=
k
t
z
j
t
y
i
t
x
t
r
r
r
r
r
)
(
)
(
)
(
)
(
+
+
=
=
=
=
)
(
)
(
)
(
t
z
z
t
y
y
t
x
x
k
t
z
j
t
y
i
t
x
t
r
a
r
r
r
r
r
2
2
2
2
2
2
2
2
d
d
d
d
d
d
d
d
+
+
=
=

5
2
2
1
1
2
3
N
ma
N
N
ma
N
F
ma
=
−
=
−
=
m
F
m
m
m
F
a
6
3
2
=
+
+
=
const
m
F
t
x
=
=
6
d
d
2
2
2
6
)
(
2
t
m
F
t
x
=
r
k
a
m
r
r −
=
0
d
d
2
2
=
+ r
m
k
t
r
r
r
t
B
t
A
t
x
x
x
ω
ω
sin
cos
)
(
+
=
r
k
F
r
r −
=
0
d
d
2
2
=
+ x
m
k
t
x
0
d
d
2
2
=
+ y
m
k
t
y
0
d
d
2
2
=
+ z
m
k
t
z
t
B
t
A
t
y
y
y
ω
ω
sin
cos
)
(
+
=
t
B
t
A
t
z
z
z
ω
ω
sin
cos
)
(
+
=
t
B
t
A
t
r
ω
ω
sin
cos
)
(
r
r
r
+
=
k
A
j
A
i
A
A
z
y
x
r
r
r
r
+
+
=
k
B
j
B
i
B
B
z
y
x
r
r
r
r
+
+
=
m
k
=
ω
6
a
m
m
F
r
r
)
(
2
1
+
=
a
m
F
K
r
r
2
=
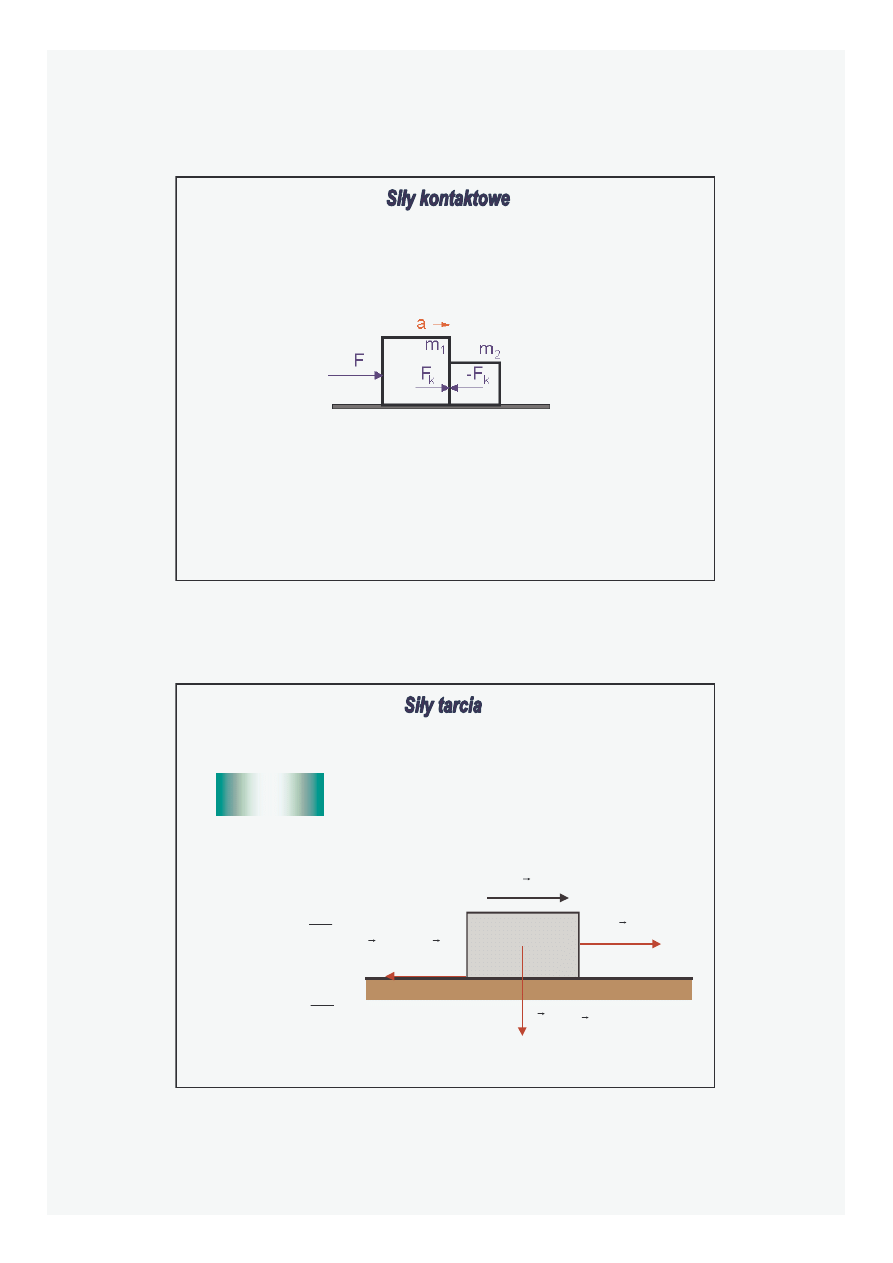
Siły kontaktowe s
ą
normalne (prostopadłe) do powierzchni.
Istnieje jednak składowa siły kontaktowej le
żą
ca w płaszczy
ź
nie powierzchni.
Je
ż
eli ciało pchniemy wzdłu
ż
stołu to po pewnym czasie ciało to zatrzyma si
ę
.
Z drugiej zasady dynamiki wiemy,
ż
e je
ż
eli ciało porusza si
ę
z przyspieszeniem
(opó
ź
nieniem) to musi działa
ć
siła. T
ę
sił
ę
, która przeciwstawia si
ę
ruchowi
nazywamy
sił
ą
tarcia.
N
F
T
r
r
µ
=
T
jest w przybli
ż
eniu niezale
ż
na od wielko
ś
ci pola powierzchni styku ciał;
T
jest proporcjonalna do siły z jak
ą
jedna powierzchnia naciska na drug
ą
.
N
S
s
F
T
r
r
=
µ
N
K
K
F
T
r
r
=
µ
Tarcie statyczne
:
Tarcie kinetyczne
:
−
N
F
r
−
µ
współczynnik tarcia
siła nacisku
n
v
T
F
i
F
µ
−
=
g
m
F
n
=
F
v

7
Przyspieszenia w obu układach s
ą
równe tylko wtedy gdy a
0
= 0 wi
ę
c gdy układ x'y’
porusza si
ę
wzgl
ę
dem układu xy ruchem jednostajnym lub wzgl
ę
dem niego
spoczywa to znaczy gdy układ x'y' te
ż
jest układem inercjalnym tak jak xy.
Natomiast gdy a
0
ró
ż
ne od 0 to układ x'y' nazywamy
układem nieinercjalnym
,
a jego przyspieszenie a
0
przyspieszeniem unoszenia
. Przyspieszenie ciała zale
ż
y
od przyspieszenia układu odniesienia (od przyspieszenia obserwatora),
w którym jest mierzone wi
ę
c druga zasada dynamiki jest słuszna tylko,
gdy obserwator znajduje si
ę
w układzie inercjalnym. Inaczej mówi
ą
c,
prawa strona równania F = ma zmienia si
ę
w zale
ż
no
ś
ci od przyspieszenia obserwatora
.
)
(
)
(
)
(
0
'
t
x
t
x
t
x
−
=
2
2
d
)
(
d
d
)
(
d
)
(
t
t
x
t
t
v
t
a
=
=
)
(
)
(
)
(
0
'
t
a
t
a
t
a
−
=
0
'
ma
F
ma
−
=
)
(
2
d
d
'
'
'
r
v
r
t
a
a
tr
u
r
r
r
r
r
r
r
r
r
×
×
+
×
+
×
+
=
ω
ω
ω
ω
tr
b
a
m
F
r
r =
'
2
v
m
F
C
r
r
r
×
=
ω
)
(
'
r
m
F
d
r
r
r
r
×
×
=
ω
ω
'
d
d
r
t
m
F
bo
r
r
r
×
=
ω
8
t
p
r
F
r
d
dr
r
r
r
×
=
×
t
p
r
v
m
v
t
p
r
p
t
r
t
p
r
t
p
r
d
)
(
d
d
)
(
d
d
d
d
)
(
d
d
d
r
r
v
r
r
r
r
r
r
r
r
r
×
=
×
−
×
=
×
−
×
=
×
F
r
M
r
r
v
×
=
p
r
L
v
r
r
×
=
(
)
t
p
r
F
r
d
d
r
r
r
r
×
=
×
r
p
r
L
×
=
p
α
sin
r
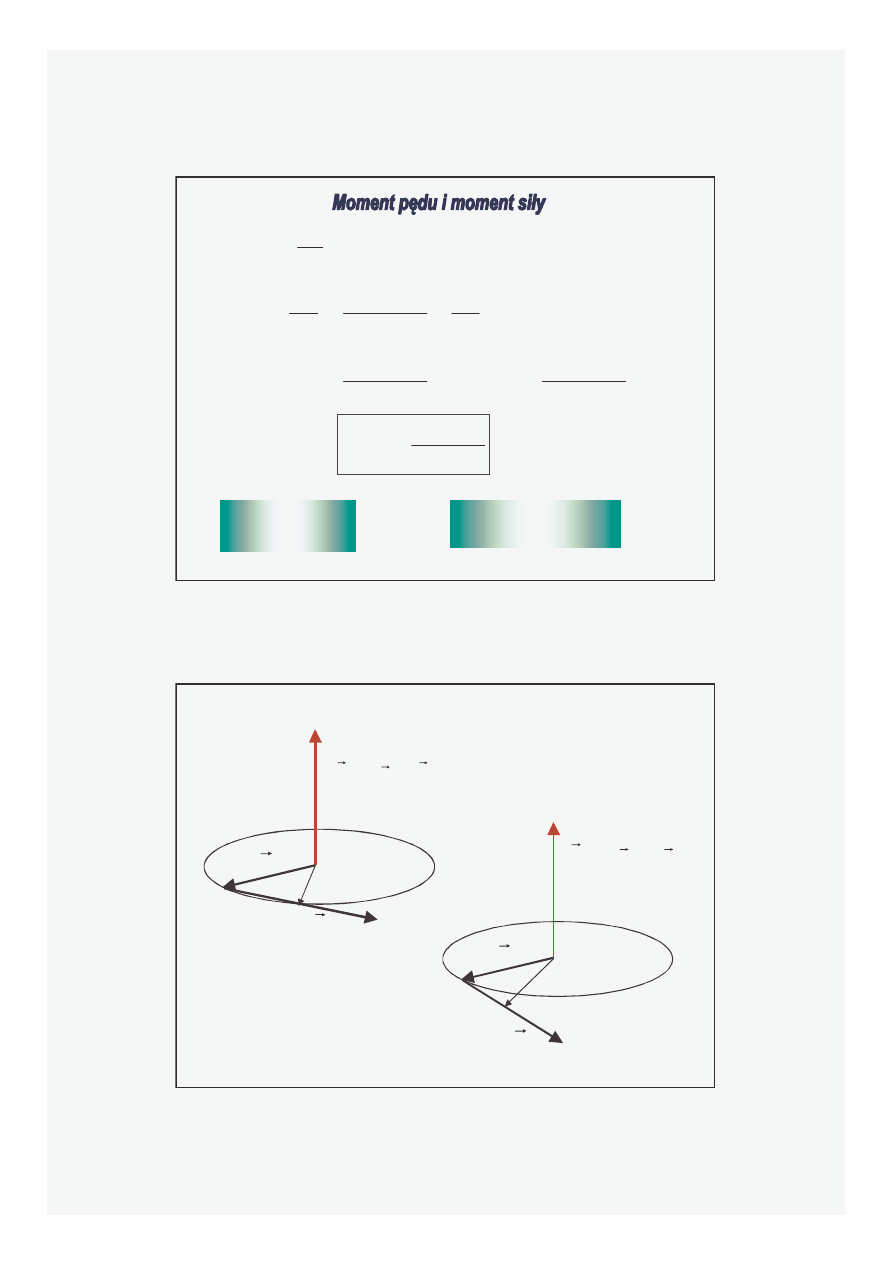
Moment siły
Moment p
ę
du
α
sin
r
F
r
F
r
M
×
=
9
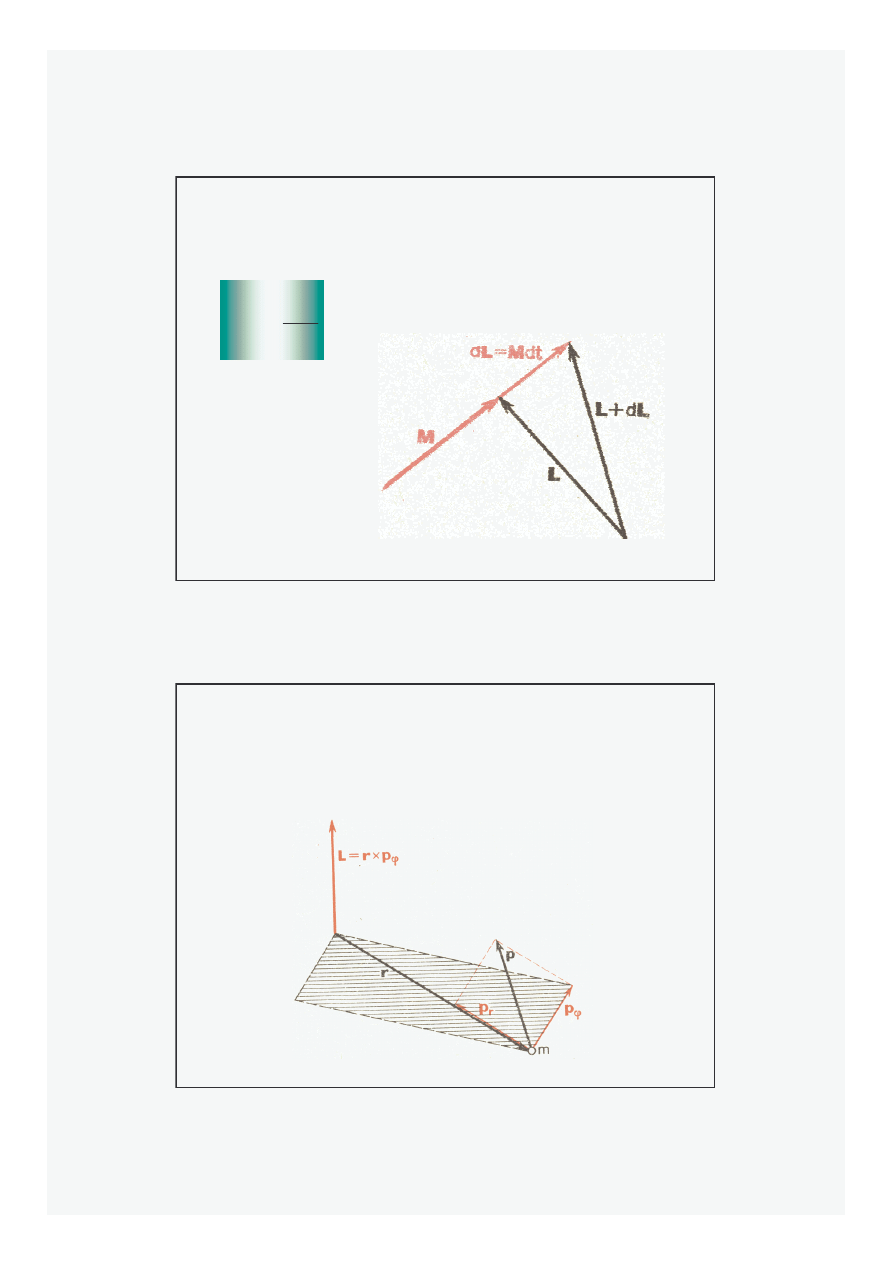
t
L
M
d
d
r
r
=
II zasada Newtona dla ruchu obrotowego:
Zmiana momentu p
ę
du ciała jest równe momentowi
siły wypadkowej działaj
ą
cemu na to ciało.
ω
ϕ
ϕ
ϕ
2
0
mr
v
m
r
p
r
L
p
r
L
r
r
=
×
=
×
=
=
×
=
r
r
r
r
r
r
r
r

10
t
I
t
L
M
d
)
d(
d
d
ω
r
r
r
=
=
ε
ω
r
r
r
I
t
I
M
=
=
d
)
d(
ω
ϕ
v
r
r
I
L
L
=
=
2
mr
I
=
Moment bezwładno
ś
ci
∫
=
−
=
B
A
t
t
A
B
t
F
p
p
t
F
p
d
d
d
r
r
r
r
r
∫
=
−
=
B
A
t
t
A
B
t
M
L
L
t
M
L
d
d
d
r
r
v
r
r
Zmiana p
ę
du (momentu p
ę
du) jest równa (wektorowo)
pop
ę
dowi siły (momentu siły). Je
ś
li siła (moment siły)
znika to p
ę
d (moment p
ę
du) cz
ą
stki jest stały.
const
to
0
=
=
L
M
v
r
const
to
0
=
=
p
F
r
r
Wyszukiwarka
Podobne podstrony:
Prawa ruchu dynamika
zm. prawa o ruchu dr. rowerzysci
Prawa ruchu
Prawa Ruchu
Maszyny Elektryczne Zadanie 2 Podstawowe Prawa Elektromagnetyczne Z Dynamiki Mechanicznej
Maszyny Elektryczne Zadanie 1 Podstawowe Prawa Elektromagnetyczne Z Dynamiki Mechanicznej (2)
Pytania z Prawa o Ruchu Drogowym, materiały dla instruktorów i przyszłych instruktorów nauki jazdy,
zm prawa o ruchu dr rowerzysci
prawa ruchu newtona
Prawa Ruchu
7 Dynamika ruchu obrotowego bry Nieznany
Jazda pasem ruchu oraz po łuku do przodu i do tyłu, Kurs Instruktora Prawa Jazdy, Egzamin praktyczny
więcej podobnych podstron