04-10-22

Reinhard Kulessa

1

Wykład 6

3 Prawa ruchu

3.1 I zasada dynamiki
Newtona

3.2 II zasada dynamiki Newtona

04-10-22

Reinhard Kulessa

2

3 Prawa ruchu

Ruch ciała możemy zmienić, jeśli poddamy
ciało oddziaływaniu. Będziemy chcieli
zastanowić się nad tym w jaki sposób dochodzi
do ruchu ciała. Będziemy chcieli zrozumieć,
dlaczego ciało drga na sprężynie, dlaczego
zatrzymuje się po pewnym czasie, dlaczego w
pewnych przypadkach wprawiamy ciało w ruch
nawet wtedy, gdy na
na to ciało bezpośrednio nie oddziałujemy.

3.1 I zasada dynamiki
Newtona

Już Galileusz zauważył, że każde ciało, jeśli na
nie nie działa żadne zewnętrzne zaburzenie
spoczywa, lub porusza się ze stałą prędkością.

Aby wprawić ciało w ruch, musimy pokonać
pewną jego własność zwaną

bezwładnością

.

04-10-22

Reinhard Kulessa

3

Newton przyjął obserwacje Galileusza i
sformułował

I Zasadę

Dynamiki

zwaną też

Zasadą Bezwładności.

Ciało odosobnione zawsze pozostaje w
spoczynku, lub porusza się ruchem
jednostajnym po linii prostej.

04-10-22

Reinhard Kulessa

4

04-10-22

Reinhard Kulessa

5

Opis odosobnionej cząstki, o której mówimy
w I zasadzie dynamiki Newtona zależy
również od układu odniesienia.

Taki układ odniesienia względem którego
cząstka nie podlega oddziaływaniu, spoczywa
lub porusza się ruchem jednostajnym po linii
prostej, nazywamy

układem inercjalnym.

Chcielibyśmy jakościowo sformułować
własność ciała zwaną

bezwładnością.

Z obserwacji wiemy, że

aby zmienić stan ciała

poruszającego się np. ruchem jednostajnym,
musimy ciało „popchnąć” lub „pociągnąć”.

Musimy na to ciało zadziałać pewną siłą.

Możemy więc powiedzieć, że ze względu na
bezwładność materii konieczna jest siła aby
zmienić stan ruchu ciała.

Zapytamy się jaka siła będzie potrzebna aby
nadać ciału określone przyśpieszenie.

04-10-22

Reinhard Kulessa

6

3.1.1 Statyczny pomiar siły

Zastanówmy się w jaki sposób dochodzimy do
pojęcia siły. Co jest wspólnego w naszych
poczynaniach co prowadzi do pojęcia siły?
Podstawową własnością siły jest to, że możemy
ją zmierzyć, tzn. w pewien sposób porównać ją
z inną siłą. Jako miernik siły weźmy sobie
sprężynę.

04-10-22

Reinhard Kulessa

7

Dynamometr

Dochodzimy do wniosku, że

sile musimy

przyporządkować punkt zaczepienia, oraz
kierunek

.

Oznacza to, że możemy ją opisać

przez jakiś wektor F.

Wielkość siły możemy określić z wydłużenia
sprężyny.

04-10-22

Reinhard Kulessa

8

Ponieważ wielkość wydłużenia zależy od
materiału, musimy sprężynę wycechować, tzn.
porównać z siłą, która zawsze i wszędzie jest
zdefiniowana w ten sam sposób, np. z siłą
wynikającą z prawa
powszechnego
ciążenia.

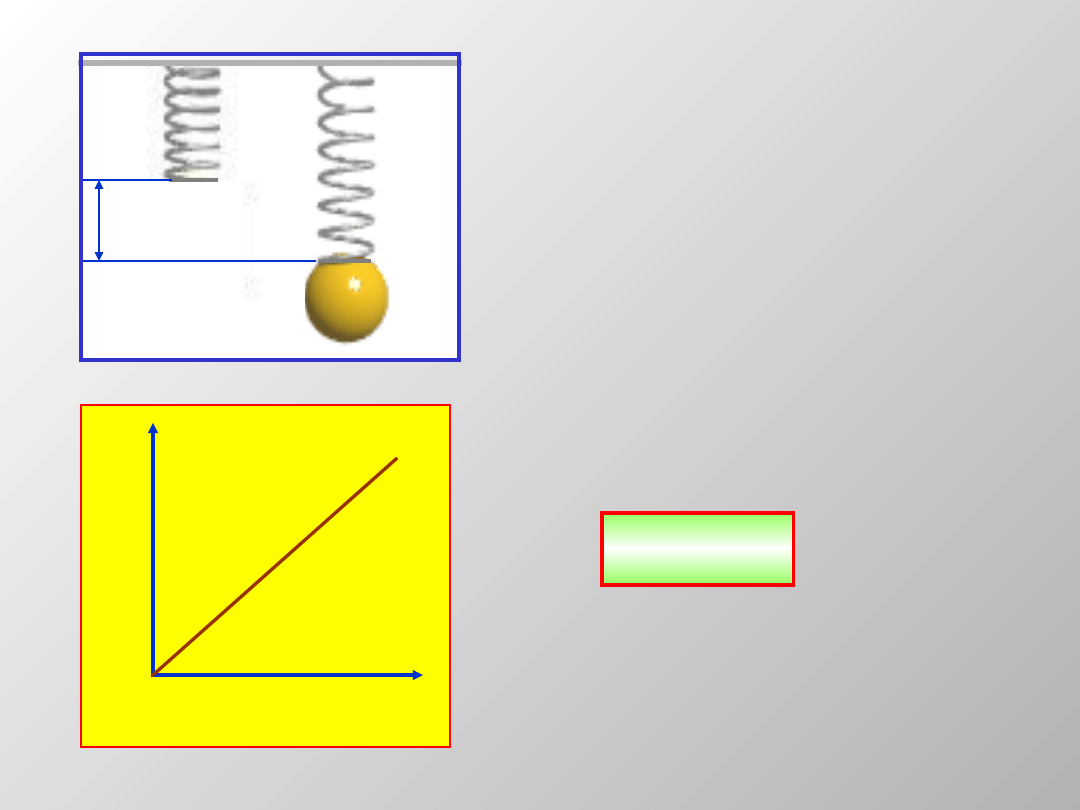
Jeśli sprężynę obciążymy masą, to sprężyna
wydłuży się o

l

.

Dlaczego? – bo masa jest przyciągana przez siłę
grawitacji. Gdy sprężyna znajdzie się w
spoczynku, siła grawitacji jest równoważona
przez siłę sprężystości.

04-10-22

Reinhard Kulessa

9

l

m

1

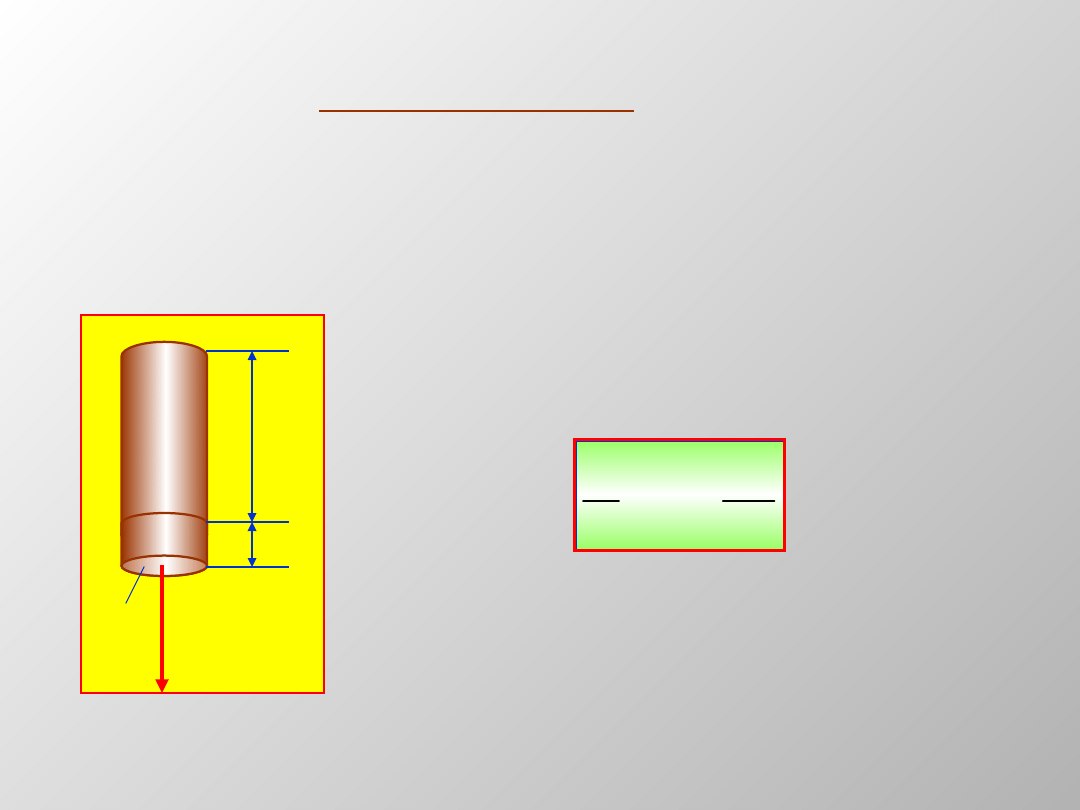
Jeśli obciążymy sprężynę
następną kulką o masie
m

1

sprężyna wydłuży się

ponownie o l., itd..

Możemy więc wyciągnąć
wniosek, że wydłużenie
sprężyny z zwiększa się

liniowo w stosunku do
przyłożonej siły.



z

m

s

Możemy to zapisać jako:

l

c

F











(3.1)

.

Znak siły jest ujemny,
gdyż siła sprężystości
sprężyny sprzeciwia się
wydłużaniu.

04-10-22

Reinhard Kulessa

10

Wyrażenie podane we wzorze

(3.1)

jest

znane jako Prawo Hooke’a.

Prawo to jest ważne dla wszystkich
materiałów i rodzajów deformacji, o ile
deformacja jest mała.
Bardzo często zamiast sprężyny stosujemy
pręt z danego materiału.

S

F

l

l

Dla przypadku podanego na
rysunku,

Prawo Hooke’a

można napisać

następująco;

l

l

E

S

F











.

(3.2)

Zakładamy przy tym, że

l

jest małe.

Zgodnie z równaniem

(3.1),

możemy mierzyć siłę przez
wydłużenie ciała.

04-10-22

Reinhard Kulessa

11

)

(

0

l

l

c

F













.

Pomiar ten odbywa się w jednostkach względnych.

W dalszym ciągu zastanowimy się nad

dynamicznymi skutkami działania siły

, czyli

m.in. jej wpływem na ruch.

3.2 II zasada dynamiki Newtona

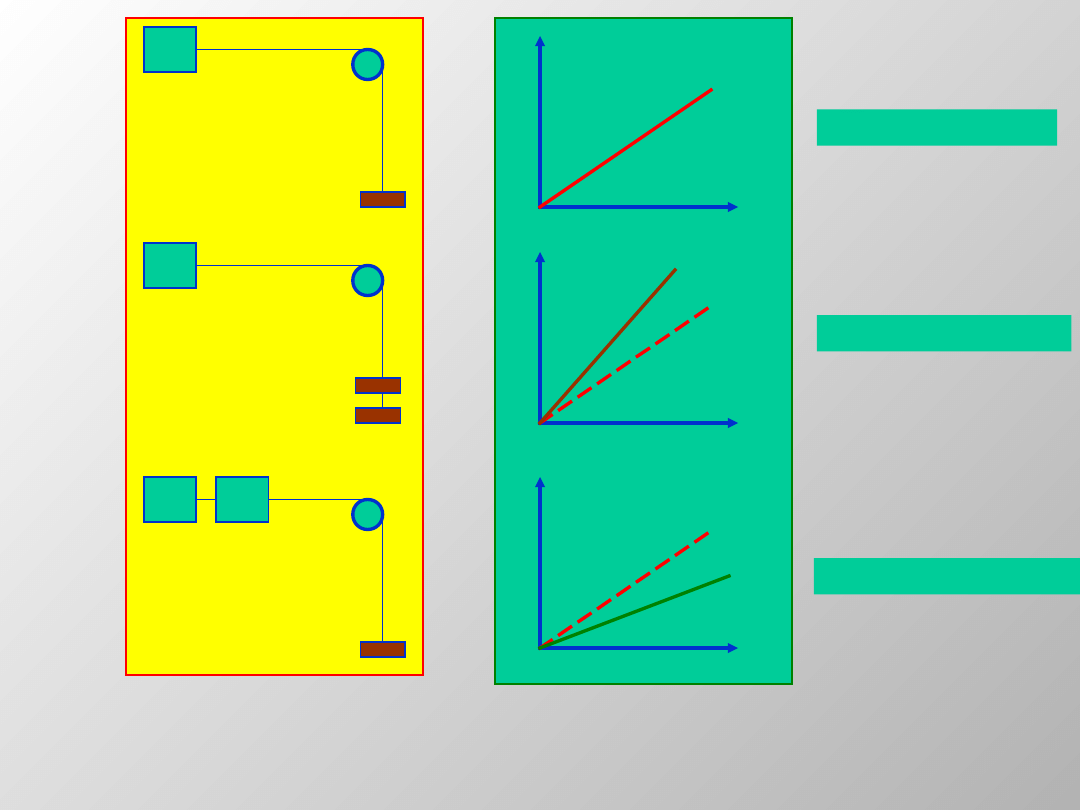
Zbadajmy na ławie powietrznej wpływ siły

F

g

na ruch wózka o masie

m

C

mogącego

poruszać się bez tarcia.
Wyznaczmy pokonaną drogę, a z niej
prędkość i przyśpieszenie w funkcji czasu
wykonując eksperyment przedstawiony na
następnej stronie.

04-10-22

Reinhard Kulessa

12

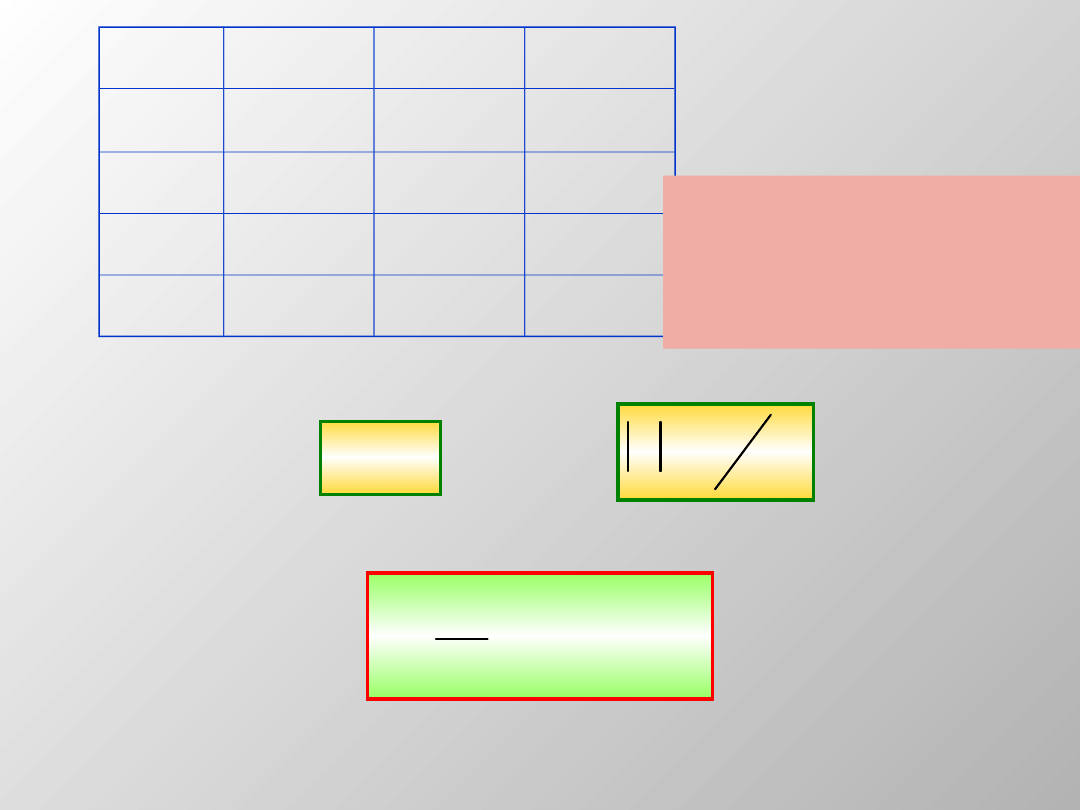
v

v

v

t

t

t

1 blok = m

C

1 blok

2 bloki

1 ciężar =F

g

1 ciężar

2 ciężary

Przyśpieszenie = a

Przyśpieszenie = 2a

Przyśpieszenie = 1/2a

04-10-22

Reinhard Kulessa

13

g

a F

�

r

r

C

1

a

m

�

r

F

m

t

a

1

1

4.275 0.219

2

1

3.125 0.32

2

2

4.125 0.235

1

2

5.9

0.169

Wyniki doświadczenia, da się zapisać
jako:

a

m

F

m

F

a

C

C

g













lub

(3.3)

Masa m pokonywała w
każdym przypadku drogę
2 m.

Aby uzyskać dobre wyniki,
należy doświadczenie
wielokrotnie powtórzyć dla
różnych wartości masy, siły
i drogi.

Widzimy,
że

oraz

.

04-10-22

Reinhard Kulessa

14

Siła działająca na cząstkę jest równa
iloczynowi masy bezwładnej razy
przyśpieszenie cząstki, które to
przyśpieszenie cząstka uzyskała pod wpływem
działania siły w układzie inercjalnym.

Inaczej mówiąc:

Jeżeli cząstka porusza się z przyśpieszeniem

a

w układzie inercjalnym, to działa na nią siła
równa iloczynowi masy bezwładnej cząstki i jej
przyśpieszenia.

Jest to II zasada dynamiki Newtona.

Jednostką siły w układzie SI jest jeden

niuton [1N].

2

1

1

1

s

m

kg

N





.

04-10-22

Reinhard Kulessa

15

Jeśli na dwie różne masy podziałamy tą samą
siłą, to możemy napisać:

2

2

1

1

a

m

F

a

m

F













stąd
wynika, że

Widzimy więc, że pod wpływem tej samej siły
większa masa ulega mniejszemu
przyśpieszeniu, a mniejsza większemu.

Masa bezwładna jest miarą oporu jaki cząstka
stawia przyśpieszeniom.

(demonstracje bezwładność)

Siłą jaka działa na cząstkę najczęściej zależy
od położenia cząstki, czyli od wektora r
definiującego to położenie. Siła ta
może jednak zależeć również od prędkości
cząstki, ,

dt

r

d

v







.

1

2

2

1

m

a

m

a



04-10-22

Reinhard Kulessa

16

oraz od czasu. Możemy więc napisać, że

)

,

,

(

t

dt

r

d

r

F

F











.

Ruch cząstki znajdujemy rozwiązując
równanie:

)

,

,

(

)

(

2

2

t

dt

r

d

r

F

dt

t

r

d

m











.

(3.4)

Równanie

(3.4)

nazywamy równaniem ruchu

Newtona

.

Jest ono równoważne trzem równaniom dla
poszczególnych składowych.

)

,

,

,

,

,

,

(

)

(

)

,

,

,

,

,

,

(

)

(

)

,

,

,

,

,

,

(

)

(

2

2

2

2

2

2

t

dt

dz

dt

dy

dt

dx

z

y

x

F

dt

t

z

d

m

t

dt

dz

dt

dy

dt

dx

z

y

x

F

dt

t

y

d

m

t

dt

dz

dt

dy

dt

dx

z

y

x

F

dt

t

x

d

m

z

y

x







.

04-10-22

Reinhard Kulessa

17

Znając warunki początkowe, czyli wartości
, możemy równanie to rozwiązać
jednoznacznie,czyli podać funkcję położenia
cząstki dla dowolnej chwili

t > t

0

.

0

0

0

,

,

t

v

r 



)

(t

r