
http://www.if.pwr.wroc.pl/~wozniak/
fizyka1.html
Dr hab. inż. Władysław Artur Woźniak
Instytut Fizyki Politechniki Wrocławskiej
Dr hab. inż. Władysław Artur Woźniak
Wykład FIZYKA I
7. Dynamika ruchu obrotowego

ŚRODEK MASY
Każde ciało można traktować jako układ punktów materialnych.
Dlatego
pęd ciała możemy obliczyć jako sumę pędów wszystkich
punktów materialnych ciała:
Dr hab. inż. Władysław Artur Woźniak
n
i
i
i
v
m
p
1
Podstawiając wyrażenie na prędkość każdego punktu materialnego:
n
i
i
i
n
i
i
i
n
i
i
i
r
m
dt
d
dt
r
d
m
v
m
p
1
1
1
Środkiem masy albo środkiem bezwładności układu punktów materialnych
nazywamy punkt, którego położenie dane jest wzorem:
n
i
i
i
S
r
m
M
r
1
1
gdzie:
n
i
i
m
M
1
r
d
r
M
r
S
1
(w przypadku „ciągłym”:
, gdzie
jest gęstością ciała)
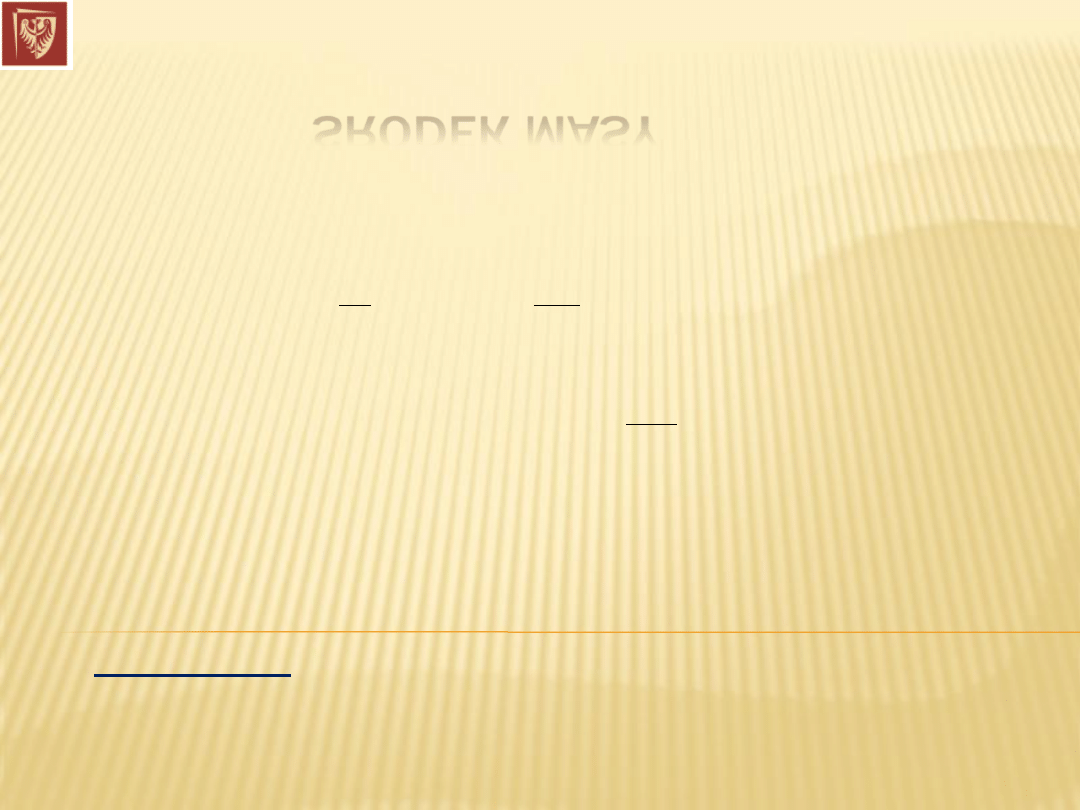
ŚRODEK MASY
Po podstawieniu do wyrażenia na pęd, otrzymamy:
Dr hab. inż. Władysław Artur Woźniak
S
S
S
v
M
dt
r
d
M
r
M
dt
d
p
Równanie ruchu środka masy układu:
wyp
S
S
F
a
M
dt
v
d
M
Środek masy układu porusza się jak punkt materialny, w którym
skupiona jest cała masa układu, i na który działa siła, równa wypadkowej
sił zewnętrznych przyłożonych do układu.
Środek ciężkości ciała to punkt przyłożenia wypadkowej sił ciężkości („ciężarów”)
wszystkich
punktów materialnych ciała. Gdy wielkość g (przyspieszenie grawitacyjne)
jest jednakowa dla wszystkich
punktów układu, mamy:
S
C
r
r

DYNAMIKA RUCHU OBROTOWEGO CIAŁA SZTYWNEGO
Każde ciało możemy uważać za układ n punktów materialnych,
których suma mas równa się całkowitej masie M ciała:
Dr hab. inż. Władysław Artur Woźniak
n
i
i
m
M
1
Ciało doskonale sztywne to takie ciało, w którym odległości między
dwoma dowolnymi jego punktami materialnymi nie zmieniają się w
trakcie ruchu (dalej nazwiemy je ciałem sztywnym lub bryłą sztywną).

DYNAMIKA RUCHU OBROTOWEGO CIAŁA SZTYWNEGO
Rozważmy ruch ciała sztywnego wokół punktu O, zwanego środkiem obrotu
ciała. Umieśćmy w tym punkcie początek układu współrzędnych. Niech
oznacza
siłę, z jaką k-ty punkt działa na punkt i-ty (siły wewnętrzne) a
wypadkową wszystkich sił zewnętrznych, przyłożonych do punktu i-tego.
Dr hab. inż. Władysław Artur Woźniak
ik
F
i
F
i
k
ik
F
II zasada dynamiki Newtona dla i-tego punktu:
n
i
k
k
i
ik
i
i
F
F
v
m
dt
d
,
1

DYNAMIKA RUCHU OBROTOWEGO CIAŁA SZTYWNEGO
Mnożymy równanie ruchu stronami wektorowo przez :
Dr hab. inż. Władysław Artur Woźniak
i
r
n
i
k
k
i
i
ik
i
i
i
i
F
r
F
r
v
m
dt
d
r
,
1
Pochodną względem czasu z lewej strony równania możemy wyłączyć
przed znak iloczynu wektorowego
(dlaczego!?
– ćwiczenia rachunkowe):
i
i
i
i
K
dt
d
v
m
r
dt
d
nazywamy
momentem
pędu (krętem) punktu materialnego i
względem osi O.
i
K

DYNAMIKA RUCHU OBROTOWEGO CIAŁA SZTYWNEGO
Moment pędu (kręt) punktu materialnego i względem osi O.
Dr hab. inż. Władysław Artur Woźniak
i
i
i
i
v
m
r
K
Moment siły
względem punktu O:
i
F
i
i
i
F
r
M
czyli:
„moment” oznacza (matematycznie) mnożenie lewostronne przez
wektor
położenia (promień wodzący)
i
r

DYNAMIKA RUCHU OBROTOWEGO CIAŁA SZTYWNEGO
Używając opisanej symboliki, możemy zapisać nasze równanie jako:
Dr hab. inż. Władysław Artur Woźniak
i
n
i
k
k
ik
i
i
M
F
r
dt
K
d
,
1
Dodajemy stronami równania wszystkich punktów materialnych ciała:
n
i
i
n
i
n
i
k
k
ik
i
n
i
i
M
F
r
dt
K
d
1
1
,
1
1
dt
K
d
dt
K
d
n
i
i
1
M
M
n
i
i
1
0
1
,
1
n
i
n
i
k
k
ik
i
F
r
- to moment główny sił zewnętrznych (wypadkowy)
to moment pędu ciała względem punktu O
K
(dlaczego?!
– ćwiczenia rachunkowe)

DYNAMIKA RUCHU OBROTOWEGO CIAŁA SZTYWNEGO
Ostatecznie:
Szybkość zmiany momentu pędu ciała obracającego się dookoła
nieruchomego
punktu
równa się wypadkowemu momentowi
(względem tego punktu) wszystkich sił zewnętrznych, przyłożonych
do
ciała – zasada dynamiki ruchu obrotowego ciała zamocowanego
w jednym, nieruchomym punkcie.
Dr hab. inż. Władysław Artur Woźniak
M
dt
K
d

DYNAMIKA RUCHU OBROTOWEGO CIAŁA SZTYWNEGO
Załóżmy teraz, że ciało sztywne umocowane jest w dwóch punktach tak,
że może obracać się wokół nieruchomej osi przechodzącej przez te punkty
– przyjmijmy, że jest to oś „z”. Wtedy składowe „x” i „y” momentu siły
są
zrównoważone przez siły reakcji zamocowania, a obrót wokół osi „z”
odbywa
się pod działaniem składowej
momentu
sił zewnętrznych:
Dr hab. inż. Władysław Artur Woźniak
M
z
M
z
z
M
dt
dK
Szybkość zmiany momentu pędu ciała względem nieruchomej osi
obrotu
równa się wypadkowemu momentowi (względem tej osi) sił
zewnętrznych działających na ciało.
z
O
K
F
r
M
DYNAMIKA RUCHU OBROTOWEGO CIAŁA SZTYWNEGO
Całkowity moment pędu ciała względem osi „z” jest równy sumie
momentów pędu każdego punktu materialnego:
Dr hab. inż. Władysław Artur Woźniak
n
i
iz
z
K
K
1
2
cos
cos
i
i
i
i
i
i
i
i
i
i
z
iz
m
v
m
v
m
r
K
K
We współrzędnych biegunowych:
wobec tego całkowity moment pędu ciała:
n
i
i
i
z
m
K
1
2

DYNAMIKA RUCHU OBROTOWEGO CIAŁA SZTYWNEGO
Wielkość:
nazywamy
momentem bezwładności ciała względem osi „z”.
Dr hab. inż. Władysław Artur Woźniak
n
i
i
i
z
m
I
1
2
W przypadku granicznym ciała „rozciągłego” sumowanie zastępujemy
całkowaniem:
m
z
dm
I
0
2
Ostatecznie otrzymujemy związek między momentem pędu ciała i prędkością
kątową obrotu:
z
z
I
K

DYNAMIKA RUCHU OBROTOWEGO CIAŁA SZTYWNEGO
Wykorzystanie
związku:
pozwala na
wyrażenie
podstawowej zasady dynamiki ruchu obrotowego:
Dr hab. inż. Władysław Artur Woźniak
z
z
M
dt
dK
z
z
z
z
I
dt
d
I
I
dt
d
M
Przyspieszenie kątowe ciała sztywnego obracającego się wokół
nieruchomej osi jest wprost proporcjonalne do wypadkowego
momentu (względem tej osi) wszystkich sił zewnętrznych działających
na ciało i odwrotnie proporcjonalny do momentu bezwładności ciała
względem tej osi.
z
z
I
M
m
F
a

MOMENT BEZWŁADNOŚCI
Moment
bezwładności jest więc miarą bezwładności ciała w ruchu
obrotowym
(analog
masy
jako
miary
bezwładności w ruchu
postępowym).
Dr hab. inż. Władysław Artur Woźniak
Przykładowe momenty bezwładności brył:
Ciało
Położenie osi
Moment bezwładności
pusty cienkościenny walec o
masie m i promieniu R
oś symetrii
pełny walec (tarcza) o masie
m i promieniu R
oś symetrii
kula o masie m i promieniu R
oś symetrii
cienki pręt o masie m i
długości L
oś prostopadła do pręta,
przechodzi przez jego środek
2
mR
I
2
2
1
mR
I
2
5
2
mR
I
2
12
1
mR
I
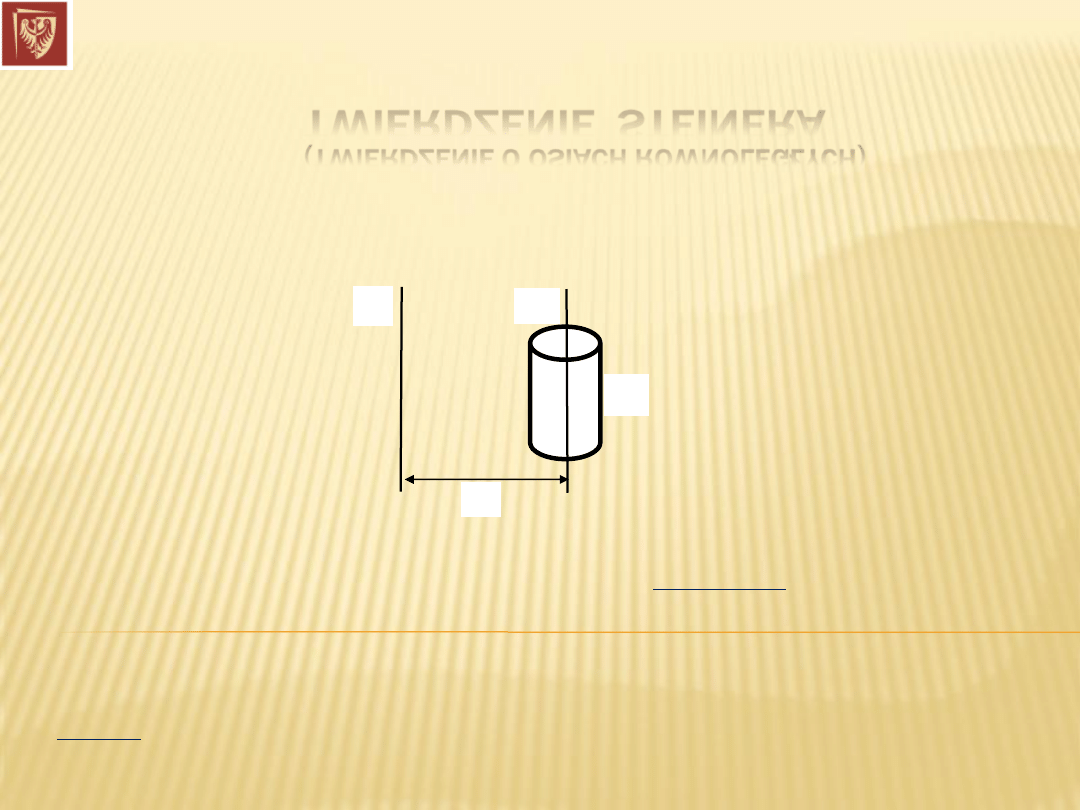
TWIERDZENIE STEINERA
(TWIERDZENIE O OSIACH RÓWNOLEGŁYCH)
Załóżmy, że znamy moment bezwładności ciała względem pewnej osi
obrotu, ale
ciało obraca się względem innej osi, równoległej do niej:
Dr hab. inż. Władysław Artur Woźniak
d
O
O’
m
Moment bezwładności ciała I względem dowolnej osi O równa się momentowi
bezwładności I’ tego ciała względem innej, równoległej do niej osi O’,
powiększonemu o iloczyn masy tego ciała przez kwadrat odległości między tymi
osiami:
2
' md
I
I
Wniosek: Gdy środek masy ciała oddala się od osi obrotu, to moment bezwładności ciała względem tej osi
wzrasta.

ZASADA ZACHOWANIA MOMENTU PĘDU
Z zasady dynamiki ruchu obrotowego:
wynika wprost:
Dr hab. inż. Władysław Artur Woźniak
M
dt
K
d
t
const
K
dt
K
d
M
0
0
Jeżeli wypadkowy moment sił zewnętrznych względem nieruchomego
punktu ciała równa się zeru, to moment pędu ciała względem tego
punktu nie zmienia się w czasie.
Można pokazać, że również: moment pędu zamkniętego układu ciał
względem dowolnego punktu nieruchomego jest stały.
Podobnie: jeśli siły zewnętrzne dają moment względem nieruchomej osi równy
zeru, to moment pędu ciała względem tej osi nie zmienia się podczas ruchu.

TENSOR MOMENTU BEZWŁADNOŚCI
Rozważmy obrót ciała o dowolnym kształcie wokół osi przechodzącej
przez
początek układu współrzędnych.
Prędkość i-tego punktu względem początku układu:
Stąd wyrażenie na moment pędu całego ciała:
Skorzystamy z
tożsamości wektorowej:
Podstawiając, otrzymujemy:
Dr hab. inż. Władysław Artur Woźniak
i
i
r
v
n
i
i
i
i
n
i
i
i
i
r
r
m
v
m
r
K
1
1
b
a
c
c
a
b
c
b
a
n
i
i
i
i
i
r
r
r
m
K
1
2

TENSOR MOMENTU BEZWŁADNOŚCI
Wszystkie punkty
mają tę samą prędkość kątową, możemy więc
zapisać powyższe równanie wektorowe jako układ trzech równań dla
poszczególnych składowych
(tu tylko dla
„x”):
Dr hab. inż. Władysław Artur Woźniak
n
i
i
i
i
n
i
i
i
x
x
r
x
m
r
m
K
1
1
2
Ponieważ:
otrzymujemy:
z
i
y
i
x
i
i
z
y
x
r
i
i
i
z
i
i
i
y
i
i
i
x
x
z
x
m
y
x
m
x
r
m
K
2
2
(znak sumowania po i pominięty dla uproszczenia)

TENSOR MOMENTU BEZWŁADNOŚCI
Podobne
równania możemy napisać dla składowych „y” i „z” i
ostatecznie
równanie,
wiążące
wektor
momentu
pędu
z
pseudowektorem
prędkości kątowej
, przyjmie
postać:
Dr hab. inż. Władysław Artur Woźniak
K
z
y
x
zz
zy
zx
yz
yy
yx
xz
xy
xx
z
y
x
I
I
I
I
I
I
I
I
I
K
K
K
,
,
Macierz z prawej strony równania to tensor bezwładności a jego
elementy nazywamy współczynnikami bezwładności lub momentami
bezwładności.
Tensor
bezwładności jest symetryczny, to znaczy:
yx
xy
I
I

TENSOR MOMENTU BEZWŁADNOŚCI
Wyraz
przekątny (tu np. „xx”):
jest
sumą iloczynów każdej z mas cząstkowych przez kwadrat jej
odległości od danej osi (tu „x”), więc możemy go nazwać momentem
bezwładności względem tej osi.
Dr hab. inż. Władysław Artur Woźniak
2
2
2
2
i
i
i
i
i
i
xx
z
y
m
x
r
m
I
W przypadku ciągłego rozkładu masy z gęstością
współczynniki tensora
możemy zapisać w postaci całek, na przykład:
r
dV
x
r
r
I
xx
2
2
xydV
r
I
xy
Wyszukiwarka
Podobne podstrony:
9 Cw. II zasady dynamiki Newtona dla ruchu obrotowego bry+é, Politechnika Rzeszowska, Fizyka, Sprawo
dynamika ruchu obrotowego
Dynamika ruchu obrotowego, 6
Dynamika ruchu obrotowego, 5
Dynamika ruchu obrotowego, 5
Dynamika ruchu obrotowego bryly
Dynamika ruchu obrotowego, 4
III01 Dynamika ruchu obrotowego bryly sztywnej
2?DANIE DYNAMIKI RUCHU OBROTOWEGO BRYŁY SZTYWNEJ
7 Dynamika ruchu obrotowego właściwe
1 Badanie dynamiki ruchu obrotowego 12
Dynamika ruchu obrotowego, 2
07 Dynamika ruchu obrotowego bryly sztywnej, Domumenty
pawlikowski, fizyka, dynamika ruchu obrotowego i drgającego
Dynamika ruchu obrotowego, 1
Dynamika ruchu obrotowego
6 Dynamika ruchu obrotowego ciala sztywnego, Politechnika Wrocławska Energetyka, I semestr, Fizyka 1
14 DYNAMIKA RUCHU OBROTOWEGO
więcej podobnych podstron