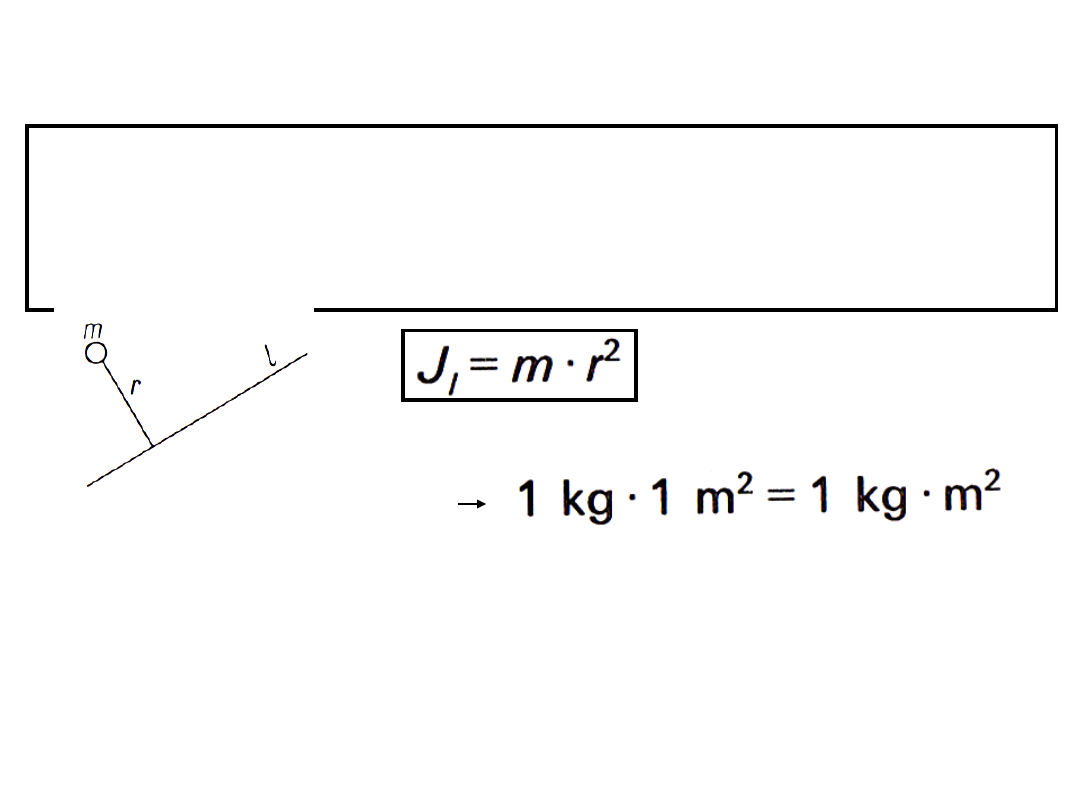
Momentem bezwładności punktu materialnego
względem bieguna (punktu), płaszczyzny lub osi
nazywamy iloczyn masy tego punktu i kwadratu jego
odległości od bieguna, płaszczyzny lub osi.

MOMENT BEZWŁADNOŚCI

Z powyższej definicji wynika, że istnieją trzy rodzaje momentów
bezwładności:

1) biegunowe (momenty bezwładności względem punktu),

2) względem płaszczyzn,

3) względem osi (osiowe momenty bezwładności).

Jednostka momentu

Moment bezwładności ciała

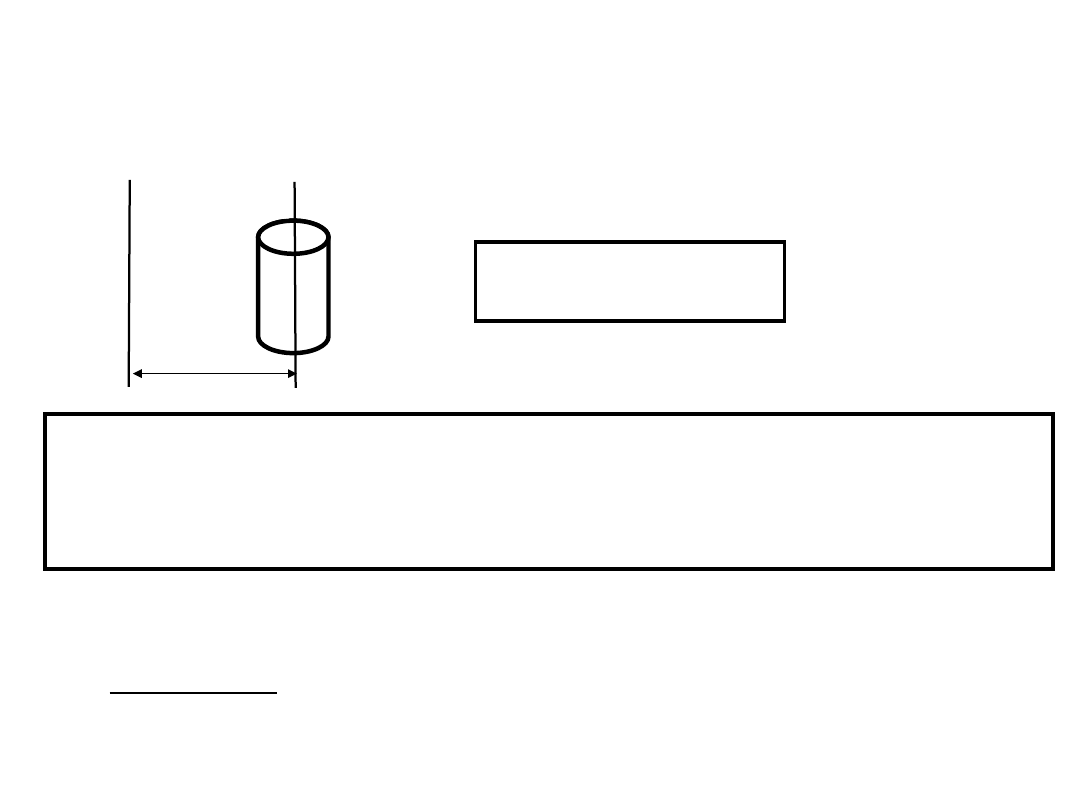
Twierdzenie Steinera

Załóżmy, że znamy moment bezwładności ciała
względem pewnej osi obrotu, ale ciało obraca się
względem innej osi, równoległej do niej:

d

O

O’

m

Moment bezwładności ciała względem dowolnej osi równa się
momentowi bezwładności tego ciała względem innej,
równoległej do niej osi , powiększonemu o iloczyn masy tego
ciała przez kwadrat odległości między tymi osiami

2

' md

I

I





Wniosek: Gdy środek masy ciała oddala się od osi
obrotu, to moment bezwładności ciała względem
tej osi wzrasta

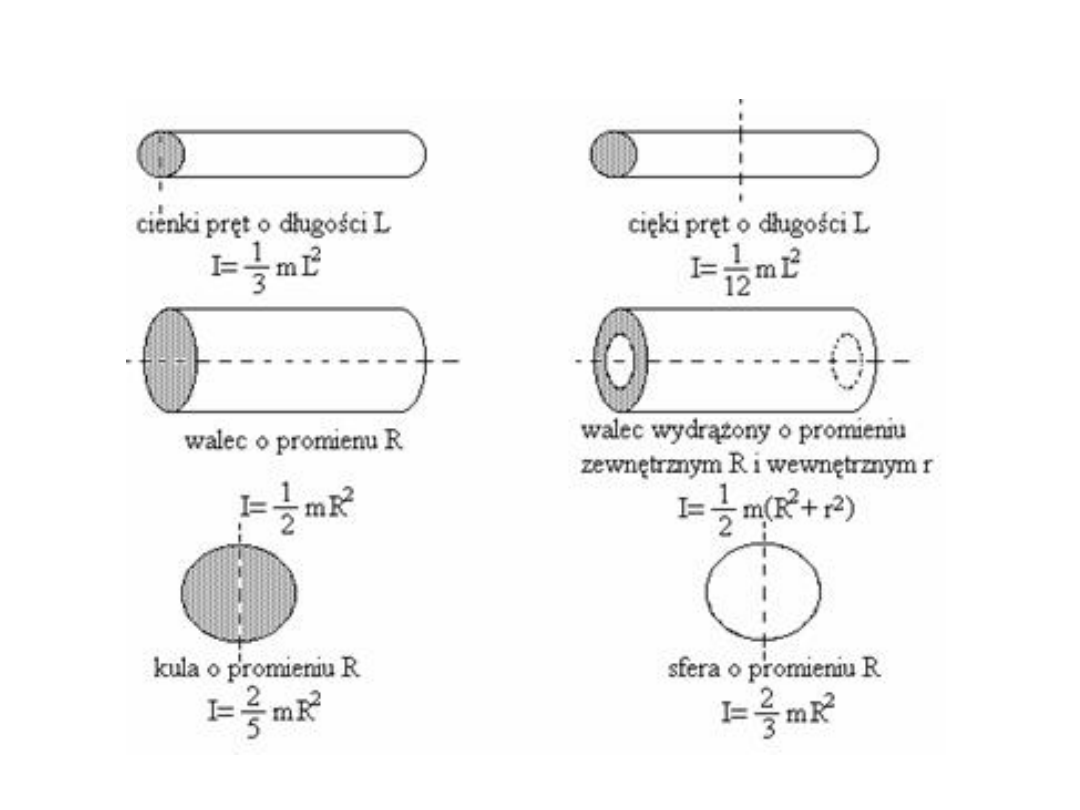
Momenty bezwładności wybranych brył

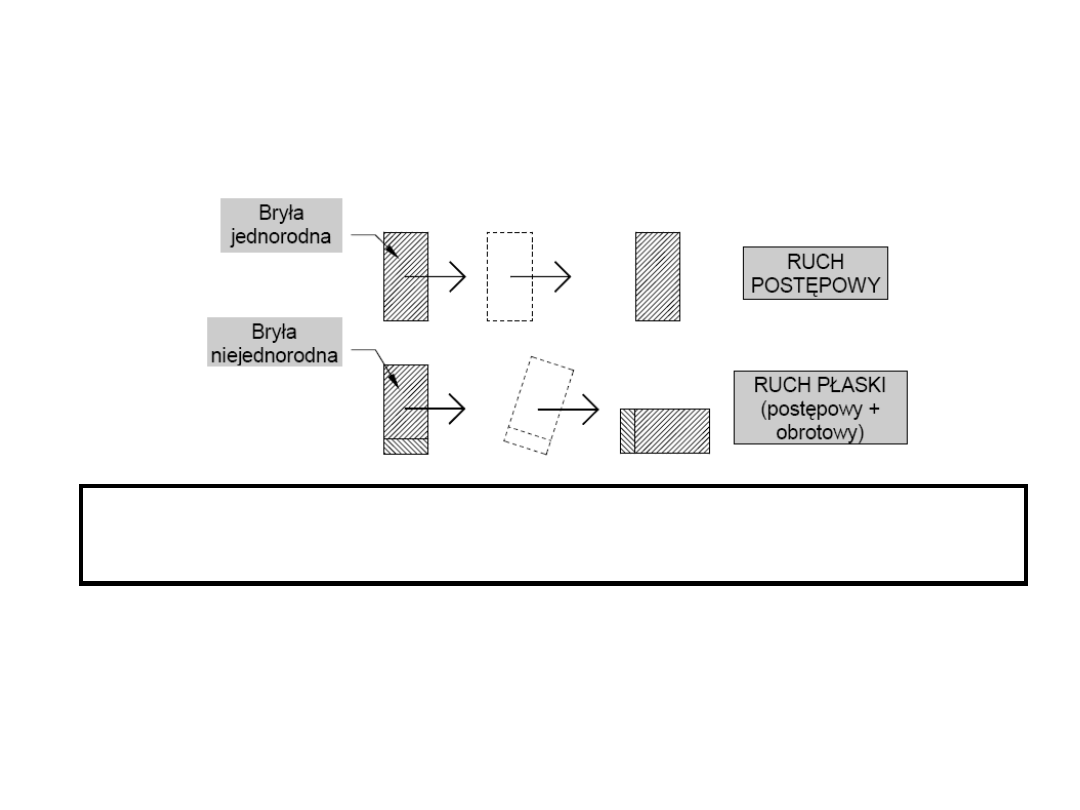
MOMENTY BEZWŁADNOŚCI

Momenty bezwładności charakteryzują rozkład w
przestrzeni masy danego układu punktów
materialnych lub bryły.

Na skutek nierównomiernego rozkładu masy, przy
tej samej masie występują różne rodzaje ruchu.

Moment bezwładności to miara bezwładności ciała w
ruchu obrotowym. Im większy moment tym trudniej
rozkręcić dane ciało lub zmniejszyć jego prędkość
obrotową.

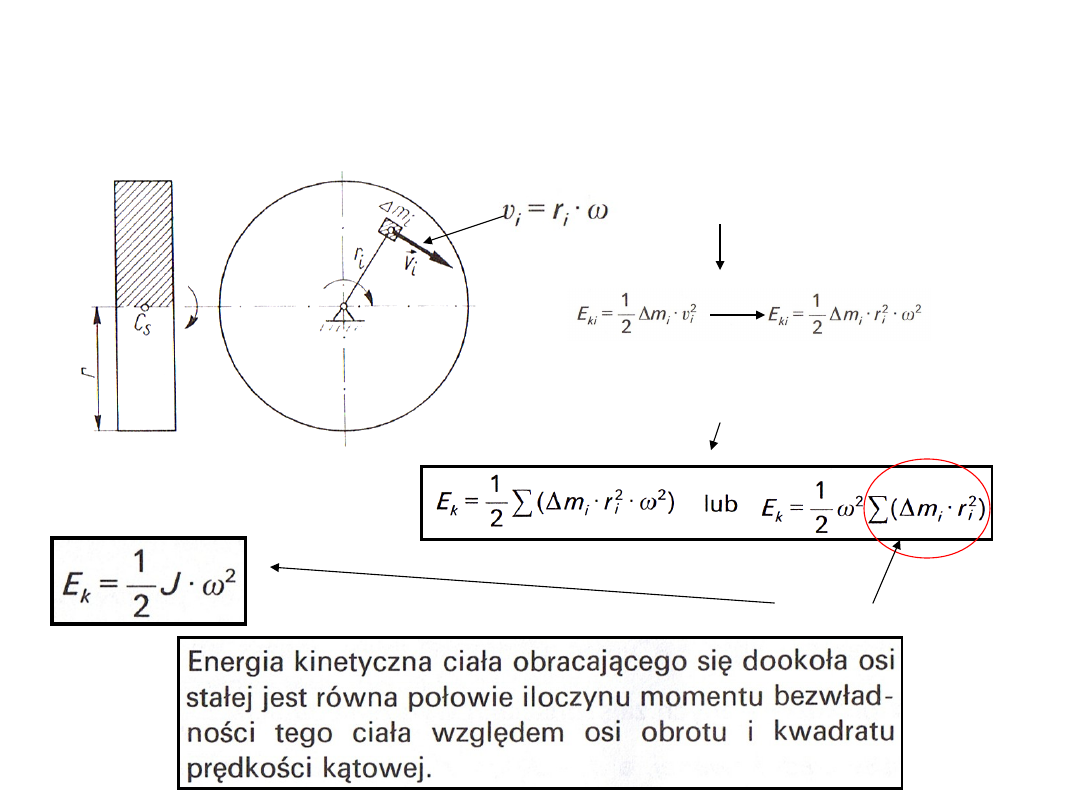
Energia kinetyczna w ruchu obrotowym

Tarcza o promieniu r i masie m obraca się dookoła osi z
prędkością ω

Prędkość punktu

Energia punktu

Energia kinetyczna całej tarczy

Moment bezwładności J

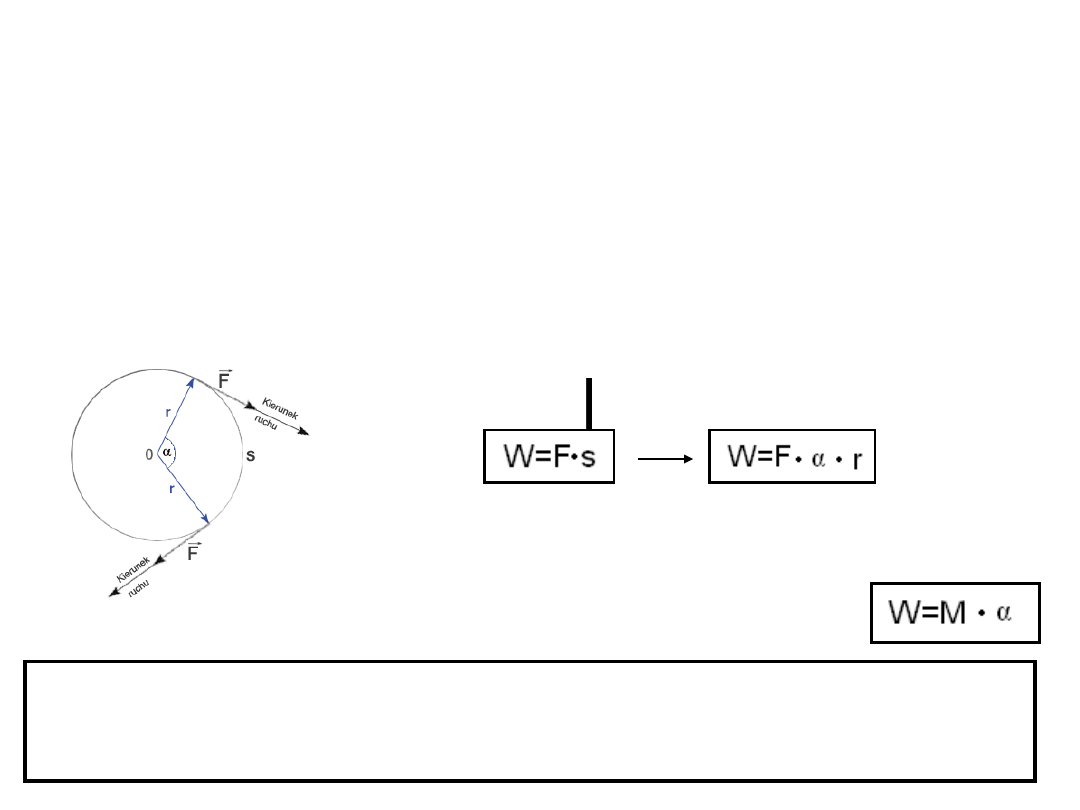
Praca i moc w ruchu obrotowym

Wprawienie ciała w ruch obrotowy związane jest z wykonaniem
pracy.Również utrzymanie ciała w ruchu obrotowym
jednostajnym, pokonując siły przeciwdziałające mu, wiąże się z
wykonaniem pracy. Załóżmy, że na obwodzie tarczy obracającej
się jednostajnie dookoła osi, dział stała siła F, pokonująca opory
ruchu

Po czasie t siła pokonała drogę liniową s.
Wykonana praca przez tę siłę, wyraża się
wzorem

Podstawiając do wzoru moment siły, otrzymujemy

Jeśli moment siły utrzymujący ciało w ruchu obrotowym
zachowuje stałą wartość, to wykonana przez niego praca jest
równa iloczynowi momentu siły i drogi kątowej

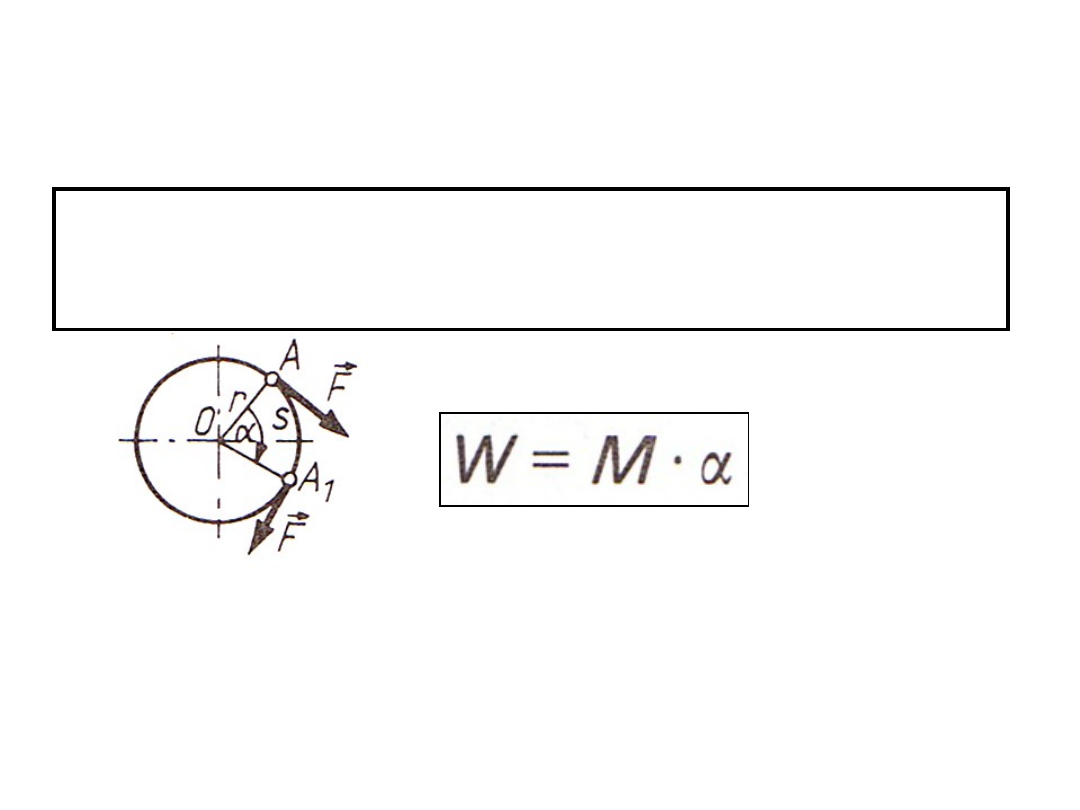
PRACA SIŁY W RUCHU OBROTOWYM

Praca siły w ruchu obrotowym równa jest
iloczynowi momentu siły względem osi obrotu i
kąta, o jakie obróci się ciało

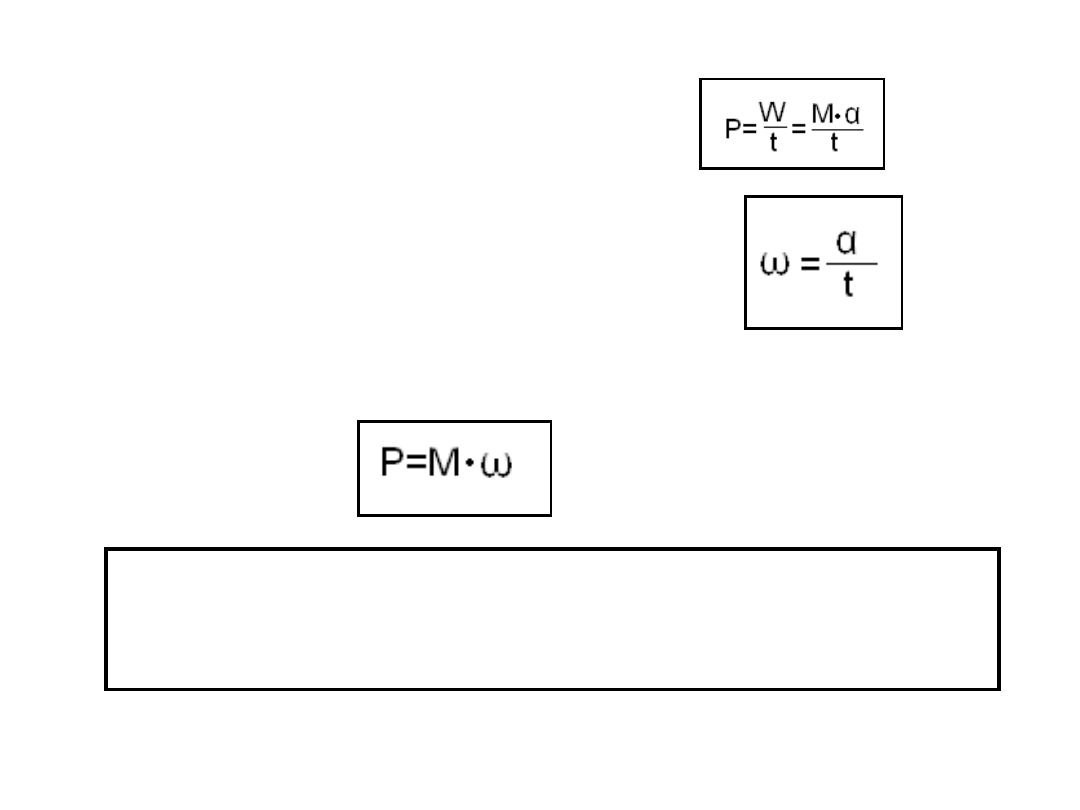
Moc wyraża się stosunkiem pracy do czasu, w
którym ta praca została wykonana

W ruchu obrotowym jednostajnym

Podstawiając to wyrażenie do wzoru na moc,
otrzymujemy:

Moc w ruchu obrotowym jednostajnym jest
iloczynem działającego na ciało momentu
obrotowego i jego prędkości kątowej.

Podstawowe równanie dynamiki ruchu obrotowego

Zgodnie z zasadą bezwładności tylko siła zewnętrzna może
zmienić ruch ciała. Jeżeli natomiast działające siły równoważą
się, to ciało pozostaje w spoczynku lub porusza się ruchem
jednostajnym. Zasada ta obowiązuje również w ruchu
obrotowym, ale trochę w zmienionej treści:

Jeśli momenty wszystkich sił działających na ciało równoważą
się wzajemnie, to ciało pozostaje w spoczynku lub porusza się
ruchem obrotowym jednostajnym (z prędkością kątową stałą
co do wielkości i kierunku).

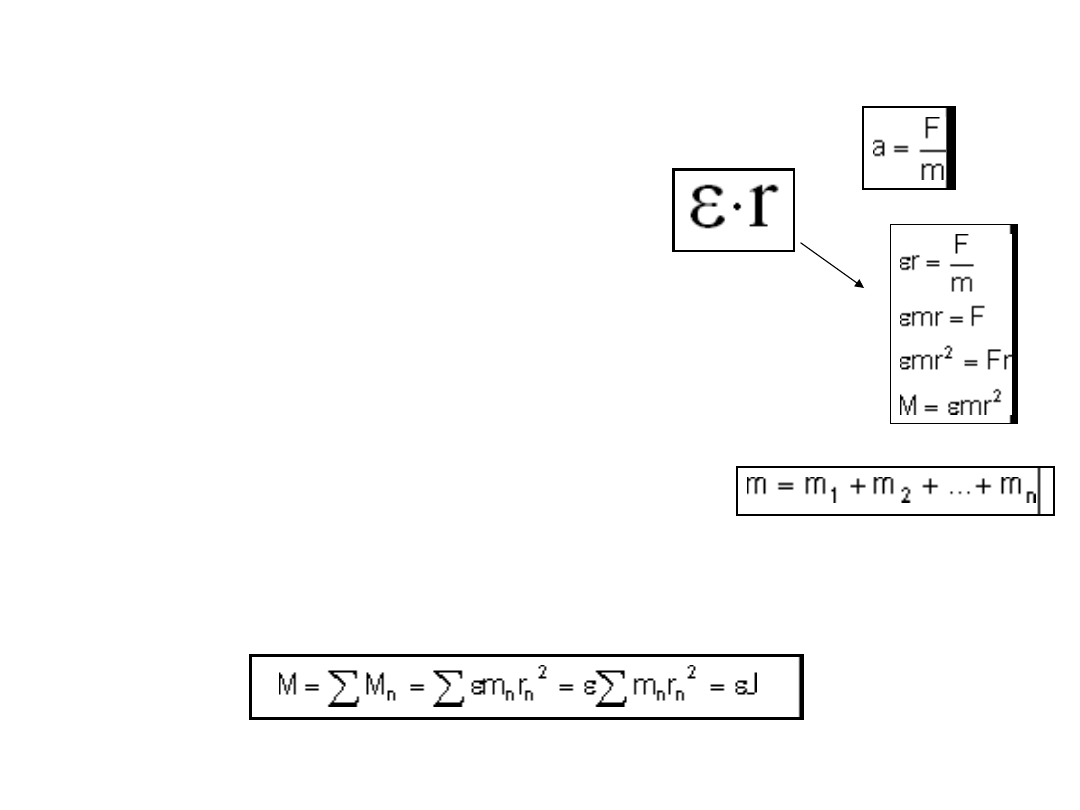
Rozważmy przypadek, gdy na punkt materialny o masie m związany z
osią obrotu i mogący się wokół niej obracać po torze o promieniu r,
działa stała siła F (co do wielkości), której moment M wynosi F*r. Pod
wpływem tej siły, punkt materialny uzyska przyspieszenie a

t

Podstawiamy zamiast a wyrażenie

Uzyskaliśmy wzór na moment siły, działający na
ten punkt materialny. Podobne rozważanie
moglibyśmy przeprowadzić dla każdego elementu
ciała obracającego się dookoła osi przechodzącej
przez środek ciężkości, którego masa wynosi

aby ciało uzyskało przyspieszenie kątowe , trzeba na nie
działać momentem obrotowym M, równym sumie momentów
obrotowych poruszających poszczególne elementy:

ε

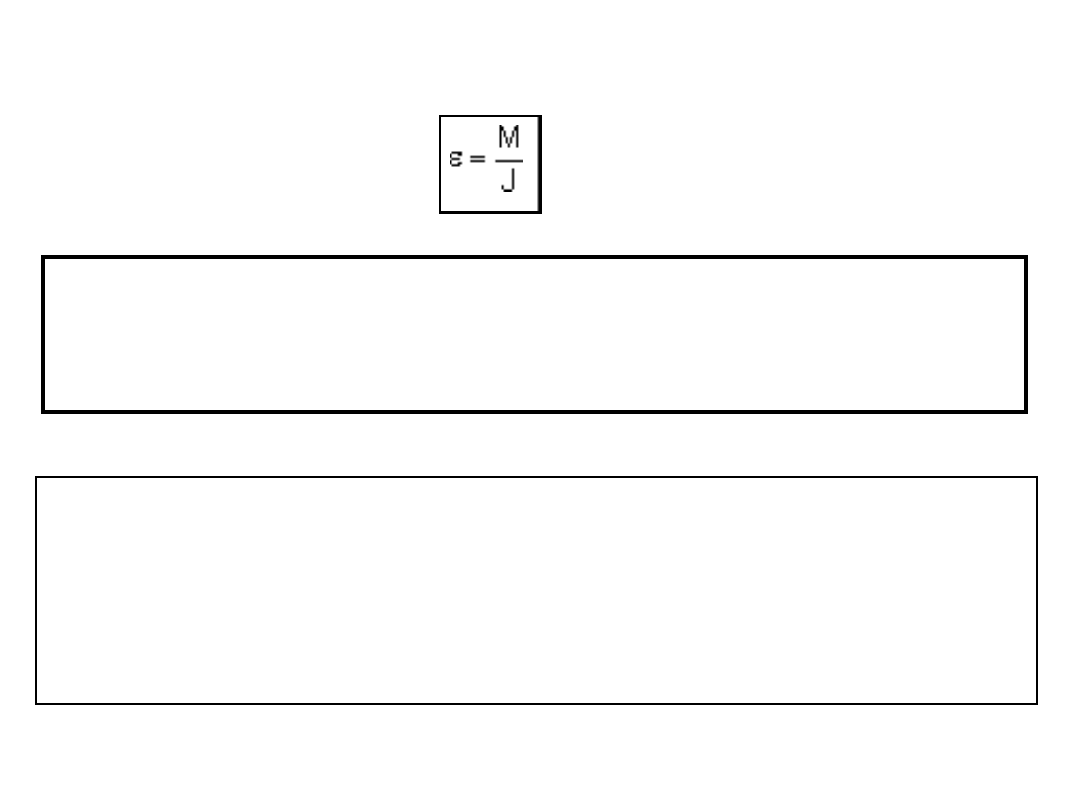
podstawowe równanie dynamiki ruchu obrotowego

Niezrównoważony moment siły działając na ciało nadaje mu
przyspieszenie kątowe, które jest wprost proporcjonalne do
momentu bezwładności ciała, przy czym jest ono skierowane
tak samo jak moment siły.

Porównując wzory dynamiki ruchu obrotowego i ruchu
postępowego widzimy, iż:

•moment bezwładności w ruchu obrotowym spełnia taką samą
rolę jak masa w ruchu postępowym,

•moment siły odgrywa w ruchu obrotowym taką rolę jak siła w
ruchu postępowym

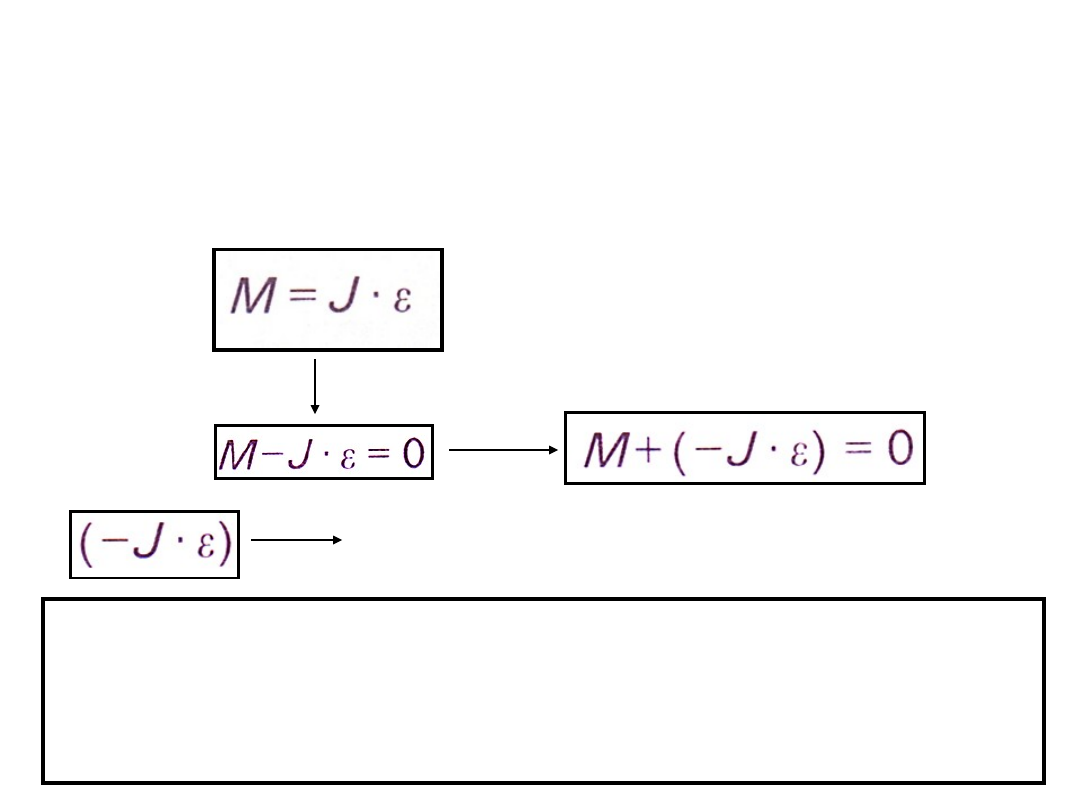
ZASADA D’ALAMBERTA DLA RUCHU OBROTOWEGO

Ciało wykonuje ruch obrotowy z
przyspieszeniem kątowym

ε

tylko wtedy , gdy

działa moment obrotowy równy:

Przekształcenia wzorów

Moment sił bezwładności w ruchu obrotowym ciała

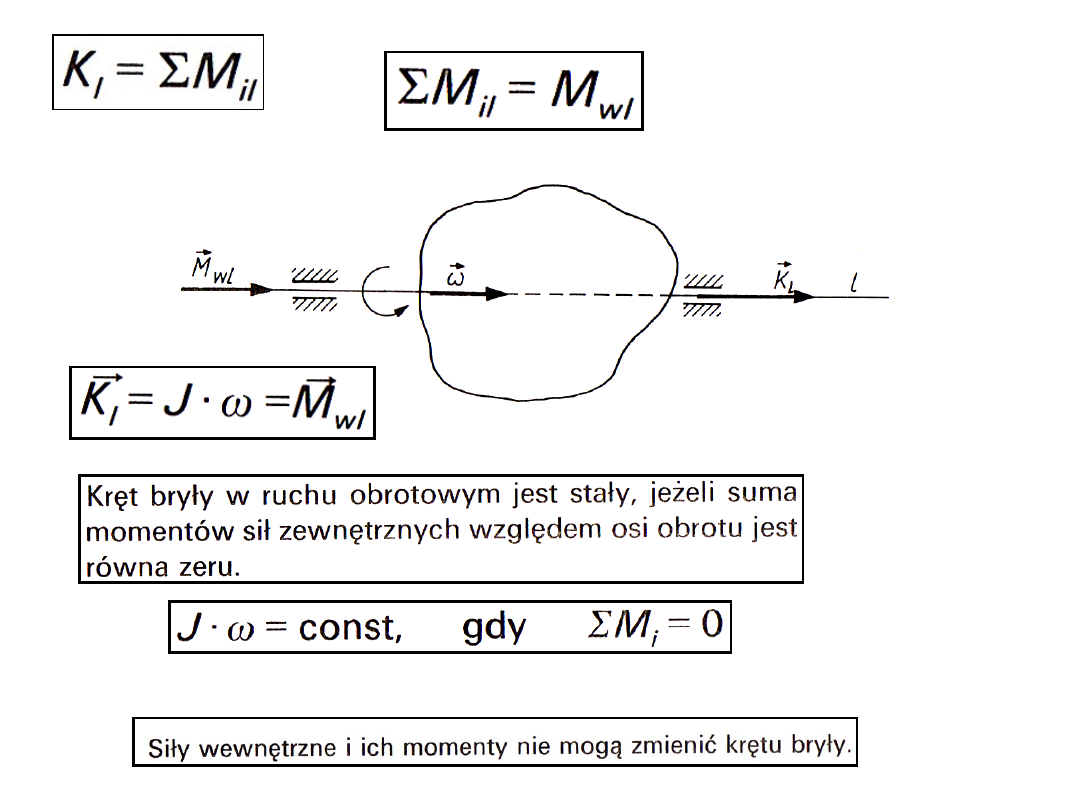
W ruchu obrotowym moment sił zewnętrznych
równoważy się z momentem sił bezwładności.

(Suma momentów sił zewnętrznych i momentów sił
bezwładności jest równa zeru.)

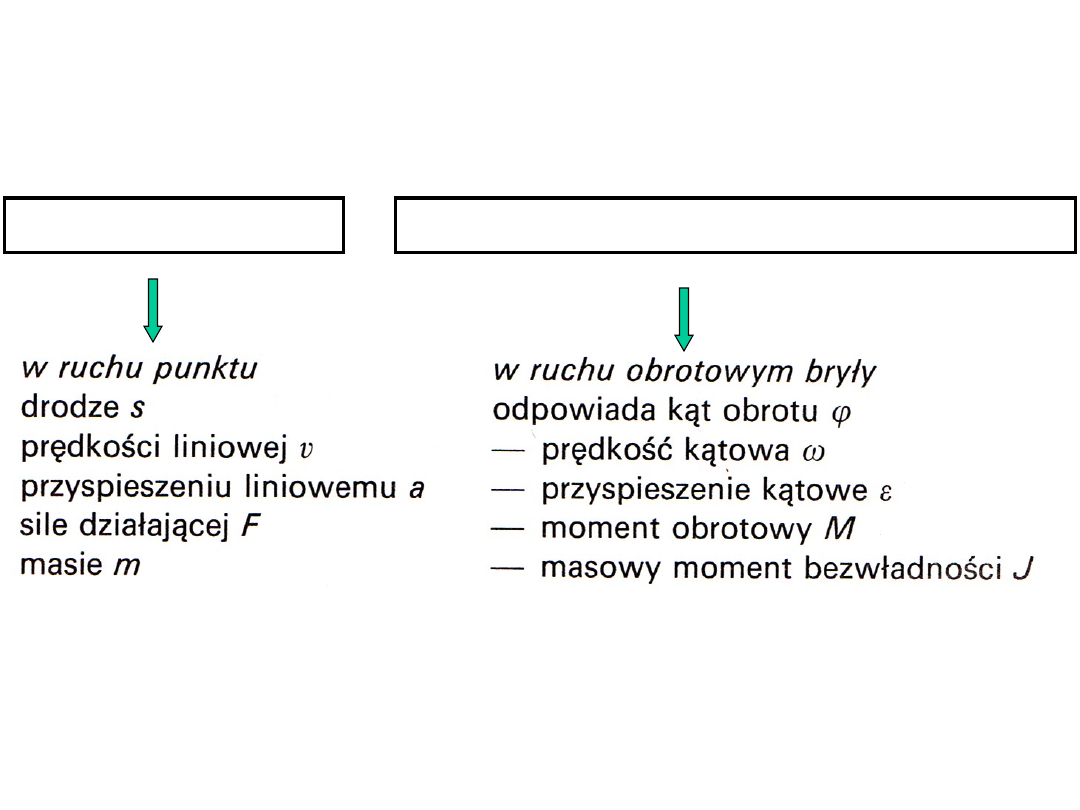
podobieństwa

dynamika punktu

dynamika bryły w ruchu obrotowym

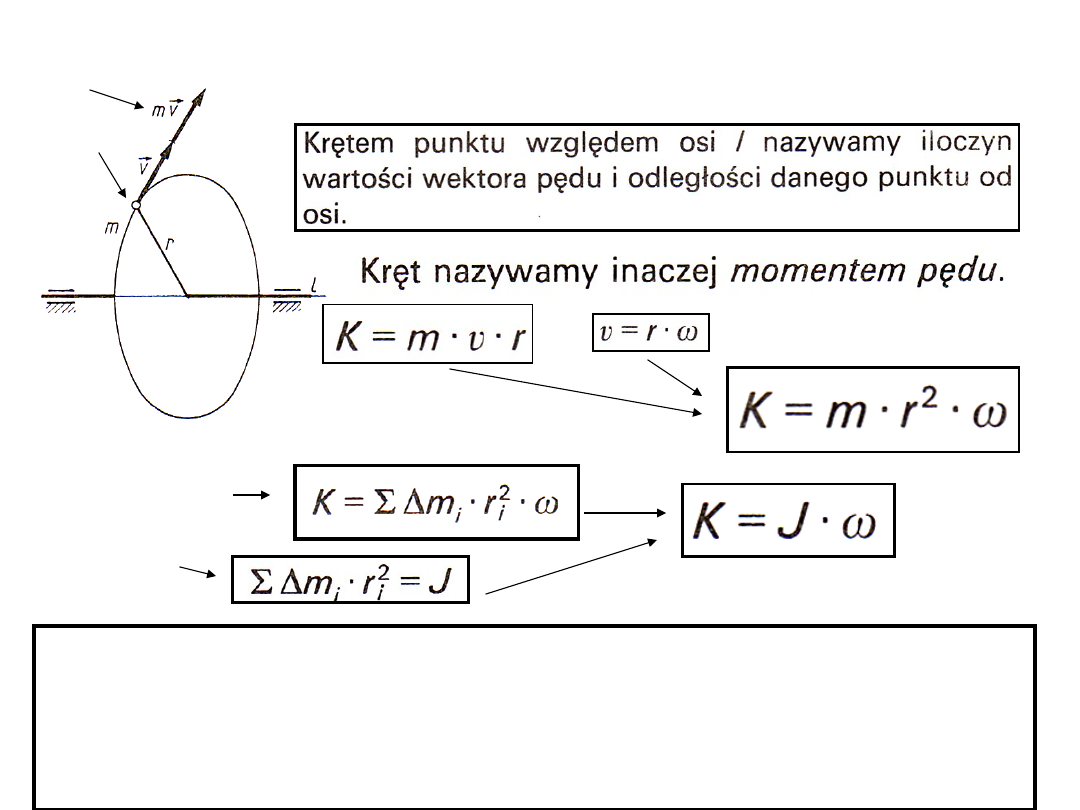
ZASADA ZACHOWANIA KRĘTU

ale

Dla całej bryły

ponieważ

pęd

Krętem bryły względem stałej osi obrotu nazywamy
iloczyn masowego momentu bezwładności bryły
względem osi obrotu
i prędkości kątowej.

Punkt bryły