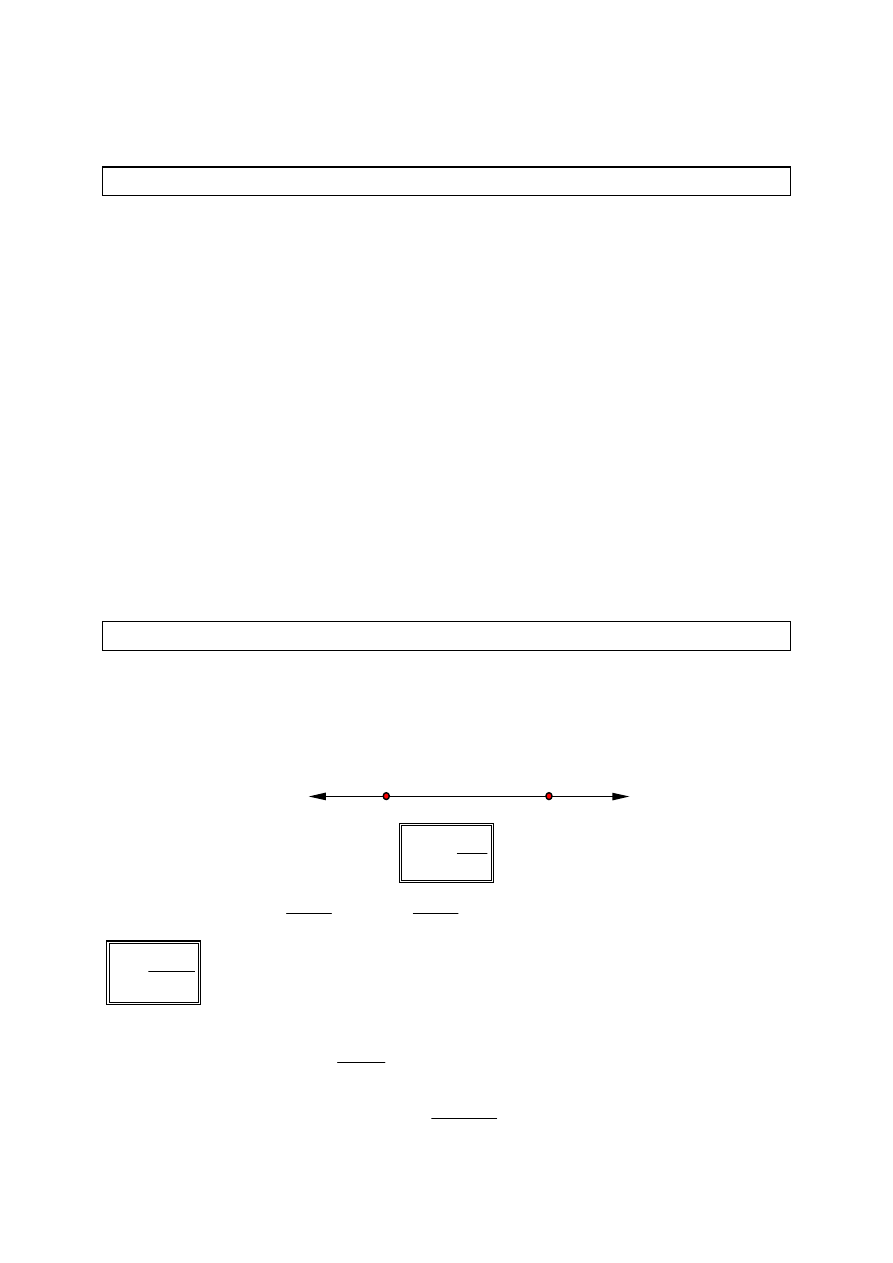
42

ELEKTROSTATYKA

Ładunek elektryczny

Ładunek elektryczny jest obok masy cechą charakterystyczną każdej
najmniejszej cząstki materii. Cząstki elementarne, do których zaliczamy
między innymi elektrony, protony i neutrony albo mają ładunek taki jak
elektron (-e), albo mają ładunek taki jak proton (+e), względnie nie mają
ładunku. Te ostatnie jednak, jeśli ulegają rozpadowi, to mogą tworzyć pary
cząstek, z których jedna ma ładunek +e, a druga -e.

Stwierdzenie, że ciało ma ładunek elektryczny oznacza, że w obrębie tego ciała
została naruszona równowaga między liczbą cząstek obdarzonych ładunkiem +e
i -e, praktycznie chodzi tu o liczby protonów zawartych w jądrach atomowych i
elektronów tworzących powłoki elektronowe. Ciało obdarzone ładunkiem
dodatnim ma za mało elektronów, a obdarzone ładunkiem ujemnym - za dużo.

Kulomb (C) jest ładunkiem, który przepływa przez przekrój poprzeczny
przewodnika w ciągu sekundy jeśli w przewodniku płynie prąd o natężeniu
jednego ampera. Ładunek elementarny ma wartość:

e = (1,60217733 ± 0,00000049) . 10

-19

C

Prawo Coulomba

Każde dwa ładunki elektryczne przyciągają się lub odpychają z siłą wprost
proporcjonalną do iloczynu ich wartości i odwrotnie proporcjonalną do
kwadratu odległości między nimi.

F

k

Qq

r

====

2

k = 8,987551 . 109

Nm

C

Nm

C

2

9

2

2

9 10

≈≈≈≈ ⋅⋅⋅⋅

- stała elektrostatyczna

k

====

1

4

0

πε

πε

πε

πε

εεεε

0

12

2

2

8 854187817 10

====

⋅⋅⋅⋅

−−−−

,

C

Nm

- przenikalność elektryczna próżni

F

Qq

r

====

4

0

2

πε

πε

πε

πε

F

r

r

F

r

−−−−

q

Q

+

+

43

J

eśli oddziaływanie zachodzi nie w próżni lecz w jakimś ośrodku, to prawo

Coulomba przyjmuje postać:

F

kQq

r

Qq

r

====

====

εεεε

πεε

πεε

πεε

πεε

2

0

2

4

r

r

r

4

Qq

F

2

0

r

r

⋅⋅⋅⋅

πεε

πεε

πεε

πεε

====

-

prawo

Coulomba w zapisie wektorowym

r

r

r

- wektor jednostkowy o kierunku i zwrocie r

r

εεεε

- liczba niemianowana charakterystyczna dla danego ośrodka, zwana

względną przenikalnością elektryczną ośrodka. Jest także oznaczana

εεεε

r

.

Powyższe prawo zostało ustalone doświadczalnie w 1785 r. przez Charlesa
Coulomba (1736 - 1806).

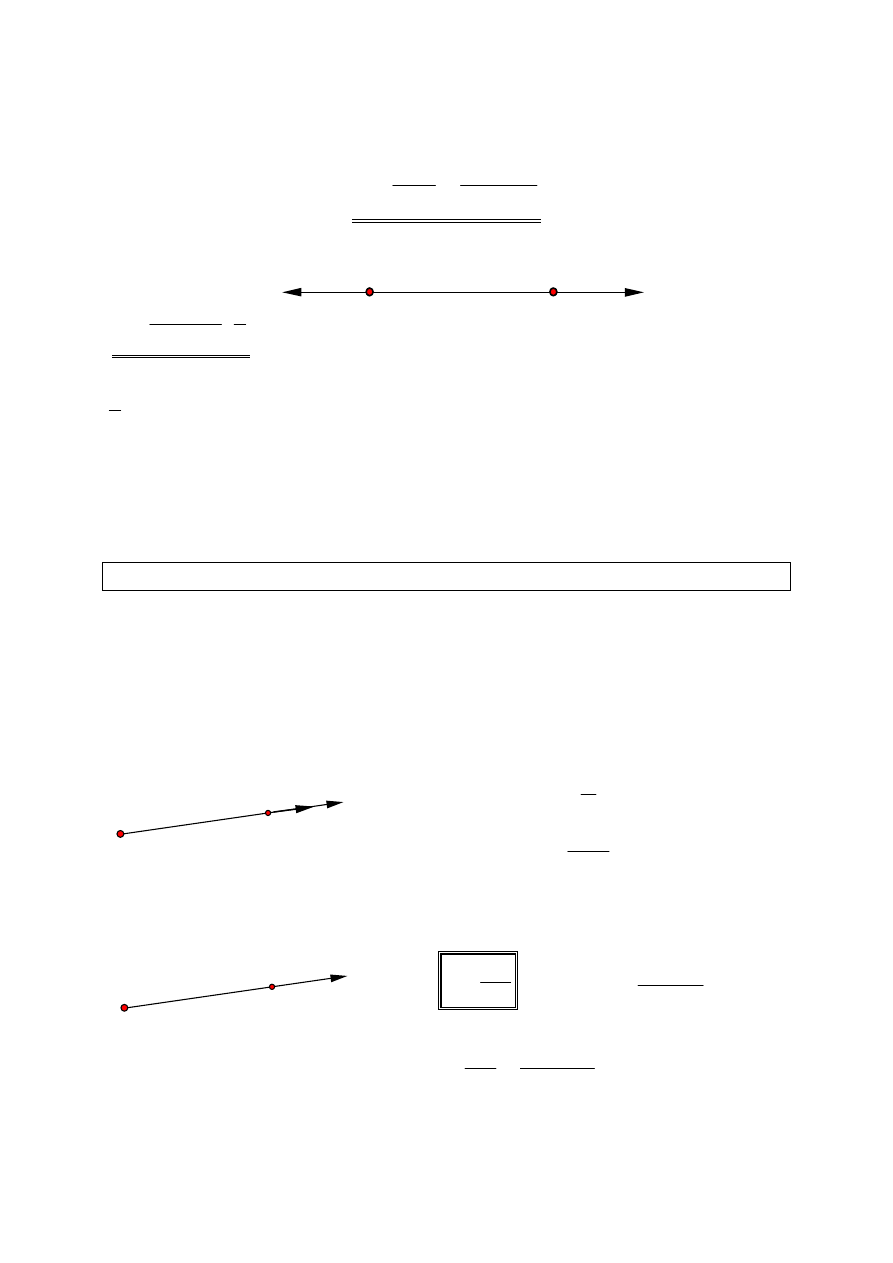
Natężenie pola elektrycznego

Przestrzeń wokół ładunku elektrycznego, w której nieruchome ładunki doznają
oddziaływań kulombowskich nazywamy polem elektrycznym.

Każdemu punktowi pola można przypisać wektor charakterystyczny dla tego
punktu zwany natężeniem pola elektrycznego. Miarą natężenia pola jest
stosunek siły działającej na ładunek umieszczony w danym punkcie pola do
wartości tego ładunku.

q

F

E

r

r

====

F

kQq

r

====

2

W przypadku, gdy źródłem pola jest ładunek punktowy Q otrzymujemy:

E

kQ

r

====

2

lub

E

Q

r

====

4

0

2

πε

πε

πε

πε

w ośrodku :

E

kQ

r

Q

r

====

====

εεεε

πεε

πεε

πεε

πεε

2

0

2

4

F

r

r

r

F

r

−−−−

q

Q

+

+

r

q

(+)

F

r

(+)

Q

E

r

r

r

q

(+)

(+)

Q

E

r

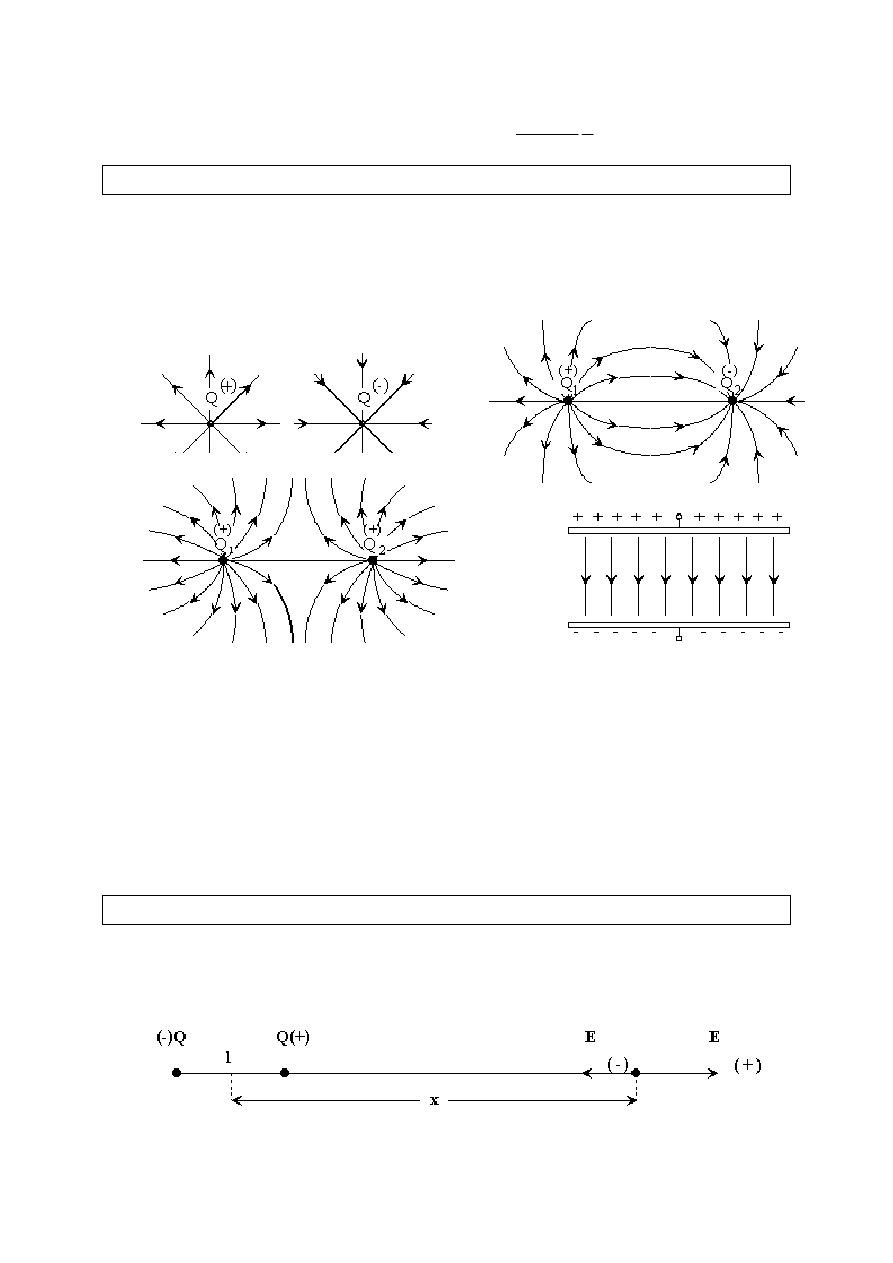
44

Stosując zapis wektorowy otrzymujemy:

r

r

r

4

Q

E

2

0

r

r

πε

πε

πε

πε

====

Linie sił pola elektrycznego

Linie poprowadzone w polu elektrycznym w taki sposób, że wektor natężenia
jest zawsze styczny do linii przechodzącej przez ten punkt pola nazywamy
liniami sił pola elektrycznego.

Powyższe rysunki przedstawiają kształt linii sił pola wytworzonego przez
pojedynczy ładunek dodatni, pojedynczy ładunek ujemny, dwa ładunki różnego
znaku, dwa ładunki dodatnie, oraz linie sił tzw. pola jednorodnego jakie istnieje
między dwiema płaskimi powierzchniami obdarzonymi ładunkami przeciwnych
znaków. W polu jednorodnym linie sił są do siebie równoległe, a natężenie pola
ma wszędzie taką samą wartość.

Nat

ęż

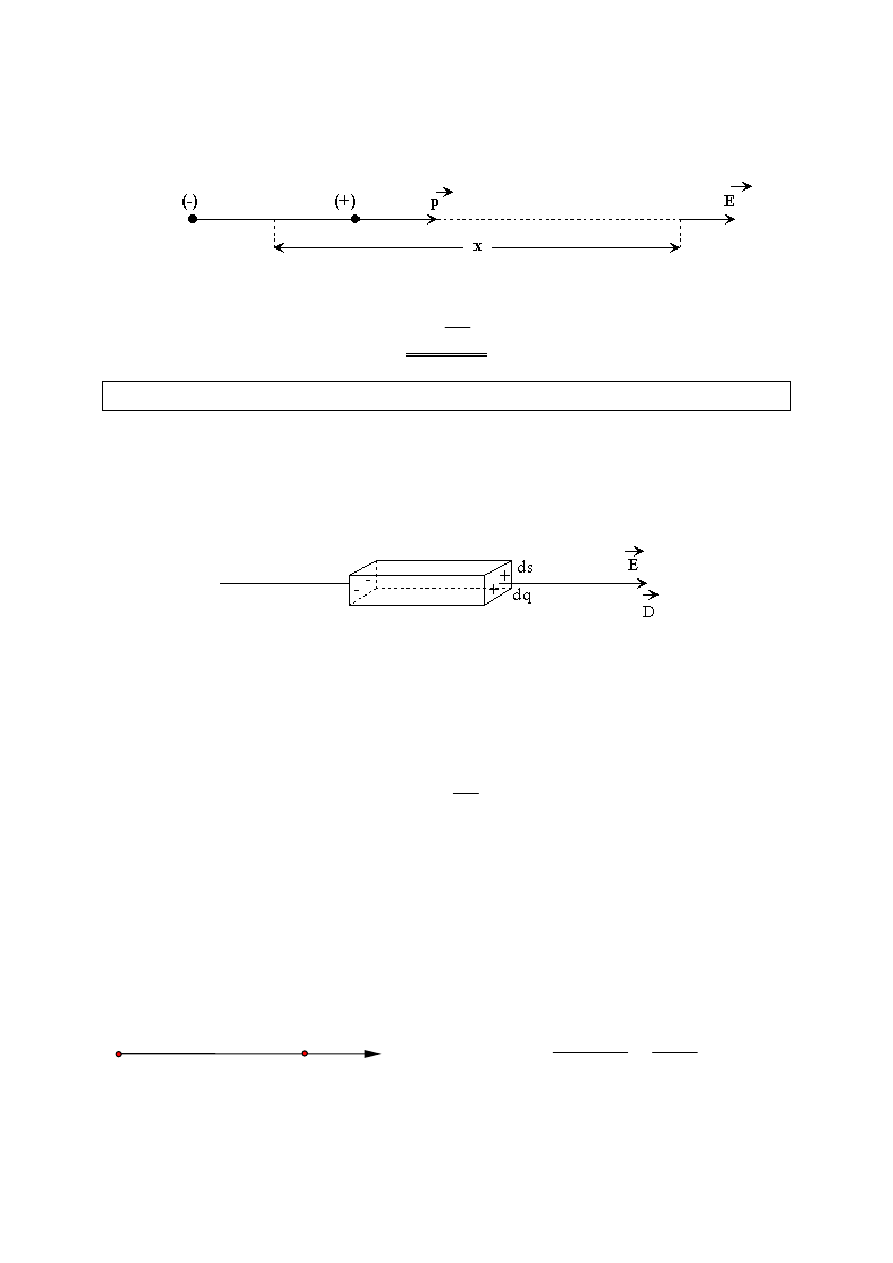
enie pola na osi dipola elektrycznego

Dipol elektryczny stanowią dwa ładunki o jednakowych wartościach i różnych
znakach umieszczone na niewielkiej odległości od siebie.

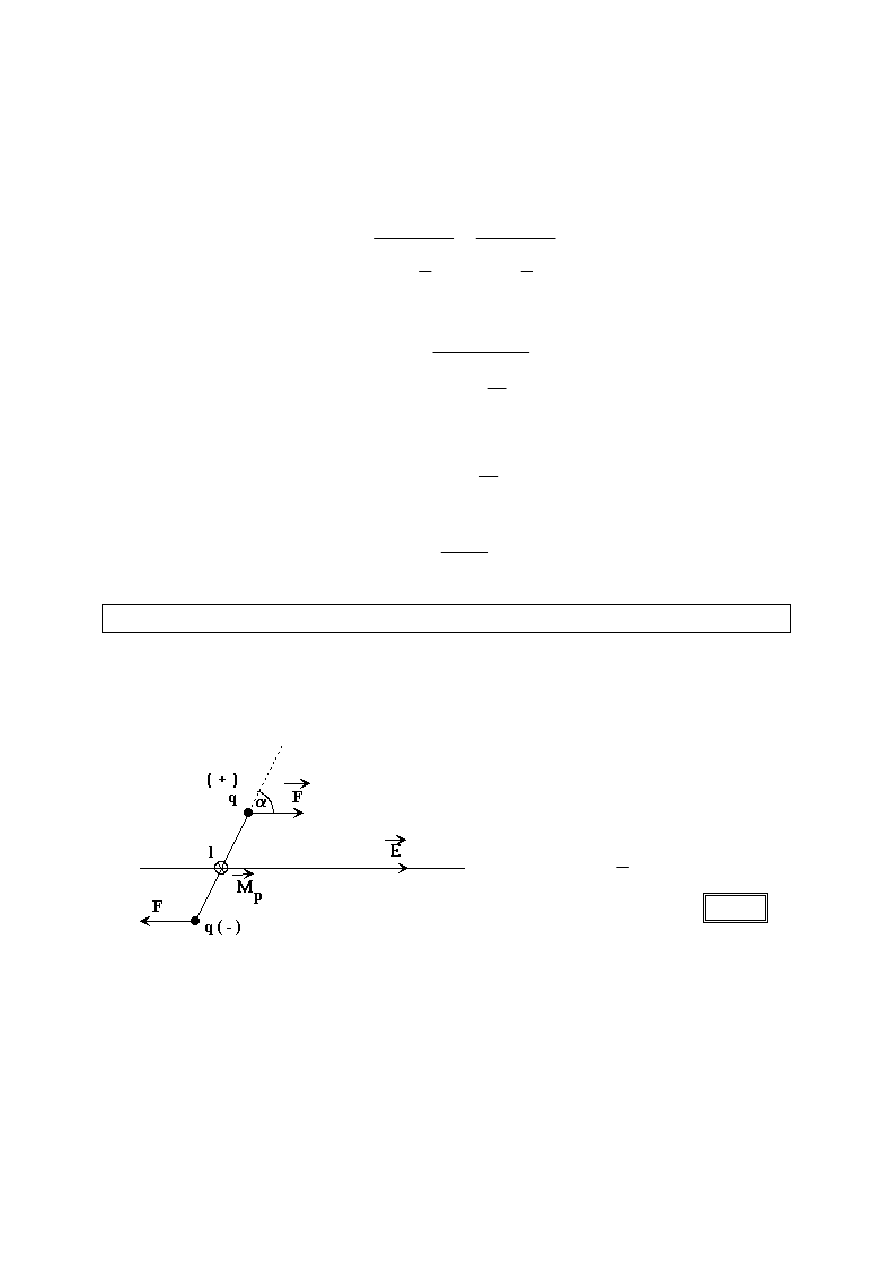
45

Natężenie pola w odległości

x

od środka dipola jest różnicą natężeń

pochodzących od poszczególnych ładunków.

E = E(+) - E(-)

E

kQ

x

l

kQ

x

l

====

−−−−











−−−−

++++











2

2

2

2

E

kQ

xl

x

l

====

−−−−











2

4

2

2

2

x

l

x

l

x

>>

>>

>>

>>

⇒

⇒

⇒

⇒

−−−−

≈≈≈≈

2

2

2

4

E

kQl

x

≈≈≈≈

2

3

Moment elektryczny dipola

Momentem elektrycznym dipola nazywamy wektor charakterystyczny dla
danego dipola, dobrany w taki sposób, żeby iloczyn wektorowy tego wektora
przez wektor natężenia pola był równy momentowi pary sił obracających ten

dipol.

E

p

M

p

r

r

r

××××

====

- def.

M

F

l

p

====

⋅⋅⋅⋅

2

2

sin

αααα

; F = q

⋅⋅⋅⋅

E

M

p

= q l E sin

αααα

ql

p

====

M

p

= p E sin

αααα

Aby powyższy związek można było zapisać w postaci

E

p

M

p

r

r

r

××××

====

, to

p

r

musi

być skierowany wzdłuż osi dipola, ze zwrotem od ładunku ujemnego do
dodatniego. Im większy jest moment elektryczny dipola (moment dipolowy)
tym większy jest moment pary sił obracających ten dipol, po umieszczeniu go w
polu elektrycznym.

46

Dipolami elektrycznymi są niektóre cząsteczki chemiczne.

p

x

k

2

E

3

r

r

====

Indukcja elektryczna

Indukcją elektryczną nazywamy wektor, który podobnie jak wektor natężenia
charakteryzuje pole elektryczne, ale w odróżnieniu od wektora natężenia,
wartość wektora indukcji elektrycznej nie zależy od rodzaju ośrodka
otaczającego źródło pola.

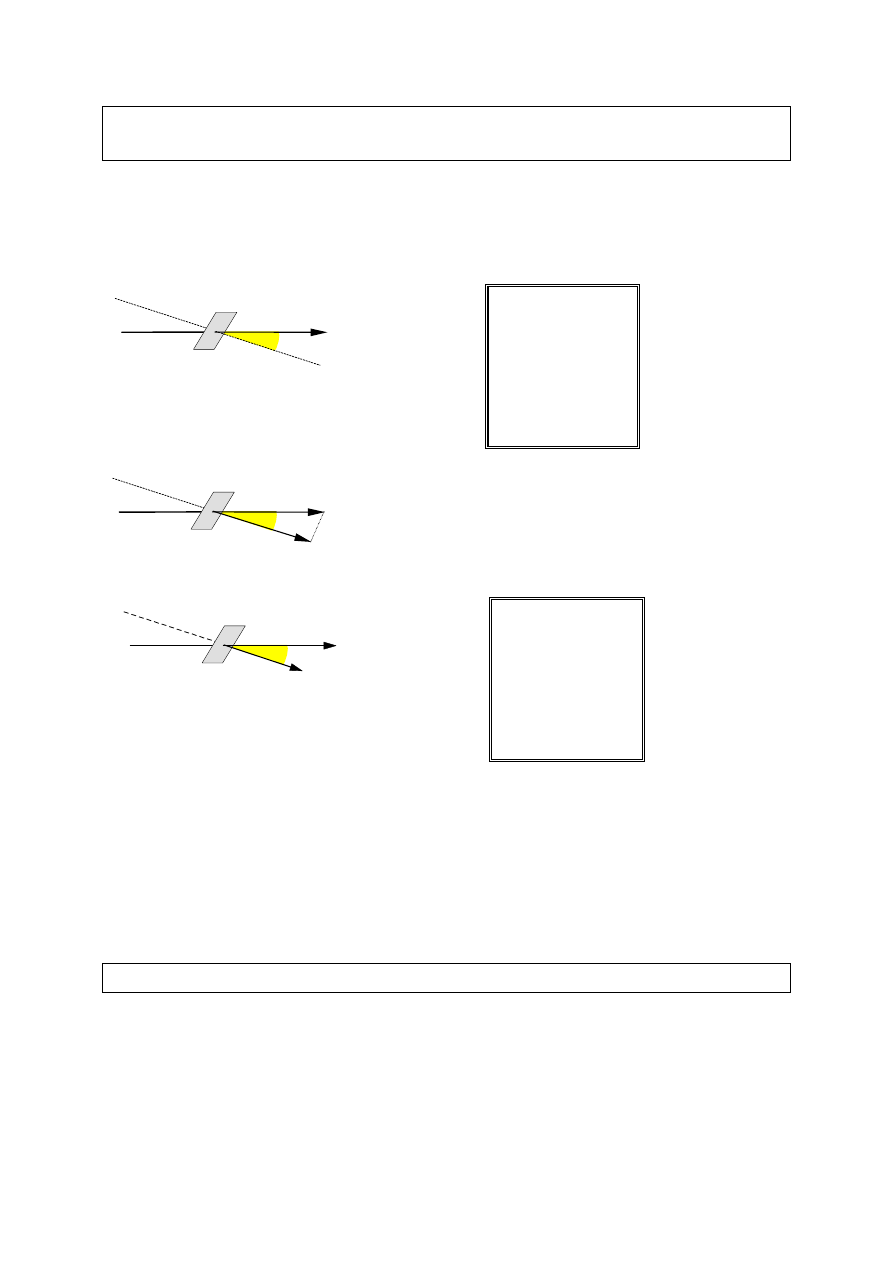
Pole elektryczne działając na ładunki zawarte w materiale umieszczonym w
polu elektrycznym powoduje przemieszczenie tych ładunków, w wyniku czego
na powierzchni

ds

indukuje się ładunek

dq

. Miarą indukcji elektrycznej jest

stosunek ładunku wyindukowanego na danej powierzchni do wielkości tej
powierzchni.

D

dq

ds

====

Jeśli ośrodek sam nie wytwarza pola elektrycznego, to wektory

D

r

i

E

r

są

współliniowe, przy czym zachodzi między nimi związek:

E

D

0

r

r

εε

εε

εε

εε

====

Indukcja elektryczna w odległości r od ładunku punktowego Q wynosi:

D

Q

r

Q

r

====

====

εε

εε

εε

εε

πεε

πεε

πεε

πεε

ππππ

0

0

2

2

4

4

Q

r

D

r

47

Strumie

ń

nat

ęż

enia pola elektrycznego

Strumie

ń

indukcji elektrycznej

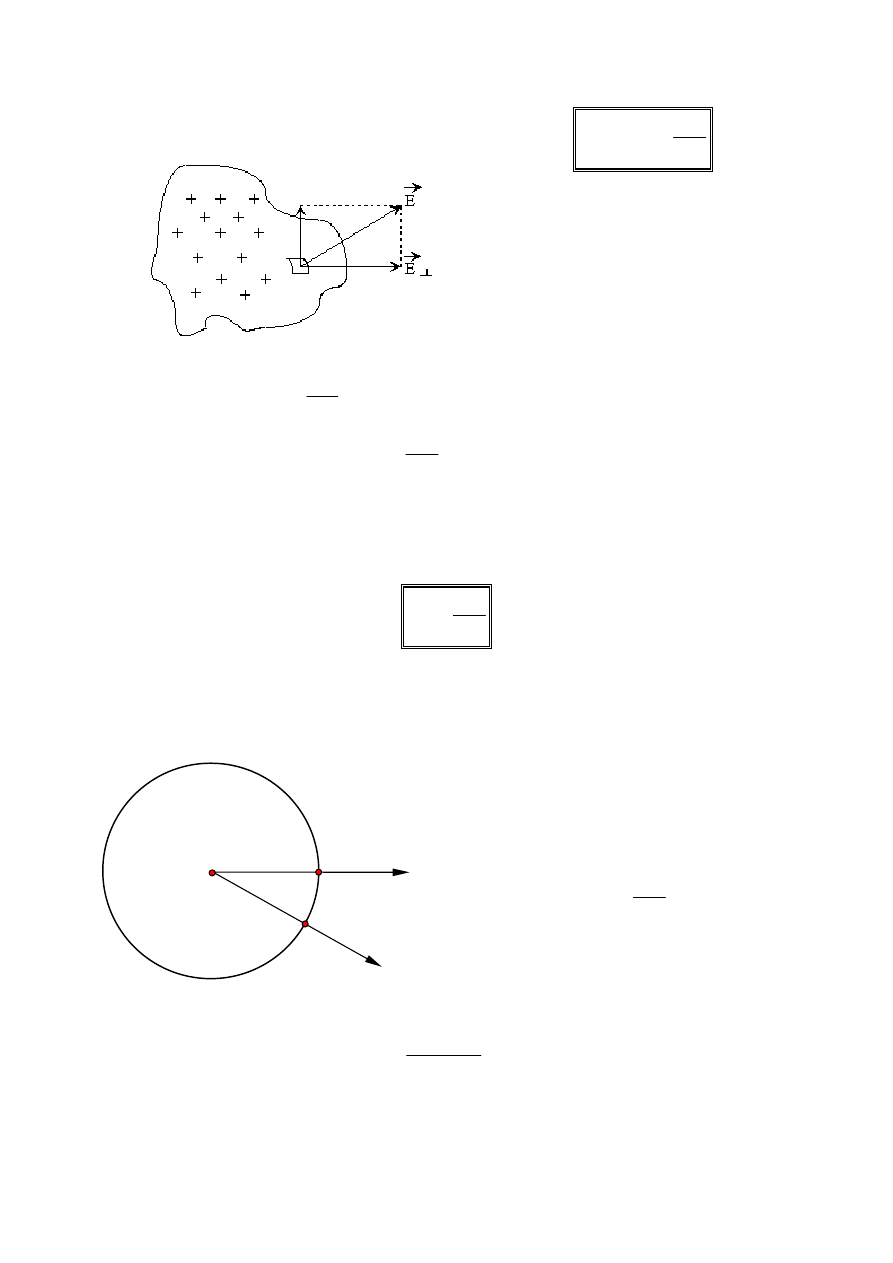
W polu elektrycznym o natężeniu E jest umieszczony element powierzchni ds.
Strumień elementarny natężenia pola przenikający powierzchnię ds jest
określony równaniem:

s

d

E

d

ds

E

d

cos

Eds

d

E

E

E

r

o

r

====

Φ

Φ

Φ

Φ

====

Φ

Φ

Φ

Φ

αααα

====

Φ

Φ

Φ

Φ

⊥

⊥⊥

⊥

Analogicznie jest określony strumień elementarny
indukcji elektrycznej:

s

d

D

d

ds

D

d

cos

Dds

d

D

D

D

r

o

r

====

Φ

Φ

Φ

Φ

====

Φ

Φ

Φ

Φ

αααα

====

Φ

Φ

Φ

Φ

⊥

⊥⊥

⊥

Strumień

całkowity

indukcji

elektrycznej

stanowi

sumę

strumieni

elementarnych przenikających przez dowolnie dużą powierzchnię umieszczoną
w polu elektrycznym.

Φ

Φ

Φ

Φ

Φ

Φ

Φ

Φ

D

D

d

====

∑

∑

∑

∑

Prawo Gaussa

Rozważamy przestrzennie rozłożony ładunek

Q

zamknięty wewnątrz

powierzchni dowolnego kształtu. Strumień całkowity natężenia pola
elektrycznego, który przenika przez rozpatrywaną powierzchnię jest
proporcjonalny do zamkniętego w niej ładunku i wynosi:

αααα

ds

E

r

αααα

ds

⊥

⊥⊥

⊥

E

r

αααα

ds

r

ds

r

E

48

E ds

Q

⊥

⊥⊥

⊥

====

∑

∑

∑

∑

εε

εε

εε

εε

0

Prawo to zostało sformułowane
przez

wielkiego

matematyka

niemieckiego Carla Friedricha
Gaussa (1777 - 1855). Istnieje
wiele sposobów zapisania tego
prawa. Oto niektóre z nich:

∑

∑

∑

∑

εε

εε

εε

εε

====

0

Q

s

d

E

r

o

r

D ds

Q

⊥

⊥⊥

⊥

====

∑

∑

∑

∑

∑

∑

∑

∑

====

Q

s

d

D

r

o

r

Φ

Φ

Φ

Φ

E

Q

====

εε

εε

εε

εε

0

Φ

Φ

Φ

Φ

D

Q

====

Jeśli w każdym punkcie powierzchni zamykającej ładunek Q wektor natężenia
jest prostopadły do odpowiedniego fragmentu powierzchni i ma tą samą
wartość, to prawo Gaussa przyjmuje postać:

E

Q

s

====

εε

εε

εε

εε

0

Korzystając z prawa Gaussa można wykazać co następuje:

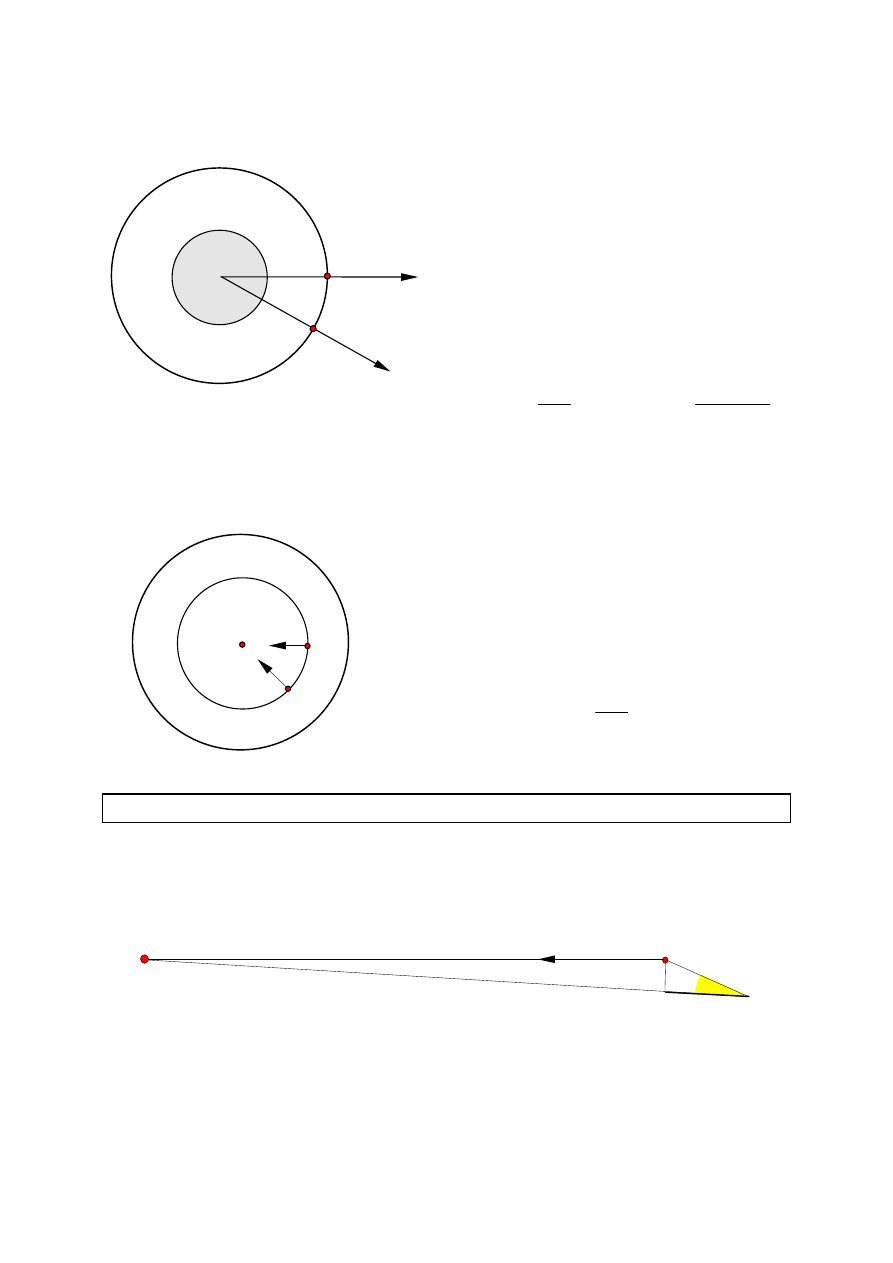
1. Prawo Coulomba wynika z prawa Gaussa.

Rozważamy

powierzchnię

kulistą

otaczającą punktowy ładunek

Q

. Ponieważ

spełnione są warunki, o których była
mowa,

otrzymujemy:

E

r

Q

⋅⋅⋅⋅

====

4

2

0

ππππ

εε

εε

εε

εε

Siła działająca na ładunek

q

umieszczony

w odległości

r

od ładunku

Q

wynosi

zatem:

F

qE

Qq

r

====

====

4

0

2

πεε

πεε

πεε

πεε

c.n.d.

Q

E

r

E

r

r

q

49

2. Równomiernie naładowana kula wytwarza takie pole elektryczne jakie
wytwarzałby ładunek tej kuli umieszczony w jej środku.

Rozważamy

powierzchnię

kulistą

otaczającą kulę obdarzoną ładunkiem Q.
Ponieważ natężenie pola elektrycznego w
każdym punkcie kuli o promieniu r
zamykającej

kulę

naładowaną

jest

prostopadłe

do

rozpatrywanej

powierzchni i wszędzie ma tą samą
wartość, otrzymujemy:

E

r

Q

⋅⋅⋅⋅

====

4

2

0

ππππ

εε

εε

εε

εε

E

Q

r

====

4

0

2

πεε

πεε

πεε

πεε

c.n.d.

3. Wewnątrz równomiernie naładowanej powierzchni sferycznej E = 0.

Rozważamy powierzchnię kulistą położoną
wewnątrz naładowanej powierzchni sferycznej,
do której należy punkt

P

. Gdyby w tym punkcie

istniało pole elektryczne to

E

r

powinien mieć

kierunek promienia (tylko na tym kierunku
istnieje asymetria układu). Stosując prawo
Gaussa otrzymujemy:

E S

⋅⋅⋅⋅ ====

0

0

εε

εε

εε

εε

Ponieważ jednak

S

≠≠≠≠

0

⇒

⇒

⇒

⇒

E = 0

c.n.d.

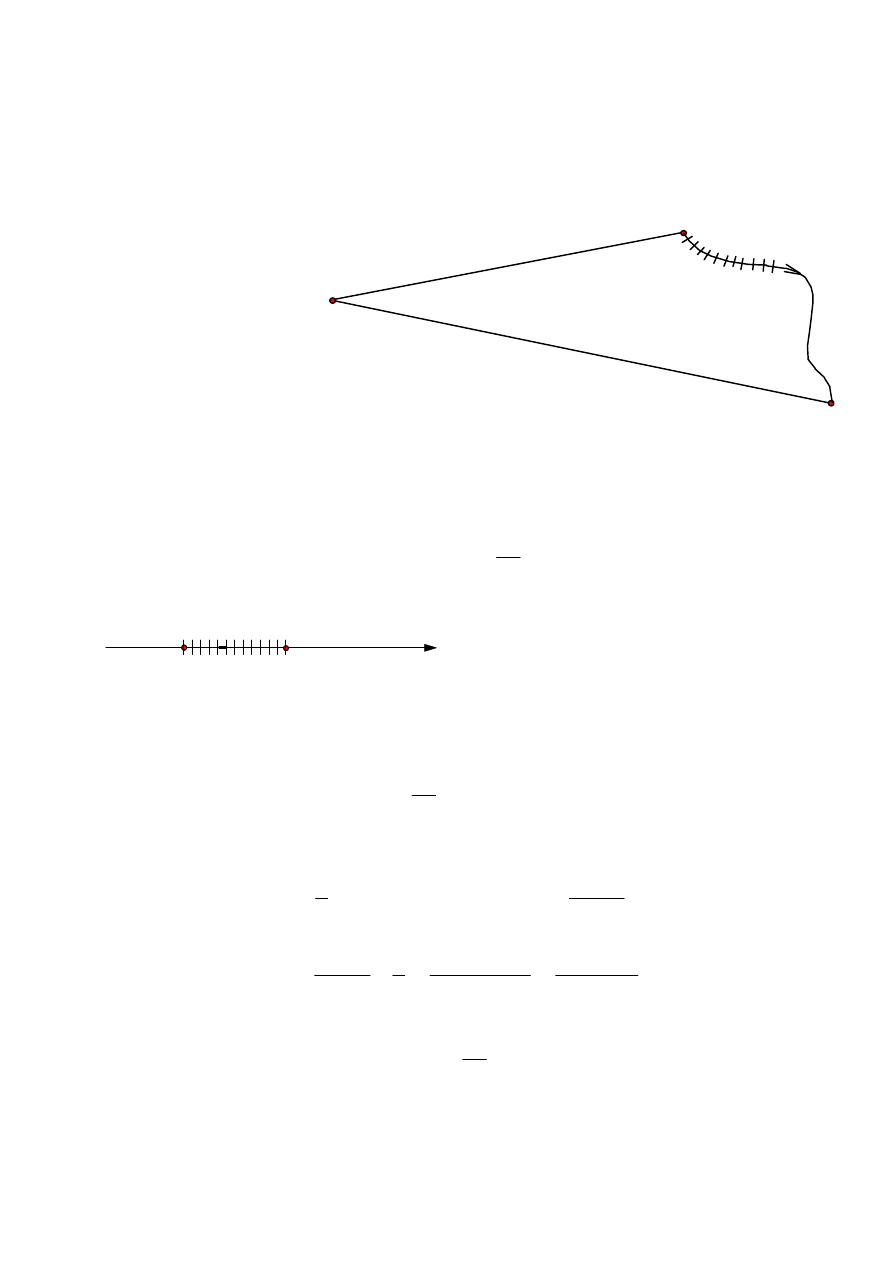
Praca w polu elektrycznym

Ładunek punktowy

q

umieszczony w odległości

r

od innego ładunku

Q

przesuwamy na odcinku

ds

, zwiększając odległość między ładunkami o

dr.

Wykonana przy tym praca elementarna wynosi:

dW = F

⋅⋅⋅⋅

ds

⋅⋅⋅⋅

cos(180

0

-

αααα

)

dW = - F

⋅⋅⋅⋅

ds

⋅⋅⋅⋅

cos

αααα

Q

r

E

r

E

r

+

+ + +

+

+

+

+

+

+

+

+

P

S

E

r

E

r

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

dr

(+)

Q

q

(+)

d

αααα

ds

F

r

50

Praca elementarna nie zależy zatem od drogi, a zależy jedynie od zmiany
odległości między ładunkami. Praca wykonana przy dowolnie dużej zmianie
odległości między ładunkami stanowi sumę prac elementarnych.

W

dW

W

Fdr

W

kqQ

dr

r

====

==== −−−−

==== −−−−

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

2

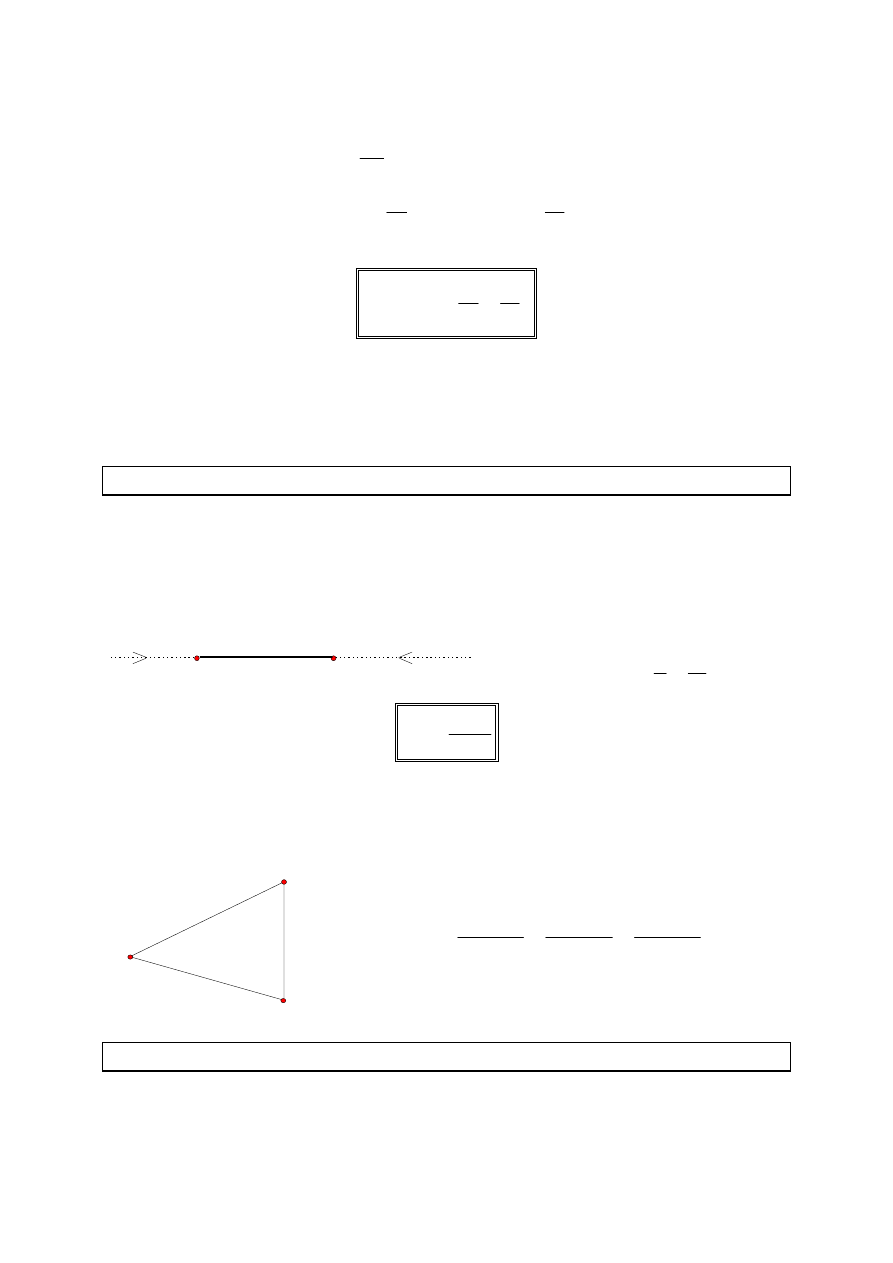
Powstaje problem obliczenia sumy prac elementarnych.

dx

x

x

====

−−−−

∑

∑

∑

∑

2

1

Suma nieskończenie wielu przyrostów zmiennej x jest równa x

2

- x

1

. Zmienną r

zastępujemy odpowiednio dobraną zmienną z, tak aby był spełniony warunek:

dr

r

dz

2

====

Aby powyższy warunek był spełniony poszukiwana zmienna powinna być
równa:

z

r

==== −−−−

1

z

dz

r

dr

−−−−

==== −−−−

++++

1

((((

))))

dz

r

dr

r

r

r

dr

r

dr r

dr

r

dr r

==== −−−−

++++

++++ ==== −−−− ++++ ++++

++++

====

++++

1

1

(

)

dr

dz

dr

r

≈≈≈≈

⇒

⇒

⇒

⇒

====

0

2

c.n.d.

Praca wykonana przy przesuwaniu ładunku w polu elektrycznym wynosi:

dW = - F

⋅⋅⋅⋅

dr

q

r

2

r

1

Q

dx

x

2

x

1

x

51

((((

))))

W

kqQ

dr

r

kqQ

dz

kqQ z

z

==== −−−−

==== −−−−

==== −−−−

−−−−

∑

∑

∑

∑

∑

∑

∑

∑

2

2

1

z

r

2

2

1

==== −−−−

z

r

1

1

1

==== −−−−

W

kqQ

r

r

====

−−−−











1

1

2

1

Powyższa zależność wyraża pracę sił zewnętrznych jaka musi być wykonana
przy zmianie odległości między ładunkami

Q

,

q

z

r

1

na

r

2

.

Energia potencjalna układu ładunków

Energia potencjalna układu ładunków

Q

,

q

umieszczonych w odległości

wzajemnej

r

równa jest pracy jaką trzeba wykonać przenosząc ten układ ze

stanu energii zerowej (gdy ładunki są nieskończenie od siebie odległe

i na

siebie nie działają) do danego stanu energii (gdy ładunki są w odległości

r

).

E

kqQ

r

p

====

−−−−

∞

∞

∞

∞











1

1

E

kqQ

r

p

====

W przypadku układu złożonego z większej ilości ładunków, energia potencjalna
układu stanowi sumę energii potencjalnych poszczególnych par.

E

kQ Q

r

kQ Q

r

kQ Q

r

p

====

++++

++++

1

2

1

2

3

2

1

3

3

Potencjał

Każdemu punktowi pola elektrycznego można przypisać wielkość skalarną
charakterystyczną dla danego punktu pola zwaną potencjałem. Miarą potencjału

Q

q

r

Q

3

Q

2

Q

1

r

3

r

1

52

jest stosunek energii potencjalnej jaką ma dowolny ładunek umieszczony w
danym punkcie pola do wartości tego ładunku.

V

E

q

p

====

Potencjał w odległości r od ładunku punktowego Q jest równy:

V

kqQ

rq

====

V

kQ

r

====

Praca wykonana przy przenoszeniu ładunku

q

z odległości

r

1

na odległość

r

2

od

ładunku

Q

wynosi:

W

kqQ

r

r

q

kQ

r

kQ

r

====

−−−−











====

−−−−











1

1

2

1

2

1

W = q (V

2

- V

1

) = q

⋅⋅⋅⋅

U

;

U

- napięcie

Wolt jest potencjałem takiego punktu pola, w którym ładunek jednego kulomba
ma energię potencjalną jednego dżula.

V

J

C

====

Elektronowolt jest pracą jaką trzeba wykonać przenosząc ładunek elektronu
między dwoma punktami pola o różnicy potencjałów 1 V.

1eV = 1e . 1V = 1,602 . 10-19 C . 1V

1eV = 1,602 . 10-19 J

Zwi

ą

zek mi

ę

dzy nat

ęż

eniem pola i potencjałem

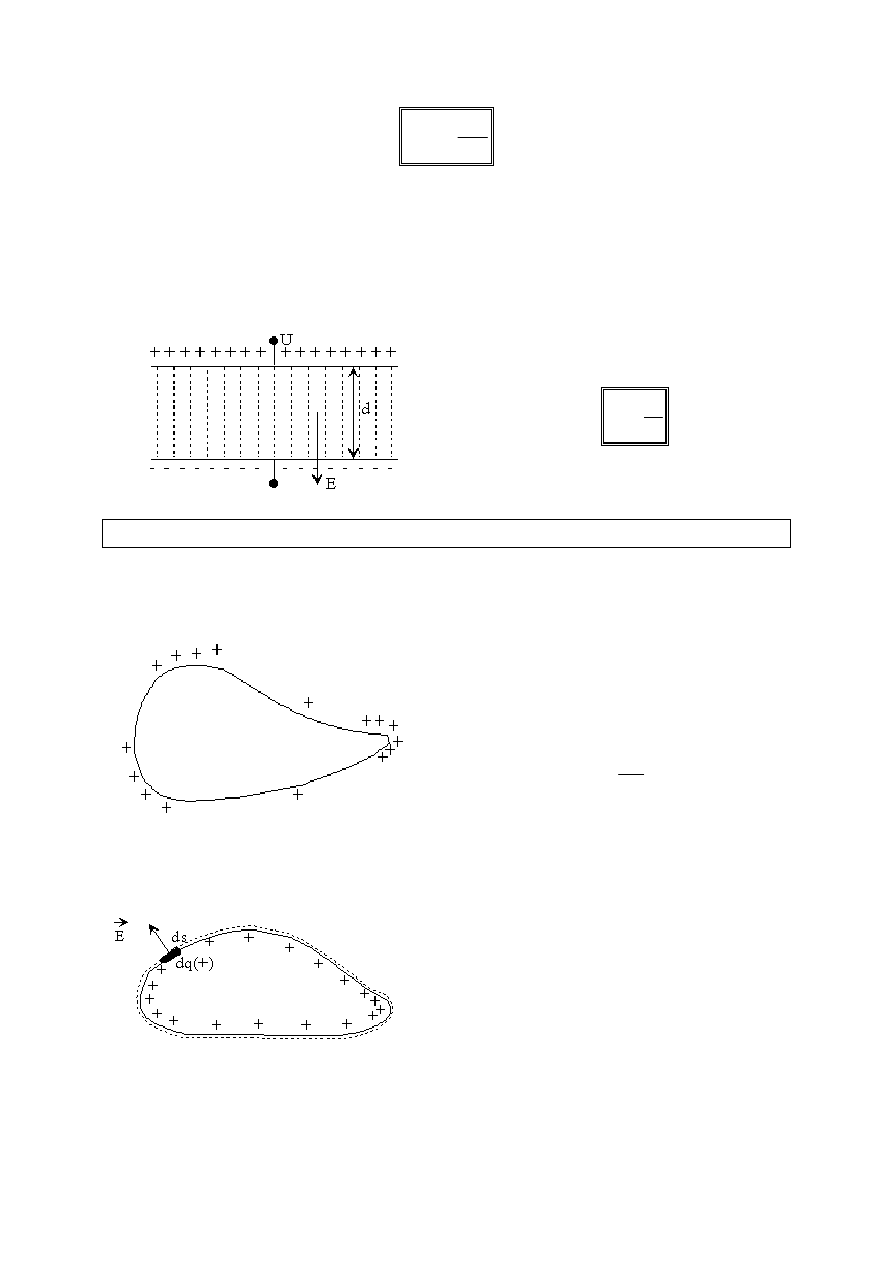
Ładunek

q

przesuwamy na odcinku

dr

wzdłuż linii sił pola elektrycznego.

Wykonaną przy tym pracę można wyrazić na dwa sposoby.

dW = Fdr cos 180

0

dW = -Fdr

dW = -qEdr lub dW = qdV

-qEdr = qdV

V

r

Q

F

r

Q

q

(2)

(1)

(+)

dr = r

2

-r

1

dV = V

2

- V

1

53

E

dV

dr

==== −−−−

Znak "-" informuje o tym, że wektor natężenia ma zwrot w stronę punktu o
mniejszym potencjale.

W przypadku pola jednorodnego, jakie istnieje między dwiema płaskimi
powierzchniami równomiernie naładowanymi ładunkami o przeciwnych
znakach, między natężeniem pola i napięciem istnieje związek:

E

U

d

====

Rozkład ładunku na powierzchni przewodnika

W wyniku elektrostatycznego odpychania ładunków tego samego znaku,

ładunki te gromadzą się na powierzchni
przewodnika. Gęstością powierzchniową
ładunku nazywamy stosunek ładunku

dq

zgromadzonego na powierzchni

ds

do

wielkości tej powierzchni

σσσσ ====

dq

ds

Największa gęstość powierzchniowa

ładunku jest w miejscach silnie zakrzywionych.

Rozważamy powierzchnię przylegającą
do

powierzchni

naładowanego

przewodnika.

O

natężeniu

pola

elektrycznego w różnych punktach takiej
powierzchni

decyduje

ładunek

dq

znajdujący

się

w

najbliższym

sąsiedztwie. Stosując prawo Gaussa do
powierzchni

przylegającej

do

powierzchni naładowanego przewodnika otrzymujemy:

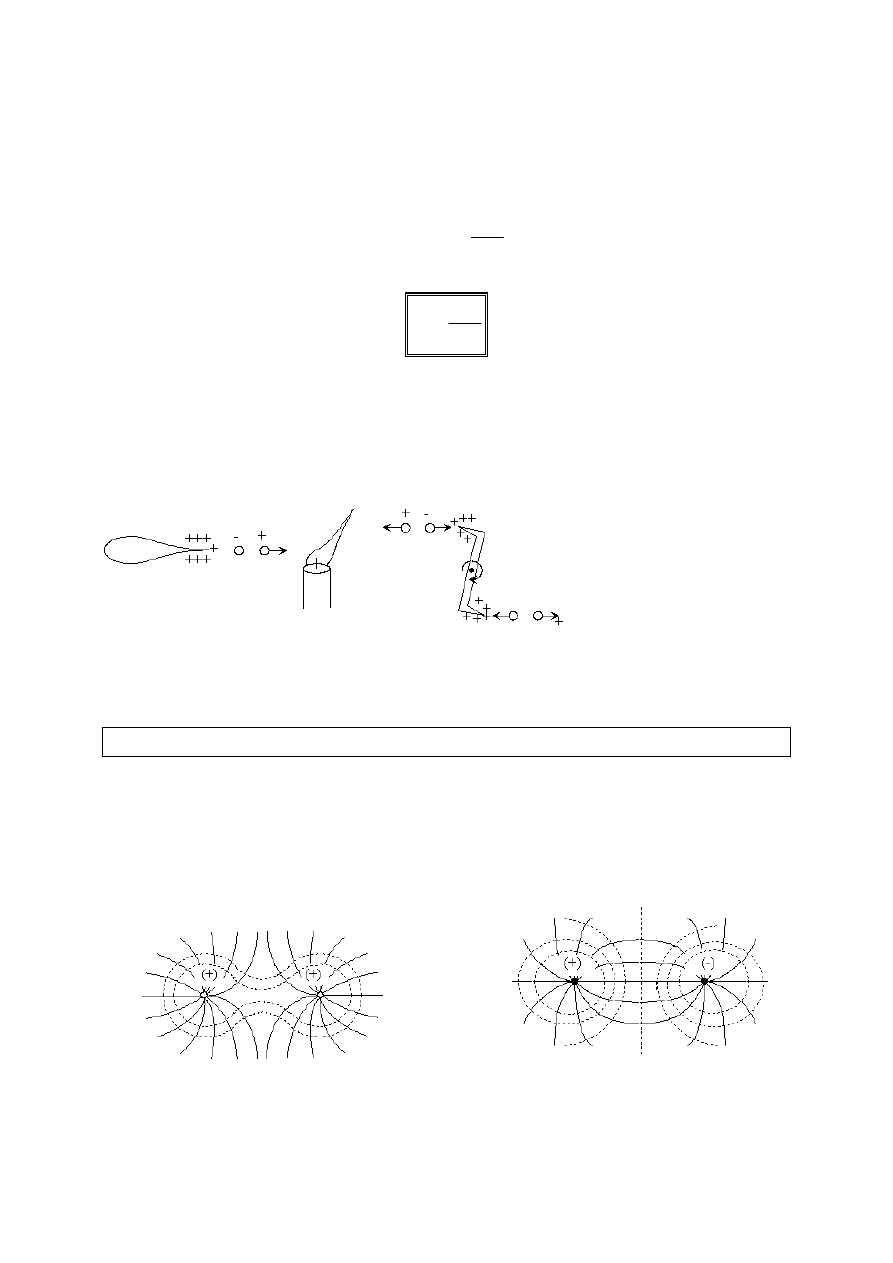
54

E

1

ds

1

+ E

2

ds

2

+ … = (dq

1

+ dq

2

+ … )

Każdemu składnikowi sumy po jednej stronie równania odpowiada jeden
składnik sumy po drugiej stronie.

Eds

dq

====

1

0

εε

εε

εε

εε

E

==== σσσσ

εε

εε

εε

εε

0

Natężenie pola elektrycznego na powierzchni przewodnika jest skierowane
prostopadle do powierzchni, a jego wartość jest wprost proporcjonalna do
gęstości powierzchniowej ładunku. Wewnątrz naładowanego przewodnika nie
ma pola elektrycznego.

W sąsiedztwie ostrzy
istnieje pole elektryczne
o

dużym

natężeniu.

Powoduje ono jonizację
powietrza. Jony tego
samego znaku co ostrze
są od niego odpychane.

Powstaje tzw. wiatr elektryczny. Siła reakcji działa na ostrze, co tłumaczy
obracanie się młynka Franklina.

Powierzchnie ekwipotencjalne

Nazywamy tak powierzchnie o jednakowym potencjale. Powierzchnia
przewodnika,

niezależnie

od

swojego

kształtu

jest

powierzchnią

ekwipotencjalną. Linie sił pola elektrycznego zawsze są prostopadłe do
powierzchni ekwipotencjalnych.

55

Powyższe rysunki przedstawiają typowy układ linii sił pola elektrycznego i
kształt powierzchni ekwipotencjalnych.

Przesunięcie ładunku po powierzchni ekwipotencjalnej nie wymaga pracy.

Model atomu Bohra

1. Model atomu Thomsona.

Odkrycie przez J.J. Thomsona (1856 - 1940) elektronu (1897 r.) umożliwiło
powstanie pierwszego modelu atomu. Thomson wyobraził sobie atom jako
dodatnio naładowaną kulę, w której umieszczone są elektrony. Model ten,
nazwany przez autora "ciastem z rodzynkami", tłumaczył wiele zjawisk. Na
jego podstawie można było wyjaśnić zjawisko elektrolizy i emisji elektronów z
rozgrzanej powierzchni, a także zjawisko emisji promieniowania świetlnego.

2. Model Rutherforda.

Ernest Rutherford (1871 - 1937) był Nowozelandczykiem. Po ukończeniu
uniwersytetu w Nowej Zelandii uzyskał stypendium na uniwersytecie w
Cambridge. Pracował tam w Laboratorium Cavendisha pod kierunkiem J.J.
Thomsona. W wieku 27 lat był już profesorem katedry fizyki na Uniwersytecie
McGila w Montrealu. W roku 1907 Rutherford wraca do Anglii i zostaje
profesorem uniwersytetu w Manchesterze. Pod jego kierunkiem dwaj jego
asystenci - Geiger i Marsden

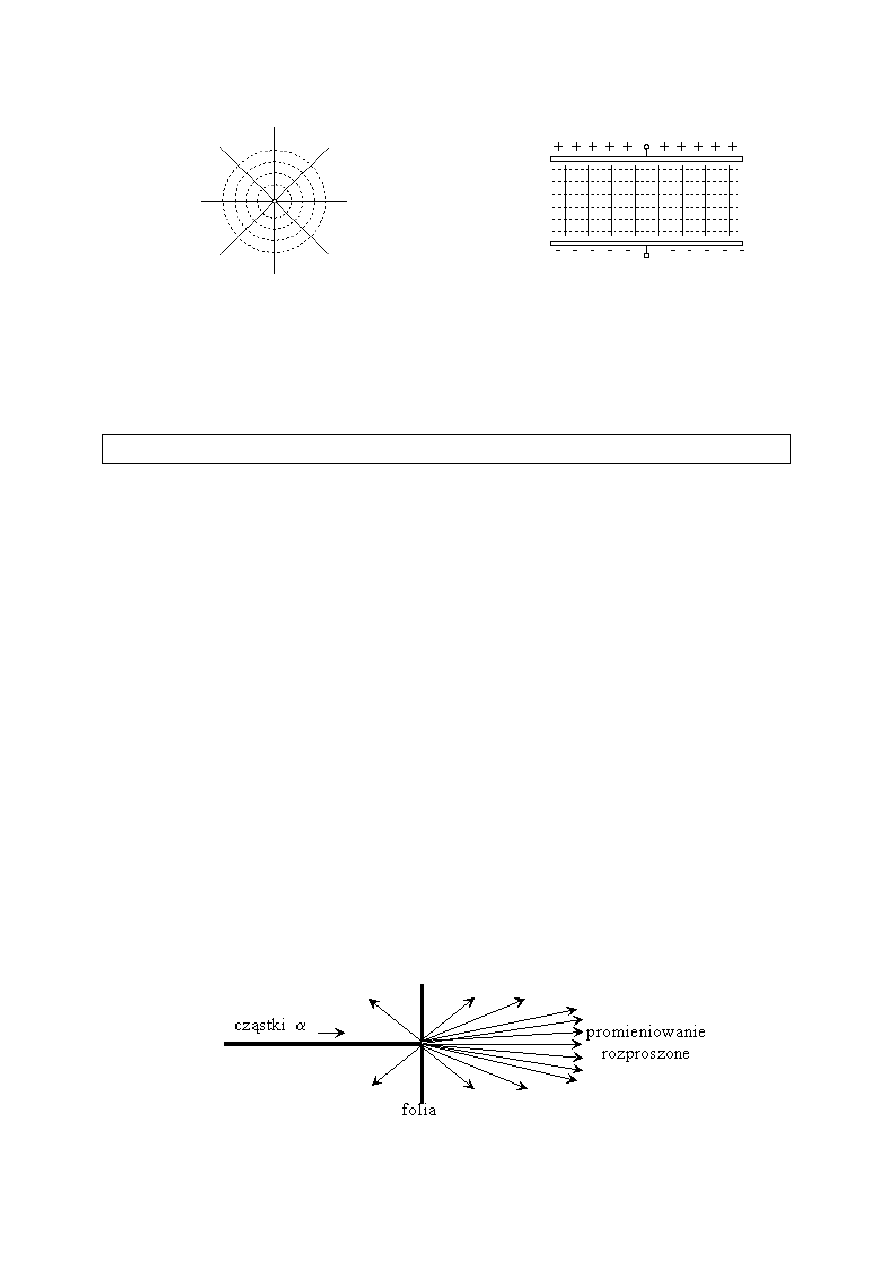
przeprowadzili badania nad rozpraszaniem cząstek

αααα

w cienkich foliach

metalowych (1909 r.). Cząstki

αααα

są to jądra helu wysyłane z jąder niektórych

pierwiastków promieniotwórczych. Mają one dodatni ładunek elektryczny o

56

wartości

2e

. Przyjmując, że atom ma taką budowę jaką przewidywał model

Thomsona, wyliczono rozkład kątowy promieniowania rozproszonego w danej
folii, tj. jaki procent cząstek powinien być rozproszony pod danym kątem.
Okazało się jednak, że niektóre cząstki ulegały wręcz odbiciu od folii. Był to
fakt zaskakujący. To tak jakby kula karabinowa mogła odbić się od kartki
papieru. Aby to zjawisko wytłumaczyć trzeba było przyjąć, że cały ładunek
dodatni atomu jest skupiony w jego centrum. Tak powstała koncepcja jądra
atomowego i planetarny model atomu ogłoszony w 1911 r.

3. Postulaty Bohra.

W 1911 roku przyjechał do Manchesteru młody Duńczyk - Niels Bohr (1885 -
1962). W wyniku współpracy z Ernestem Rutherfordem udało mu się usunąć
trudności stojące przed modelem planetarnym. Dokonał tego przez
wprowadzenie do atomistyki pojęcia kwantu. Sformułował on postulaty
kwantowe, którymi uzupełnił model Rutherforda:

1. Elektrony mogą krążyć wokół jądra atomowego jedynie po takich orbitach
kołowych, na których moment pędu jest wielokrotnością pewnej stałej.

mVr

n

====

h

;

ππππ

====

2

h

h

h = (6,6260755 ± 0,0000040) . 10-34 J . s

n

∈

∈

∈

∈

N

h

- stała Plancka

n

- główna liczba kwantowa.

2. Elektron krążący po ustalonym torze nie traci energii.

3. Przejściu elektronu z jednej orbity na drugą towarzyszy emisja lub absorpcja
kwantu energii:

∆∆∆∆

E

h

==== νννν

;

νννν

λλλλ

====

c

c = 2,99792458 . 108

m

s

m

s

≈≈≈≈ ⋅⋅⋅⋅

3 10

8

νννν

- częstość kwantu,

λλλλ

- długość fali promieniowania wysłanego lub pochłoniętego

c

- prędkość światła w próżni.

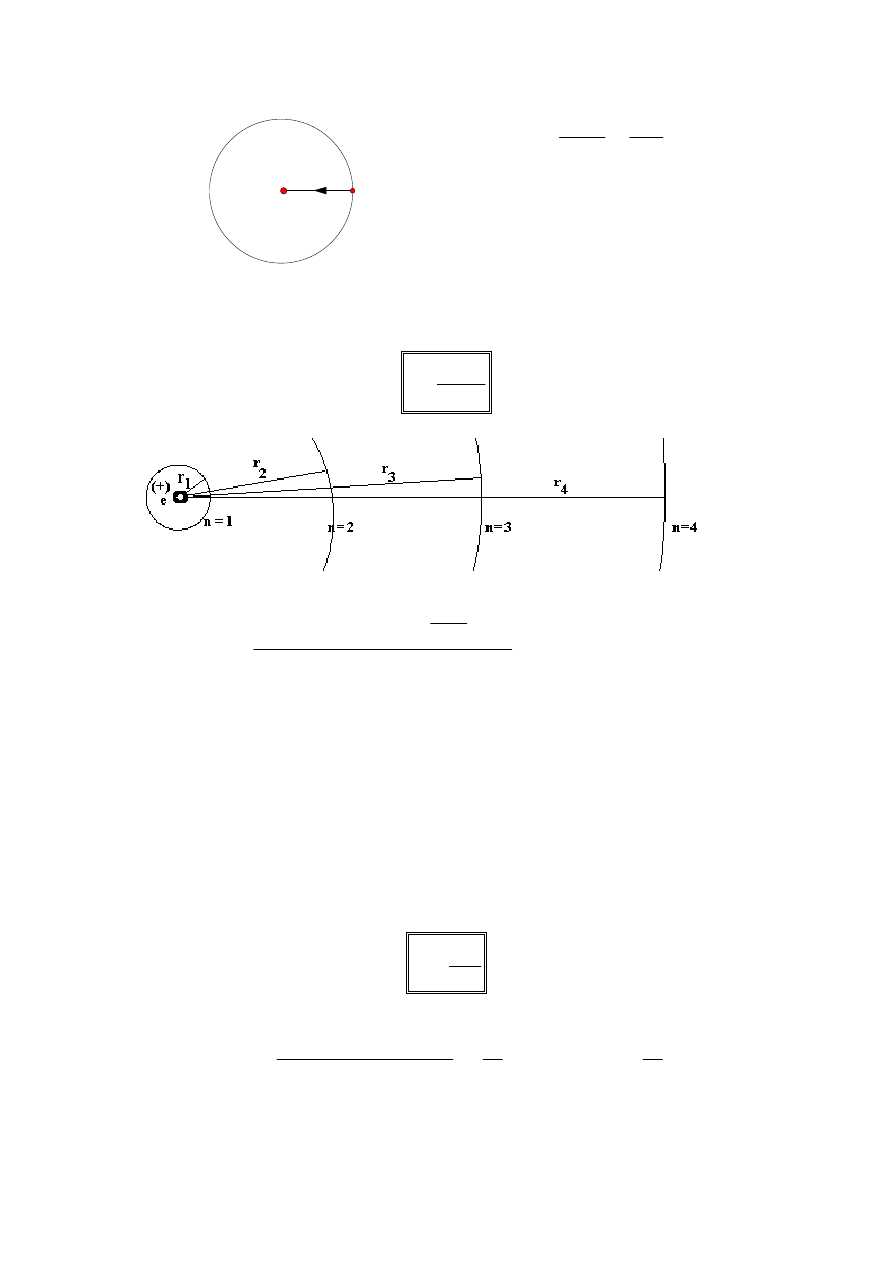
4. Promie

ń

orbity dozwolonej.

Na elektron poruszający się po orbicie działa siła dośrodkowa, którą jest siła
kulombowska.

57

F

mV

r

ke

r

r

====

====

2

2

2







====

====

h

n

mVr

ke

r

mV

2

2

Podnosząc drugie równanie stronami do kwadratu i dzieląc stronami przez
pierwsze otrzymujemy:

m

ke

n

r

2

2

2

h

====

((((

))))

((((

))))

r

m

m

1

34

2

2

9

19

2

31

10

6 62 10

1

4

9 10 1 6 10

9 1 10

0 529 10

====

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

≈≈≈≈

⋅⋅⋅⋅

−−−−

−−−−

−−−−

−−−−

,

,

,

,

ππππ

r

2

= 4r

1

;

r

3

= 9r

1

;

r

4

= 16r

1

…

5. Pr

ę

dko

ść

elektronu na orbicie.

Ten sam układ równań pozwala określić prędkość elektronu krążącego wokół
jądra atomowego:







====

====

h

n

mVr

ke

r

mV

2

2

h

n

ke

V

2

====

((((

))))

V

m

s

1

9

19

2

34

9 10

1 6 10

6 62 10

2

====

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

−−−−

−−−−

,

,

ππππ

V

1

≈≈≈≈

2,2

⋅⋅⋅⋅

10

6

m

s

F

r

r

(-)

e

(+)

e

58

Posługując się wyjściowym układem równań można również określić inne
parametry elektronu związanego z atomem wodoru.

6. Energia elektronu na orbicie.

Elektron związany z jądrem atomowym posiada energię kinetyczną i
potencjalną:

(((( ))))

E

mV

ke

e

r

====

++++

−−−−

2

2

;

mV r

ke

2

2

====

E

ke

r

ke

r

====

−−−−

2

2

2

;

m

ke

n

r

2

2

2

h

====

2

2

4

2

n

2

m

e

k

E

h

−−−−

====

E

R

n

==== −−−−

'

1

2

;

R

k e m

'

====

2

4

2

2

h

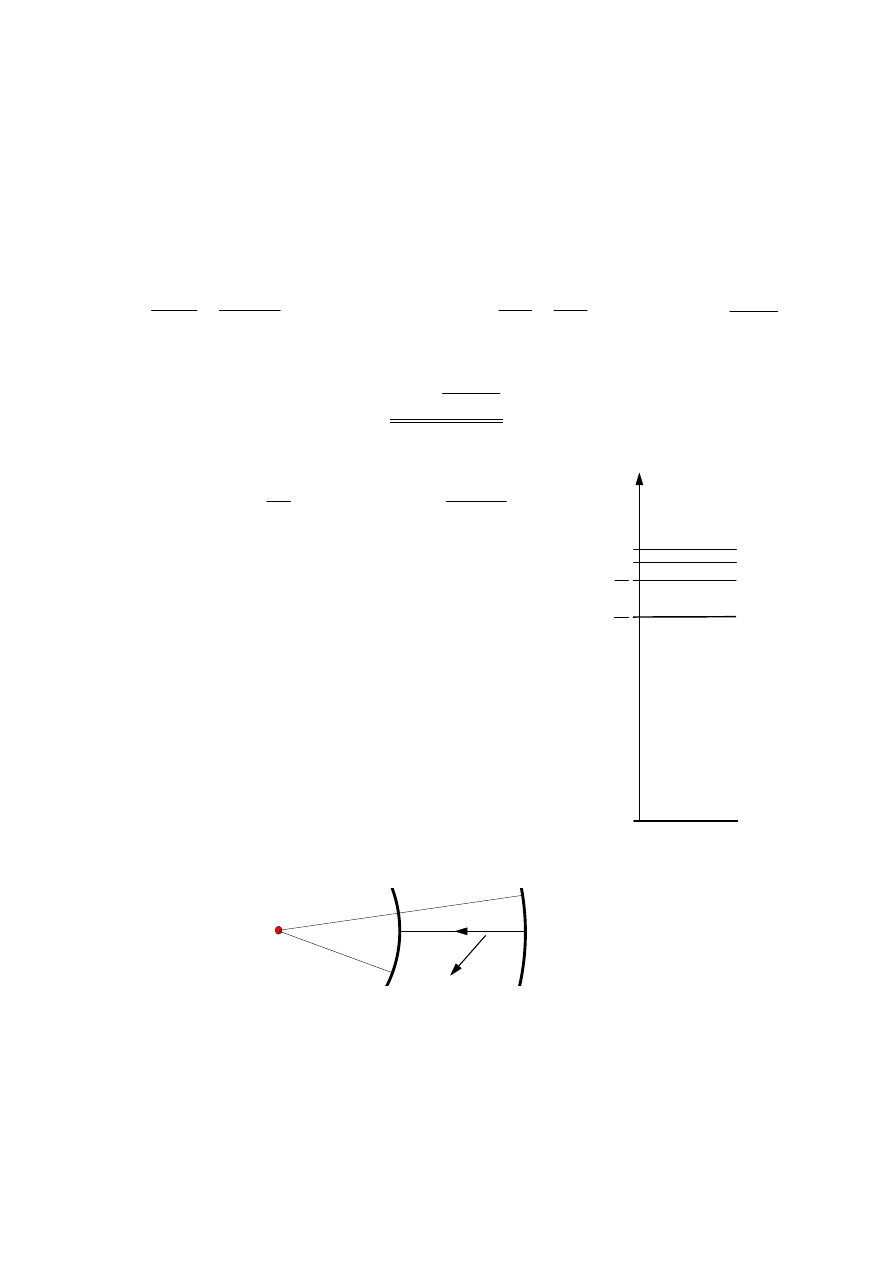
Różnice między kolejnymi dozwolonymi poziomami
energii szybko maleją.

7. Zmiany energii przy zmianie orbity elektronu.

Jeśli

energia

elektronu

krążącego

wokół

jądra

atomowego jest najmniejsza, to mówimy, że atom jest w
stanie podstawowym. Efektem dostarczenia energii jest
powstanie tzw. stanu wzbudzonego atomu. Czas
pozostawania w stanie wzbudzonym wynosi ok. 10

-8

s,

po czym atom przechodzi do innego stanu wzbudzonego,
względnie do stanu podstawowego.

Energia kwantu wysłanego przez atom podczas przechodzenia do niższego
stanu energii wynosi:

n = 3

n = 2

n

→

→

→

→∞

∞

∞

∞

n = 1

−−−−

R '

9

−−−−

R'

4

0

E

∆Ε

∆Ε

∆Ε

∆Ε

n

2

n

1

e

59

∆∆∆∆

E

E

E

R

n

R

n

R

n

n

====

−−−−

==== −−−−

++++

====

−−−−











2

1

1

2

2

2

1

2

2

2

1

1

1

1

'

'

'

hc

R

n

n

λλλλ

====

−−−−











'

1

1

1

2

2

2













−−−−

====

λλλλ

2
2

2

1

n

1

n

1

R

1

gdzie

((((

))))

m

1

10

097

,

1

m

1

10

0000000013

,

0

0973731534

,

1

hc

2

m

e

k

hc

'

R

R

7

7

2

4

2

⋅⋅⋅⋅

≈≈≈≈

⋅⋅⋅⋅

±±±±

====

====

====

h

R -

stała Rydberga

Zmianę energii atomu przechodzącego z jednego stanu wzbudzonego do innego
stanu wzbudzonego lub do stanu podstawowego można zatem określić
równaniem:

∆∆∆∆

E

Rhc

n

n

====

−−−−











1

1

1

2

2

2

Energia stanu podstawowego wyraża się wzorem:

E

Rhc

0

====

i wynosi E

0

= 13,6 eV

Uwzględniając, że elektron i jądro krążą wokół wspólnego środka masy stała
Rydberga wynosi:

R

H

= (1,096775854 ± 0,0000000083) . 107

1

m

8. Dalsze liczby kwantowe.

Model atomu Bohra tłumaczył powstawanie widm promieniowania wysyłanego
przez różne atomy, ale do czasu. Coraz lepsze metody badawcze doprowadziły
do wykrycia zjawisk, których model nie przewidywał. Analiza światła
wysyłanego przez atomy umieszczone w silnym polu magnetycznym wykazała,
ż

e widziane dotychczas pojedyncze linie, przy bliższym poznaniu mają

strukturę subtelną tzn. składają się z kilku linii położonych w niewielkich
odległościach. Odpowiada to kilku długościom fali. Aby znaleźć
wytłumaczenie subtelnej struktury widm przyjęto, że elektrony mogą poruszać
się również po torach eliptycznych, podlegająch także warunkom kwantowym.

60

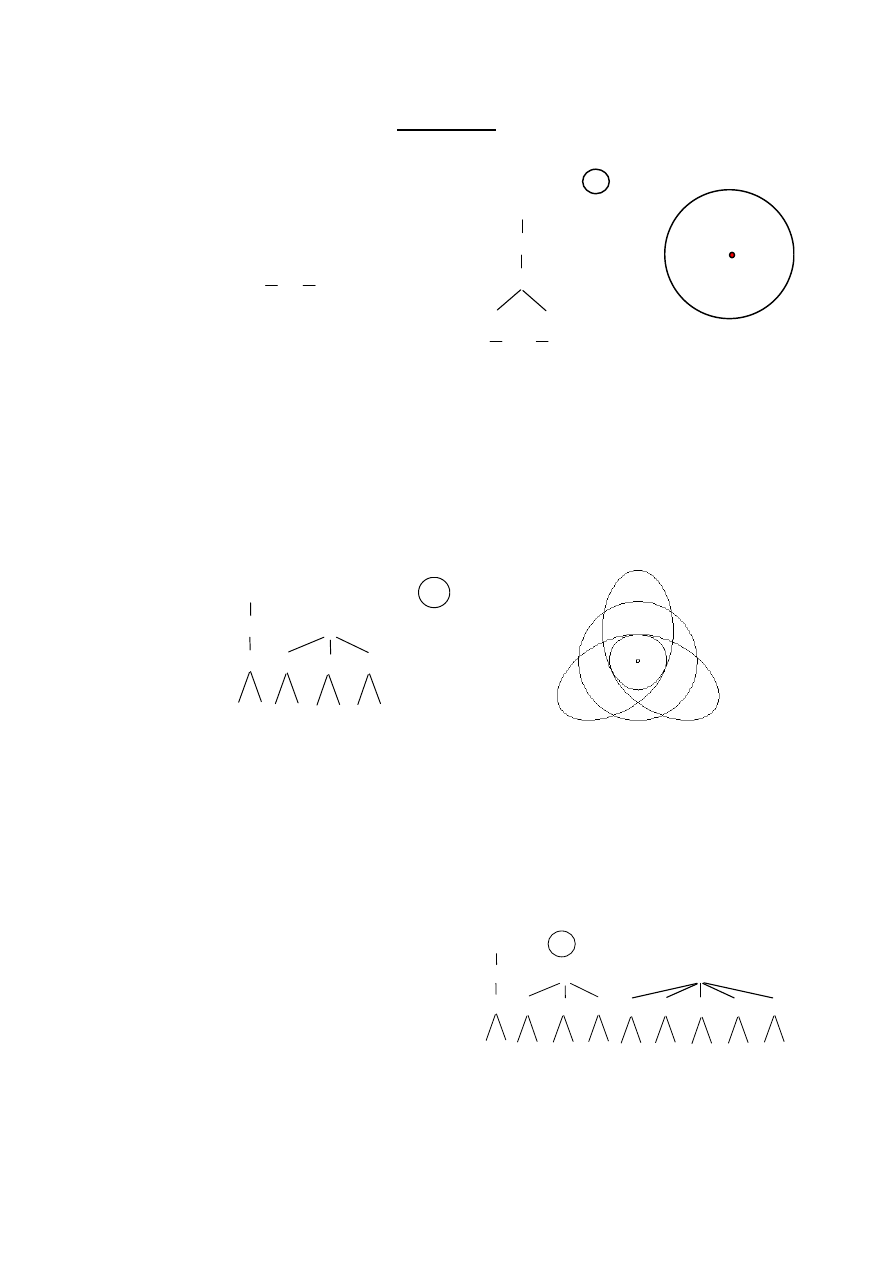
Orbity eliptyczne do modelu atomu Bohra wprowadził w latach dwudziestych
Arnold Sommerfeld (1868 - 1951).

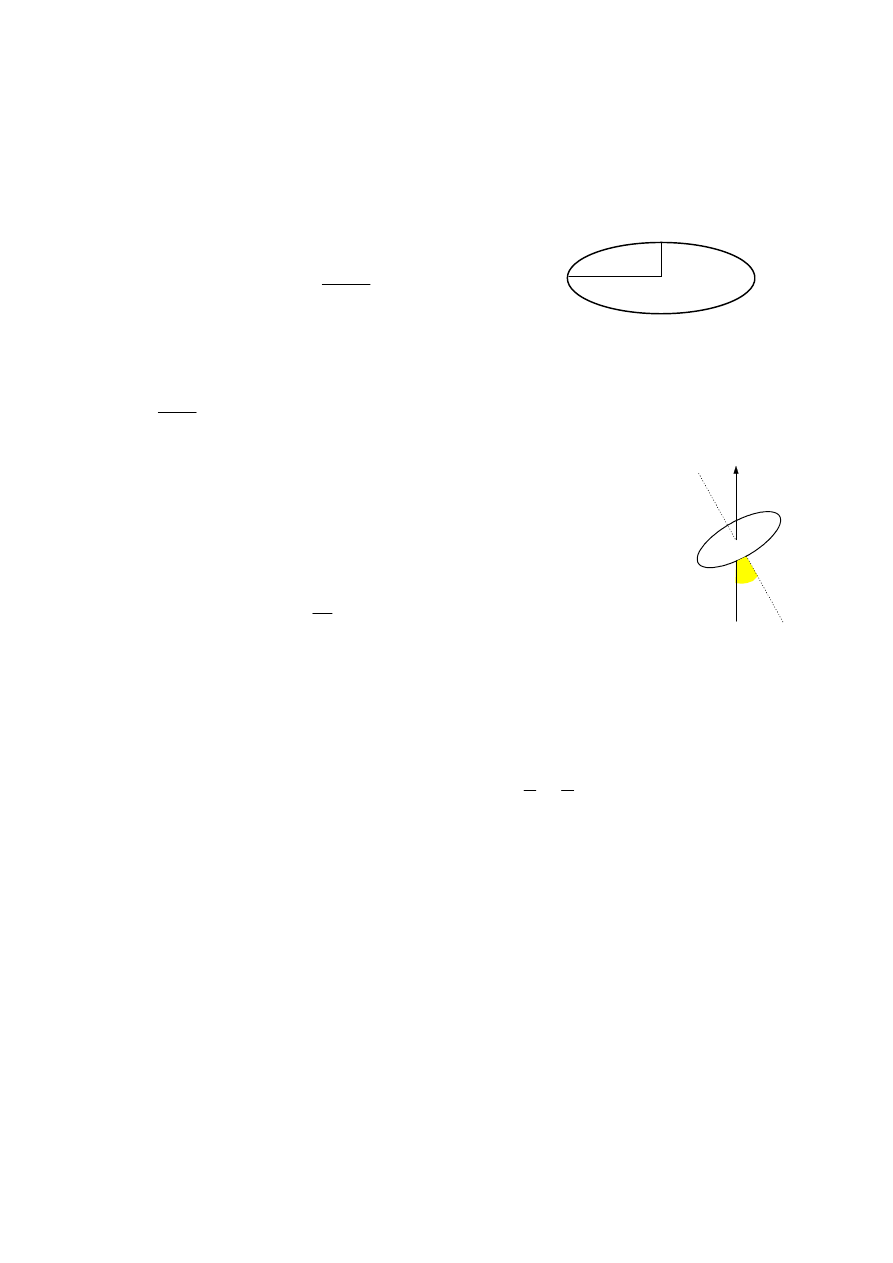
W wyniku wprowadzenia orbit eliptycznych, główna liczba kwantowa określa
wielkość dużej półosi orbity eliptycznej.

m

ke

n

a

2

2

2

h

====

Wielkość małej półosi określa tzw. poboczna, lub orbitalna liczba kwantowa (l).

b

a

l

n

====

++++

1

;

l

∈

∈

∈

∈

{0, 1, 2 … n-1}

Jeśli atom znajduje się w polu magnetycznym, to poszczególne orbity ustawiają
się pod pewnym kątem w stosunku do kierunku pola. Ustawienie
nie jest dowolne i określa je tzw. magnetyczna liczba kwantowa
(m).

cos

αααα ====

m

l

; m

∈

∈

∈

∈

{-l, …0 … +l}

Oprócz ruchu obiegowego, każdy elektron porusza się ruchem wirowym wokół
własnej osi. Moment pędu związany z ruchem wirowym określa spinowa liczba
kwantowa (s).

h

s

L

s

====

;

s

∈

∈

∈

∈ −−−− ++++













1

2

1

2

,

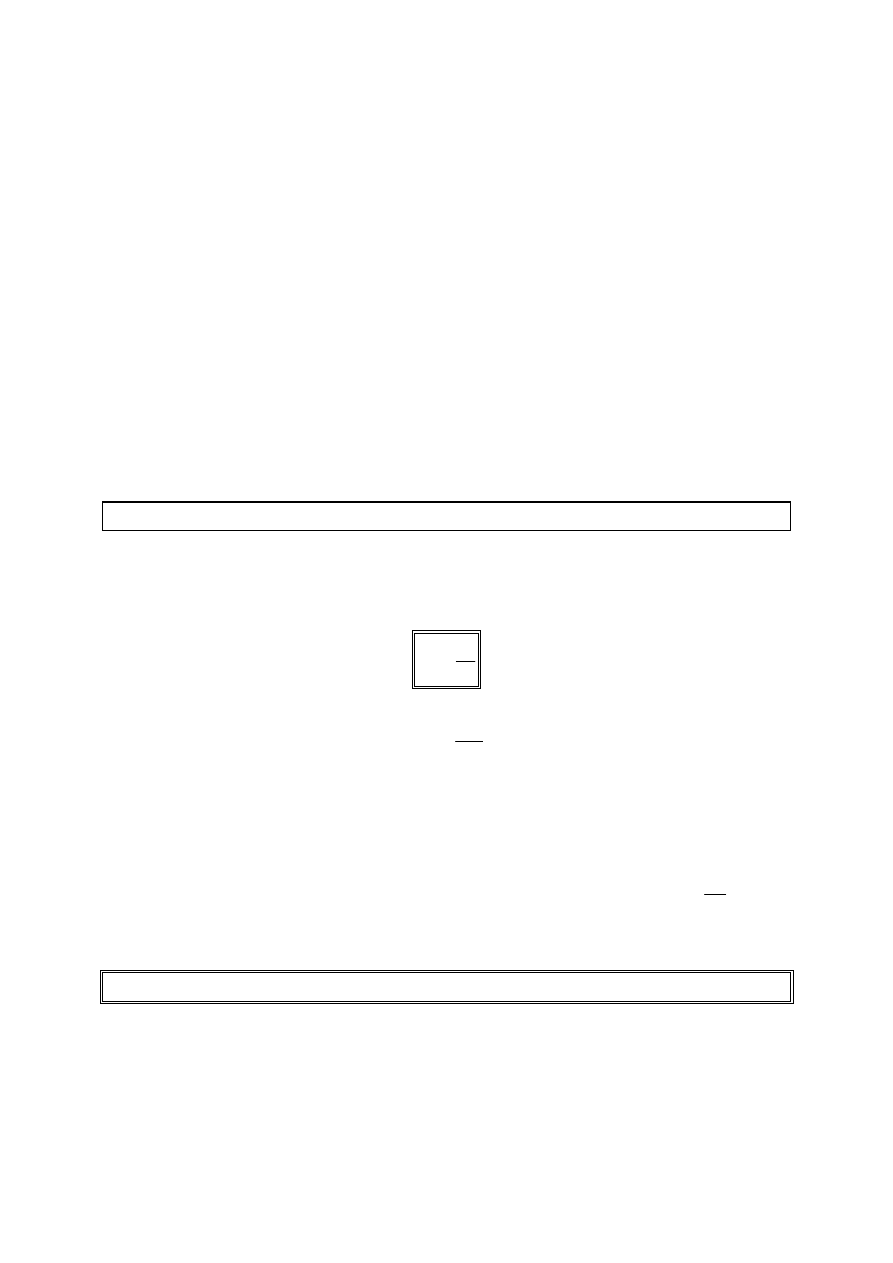
9. Zakaz Pauliego. Budowa powłok elektronowych.

Stan elektronu krążącego wokół jądra atomowego można określić przy użyciu
czterech liczb kwantowych. Zgodnie z zakazem Pauliego, w obrębie jednego
atomu mogą znaleźć się elektrony różniące się co najmniej jedną liczbą
kwantową. Przyjęcie tej zasady tłumaczy budowę powłok elektronowych.
Elektrony krążące wokół jądra atomowego poruszają się po orbitach o różnych
rozmiarach i kształcie, różnie ustawionych w przestrzeni. Elektrony wirują
także wokół własnej osi. Zbiór orbit o jednakowej wartości dużej półosi, ale o
różnych kształtach i różnie ustawionych w przestrzeni tworzy powłokę
elektronową. Kolejne powłoki są oznaczane: K, L, M, N, …

b

a

r

B

α

αα

α

61

Powłoka K

n = 1

⇒

⇒

⇒

⇒

l

∈

∈

∈

∈

{ 0 }

l = 0

⇒

⇒

⇒

⇒

m

∈

∈

∈

∈

{ 0 }

s

∈

∈

∈

∈ −−−− ++++













1

2

1

2

,

W powłoce K mogą znaleźć się tylko dwa elektrony.

Powłoka L

n = 2

⇒

⇒

⇒

⇒

l

∈

∈

∈

∈

{ 0 , 1}

l = 0

⇒

⇒

⇒

⇒

m

∈

∈

∈

∈

{ 0 }

l = 1

⇒

⇒

⇒

⇒

m

∈

∈

∈

∈

{ -1 , 0 +1}

W powłoce L może znaleźć się 8 elektronów. Tworzą one dwie powłoki.
Przez podpowłokę rozumiemy zbiór orbit o jednakowych rozmiarach i kształcie,
lecz różnie zorientowanych w przestrzeni. Kolejne podpowłoki oznaczamy: s
(sharp), p (principal), d (diffuse), f (fundamental).

Powłoka M

n = 3

⇒

⇒

⇒

⇒

l

∈

∈

∈

∈

{ 0 , 1 , 2}

l = 0

⇒

⇒

⇒

⇒

m

∈

∈

∈

∈

{ 0 }

l = 1

⇒

⇒

⇒

⇒

m

∈

∈

∈

∈

{ -1 , 0 +1}

l = 2

⇒

⇒

⇒

⇒

m

∈

∈

∈

∈

{ -2 ,-1 , 0 +1 +2}

K

l = 0

m = 0

n = 1

s

==== −−−−

++++

1

2

1

2

L

n = 2

m = 0 -1 0

1

l = 0

1

{

4

4 3

4

4 2

1

p

s

s

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

{

4

4

4

4

3

4

4

4

4

2

1

4

4 3

4

4 2

1

d

p

s

s

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

M

n = 2

m = 0 -1 0

1 -2 -1 0 1 2

l = 0

1

2

62

W powłoce M może znaleźć się 18 elektronów. Tworzą one trzy podpowłoki.
Energię elektronu określa główna liczba kwantowa, ale jeśli atom znajduje się
w polu magnetycznym to poszczególne orbity wykonują ruchy precesyjne, z
którymi jest także związana pewna energia. Wpływ na energię ma również
magnetyczna i spinowa liczba kwantowa. Ma to istotne znaczenie w przypadku
dalekich powłok. Już dla potasu energia stanu 4s jest mniejsza od energii stanu
3d. Oznacza to, że energia elektronu znajdującego się w powłoce N może być
mniejsza jak w powłoce M. Model atomu Bohra, nawet po wprowadzeniu orbit
eliptycznych nie tłumaczy takich zjawisk jak np. zjawisko nadprzewodnictwa,
nadciekłości, czy efekt tunelowy w półprzewodnikach. Do wyjaśnienia tych
zjawisk jest używany model falowy atomu opracowany w latach dwudziestych
naszego stulecia. Jest to model matematyczny i jego wadą jest to, że nie
pozwala na poglądowe wyjaśnienie zjawisk atomowych. Z tego względu model
atomu Bohra jest ciągle używany. Modelu atomu nie wolno jednak utożsamiać z
atomem.

Pojemność elektryczna

Miarą pojemności elektrycznej przewodnika jest stosunek ładunku skupionego
na przewodniku do potencjału tego przewodnika.

C

Q

V

====

1

1

1

F

C

V

====

Przewodnik ma pojemność elektryczną jednego farada, jeśli ładunek 1 C
umieszczony na powierzchni tego przewodnika wytwarza potencjał 1 V.

1mF = 10

-3

F

1nF =10

-9

F 1 cm =

9

10

pF

1F = 10

-6

F

1pF = 10

-12

F

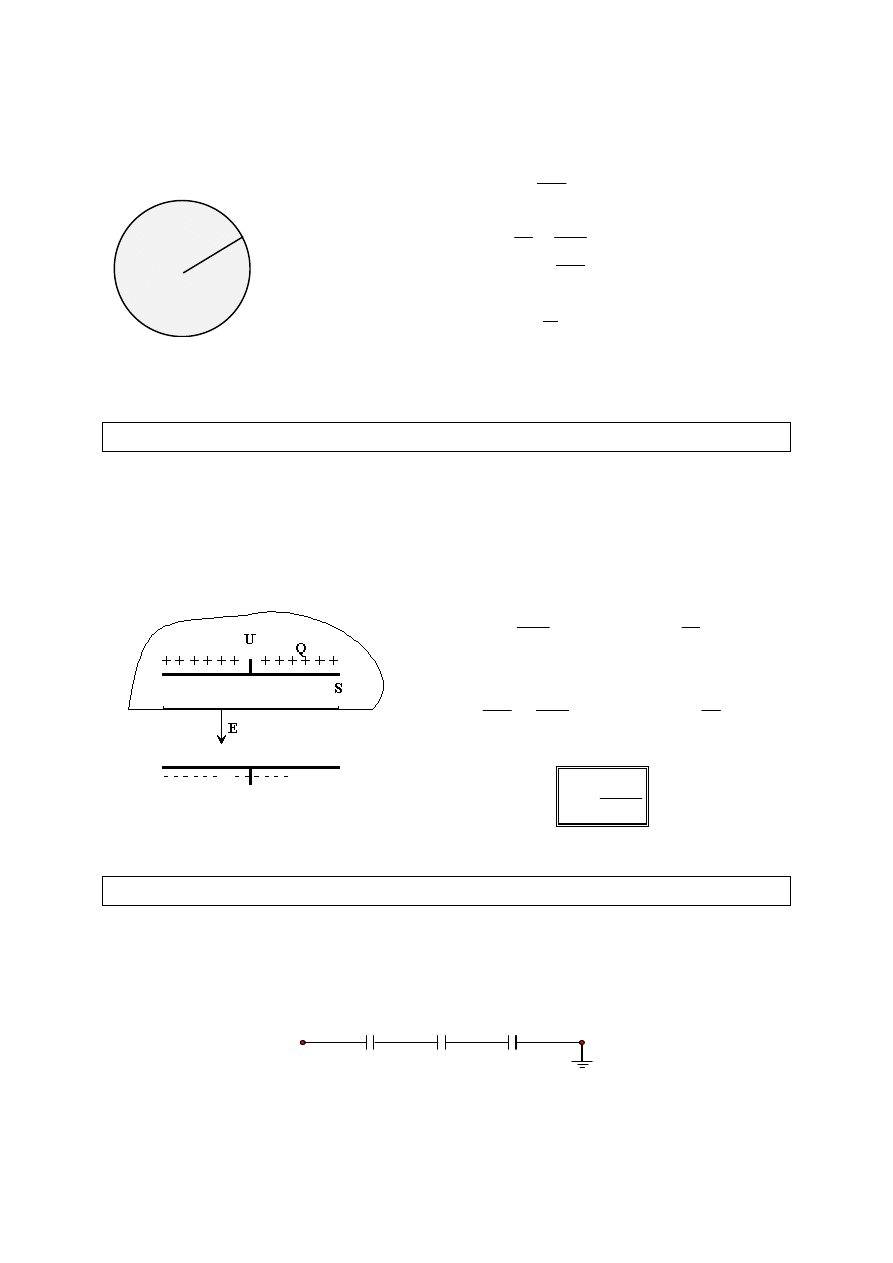
Pojemność elektryczna kuli

63

Ładunek elektryczny kuli wytwarza takie pole elektryczne jak ładunek
punktowy umieszczony w jej centrum.

r

kQ

V

====

k

r

C

r

kQ

Q

V

Q

C

====

====

====

Pojemność elektryczna kuli jest wprost proporcjonalna do jej promienia.

Pojemność kondensatora płaskiego

Kondensator płaski stanowią dwie płaskie, równoległe płyty umieszczone w
odległości wzajemnej d. Naładowany kondensator wytwarza pole elektryczne
jedynie w przestrzeni między płytami. Stosując prawo Gaussa dla powierzchni
zamykającej ładunek jednej z płyt, otrzymujemy:

ES

Q

E

U

d

====

====

εε

εε

εε

εε

0

;

US

d

Q

C

Q

U

====

====

εε

εε

εε

εε

0

;

C

S

d

====

εε

εε

εε

εε

0

Szeregowe łączenie kondensatorów

Cechą charakterystyczną łączenia szeregowego kondensatorów jest jednakowy
ładunek elektryczny na okładkach każdego kondensatora.

C

2

C

3

C

1

Q

Q

Q

-

+

-

+

-

+

Napięcie na okładkach baterii kondensatorów jest równe sumie napięć na
okładkach poszczególnych kondensatorów.

Q

V

r

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

+

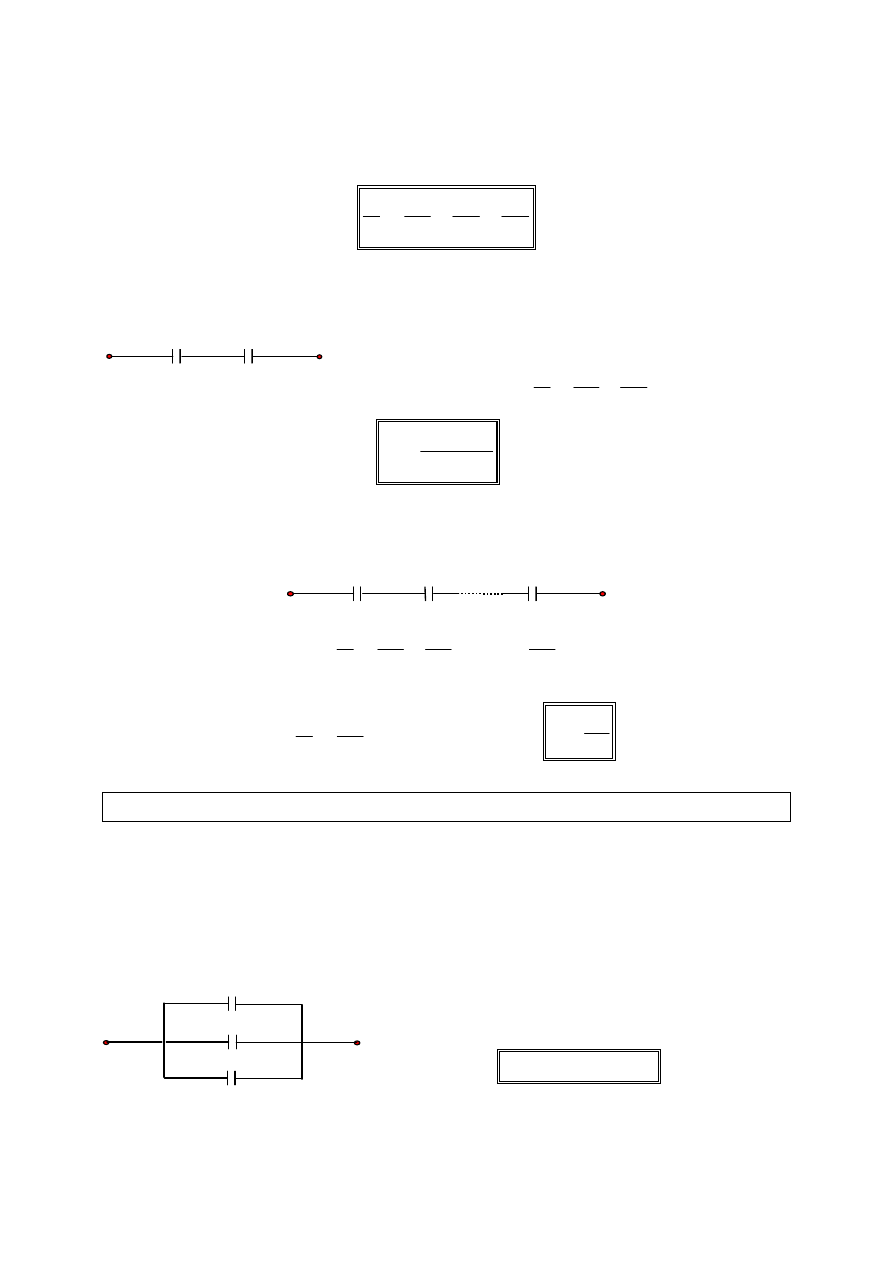
64

U = U

1

+ U

2

+ U

3

|: Q

1

1

1

1

1

2

3

C

C

C

C

====

++++

++++

W przypadku dwóch kondensatorów połączonych szeregowo otrzymujemy:

C

2

C

1

2

1

C

1

C

1

C

1

++++

====

C

C C

C

C

====

++++

1

2

1

2

W przypadku n jednakowych kondensatorów o pojemności C

1

każdy,

połączonych szeregowo otrzymujemy:

C

1

C

1

C

1

1

1

1

1

1

1

1

C

C

C

C

====

++++

++++ ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ ++++

1

1

C

n

C

====

⇒

⇒

⇒

⇒

n

C

C

1

====

Równoległe łączenie kondensatorów

Cechą charakterystyczną tego połączenia jest jednakowe napięcie na okładkach
każdego kondensatora. Ładunek na okładkach baterii kondensatorów
połączonych równolegle jest sumą ładunków na okładkach poszczególnych
kondensatorów.

Q = Q

1

+ Q

2

+ Q

3

|:U

C

C

C

C

====

++++

++++

1

2

3

C

2

C

3

C

1

Q

3

Q

2

Q

1

-

+

-

+

-

+

65

Kondensator wielookładkowy

Pomiędzy płytkami takiego kondensatora istnieje pole elektryczne.
Jeśli kondensator liczy n płyt, to istnieje n -1 obszarów pola elektrycznego.

Kondensator taki można traktować

jak n-1 kondensatorów połączonych równolegle. Jego pojemność wynosi:

((((

))))

C

n

S

d

====

−−−−

1

0

εεεε

Energia naładowanego kondensatora

Okładki kondensatora o pojemności C mają ładunek q. Przeniesienie ładunku
dq podczas ładowania takiego kondensatora wymaga pracy dw:

dW = dq

⋅⋅⋅⋅

u

u

C

q

====

1

Zależność napięcia na okładkach kondensatora od zgromadzonego na nich
ładunku jest funkcją liniową. Miarą pracy elementarnej jest pole wąskiego
prostokąta pod wykresem u(q). Praca wykonana podczas ładowania
kondensatora ładunkiem Q stanowi sumę prac elementarnych i odpowiada jej
pole trójkąta pod wykresem u(q).

W

QU

====

2

;

C

Q

U

====

W

Q

C

====

2

2

W

CU

====

2

2

(n = 5)

66

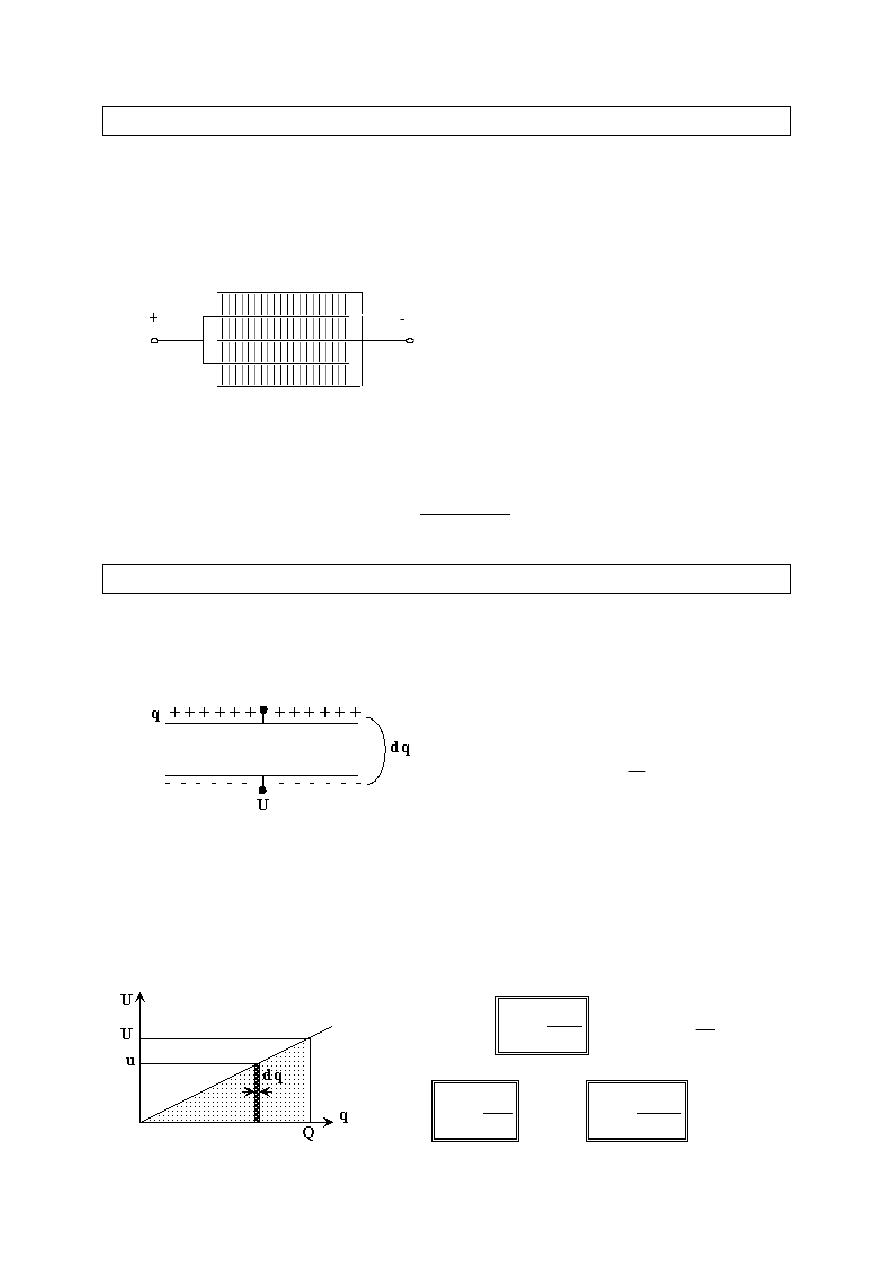
Polaryzacja dielektryka

Kondensator próżniowy ma pojemność Co i po naładowaniu ładunkiem Qo,
między jego okładkami jest napięcie Uo, natężenie pola elektrycznego Eo i
indukcja elektryczna Do.

Wsunięcie dielektryka między okładki takiego kondensatora powoduje
polaryzację. Jeśli dielektryk zawiera cząsteczki stanowiące dipole elektryczne,
to w wyniku obrotów tych dipoli, na powierzchniach dielektryka sąsiadujących
z okładkami wyindukują się odpowiednie ładunki. Parametry kondensatora
zmienią się na C, Q, U, E i D.

Przyjmując założenie, że ładunek kondensatora nie uległ zmianie (Qo = Q),
otrzymujemy:

E = Eo - E'

(((( ))))

E

E

r

0

==== εεεε

εεεε



r

- względna przenikalność elektryczna (stała dielektryczna) dielektryka

E

E

====

1

0

0

εεεε

Umieszczenie dielektryka między okładkami kondensatora powoduje zatem
zmniejszenie natężenia pola elektrycznego.

E

U

d

====

;

E

U

d

0

0

====

⇒

⇒

⇒

⇒

U

d

U

d

====

1

0

0

εεεε

⇒

U

U

====

1

0

εεεε

Obecność dielektryka powoduje zatem zmniejszenie napięcia między płytami
kondensatora.

- - - - - - - - - - - - - - - - - -

+ + + + + + + + + + + + +

Q

0

C

0

U

0

D

0

E

0

- - - - - - - - - - - - - - - - - -

+ + + + + + + + + + + + +

Q

C

U

D

E’

E

0

+

-

67

C

S

d

====

εε

εε

εε

εε

0

;

C

S

d

0

0

====

εεεε

⇒

⇒

⇒

⇒

C

C

==== εεεε

0

Dielektryk powoduje wzrost pojemności elektrycznej kondensatora.

D =

εεεεεεεε

0

E

;

D

0

=

εεεε

0

E

⇒

⇒

⇒

⇒

D

D

====

0

Dielektryk nie powoduje zmiany indukcji elektrycznej między okładkami
kondensatora.
Jeśli dielektryk nie zawiera dipoli elektrycznych, to pod wpływem pola
elektrycznego powstają tzw. dipole indukowane. Tworzą się one w wyniku
przesunięcia chmury elektronowej atomu względem jądra atomowego.
Analogicznie, przyjmując że U = Uo otrzymujemy:

E = Eo ;

Q =

εεεε

Qo ;

C =

εεεε

Co ;

D =

εεεε

D

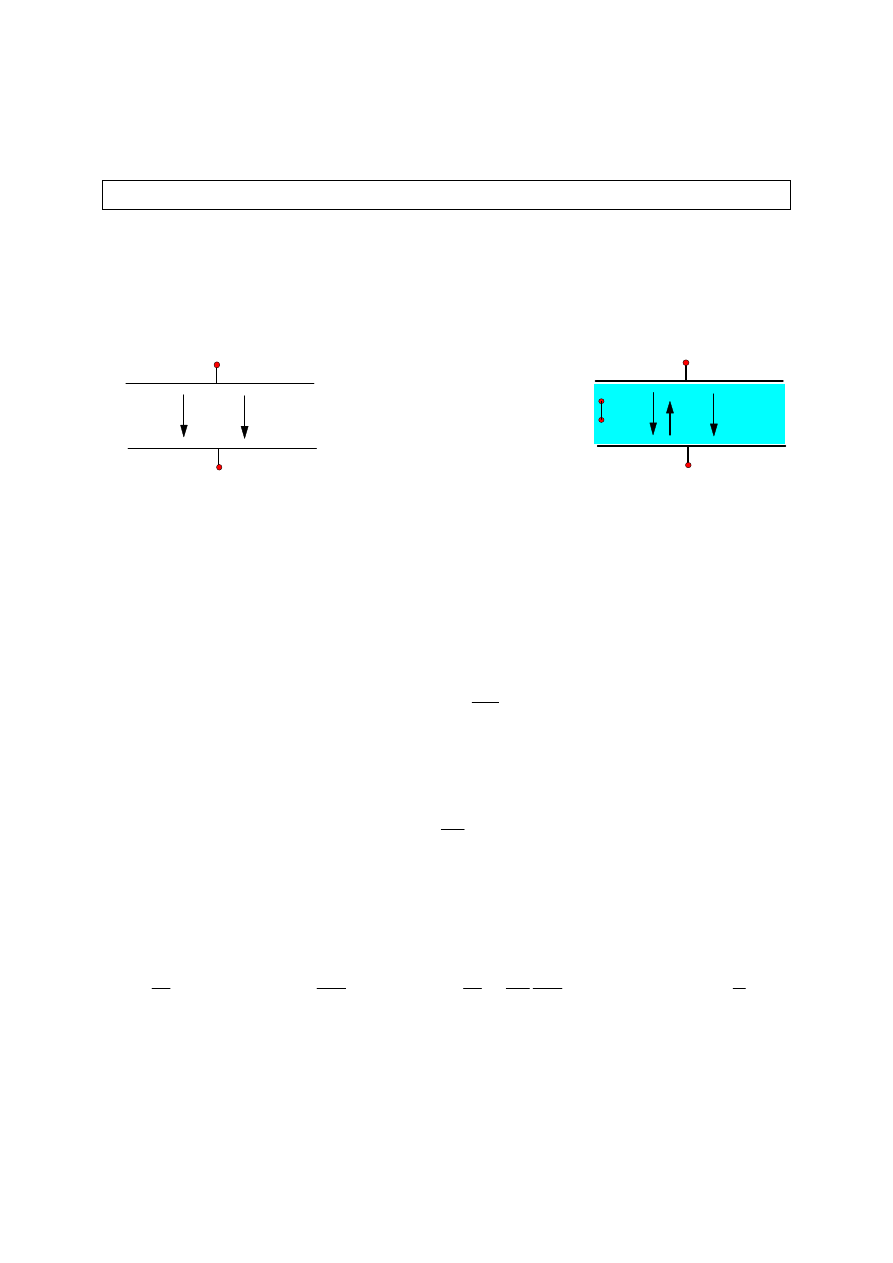
Ruch ładunku w polu elektrycznym

Na ładunek umieszczony w polu elektrycznym o natężeniu E działa siła:

F = qE

Jeśli pole to jest jednorodne (np. między okładkami kondensatora płaskiego), to
siła działająca na ładunek wynosi:

F

q

U

d

====

Pod wpływem tej siły ładunek uzyskuje przyspieszenie:

a

qE

m

qU

dm

====

====

Praca wykonana przez pole elektryczne jest równa energii kinetycznej
przyspieszonego ładunku.

68

qU

mV

====

2

2

⇒

⇒

⇒

⇒

V

qU

m

====

2

Powyższa zależność może być stosowana tylko wtedy, gdy prędkość uzyskana
przez ładunek jest znacznie mniejsza od prędkości światła w próżni.

c = 3 . 10

8

m

s

Przy większych napięciach należy stosować zależność relatywistyczną:

((((

))))

qU

m c

k

====

⋅⋅⋅⋅

−−−−

0

2

1

gdzie m

0

- masa spoczynkowa cząstki

k

v

c

====

−−−−











1

1

2

- współczynnik relatywistyczny

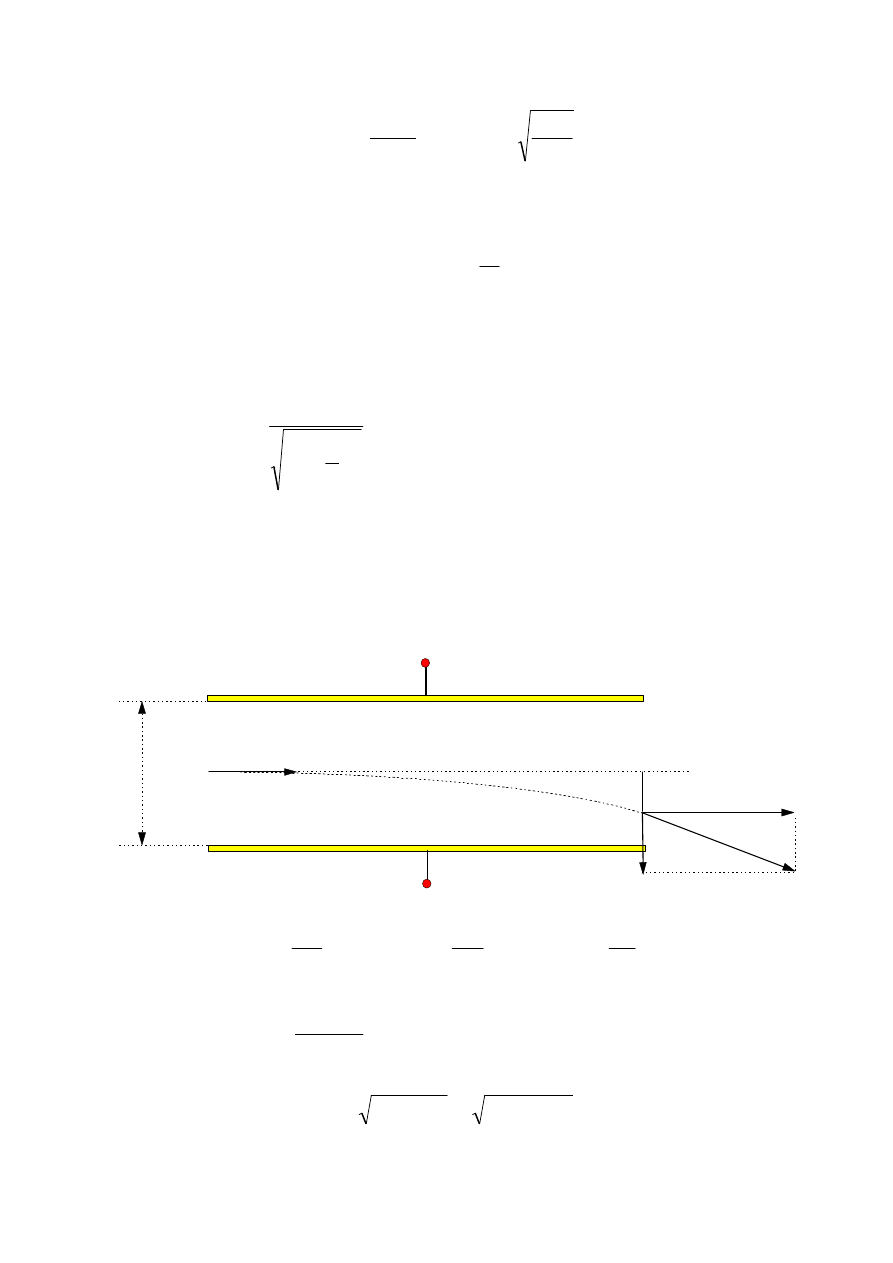
Jeśli ładunek wpada w obszar pola elektrycznego między okładkami płaskiego
kondensatora, poruszając się prostopadle do linii sił tego pola, to ruch takiego
ładunku jest złożony. Przy stałej prędkości skierowanej prostopadle do linii sił
pola ładunek uzyskuje rosnącą prędkość skierowaną wzdłuż linii sił pola, w
wyniku czego porusza się on po torze parabolicznym, doznając odchylenia (x).

x

at

a

qU

dm

t

l

V

====

====

====

2

0

2

;

;

x

qUl

dmV

====

2

0

2

2

-

odchylenie ładunku

V

V

V

a t

V

====

++++

====

++++

1

2

2

2

2 2

0

2

V

0

V

V

1

x

l

U

V

0

d

69

V

q U l

d m V

V

====

++++

2

2 2

2

2

0

2

0

2

-

prędkość końcowa