Geoinformatyka

Ćwiczenie 3
Odwzorowania kartograficzne i systemy odniesień
przestrzennych

Opracowanie: Mateusz Troll
[e-mail]

Zakład Systemów Informacji Geograficznej, Kartografii i Teledetekcji
Instytut Geografii i Gospodarki Przestrzennej UJ

Kraków 2009

2

Wprowadzenie

Konstrukcja odwzorowań oparta jest na regułach matematycznych. Reguły opracowane przez kartografów mogą
być obecnie łatwo zastosowane w programach komputerowych, zarówno kartograficznych (jak np. Flex
Projector) jak i programach z rodziny GIS (np. ArcGIS). Dlatego nie ma potrzeby abyśmy konstruowali siatki
kartograficzne manualnie – komputery zrealizują to zadanie znacznie szybciej i lepiej niż ludzie pod warunkiem,
że zostaną umiejętnie wykorzystane ☺ Aby w pełni wykorzystać do tego celu możliwości komputerów należy
mieć przygotowanie teoretyczne w zakresie teorii odwzorowań i zniekształceń (ten warunek należało spełnić
przed ćwiczeniami) oraz posiadać umiejętności praktyczne – ich nabycie jest celem ćwiczenia.

Wymagania wstępne

Znajomość pojęć:

sfera, siatka geograficzna, współrzędne geograficzne

koło wielkie, ortodroma, loksodroma

system odniesienia, elipsoida, współrzędne geodezyjne (elipsoidalne)

układ współrzędnych prostokątnych płaskich

odwzorowanie azymutalne, walcowe, stożkowe, umowne

odwzorowanie równokątne, równopolowe i równodługościowe

współczynnik skali, ekwideformata

koło elementarne, elipsa zniekształceń

Zalecana jest znajomość najważniejszych własności odwzorowań:

odwzorowanie kwadratowe (walcowe proste)

odwzorowanie walcowe wiernokątne Merkatora

odwzorowanie walcowe wiernokątne UTM i Gaussa-Krügera

układy współrzędnych: 1942, 1965, 1992 i 2000

odwzorowanie równopolowe Mollweidego

odwzorowanie stożkowe równokątne Lamberta (LCC)

odwzorowanie azymutalne równopolowe Lamberta (LAEA)

Po zrealizowaniu ćwiczenia będziecie umieli:

ocenić zniekształcenia odwzorowawcze w najczęściej stosowanych odwzorowaniach,

skorzystać z gotowych definicji odwzorowań i układów współrzędnych dostępnych w programach GIS,

wprowadzić pożądane parametry odwzorowania wraz z pozostałymi elementami definicji systemu odniesień
przestrzennych w jakim opracowana jest mapa, bądź do jakiego mapa ma być transformowana,

przeprowadzić transformację odwzorowania, układu współrzędnych, układu odniesienia bądź całego
systemu odniesień przestrzennych.

CZĘŚĆ 1. WSPÓŁRZĘDNE GEOGRAFICZNE I PROSTOKĄTNE PŁASKIE NA
PRZYKŁADZIE ODWZOROWANIA WALCOWEGO PROSTEGO

Odwzorowanie kartograficzne to umowny, określony matematycznie sposób jednoznacznego przypisania każdej
parze współrzędnych geodezyjnych pary współrzędnych płaskich (Ogorzelska 2006). Współrzędne geodezyjne,
nazywane czasem geograficznymi współrzędnymi geodezyjnymi będziemy w niniejszym ćwiczeniu określać dla
uproszczenia mianem współrzędnych geograficznych, pamiętając przy tym, że mogą one być opisane na
elipsoidzie lub na sferze.

Zasadę odwzorowania kartograficznego, a więc przypisania parze współrzędnych geograficznych pary
współrzędnych prostokątnych płaskich, poznamy na przykładzie odwzorowania walcowego prostego. W
odwzorowaniu tym najprostszym sposobem wyprowadzenia wzorów wiążących współrzędne geograficzne z
prostokątnymi płaskimi jest proporcja opisująca związek kąta środkowego (α) z długościami łuku okręgu
wyznaczonego przez ramiona tego kąta (L), dla kuli o promieniu R:

°

=

° 360

2 R

L

π

α

3

Z proporcji tej otrzymujemy wzór na L:

°

°

=

180

α

π

R

L

Zadanie 1
Oblicz długości łuku koła wielkiego (południka) dla α° = φ = 30° i R = 6371 km.

?

Jaka będzie długość łuku koła wielkiego dla α° =

Δλ = 30°? Co to za koło wielkie?

W wyniku odwzorowania sfery (lub elipsoidy) na płaszczyznę współrzędne geograficzne transformowane są na
współrzędne prostokątne płaskie. W geodezji i kartografii operuje się układem prawoskrętnym natomiast w
systemach informacji geograficznej bardzo często stosuje się układ matematyczny lewoskrętny.

!

Korzystając z instrukcji geodezyjnych przy wprowadzaniu parametrów układu do programu GIS

zamieniamy x z y!

Obliczanie współrzędnych prostokątnych płaskich punktu na podstawie jego współrzędnych
geograficznych – a więc odwzorowanie punktu P na punkt P’ na przykładzie odwzorowania walcowego
prostego (równodługościowego, kwadratowego).

Rozpatrzymy przypadek odwzorowania walcowego w położeniu normalnym, a więc kiedy walec jest styczny
wzdłuż równika:

obrazami południków i równoleżników są w takim przypadku zawsze linie proste prostopadłe względem
siebie,

obrazy południków mają długości wierne oryginałom, czyli

πR

odległości między nimi są jednakowe i odpowiadają odległościom na równiku, a więc można je obliczyć ze
wzoru na długość łuku koła wielkiego:

°

°

Δ

=

180

λ

π

R

y

gdzie:

Δλ jest różnicą długości geograficznej pomiędzy południkiem środkowym odwzorowania (np. 0°)
a południkiem punktu P

wszystkie równoleżniki (i obydwa bieguny) mają długość równą długości równika, czyli 2

πR

odległości między równoleżnikami są jednakowe i zgodne z oryginałem; oznacza to, że odległość obrazu
równoleżnika o szerokości φ od równika odpowiada długości łuku południka pomiędzy równikiem a
szerokością φ, zgodnie ze wzorem:

°

°

=

180

ϕ

π

R

x

Dla każdego φ =

Δλ mamy x = y a więc siatka kartograficzna tworzy siatkę kwadratów.

!

Dla

półkuli W i S współrzędne geograficzne i prostokątne płaskie mają znak ujemny!

Konstrukcja siatki odwzorowania walcowego prostego (równodługościowego) sprowadza się więc do
narysowania siatki kwadratów o wymiarach 2

πR × πR w przyjętej skali oraz przyjętej wielkości oczka siatki

geograficznej.

Zadanie 2
Oblicz współrzędne x, y w odwzorowaniu walcowym prostym dla dwóch punktów o współrzędnych P

1

(φ = 50°N,

λ = 20°E) i P

2

(50°S, 20°W). Południkiem środkowym jest południk początkowy 0°. Pamiętaj aby

współrzędne x, y wyrazić w metrach!
Następnie przelicz te współrzędne przyjmując, że mapa ma skalę 1:100 000 000 a współrzędne wyrażone są w
cm. R = 6371 km

4

Zadanie ilustruje zależność wartości współrzędnych prostokątnych płaskich od wartości R - należy
rozróżniać współrzędne prostokątne płaskie związane z danym układem, które są obliczane dla rzeczywistego R
kuli ziemskiej (względnie dla rzeczywistych parametrów elipsoidy odniesienia) – z takimi współrzędnymi
spotykamy się na mapach papierowych i w systemach informacji geograficznej – od współrzędnych obliczonych
dla R w konkretnej skali mapy – z takimi współrzędnymi mamy do czynienia podczas manualnej konstrukcji
siatki.

Uwaga: odwzorowanie walcowe proste jest jedynym przypadkiem odwzorowania, w którym obydwa układy
współrzędnych – geograficznych i prostokątnych płaskich mają identyczną geometrię. Inaczej mówiąc siatka
kartograficzna jest przedstawiona w układzie współrzędnych prostokątnych płaskich.

CZĘŚĆ 2. WIZUALIZACJA ODWZOROWAŃ I ROZKŁADU ZNIEKSZTAŁCEŃ;
TRANSFORMACJE ODWZOROWAŃ

CZĘŚĆ 2A ĆWICZENIA W PROGRAMIE FLEX PROJECTOR

Wprowadzenie

Program Flex Projector jest darmowym programem kartograficznym umożliwiającym wizualizację odwzorowań
wraz z rozkładem zniekształceń, a także samodzielne projektowanie odwzorowań dla świata. Autorem programu
jest Bernhard Jenny z Instytutu Kartografii ETH w Zurychu. Program jest dostępny na stronie

http://www.flexprojector.com

.

!

Program wymaga instalacji Javy

1. Uruchom program Flex Projector.

Domyślnie program wyświetla mapę świata w odwzorowaniu Robinsona, które zainspirowało autora do
napisania programu Flex Projector (

http://www.flexprojector.com/about.html

). Zapoznamy się z niektórymi

narzędziami programu zaczynając pracę od zmiany odwzorowania na znane nam już odwzorowanie walcowe
równodługościowe.

2. Zmień odwzorowanie wybierając ikonę Options (po prawej u góry); w wyświetlonym menu wybierz

Reset to Projection

a następnie w wykazie odwzorowań znajdź Equidistant Cylindrical (Plate

Carrée).

3. Zmień zakładkę po prawej stronie z Flex Projection na Display; okno programu powinno

wyglądać jak na rycinie poniżej (ryc. 3.1).

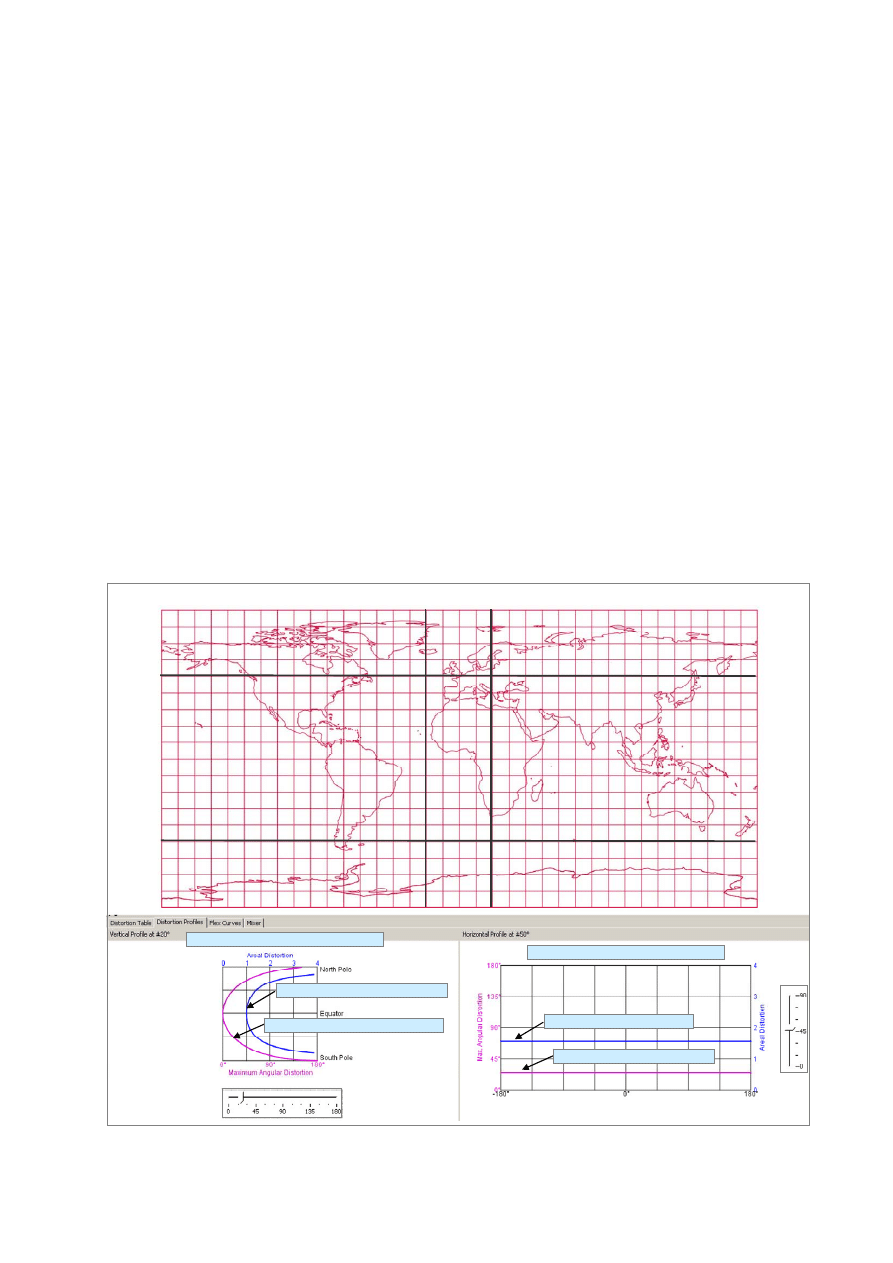
Ryc. 3.1. Wybrane narzędzia programu Flex Projector

współrzędne

geogr.

współrzędne

płaskie

aktualna

skala mapy

zniekształcenie pow.

zniekształcenie kątów

południk środkowy

siatka geogr. i jej gęstość

elipsy zniekształceń i ich gęstość

ekwideformaty pow. i ich interwał

ekwideformaty kątów i ich interwał

obszar akceptowalnych zniekształceń

wybrane

odwzorowania

średnie ważone zniekształceń dla całego globu i dla lądów (Cont.):

skali powierzchni kątów

powierzchnia obszaru akceptowalnych zniekształceń (%)

5

4. Zmień gęstość siatki geograficznej z 30 na 10° a następnie powiększ mapę w okolicach Krakowa i ustaw się

kursorem w miejscu przecięcia się południka 20°E i równoleżnika 50°N – odczytaj współrzędne prostokątne
płaskie i porównaj jej z wynikami obliczeń w zadaniu 2.

?

W którym miejscu w tym odwzorowaniu współrzędne geograficzne mają takie same wartości, jak

współrzędne prostokątne płaskie?

5. Wyświetl elipsy zniekształceń Tissota – zostaną one wyświetlone dla węzłów siatki geogr. zgodnie z

domyślą gęstością (30°); zinterpretuj przestrzenny rozkład zniekształceń.

6. Wyświetl ekwideformaty powierzchni zmieniając interwał izolinii równych zniekształceń na 1; zinterpretuj

rozkład przestrzenny zniekształceń powierzchni.

7. Wyświetl ekwideformaty kątowe zmieniając interwał izolinii równych zniekształceń na 30°; zinterpretuj

rozkład przestrzenny zniekształceń kątów.

8. Sprawdź jaki obszar globu posiada w tym odwzorowaniu akceptowalne zniekształcenia kątów i powierzchni

przyjmując domyślne maksymalne wartości zniekształceń, tj. 40° i 150% pow.; sprawdź, jakie
ekwideformaty wyznaczają faktyczne granice obszaru o dopuszczalnych zniekształceniach.

9. Sprawdź wartość średnią indeksu dopuszczalnych zniekształceń w tabeli zniekształceń (kolumna Acc.

40° i 150%); klikając dwukrotnie na nagłówek kolumny otwórz okno dialogowe Acceptance Index i
zmień wartości maksymalnych dopuszczalnych zniekształceń kątowych i powierzchniowych obserwując
zmiany indeksu w tabeli oraz zasięg obszaru o dopuszczalnych zniekształceniach na mapie.

10. Sprawdź pozostałe statystyki w tabeli zniekształceń skali, kątów i powierzchni – przedstawione jako średnie

ważone zniekształceń dla całego globu i osobno dla lądów (por. ryc. 3.1).

11. Sprawdź zmienność równoleżnikową i południkową zniekształceń kątowych i powierzchniowych

wybierając zakładkę Distortion Profiles (ryc. 3.2); ustaw suwaki na równoleżniku i południku
Krakowa (20°E i 50°N); zinterpretuj diagramy oraz powiąż wartości odczytane z diagramów z wartościami
wyświetlanymi nad mapą – w tym celu powiększ mapę tak, aby precyzyjnie wskazać kursorem myszy
przecięcie się południka 20°E z równoleżnikiem 50°N.

Ryc. 3.2. Południkowe i równoleżnikowe profile zniekształceń w programie Flex Projector

50°N

50°S

20°W 20°E

Profil równoleżnikowy (50°N/S)

stałe zniekształcenie pow.

stałe zniekształcenie kątowe

Profil południkowy (20°E/W)

zmienne zniekształcenie pow.

zmienne zniekształcenie kątowe

6

!

Wartość zniekształcenia powierzchni w programie Flex Projector jest wyrażana na kilka sposobów:

w tabeli zniekształceń (Distortion Table) brak zniekształceń wyraża wartość zero,

na profilach równoleżnikowych i południkowych (Distortion Profiles) brak zniekształceń wyraża
wartość 1,

na mapie wartość miejscowego zniekształcenia powierzchni (Area Dist.) wyrażana jest w procentach –
brak zniekształceń wyraża wartość 100%.

?

Które ze znanych Ci odwzorowań równopolowych i równokątnych możesz zidentyfikować na podstawie

informacji wyświetlanych w tabeli zniekształceń?

12. Zmień odwzorowanie na mapie z walcowego prostego na odwzorowanie Merkatora; odwzorowanie to jest

dostępne jedynie w zakładce Display, po zaznaczeniu Show Second Projection; odznacz
jednocześnie Show Flex Projection – inaczej mapa świata zostałaby wyświetlona w dwóch
odwzorowaniach jednocześnie.

13. Wyświetl ekwideformaty powierzchni a następnie kątów w odwzorowaniu Merkatora.

?

Dlaczego ekwideformaty kątów się nie wyświetlają? Jak to się odzwierciedla w kształtach elips

zniekształceń? Czym różni się więc odwzorowanie walcowe proste (kwadratowe) od odwzorowania
Merkatora?

14. Odznacz Show Second Projection a następnie w zakładce Flex Projection podstaw

odwzorowanie Mollweidego; na profilach zniekształceń sprawdź rozkład zniekształceń kątowych i
powierzchniowych.

?

Czy powierzchnie odwzorowują się wiernie w tym odwzorowaniu na całej kuli ziemskiej?

?

Odwzorowanie to jest często stosowane w polskich atlasach dla obrazowania zjawisk w skali globalnej. Czy

wiesz czym różni się wersja tego odwzorowania stosowane w Polsce od wersji, którą oglądasz obecnie na
monitorze?

15. Przejdź do zakładki Display, korzystając tym razem z możliwości zmiany południka środkowego z 0° na

10°.

?

Jaką zaletę ma odwzorowanie świata przy tak dobranym południku środkowym?

CZĘŚĆ 2B ĆWICZENIA W PROGRAMIE ARCGIS

Dane
Projekt o nazwie Swiat_Europa_Polska.mxd zawierający następujące mapy (warstwy):

Swiat_panstwa – mapa świata z siatką geograficzną (Swiat_siatka),

Europa_panstwa – mapa Europy z siatką geograficzną (Europa_siatka),

Polska – mapa Polski (w podziale na województwa) z siatką geograficzną (Polska_siatka),

Polska_2 – mapa Polski w innym układzie odniesienia,

Malopolska – mapa woj. małopolskiego (w podziale na gminy) z siatką geograficzną (Malopolska_siatka),

UTM_strefy – mapa podziału świata na strefy odwzorowawcze UTM.

Odwzorowania dla całego świata, które będziesz oglądać:

odwzorowanie „Geographic” często stosowane w zapisie cyfrowych danych geograficznych
udostępnianych w Internecie,

odwzorowanie równopolowe Mollweidego – popularne odwzorowanie atlasowe dla map świata.

1. Uruchom program ArcGIS; w ramce Start using ArcMap with: wybierz opcję An existing

map a następnie znajdź w katalogu roboczym plik projektu o nazwie Swiat_Europa_Polska.mxd i otwórz go
– wyświetlisz w ten sposób mapę świata w znanym Ci odwzorowaniu.

2. Sprawdź jakie współrzędne wyświetlają się w prawym dolnym narożniku okna mapy – zauważ, że nie są to

współrzędne prostokątne płaskie odwzorowania walcowego prostego, jakie obliczaliśmy i odczytywaliśmy
w programie Flex w części pierwszej ćwiczenia.

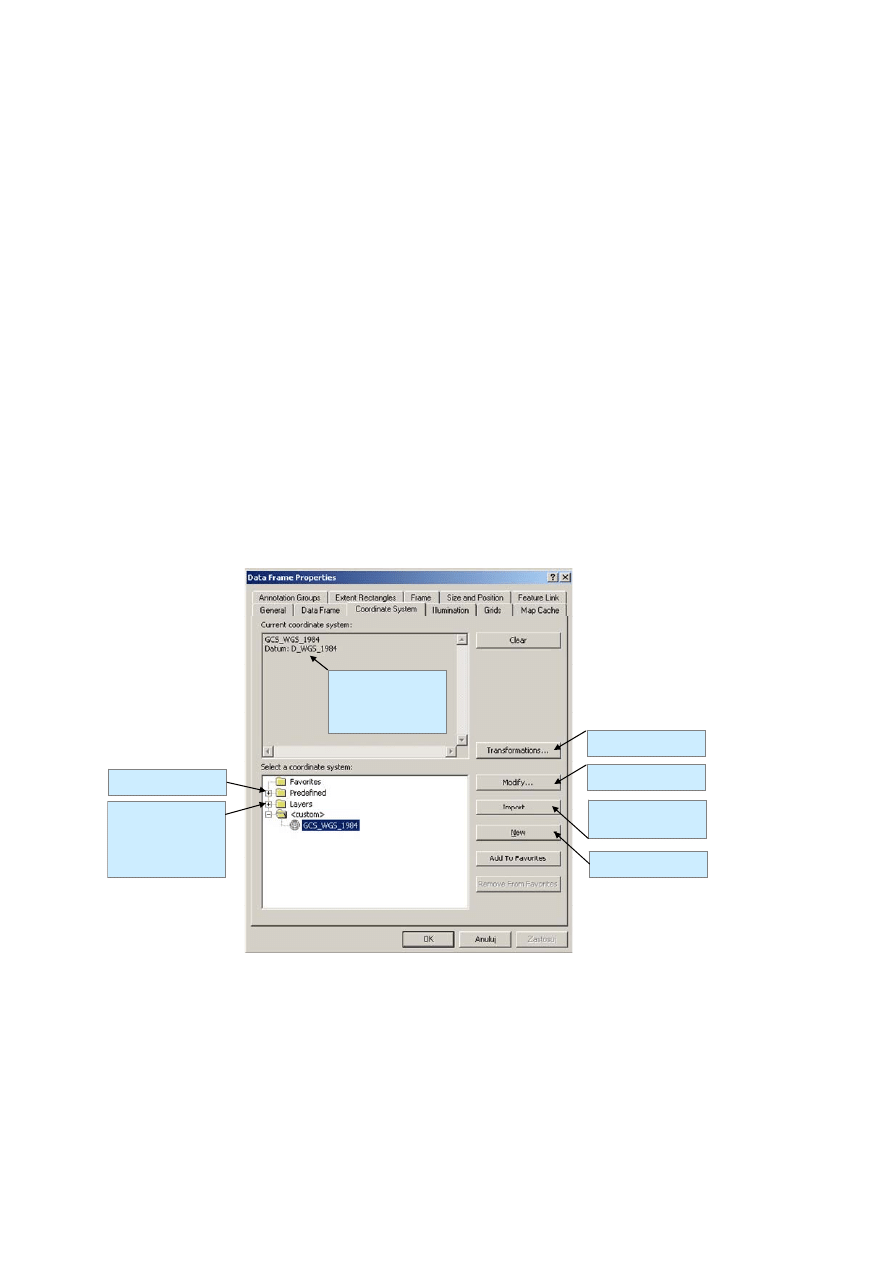
3. Sprawdź właściwości mapy świata wybierając PPKW (pod prawym klawiszem myszy) > Properties, a

następnie przejdź do zakładki Source; w wyświetlonej dokumentacji mapy znajdź informacje o systemie
odniesień przestrzennych:

7

Geographic Coordinate System: GCS_WGS_1984

Datum (układ odniesienia): D_WGS_1984

Prime Meridian (południk zerowy): Greenwich
Angular Unit (jednostka): Degree

Wynika z tego, że mapa zapisana jest w układzie geograficznych współrzędnych geodezyjnych, będących
współrzędnymi elipsoidalnymi (elipsoida WGS-84). Program wyświetlając taką mapę traktuje współrzędne
geograficzne jak współrzędne prostokątne płaskie – w ten sposób mapa wygląda identycznie, jak w przypadku
odwzorowania walcowego prostego.

!

Układ współrzędnych geograficznych jest często stosowany w zapisie danych udostępnianych w Internecie

– mapy wyglądają wówczas tak jak w odwzorowaniu walcowym prostym choć nie posiadają one informacji
o współrzędnych prostokątnych płaskich.

Mapę zapisaną w określonym odwzorowaniu można łatwo transformować do innego odwzorowania zmieniając
ustawienia w właściwościach okna projektu (Data Frame).

!

System

odniesień przestrzennych zdefiniowany w oknie Data Frame obowiązuje dla wszystkich warstw,

które są wyświetlone w projekcie.

4. Wyświetl właściwości okna projektu Properties, klikając dwukrotnie na nagłówek Layers w wykazie

warstw po lewej (Table of Contents).

5. W oknie właściwości wybierz zakładkę Coordinate System i zapoznaj się z opcjami dostępnymi w

tym oknie (ryc. 3.3).

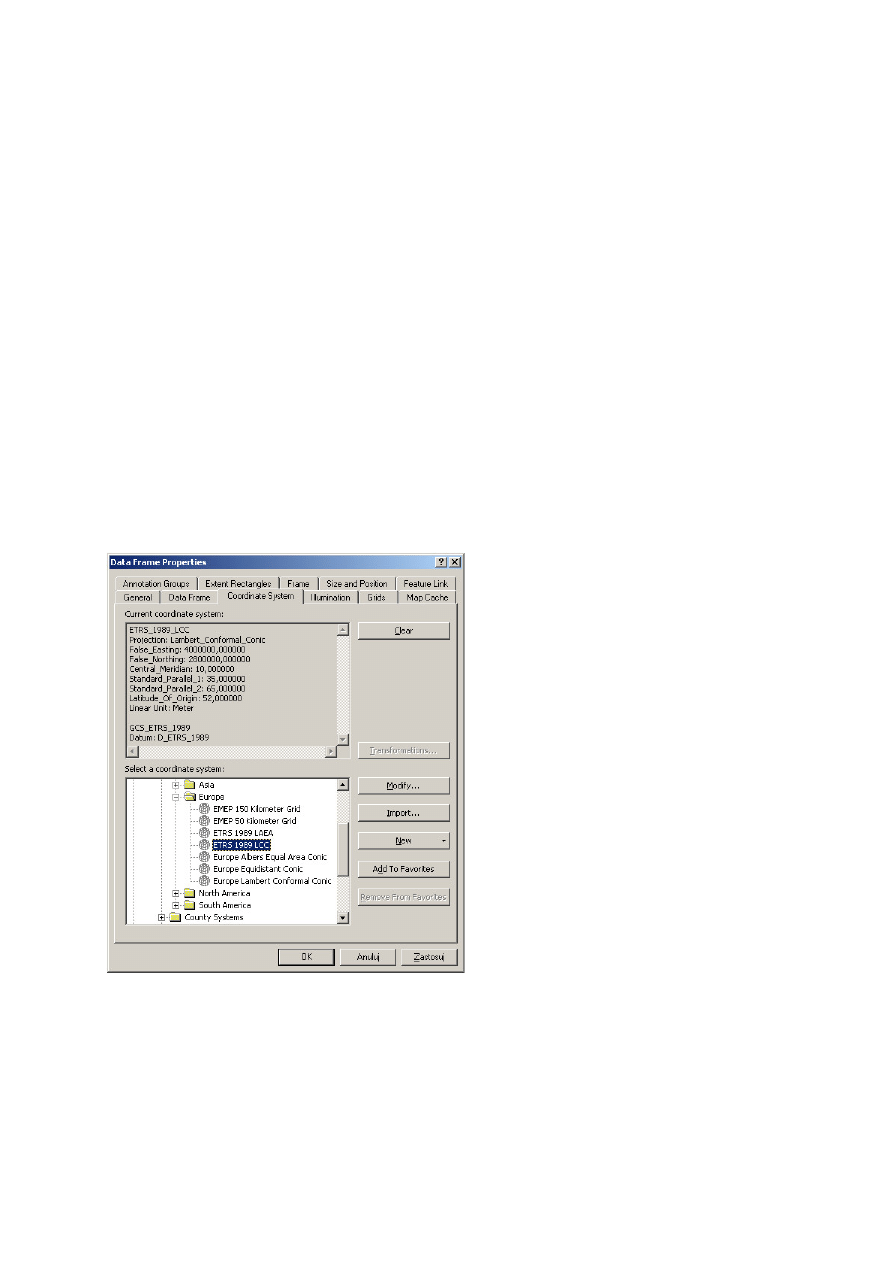
Ryc. 3.3. Okno definiowania systemu odniesień przestrzennych, w którym wizualizowane są mapy w ArcMap

6. Sprawdź obowiązujący aktualnie system odniesień przestrzennych – jest to ten sam system, w którym

zapisana jest oglądana wcześniej warstwa Swiat_panstwa.

!

Nie wszystkie warstwy wizualizowane w odwzorowaniu aktualnie zdefiniowanym w oknie projektu muszą

być w tym odwzorowaniu zapisane na dysku – nie ma tu żadnej zależności.

System odniesień

przestrzennych, w

którym wizualizowane

są aktualnie mapy w

oknie projektu

Katalog gotowych

definicji odwzorowań

Możliwość skorzystania

z definicji systemu w

którym zapisana jest

dowolna warstwa

wyświetlona aktualnie w

projekcie

Edycja parametrów

wybranej definicji

Import definicji z

dowolnej warstwy

zapisanej na dysku

Samodzielne

definiowanie systemu

Transformacje układów

odniesienia

8

7. Sprawdź, w jakich odwzorowaniach/systemach odniesień zapisane są wszystkie pozostałe warstwy

zgromadzone w projekcie. Nie musisz w tym celu wyświetlać okna właściwości wszystkich map, ponieważ
definicje wszystkich warstw dostępne są w oknie Coordinate System, a ściślej Select
Coordinate System. Aby je zobaczyć rozwiń Layers wskazując plus po lewej; powinieneś znaleźć
tam dwie warstwy w innych odwzorowaniach.

8. Dokonaj transformacji odwzorowania z Geographic do odwzorowania Mollweidego korzystając z gotowej

definicji tego odwzorowania, którą znajdziesz w katalogu: Predefined > Projected Coordinate
Systems > World > Mollweide (World); zatwierdź wybór.

9. Wyłącz mapę świata w tabeli po lewej odznaczając kwadracik obok nazwy Swiat, podobnie zrób z siatką

geograficzną Swiat_siatka.

10. Włącz warstwy Europa i Europa_siatka, a następnie zwróć uwagę na kształt Europy na mapie świata.

?

Czy odwzorowanie Mollweidego jest odpowiednim dla przedstawiania wybranej części świata, np.
Europy?

Odwzorowania dla Europy, które będziesz oglądać:

odwzorowanie stożkowe wiernokątne Lamberta LCC (35°N/65°N) – standard odwzorowania konforemnego
dla map Europy w skalach 1:500 000 i mniejszych (gotowa definicja w ArcGIS)

odwzorowanie azymutalne równopolowe Lamberta LAEA (52°N/10°E) – standard dla map statystycznych
Europy (gotowa definicja w ArcGIS).

11. Zmień odwzorowanie z Mollweidego na LCC dla Europy korzystając z gotowej definicji; tym razem

zamiast w katalogu World wejdź do katalogu Continental > Europe i wybierz ETRS 1989 LCC;
następnie sprawdź parametry wybranego odwzorowania w okienku powyżej (ryc. 3.4).

Ryc. 3.4. Definicja odwzorowania LCC dla Europy w programie ArcGIS

12. Zatwierdź wybór odwzorowania i oceń efekt na mapie Europy.
13. Przeprowadź ponownie transformację dla Europy zmieniając odwzorowanie LCC na LAEA (ETRS 1989

LAEA).

?

Czym różni się odwzorowanie LAEA od LCC?

9

Gdybyśmy obliczyli powierzchnie państw Europy w obydwóch odwzorowaniach i porównali je okazałoby się,
że te, które zostały obliczone w odwzorowaniu LAEA są bardziej zbliżone do rzeczywistych.

?

Dlaczego obliczone tak powierzchnie będą tylko zbliżone a nie identyczne z rzeczywistymi?

14. Ponownie wróć do odwzorowania LCC korzystając tym razem z możliwości wczytania definicji,

przypisanej konkretnej warstwie; w odwzorowaniu LCC zapisana jest warstwa Europa_państwa; podstaw
jej odwzorowanie wskazując plus na lewo od nazwy warstwy w oknie Data Frame Properties a
następnie wskazując nazwę systemu odniesień przestrzennych ETRS_1989_LCC.

Odwzorowanie dla Polski, które będziesz oglądać:

odwzorowanie poprzeczne Merkatora (Gaussa-Krügera) w układzie 1992 będące elementem
obowiązującego w Polsce systemu odniesień przestrzennych.

Zdefiniujesz teraz układ 1992; bazując na ogólnej definicji odwzorowania poprzecznego Merkatora dobierzesz
wszystkie parametry tak, aby w efekcie otrzymać pełna definicję obowiązującego w Polsce systemu odniesień
przestrzennych. Pomoże Ci w tym treść rozporządzenia Rady Ministrów z dnia 8 sierpnia 2000 r. w sprawie
państwowego systemu odniesień przestrzennych dostępna w katalogu roboczym (Rozporzadzenie_2000.pdf).

15. Wyświetl treść rozporządzenia w sprawie Państwowego Systemu Odniesień Przestrzennych w programie

Acrobat Reader.

16. Porównaj nazwę odwzorowania zastosowaną w rozporządzeniu z nazwą użytą na mapie topograficznej w

skali 1:10 000 (plik Topo_10k_skan.jpg w katalogu Materialy) oraz z nazewnictwem na rycinie 7.2 w
podręczniku pod redakcją J. Pasławskiego (s. 237).

17. W ArcMap wyłącz mapę Europy oraz jej siatkę i włącz kolejne warstwy: Polska oraz Polska_siatka
18. Wyświetl okno Coordinate System a następnie wybierz New > Projected Coordinate

System.

19. Nadaj nazwę Uklad 1992 w pozycji Name a następnie wybierz odwzorowanie Transverse Mercator

w ramce Projection i dokonaj edycji parametrów wyświetlonych poniżej, zgodnie z treścią
rozporządzenia.

!

Pamiętaj, że w systemach informacji geograficznej stosowany jest matematyczny lewoskrętny układ

współrzędnych x, y!

20. Po zdefiniowaniu wszystkich parametrów wybierz układ odniesienia ETRS 1989 w oknie Geographic

Coordinate System korzystając z Select > Europe > ETRS 1989; zatwierdź całą definicję a
następnie także okno informujące o zmianie układu odniesienia (ryc. 3.5); sprawdź efekt transformacji.

Ryc. 3.5. Okno ArcMap informujące o transformacji układu odniesienia

21. Odczytaj współrzędne prostokątne płaskie na południku środkowym oraz w kilku innych miejscach, w tym

również poza granicami Polski; powiąż wartości odczytywanych współrzędnych z parametrami
matematycznymi układu 1992 (False_Easting z Central Meridian oraz False_Northing z
Latitude_of_Origin).

22. Wyświetl ponownie okno Coordinate System i podstaw gotową definicję układu 1992 – znajdziesz ją

w katalogu Predefined > Projected Coordinate Systems > National Grids > ETRS
1989 Poland CS92.

Definicje, z których korzystasz w ArcGIS przechowywane są na dysku systemowym w postaci plików PRJ.
Przykładowo definicja układu 1992 znajduje się w katalogu:

10

C:\Program Files\ArcGIS\Coordinate Systems\Projected Coordinate Systems\National Grids

23. Sprawdź zawartość katalogu National Grids w Eksploratorze Windows; znajdziesz tam szereg plików o

rozszerzeniu *.prj.

24. Otwórz plik ETRS 1989 Poland CS92.prj wybierając PPKW > Otwórz za pomocą > Notatnik.
25. Spróbuj zidentyfikować w wyświetlonej zawartości pliku prj elementy definicji układu 1992.

!

Pliki PRJ z definicjami wszystkich najważniejszych odwzorowań stosowanych w Polsce powojennej są

udostępnione przez polskiego przedstawiciela producenta programu ArcGIS – firmę ESRI Polska.
Spakowany zbiór z tymi definicjami dostępny jest w katalogu ćwiczenia 3 (PolskieUklady.zip).

26. Włącz mapę województwa małopolskiego Malopolska oraz Malopolska_siatka.

?

Czy zdefiniowane obecnie odwzorowanie i układ 1992 może być stosowane dla mapy woj. małopolskiego

zgodnie z obowiązującym rozporządzeniem w sprawie systemu odniesień przestrzennych?

27. Wyłącz mapę województwa małopolskiego Malopolska oraz Malopolska_siatka.
28. Zmień ponownie system odniesień przestrzennych okna ArcMap podstawiając układ współrzędnych

geograficznych WGS-84 z wybranej warstwy zapisanej w tym układzie (okno Data Frame).

Transformacja układu odniesienia

W tej części ćwiczenia zapoznasz się z wielkością błędów wynikających z pominięcia różnic w układach
odniesienia nakładanych map.

29. Do okna ArcMap dodaj warstwę Polska_2

; podczas jej wczytywania program wyświetli komunikat o

różnicy pomiędzy układem odniesienia dodawanej mapy a układem zdefiniowanym w oknie ArcMap:
Geographic Coordinate System Warning; zamknij okno wybierając Close.

30. Po wyświetleniu mapy Polska_2 powiększ okolice SE kranców Polski w Bieszczadach.
31. Porównaj przebieg granicy państwa na warstwach Polska, Polska_2 i Swiat_panstwa.

?

Z czego wynikają różnice pomiędzy przebiegiem granicy państwa na warstwie Polska i Swiat_panstwa?

32. Porównaj przebieg granicy państwa na warstwach Polska i Polska_2.
33. Zmierz narzędziem odległości pomiędzy równoległymi do siebie obrazami tej samej granicy państwa;

pomiaru dokonaj w kilku miejscach.

?

Z czego wynikają te różnice w przebiegu granicy państwa na warstwach Polska i Polska_2?

34. Aby dokonać koniecznej transformacji otwórz okno Data Frame Properties > Coordinate

System i znajdź guzik Transformations (por. ryc. 3.3).

35. Po wyświetleniu okna Geographic Coordinate System Transformation upewnij się, że w

pozycji Convert from podstawiony jest układ D_Pulkovo_42 zaś pod Into GCS_WGS_84; zauważ, że
w pozycji Using mamy <None>; wybierz New.

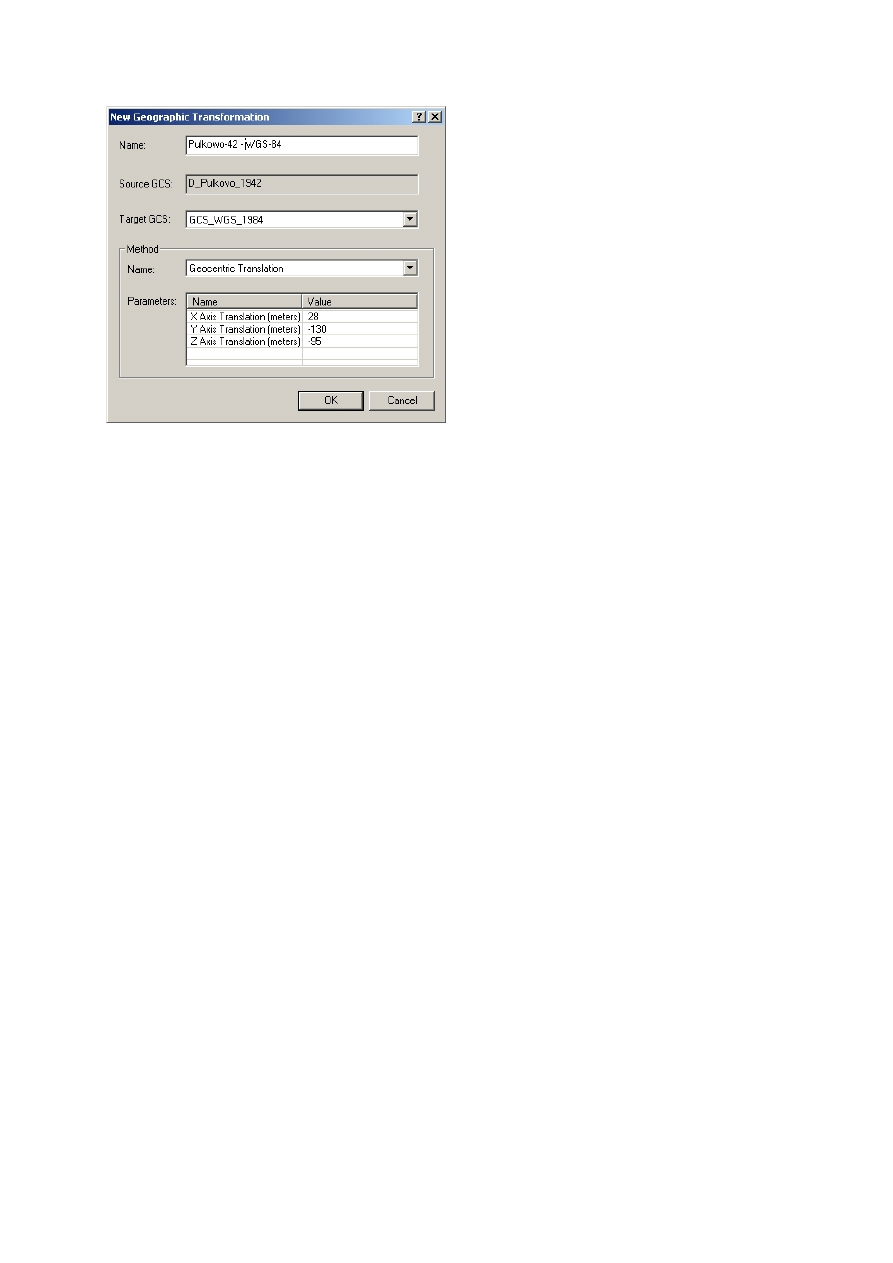
36. W oknie New Geographic Transformation pozostaw domyślną metodę transformacji

geocentrycznej a następnie wpisz parametry tej transformacji pokazane na rycinie 3.5.

!

Parametry te są wyrażonymi w metrach wektorami przesunięcia środka elipsoidy Krasowskiego (stosowanej

w układzie Pułkowo-42) względem elipsoidy WGS-84.

11

Ryc. 3.5. Okno edycji parametrów układu odniesienia Pułkowo-42

37. W polu Name podaj nazwę dla zestawu wpisanych parametrów Pulkowo-42 – WGS-84 a następnie

zatwierdź definicję.

38. Po zamknięciu okna Data Frame Properties sprawdź powtórnie nakładanie się granicy państwa dla

warstw Polska i Polska_2.

Powyższa część ćwiczenia powinna uświadomić Ci, jak duże błędy można popełnić ignorując różnice w
układach odniesienia różnych zbiorów danych geograficznych.

Odwzorowanie strefowe, które będziesz oglądać:

odwzorowanie i układ współrzędnych UTM (Universal Transverse Mercator – Uniwersalne Poprzeczne
odwzorowanie Merkatora) – światowy standard odwzorowania konforemnego dla map topograficznych w
skalach większych niż 1:500 000.

Zanim skorzystasz z definicji odwzorowania UTM musimy dokonać wyboru strefy odwzorowawczej właściwej
dla woj. małopolskiego.

40. Włącz mapę podziału świata na strefy UTM_strefy i sprawdź, która strefa jest właściwa dla woj.

małopolskiego.

41. Przeprowadź transformację map Polski i woj. małopolskiego do UTM korzystając z gotowej definicji, którą

znajdziesz w katalogu Projected Coordinate Systems > UTM > Wgs 1984 > WGS 1984
UTM Zone 34N.

42. Wskaż granice wybranej strefy odwzorowawczej na mapie.

?

Czy przyjęcie odwzorowania strefowego UTM dla mapy całej Polski jest poprawne? Dlaczego?

43. Włącz warstwę Swiat i Swiat_siatka i zobacz jak odwzorowują się w przypadku zastosowania UTM obszary

okołobiegunowe.

Odwzorowanie UTM nie nadaje się do przedstawiania obszarów okołobiegunowych ze względu na zbyt duże
zniekształcenia. Stosuje się go do szerokości geograficznych 80°N/S. Dla obszarów podbiegunowych stosuje się
najczęściej odwzorowanie stereograficzne w tzw. Uniwersalnym Biegunowym Odwzorowaniu Stereograficznym
UPS (Universal Polar Stereographic).


Trwała zmiana systemu odniesień przestrzennych dla wybranej warstwy

Dotychczasowe transformacje dokonywane były „w locie” i znajdowały odzwierciedlenie jedynie w sposobie
wyświetlania map w oknie ArcMap. Czasem może zaistnieć konieczność trwałej zmiany systemu odniesień

12

przestrzennych bądź jakiegoś wybranego elementu jego definicji. Wówczas mamy w ArcGIS do dyspozycji
dwóch narzędzi:

najprostszym jest transformacja w oknie ArcMap i eksport transformowanej mapy z parametrami
zdefiniowanymi w oknie Data Frame,

drugie narzędzie dostępne jest w ArcToolbox

.

44. Mając zdefiniowane odwzorowanie UTM dokonaj eksportu mapy woj. małopolskiego wybierając pod

prawym klawiszem myszy Data > Export Data.

45. W oknie Export Data zaznacz Use the same coordinate system as: the data frame

(zastosuj ten sam system współrzędnych jaki jest zdefiniowany na poziomie Data Frame).

46. Ustaw ścieżkę dostępu na katalog Cwiczenie_3/Dane i wpisz nazwę Malopolska_UTM a następnie

zatwierdź polecenie.

47. Potwierdź dodanie warstwy do okna ArcMap i sprawdź czy warstwa ta posiada obecnie zdefiniowane

odwzorowanie UTM.

ZADANIE DOMOWE

Uzupełnieniem niniejszego ćwiczenia jest moduł trzeci kursu VC ESRI Learning ArcGIS Desktop pt.
Referencing Data to Real Locations. Zapoznaj się z teorią oraz wykonaj obydwa ćwiczenia zawarte w tym
module. Zaliczenie modułu należy potwierdzić certyfikatem.
Uwaga: treści zawarte w tym module należy traktować jako obligatoryjne.


LITERATURA DLA ZAINTERESOWNYCH

Annoni A., Luzet C., Gubler E., Ihde J. (red.), 2003, Map Projection for Europe, Institute for Environment and

Sustainability, European Commision, 131 ss.

Drabek J., Piątkowski F. 1989, 1000 słów o mapach i kartografii, Wyd. MON, W-wa.

Kadaj R.J., 2002, Polskie układy współrzędnych. Formuły transformacyjne, algorytmy i programy, Rzeszów, ss. 52.

Ogorzelska B., 2006, Odwzorowania kartograficzne, [w:] Pasławski J. (red.), Wprowadzenie do kartografii i topografii, Wyd.

Nowa Era

Pasławski J. (red.), 2006, Wprowadzenie do kartografii i topografii, Wyd. Nowa Era, ss. 399.

Projekt nowelizacji RRM w sprawie systemu odniesień przestrzennych z dnia 10.01.2008r. Dostępne w Internecie:

http://www.gugik.gov.pl/gugik/dw_files/891_rrm_10_01_2008_1.pdf

Robinson A., Sale R., Morrison J., 1988, Podstawy kartografii, PWN, W-wa

Rozporządzenia Rady Ministrów z dnia 8 sierpnia 2000 r. w sprawie państwowego systemu odniesień przestrzennych, Dz. U.

z dnia 24 sierpnia 2000 r., nr 70, poz. 821. Dostępne w Internecie:

http://www.gugik.gov.pl/gugik/dw_files/86_rozp_25.pdf

ZAGADNIENIA DO EGZAMINU

1. Zniekształcenia: elipsa zniekształceń a koło elementarne w odwzorowaniu równodługościowym

równopolowym i równokątnym; obliczanie współczynnika zniekształcenia całej kuli w odwzorowaniu
walcowym prostym i całej półkuli w rzucie ortograficznym w położeniu normalnym; obliczanie
współczynnika zniekształcenia długości połowy południka w rzucie ortograficznym w położeniu
normalnym,

2. Klasyfikacja odwzorowań wg Drabka, Piątkowskiego (1989), zamieszczona w podręczniku Pasławskiego

(nie mylić z klasyfikacją studentów Geoinformatyki 2009:),

3. Najważniejsze własności wybranych odwzorowań: odwzorowanie równopolowe Mollweidego,

odwzorowanie stożkowe równokątne Lamberta (LCC), odwzorowanie azymutalne równopolowe Lamberta
(LAEA), odwzorowania równokątne Merkatora i poprzeczne Merkatora (Gaussa-Krügera), odwzorowanie
kwadratowe (walcowe proste); przykład pytania o własności odwzorowań: Które z poniższych odwzorowań
są równopolowymi: LAEA, LCC, Mollweidego, poprzeczne Merkatora,

4. Odwzorowania map prezentowanych na korytarzach i klatkach schodowych IGiGP UJ (bez sal

dydaktycznych, gabinetów pracowniczych, posterów, plakatów i innych „mapek”:),

13

5. Pełna definicja systemu odniesień przestrzennych na przykładzie układu 1992,
6. Różnice pomiędzy układami współrzędnych opartymi na odwzorowaniu poprzecznym Merkatora (Gaussa-

Krügera): UTM, 1992, 1942,

7. Różnice pomiędzy „Geographic” a odwzorowaniem walcowym prostym (kwadratowym),
8. Systemy/układy odniesienia WGS-84, ETRF-89/EUREF-89, Pułkowo-42.

Obowiązujący podręcznik:

Pasławski J. (red.), 2006, Wprowadzenie do kartografii i topografii, Wyd. Nowa Era, ss. 399.


ZAGADNIENIA DO TESTU ZALICZENIOWEGO Z ĆWICZEŃ

1. Zmiana systemu odniesień przestrzennych przez skorzystanie z gotowych definicji oraz przez wybór

systemu zdefiniowanego dla innej warstwy tego samego projektu,

2. Definiowanie parametrów układu 1992,
3. Definiowanie układu UTM przez wybór strefy odwzorowawczej właściwej dla danego obszaru.