ZAGADNIENIE TRASOWANIA POJAZDÓW Z OGRANICZENIAMI 

CZASOWYMI ORAZ OGRANICZONĄ LICZBĄ POJAZDÓW. 

METODA WYZNACZANIA GÓRNEGO OGRANICZENIA DLA 

CAŁKOWITEJ LICZBY ODBIORCÓW 

 

Tomasz AMBROZIAK, Renata PIĘTKA 

Politechnika Warszawska  

Wydział Transportu  

Zakład Logistyki i Systemów Transportowych 

ul. Koszykowa 75, 00-662 Warszawa 

e–mail: pietkar@gazeta.pl 

STRESZCZENIE 

W  artykule  przedstawiono  wprowadzenie  do  problemu  trasowania  pojazdów  z  ograniczeniami 

czasowymi  oraz  ograniczoną  liczbą  pojazdów.  Przedstawiono  również  metodę  wyznaczania  górnego 
ograniczenia całkowitej liczby odbiorców możliwych do obsłużenia daną ograniczoną liczbą pojazdów. 

 

1.  WSTĘP 

Wiele  praktycznych  problemów  logistyki  transportu  i  dystrybucji  może  być 

sformułowanych  jako  zagadnienie  trasowania  pojazdów  z  ograniczeniami  czasowymi. 
Rozwiązaniem  tego  typu  problemów  jest  znalezienie  takiej  organizacja  przewozów,  której 
celem  jest  uzyskanie  planu  tras  o  minimalnym  koszcie  obsługującego  zbiór  odbiorców 
ze znanymi popytami. Zakładamy, że każdy odbiorca jest przyporządkowywany do dokładnie 
jednej  trasy  pojazdu,  a  całkowity  popyt  każdej  z  tras  nie  może  przekraczać  pojemności 
pojazdu. 

Większość  proponowanych  metod  znalezienia  ww.  planu  tras  zakłada,  że  liczba 

dostępnych  pojazdów  jest  nieograniczona,  a  celem  jest  uzyskanie  rozwiązania, 
które  minimalizuje  ich  liczbą  i/lub  całkowity  koszt  przejazdu.  Jednakże  w  rzeczywistości 
operatorzy transportowi dysponują ograniczonymi zasobami pojazdów. 

 

POLITECHNIKA WARSZAWSKA 

Wydział Transportu 

Polska Akademia Nauk 

Komitet Transportu 

2.  CHARAKTERYSTYKA PROBLEMU 

2.1. 

CHARAKTERYSTYKA 

PROBLEMU 

TRASOWANIA 

POJAZDÓW 

Z  OGRANICZENIAMI  CZASOWYMI  ORAZ  OGRANICZONA  ILOŚCIĄ 
POJAZDÓW 

W  artykule  omówiony  zostanie  problem  trasowania  pojazdów  z  ograniczeniami 

czasowymi  oraz  ograniczoną  liczbą  dostępnych  pojazdów  polegający  na  rozwózce  lub 
zwózce  towarów  bądź  osób,  w  zależności  od  rodzaju  zagadnienia(np.  przewozy  z  i  do 
szkoły). Zakładamy, że równoczesna zwózka i rozwózka nie jest dopuszczalna. Przykładowy 
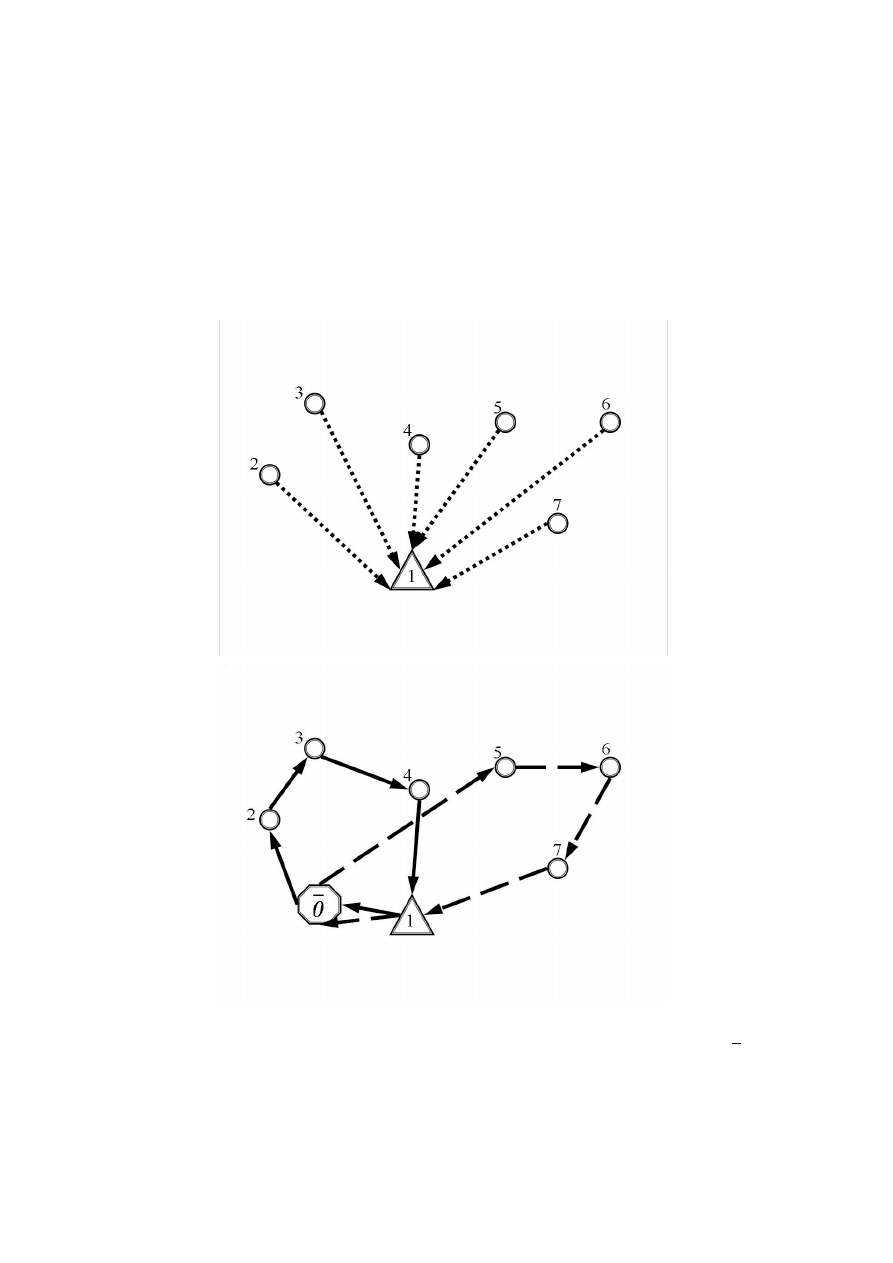
schemat problemu zwózki oraz przykład rozwiązania przedstawione został na rys. 1. 

 

 

 

Rys. 1. Przykładowy problem zwózki z 7 odbiorcami wraz przykładowym rozwiązaniem. Wierzchołek 

0

- baza, 

wierzchołek 1 – wierzchołek końcowy. 

Wyżej przedstawiony problem można sformułować następująco. Niech n będzie liczbą 

odbiorców  zgłaszających  zapotrzebowanie  na  przewóz.  Tworzymy  zbiór  N  ={2,…,  n+1} 
numerów  wierzchołków  oznaczających  poszczególnych  odbiorców.  Wierzchołek  1 
reprezentować  będzie  punkt  początkowy(w  przypadku  rozwózki)  bądź  punkt  końcowy  (w 
przypadku zwózki) zlecenia, zaś 0  reprezentować będzie bazę pojazdów. 

Dla  każdego  wierzchołka  i∈  N  mamy  określony  czas  obsługi  o

i

,  który  przykładowo 

określać  może  czas  potrzebny  do  wsiadania  bądź  wysiadania  z  pojazdu  osób,  zależny 
chociażby  w  przypadku  przewozu  osób  niepełnosprawnych  od  stopnia  niepełnosprawności 
pasażera. 

Wielkość q

i

 określa popyt każdego z odbiorców(przykładowo liczbę osób jaką należy 

zabrać z i-tego wierzchołka). Zakładamy, że podział wielkości q

i

 jest zabroniony. W związku 

z  tym  popyt  każdego  odbiorcy  musi  być  mniejszy  niż  największa  dostępna  pojemności 
pojazdu: 

max{ } max{ }

a

i

a

i

!

q

q  

(2.1) 

gdzie a określa typ dostępnego pojazdu. 

Zakładamy  dodatkowo,  że  łączny  popyt  odbiorców  jest  znacznie  większy 

od największej dostępnej pojemność pojazdu: 

1

2

max{ }

a

i

a

i

+

=

>>

!

n

q

Q  

(2.2) 

 
Zakładamy,  że  przewozy  odbywać  się  będą  uwzględniając  w  każdym  i-tym  zleceniu 

następujące kryteria jakości: 
- 

dla każdego odbiorcy i∈ N obsługa w wierzchołku 1 nie może w przypadku rozwózki 
rozpocząć  się  wcześniej  niż  wartość 

ro

T

1

dla  wierzchołka  1,  zaś  w  przypadku  zwózki 

zakończyć później niż 

pr

T

1

; 

- 

rzeczywisty  czas  jazdy  każdego  klienta  nie  może  przekraczać  maksymalnej  wartości 

max

,

1 i

t

  dla  rozwózki,  a 

max

1

,

i

t

dla  zwózki,  będącej  pewną  funkcją  bezpośredniego  czasu 

jazdy t

1,i

 (dla rozwózki) lub t

i,1

 (dla zwózki) między wierzchołkiem 1 a wierzchołkiem 

i∈  N  (np.  podwojonej  wartości  bezpośredniego  czasu  jazdy  między  tymi 
wierzchołkami); 

- 

różnica  („czas  odchylenia”)  pomiędzy  rzeczywistym  momentem  odbioru(dowozu)  a 
pożądanym  momentem  odbioru(dowozu)  nie  może  przekraczać  ustalonej  wartości 
maksymalnej 

max

od

t

. 

Na  podstawie  podanych  powyżej  kryteriów  jakości  dla  każdego  i∈  N  wyznaczamy, 

okna czasowe [a

i

, b

i

], określające przedziały, w zakresie których należy rozpocząć/zakończyć 

obsługę w i-tym wierzchołku. 

 
Dla problemu rozwózki okna te wyznaczamy z następujących zależności: 

-  najwcześniejszy możliwy moment rozpoczęcia obsługi w wierzchołku 1 

 

ro

T

a

1

1

=

 

(2.3) 

 

 

-  najpóźniejszy dopuszczalny moment rozpoczęcia obsługi w wierzchołku 1 

 

max

1

1

od

t

a

b

+

=

 

(2.4) 

 

-  najwcześniejszy możliwy moment rozpoczęcia obsługi w wierzchołku i 

 

i

i

t

a

a

,

1

1

+

=

 

(2.5) 

 

-  najpóźniejszy dopuszczalny moment rozpoczęcia obsługi w wierzchołku i 

 

max

,

1

1

i

i

t

b

b

+

=

 

(2.6) 

 
natomiast dla problemów zwózki zależności te są następujące: 

-  najpóźniejszy możliwy moment rozpoczęcia obsługi w wierzchołku 1 

 

pr

T

b

1

1

=

 

(2.7) 

 

-  najwcześniejszy dopuszczalny moment rozpoczęcia obsługi w wierzchołku 1 

 

max

1

1

od

t

b

a

!

=

 

(2.8) 

 

-  najwcześniejszy możliwy moment rozpoczęcia obsługi w wierzchołku i 

 

1

,

1

i

i

t

a

a

!

=

 

(2.9) 

 

-  najpóźniejszy dopuszczalny moment rozpoczęcia obsługi w wierzchołku i 

 

max

1

,

1

i

i

t

b

b

!

=

 

(2.10) 

 
Na rys. 2. powyższe zależności zostały przedstawione graficznie dla obu przypadków. 
 
Określony  jest  również  dla  każdej  pary  wierzchołków  i,j∈  N  ∪{ 0 ,1}  ∧  (i≠j)  czas 

podróży t

i,j

 oraz odległość d

i,j

 między wierzchołkami i oraz j  . 

Zakładamy, że w bazie  0  z oknem czasowym 

0

0

[ , ]

a b

mamy do dyspozycji A typów 

pojazdów. Zbiór A={1,…, a,…, A} oznacza zbiór numerów typów pojazdów. Każdy pojazd 
typu a charakteryzuje się pojemnością Q

a

∈

/{0}, oraz ustalonym kosztem eksploatacyjnym 

a

c

  określonym  na  jednostkę  odległości.    Niech  zbiór  P(a)={1

a

,…,L(a)

a

}  określa  zbiór 

numerów  pojazdów  typu  a,  przy  czym  L(a)  określa  liczbę  pojazdów  typu  a.  Niech 
P=

a !

U

A

P(a) będzie zbiorem numerów wszystkich dostępnych pojazdów. 

 

 

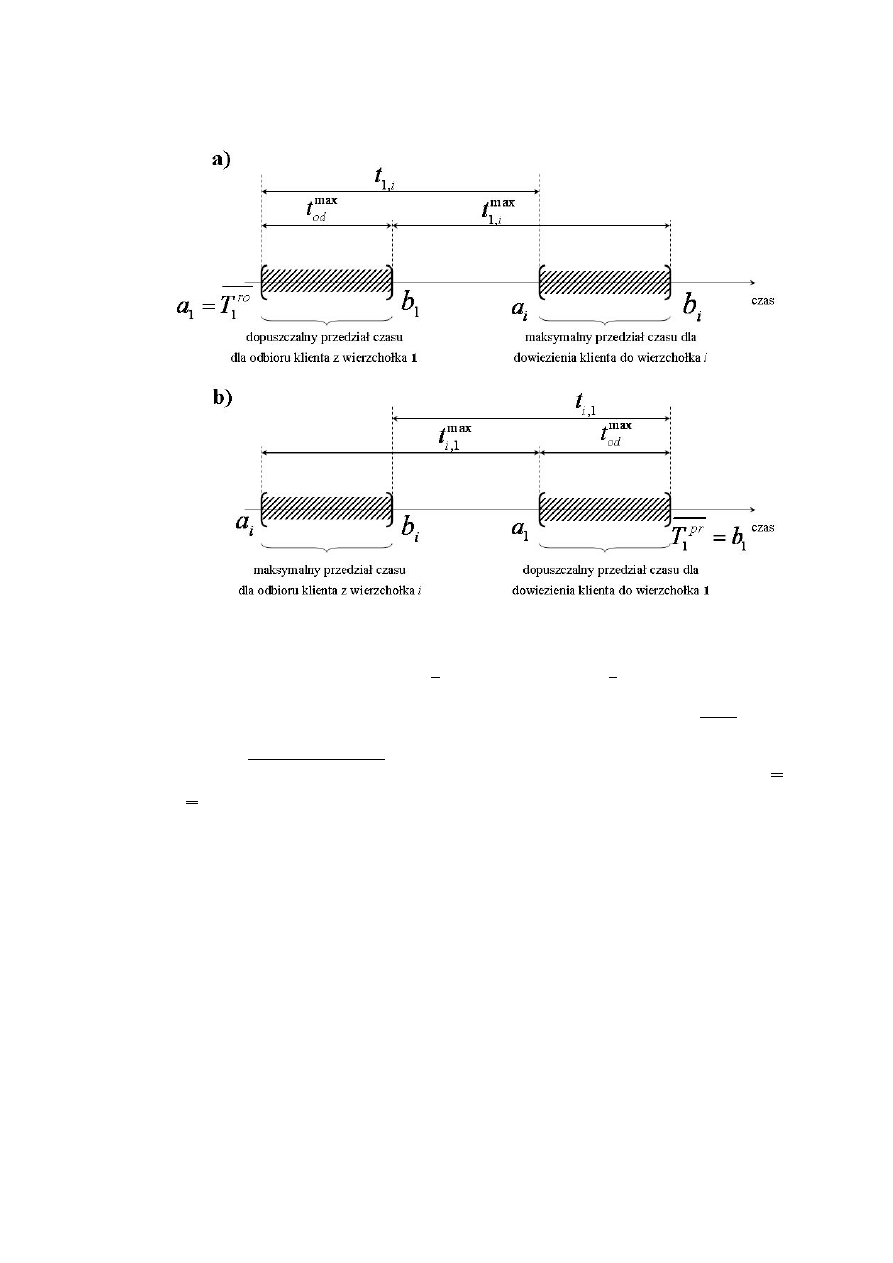
Rys. 2. Schemat okien czasowych: a) przypadek rozwózki; b) przypadek zwózki. 

 

Ciąg wierzchołków T = 〈 1, i

1

,…, i

m

,  0 〉(rozwózka) lub T = 〈0 , i

1

,…, i

m

, 1 〉(zwózka) 

gdzie i

1

,…, i

m

 jest m-elementowym ciągiem liczb ze zbioru N nazywać będziemy trasą. Zbiór 

tras  mających  tę  własność,  że  każdy  wierzchołek  występuje  dokładnie  raz  w  jednej  z  tras 
nazywać będziemy planem przewozów. 

Zadaniem jest uzyskanie takiego planu przewozów składającego się maksymalnie z 

P

 

tras(gdzie 

P

 moc zbioru P równa liczbie dostępnych pojazdów), spełniającego następujące 

ograniczenia: 
- 

każda trasa rozpoczyna się/kończy w bazie i kończyć/rozpoczynać w wierzchołku 1; 

- 

każdy wierzchołek(odbiorca) obsługiwany jest dokładnie raz; 

- 

całkowity  popyt  wszystkich  odbiorców  obsługiwanych  na  trasie  nie  przekracza 
pojemności pojazdu przypisanego do tej trasy; 

- 

obsługa  w  każdym  punkcie  musi  rozpocząć  się/zakończyć  w  przedziale  czasu 
określonym oknem czasowym; 

- 

liczba użytych do przewozów pojazdów nie może przekraczać dostępnej ilości. 

- 

czas  pracy  pojazdu  nie  może  przekraczać  danej  wartości  maksymalnej(np. 
dopuszczalny czas pracy kierowców); 

gdzie funkcja celu: 
- 

maksymalizuje całkowitą liczbę obsługiwanych odbiorców; 

- 

minimalizuje całkowitą liczbę odbiorców obsługiwanych później (jeśli dozwolone); 

- 

minimalizuje całkowity czas trwania zwłoki (jeśli dozwolone); 

- 

minimalizuje całkowitą liczbę użytych pojazdów; 

- 

minimalizuje całkowitą odległości przejazdu. 

 

Jednym  z  możliwym  sposobów  uchwycenia  tak  wielokryterialnego  celu  jest 

zdefiniowanie  funkcji  kosztów  będącej  sumą  kosztów  odpowiadających  poszczególnym 
kryteriom z przypisaniem im odpowiednich wag. Jednakże, określenie poprawnych wag może 
stać  się    trudne  (lub  wręcz  niemożliwy),  a  wynikowa  funkcja  stanie  się  bezsensowna 
do zinterpretowania. 

Innym  z  podejść  do  problemu  jest  zdefiniowanie  hierarchicznej  struktury  kosztów 

jak zaproponowano w [1]. Dla przykładu, obsłużenie większej liczby odbiorców jest zawsze 
lepsze  niezależnie  od  liczby  użytych  pojazdów.  Zaproponowana  hierarchiczna  struktura 
kosztów  odpowiadała  w  malejący  kolejność  pierwszeństwa  przedstawionej  powyżej  liście 
celów.  Dla  dokładniejszego  opisu  hierarchicznej  struktury  kosztów  odsyłamy  do  publikacji 
Lau H.C., Sim M., Teo K.M. [1]. 

 

2.2. METODA  WYZNACZANIA  GÓRNEGO  OGRANICZENIA  DLA  CAŁKOWITEJ 

LICZBY ODBIORCÓW  
Do wyznaczania górnego ograniczenia dla całkowitej liczby odbiorców, którzy mogą być 

obsłużeni ograniczoną liczbą pojazdów w problemach trasowania pojazdów z ograniczeniami 
czasowymi Lau H.C., Sim M., Teo K.M. [1] zaproponowali sformułowanie w postaci zadania 
programowania  całkowitoliczbowego.  Sformułowanie  takie  dzięki  swojej  prostocie  jest 
w  stanie  zapisać  problemy  dużych  rozmiarów,  nie  jest  jednak  na  tyle  uproszone  aby  jego 
wynik odbiegał znacznie od poszukiwanego rozwiązania optymalnego. 

Przykładowo  dla  problemu  rozwózki  w  zastosowanym  sformułowaniu  będzie  brało  się 

pod  uwagę  ograniczenia  pojemności  pojazdów,  jaki  i  ograniczenia  czasu  narzucone  przez 
najpóźniejsze  momenty  powrotu  każdego  pojazdu  do  bazy.  W  tym  przypadku  górne 
ograniczenie  liczbą  odbiorców  możliwych  do  obsłużenia  jest  wynikiem  rozwiązywania 
następującego sformułowania programowania całkowitoliczbowego. 
Niech  P  =

a !

U

A

P(a)  będzie  zbiorem  numerów  wszystkich  dostępnych  pojazdów,  zaś 

N

c

=N∪{

0

,1}  będzie  zbiorem  numerów  wierzchołków  reprezentujących  odbiorców 

wyłączając  wierzchołek  bazy  oraz  wierzchołek  początkowy.  Zdefiniujmy  wielkość 

,

min

i

j i j

r

t

=

 dla i,j∈ N

c

 ∧ (i≠j), określającą czas przejazdu z wierzchołka i do najbliższego 

sąsiada  i  jest  dolnym  ograniczeniem  czasu  przejazdu  z  wierzchołka  i  do  każdego  innego 
wierzchołka. 
Niech 

,0

i

i

i

i

w

b o

t

=

+

+

 dla i∈ N

c

 oznacza moment powrotu do bazy po obsłużeniu odbiorcy 

w  wierzchołku  i  jako  ostatniego  odbiorcy,  przy  czym  obsługa  odbiorcy  i  rozpoczęło  się 
w  najpóźniejszym  momencie  rozpoczęcia  obsługi.  Bez  utraty  uogólnienia  załóżmy, 
że wszystkie wartości w

i

 nie przekraczają okna czasowego dla bazy. 

Niech  G={g

1

,  g

2

,…, 

P

g

}  będzie  listą 

P

  niepowtarzalnych  odbiorców,  dla  których  w

i

≥w

j 

dla wszystkich i∈ G ∧ j∉ G. Zakładamy, że wszystkie pojazdy są identyczne, a 

P

 elementów 

zbioru  G  reprezentują  najpóźniejsze  możliwe  momenty  powrotu  do  bazy  dla  każdego  z 

P

 

pojazdów, dla wykonalności rozwiązania. 

Zmienną decyzyjną oznaczamy przez 

P

!

"

p

,

1,

0,

i p

je¿eli wierzcholek

jest obslugiwany przez pojazd ,

x

w przeciwnym razie

!

"

= #

$

i N

p

       (2.11) 

 

Znaleźć maksimum funkcji 

ƒ(x) = 

i,p

p

i

x

!

!

" "

c

P

N

→ max 

(2.12) 

spełniającej ograniczenia: 
 

,

1

i p

i

p

x

!

!

"

#

$

c

N

P

 

(2.12) 

 

,

i p

i

p

i

x

q

Q

!

!

"

#

$

%

c

P

N

 

(2.13) 

 

,

0

(

)

i p

i

i

g

p

i

x

o

r

r

w

!

!

"

#

+

+

$

%

c

p

P

N

 

(2.14) 

 

 

Ograniczenia (2.12) zapewnia, że wszyscy odbiorcy muszą być przyporządkowywani 

co  najwyżej  do  jednego  pojazdu.  Ograniczenia  (2.13)  zapewnia,  że  pojemność  każdego 
z  pojazdów  nie  jest  przekroczona.  Ograniczenia  (2.14)  narzuca,  że  dla  każdego  pojazdu, 
najwcześniejszy  możliwy  moment  powrotu  do  bazy  nie  może  przekraczać  najpóźniejszego 
możliwego momentu powrotu (narzuconego przez G).  

Zauważmy, że w tym sformułowaniu, zignorowane zostało całkowicie rozpatrywanie 

ograniczeń  okien  czasowych  i  rzeczywistego  czasu  przejazdu  pomiędzy  dwoma 
wierzchołkami.  Będzie  ono  więc  mniej  efektywne  dla  problemów  z  wąskimi  oknami 
czasowymi. 
 

 

3.  WNIOSKI 

Występowanie  w  problemach  trasowania  pojazdów  ograniczeń  na  czas  pracy 

pojazdów,  godzin  otwarcia  bazy  i  pożądanych  czasów  obsługi  odbiorców  znacząco 
komplikuje  problem.  W  rzeczywistych  problemach  mamy  jednak  do  czynienia  jeszcze 
dodatkowo  z  ograniczoną  liczbą  pojazdów,  będących  w  dyspozycji  przewoźników. 
Konsekwencją  tak  wielu  ograniczeń  może  być  trudność  w  skonstruowaniu  planu 
dopuszczalnego, zwłaszcza, kiedy w problemie ograniczenia czasu są restrykcyjne. 

Wyznaczenie  górnego  ograniczenia  dla  całkowitej  liczby  odbiorców,  którzy  mogą 

być 

obsłużeni 

ograniczoną 

liczbą 

pojazdów 

w 

problemach 

trasowania  

z  ograniczeniami  czasowymi  pozwala  na  wstępne  określenie    możliwości  realizacji 
założonych przez przewoźnika zadań. 

 
 

 

LITERATURA 

[1]  Lau H.C., Sim M., Teo K.M.: Vehicle routing problem with time windows and limited number of 

vehicles,

 

European Journal of Operational Research 148 (2003) 559–569. 

[2]  Savelsbergh M.W.P., Sol M.: The general pickup and delivery problem. Transportation Science 

29 (1995). 

[3]  Solomon  M.  M.,  Desrosiers  J.:  Time  window  constrained  routing  and  scheduling  problems. 

Transportation Science 22 (1988) 

[4]  Piasecki  S.  Optymalizacja  systemów  przewozowych.  Wydawnictwa  Komunikacji  i  Łączności. 

Warszawa 1973. 

[5]  Ambroziak  T.,  Piętka  R.  Metoda  wyznaczania  suboptymalnej  organizacji  przewozów 

terminowych.  Materiały  Konferencyjne  VIII.  Konferencji  Logistyki  Stosowanej  "TOTAL 
LOGISTIC MANAGEMENT" Zakopane 2004. 

[6]  Piętka  R.  Zagadnienie  przewozów  terminowych.  Sformułowanie  zadania  optymalizacyjnego, 

metoda rozwiązania. Zeszyty Naukowe Politechniki Śląskiej Nr 1621 Transport 52 (2004). 

VEHICLE ROUTING PROBLEM WITH TIME WINDOWS 

AND A LIMITED NUMBER OF VEHICLES. 

METOD OF DETERMINING AN UPPER BOUND FOR THE TOTAL NUMBER OF CUSTOMERS. 

ABSTRACT 

This paper introduces a variant of the vehicle routing problem with time windows where a limited number of vehicles 
is given. There is also presented the method of 

determining  an  upper  bound for  the  total  number  of customers  that 

can be served by a given fixed number of vehicles.