KRYSTALOCHEMIA /ćwiczenia/                      I ROK II STOPNIA / MSG 
 

ZAGADNIENIA: 

 



 

Kryształ,  komórka  elementarna,  motyw,  sieć  przestrzenna  (węzeł  sieci,  parametry 
sieci).  



 

Proste  sieciowe,  płaszczyzny  sieciowe  (równanie  prostej  sieciowej  i  płaszczyzny 
sieciowej), wektor identyczności. 



 

Pas płaszczyzn, relacja pasowa. 

 

ZESTAW ZADAŃ NR 1 

 
Zadanie 1  
Oblicz  symbol  [uvw]  dla  kierunku  przeprowadzonego  przez  węzły  sieci  przestrzennej  A  i  B  
o współrzędnych A = (0,½,½), B = (½,0,½). Narysuj tą prostą w układzie rombowym. 
 
Zadanie 2 
Jakie  wskaźniki  Millera  mają  płaszczyzny  odcinające  na  osiach  X,  Y,  Z  układu 
współrzędnych  odcinki:  ½a,  1b,  ∞c  oraz  1a,  ½b,  ¼c.  Narysuj  te  płaszczyzny  
w tetragonalnym układzie współrzędnych. 
 
Zadanie 3 
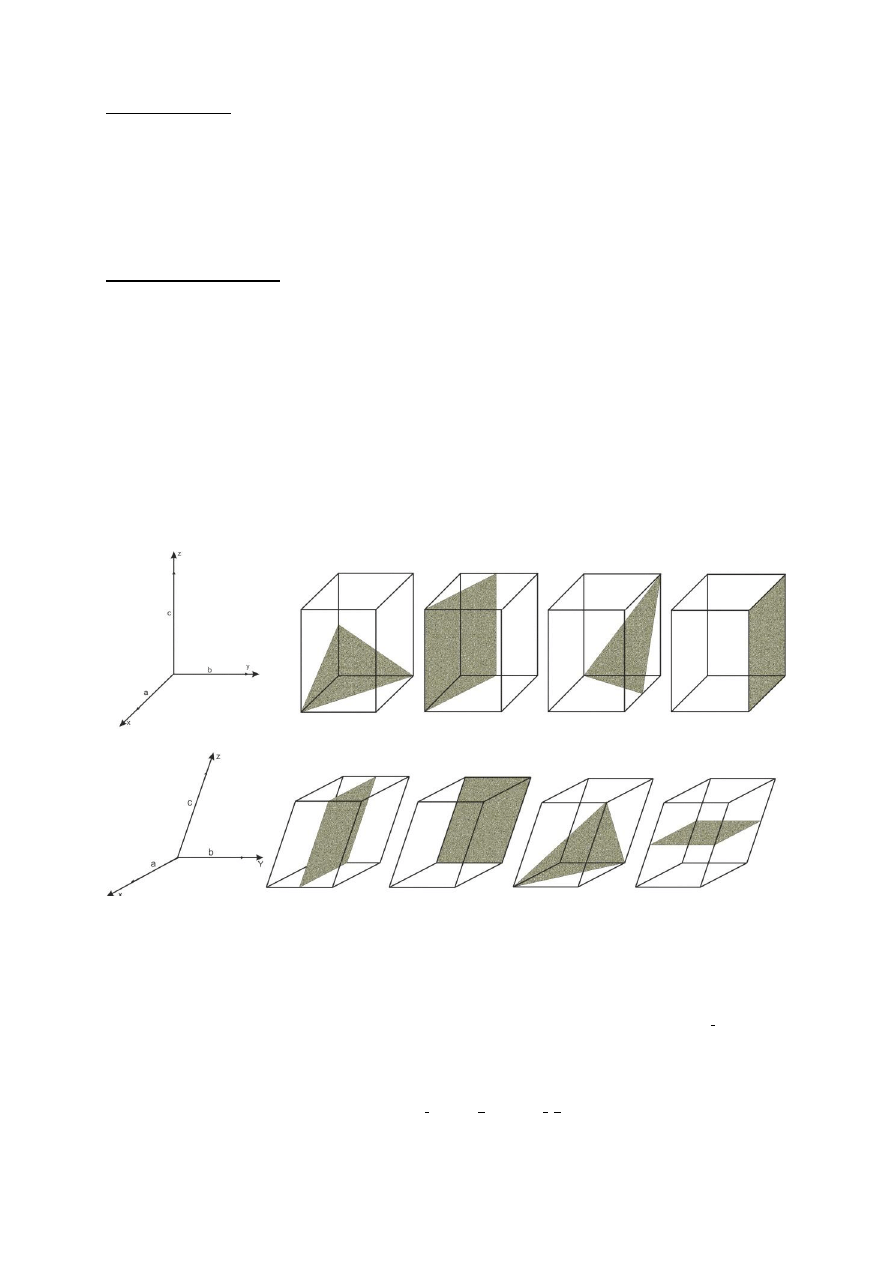
Określ wskaźniki Millera dla poniższych płaszczyzn: 
 

 

 
Zadanie 4 
Narysuj płaszczyzny sieciowe o wskaźnikach Millera (100), (010), (001), (123), (420), (1



11) 

(120) w dwóch układach krystalograficznych: regularnym i trójskośnym.  
 
Zadanie 5 
Sprawdź,  czy  istnieje  płaszczyzna  należąca  do  trzech  pasów  o  osiach  [210],  [20

1

]  i  [011]. 

Jeśli tak, wyznacz wskaźniki (hkl) tej płaszczyzny i narysuj ją w układzie tetragonalnym. 
 
Zadanie 6 
Sprawdź,  czy  płaszczyzny  o  symbolach  (

1

10),  (

3 11)  i  (

1

3 2)  należą  do  wspólnego  pasa 

płaszczyzn. Jeśli tak, podaj wskaźniki [uvw] osi tego pasa.